1-1函数
3.1.1 函数的概念 课件(1)-人教A版高中数学必修第一册(共35张PPT)

不正确。
对应关系应为S=350t,其中,t A1 {t | 0 t 0.5}, s B1 {s | 0 s 175}
问题2 某电气维修告诉要求工人每周工作至少1天,至多不超过6天。如果 公司确定的工资标准是每人每天350元,而且每周付一次工资,那么你认为 该怎样确定一个工人每周的工资?一个工人的工资w(单位:元)是他工作 天数d的函数吗?
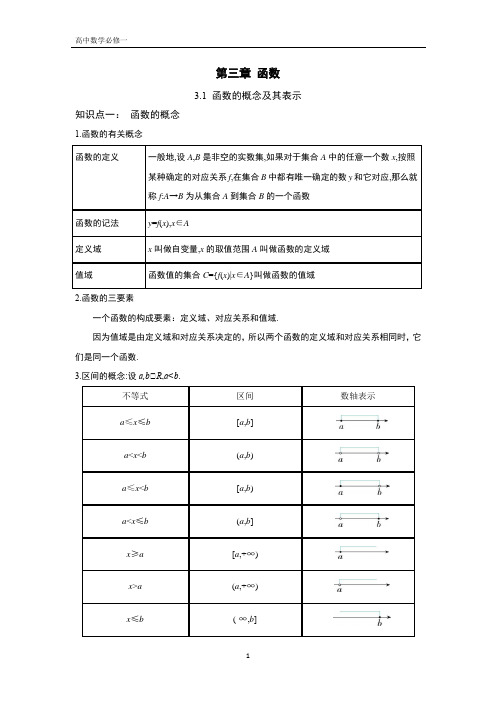
ab ab
实数集R可以表示为(-∞,+ ∞)
x≥a
x >a
x≤b
x<b
[a,+∞) (a,+∞) ( -∞ ,b] (-∞,b)
注意: 1.区间(a,b),必须有b>a 2.区间只能表示数集 3.区间不能表示单元素集 4.区间不能表示不连续的数集 5.区间的左端点必须小于右端点; 6.区间都可以用数轴表示; 7.以“-∞”或“+∞”为区间的一端时,这一端必须是小括号.
第三章
人教2019A版必修 第一册
函数概念与性质
3.1.1 函数的概念
1.初中学习的函数的定义是什么?
设在一个变化过程中有两个变量x和y, 如果对于x的每一个值,y都有唯一的值与 它对应,那么就说y是x的函数.其中x叫自 变量,y叫因变量.
2.回顾初中学过哪些函数?
(1)一次函数 y ax b,(a 0)
(2)正比例函数
y k , (k 0) x
(3)反比例函数 y kx, (k 0)
(4)二次函数 y ax2 bx c,(a 0)
问题1. 某“复兴号”高速列车到350km/h后保持匀速运行半小时。这段时间内, 列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示 为 S=350t。
高中数学 第2章 函数2.1.1函数的概念和图象(一)配套课件 苏教版必修1

2.1.1 函数的概念和图象(一)
【学习要求】 1.理解函数的概念,明确决定函数的三个要素; 2.学会求某些函数的定义域; 3.掌握判定两个函数是否相同的方法; 4.理解静与动的辩证关系. 【学法指导】 通过实例,进一步体会函数是描述变量之间的依赖关系的重要 数学模型,在此基础上学习用集合与对应的语言来刻画函数, 体会对应法则在刻画函数概念中的作用,感受学习函数的必要 性与重要性.
第二十一页,共24页。
练一练•当堂检测(jiǎn cè)、目标达成 落实处 2.下列关于函数与区间的说法正确的是___④_____.(填序号)
①函数定义域必不是空集,但值域可以是空集; ②函数定义域和值域确定后,其对应法则也就确定了; ③数集都能用区间表示; ④函数中一个函数值可以有多个自变量值与之对应. 解析 函数的值域不可能为空集,故①错; 当两函数的定义域和值域分别相同时,但两函数的对应法则可 以不同,故②错; 由于整数集没法用区间表示,故③错. 只有④正确.
(3) 若 f(x) 是 偶 次 根 式 , 那 么 函 数 的 定 义 域 是 ____根__号__(ɡ_ē_n__h_à_o_)_内__的_式__子__不__小__于__零___的实数的集合; (4)若 f(x)是由几个部分的数学式子构成的,那么函数的定义域是 ____使__各__部__分__式__子_都__有__意__义___________的实数的集合(即使每个部 分有意义的实数的集合的交集); (5)若 f(x)是由实际问题列出的,那么函数的定义域是使解析式本 身有意义且符合____实__际__意__义______的实数的集合.
第三页,共24页。
填一填·知识要点(yàodiǎn)、记下 疑难点 2.求函数的定义域实质上是求使函数表达式有意义的自变量的取
tan-1的计算方式

tan-1的计算方式标题:如何使用tan-1函数计算角度?摘要:本文将介绍如何使用tan-1函数计算角度的方法和步骤,包括计算原理、使用示例和注意事项等内容。
第一节:tan-1函数的计算原理tan-1函数,也称为反正切函数,是三角函数中的一种,用于计算给定正切值的角度。
在计算机科学和数学领域中,tan-1函数被广泛应用。
其计算原理如下:1. 根据给定的正切值,使用tan-1函数可以计算出对应的角度。
2. tan-1函数的结果范围在-π/2到π/2之间,表示的是弧度制的角度。
3. tan-1函数的输入参数是一个实数,表示正切值,输出结果是一个实数,表示角度。
第二节:如何使用tan-1函数计算角度?使用tan-1函数计算角度的步骤如下:1. 确定要计算的正切值。
2. 将正切值作为tan-1函数的输入参数。
3. 使用计算器或数学软件,调用tan-1函数并输入正切值,得到对应的角度结果。
例如,要计算正切值为1的角度,可以按照以下步骤进行:1. 将正切值1作为tan-1函数的输入参数。
2. 调用计算器或数学软件中的tan-1函数。
3. 输入正切值1,得到结果0.785398163,表示该角度为约45度。
第三节:tan-1函数的使用示例下面通过一些具体的示例来展示tan-1函数的使用方法:示例1:计算正切值为0的角度1. 将正切值0作为tan-1函数的输入参数。
2. 调用计算器或数学软件中的tan-1函数。
3. 输入正切值0,得到结果0,表示该角度为0度。
示例2:计算正切值为√3的角度1. 将正切值√3作为tan-1函数的输入参数。
2. 调用计算器或数学软件中的tan-1函数。
3. 输入正切值√3,得到结果1.047197551,表示该角度为约60度。
示例3:计算正切值为-1的角度1. 将正切值-1作为tan-1函数的输入参数。
2. 调用计算器或数学软件中的tan-1函数。
3. 输入正切值-1,得到结果-0.785398163,表示该角度为约-45度。
高中数学必修一-第三章-3.1 函数的概念及其表示
第三章函数3.1 函数的概念及其表示知识点一:函数的概念1.函数的有关概念2.函数的三要素一个函数的构成要素:定义域、对应关系和值域.因为值域是由定义域和对应关系决定的,所以两个函数的定义域和对应关系相同时,它们是同一个函数.3.区间的概念:设a,b∈R,a<b.实数集R可以用区间表示为(-∞,+∞).知识点二:函数的表示法1.函数的三种表示法2.分段函数已知函数y=f(x),x∈A,如果自变量x在不同的取值范围内,函数有着不同的对应关系,那么我们称这样的函数为分段函数.【思考】1.函数的定义域和值域是否一定是无限集?2.区间是数集的另一种表示方法,是否任何数集都能用区间表示?3.根据函数的定义,任何一个自变量x是否都有唯一的函数值y与之对应?任何一个函数值y 是否都有唯一的自变量x与之对应?4.如何确定分段函数的定义域和值域?【解析】1.不一定.函数的定义域和值域也可能是有限集,如f(x)=1,x∈{1,2,3}.2.不是.如集合{0,1}就不能用区间表示.3.任何一个自变量x都有唯一的函数值y与之对应,但是函数值y不一定有唯一的自变量x 与之对应。
如f(x)=x2中,函数值4有两个自变量2、-2与之对应。
函数中x,y的对应关系是“一对一”或“多对一”,不能“一对多”.4.分段函数的定义域是每一段自变量取值范围的并集,值域也是每一段函数值取值范围的并集.3.1.1 函数的概念基础练一函数的概念1.(多选题)下面选项中,变量y是变量x的函数的是()A.x表示某一天中的时刻,y表示对应的某地区的气温B.x表示年份,y表示对应的某地区的GDP(国内生产总值)C.x表示某地区学生的某次数学考试成绩,y表示该地区学生对应的考试号D.x表示某人的月收入,y表示对应的个税2.下列四组函数中,表示同一个函数的是()3A.y=|x|与y=√x3B.y=√x2与s=(√t)2C.y=2t+1与y=2u+1D.y=1与y=x03.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示以集合M为定义域,集合N为值域的函数关系的有()A.①②③④B.①②③C.②③D.②④二函数的定义域4.函数f(x)=√x−1的定义域为() x−2A.[1,+∞)B.[1,2)C.[1,2)∪(2,+∞)D.(1,2)∪(2,+∞)5.已知某矩形的周长为定值a,若该矩形的面积S是这个矩形的一边长x的函数,则这个函数的定义域是.6.已知函数y=f(x)的定义域为[-2,3],则函数y=f(2x+1)的定义域为.x+1三函数值及函数的值域7.已知集合P={x|y=√x−1},集合Q={y|y=√x−1},则()A.P=QB.P⫋QC.Q⫋PD.P∩Q=⌀8.函数y=√x2−2x+3的值域为.,则f(x)的值域为.9.已知函数f(x)=1x2−2x10.已知函数f(x)的定义域是[0,1],值域是[1,2],则这样的函数可以是f(x)=.11.已知函数f(x)=x2+x-1.);(1)求f(2), f(1x(2)若f(x)=5,求x的值.3.1.2 函数的表示法基础练一 函数的表示法及其应用 1.函数y =x x+1的图象大致是 ( )A B C D2.某同学从家里到学校,为了不迟到,先匀速跑一段时间,跑累了再匀速走余下的路,设在途中花费的时间为t ,离开家的距离为d ,则下面图象中,能正确表示d 与t 的关系的是( )A B C D3.已知函数y =f (x )的对应关系如表,函数y =g (x )的图象为如图所示的曲线ABC ,则g (f (3))的值为 .二 函数解析式的求法5.已知函数f (x +2)=x 2+6x +8,则函数f (x )的解析式为( ) A.f (x )=x 2+2x B.f (x )=x 2+6x +8 C.f (x )=x 2+4x D.f (x )=x 2+8x +66.函数f (x )满足f (1-2x )=-1x ,则f (2)=( )A.2B.-2C.12 D.-12 7.已知函数f (2x -1)=3x -5,若f (x 0)=4,则x 0= .8.已知f (x )是一次函数,2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )= .9.(1)已知函数g (√x +1)=2x +1,求g (x )的解析式;(2)已知f (x )为二次函数,且f (0)=2, f (2)=f (-1)=0,求f (x )的解析式.三 分段函数问题10.已知函数f (x )={√x,x >0,|x +1|,x ≤0,则f (f (-3))=( )A.√3B.1C.2D.√2 11.已知f (x )={x +2,x ≤−1,x 2,−1<x <2,2x,x ≥2,若f (x )=3,则x 的值是( )A.1B.1或32C.1,32或±√3 D.√312.函数f (x )=x +|x |x 的图象是( )A B C D13.(2022山西大同期中)已知函数f (x )={x 2,x ≤0,4−2x,x >0.(1)画出函数f (x )的图象;(2)当f (x )≥2时,求实数x 的取值范围.。
第5章 函数1

第5章 函数
(2) A到B的所有不同的满射有6个, 分别为 f1={(a, g1), (b, g1 ), (c, g2)} f2={(a, g1 ), (b, g2), (c, g1 )} f3={(a, g1 ), (b, g2), (c, g2)} f4={(a, g2), (b, g1 ), (c, g2)} f5={(a, g1 ), (b, g2), (c, g1 )} f6={(a, g1 ), (b, g2), (c, g2)}
p: A→A是双射, 则称p为集合A上的n阶置换 记为 阶置换, 阶置换
a1 p= p( a1 )
a2 L an p ( a2 ) L p ( an )
第5章 函数
例2 若A={1, 2, 3}, 试写出A上的全部置换。 解 A上的全部置换有3!=6个,分别为
1 p1 = 1 1 p3 = 2
第5章 函数
定义 5.1 ― 2 设有函数f: A→B, g: C→D, 若 有A=C、 B=D且对所有的x∈A, 有f(x)=g(x), 则称 函数f和g相等, 记为f=g。 定义 5.1 ― 3 集合A到集合B的所有函数的集合记 为BA, 即 BA={f|f: A→B}
第5章 函数
定理 5.1 ― 1 当A和B是有限集合时,有 |BA|=|B||A| 证明 设|A|=m, |B|=n(m, n∈N); 又设A={a1, a2, …, am}。 因为 Df=A,所以 f={(a1, f(a1)), (a2, f(a2)), …, (am , f(am))}。 , 而每个f(ai)(i∈Nm)都有n种可能,所以A到B的不 同函数共有 {n·n·…·n } =n m个 M个 即 |BA|=|B||A|
第5章 函数
19.1.1函数教案

一、教学内容
本节课选自教材第十九章第一节第一部分,主题为“函数教案”。教学内容主要包括以下方面:
1.函数的定义:介绍函数的概念,使学生理解函数表示两个变量之间的依赖关系。
2.函数的表示方法:学习图像法、表格法和解析式法表示函数,并学会在不同情况下选择合适的表示方法。
3.函数的性质:探讨函数的单调性、奇偶性、周期性等基本性质,培养学生观察和分析函数图像的能力。
举例解释:
-函数定义:通过实际例子(如气温随时间的变化),让学生明确函数是一种特殊的关系,其中一个变量的值决定了另一个变量的值。
-函数表示方法:以一次函数为例,展示如何从图像、表格和解析式三种方式来描述同一个函数,强调各自的优势和适用场景。
-函数性质:以二次函数为例,讲解如何判断其单调性、奇偶性和周期性,以及这些性质如何影响函数图像。
-函数定义:强调函数表示两个变量之间的依赖关系,理解函数的输入和输出概念。
-函数表示方法:掌握图像法、表格法和解析式法,并能够根据具体情况选择合适的表示方法。
-函数性质:理解和掌握函数的单调性、奇偶性、周期性等核心性质,并能运用这些性质分析函数。
-实例应用:学会将函数知识应用于解决实际问题,例如在物理、经济等领域的建模。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了函数的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对函数的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
专题2一次函数的图象与性质-重难点题型(举一反三)(浙教版)(原卷版)
专题5.3 一次函数的图象与性质-重难点题型【浙教版】函数图像一次函数变为正比例函数,正比例函数是一次函数的特例。
)A.B.C.D.【变式1-1】函数y=ax+b﹣2的图象如图所示,则函数y=﹣ax﹣b的大致图象是()A.B.C.D.【变式1-2】(2019•杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是()A.B.C.D.【变式1-3】函数y=|x﹣2|的图象大致是()A.B.C.D.【题型2 正比例函数的图象】【例2】如图,三个正比例函数的图象分别对应函数关系式:①y=ax,①y=bx,①y=cx,将a,b,c从小到大排列并用“<”连接为()A.a<b<c B.c<a<b C.c<b<a D.a<c<b【变式2-1】(2020秋•达川区期末)如图,四个一次函数y=ax,y=bx,y=cx+1,y=dx﹣3的图象如图所示,则a,b,c,d的大小关系是()A.b>a>d>c B.a>b>c>d C.a>b>d>c D.b>a>c>d【变式2-2】(2021秋•茂名期中)直线y=2kx的图象如图所示,则y=(k﹣2)x+1﹣k的图象大致是()A.B.C.D.【变式2-3】(2021春•新田县期末)如图,直线l1①x轴于点(1,0),直线l2①x轴于点(2,0),直线l3①x轴于点(3,0),…直线l n①x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,l n分别交于点A1,A2,A3,…,A n ;函数y =3x 的图象与直线l 1,l 2,l 3,…,l n 分别交于点B 1,B 2,B 3,…,B n ,如果①OA 1B 1的面积记的作S 1,四边形A 1A 2B 2B 1的面积记作S 2,四边形A 2A 3B 3B 2的面积记作S 3,…四边形A n ﹣1A n B n B n ﹣1的面积记作S n ,那么S 2021= ..) C .第一、三、四象限D .第二、三、四象限【变式3-1】(2021•黄州区校级自主招生)已知过点(2,3)的直线y =ax +b (a ≠0)不经过第四象限,设s =a ﹣2b ,则s 的取值范围是( ) A .32≤s <6B .﹣3<s ≤3C .﹣6<s ≤32D .32≤s ≤5【变式3-2】(2021春•忠县期末)已知一次函数y =(5﹣a )x +a +1的图象不经过第四象限,且关于x 的分式方程102−x=2−axx−2有整数解,则满足条件的所有整数a 的和为( )A .6B .7C .8D .9【变式3-3】(2021•渝中区模拟)若关于x 的一元一次不等式组{23x >x −14x +1≥a恰有3个整数解,且一次函数y =(a﹣2)x +a +1不经过第三象限,则所有满足条件的整数a 的值之和是( ) A .﹣2B .﹣1C .0D .1【题型4 一次函数图象与系数的关系】【例4】(2021春•鄢陵县期末)已知A (x 1,y 1)、B (x 2,y 2)是一次函数y =(2﹣m )x +3图象上两点,且(x 1﹣x 2)(y 1﹣y 2)<0,则m 的取值范围为 .【变式4-1】如图,平面直角坐标系中,若点A (3,0)、B (4,1)到一次函数y =kx +4(k ≠0)图象的距离相等,则k 的值为 .【变式4-2】(2020•成都模拟)在平面直角坐标系xOy 中,直线l :y =kx ﹣1(k ≠0)与直线x =﹣k ,y =﹣k 分别交于点A ,B .直线x =﹣k 与y =﹣k 交于点C .记线段AB ,BC ,AC 围成的区域(不含边界)为W ;横,纵坐标都是整数的点叫做整点.(1)当k =﹣2时,区域W 内的整点个数为 ; (2)若区域W 内没有整点,则k 的取值范围是 . 【变式4-3】已知一次函数y =(6+3m )x +(n ﹣2).求(1)当m ,n 为何值时,y 值随x 的增大而减小,且与y 轴交点在x 轴下方? (2)当m ,n 为何值时,此一次函数也是正比例函数?(3)当m =﹣1,n =﹣2时,设此一次函数与x 轴交于点A ,与y 轴交于点B ,并求出①AOB 的面积(O 为坐标原点)【题型5 一次函数图象上点的坐标特征】 【例5】已知一次函数y =(6+3m )x +(n ﹣2).求(1)当m ,n 为何值时,y 值随x 的增大而减小,且与y 轴交点在x 轴下方? (2)当m ,n 为何值时,此一次函数也是正比例函数?(3)当m =﹣1,n =﹣2时,设此一次函数与x 轴交于点A ,与y 轴交于点B ,并求出①AOB 的面积(O 为坐标原点)【变式5-1】如图,直线y =2x +3与x 轴相交于点A ,与y 轴相交于点B .(1)求①AOB 的面积;(2)过B 点作直线BP 与x 轴相交于P ,①ABP 的面积是92,求点P 的坐标.【变式5-2】如图,直线y =kx +6与x 轴y 轴分别相交于点E ,F .点E 的坐标(8,0),点A 的坐标为(6,0).点P (x ,y )是第一象限内的直线上的一个动点(点P 不与点E ,F 重合). (1)求k 的值;(2)在点P 运动的过程中,求出①OP A 的面积S 与x 的函数关系式. (3)若①OP A 的面积为278,求此时点P 的坐标.【变式5-3】(2021春•青县期末)如图,直线y =﹣x +10与x 轴、y 轴分别交于点B ,C ,点A 的坐标为(8,0),P (x ,y )是直线y =﹣x +10在第一象限内一个动点.(1)求①OP A 的面积S 与x 的函数关系式,并写出自变量的x 的取值范围; (2)当①OP A 的面积为10时,求点P 的坐标.【题型6 一次函数图象与几何变换】【例6】已知一次函数y =kx +b 的图象过点A (﹣4,﹣2)和点B (2,4) (1)求直线AB 的解析式;(2)将直线AB 平移,使其经过原点O ,则线段AB 扫过的面积为 .【变式6-1】若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为()A.k=2、b=﹣3B.k=﹣2、b=﹣3C.k=﹣2、b=1D.k=﹣2、b=﹣1【变式6-2】(2018春•沙坪坝区校级期末)如图:一次函数y=13x+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.(1)求点B的坐标;(2)求四边形ABCO的面积;(3)求直线CD的解析式.【变式6-3】(2018•沙坪坝区模拟)如图,正比例函数y=kx(k≠0)的图象过点A(2,﹣3).直线y=x+b沿y 轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.(1)若点D在线段OA上(含端点),求b的取值范围;(2)当点A关于直线BC的对称点A'恰好落在y轴上时,求①OBD的面积.。
专题一 微重点1 函数的新定义问题
规律方法 以某些特殊函数为背景考查函数的基本概念及应用时,关 键是理解函数的实质,与熟悉的函数类比,通过赋特殊值 或数形结合解决.
跟踪演练1
1,x>0, (1)(2022·东北师大附中模拟)已知符号函数sgn x=0,x=0,
-1,x<0,
偶函数f(x)满足f(x+2)=f(x),当x∈[0,1]时,f(x)=x,则
得 3sin x=-cos x,即 tan x=-13, 因为函数y=tan x的周期为π, 所以 tan x=-13的根有无数个, 故函数g(x)有无数个“新不动点”,不符合题意.
(2)(多选)在实数集R上定义一种运算“★”,对于任意给定的a,b∈R,
a★b为唯一确定的实数,且具有下列三条性质:
f
-2
0522=-f
2
0522=-f
4×101+25
=-f 25=-R25=-15,
∴f(2
022)+f
-2
0522=-15.
考向4 欧拉函数
例4 (多选)(2022·重庆八中调研)若正整数m,n只有1为公约数,则称m,
n互质.对于正整数n,φ(n)是小于或等于n的正整数中与n互质的数的个数,
A.sgn[f(x)]>0
√C.sgn[f(2k+1)]=1(k∈Z)
B.f
2
0221=1
D.sgn[f(k)]=|sgn k|(k∈Z)
对于A选项,sgn[f(0)]=sgn 0=0,A错;
对于
B
选项,f
2
0221=f
1
010+12=f
12=12,B
错;
对于C选项,
对任意的k∈Z,f(2k+1)=f(1)=1,
欧拉函数φ1
欧拉函数φ1欧拉函数φ1(Eulertotientfunction)也称为欧拉和函数,是欧拉在1760年在其数论作品“Introductio in Analysis infinitorum”中首次提出的一种函数。
欧拉函数φ1以数学上表示整数n中小于等于n且与n互质的正整数的个数。
与费马小定理相反,欧拉函数φ1有助于求解从一个正整数a获得正整数b的正整数m数量。
欧拉函数φ1有着重要的意义。
它可以用来求解欧拉恒等式,即φ1(n)=n(1-1/p1)(1-1/p2)(1-1/p3)...(1-1/pn),其中p1,p2...pn 是n的质因数。
该等式在求解环上的问题中得到了广泛的应用,如求解有关两个互质整数模上的乘法运算问题以及有关费马素数序列和欧拉函数之间的关系问题。
此外,欧拉函数φ1还可以用于组合学中关于几何分布的研究,有助于确定某个数字模型是否是正确的。
另外,欧拉函数φ1可以用来计算某个整数的质因子,也可以用于计算多个整数的最大公约数和最小公倍数。
欧拉函数φ1也与高等数学中的一些重要概念有关,如模代数及它的应用、解析几何及群论的一些重要的理论。
它也与编码理论密切相关,因为它可以用来计算数字信号的混合度及它们之间的熵值。
另外,欧拉函数φ1也可以用来计算求解大整数因式分解问题,给人们带来了很大的帮助。
欧拉函数φ1的计算是以费马函数为基础的,费马函数是一种重要的算法,它可以用来计算某个数的质因子个数。
费马函数可以用分解质因数表示法将数n表示为p1p2p3...pn的乘积,其中p1,p2...pn为质因数。
由于费马函数的乘法准则也是欧拉函数φ1的乘法准则,因此可以根据费马函数求出欧拉函数φ1的值,在求某个数的质因式分解的时候也可以使用欧拉函数φ1,从而得出n所对应的费马素数序列。
总之,欧拉函数φ1是一个重要的函数,它不仅可以用来求解欧拉恒等式,而且也有助于求解环和费马小定理的问题,与几何分布和编码理论也有关系,能够用来计算某个整数的质因子以及求解大整数因式分解问题,因此在数学上具有重要的意义。
高中数学必修一第二章:函数.第一节:值域
高中数学(人教B 版)必修一:第二章 函数2.1.1 函数函数的值域一.值域:在函数y=f(x)中,由所有函数值构成的集合:{y |y=f(x),y ∈A},叫做这个函数的值域。
值域即因变量y 的取值范围,是函数的象的集合。
二.基本函数的值域: ①.一次函数y=kx+b [ y ∈R 或(-∞,+∞) ]②.二次函数y=ax 2+bx+c (a >0) ( , +∞)③.二次函数y=ax 2+bx+c (a <0) (-∞, ) ④.反比例函数y= [ y ≠0或(-∞,0) ∪(0,+∞)] 二.求函数的值域的方法:方法一.观察法:例一:求函数y= 的值域.例二:求函数y= 的值域.规律总结:当x ≥2时, = 。
当x ≤2时, = 。
当x ≥-2时, = 。
当x ≤-2时, = 。
方法二.分离常数法:——适用于分式。
例三:求函数y= 的值域.4a 4ac-b 2 4a 4ac-b 2 k x 1 1 x 2+1 x 2-1 x 1 x 1 x 1 x 1 2x-1 x+1例四:求函数y= 的值域.方法三.反表示法:用y 表示f(x).——适用于形如y= 的函数。
例五:求函数y= 的值域.方法四.二次函数配方法:配方、画图、截断——适用于形如F(x)=af(x)2+bf(x)+c 的函数。
例六:求函数y=x 2-4x+5的值域.方法五.换元法:——适用于带根号且根号下为一次式的函数。
例七:求函数y=x+ 的值域.方法六.判别式法:——适用于二次分式函数。
例八:求函数y= 的值域.x 2-1 x 2+1 af(x)+b cf(x)+d 2x-1 x+1 2x+1 x 2-3x+4 x +3x+4。
