初二数学《全等三角形》题型归类,充分掌握12种解题思路(附打印版)
初二年级数学八上第十二章全等三角形知识点总结复习及常考题型练习

第十二章全等三角形一、知识框架:二、知识概念:1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形;③三角形全等不因位置发生变化而改变。
&⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边.⑸对应角:全等三角形中互相重合的角叫做对应角.2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角。
(3)全等三角形的周长相等、面积相等。
](4)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3.全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4.证明两个三角形全等的基本思路::5.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.(4)三角形的三条角平分线交于三角形内部一点,并且这点到三边的距离相等6.证明的基本方法:—⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程.7.学习全等三角形应注意以下几个问题:(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4)中线倍长法、截长补短法证三角形全等。
(文末带解析)八年级数学全等三角形常考必考知识点总结

(文末带解析)八年级数学全等三角形常考必考知识点总结单选题1、工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是()A.SAS B.ASA C.AAS D.SSS2、小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带()A.第1块B.第2块 C.第3块D.第4块3、如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是( )A.AB=EDB.AC=EFC.AC∥EFD.BF=DC4、如图,AB//DC,AB=DC,要使∠A=∠C,直接利用三角形全等的判定方法是()A.AASB.SASC.ASAD.SSS∠AOB,则OC是∠AOB的平分线③a>b,则5、下列说法:①若AC=BC,则C为AB的中点②若∠AOC=12a2>b2④若a=b,则|a|=|b|,其中正确的有()A.1个B.2个C.3个D.4个6、如图是作ΔABC的作图痕迹,则此作图的已知条件是()A.已知两边及夹角B.已知三边C.已知两角及夹边D.已知两边及一边对角7、作∠AOB平分线的作图过程如下:作法:(1)在OA和OB上分别截取OD、OE,使OD=OE.DE的长为半径作弧,两弧交于点C.(2)分别以D,E为圆心,大于12(3)作射线OC,则OC就是∠AOB的平分线.用下面的三角形全等的判定解释作图原理,最为恰当的是()A.SSS B.SAS C.ASA D.AAS8、如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是()A.1个B.2个C.3个D.4个填空题9、如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是_____.(不添加任何字母和辅助线)10、如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,若∠A=50°,则∠DFE的度数为________.11、如图,△ABC≌△DEF,BE=5,BF=1,则CF=_____.12、如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动______分钟后△CAP与△PQB全等.13、如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=_____cm.解答题14、如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.15、如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.(文末带解析)八年级数学全等三角形_009参考答案1、答案:D解析:根据全等三角形的判定条件判断即可.解:由题意可知OC=OD,MC=MD在△OCM和△ODM中{OC=OD OM=OM MC=MD∴△OCM≅△ODM(SSS)∴∠COM=∠DOM∴OM就是∠AOB的平分线故选:D小提示:本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.2、答案:B解析:本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.故选:B.小提示:本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3、答案:C解析:根据全等三角形的判定方法即可判断.A. AB=ED,可用ASA判定△ABC≌△EDF;B. AC=EF,可用AAS判定△ABC≌△EDF;C. AC∥EF,不能用AAA判定△ABC≌△EDF,故错误;D. BF=DC,可用AAS判定△ABC≌△EDF;故选C.小提示:此题主要考查全等三角形的判定,解题的关键是熟知全等三角形的判定方法.4、答案:B解析:根据平行线性质得出∠ABD=∠CDB,再加上AB=DC,BD=DB,根据全等三角形的判定定理SAS即可推出△ABD≌△CDB,从而推出∠A=∠C,即可得出答案.∵AB//DC,∴∠ABD=∠CDB,在△ABD和△CDB中,{AB=CD∠ABD=∠CDBBD=BD,∴△ABD≌△CDB(SAS),∴∠A=∠C,故选B.小提示:本题考查了平行线性质、全等三角形的判定与性质的应用,熟练掌握全等三角形的判定与性质定理是解题的关键.5、答案:A解析:根据直线中点、角平分线、有理数大小比较以及绝对值的性质,逐一判定即可.当三点不在同一直线上的时候,点C不是AB的中点,故错误;当OC位于∠AOB的内部时候,此结论成立,故错误;当a、b为负数时,a2<b2,故错误;若a=b,则|a|=|b|,故正确;故选:A.小提示:此题主要考查直线中点、角平分线、有理数大小比较以及绝对值的性质,熟练掌握,即可解题.6、答案:C解析:观察ΔABC的作图痕迹,可得此作图的条件.解:观察ΔABC的作图痕迹,可得此作图的已知条件为:∠α,∠β,及线段AB,故已知条件为:两角及夹边,故选C.小提示:本题主要考查三角形作图及三角形全等的相关知识.7、答案:A解析:根据作图过程可得OD=OE,CE=CD,根据OC为公共边,利用SSS即可证明△OCE≌△OCD,即可得答案.∵分别以D,E为圆心,大于12DE的长为半径作弧,两弧交于点C;∴CE=CD,在△OCE和△OCD中,{OE=OD CD=CE OC=OC,∴△OCE≌△OCD(SSS),故选:A.小提示:本题考查全等三角形的判定,正确找出相等的线段并熟练掌握全等三角形的判定定理是解题关键.8、答案:C解析:根据全等三角形对应边相等,对应角相等,结合图象逐个分析即可.解:∵△ABC≌△AEF,∴AC=AF,EF=BC,∠EAF=∠BAC,故①③正确;∵∠EAF=∠EAB+∠BAF,∠BAC=∠FAC+∠BAF,∴∠EAB=∠FAC,故④正确;条件不足,无法证明∠FAB=∠EAB,故②错误;综上所述,结论正确的是①③④共3个.故选:C.小提示:本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.9、答案:AB=AC或∠ADC=∠AEB或∠ABE=∠ACD.解析:根据图形可知证明△ADC≌△AEB已经具备了一个公共角和一对相等边,因此可以利用ASA、SAS、AAS证明两三角形全等.∵∠A=∠A,AD=AE,∴可以添加AB=AC,此时满足SAS;添加条件∠ADC=∠AEB,此时满足ASA;添加条件∠ABE=∠ACD,此时满足AAS,故答案为AB=AC或∠ADC=∠AEB或∠ABE=∠ACD;小提示:本题考查了全等三角形的判定,是一道开放题,解题的关键是牢记全等三角形的判定方法.10、答案:40°解析:先利用HL定理证明Rt△ABC≌Rt△DEF,得出∠D的度数,再根据直角三角形两锐角互余即可得出∠DFE的度数.解:在Rt△ABC与Rt△DEF中,∵∠B=∠E=90°,AC=DF,AB=DE,∴Rt△ABC≌Rt△DEF(HL)∴∠D=∠A=50°,∴∠DFE=90°-∠D=90°-50°=40°.所以答案是:40°.小提示:此题主要考查直角三角形全等的HL定理.理解斜边和一组直角边对应相等的两个直角三角形全等是解题关键.11、答案:3解析:先利用线段和差求EF=BE﹣BF=4,根据全等三角形的性质BC=EF,再结合线段和差求出FC 可得答案.解:∵BE=5,BF=1,∴EF=BE﹣BF=4,∵△ABC≌△DEF,∴BC=EF=4,∴CF=BC﹣BF=4-1=3,所以答案是:3.小提示:本题考查全等三角形的性质,线段和差,解题的关键是根据全等三角形的性质得出BC=EF.12、答案:4解析:分当△CPA≌△PQB时和当△CPA≌△PQB时,两种情况进行讨论,求得BQ和BP的长,分别求得P和Q运动的时间,若时间相同即可,满足全等,若不等,则不能成立.当△CPA≌△PQB时,BP=AC=4(米),则BQ=AP=AB-BP=12-4=8(米),P的运动时间是:4÷1=4(分钟),Q的运动时间是:8÷2=4(分钟),则当t=4分钟时,两个三角形全等;当△CPA≌△QPB时,BQ=AC=4(米),AB=6(米),AP=BP=12则P运动的时间是:6÷1=6(分钟),Q运动的时间是:4÷2=2(分钟),故不能成立.综上,运动4分钟后,△CPA与△PQB全等,所以答案是:4.小提示:本题考查了全等三角形的判定,注意分△CPA≌△PQB和△CPA≌△QPB两种情况讨论是关键.13、答案:5解析:由D为AC的中点可得AD=CD,由CF∥AB可得∠AED=∠F,∠A=∠FCD,根据全等三角形的判定定理AAS证得结论即可.解:∵D为AC的中点∴AD=CD∵CF∥AB∴∠AED=∠F,∠A=∠FCD在△AED和△CFD中{AD=CD∠AED=∠F∠A=∠FCD∴△AED≌△CFD(AAS)∴AE=CF∵AB=15cm,CF=10cm,BE=AB-AE=AB-CF=15-10=5cm所以答案是:5小提示:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL根据具体情况选择恰当的判定方法是解题关键14、答案:(1)全等,理由见详解;PC⊥PQ,理由见解析;(2)存在,{t=1x=1或{t=2x=32.解析:(1)利用SAS 证得△ACP ≌△BPQ ,得出∠ACP=∠BPQ ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;(2)由△ACP ≌△BPQ ,分两种情况:①AC=BP ,AP=BQ ,②AC=BQ ,AP=BP ,建立方程组求得答案即可. 解:(1)当t =1时,AP =BQ =1,BP =AC =3,又∵∠A =∠B =90°,在ΔACP 和ΔBPQ 中,{AP =BQ ∠A =∠B AC =BP∴ΔACP ≅ΔBPQ (SAS ).∴∠ACP =∠BPQ ,∴∠APC +∠BPQ =∠APC +∠ACP =90°.∴∠CPQ =90°,即线段PC 与线段PQ 垂直.(2)①若ΔACP ≅ΔBPC ,则AC =BP ,AP =BQ ,则{3=4−t t =xt, 解得:{t =1x =1; ②若ΔACP ≅ΔBQP ,则AC =BQ ,AP =BP ,则{3=xt t =4−t, 解得:{t =2x =32 ;综上所述,存在{t =1x =1 或{t =2x =32使得ΔACP 与ΔBPQ 全等. 小提示:本题主要考查了全等三角形的判定与性质,两边及其夹角分别对应相等的两个三角形全等.在解题时注意分类讨论思想的运用.15、答案:证明见解析.解析:延长CE 、BA 交于F ,根据角边角定理,证明△BEF ≌△BEC ,进而得到CF=2CE 的关系.再证明∠ACF=∠1,根据角边角定理证明△ACF ≌△ABD ,得到BD=CF ,至此问题得解.证明:分别延长BA ,CE 交于点F.∵BE ⊥CE ,∴∠BEF =∠BEC =90°.又∵∠1=∠2,BE =BE ,∴△BEF ≌△BEC(ASA),∴CE =FE =12CF. ∵∠1+∠F =90°,∠ACF +∠F =90°,∴∠1=∠ACF.又∵AB =AC ,∠BAD =∠CAF =90°,∴△ABD ≌△ACF(ASA),∴BD=CF,∴BD=2CE小提示:本题考查了全等三角形的判定与性质.解题的关键是恰当添加辅助线,构造全等三角形,将所求问题转化为全等三角形内边间的关系来解决.。
八年级数学上册丨专题2.三角形全等证明的解题思路【2019年版】
∴∠ABE=∠CDF C
在△ABE和△CDF中
∠ABE=∠CDF BE=DF ∴△ABE≌△CDF(
SAS)
∴AE=CF
方法总结 两个待证的全等三角形如果位置较为特殊,我们可以从平移、翻折、旋转
等角度找用于证明全等的等边或等角,同时要根据有利条件选择合适的证明方 法.
优翼微课
B
P
C
在△ABE和△CAF中
E ∴△ABE≌△CAF
∠ABE=∠CAF
∴CF=AE,AF=BE
∠AEB=∠CFA
∴EF=AE-AF=CF-BE
AB=AC
典例精解
类型二:线段和差问题的证明
二 截长补短法
如图,在四边形ABCD中,AD∥BC,∠A与∠B的平分线交于点E,点E在CD
上,求证:AD+BC=AB
AD
21
E
3
4
B
C
典例精解
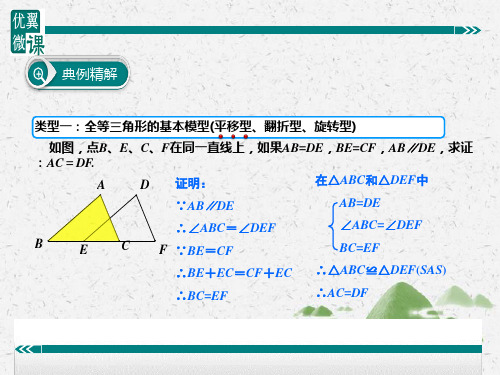
类型一:全等三角形的基本模型(平移型、翻折型、旋转型)
如图,点B、E、C、F在同一直线上,如果AB=DE,BE=CF,AB∥DE,求证
:AC=DF.
A
D 证明:
在△ABC和△DEF中
∵AB∥DE
AB=DE
∴∠ABC=∠DEF
B
E
C F ∵BE=CF
∠ABC=∠DEF BC=EF
∴BE+EC=CF+EC ∴△ABC≌△DEF(SAS)
∴∠MOP=∠NOP
OP=OP
O
BN
∴△AOP≌△BOP(AAS)
∴AO = BO
典例精解
类型一:全等三角形的基本模型(平移型、翻折型、旋转型) 如图,已知四边形ABCD中,AB=CD且AB∥CD,连接BD,在BD上截取BE=
初中数学—全等三角形解题方法、思路及技巧汇总

初中数学—全等三角形解题方法、思路及技巧汇总全等三角形是初中数学中非常重要的内容,今天我们就把初二数学中,与全等三角形相关的方法、思路及技巧都来整理一下。
一、全等三角形的性质与判定。
五种判定方法:SSS,SAS,AAS,ASA,HL,其中HL是边边角(SSA的特例)。
全等三角形的对应边相等,对应角相等,一句话,凡是对应的,都相等。
二、寻找全等三角形常用方法1、直接从结论入手一般会有以下几种要求证的方向:•线段相等•角相等•度数•线段或者线段的和、差、倍、分关系然后根据题目要求证的方向,找到要证明的相关量分别在哪两个三角形中,再围绕这两个三角形进行研究。
2、从已知条件入手把所有能标注在图上的已经条件标注出来,注意用不同的标示进行区分,比如第一组相等的线段用一条短竖,第二组相等的线段用两条短竖,再比如第一组相等的角用一个小圆弧,第二组相等的角就用两个小圆弧等。
然后通过已知条件找到相关的两个三角形,再进行分析。
记住一句话:“充分利用已知条件”。
3、把已经条件和结论综合起来考虑找到所有的已知条件和隐藏条件,结合结论,找出可能全等的两个三角形,再进行分析。
4、如果上述方法都确定行不通,就考虑添加辅助线来构造全等三角形。
三、构造全等三角形的一般方法1、题目中出现角平分线(1)通过角平分线上的某个已知点,向两边作垂线,这是利用角平分线的性质定理或者逆定理来构造的全等三角形(2)在角平分线的某个已知点,作角平分线的垂线和两边相交,构造全等三角形。
(3)在该角的两边,距离角的顶点相等长度的位置上截取两点,分别连接这两点与角平分线上的某已知点,构造全等三角形2、题目中出现中点或者中线(中位线)(1)倍长中线法,把中线延长至二倍位置(2)过中点作某一条边的平行线3、题目中出现等腰或者等边三角形(1)找中点,倍长中线(2)过顶点作底边的垂线(3)过某已知点作一条边的平行线(4)三线合一4、题目中出现三条线段之间的关系通常用截长补短法,在某条线段上截取一段线段,使之与特定的线段相等,或者将某条线段延长,使之与特定线段相等。
全等三角形解题方法、思路和技巧汇总

全等三角形解题方法、思路和技巧汇总本文主要介绍全等三角形的解题方法、思路和技巧。
全等三角形有五种判定方法:SSS,SAS,AAS,ASA,HL(边边角的特例)。
全等三角形的对应边相等,对应角相等。
因此,我们可以从结论、已知条件入手,或将已知条件和结论综合考虑,寻找可能全等的两个三角形,或者添加辅助线来构造全等三角形。
构造全等三角形的方法有多种。
如果题目中出现角平分线,可以通过角平分线上的某个已知点,向两边作垂线,或在角平分线的某个已知点,作角平分线的垂线和两边相交,或在该角的两边,距离角的顶点相等长度的位置上截取两点,分别连接这两点与角平分线上的某已知点,构造全等三角形。
如果题目中出现中点或者中线,可以倍长中线法,或过中点作某一条边的平行线。
如果题目中出现等腰或者等边三角形,可以找中点,倍长中线,或过顶点作底边的垂线,或过某已知点作一条边的平行线,或三线合一。
如果题目中出现三条线段之间的关系,可以用截长补短法,在某条线段上截取一段线段,或将某条线段延长,使之与特定线段相等。
如果题目中出现垂直平分线,可以把线段两端点与垂直平分线上的某点连接。
在某些特定题目中还可以使用旋转法、翻折法等。
最后,需要注意的是,在等腰直角三角形中,除了两腰相等、两底角相等外,还有三个度数:45,45,90.这是一个常见的隐藏条件,需要注意。
2、等边三角形除了三条边相等和三个角相等外,还要注意其中每个角都是60度。
通过三线合一,我们还能得到一个30度角。
3、平角的度数是180度,这是我们在计算角度时最容易忽略的。
4、外角和是指一个三角形的所有外角的度数之和,而内角和则是指所有内角的度数之和。
八年级数学第12章全等三角形知识点

第十一章 全等三角形知识点及常见题型一、全等三角形1、定义:能够完全重合的两个三角形叫做全等三角形。
①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形; ③三角形全等不因位置发生变化而改变。
2、全等三角形性质.. (1)全等三角形的对应边相等、对应角相等。
①长边对长边,短边对短边;最大角对最大角,最小角对最小角; ②对应角的对边为对应边,对应边对的角为对应角。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3、全等三角形的判定..边边边:三边对应相等的两个三角形全等(可简写成“SSS ”)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS ”) 角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA ”) 角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS ”) 斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL ”) 4、证明两个三角形全等的基本思路: 方法指引证明两个三角形全等的基本思路:(1):已知两边----找第三边(SSS )找夹角(SAS )(2):已知一边一角---已知一边和它的邻角找是否有直角(HL )已知一边和它的对角找这边的另一个邻角(ASA )找这个角的另一个边(SAS)找这边的对角(AAS )找一角(AAS )已知角是直角,找一边(HL )(3):已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS )练习二、角的平分线:从一个角的顶点得出一条射线把这个角分成两个相等的角,称这条射线为这个角的平分线。
性质:角的平分线上的点到角的两边的距离相等.判定:角的内部到角的两边的距离相等的点在角的平分线上。
三、学习全等三角形应注意以下几个问题:1、要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;2、表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;3、时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”检测题1、下列命题中正确的是( )A .全等三角形的高相等B .全等三角形的中线相等C .全等三角形的角平分线相等D .全等三角形对应角的平分线相等2、将五边形纸片ABCDE 按如图所示方式折叠,折痕为AF ,点E 、D 分别落在E ′,D ′,已知∠AFC=76°,则∠CFD ′等于( )A .31°B .28°C .24°D .22°第2题 第3题 第4题3、如图所示,在菱形ABCD 中,E 、F 分别是AB 、AC 的中点,如果EF=2,那么菱形ABCD 的周长是( )A .4B .8C .12D .164、如图所示,在锐角△ABC 中,点D 、E 分别是边AC 、BC 的中点,且DA=DE ,那么下列结论错误的是( )A .∠1=∠2B .∠1=∠3C .∠B=∠CD .∠3=∠B 5、将一张长方形纸片按如图所示的方式折叠,BC BD ,为折痕, 则CBD ∠的度数为( ) A .60° B .75° C .90° D .95°6、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )A .带①去B .带②去 C.带③去 D .带①②③去第6题 第7题7、如图,在Rt ABC △中, ,ED 是AC 的垂直平分线,交AC 于点D ,交BC于点E .已知 10=∠BAE ,则C ∠的度数为( )90 = ∠ B AE CB A ′ E ′ DADBA . 30B . 40C . 50D .60 8、如果△ABC ≌△DEF ,△DEF 的周长为13,DE=3,EF=4,则AC 的长( ) A .13 B .3 C .4 D .6 9、下列各条件中,不能作出惟一三角形的是( )A .已知两边和夹角B .已知两角和夹边 C.已知两边和其中一边的对角 D .已知三边二、填空题10、如图,在△ABC 中,∠C=90°,AD 平分∠BAC ,BC=12cm ,BD=8cm 则点D 到 AB 的距离为 。
最新初二数学全等三角形常见几何模型总结归类大全
最新初二数学全等三角形常见几何模型总结归类大全一、角平分线模型应用1.角平分性质模型: 辅助线:过点G 作GE ⊥射线AC(1).例题应用:①如图1,在中ABC ∆,,cm 4,6,900==∠=∠BD cm BC CAB AD C 平分,那么点D 到直线AB 的距离是 cm.②如图2,已知,21∠=∠,43∠=∠.BAC AP ∠平分求证:.图1 图2①2 (提示:作DE ⊥AB 交AB 于点E )②21∠=∠ ,PN PM =∴,43∠=∠ ,PQ PN =∴,BAC PA PQ PM ∠∴=∴平分,.(2).模型巩固:练习一:如图3,在四边形ABCD 中,BC>AB ,AD=CD ,BD 平分BAC ∠..求证:︒=∠+∠180C A图3练习二:已知如图4,四边形ABCD 中,..,1800BAD AC CD BC D B ∠==∠+∠平分求证:图4练习三:如图5,,,900CAB AF D AB CD ACB ABC Rt ∠⊥=∠∆平分,垂足为,中,交CD 于点E ,交CB 于点F. (1)求证:CE=CF.(2)将图5中的△ADE 沿AB 向右平移到'''E D A ∆的位置,使点'E 落在BC 边上,其他条件不变,如图6所示,是猜想:'BE 于CF 又怎样的数量关系?请证明你的结论.图5 图6练习四:如图7,90A AD BC =︒,∠∥,P 是AB 的中点,PD 平分∠ADC . 求证:CP 平分∠DCB .图7 练习五:如图8,AB >AC ,∠A 的平分线与BC 的垂直平分线相交于D ,自D 作DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F .求证:BE=CF .图8练习六:如图9所示,在△ABC 中,BC 边的垂直平分线DF 交△BAC 的外角平分线AD 于点D ,F 为垂足,DE ⊥AB 于E ,并且AB>AC 。
求证:BE -AC=AE 。
八年级数学上册第十二章全等三角形解题技巧总结(带答案)
八年级数学上册第十二章全等三角形解题技巧总结单选题1、在△ABC中,AB=4,AC=6,AD是BC边上的中线,则AD的取值范围是()A.0<AD<10B.1<AD<5C.2<AD<10D.0<AD<5答案:B分析:延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,即可解题.解:延长AD至点E,使得DE=AD,∵在△ABD和△CDE中,∵{AD=DE∠ADB=∠CDEBD=CD,∴△ABD≌△CDE(SAS),∴AB=CE,AD=DE∵△ACE中,AC﹣AB<AE<AC+AB,∴2<AE<10,∴1<AD<5.故选:B.小提示:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD≌△CDE是解题的关键.2、“经过已知角一边上的一点作“个角等于已知角”的尺规作图过程如下:已知:如图(1),∠AOB和OA上一点C.求作:一个角等于∠AOB,使它的顶点为C,一边为CA.作法:如图(2),(1)在0A上取一点D(OD<OC),以点O为圆心,OD长为半径画弧,交OB于点E;(2)以点C为圆心,OD长为半径画弧,交CA于点F,以点F为圆心,DE长为半径画弧,两弧交于点C;(3)作射线CC.所以∠CCA就是所求作的角此作图的依据中不含有()A.三边分别相等的两个三角形全等B.全等三角形的对应角相等C.两直线平行同位角相等D.两点确定一条直线答案:C分析:根据题意知,作图依据有全等三角形的判定定理SSS,全等三角形的性质和两点确定一条直线,直接判断即可.解:由题意可得:由全等三角形的判定定理SSS可以推知△EOD≌△GCF,故A正确;结合该全等三角形的性质对应角相等,故B正确;作射线CG,利用两点确定一条直线,故D正确;故选:C.小提示:本题考查作一个角等于已知角和三角形全等的判定与性质,解题关键是明确作图原理,准确进行判断.3、如图,在△ABC中,∠C=90°,BD平分∠ABC,AB=10,CD=3,则△ABD的面积为()A.30B.20C.15D.10答案:C分析:根据角平分线上的点到角两边的距离相等的性质作出辅助线,即可得出AB边上的高线长度,根据面积公式计算,解:如图,过D作DE⊥AB于E,∵BD平分∠ABC,DE⊥AB,DC⊥BC,∴DE=DC=3,∴S△ABD=12AB⋅DE=12×10×3=15.故选:C.小提示:本题主要考查了角平分线的性质,根据性质作出辅助线是解答此题的关键.4、如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为()A.3B.4C.5D.6答案:B分析:先证明△MQP≌△NQH,再由全等三角形的性质可得PQ=QH=5,根据MQ=NQ=9,即可得到答案.解:∵MQ⊥PN,NR⊥PM,∴∠NQH=∠NRP=∠HRM=90°,∵∠RHM=∠QHN,∴∠PMH=∠HNQ,在△MQP和△NQH中,{∠PMQ=∠QNHMQ=NQ∠MQP=∠NQH=90°,∴△MQP≌△NQH(ASA),∴PQ=QH=5,∵NQ=MQ=9,∴MH=MQ﹣HQ=9﹣5=4,故选:B.小提示:本题考查全等三角形的判定和性质,解题的关键是推理证明三角形的全等三角形,找到边与边的关系解决问题.5、如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD 的面积是()A.24B.30C.36D.42答案:B分析:过D作DE⊥AB交BA的延长线于E,根据角平分线的性质得到DE=CD=4,根据三角形的面积公式即可得到结论.如图,过D作DE⊥AB交BA的延长线于E,∵BD平分∠ABC,∠BCD=90°,∴DE=CD=4,∴四边形ABCD的面积=S△ABD+SΔBCD=12AB⋅DE+12BC⋅CD=12×6×4+12×9×4=30故选B.小提示:本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.6、如图,已知△ABC与△DEF,B,E,C,D四点在同一条直线上,其中AB=DF,BC=EF,AC=DE,则∠ACB等于()A.∠EFD B.∠ABC C.2∠D D.12∠AFE答案:D分析:根据已知条件可证△ABC≌△DFE,则∠ACB=DEF,再利用三角形的外角的性质可得∠AFE=∠ACB+∠DEF,进而可求解.在△ABC和△DFE{AB=DF BC=EF AC=DE∴△ABC≌△DFE∴∠ACB=DEF∵∠AFE=∠ACB+∠DEF∴∠AFE=2∠ACB,即∠ACB=1∠AFE2故选:D小提示:本题考查了三角形全等的判定和性质,三角形外角的性质,解题关键是利用三角形全等得出对应角相等.7、如图,若∠B=∠C=90°,AB=AC,则△ABD≌△ACD的理由是()A.SAS B.AAS C.ASA D.HL答案:D分析:根据两直角三角形全等的判定定理HL推出即可.解:∠B=∠C=90°,在Rt△ABD和Rt△ACD中,,{AD=ADAB=AC∴Rt△ABD≌Rt△ACD(HL),故选:D.小提示:本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.8、如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是()A.SSS B.SAS C.AAS D.HL答案:B分析:根据OA=OD,OB=OC,∠AOB=∠COD正好是两边一夹角,即可得出答案.解:∵在△ABO和△DCO中,{OA=OD∠AOB=∠CODOB=OC,∴△ABO≌△DCO(SAS),故B正确.故选:B.小提示:本题主要考查了全等三角形的判定,熟练掌握两边对应相等,且其夹角也对应相等的两个三角形全等,是解题的关键.9、如图,BD是△ABC的角平分线,AE⊥BD,垂足为M.若∠ABC=30°,∠C=38°,则∠CDE的度数为()A.68°B.70°C.71°D.74°答案:D分析:利用三角形内角和定理求出∠BAC=112°,利用全等三角形的性质证明∠BED=∠BAD即可解决问题.解:∵∠ABC=30°,∠C=38°,∴∠BAC=112°,在△BMA和△BME中,{∠ABM =∠EBMBM =BM ∠BMA =∠BME =90°.∴△BMA ≌△BME (ASA ),∴BA =BE ,在△BDA 和△BDE 中,{BA =BE∠ABD =∠EBD BD =BD,∴△BDA ≌△BDE (SAS ),∴∠BED =∠BAD =112°,∴∠CED =68°,∴∠CDE =180°-∠C -∠CED =74°,故选:D .小提示:本题考查三角形内角和定理,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.10、如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 的面积是30cm 2,AB =13cm ,AC =7cm ,则DE 的长( )A .3cmB .4cmC .5cmD .6cm答案:A分析:根据角平分线的性质求出DE =DF ,根据三角形的面积公式列式计算即可.解:∵AD 是∠BAC 的平分线,DE ⊥AB 于点E ,DF ⊥AC 于点F ,∴DE =DF ,∴12×AB ×DE +12AC ×DF =S △ABC =30,即12×13DE +12×7DE =30,解得DE =3. 故选:A .小提示:本题主要考查了角平分线的性质以及三角形的面积,灵活运用角平分线的性质成为解答本题的关键. 填空题11、如图,在△ABC 中,∠A =90°,DE ⊥BC ,垂足为E .若AD =DE 且∠C =50°,则∠ABD =_____°.答案:20分析:利用三角形的内角和定理先求解∠ABC ,再利用角平分线的性质定理的逆定理证明:BD 平分∠ABC, 从而可得答案.解:∵∠A =90°,∠C =50°,∴∠ABC =180°−90°−50°=40°,∵∠A =90°,DE ⊥BC,DA =DE,∴BD 平分∠ABC,∠ABD =12∠ABC =20°, 所以答案是:20小提示:本题考查的是三角形的内角和定理,角平分线的定义及性质定理的逆定理,掌握角平分线的性质定理的逆定理是解题的关键.12、如图,已知AB =CB ,要使△ABD ≌△CBD (SSS),还需添加一个条件,你添加的条件是__________.答案:AD =CD分析:要利用SSS 判定△ABD ≌△CBD ,已知AB =CB ,公共边BD =BD ,只需要再添加一组对边相等即可.解:∵AB=CB,BD=BD,∴要利用SSS判定△ABD≌△CBD,只需要在添加一组对边相等即可.∴AD=CD,所以答案是:AD=CD.小提示:本题考查用三边对应相等判定三角形全等,根据图形找到相关的条件是解题关键.13、如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB=___.答案:40°分析:根据AP平分∠CAB,BP平分∠CBD,可得∠CAB=2∠PAB,∠CBD=2∠PBD,再根据外角的性质可得∠CBD=∠CAB+∠ACB,∠PBD=∠PAB+∠APB,化简得2∠APB=∠ACB;过P作PE1⊥AB于点E1,PE2⊥BC于点E2,PE3⊥AC延长线于点E3,易得PE1=PE2=PE3,可得CP平分∠E3CE2,即有∠E3CP=∠E2CP,根据∠ACP=130°,可得∠E3CP=50°,∠E3CE2=2∠E3CP=100°,则有∠ACB=80°,再根据∠APB=1∠ACB求解即可.2解:∵AP平分∠CAB,BP平分∠CBD,∴∠CAB=2∠PAB,∠CBD=2∠PBD,又∵∠CBD=∠CAB+∠ACB,∠PBD=∠PAB+∠APB,∴2∠PBD=2∠PAB+∠ACB∴2(∠PAB+∠APB)=2∠PAB+∠ACB∴2∠APB=∠ACB如图示,过P作PE1⊥AB于点E1,PE2⊥BC于点E2,PE3⊥AC延长线于点E3,∵AP平分∠CAB,BP平分∠CBD,∴PE1=PE3,PE2=PE1,即PE1=PE2=PE3∴CP平分∠E3CE2,∴∠E3CP=∠E2CP又∵∠ACP=130°∴∠E3CP=180°−∠ACP=180°−130°=50°∴∠E3CE2=2∠E3CP=100°∴∠ACB=180°−∠E3CE2=180°−100°=80°∴∠APB=12∠ACB=12×80°=40°故答案是:40°.小提示:本题主要考查了角平分线的判定与性质,外角的性质,熟悉相关性质是解题的关键.14、三角形全等的判定方法——“角边角”(即ASA)指的是_______________________________答案:两角和它们的夹边分别相等的两个三角形全等.分析:角边角公理:两角和它们的夹边分别相等的两个三角形全等,根据公理直接作答即可.解:三角形全等的判定方法——“角边角”(即ASA)指的是:两角和它们的夹边分别相等的两个三角形全等.所以答案是:两角和它们的夹边分别相等的两个三角形全等.小提示:本题考查的是全等三角形的判定,掌握角边角公理是解题的关键.15、如图,在ΔABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°−12∠A;③点O到ΔABC各边的距离相等;④设OD=m,AE+AF=n,则SΔAEF=12mn.其中正确的结论有________(填写序号).答案:①③④分析:由角平分线的性质,平行的性质,三角形的性质等对结论进行判定即可.解:在ΔABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°−12∠A,∴∠BOC=180°−(∠OBC+∠OCB)=90°+12∠A;故②错误;在ΔABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF,∵EF//BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,在ΔABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴SΔAEF=SΔAOE+SΔAOF=12AE·OM+12AF·OD=12OD·(AE+AF)=12mn;故④正确;在ΔABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到ΔABC各边的距离相等,故③正确.所以答案是:①③④.小提示:本题考查了三角形内的有关角平分线的综合问题,一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线,角的平分线上的点到角的两边的距离相等.也就是说,一个点只要在角的平分线上,那么这个点到该角的两边的距离相等.解答题16、如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.答案:见解析分析:利用SSS证明△ABC≌△DCB,根据全等三角形的性质可得∠ABC=∠DCB,再由SAS定理证明△ABE≌△CED,即可证得AE=DE.证明:在△ABC和△DCB中,{AB=DC AC=DBBC=CB,∴△ABC≌△DCB(SSS).∴∠ABC=∠DCB.在△ABE和△DCE中,{AB=DC∠ABC=∠DCB BE=CE ,∴△ABE≌△DCE(SAS).∴AE=DE.小提示:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.17、命题:如图,已知AC∥EF,AC=FE,A,D,B,F共线,(1),那么ΔABC≅ΔFDE.(1)从①AB=FD和②BC=DE两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);(2)根据你选择的条件,判定ΔABC≅ΔFDE的方法是________;(3)根据你选择的条件,完成ΔABC≅ΔFDE的证明.答案:(1)①(2)SAS(3)见解析分析:(1)根据全等三角形的判定方法分析得出答案;(2)根据(1)直接填写即可;(3)利用SAS进行证明.(1)解:∵AC∥EF,∴∠A=∠F,∵AC=EF,∴当AB=FD时,可根据SAS证明ΔABC≅ΔFDE;当BC=DE时,不能证明ΔABC≅ΔFDE,所以答案是:①;(2)解:当AB=FD时,可根据SAS证明ΔABC≅ΔFDE,所以答案是:SAS;(3)证明:在△ABC和△FDE中,{AC=EF∠A=∠F AB=FD,∴ΔABC≅ΔFDE.小提示:此题考查了添加条件证明两个三角形全等,正确掌握全等三角形的判定定理是解题的关键.18、如图,在△ABC中,∠A=100°,AB=AC,BE是∠ABC的平分线,求证:AE+BE=BC.答案:见解析分析:延长BE到F,使BF=BC,连接FC,由AB=AC,∠A=100°,得到∠ABC=∠ACB=40°,由于BE平分∠ABC,于是得到∠ABE=∠EBC=20°,通过△FCE≌△F′CE,得到EF=EF′,∠EF′C=∠F=80°,证得△ABE≌△F′BE,于是得到AE=EF′,于是得到结论.解:如图,延长BE到F,使BF=BC,连接FC,∵AB=AC,∠A=100°,∴∠ABC=∠ACB=40°,∵BE平分∠ABC,∴∠ABE=∠EBC=20°,∵BF=BC,∴∠F=∠BCF=80°,∴∠FCE=∠ACB=40°,在BC上取CF′=CF,连接EF′,在△FCE与△F′CE中,{CF=CF′∠F′CE=∠FCECE=CE,∴△FCE≌△F′CE(SAS),∴EF=EF′,∠EF′C=∠F=80°,∴∠BF′E=100°,∴∠A=∠BF′E,在△ABE与△F′BE中,{∠A=∠BF′E∠ABE=∠F′BEBE=BE,∴△ABE≌△F′BE(AAS),∴AE=EF′,∴AE=EF,∴AE+BE=BE+EF=BC.小提示:本题考查了全等三角形的判定和性质,角平分线的性质,等腰三角形的性质,作辅助线构建全等三角形是解题的关键.。
人教版八年级数学上册第十二章全等三角形题型归纳
人教版八年级数学上册第十二章全等三角形题型归纳(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--全等三角形经典题型分类和归纳一,证明边或角相等方法:证明两条线段相等或角相等,如果这两条线段或角在两个三角形内,就证明这两个三角形全等;如果这两条线段或角在同一个三角形内,就证明这个三角形是等腰三角形;如果看图时两条线段既不在同一个三角形内,也不在两个全等三角形内,那么就利用辅助线进行等量代换,同样如果角不在同一个三角形内,也不在两个全等三角形内,也是用等量代换(方法是:(1)同角(等角)的余角相等(2)同角(等角)的补角相等,此类型问题一般不单独作一大题,往往是通过得出角相等后用来证明三角形全等,而且一般是在双垂直的图形中)1.已知,如图,AB⊥AC,AB=AC,AD⊥AE,AD=AE。
求证:BE=CD。
2.如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.3.已知:如图△ABC中,AB=AC,BD⊥AC,CE⊥AB,BD、CE交于H。
求证:HB=HC。
2、如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求证:AC=EF.AEDCB654321EDCAEDCBA二.证明线段和差问题 (形如:证明两条线段和等于另一条线段,常常使即为在这三条最长的线段截取一段使它等于较短线段中的一条,然后证明剩下的一段等于另一条较短的线段。
②补短法即为在较短的一条线段上延长一段,使它们等于最长的线段,然后证明延长的这一线段等于另一条较短的线段。
证明两条线段差等于另一条线段,只需把差化成和来解决即可。
1.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .2、如图,已知:△ABC 中,∠BAC =90, AB =AC ,AE 是过A 一直线,且点B 、C 在AE 的异侧,BD ⊥AE 于D ,CE ⊥AE 于E . 求证:BD =DE +CE ;PEDCBA FGE D CB A3、如图,AB ∥CD ,DE 平分∠ADC ,AE 平分∠BAD ,求证:AB=AD - CD三.证明线段的2倍或21关系 ( AB CE =2, MN BN =12) 1. 利用含30 角的直角三角形的性质证明例1. 已知,如图1,∆ABC 是等边三角形,在AC 、BC 上分别取点D 、E ,且AD =CE ,连结AE 、BD 交于点N ,过B 作BM AE ⊥,垂足为M ,求证:MN BN =12(提示:先证∠=BNE 60)2. 利用等线段代换(充分利用中点)例1.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .FE DCB A3.转化为线段和问题,利用截长补短法例5. 已知:如图5,四边形ABCD 中,∠=D 90 ,对角线AC 平分∠BAD ,AC BC =,求证:ADAB =12四.证明二倍角关系利用三角形外角和定理和等量代换如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠BD CBA。
人教版八年级数学上册考点与题型归纳第十二章全等三角形12.2全等三角形的判定(含解析)
人教版八年级数学上册考点与题型归纳第十二章全等三角形12.2 全等三角形的判定一:考点归纳考点一、三角形全等的判定定理:(1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS ”)(2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA ”)(3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS ”)。
考点二、直角三角形全等的判定:对于特殊的直角三角形,判定它们全等时,还有HL 定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL ”).考点三、证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程.二:【题型归纳】题型一:直角三角形全等的判定1.如图,已知,,AE BD AC BC DF EF =⊥⊥,垂足分别为点,C F ,且BC EF =.求证:ABC DEF ∆≅∆题型二:SAS的判定2.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;(2)若∠1=48°,求∠BDE的度数.题型三:全等三角形判定与性质的综合3.如图,∆ABC中,AC=CB,∠ACB=90°,D为AC延长线上的一点,E在BC边上,连接AE,DE,BD,AE=BD,∆≅∆(1)求证:ACE BCD(2)若∠CAE=15°,求∠EDB的度数.4.如图,AD为ABC的高,AD=BD,E为AC上一点,BE交AD于F,且FD=CD.(1)求证:BFD≌ACD;(2)判断BE与AC的位置关系,并说明理由.三:基础巩固和培优一、单选题1.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是()A .∠A =∠EB .BA =BEC .∠C =∠D D .AC =DE2.如图,下列条件中,不能证明ABD ≌ACD 的是( )A .BD DC =,AB AC =B .ADB ADC ∠∠=,BD DC =C .B C ∠=∠,BAD CAD ∠=∠D .B C ∠=∠,BD DC =3.如图,下列条件不能证明ABC DCB △≌△的是( )A .AB =DC ,AC =DBB .AB =DC ,∠ABC =∠DCB C .BO =CO ,∠A =∠D D .AB =DC ,∠ACB =∠DBC4.如图,BE=CF ,AB=DE ,添加下列哪一个条件可以推证△ABC ≌△DEF ( )A .BC=EFB .∠A=∠DC .AC//DFD .∠B=∠DEF5.如图,∆ABC 的面积为102cm ,BP 平分∠ABC ,AP 垂直于BP 于P .连接CP ,若∆ACP 的面积为22cm ,则∆ABP 的面积为( )A .12cmB .22cmC .32cmD .42cm6.如图,已知AD 是ABC 的角平分线,增加以下条件:①AB =AC ;②∠B =∠C ;③AD ⊥BC ;④ABD ACD S S ,其中能使BD =CD 的条件有 ( )A .①B .①②C .①②③D .①②③④7.如图,已知AE=CF ,∠AFD=∠CEB ,那么添加下列一个条件后,仍无法判定△ADF ≌△CBE 的是( )A .∠B=∠DB .BE=DFC .AD=CBD .AD ∥BC8.如图,在△ABC 和△DEC 中,已知CB CE =,还需添加两个条件才能使△ABC ≌△DEC ,不能添加的一组条件是( ).A .AB DE =,B E ∠=∠B .AB DE =,AC DC = C .AB DE =,AD ∠=∠ D .A D ∠=∠,BE ∠=∠9.如图,90ACB ∠=︒,AC=BC .AD CE ⊥,BE CE ⊥,垂足分别是点D 、E .若AD=6,BE=2,则DE 的长是( )A .2B .3C .4D .510.如图,△ABC 的面积为1cm 2, AP 垂直∠B 的平分线BP 于P ,则△PBC 的面积为( )A .0.4 cm 2B .0.5 cm 2C .13 cm 2D .0.6 cm 2二、填空题 11.如图所示,在△ABC 中,AB =CB ,∠ABC =90°,D 为AB 延长线上一点,点E 在BC 上,且BE =BD ,连接AE 、DE 、DC .若∠CAE =25°,则∠BDC =_____.12.在△ABC 和△A ′B ′C ′中,若∠A =∠A ′,AB =A ′B ′,请你补充一个条件_____,使得△ABC ≌△A ′B ′C ′.13.如图,在ABC 中,点D 、E 、F 分别是BC ,AB ,AC 上的点,若∠B =∠C ,BF =CD ,BD =CE ,∠EDF =56°,则∠A =_____°.14.如图,已知在ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;≌;④BP=CP中,正确的是________.③BPR CPS15.如图,在△ABC 中,AB=AC=12,BC=8,D 为AB 的中点,点P 在线段BC 上以每秒2 个单位的速度由B 点向C 点运动,同时,点Q 在线段CA 上以每秒x 个单位的速度由C 点向A 点运动.当△BPD 与以C、Q、P 为顶点的三角形全等时,x 的值为_____.三、解答题16.如图所示,在四边形ABCD中,CD∥AB,∠ABC的平分线与∠BC D的平分线相交于点F,BF与CD的延长线交于点E,连接CE.求证:(1)△BCE是等腰三角形.(2)BC=AB+CD17.如图,点B,E,C,F在一条直线上,AB=DE,AC =DF,BE=CF.求证:△ABC ≌△DEF;18.如图,D为△ABC外一点,∠DAB=∠B,CD⊥AD,∠1=∠2,若AC=7,BC=4,求AD的长.19.如图,在△ABC中,AB<AC,边BC的垂直平分线DE交△ABC的外角∠CAM平分线于点D,垂足为E,DF⊥AC于点F,DG⊥AM于点G,连接CD.(1)求证:BG=CF;(2)若AB=10cm,AC=14cm,求AG的长.20.在ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.10参考答案题型归纳1.证明:,AC BC DF EF ⊥⊥ 90C F ︒∴∠=∠=AE BD =AB DE ∴=在Rt ABC ∆和Rt DEF ∆中AB DEBC EF =⎧⎨=⎩()Rt ABC Rt DEF HL ∴∆≅∆ 2.解:(1)证明:∵AE 和BD 相交于点O , ∴∠AOD =∠BOE .在△AOD 和△BOE 中,∠A =∠B ,∴∠BEO =∠2. 又∵∠1=∠2,∴∠1=∠BEO ,∴∠AEC =∠BED .在△AEC 和△BED 中,A BAE BE AEC BED ∠=∠⎧⎪=⎨⎪∠=∠⎩(2)∵△AEC ≌△BED ,∴EC =ED ,∠C =∠BDE .在△EDC 中,∵EC =ED ,∠1=48°,∴∠C =∠EDC =66°,∴∠BDE =∠C =66°.3.(1)证明:在Rt △ACE 和Rt △BCD 中,AC BCAE BD =⎧⎨=⎩,∴△ACE ≌△BCD (HL );(2)∵△ACE ≌△BCD ,∠CAE=15°,∴CE=CD,∠CBD=∠CAE=15°∴∠CDE=∠CED ,∵∠ACB=90°,∴∠CED=45°,∵∠CED 为△BDE 的外角,∴∠EDB=∠CED-∠CBD=45°-15°=30°.4.证明:(1)在△BDF 和△ADC 中,90AD BDADC BDF CD DF,(2)BE⊥AC,理由如下:∵△BDF≌△ADC,∴∠DAC=∠DBF,∵∠DAC+∠C=90°,∴∠DBF+∠C=90°,∴∠BEC=90°,∴BE⊥AC.三:基础巩固和培优1.D解:∵∠ABD =∠EBC ,BC=BD ,∴∠ABC=∠EBD ,A.当添加∠A=∠E 时,可根据“AAS”判断△ABC ≌△EBD ,故正确;B.当添加BA=BE 时,可根据“SAS”判断△ABC ≌△EBD ,故正确;C.当添加∠C=∠D 时,可根据“ASA”判断△ABC ≌△EBD ,故正确;D.当添加AC =DE 时,无法判断△ABC ≌△EBD ,故错误;故选:D .2.D解:A 、因为BD DC =,AB AC =,又因为AD=AD ,所以ABD ≌ACD (SSS ),故本选项不符合题意; B 、因为ADB ADC ∠∠=,BD DC =,又因为AD=AD ,所以ABD ≌ACD (SAS ),故本选项不符合题意;C 、因为B C ∠=∠,BAD CAD ∠=∠,又因为AD=AD ,所以ABD ≌ACD (AAS ),故本选项不符合题意;D 、因为B C ∠=∠,BD DC =,AD=AD ,这是边边角,不能证明ABD ≌ACD ,故本选项符合题意. 故选:D .3.D解:AB =DC ,AC =DB ,BC =BC ,符合全等三角形的判定定理“SSS”,能推出ABC DCB △≌△ ,故A 选项错误;AB =DC ,ABC DCB ∠=∠,BC =CB符合全等三角形的判定定理“SAS”,能推出ABC DCB △≌△ ,故B 选项错误;在△AOB 和△DOC 中,AOB DOCA D OB OC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴AOB DOC △≌△ (AAS ),∴AB =DC ,∠ABO =∠DCO ,∵OB =OC ,∴∠OBC =∠OCB ,∴∠ABC =∠DCB ,在△ABC 和△DCB 中,AB DCABC DCB BC CB=⎧⎪∠=∠⎨⎪=⎩ ,能推出ABC DCB △≌△,故C 选项错误;BC =CB ,AB =DC ,∠ACB =∠DBC ,SSA 不符合全等三角形的判定定理,即不能推出ABC DCB △≌△,故D 选项正确.故选D .4.D解:∵BE =CF ,∴BC =EF ,又∵AB=DE ,A 、添加BC =EF 不能证明△ABC ≌△DEF ,故此选项错误;B 、添加∠A =∠D 不能证明△ABC ≌△DEF ,故此选项错误;C 、添加AC ∥DF 可得∠ACB =∠F ,不能证明△ABC ≌△DEF ,故此选项错误;D 、添加∠B=∠DEF 可利用SAS 判定△ABC ≌△DEF ,故此选项正确;故选:D .5.C解:延长AP 交BC 于D ,∵BP 平分∠ABC ,AP ⊥BP ,∴∠ABP=∠DBP ,∠APB=∠DPB=90°,在△ABP 与△DBP 中,ABP DBP PB PBAPB DPB ∠∠⎧⎪⎨⎪∠∠⎩===,∴AP=PD ,S △PBD =S △ABP∴2ACP PCD S S ∆∆==2cm∴S △ABD =10-4=62cm ,∴△ABP 的面积=3cm 2,故选:C .6.D解:∵AD 平分∠BAC ,∴∠BAD=∠CAD ,∵AB=AC ,AD=AD ,∴△BAD ≌△CAD (SAS ),∴BD=CD ,故①符合题意;∵∠B=∠C ,AD=AD ,∴△BAD ≌△CAD (AAS ),∴BD=CD ,故②符合题意;∵AD ⊥BC ,∴∠ADB=∠ADC=90°,∵AD=AD ,∴△BAD ≌△CAD (ASA ),∴BD=DC ,故③符合题意;∵ABD ACD S S ,∴BD=DC ,故④符合题意;∴①②③④都可以得到BD=CD ;故选D .7.C解:∵AE=CF ,∴AE+EF=CF+EF ,∴AF=CE ,A 、∠B=∠D ,∠AFD=∠CEB ,AF=CE ,满足AAS ,能判定△ADF ≌△CBE ;B 、BE=DF ,∠AFD=∠CEB ,AF=CE ,满足SAS ,能判定△ADF ≌△CBE ;C 、AD=CB ,AF=CE ,∠AFD=∠CEB ,满足SSA ,不能判定△ADF ≌△CBE ;D 、AD ∥BC ,则∠A=∠C ,又AF=CE ,∠AFD=∠CEB ,满足ASA ,能判定△ADF ≌△CBE ; 故选:C .8.C解:∵CB=CE.∴当AB DE =,B E ∠=∠时,满足SAS ,可证△ABC ≌△DEC ,故A 不符合题意; 当AB DE =,AC DC =时,满足SSS ,可证△ABC ≌△DEC ,故B 不符合题意;当AB DE =,A D ∠=∠时,满足是ASS ,不能证明△ABC ≌△DEC ,故C 符合题意; 当A D ∠=∠,B E ∠=∠时,满足AAS ,可证△ABC ≌△DEC ,故D 不符合题意. 故选C .9.C解:∵90ACB ∠=︒,∴∠ACD+∠ECB=90º,∵AD CE ⊥,BE CE ⊥,∴∠ADC=∠CEB=90º,∴∠ECB+∠CBE=90º,∴∠ACD=∠CBE,在△ACD和△CBE中,∵∠ADC=∠CEB=90º,∠ACD=∠CBE,AC=BC,∴△ACD≌△CBE(AAS),∴AD=CE=6,CD=BE=2,∴ED=EC-CD=6-2=4.故选择:C.10.B解:如图,延长AP交BC于T.∵BP⊥AT,∴∠BPA=∠BPT=90°,∵BP=BP,∠PBA=∠PBT,∴△BPA≌△BPT(ASA),∴PA=PT,∴S△BPA=S△BPT,S△CAP=S△CPT,∴S △PBC =12S △ABC =12=0.5, 故选:B .11.70°解: ∵∠ABC=90°,∴∠CBD=∠ABC =90°,在Rt △ABE 与Rt △CBD 中,BE BD CBD ABC AB BC =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CBD ,∴∠AEB=∠BDC ,∵AB=BC ,∴∠BAC=∠ACB=45°,∵∠AEB 为△AEC 的外角,∠CAE=25°,∴∠AEB=∠ACB+∠CAE=45°+25°=70°,∴∠BDC=70°.故答案为:70°.12.∠B =∠B ′或∠C =∠C ′或AC =A ′C ′.解:在△ABC 和△A ′B ′C ′中,AB =A ′B ′,∠A =∠A ′, 当添加∠B =∠B ′可利用“ASA ”判断△ABC ≌△A ′B ′C ′; 当添加∠C =∠C ′可利用“AAS ”判断△ABC ≌△A ′B ′C ′; 当添加AC =∠A ′C ′可利用“SAS ”判断△ABC ≌△A ′B ′C ′. 故答案为:∠B =∠B ′或∠C =∠C ′或AC =A ′C ′. 13.68°.解:在△BDF和△CED中∴△BDF ≌△CED (SAS ),∴∠BFD=∠CDE ,∠BDF=∠CED ,∴∠BDF+∠CDE=180º-∠EDF=180º-56º=124º,∴∠BFD+∠BDF=∠BDF+∠CDE=124º,∴∠C=∠B=180º-∠BFD-∠BDF=56º,∴∠A=180º-∠B-∠C=180º-56º-56º=68º.故答案为:68º.14.①② 解:在Rt APR ∆和Rt APS ∆中,PS PR AP AP =⎧⎨=⎩, Rt APR Rt APS ∴∆≅∆,()HLAR AS ∴=,①正确,∴1BAP ∠=∠,12∠=∠,2BAP ∴∠=∠,//QP AB ∴,②正确,BRP ∆和QSP ∆中,只有一个条件PR PS =,再没有其余条件可以证明 BRP QSP ∆≅∆,故③④错误; 故答案是:①②.15.2 或 3解:设经过 t 秒后,使△BPD 与△CQP 全等. ∵AB =AC =12,点 D 为 AB 的中点.∴BD =6.∵∠ABC =∠ACB .∴要使△BPD 与△CQP 全等,必须 BD =CP 或 BP =CP . 即 6=8﹣2t 或 2t =8﹣2t .1t =1,2t =2.当t =1 时,BP =CQ =2,2÷1=2.当t =2 时,BD =CQ =6,6÷2=3.即点 Q 的运动速度是 2 或 3,故答案为:2 或 3.16.解:(1)∵BF 平分∠ABC , ∴12ABF CBF ABC ∠=∠=∠,∵CD ∥AB ,∴ABF E ∠=∠,∴E CBF ∠=∠,∴BC=CE ,∴△BCE 是等腰三角形.(2)∵CF 平分∠BCE , ∴12BCF BCE ∠=,∵CD ∥AB ,∴180ABC BCE ∠+∠=︒,∴90CBF BCF ∠+∠=︒,∴90BFC ∠=︒,即 CF ⊥BE ,又BC=CE ,∴BF=EF ,在△ABF 和△DEF 中,∵ABF EAFB DFE BF EF∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABF ≌△DEF ;∴AB=DE ,∴BC=CE=DE+CD=AB+CD ,因此 BC=AB+CD .17.解:证明:∵BE =CF ,∴BE +EC =CF +EC ,∴BC =EF ,在△ABC 和△DEF 中,∵AB DEAC DF BC EF=⎧⎪=⎨⎪=⎩,∴△ABC ≌△DEF (SSS ).18.解:证明:延长AD ,BC 交于点E .∵CD ⊥AD ,∴∠ADC =∠EDC =90°.在△ADC 和△EDC 中12ADC EDCCD CD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADC ≌△EDC (ASA ).∴∠DAC =∠DEC ,AC =EC ,AD =ED .∵AC =7,∴EC =7.∵BC =4∴BE =11∵∠DAB =∠B ,∴AE =BE =11.∴AD =5.5.答:AD 的长为5.5.19.解:(1)证明:如图所示,连接DB .∵AD 是△ABC 的外角平分线,DG ⊥AB ,DF ⊥CA , ∴DF=DG .∵DE 垂直平分BC ,∴DC=DB ,在Rt △CDF 与Rt △BDG 中DF DG DC DB =⎧⎨=⎩∴Rt △CDF ≌Rt △BDG (HL ),∴BG=CF .(2)解:∵∠GAD=∠FAD ,∠AGD=∠AFD ,AD=AD , ∴在△ADG 与△ADF 中GAD FADAGD AFD AD AD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADG ≌△ADF (AAS ),∴AG=AF ,∵BG=CF∴AG=()()111410222AC AB -=-=(cm).20.解:(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,∴∠DAC+∠ACD =90°,∵∠ACB =90°,∴∠BCE+∠ACD =90°,∴∠DAC =∠BCE ,在△ADC 和△CEB ,ADC CEBDAC ECB AC CB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴CD =BE ,AD =CE ,∴DE =CE+CD =AD+BE ;(2)证明:∵AD ⊥MN ,BE ⊥MN , ∴∠ADC =∠CEB =90°,∴∠DAC+∠ACD =90°,∵∠ACB =90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠BCE,∵AC=BC,∴△ADC≌△CEB,∴CD=BE,AD=CE,∴DE=CE﹣CD=AD﹣BE;(3)解:DE=BE﹣AD,理由如下:∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠BCE,∵AC=BC,∴△ADC≌△CEB,∴CD=BE,AD=CE,∴DE=BE﹣AD.。
