材料力学组合变形习题
材料力学习题答案
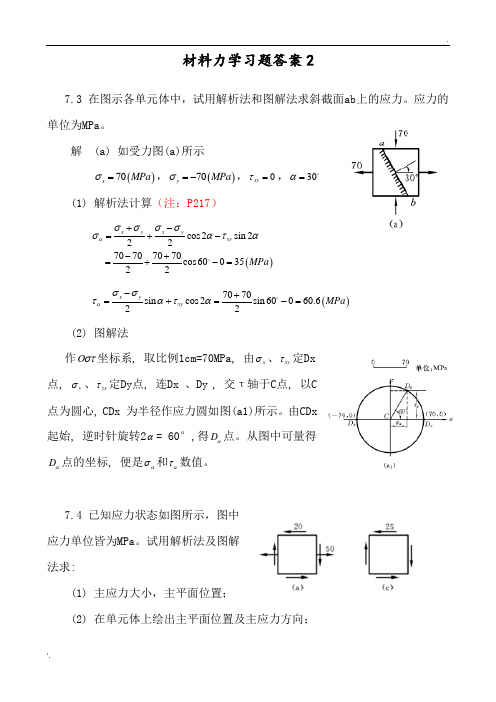
.材料力学习题答案27.3在图示各单元体中,试用解析法和图解法求斜截面ab上的应力。
应力的单位为MPa。
解(a) 如受力图(a)所示()70xMPaσ=,()70yMPaσ=-,0xyτ=,30α=(1) 解析法计算(注:P217)()cos2sin22270707070cos6003522x y x yxyMPaασσσσσατα+-=+--+=+-=()7070sin cos2sin60060.622x yxyMPaασστατα-+=+=-=(2) 图解法作Oστ坐标系, 取比例1cm=70MPa, 由xσ、xyτ定Dx点,yσ、yxτ定Dy点, 连Dx 、Dy , 交τ轴于C点, 以C点为圆心, CDx 为半径作应力圆如图(a1)所示。
由CDx起始, 逆时针旋转2α= 60°,得Dα点。
从图中可量得Dα点的坐标, 便是ασ和ατ数值。
7.4 已知应力状态如图所示,图中应力单位皆为MPa。
试用解析法及图解法求:(1) 主应力大小,主平面位置;(2) 在单元体上绘出主平面位置及主应力方向;.(3) 最大切应力。
解 (a) 受力如图(a)所示()50x MPa σ=,0y σ=,()20xy MPa τ=(1) 解析法 (数P218)2max 2min 22x y x y xy σσσσστσ+-⎛⎫⎫=±+⎬ ⎪⎭⎝⎭()()225750050020722MPa MPa ⎧+-⎪⎛⎫=±+=⎨ ⎪-⎝⎭⎪⎩ 按照主应力的记号规定()157MPa σ=,20σ=,()37MPa σ=-02220tan 20.8500xyx yτασσ⨯=-=-=---,019.3α=-()13max 5773222MPa σστ-+=== (2) 图解法作应力圆如图(a1)所示。
应力圆与σ轴的两个交点对应着两个主应力1σ、3σ 的数值。
由x CD 顺时针旋转02α,可确定主平面的方位。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
吉林大学考研材料力学题型四:组合变形

(2000)四、钢制平面直角曲拐ABC,受力如图。
q=2.5πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P x=qL,试设计AB段的直径d。
(15分)(2001)三、已知直径为d的钢制圆轴受力如图。
(1)试确定可能危险点的位置,并用单元体表示其应力状态;(2)若此圆轴单向拉伸时的许用应力为[σ],试列出校核此轴强度的强度条件。
(10分)(2001)九、试指出下面各截面梁在P的作用下,将产生什么变形?(6分)(2002)二、图示矩形截面杆,上、下表面的轴向线应变分别为:εa=1×10-3,εb=0.4×10-3,E=210Gpa1)试求拉力P和偏心距e;2)并画出横截面上的正应力分布图。
(10分)(2002)五、直径为d的钢制圆轴受力如图。
已知:P1=20KN,P2=10KN,m=20KN·m,q=5KN/m,[σ]=160Mpa,试设计AB 轴的直径。
(10分)(2003)三、钢制实心圆截面轴AC,[σ]=140Mpa,L=100cm,a=15cm,皮带轮直径D=80cm,重Q=2KN,皮带水平拉力F1=8KN,F2=2KN,试设计AC轴的直径d。
(15分)m=qL2,P=qL,试用第三强度理论设计该圆周的直径d。
(15分)L、P、M=4PL,试用第三强度理论设计该轴的直径D。
(15分)(2005)十一、图示为一等直杆受偏心拉伸,试确定其任意X截面上的中性轴方程。
若设Y P=H/6,Z P=B/6,求其中性轴在Y轴和Z轴上的截距(A Y=?、A Z=?)各为多少?(8分)(2006)六、直径为D的钢制平面曲拐圆轴受力如图所示,已知材料的许用应力为[Σ]=160MP A,Q=20KN/M,F1=10KN,F2=20KN,L=1M,试设计AB轴的直径D。
(2006)九、已知矩形截面铝合金杆A点处的纵向线应变ΕX=5×10-4,E=70GP A,H=18CM,B=12CM,试求荷载F。
材料力学试卷组合+压杆
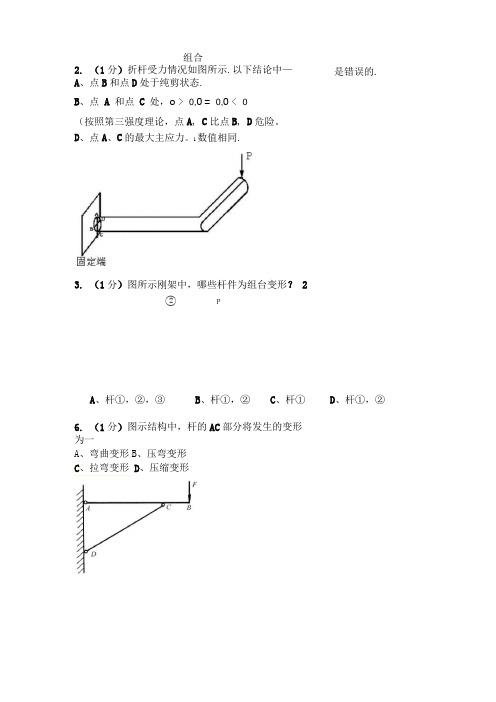
组合2.(1分)折杆受力情况如图所示.以下结论中—A、点B和点D处于纯剪状态.B、点A 和点C 处,o > 0,0 = 0,0 < 0(按照第三强度理论,点A, C比点B, D危险。
3.(1分)图所示刚架中,哪些杆件为组台变形? 2②PA、杆①,②,③B、杆①,②C、杆①6.(1分)图示结构中,杆的AC部分将发生的变形为一A、弯曲变形B、压弯变形C、拉弯变形D、压缩变形是错误的.D、杆①,②D、点A、C的最大主应力。
1数值相同.7.(1分)在图示刚架中,―B一段发生拉弯组合变形。
㈤(A) (C)I 如F9.(1分)图示简支斜梁ACB,在C处承受铅垂力P的作用。
该梁的A、AC段发生弯曲变形,CB段发生拉弯组合变形B、AC段发生压弯组合变形,CB段发生弯曲变形C、AC段发生压弯组合变形,CB段发生拉弯组合变形D、AC段和CB段均只发生弯曲变形10.(1分)图示两个起重机构,在机构(a)中滑轮通过轴承安装在悬臂圆杆AB的自由端B;在机构(b)中,滑轮通过方键固定在轴CD上,起吊重物P时,杆AB、轴CD的变形状态。
A、分别为扭转和弯曲;C、分别为弯曲和弯扭组合; B、分别为扭转和弯扭组合;D、均为弯扭组合。
11.(1分)图示圆轴,垂直集中力P作用于自由端B,扭转力偶作用于截面C 处,该轴的。
A、AC段发生扭转变形,CB段发生弯曲变形;D、AC段和CB段均发生弯扭组合变形。
14. (1分)图示三角形支架的AB杆均为高h、宽b的矩形截面杆,杆长l >5h。
在图(a)、(b)两种受载情况下,图(a)所示AB杆的变形是—拉压__ ,图(b)所示杆的变形是_拉弯。
两种受载情况下,AB杆的最大正应力关系是。
A、o >o bB、o =o bC、o <o b1. (1分)图示受扭转与弯曲联合作用的圆杆,a、b两点的应力状态是否正确?5.下面 B 单元体表示构件A点的应力状态。
(C) (D)8. 一压力机框架受力F, m-m截面如图。
材料力学(单辉祖)第十章组合变形

弯压组合
可见,危险截面为C截面 其轴力和弯矩分别为
FNC 3 kN M c M max 4 2 8kN m
A
FAy
10kN m a x
g g f
C m
FBy
B
危险点 截面C上的最低点f 和最高点g
FN M c s A W
f
18
弯压组合
A I
4
10kN
解 首先计算折杆的支座反力 由平衡方程可得 FAx A
FAx 0, FAy 5kN, FBy 5kN
FAy
m
10kN
C 1.2m B 1.6m FBy
a x 1.6m
m
由于折杆左右对称,所以只需分析一半即可。 折杆AC部分任一截面上的内力
FN FAy sin 3 kN FS FAy cos 4 kN M xFAy cos
杆件变形分析步骤 首先, 在杆件原始尺寸上分别计算由横向力和 轴向力引起变形、应力 然后, 利用叠加原理,合成在横向力和轴向力 共同作用下杆件变形、应变和应力等物理量 若杆件抗弯刚度EI较大,轴力引起杆件的弯曲 变形较小,可以忽略
10
弯拉组合
细长杆件强度问题, 受力如图,抗弯刚度 EI,截面抗弯模量W , 横截面面积A。
n
e n
P
z b h y
30
偏心拉伸(压缩)
解: 1. 力系简化 力P对竖直杆作用等效于作 用在杆轴线上一对轴力P和 一对作用在竖直平面内力 偶mz=Pe
FN P 2000 N, M z mz Pe 120 N m
mz P
n
e n
P
mz P
可见,竖直杆发生弯拉组合变形
材料力学作业及练习题参考答案(8、9章)

八章2题: 解:查槽钢表,每根槽钢,A=25.669 cm2,W=141 cm3, 则两根槽钢制成的梁:A=2A=51.538 cm2, W=2W=282 cm3 在B截面左侧的上边缘处: =-FN/A+M/W=-50×103/(51.538×10-4)+37.5×103/(282×10-6) =123.24×106 Pa, 即在该处为拉应力123.24 MPa ; 在B截面左侧的下边缘处: =-FN/A-M/W=-50×103/(51.538×10-4)-37.5×103/(282×10-6) =-142.72×106 Pa, 即在该处为压应力142.72 MPa ; 在B截面右侧的上边缘处: =M/W=37.5×103/(282×10-6)=132.98×106 Pa, 即在该处为拉应力132.98 MPa ; 在B截面右侧的下边缘处: =-M/W=-37.5×103/(282×10-6)=-132.98×106 Pa, 即在该处为压应力132.98 MPa。
材料力学第十二章 组合变形
T Fa T
Wp
按照Treca和Mises强度设计准则,
M Fl M
W
r3 2 4 2 [ ]
r4 2 3 2 [ ]
r3
M 2 T 2 [ ] W
r4
M 2 0.75T 2 [ ] W
12.4.2弯拉(压)扭组合强度计算
r3
M
N 2
4
2 T
[ ]
r4
M
N 2
3
2 T
[ ]
12.5例题编程
例12-1 小型压力机的铸铁框架如图12-6a所示。已知材料的许用拉应力[ t ] 30MPa , 许用压应力为[ c ] 160MPa 。试按立柱的强度确定压力机的最大许可压力 F 。立柱的截
面尺寸如图12-6b所示。
图12-6例12-1
已知:
[ t ] 30MPa
h1 50mm
求: F
[ c ] 160 MPa h2 150 mm
b1 150 mm a 350mm
b2 50mm
解:●建模 立柱受①力计:算F 立F柱N 横M截y 面面积A;
② 确定立柱横截面形心的位置; ③ 计算立柱横截面对形心轴 y 的惯性矩I y ; ④ 计算立柱任意横截面上的轴力FN 和弯矩M y ; ⑤ 计算在弯矩 M 作用下的最大拉应力和最大压应力 ; ⑥计算在轴力 FN 作用下的拉应力 ; ⑦按抗拉强度条件和抗压强度条件确定许可载荷。
#各矩形的面积。 #立柱横截面面积。 #立柱左表面距形心距离。 #立柱右表面距形心距离。
>
+A2*(h1+h2/2-z0)^2+b2*h2^3/12:
组合变形习题讲解[1]
第八章 组合变形习题讲解【习题5-29】解:矩形截面木榫头在力F 作用下可能发生挤压、剪切、横截面强度破坏,因此应分别满足这三方面的强度条件。
(1)挤压强度校核挤压面:BC 面,挤压面积:0.25b s A a=;挤压力:50b sF F k N==于是有,35010[]0.25b s b sb s b sF A a σσ⨯==≤⨯ 则20a m m≥(2)剪切强度校核剪切面:BE 和CD 面,剪切面积:0.25sA l=;剪切力:50sF F k N==于是有,35010[]0.25s ssF A l στ⨯==≤⨯则 200l m m ≥ (3)横截面强度校核1-1截面(如图(a )所示):由于只有轴力150N k N=,所以按照轴向拉压强度条件进行强度校核。
即:31115010[](2)0.25t N A a c σσ⨯==≤+⨯则 233.3a c m m+≥。
2-2截面:截面上存在轴力250N k N=,弯矩0.5()M F a c =+,所以应按照组合变形(偏心拉伸)来考虑。
根据2-2截面上的内力分量可知:危险点位于该截面的下边缘,应力为:题 5-29 图(a )题 5-29 图(b )233222250100.55010()[]10.250.256t N M a c A Wccσσ⨯⨯⨯⨯+=+=+≤⨯⨯⨯则146.9c m m≥【习题5-32】解:(1)外力分析以ABC 横梁为研究对象,受力图如图所示(a )。
列静力平衡方程()00.1120A B D x B D y M F F F F =⨯+⨯-⨯=∑其中,B D xB D yF F =。
则27.272B D xB D y F F k N==绘制ABC 横梁的受力简图如图(b )所示。
其中0.1 2.7272B D x M F k N m=⨯=⋅(2)内力分析根据横梁上作用的载荷可知,AE 段发生弯曲与拉伸的组合变形,EC 段发生平面弯曲变形。
刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(组合变形)【圣才出品】
(3)根据叠加原理,总正应力:
FN M z gy
A Iz
5.强度计算 危险点通常位于截面上距中性轴最远处。 (1)强度条件 危险点处于单向应力状态,强度条件 σmax≤[σ]。 当材料的许用拉应力和许用压应力不相等时,应分别建立杆件的抗拉和抗压强度条件: σtmax≤[σt],σcmax≤[σc]。 (2)强度计算步骤 ①作内力图,确定危险截面; ②计算截面应力并作其分布图,确定危险点;
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 8 章 组合变形
8.1 复习笔记
一、组合变形和叠加原理 组合变形是指构件在荷载作用下发生两种或两种以上的基本变形。在下述情况下组合变 形可用叠加法求解:①内力、应力、应变、变形等与外力之间成线性关系,即满足胡克定律; ②变形是小变形,可以用原始尺寸原理。
W
其中,W 为抗弯截面系数。 8.2 课后习题详解
8.1 试求图 8-2-1 所示各构件在指定截面上的内力分量。
9 / 67
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 8-2-1 解:(a)FN=Fcosθ,FS=Fsinθ,M=Facosθ+Flsinθ (b)FN=Fy,FSx=Fx,FSz=Fz,Mx=2Fy-FzL,Mz=FxL-3Fy,T=2Fx-3Fz (c)截面 1-1:FSy=F1/2,FSz=F2/2,Mz=F1a,My=F2a,T=-F1a/2;
图 8-1-1 3.内力分析 横截面上的内力包括:轴力 FN、弯矩 Mz 和剪力 FS。其中,由于剪力引起的切应力较 小,因此,一般不考虑。
2 / 67
圣才电子书 十万种考研考证电子书、题库视频学习平台
4.应力分析 (1)拉伸正应力:
材料力学第8章组合变形
B B
危险点:B
A
安全
8.17 图示皮带轮传动轴,传递功率P=7kW,转速n=200r/min。皮带
轮重量W=1.8kN。
(P286)
Fr
T
Ft
3F2
T/Nm 162.2
Mz/Nm
W 334.25
危险截面:
My/Nm 445.6
360 802.2
d=49mm
圆 截 面 折 杆 ABC 如 图 示 , A R=500mm , l=400mm ,
对称弯曲一定是平面弯 曲,而平面弯曲能保证 弯曲应力公式成立。
对称弯曲:截面有一个纵向对称 面,载荷作用在此对称面内。
无纵向对称面,载荷沿主惯轴依 然是平面弯曲。
求:max及自由端形心位移。
危险截面:根部。
Mz=Flcos My=Flsi
危险点:A、B
n
方位角:
A
B
F
F
Mz +
My + - -
z a
已 知 : l1=3m , l2=0.5m , []=160MPa , A=8010-4m2 ,
W=10010-6m3 , Wt=200 10-6m3 ,
试校核强度
作业 8-2
T1
400
T2 800
T
250
已知: T=3kN, T1=2T2,D=60cm, []=80MPa,试确定轴的直径。
D
Q2 Pz
F
F F
F
压弯
弯扭
拉弯扭
1
一.组合变形解法:
○ 将外载荷向轴线简化 ○ 组合变形分解为多个基本
变形 ○ 分别计算基本变形的各个
量 ○ 对应的量进行叠加
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学组合变形习题 L 1AL101ADB (3) 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案: (A) e=d; (B) e>d; (C) e越小,d越大; (D) e越大,d越小。 正确答案是______。 答案(C)
1BL102ADB (3) 三种受压杆件如图。设杆1、杆2和杆3中的最大压应力(绝对值)分别用
max1、max2和max3表示,现有下列四种答案:
(A)max1=max2=max3; (B)max1>max2=max3; (C)max2>max1=max3; (D)max2<max1=max3。 正确答案是______。
答案(C) 1BL103ADD (1) 在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案: (A)A点; (B)B点; (C)C点; (D)D点。 正确答案是______。
答案(C) 1AL104ADC (2) 一空心立柱,横截面外边界为正方形, 内边界为等边三角形(二图形形心重 合)。当立柱受沿图示a-a线的压力时,此立柱变形形态有四种答案: (A)斜弯曲与中心压缩组合; (B)平面弯曲与中心压缩组合; (C)斜弯曲; (D)平面弯曲。 正确答案是______。
答案(B) 1BL105ADC (2) 铸铁构件受力如图所示,其危险点的位置有四种答案: (A)①点; (B)②点; (C)③点; (D)④点。 正确答案是______。
答案(D) 1BL106ADC (2) 图示矩形截面拉杆中间开一深度为h/2的缺口,与不开口的拉杆相比,开口处 的最大应力的增大倍数有四种答案: (A)2倍; (B)4倍; (C)8倍; (D)16倍。 正确答案是______。
答案(C) 1BL107ADB (3) 三种受压杆件如图,设杆1、杆2和杆3中的最大压应力(绝对值)分别用
max1、max2和max3表示,它们之间的关系有四种答案: (A)max1<max2<max3; (B)max1<max2=max3; (C)max1<max3<max2; (D)max1=max3<max2。 正确答案是______。
答案(C) 1AL108ADB (3) 图示正方形截面直柱,受纵向力F的压缩作用。则当F力作用点由A点移至B点
时柱内最大压应力的比值maxA/maxB有四种答案: (A)1:2; (B)2:5; (C)4:7; (D)5:2。 正确答案是______。
答案(C) 1AL109ADC (2) 一空间折杆受力如图所示,则AB杆的变形有四种答案: (A)偏心拉伸; (B)纵横弯曲; (C)弯扭组合; (D)拉、弯、扭组合。 正确答案是______。 答案(A) 1AL110ADD (1) 图示矩形截面偏心受压杆发生的变形有下列四种答案: (A)轴向压缩和平面弯曲组合; (B)轴向压缩,平面弯曲和扭转组合; (C)轴向压缩和斜弯曲组合; (D)轴向压缩,斜弯曲和扭转组合。 正确答案是______。
答案(C) 1BL111BDC (2) 图示受压柱横截面上最大压应力的位置在____点处。
答案 切口段各横截面的b,e各点 1BL112BDD (1) 图示杆中的最大压应力的数值是____。
答案 最大压应力数值max2/Fbh 1AL113BDD (1) 图示立柱AB,其危险截面上的内力分量(不计剪力)是________; _________;___________。
答案 轴力NFF(拉);弯矩3yMFe;zMFl。 1BL114BDD (1) 偏心压缩实际上就是____和____的组合变形问题。 答案 轴向压缩 弯曲
1AL115CCA 短柱受力如图,试导出柱的底面上中性轴的方程。
答案 3()/12zIab 3()/12yIba 固定端截面上的内力 NFF (/2)zMFbg yMFh
任一点(y,z)处的应力 /()/(/2)/yzFAFhzIFbyIg
令max/6eb0得中性轴方程为226120aybhzab
3AL116CCA 证明:在矩形截面杆的两个端面上,当偏心拉力F作用在图示三分点上如1
点,或2点,···时,截面上max=2F/(bh),min=0。 答案 在h/3两边的点NFF /6MFh max//2/()FAMWFbh min0同理可证在b/3两边的点max2/()Fbh min0
1AL117CCC 证明当图示柱中去掉其中一个力F时,最大压应力值不变。
答案 两力作用时2/()Fbh 去掉一个F后/()(/6)/2/()FbhFhWFbhg 两者相等
1BL118DBC 具有切槽的正方形木杆,受力如图。求
(1)m-m截面上的maxt和maxc;
(2)此maxt是截面削弱前的t值的几倍? 答案 (1)2max()//8/tFAMWFa 2max()//4/cMWFAFa
(2)max()/8tt
1BL119DBB 结构如图,折杆AB与直杆BC的横截面面积为A=422cm,yzWW=4203cm [σ]=100Mpa 。求此结构的许可载荷[P]。
答案 竖杆横截面上的内力2/3NFF 24/3BMFF max()//tNFAMW
30FKN 30FKN
1BL120DBC 矩形截面杆受轴向力F的作用,若在杆上开了个图示槽口,已知F=60KN, a=60mm。作出Ⅰ-Ⅰ,Ⅱ-Ⅱ截面上的应力分布图。
答案Ⅰ-Ⅰ截面 11/16.7NFAMpa Ⅱ-Ⅱ截面 max222()//66.7tNFAMWMPa
max222()//33.3cNFAMWMPa
1BL121DBB 矩形截面木接头受力如图, 已知顺纹许用挤压应力10bsMPa,
[τ]=1MPa,t=6MPa,c=10MPa。求接头尺 寸a和c。
答案 3(5010)/(250)l 200lmm 3(5010)/(250)bsbsa 20amm
332
max()(5010)/(250)5010()/2/(250/6)ttcacc
147cmm 取200lmm,a=20mm,c=147mm
1BL122DBD 图示偏心受压杆。试求该杆中不出现拉应力时的最大偏心距。 答案 //0tyFeWFA 即2max/1/(6)/0tFehbFbh 由此得max/6eb
1AL123DBC 矩形截面杆受力如图,求固定端截面上A、B、C、D各点的正应力。
答案 max2222()//294.9cNcFAMWKPa/2.5NNFAMPa(拉) /2.5MZZZMWMPa (B.C拉,A.D压)
/6MyyyMWMPa (C.D拉,A.B压)
2.52.561BMPa 2.52.566AMPa 2.52.5611CMPa 2.52.566DMPa
1BL124DBC 已知一矩形截面梁,高度h=100mm,跨度l=1m。梁中点受集中力F, 两端受拉力S=30KN。此拉力作用在横截面的对称轴y上,距上表面a= 40mm。若横截面内最大正应力与最小正应力之比为5/3。试求F值。 答案 偏心距/210pyhamm 最大弯矩在跨中央截面内max/4pMFlSy 轴力NFS
22maxmin//()6(/4)/()//()6(/4)/()5/3NpNpFbhFlSybhFbhFlSybh
F=1.7KN
1BL125DBA 偏心拉伸杆,弹性模量为E,尺寸、受力如图所示。试求: ⑴最大拉应力和最大压应力的位置和数值; ⑵AB长度的改变量。
答案 (1)最大拉应力在AB线上,最大压应力在CD线上。 22max(/2)/(/6)(/2)/(/6)/()7/()tFbhbFhhbFbhFbh
max3/()3/()/()5/()cFbhFbhFbhFbh (2)/7/()ABllEFlbhE
1AL126DCA 图示矩形截面梁。已知b、h、l、E和F。试求AB纤维的伸长量l。
