类比探究(讲义及答案)
中考数学类比探究(一)——直角、平行(习题及答案).
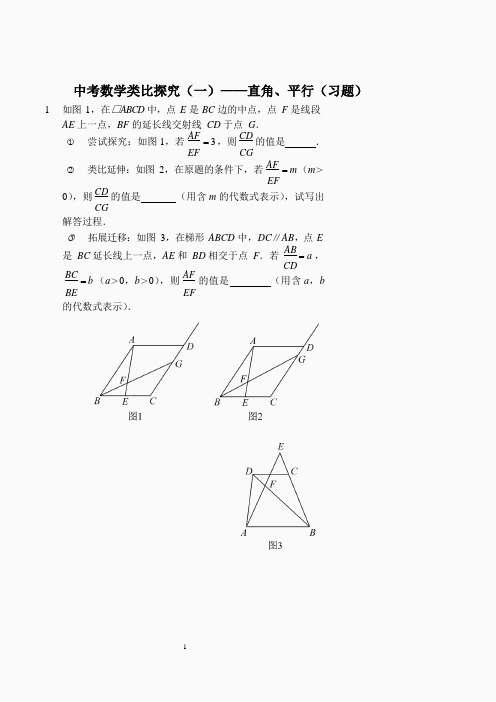
中考数学类比探究(一)——直角、平行(习题)1. 如图 1,在□ABCD 中,点 E 是 BC 边的中点,点 F 是线段AE 上一点,BF 的延长线交射线 CD 于点 G . (1) 尝试探究:如图 1,若 AF = 3 ,则 CD 的值是 .EF CG(2) 类比延伸:如图 2,在原题的条件下,若 AF = m (m > EF0),则 CD 的值是 (用含 m 的代数式表示),试写出CG解答过程.(3) 拓展迁移:如图 3,在梯形 ABCD 中,DC ∥AB ,点 E是 BC 延长线上一点,AE 和 BD 相交于点 F .若 AB = a , CD BC = b (a >0,b >0),则 AF 的值是 (用含 a ,bBE EF的代数式表示).2.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°.【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P,边EF 与边BC 交于点Q.【探究】在旋转过程中,(1)如图2,当CE=1时,EP 与EQ 满足怎样的数量关系?EA并给出证明.(2)如图3,当CE= 2 时,EP 与EQ 满足怎样的数量关系?EA并给出证明.(3)根据你对(1),(2)的探究结果,试写出当CE=m时,EAEP 与EQ 满足的数量关系式为.3.在△ABC 中,已知D 是BC 边的中点,G 是△ABC 的重心,过点G 的直线分别交AB,AC 于点E,F.(1)如图1,当点E 与点B 重合时,AG=GD(2)如图2,当EF∥BC 时,求证:BE+CF.= 1 .AE AF(3)如图3,当EF 和BC 不平行,且点E,F 分别在线段AB,AC 上时,(2)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.提示:①过点 A 作AM∥BC,交EF 于点M,直线FE 交BC 于N;②NB+NC=2ND.(4)如图4,当点E 在AB 的延长线上或点F 在AC 的延长线上时,(2)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.【参考答案】 1. 1 3 ( ) ; 2(2) m ;2(3) a b .2. (1)EP =EQ ,证明略;(2) EP = 1 2EQ ,证明略; (3) EP = 1 EQ . m3. (1)2;(2)证明略;(3)(2)中的结论仍然成立,证明略;(4)(2)中的结论不成立,理由略.。
探究类比归纳专题(含答案)

天天家教中心数学内部讲义
探究类比归纳(2012/5/26)
27. (2011年青海,27,10分)认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.
A AA
O
B CO
CDB图11-2 CBDE图11-1O
图11-3
探究1:如图11-1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,∠BOC与∠A 的关系为
探究2:如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A 有怎样的关系?请说明理由.
探究3:如图11-3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: .
25.(11·南平)(12分)
(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.
(2)类比探究:
如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.
E E
(11·辽阜新)如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PE=EB,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理寒假班暑假班周末班作业班 VIP一对一。
相似类比探究(2015)

相似之类比探究(讲义)一、知识点睛●类比探究是一类共性条件与特殊条件相结合,由特殊情形到一般情形(或由简单情形到复杂情形)逐步深入,解决思想方法一脉相承的综合性题目,常以几何综合题为主.●解决类比探究问题的通常思路解决类比探究问题的核心思想是类比(照搬),类比上一问的思路方法(如照搬字母,照搬辅助线等).探究变化过程中的不变特征(如常见结构),是类比的前提.●类比探究中的常见结构平行结构:由比例找平行,构造A字型或X型;直角结构:由斜置的直角通过作垂线构造相似三角形.二、精讲精练1.如图1,D是△ABC的边BC上一点,过点D的一条直线交BA于点F,交CA的延长线于点E.若BD=CD,BF=2AF,求(1)(2)如图2,D是△ABC的边BC上一点,过点D的一条直线交BA于点F,交CA的延长线于点E.若BD=CD,BF=mAF,求(用含m的代数式表示).(3)如图3,D是△ABC的边BC上一点,过点D的一条直线交AB的延长线于点F,交AC于点E.若BD=nCD,BF=mAF,求(用含m,n的代数式表示).2.善于学习的小敏查资料知道:对应角相等,对应边成比例的两个梯形,叫做相似梯形.他想到“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”,提出如下两个问题.图 1 图 2 图 3(1)问题一:平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似?从特殊情形入手探究.假设梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,MN是中位线,如图1.根据相似梯形的定义,能够证明梯形AMND与梯形ABCD不相似;由此推广到一般结论:平行于梯形底边的直线截两腰所得的梯形与原梯形是否相似?问题二:平行于梯形底边的直线截两腰所得的两个小梯形是否相似?(1)从特殊平行线入手探究.能够得到梯形的中位线截两腰所得的两个小梯形不相似;(2)从特殊梯形入手探究.假设梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,点P,Q在梯形的两腰上,且PQ∥BC,如图2,则当梯形APQD与梯形PBCQ相似时,求AP 的值?(3)一般结论:对于任意梯形(如图3),一定存在平行于梯形底边的直线PQ,使截得的两个小梯形相似.不妨设梯形ABCD中,AD=a,BC=b,AB=c,CD=d,PQ∥BC,若两个小梯形相似,求3.(1)如图,D是△ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.若BD=2CD,CF=mAF,求(2)如图,D是△ABC的边BC上一点,过点D的一条直线交AC的延长线于点F,交AB 于点E.若BD=aCD,CF=bAF,求图 24.如图所示,在形状和大小不确定的△ABC 中,BC=6,E ,F 分别是AB ,AC 的中点,P 在EF 或EF 的延长线上,BP 交CE 于D ,Q 在CE 上且BQ 平分∠CBP ,设BP=y ,PE=x . (1)当时,求y 与x 之间的函数关系式为(2)当,其他条件不变时,求y 与x 之间的函数关系式(3)(上接第3,4题)当(n 为不小于2的常数),其他条件不变时,求y与x 之间的函数关系式5.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.原题:如图1,在□ABCD 中,点E 是BC 边的中点,点F 是线段AE 上一点,BF 的延长线交射线CD 于点G ,若3AF EF=,求CDCG 的值. (1)尝试探究:在图1中,过点E 作EH ∥AB 交BG 于点H ,则AB 和EH 的数量关系是_____________,CG 和EH 的数量关系是_____________,CDCG的值是_________. (2)类比延伸:如图2,在原题的条件下,若AF m EF=(m >0),则CDCG 的值是_________(用含m 的代数式表示),试写出(3)拓展迁移:如图3,在梯形ABCD 中,DC ∥AB ,点E 是BC 的延长线上一点,AE 和BD 相交于点F .若AB a CD =,BC b BE=(a >0,b >0),则AFEF 的值是________(用含a ,b的代数式表示).第4题图图3BFECDA6.数学课上,魏老师出示图1和下面框中条件:(1)①当点C 与点F 重合时,如图2所示,可得AMDM的值为___________; ②在平移过程中,AMDM的值为___________(用含x 的代数式表示).(2)将图2中的三角板ABC 绕点C 逆时针旋转,原题中的其他条件保持不变.当点A 落在线段DF 上时,如图3所示,请计算AMDM的值. (3)将图1中的三角板ABC 绕点C 逆时针旋转m 度,090m ≤,原题中的其他条件保持不变,如图4所示,请计算AMDM的值(用含x 的代数式表示).如图1,两个等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上,∠ABC =∠DEF =90°,AB =1,DE =2.将直线EB 绕点E 逆时针旋转45°,交直线AD 于点M .将图1中的三角板ABC 沿直线l 向右平移,设C ,E 两点间的距离为x .图2MDABl(C )F E图1DMAB FlC E图4F lBA MDEC 图3DM AB l(C )F E7.如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD 的顶点A 重合,三角板的一边交CD 于点F ,另一边交CB 的延长线于点G .(1)求证:EF =EG .(2)如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由. (3)如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”, 且使三角板的一边经过点B ,其他条件不变,若AB =a ,BC =b ,求EFEG的值.8.如图1,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,点E 在AC 上,BE 交CD 于点G ,EF ⊥BE 交AB 于点F ,AC =mBC ,CE =nEA (m ,n 为实数).试探究线段EF 与EG 的数量关系.(1)如图2,当m =1,n =1时,EF 与EG 的数量关系是____________.(2)如图3,当m =1,n 为任意实数时,EF 与EG 的数量关系是______________,并证明你的结论.(3)如图1,当m ,n 均为任意实数时,EF 与EG 的数量关系是______________.(写出关系式,不必证明)FD A B图1GC E图2G BA D FEC图3C GBA D F E【参考答案】1.(1)AB =3EH ;CG =2EH ;32(2)2m;提示:过点E 作EH ∥AB 交BG 于点H (3)ab ;提示:过点E 作EH ∥AB 交BD 的延长线于点H 2.(1)①1;②2x(2)提示:过点B 作BE 的垂线交EM 的延长线于点G ,连接AG , 证AG ∥DE ,得△AMG ∽△DME ,所以212AM AG DM DE === GDE (C )F BAMl(3)提示:过点B 作BE 的垂线交EM 的延长线于点G ,连接AG , 证AG ∥DE ,得△AMG ∽△DME ,所以2AM AG xDM DE ==. G DE C FBAMl3.(1)提示:证明Rt △FED ≌Rt △GEB (ASA),所以EF =EG ; (2)成立.理由如下: 证明:如图,I HEAB CD FG过点E 分别作BC ,CD 的垂线,垂足分别为H ,I , 证明Rt △FEI ≌Rt △GEH (ASA),所以EF =EG ; (3)解:如图,MN G (B )FD CAE过点E 分别作BC ,CD 的垂线,垂足分别为M ,N , 证明△GME ∽△FNE ,所以 EF bEG a. 4. (1)EF =EG . (2)EF =1nEG ;作EM ⊥AB 于点M ,EN ⊥CD 于点N N M ECFAB G(3)EF =1mnEG .I H C EF DA BG相似之类比探究(每日一题)1. 在△ABC 中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交AD 于点O ,某学生在研究这一问题时,发现了如下的事实:(1)当11211==+AE AC 时,有22321==+AO AD ; (2)当11312==+AEAC 时,有22422==+AO AD ; (3)当11413==+AEAC 时,有22523==+AO AD ; (4)当11=+AEACn时,参照上述研究结论,请你猜想用n 表示AO AD 的一般结论,并给出证明(其中n 是正整数).2.在图1至图3中,直线MN 与线段AB 相交于点O ,∠1=∠2=45°. (1)如图1,若AO =OB ,请写出AO 与BD 的数量关系和位置关系.(2)将图1中的MN 绕点O 顺时针旋转得到图2,其中AO =OB .求证:AC =BD ,AC ⊥BD . (3)将图2中的OB 拉长为AO 的k 倍得到图3,求BDAC的值.第1题图OE D CBAABD OM NC 1221NM O D BA21C NMO D BA图1图2图33.已知:线段OA ⊥OB ,点C 为OB 中点,D 为线段OA 上一点.连接AC ,BD 交于点P .(1)如图1,当D 为OA 中点时,求APPC 的值; (2)如图2,当AD :DO =1:m 时,求APPC的值;(3)如图3,把题目中“点C 为OB 中点”改为“BC :CO =1:n ”,当AD :DO =1:m 时,直接写出APPC的值. ABC DOPPODC BA PODC BA 图1图2图34.(1)如图1,已知正方形ABCD ,E 是AD 上一点,F 是BC 上一点,G 是AB 上一点,H 是CD 上一点,线段EF ,GH 交于点O ,∠EOH =∠C .求证:EF =GH .(2)如图2,若将“正方形ABCD ”改为“矩形ABCD ”,且AD =mAB ,其他条件不变,探索线段EF 与线段GH 的数量关系并加以证明.(3)根据前面的探究,你能否将本题推广到一般的平行四边形情况?若能, 写出推广命题,画出图形,并证明;若不能,说明理由.A BCD EFG HOOHGF EDCBA图1图25.在矩形ABCD 中,E 是BC 的中点,点F 在BC 的延长线上,CM 平分∠DCF ,连接AE ,作EM ⊥AE 交CM 于点M .(1)如图1,当AB =BC 时,请判断AE 与EM 的数量关系并证明; (2)如图2,当AB =nBC 时,请判断AE 与EM 的数量关系并证明; (3)如图3,把题目中“E 是BC 的中点”改为“BE =mEC ”,当AB =nBC 时, 请判断AE 与EM 的数量关系并证明.图3图2图1ABCDFE M ABCDFE MME FDCBA【参考答案】1.解:当11=+AEAC n时,2=2AOAD n+FOED CBA证明如下:过点A作BC的平行线交BE的延长线于点F∵11=+AEAC n∴1AEEC n=∵AF∥BC∴△AEF∽△CEB,△AOF∽△DOB∴1AF AEBC EC n==,AF AOBD OD=∵D为BC的中点∴BD=DC∴2212AF AF AFBD BC nBC===∴2=AOOD n,即:2=2AOAD n+2.解:(1)由题意知∠BOD=∠1=45°,此时△OBD是等腰直角三角形∴OB=BD,OB⊥BD∴AO=BD,AO⊥BD(2)如图2,EFC21NMODBA图2过点B作BE//AC交CD于点E,延长AC,DB交于点F.∴∠DEB=∠DCF=∠1=45°,∠ACO=∠BEO,∠OAC=∠OBE∴△BED,△FCD是等腰直角三角形∴BD=BE,AC⊥BD∵AO=BO∴△AOC≌△BOE,∴AC=BE∴AC=BD,AC⊥BD(3)如图3,EF21C NMO D B A图3过点B 作BE //AC 交CD 于点E ,延长AC ,DB 交于点F .∴ ∠DEB =∠DCF =∠1=45°,∠ACO =∠BEO ,∠OAC =∠OBE ∴ △BED 、△FCD 是等腰直角三角形,且△AOC ∽△BOE ∴ BD =BE ,BE OBAC OA= ∵ OB 是OA 的k 倍∴ BE AC =k ∴BDk AC= 3.解:(1)如图1,E 图1BPODC A过点D 作DE ∥OB 交AC 于点E ,∠ADE =∠O ,∠AED =∠ACO ∴ △ADE ∽△AOC ∴12AE AD DE DE AC AO OC BC ==== 又∵ DE ∥OB ∴ ∠EDP =∠B ,∠DEP =∠BCP ∴ △DEP ∽△BCP ∴12EP DE PC BC ==∴ APPC=2 (2)如图2,E图2OACDPB过点D作DE∥OB交AC于点E,∠ADE=∠O,∠AED=∠ACO∴△ADE∽△AOC∴11AE AD DE DEAC AO OC BC m====+,1AE ADEC DO m==∵DE∥OB∴∠EDP=∠B,∠DEP=∠BCP∴△DEP∽△BCP∴11 EP DEPC BC m==+∴12EPEC m=+设AE=k,则EC=mk∴EP=2mkm+∴AP=AE+EP=2222mk mk kkm m++=++,PC=EC-EP=222mk m k mkmkm m+-=++∴AP PC =2 m(3)1 nm +4.证明:(1)如图1,QNMR图1OH GFE DC BA过点F作FM⊥AD于M,过点G作GN⊥CD于N则FM=GN=CD=BC,且GN⊥FM,设它们的垂足为Q,EF,GN交于点R∵∠EOH=∠GOF=∠C=90°,∴∠OGR=90°-∠GRO=90°-∠QRF=∠OFM.∵∠GNH=∠FME=90°,FM=GN,∴△GNH≌△FME.∴EF=GH(2)GH=mEF证明如下:如图2,MNRQ图2AB CDEFGHO过点F作FM⊥AD于M,过点G作GN⊥CD于N,设EF,GN交于点R,GN,MF交于点Q ∵∠EOH=∠GOF=∠C=90°,∴∠OGR=90°-∠GRO=90°-∠QRF =∠OFM.∵∠GNH=∠FME=90°,∴△GNH∽△FME.∴GH ADEF AB==m,即:GH=mEF(3)A E M DHNCQORFGB如图,已知平行四边形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD 上一点,线段EF,GH交于点O,∠EOH=∠C,AD=mAB,则GH=mEF.证明:如图,过点F作FM⊥AD于M,过点G作GN⊥CD于N,设EF,GN交于点R、GN,MF交于点Q,在四边形MQND中,∠QMD=∠QND=90°∴∠ADC+∠MQN=180°.∴∠MQN=∠C=∠EOH=∠GOF.∵∠ORG=∠QRF,∴∠HGN=∠EFM.∵∠FME=∠GNH=90°,∴△GNH∽△FME.∴GH GN EF MF=∵AB⋅GN=AD⋅MF∴GN ADFM AB==m∴GHmEF=,即:GH=mEF5.解:(1)AE=EM,理由如下:如图1,G图1ME FDCBA取AB的中点G,连接GE.∵∠AEM=90°∴∠MEC+∠AEB=90°∵∠B=90°∴∠EAG+∠AEB=90°∴∠EAG=∠MEC∵点E,G分别为正方形ABCD的边BC和AB的中点∴AG=EC ∵△BGE是等腰直角三角形∴∠AGE=135°∵CM平分∠DCF∴∠ECM=135°∴△AEG≌△EMC∴AE=EM (2)当AB=nBC时,AE=(2n-1)EM,理由如下:如图2,G图2AB CDFEM在AB上截取BG=BE,连接GE,则△BGE为等腰直角三角形∴∠BGE=45°∴∠AGE=∠ECM=135°∵∠AEM=90°∴∠MEC+∠AEB=90°∵∠B=90°∴∠EAG+∠AEB=90°∴∠EAG=∠MEC∴△AEG∽△EMC∴AE AG EM EC=∵AB=nBC,BC=2BE=2EC,BG=BE∴AG+BG=2nEC∴AG=(2n-1)EC∴AE AGEM EC==(2n-1)∴AE=(2n-1)EM(3)当AB=nBC,BE=mEC时,AE=(mn+n-m)EM,理由如下:如图3,ME FDCBA图3G在AB上截取BG=BE,连接GE,则△BGE为等腰直角三角形∴∠BGE=45°∴∠AGE=∠ECM=135°∵∠AEM=90°∴∠MEC+∠AEB=90°∵∠B=90°∴∠EAG+∠AEB=90°∴∠EAG=∠MEC∴△AEG∽△EMC∴AE AG EM EC=∵BE=mEC∴BC=BE+EC=(m+1)EC∵AB=nBC,BG=BE∴AG+BG=n(m+1)EC∴AG+mEC=n(m+1)EC∴AG=(mn+n-m)EC∴AE AGEM EC=(mn+n-m)∴AE=(mn+n-m)EM相似之类比探究(随堂测试)1. 已知:在Rt △ABC 中,∠ABC =90°,∠A =30°,点P 在AC 上,且∠MPN =90°.当点P 为线段AC 的中点,点M ,N 分别在线段AB ,BC 上时(如图1),过点P 作PE ⊥AB 于点E ,PF ⊥BC 于点F ,可证Rt △PME ∽Rt △PNF ,得出PN =3PM (不需证明).当PC =2PA ,点M ,N 分别在线段AB ,BC 或其延长线上,如图2、图3这两种情况时,请写出线段PN ,PM 之间的数量关系,并任选一种情况给予证明.【参考答案】如图2,如图3中都有结论:PN =6PM .理由略HG AN MBPCI QC MPANB图1AEFMCN PB 图2CPBMN A图3B NAPMC2.如图1,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D ,点O 是AC 边上一点,连接BO ,交AD 于点F ,OE ⊥OB 交BC 于点E . (1)求证:△ABF ∽△COE ; (2)如图2,当O 为边AC 中点,2AC AB =时,求OFOE的值; (3)如图3,当O 为边AC 中点,AC n AB =时,请直接写出OFOE的值.3.如图,在△ABC 中,∠A =60°,BD ,CE 分别是AC ,AB 上的高.求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;(3)BC =2ED .DCAEB第3题图【参考答案】1. 原题:12;(1)1m ;(2)1ab; 2. 解:(1)略(2)2OFOE=. 提示:如图,过点O 作OG ∥AB 交BC 于点G ,证明△AOF ∽△GOEGDEOCFBA(3)OFn OE=。
类比探究之类比探索(一)(含答案)

类比探究之类比探索(一)一、单选题(共6道,每道16分)1.问题情境:在特殊四边形的复习课上,老师出了这样一道题:如图2,在菱形ABCD中,E,F,G,H分别为AB,BC,CD,DA边上的动点,连接EG,FH相交于点O,若∠HOE=∠D,试探究:EG与FH的数量关系.经过小组讨论后,小聪建议分以下两步进行:(1)特殊情况,探索结论当菱形ABCD是正方形时,如图1,EG与FH有怎样的数量关系呢?小聪想:要求EG与FH的数量关系,就要构造全等三角形或相似三角形,于是,分别过点G,H作GM⊥AB于点M,HN⊥BC于点N,证明△GME≌△HNF,从而得到EG=FH.则判定△GME≌△HNF使用的条件可能是( )A.HLB.ASA或AASC.SASD.AAA答案:B解题思路:试题难度:三颗星知识点:中考数学中的类比探究2.(上接第1题)(2)特例启发,解答题目由此猜想:原题中EG与FH的数量关系是EG=FH,经过思考小聪给出了两种方案:方案一:分别过点G,H作GM⊥AB于点M,HN⊥BC于点N,即可证明结论;方案二:过点G作GM∥AD,交AB于点M,过点H作HN∥AB,交BC于点N,即可证明结论.下列说法正确的是( )A.方案一正确,方案二错误B.方案一错误,方案二正确C.两种方案都正确D.两种方案都错误答案:A解题思路:试题难度:三颗星知识点:全等三角形的判定与性质3.(上接第1,2题)(3)反思提升,拓展延伸课后小聪对本题进行了反思,提出如下猜想:将题目中的菱形ABCD改为平行四边形ABCD,如图3,若AB=a,AD=b,其他条件不变,则EG与FH的数量关系为( )A.EG=FHB.C. D.无法确定答案:B解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究4.如图1,在△ABC中,D是BC边上的点(不与点B,C重合),连接AD.问题引入:(1)当D是BC边的中点时,;当D是BC边上任意一点时,.(用图中已有线段表示)A.1:1,BD:CDB.1:2,BD:BCC.2:1,BC:BDD.1:2,CD:BC答案:B解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究5.(上接第4题)探索研究:(2)如图2,在△ABC中,O是线段AD上一点(不与点A,D重合),连接OB,OC,则.(用图中已有线段表示)A.OA:CDB.OA:ODC.OD:ADD.OA:AD答案:C解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究6.(上接第4,5题)拓展应用(3)如图3,O是线段AD上一点(不与点A,D重合),连接BO并延长,交AC于点F,连接CO并延长,交AB于点E,则的值为( )A.1B.2C.3D.无法确定答案:A解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究。
综合复习——类比探究(人教版)(含答案)

学生做题前请先回答以下问题问题1:解决类比探究问题的一般方法:(1)根据题干条件,结合____________先解决第一问;(2)用解决_______的方法类比解决下一问,整体框架照搬.问题2:整体框架照搬包括____________,____________,____________.问题3:“三角形全等”的辅助线:见中线,要________,________之后___________.问题4:当见到线段的______________考虑截长补短,构造全等或等腰转移____、转移____,然后和_________重新组合解决问题.问题5:当见到线段的______________考虑截长补短,截长补短的作用是把_________________________转化成_____________________.综合复习——类比探究(人教版)一、单选题(共7道,每道14分)1.如图1,△ABC的边BC在直线上,AC⊥BC,且AC=BC;△EFP的边FP也在直线上,边EF与边AC重合,且EF=FP.如图1,易证AB=AP,且AB⊥AP.(1)将△EFP沿直线向左平移到图2的位置时,EP交AC于点O,连接AP,BO.则在证明BO与AP所满足的数量关系及位置关系时,需要证明的全等三角形是( )A.△ABC≌△EPFB.△BAO≌△BPOC.△BCO≌△ACPD.△BPO≌△APO答案:C解题思路:(1)如图,延长BO交AP于点H,由题意可知,△ABC和△EFP均为等腰直角三角形,∴∠EPF=45°,∴△OPC为等腰直角三角形,∴OC=PC,∴△ACP≌△BCO(SAS),∴AP=BO,∠CAP=∠CBO,又∵∠AOH=∠BOC,∴∠AHO=∠BCO=90°,∴AP⊥BO,即BO=AP,且BO⊥AP.故选C试题难度:三颗星知识点:类比探究问题2.(上接第1题)(2)将△EFP沿直线继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.证明BO与AP的数量关系和位置关系时,证明三角形全等的依据是( )A.SSSB.SASC.ASAD.AAS答案:B解题思路:(2)首先对比第1问的图形和问法,可辨识这是一道类比探究问题,类比探究问题的核心是类比,类比分为三个层次:类比字母,类比辅助线,类比思路.本题中类比第1问的辅助线,如图,延长OB交AP于点H,由题意可知,△ABC和△EFP均为等腰直角三角形,∴∠EPF=45°,∴△OPC为等腰直角三角形,∴OC=PC,∴△ACP≌△BCO(SAS),∴AP=BO,∠CAP=∠CBO,又∵∠AOH=∠BOC,∴∠AHO=∠BCO=90°,∴AP⊥BO,即BO=AP,且BO⊥AP.故选B试题难度:三颗星知识点:类比探究问题3.如图1,在正方形ABCD和正方形CGEF(CG BC)中,点B,C,G在同一直线上,点M 是AE的中点.(1)探究线段MD,MF的位置关系,并证明.解题思路:(1)小明猜测MD⊥MF,看到图1中M是AE的中点,并且AD∥EF,考虑延长DM交EF于点H,如下图,先利用全等三角形的判定定理ASA,证明_____,由全等的性质可以得到_____,所以CD=EH,进而可以得到FD=FH,在等腰△DFH中,由等腰三角形三线合一可以得到_____,从而证明结论.以上横线处,依次所填正确的是( )①△ADM≌△EHM;②△FDM≌△FHM;③DM=HM,AD=HE;④FD=FH;⑤MF⊥DH;⑥FM平分∠DFH.A.①③⑥B.②④⑥C.①③⑤D.①④⑤答案:C解题思路:结合题意,由AD∥EF,可得:∠MAD=∠MEH,∵M是AE中点,∴AM=EM,∵∠AMD=∠EMH,∴△ADM≌△EHM(ASA),故第一个空填①;∴DM=HM,AD=HE,即第二个空填③;∵FC=EF,AD=CD,∴FD=FH,∴△DFH是等腰三角形,∵M是DH的中点,∴MF⊥DH(等腰三角形三线合一),即:MF⊥MD,第三个空填⑤.综上,故选C试题难度:三颗星知识点:类比探究问题4.(上接第3题)(2)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边BC在同一条直线上,如图2,其他条件不变,(1)中得到的结论是否发生改变,写出猜想并加以证明.解题思路:(2)小明类比第(1)问的解法,看到图2中M是AE的中点,并且AD∥EC,考虑延长DM交BE于点H,连接FD,FH,如下图,先证明____,由全等的性质可以得到____.因为CD=AD,所以CD=HE,结合题目中的条件FC=FE,∠DCF=∠FEH=45°,又可以利用判定定理____证得____,得到FD=FH,在等腰△DFH中,由等腰三角形三线合一,得到MF⊥DH,从而证明结论.以上横线处,依次所填正确的是( )①△ADM≌△EHM;②△DCF≌△HEF;③DM=HM,AD=HE;④FD=FH;⑤SSA;⑥ASA;⑦SAS.A.①③⑤②B.②③⑤①C.②④⑦①D.①③⑦②答案:D解题思路:本题解题思路类比上一题,首先要证明△ADM≌△EHM,然后由全等可以得到DM=HM,AD=HE,即前两个空填①③,接下来需要证明△DCF≌△HEF,判定定理是SAS,即后两个空填⑦②.综上,故选D试题难度:三颗星知识点:类比探究问题5.如图,点E是长方形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,BD=5,点P 是直线EC上的一点,且PQ⊥BC于点Q,PR⊥BD于点R.(1)如图1,当点P在线段EC上时,PR+PQ的值为( )A. B.C. D.答案:C解题思路:如图,连接BP,过点C作CF⊥BD于点F.△BCE的面积可以直接通过面积公式得到(以BE为底,CF为高),也可以通过两个三角形面积之和得到(△BPE与△BPC),即:,∵,∴,∴,∵,,,∴,∵,∴,即:.故选C试题难度:三颗星知识点:类比探究问题6.(上接第5题)(2)如图2,当点P为线段EC延长线上的任意一点时,其他条件不变,则PR与PQ之间的数量关系为( )A. B.C. D.答案:D解题思路:如图,连接BP,过点C作CF⊥BD于点F.△BCE的面积可以直接通过面积公式得到(以BE为底,CF为高),也可以通过两个三角形面积之差得到(△BPE与△BPC),即:,∵,∴,∴,∵,,,∴,∵,∴,即:.故选D试题难度:三颗星知识点:类比探究问题7.如图1所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上.连接BE,CD,M,N分别为BE,CD的中点,容易证明△AMN是等腰三角形.在图1的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图2所示的图形,则在图2中下列说法不正确的是( )A.△ADC≌△AEBB.△CAN≌△BAMC.∠CAM=∠NAED.AM=AN答案:C解题思路:∵AC=AB,AD=AE,∠CAD=∠BAE,∴△ADC≌△AEB.故选项A正确.由△ADC≌△AEB得CD=BE,∠ACN=∠MBA,∵M,N分别为BE,CD的中点,∴CN=BM,又∵AC=AB,∴△CAN≌△BAM.故选项B正确.由△CAN≌△BAM得AM=AN,故选项D正确.要证得∠CAM=∠NAE,只需证明∠CAN=∠EAM,而∠CAN不一定等于∠EAM,故选项C错误.综上,故选C试题难度:三颗星知识点:类比探究问题。
【中考数学必备专题】类比探究之图形运动(含答案)[1]
![【中考数学必备专题】类比探究之图形运动(含答案)[1]](https://img.taocdn.com/s3/m/eb50796e7e21af45b307a818.png)
类比探究之图形运动一、探究题(共2道,每道50分)1.已知:在中,,动点绕的顶点逆时针旋转,且,连结.过、的中点、作直线,直线与直线、分别相交于点、.(1)如图1,当点旋转到的延长线上时,点恰好与点重合,证明(提示取的中点,连结、,根据三角形中位线定理和平行线的性质即可证明).(2)当点旋转到图2或图3中的位置时,与有何数量关系?请分别写出猜想,并证明.答案:图2:∠AMF=∠ENB图3:∠AMF+∠ENB=180°证明:如图2,取AC的中点H,连接HE、HF∵F是DC的中点,H是AC的中点∴HF∥AD,HF=AD∴∠AMF=∠HFE同理,HE∥CB,HE=CB,∴∠ENB=∠HEF又∵∴HF=HE∴∠HEF=∠HFE∴∠ENB=∠AMF如图3,取AC的中点H,连接HE、HF∵F是DC的中点,H是AC的中点∴HF∥AD,HF=AD∴∠AMF+∠HFE=180°同理,HE∥CB,HE=CB,∴∠ENB=∠HEF又∵∴HF=HE∴∠HEF=∠HFE∴∠AMF+∠BNE=180°解题思路:两题思路基本相同,都需要作出两条辅助线,两次运用中位线定理解答.试题难度:三颗星知识点:平行线的性质2.正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.答案:(1)AP=EF,AP⊥EF,理由如下:连接AC,则AC必过点O,延长FO交AB于M;∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,∴四边形OECF是正方形,∴OM=OF=OE=AM,∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,∴△AMO≌△FOE,∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,故AP=EF,且AP⊥EF.(2)题(1)的结论仍然成立,理由如下:延长AP交BC于N,延长FP交AB于M;∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,∴四边形MBEP是正方形,∴MP=PE,∠AMP=∠FPE=90°;又∵AB-BM=AM,BC-BE=EC=PF,且AB=BC,BM=BE,∴AM=PF,∴△AMP≌△FPE,∴AP=EF,∠APM=∠FPN=∠PEF∵∠PEF+∠PFE=90°,∠FPN=∠PEF,∴∠FPN+∠PFE=90°,即AP⊥EF,故AP=EF,且AP⊥EF.(3)题(1)(2)的结论仍然成立;如图,延长AB交PF于H,证法与(2)完全相同.解题思路:(1)连接AC,则AC必过O点,延长FO交AB于M,由于O是BD中点,易证得△AOM≌△FOE,则AO=EF,且∠AOM=∠FOC=∠OFE=45°,由此可证得AP⊥EF.(2)方法与①类似,延长FP交AB于M,延长AP交BC于N,易证得四边形MBEP是正方形,可证得△APM≌△FEP,则AP=EF,∠APM=∠FEP;而∠APM=∠FPN=∠PEF,且∠PEF与∠PFE互余,故∠PFE+∠FPN=90°,由此可证得AP⊥EF,所以(1)题的结论仍然成立.(3)解题思路和方法同(2).试题难度:四颗星知识点:全等三角形的判定与性质。
类比探究专题(学习资料)
类比探究专题例1 如图1,在等腰直角△ABC 和等腰直角△CDE 中,CD>BC ,点C ,B ,D 在同一直线上,M 是AE 的中点,易证MD ⊥MB ,MD=MB .(1)如图2,将图1中的△CDE 绕点C 顺时针旋转45°,使△CDE 的斜边CE 恰好与△ABC 的边BC 垂直,题干中的其他条件不变,则上述结论是否仍然成立?(2)将图2中的△ABC 绕点C 逆时针旋转大于0°且小于45°的角,如图3所示,请直接写出你的结论.MDBA图2ABC DE M图1图3ABDM例2 如图1,在ABC △中,AC BC =,120C ∠=︒,D 在BC 边上。
BDE △为等边三角形,连接AE ,F 为AE 中点,连CF DF ,。
⑴请直接写出CF DF 、的关系,不必说明理由;⑵若将图1中的DBE △绕点B 顺时针旋转90︒,其它条件不变,请作出相应图形,并直接给出结论,不必说明理由。
⑶将图中的DBE △绕点B 顺时针旋转α(0°<α<60°),其它条件不变,如图2,试回答⑴中的结论是否成立?并说明理由。
图1AB C DEFFDCBA图2例3 (1)操作发现:如图1,在矩形ABCD 中,E 是BC 的中点,将△ABE 沿AE 折叠后得到△AFE ,点F 在矩形ABCD 内部,延长AF 交CD 于点G .猜想线段GF 与GC 有何数量关系?并证明你的结论. (2)类比探究:如图2,将(1)中的矩形ABCD 改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.GCFAFBA图1 图2例4 已知:如图所示,直线MA NB MAB ∠∥,与NBA ∠的平分线交于点C ,过点C 作一条直线l 与两条直线MA NB 、分别相交于点D E 、.(1)如图1所示,当直线l 与直线MA 垂直时,猜想线段AD BE AB 、、之间的数量关系,请直接写出结论,不用证明;(2)如图2所示,当直线l 与直线MA 不垂直且交点D E 、都在AB 的同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由;(3)当直线l 与直线MA 不垂直且交点D E 、在AB 的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段AD BE AB 、、之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.ABMCC NMBAABCDEMNl lMEDCB A图1 图2 备用图 备用图例5 在△ABC 中,∠A =90°,点D 在线段BC 上,∠EDB =12∠C ,BE ⊥DE ,垂足为E ,DE 与AB 相交于点F .(1)当AB =AC 时(如图1), ①∠EBF =_______°;②探究线段BE 与FD 的数量关系,并加以证明;(2)当AB =kAC 时(如图2),求BEFD 的值(用含k 的式子表示).。
类比探究专题(一)——平行结构(含答案)
学生做题前请先回答以下问题问题1:类比探究问题的处理思路是什么?以下是问题及答案,请对比参考:问题1:类比探究问题的处理思路是什么?答:类比探究问题的处理思路为:(1)类比探究往往会围绕一个不变结构进行考查.类比探究中常见的不变结构有:中点结构、直角结构、旋转结构、平行结构.(2)若不属于常见结构类型,则需要我们尝试着去寻找不变结构解决问题.①根据题干条件,结合支干条件先解决第一问.②类比解决下一问.如果不能,分析条件变化,寻找不变特征.③结合所求目标,依据不变特征尝试找不变结构,大胆猜测、尝试、验证.若属于类比探究常见的结构类型,调用结构类比解决.类比探究专题(一)——平行结构一、单选题(共6道,每道16分)1.如图1,D是△ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.(1)若BD=CD,CF=2AF,则的值为( )A.2B.C. D.答案:B解题思路:试题难度:三颗星知识点:平行结构2.(上接第1题)(2)如图2,若BD=CD,CF=mAF,则的值为( ) (用含m的代数式表示)A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:平行结构3.(上接第1,2题)(3)如图3,将原题改为“过点D的一条直线交AC的延长线于点F,交AB于点E”,若BD=nCD,CF=mAF,则的值为( )(用含m,n的代数式表示)A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:平行结构4.已知AD是△ABC的中线,将BC边所在直线绕点D顺时针旋转角,交AB边于点M,交射线AC于点N,设.(1)如图1,满足的函数关系式为( ) A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:平行结构5.(上接第4题)(2)如图2,当G是AD上任意一点时(点G不与点A重合),过点G的直线交AB边于点,交AC边于点,设,则满足的函数关系式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:平行结构6.(上接第4,5题)(3)如图3,当G是AD上任意一点时(点G不与点A重合),过点G 的直线交AB边于点,交AC的延长线于点,设,则满足的函数关系式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:平行结构。
类比探究—平行结构(含答案)
学生做题前请先回答以下问题问题1:类比探究属于几何综合题,类比(__________,___________,___________)是解决此问题的主要方法,做好类比需要把握变化过程中的____________.若属于类比探究常见的结构类型,调用结构类比解决.若不属于常见结构类型①根据题干条件,结合___________________先解决第一问.②类比解决下一问.如果不能,分析条件变化,寻找______________.结合所求目标,依据_____________,大胆猜测、尝试、验证问题2:想一想类比探究问题常见的不变结构有哪些,处理方式是什么?以下是问题及答案,请对比参考:问题1:类比探究属于几何综合题,类比(,,)是解决此问题的主要方法,做好类比需要把握变化过程中的.若属于类比探究常见的结构类型,调用结构类比解决.若不属于常见结构类型①根据题干条件,结合先解决第一问.②类比解决下一问.如果不能,分析条件变化,寻找.结合所求目标,依据,大胆猜测、尝试、验证答:问题2:想一想类比探究问题常见的不变结构有哪些,处理方式是什么?答:类比探究—平行结构一、单选题(共6道,每道16分)1.现有多个全等直角三角形,先取三个拼成如图1所示的形状,R为DE的中点,BR分别交AC,CD于点P,Q,则BP:PQ:QR等于( )A.3:2:1B.3:2:4C.3:1:2D.2:1:2答案:C解题思路:试题难度:三颗星知识点:类比探究问题2.(上接第1题)若取四个直角三角形拼成如图2所示的形状,S为EF的中点,BS分别交AC,CD,DE于点P,Q,R,则BP:PQ:QR:RS等于( )A.5:1:3:2B.4:1:3:2C.5:1:4:2D.3:1:3:2答案:B解题思路:试题难度:三颗星知识点:类比探究问题3.(上接第1,2题)若取五个直角三角形拼成如图3所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于点P,Q,R,S,则BP:PQ:QR:RS:ST等于( )A.5:1:4:2:3B.5:1:5:2:3C.4:1:4:2:3D.5:1:4:3:2答案:A解题思路:试题难度:三颗星知识点:类比探究问题4.问题背景:已知在△ABC中,AB边上的动点D由A向B运动(与A,B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.(1)初步尝试:如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等,则HF,AH,CF之间的数量关系为( )A.HF=AH+CFB.C.HF=2AH+CFD.答案:A解题思路:试题难度:三颗星知识点:全等三角形的判定与性质5.(上接第4题)(2)类比探究:如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC= 30°,且点D,E的运动速度之比是,则的值为( )A. B.C.2D.答案:C解题思路:试题难度:三颗星知识点:全等三角形的判定与性质6.(上接第4,5题)(3)延伸拓展:如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记,且点D,E的运动速度相等,则的值为( )(用含m的代数式表示)A.2B.C.3mD.答案:B解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究。
类比探究(一)——探究应用(习题及答案).
类比探究(一)——探究应用(习题)1.探究发现如图1,△ABC是等边三角形,∠AEF=60°,EF交等边三角形外角平分线CF所在的直线于点F,当点E是BC的中点时,有AE=EF成立.数学思考某数学兴趣小组在探究AE,EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:当点E是直线BC上(B,C除外)任意一点时(其他条件不变),结论AE=EF仍然成立.假如你是该兴趣小组中的一员,请你从“点E是线段BC上的任意一点”,“点E是线段BC延长线上的任意一点”,“点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在图2中画出图形,并证明AE=EF.拓展应用当点E在线段BC的延长线上时,若CE=BC,在图3中画出:S△AEF的值.图形,并运用上述结论求出S△ABC2.已知∠MAN=135°,正方形ABCD绕点A旋转.(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是__________.②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由.(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A 除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.3.已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1)如图1,若四边形ABCD是矩形,且DE⊥CF,求证:DE ADCF CD=.(2)如图2,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得DE ADCF CD=成立?并证明你的结论.(3)如图3,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出DECF的值.【参考答案】1.证明略;1:32.(1)①MN =BM +DN②成立,理由略(2)222MN BM DN =+3.(1)证明略(2)∠B +∠EGC =180°,证明略(3)2524。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1
A
B C D G
E
F
M
图2
A
B
C
D
G
E
F
M
图3
A
B C
D
G E
F
M
类比探究(讲义)
➢ 课前预习
1. 小明同学碰到如下问题:
如图1,在正方形ABCD 和正方形CGEF (CG >BC )中,点B ,C ,G 在同一直线上,点M 是AE 的中点.
(1)探究线段MD ,MF 的位置关系及数量关系,并证明. (2)若将图1中的正方形CGEF 绕点C 顺时针旋转,使D , C ,G 三点在同一直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明. (3)若将图1中的正方形CGEF 绕点C 顺时针旋转,使正方形CGEF 的对角线CE 恰好与正方形ABCD 的边BC 在同一直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.
小明同学分析第一问发现,问题关键在于中点的应用. 经过尝试,小明成功解决了第(1)问,并将思路记录如下:
MD ⊥MF ,MD =MF
等腰Rt △DFH ,M 为DH 中点FD =FH ,∠DFH =90°
DM =MH ,AD =EH △ADM ≌△EHM
延长DM ,交EF 于点H (平行夹中点)
仿照小明的证明方法,你能解决(2)(3)问吗?
扫一扫 看视频 对答案
2. ①如图,在△ABC 中,AF :FB =2:3,延长BC 至点D ,使得
BC =2CD ,则
AE
EC
=_________. 提示:求比例,找相似.利用平行线构造“A 型”或“X 型”
相似是我们常用的一种做法.
A B
D
C
E
F
②如图,AB =4,射线BM 和AB 相互垂直,点D 是AB 上的一个动点,点E 在射线BM 上,2BE =DB ,作EF ⊥DE 并截取EF =DE ,连接AF 并延长交射线BM 于点C .设BE =x ,BC =y ,则y 关于x 的函数解析式是( )
A .124
x
y x =--
B .21
x
y x =--
C .31x
y x =-- D .84
x y x =-- 提示:结合直角特征考虑分析,可构造一线三等角,利用相似整合信息.
M F
E D
C B A
➢知识点睛
类比探究问题的处理思路
1.若属于类比探究常见的结构类型,调用结构类比解决.
类比探究结构举例:中点结构、直角结构、旋转结构、平行结构.
2.若不属于常见结构类型:
①根据题干条件,结合_______________先解决第一问.
②类比解决下一问.
如果不能,分析条件变化,寻找______________.
③结合所求目标,依据__________,大胆猜测、尝试、验证.
➢精讲精练
1.已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,
BC=3.
(1)如图1,P为AB边上的一点,以PD,PC为边作
□PCQD,则当点P与点A重合时,PQ的长为__________.(2)如图2,若P为AB边上任意一点,以PD,PC为边作□PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
(3)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作□PCQE,请探究对角线PQ的长是否也存在最小值.如果存在,请求出最小值;如果不存在,请说明理由.
(4)如图3,若P为直线DC上任意一点,延长PA到E,使AE=nPA(n为常数),以PE,PB为边作□PBQE,请探究对角线PQ的长是否也存在最小值.如果存在,请求出最小值;如果不存在,请说明理由.
A(P)
D
Q
C
B
图1
A
P B
C
Q
D
图2
A
B C D E
P
Q
图3
A B C
D
A B C
D
2. 已知△ABC 为直角三角形,∠ACB =90°,点P 是射线CB 上
一点(点P 不与点B ,C 重合),线段AP 绕点A 顺时针旋转90°得到线段AQ ,连接QB 交射线AC 于点M .
(1)如图1,当AC =BC ,点P 在线段CB 上时,线段PB ,CM 的数量关系是__________.
(2)如图2,当AC =BC ,点P 在线段CB 的延长线上时,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由.
(3)如图3,若
5
2
AC BC ,点P 在线段CB 的延长线上时,CM =2,AP =13,求△ABP 的面积.
图1
M Q
P
A
B
C
图2
M Q
P
A
B C
M
C B
A
P
Q
图3
3. (1)问题发现
如图1,△ACB 和△DCE 均为等边三角形,点A ,D ,E 在同一直线上,连接BE .填空: ①∠AEB 的度数为___________;
②线段AD ,BE 之间的数量关系为___________.
图1
C
D
A
B
E
(2)拓展探究
如图2,△ACB 和△DCE 均为等腰直角三角形,∠ACB = ∠DCE =90°,点A ,D ,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接BE .请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系,并说明理由.
图2
M
E
D
C
B
A
(3)解决问题
如图3,在正方形ABCD 中,CD =2.若点P 满足PD =1,且∠BPD =90°,请直接写出点A 到BP 的距离.
A B
C
D
图3
4. 如图1,在Rt △ABC 中,∠B =90°,BC =2AB =8,点D ,E 分
别是边BC ,AC 的中点,连接DE .将△EDC 绕点C 按顺时针方向旋转,记旋转角为α. (1)问题发现 ①当α=0°时,
AE
BD
=______;②当α=180°
时,AE
BD
=______. (2)拓展探究
试判断:当0°≤α<360°时,AE
BD
的大小有无变化?请仅就图2的情形给出证明. (3)问题解决
当△EDC 旋转至A ,D ,E 三点共线时,直接写出线段BD 的长.
图3
图2
图1
A
B
C
A
E
B
D
C
D E
C
B A
【参考答案】 ➢ 课前预习
1. 能,证明略
2. ①2
②A
➢ 知识点睛
2. ①分支条件 ②不变特征 ③不变特征
➢ 精讲精练
1. (1)25.
(2)存在,最小值为4. (3)存在,最小值为5. (4)存在,最小值为2
(4)2
n +. 2. (1)PB =2CM .
(2)成立,证明略. (3)△ABP 的面积为25. 3. (1)①60°;②AD =BE .
(2)AE =2CM +BE . (3)点A 到BP 的距离为312+或31
2
-. 4. (1)①
52;②52
. (2)0360α︒<︒≤时,
AE
BD
的大小没有变化,证明略. (3)线段BD 的长为45或
125
5
.。
