9.4菱形(2)
菱形判定

检测反馈: 4.如图,矩形ABCD的对角线相交于点O, DE∥AC,CE∥BD.请判断四边形OCED 的形状,并说明理由.
谢谢!
苏科版 八年级数学(下)
§9.4 矩形、菱形、正方形 ——菱形的判定
复习巩固: 菱形的性质
对称性 边
既是轴对称图形,又是中心对 称图形. 四边相等,对边平行.
对角相等. 对角线互相垂直且平分. 每条对角线平分一组对角.
角
对角线
合作探究: 一 个四边形满足什么条件,它就是菱形 呢? 定义: 有一组邻边相等的平行四边形叫做菱形.
B
O
D
C
菱形的判别方法有哪些? 判别方法1: 有一组邻边相等的平行四边形叫做菱形. 判别方法2: 四条边相等的四边形是菱形. 判别方法3:
对角线互相垂直的平行四边形是菱形.
个性展示: 例1 如图,矩形ABCD(AD>AB),对角线AC 的垂直平分线与边AD、BC分别相交于点E、 F.分别连结AF和CE. (1)说明四边形AFCE是菱形; (2)若AB=4cm,BC=8cm,求BF的长.
D C
合作探究:
四边形的对角线满足什么条件,它就是 菱形呢? 两条对角线互相垂直的四边形是菱形吗? 不是,四边形可能是“筝形”.
A A B D B C
D
C
合作探究:
两条对角线互相垂直的平行四边形,它 是菱形吗?说明理由.
A B O D
C
菱形的判别方法3: 对角线互相垂直的平行四边形是菱形.
A
在□ABCD中 ∵AC⊥BD ∴□ABCD是菱形
A
在□ABCD中 ∵AB=BC ∴□ABCD是菱形
B
D
C
菱形呢?
四条边相等的四边形是菱形.请你说 明理由.
9.4.4菱形的判定

9.4.4菱形的判定知识点菱形的判定1.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,则得到的四边形ABCD 是菱形,这样作图的依据是()A.一组邻边相等的四边形是菱形B.四边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.每条对角线平分一组对角的平行四边形是菱形2.如图,在▱ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定▱ABCD是菱形的只有()A.AC⊥BD B.AB=BC C.AC=BD D.∠1=∠23.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是________(写出一个即可).4.如图,在▱ABCD中,AB=3,BC=4,平移边CD到EF,当BF=________时,四边形ABFE为菱形.第1题第2题第3题第4题5.如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB,AC于点E,F,连接DE,DF.求证:四边形AEDF是菱形.6.如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于点E.求证:四边形OCED是菱形.7.如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线分别与边AD,BC交于点E,F,连接AF,CE,四边形AFCE是菱形吗?为什么?【能力提升】8.如图所示,在▱ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE =4,AE=8,则DF的长为() A.4 B.8 C.6 D.99.2017·铜山区二模如图,用完全相同的两个矩形纸片交叉叠合得到四边形ABCD,则四边形ABCD的形状是________.第8题10.如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E,F,并且DE=DF.求证:(1)△ADE≌△CDF;(2)四边形ABCD是菱形.11.如图,在▱ABCD中,O是对角线AC的中点,过点O作AC的垂线分别与AD,BC交于点E,F.(1)求证:AE=CF;(2)连接AF,CE,试判断四边形AFCE的形状,并说明理由.12.如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:(1)∠BOD=∠C;(2)四边形OBCD是菱形.13.如图,在菱形ABCD中,∠C=60°,AB=2,E是AD边的中点,M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.(2)填空:①当AM的长为________时,四边形AMDN是矩形;②当AM的长为________时,四边形AMDN是菱形.。
9.4矩形、菱形、正方形

1ODC BA9.4矩形、菱形、正方形一、知识梳理1.矩形定义:有一个角是直角的平行四边形叫做矩形。
2.矩形的性质:(1)矩形既是中心对称图形(对角线交点),矩形又是轴对称图形(两条对称轴) (2)矩形的两组对边分别平行且相等 (3)矩形的四个角都是直角;(4) 矩形的对角线相等且会互相平分。
3、矩形中的基本图形(1)两对全等的等腰三角形 (2)四个全等的直角三角形. 二、题型分类全解【例题1】已知:如图,矩形ABCD 的两条对角线相交于点O ,且 AC =2AB . 求证:△AOB 是等边三角形.【例题2】如图,矩形ABCD 的对角线AC 、BD 相交于点O , AB=4,∠AOB=60°,求对角线AC 的长三、测试1、矩形的定义中有两个条件:一是____________,二是_________________。
2、下列性质中,矩形不一定具有的是( )A 、对角线相等B 、 四个角都相等C 、对角线垂直D 、是轴对称图形 3、矩形ABCD 中,对角线AC 、BD 把矩形分成( )对全等等腰三角形,( )个全等的直角三角形。
(A )2 (B )4 (C )6 (D )84、矩形具有而一般平行四边形不具有的性质是( )A .对角线相等B .对边相等C .对角相等D .对角线互相平分2ODC B A5.下面说法中正确的是 ( )A .平行四边形的两条对角线的长度相等B .有一个角是直角的四边形是矩形C .矩形的两条对角线互相垂直D .矩形的对角线相等且互相平分6.矩形既是轴对称图形,又是中心对称图形:每一个矩形最少有 条对称轴;矩形对称中心是 的交点.7.如图,在矩形ABCD 中,点E 为边AB 中点,过点E 作直线EF 交对边CD 于点F ,若S AEFD :S BCFE =2:1,则DF : FC=( )A .5:1B .5:2C .4:1D .3:18.矩形ABCD 的对角线AC 、BD 相交于点O ,∠BOC =2 ∠AOB ,如果对角线AC=10cm ,则AD=______cm.9.如图,矩形纸片ABCD 中,已知AD=8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF=3,求AB 的长。
苏科版数学八年级下册 9.4矩形菱形正方形大题综合练习(含答案解析)
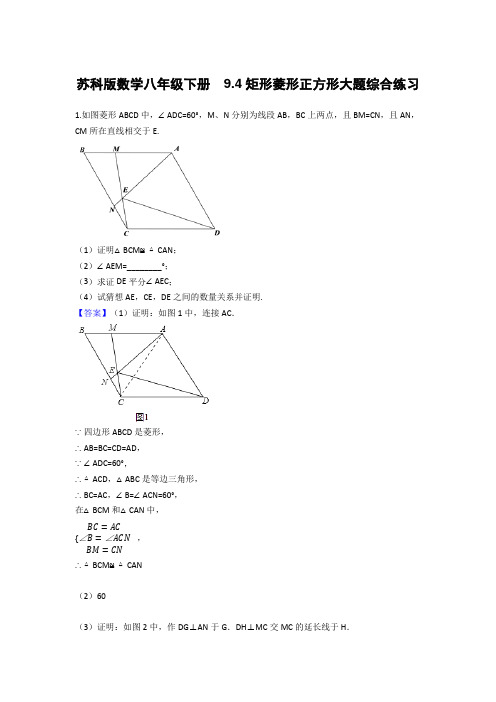
苏科版数学八年级下册9.4矩形菱形正方形大题综合练习1.如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.(1)证明△BCM≌△CAN;(2)∠AEM=________°;(3)求证DE平分∠AEC;(4)试猜想AE,CE,DE之间的数量关系并证明.【答案】(1)证明:如图1中,连接AC.∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵∠ADC=60°,∴△ACD,△ABC是等边三角形,∴BC=AC,∠B=∠ACN=60°,在△BCM和△CAN中,{BC=AC∠B=∠ACNBM=CN,∴△BCM≌△CAN(2)60(3)证明:如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.∵∠AEM=60°,∴∠AEC=120°,∵∠DGE=∠H=90°,∴∠GEH+∠GDH=180°,∴∠GDH=∠ADC=60°,∴∠ADG=∠CDH ,在△DGA 和△DHC 中,{∠DGA =∠H =90∘∠ADG =∠CDH DA =DC,∴△DGA ≌△DHC ,∴DG=DH ,∵DG ⊥AN ,DH ⊥MC ,∴∠DEG=∠DEH .∴DE 平分∠AEC .(4)证明:结论:EA+EC=ED .理由如下:如图2中,由(3)可知,∠GED=60°,在Rt △DEG 中,∵∠EDG=30°,∴DE=2EG ,易知△DEG ≌△DEH ,∴EG=EH ,∴EA+EC=EG+AG+EH-CH ,∵△DGA ≌△DHC ,∴GA=CH ,∴EA+EC=2EG=DE ,∴EA+EC=ED.【解析】【解答】解:(2)如图1中,∵△BCM ≌△CAN ,∴∠BCM=∠CAN ,∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.故答案为60.【分析】(1)连接AC,因为∠ADC=60°,利用菱形四边相等的性质,可知△ADC为等边三角形,所以AC=BC ,又因为菱形的对角线平分一组对角,所以∠ACN=60°=∠B,因为BM=CN,所以△BCM≌△CAN;(2)因为∠AEM=∠CEN,对顶角相等,由全等可知∠AEM=∠CEN=∠B=60°;(3)过点D做AE、CM两边的垂线,利用角角边可得到△DHC≌△DGA,可得DH=DG,再用角平分线的性质,到一个角两边距离相等的点在这个角的角平分线上;(4)由全等可知EA+EC=2EG,又因为在Rt△中30°的角所对的边等于斜边的一半,所以EA +EC=DE.2.综合:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为A. 平行四边形B. 菱形C. 矩形D. 正方形(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.【答案】(1)C(2)解:如图2中,①证明:∵AD=5,S□ABCD=15,∴AE=3.又∵在图2中,EF=4,∴在Rt△AEF中,AF═5.∴AF=AD=5,又∵AF∥DF',AF=DF,∴四边形AFF'D是平行四边形.∴四边形AFF'D是菱形.②解:连接AF',DF,在Rt△DE'F中,∵E'F=E'E﹣EF=5﹣4=1,DE'=3,∴DF═√E′D2+E′F2= √10.在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,∴AF'═√AE2+EF′2= √32+92=3 √10【解析】【解答】(1)解:如图1中,∵四边形ABCD是平行四边形,∴AD=BC,∵BE=CE′,∴AD∥EE′,AD=EE′,∴四边形AEE′D是平行四边形,∵∠AEE′=90°,∴四边形AEE′D是矩形,故选C.【分析】(1)根据矩形的判定方法即可判定;(2)①通过计算证明AF=AD=5,证明四边形AFF′D是平行四边形即可;②连接AF',DF,分别利用勾股定理计算即可;3.如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF 的面积为S1,△PDE的面积为S2.(1)求证:BP⊥DE.(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围.(3)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.【答案】(1)解:如图1中,延长BP交DE于M.∵四边形ABCD是正方形,∴CB=CD,∠BCP=∠DCE=90°,∵CP=CE,∴△BCP≌△DCE,∴∠BCP=∠CDE,∵∠CBP+∠CPB=90°,∠CPB=∠DPM,∴∠CDE+∠DPM=90°,∴∠DMP=90°,∴BP⊥DE.(2)解:由题意S1﹣S2= 12(4+x)•x﹣12•(4﹣x)•x=x2(0<x<4).(3)解:①如图2中,当∠PBF=30°时,∵∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,∴∠PFD=∠DPF=45°,∴DF=DP,∵AD=CD,∴AF=PC,∵AB=BC,∠A=∠BCP=90°,∴△BAF≌△BCP,∴∠ABF=∠CBP=30°,∴x=PC=BC•tan30°= 4√3,3∴S1﹣S2=x2= 16.3②如图3中,当∠PBF=45°时,在CB上截取CN=CP,理解PN.由①可知△ABF≌△BCP,∴∠ABF=∠CBP,∵∠PBF=45°,∴∠CBP=22.5°,∵∠CNP=∠NBP+∠NPB=45°,∴∠NBP=∠NPB=22.5°,∴BN=PN= √2x,∴√2x+x=4,∴x=4 √2﹣4,∴S1﹣S2=(4 √2﹣4)2=48﹣32 √2.【解析】【分析】(1)首先延长BP交DE于M.然后依据SAS可证明△BCP≌△DCE,依据全等三角形的性质可得到∠BCP=∠CDE,由∠CBP+∠CPB=90°,∠CPB=∠DPM,即可推出∠CDE+∠DPM=90°;(2)根据题意可得到S1-S2=S△PBE-S△PDE,然后依据三角形的面积公式列出函数关系式即可;(3)分当∠PBF=30°和∠PBF=45°两种情形分别求出PC 的长,最后再利用(2)中结论进行计算即可.4.如图,在矩形ABCD 中,BC >AB ,∠BAD 的平分线AF 与BD ,BC 分别交于点E ,F ,点O 是BD 的中点,直线OK ∥AF ,交AD 于点K ,交BC 于点G .(1)求证:△DOK ≌△BOG ;(2)探究线段AB 、AK 、BG 三者之间的关系,并证明你的结论;(3)若KD=KG ,BC=2 √2 ﹣1,求KD 的长度.【答案】(1)证明:∵在矩形ABCD 中,AD ∥BC ,∴∠KDO=∠GBO ,∠DKO=BGO .∵点O 是BD 的中点;∴DO=BO .在△DOK 和△BOG 中, {∠KDO =∠GBO∠DKO =∠BGO DO =BO∴△DOK ≌△BOG (AAS ).(2)解:AB+AK=BG ;证明如下:∵四边形ABCD 是矩形;∴∠BAD=∠ABC=90°,AD ∥BC .又∵AF 平分∠BAD ,∴∠BAF=∠BFA=45°.∴AB=BF .∵OK ∥AF ,AK ∥FG ,∴四边形AFGK 是平行四边形.∴AK=FG .∵BG=BF+FG ;∴BG=AB+AK .(3)解:∵四边形AFGK 是平行四边形.∴AK=FG ,AF=KG又∵△DOK ≌△BOG ,且KD=KG ,∴AF=KG=KD=BG .设AB=a ,则AF=KG=KD=BG= √2 a .∴AK=2 √2 ﹣1﹣ √2 a ,FG=BG ﹣BF= √2 a ﹣a .∴2 √2﹣1﹣√2a= √2a﹣a.解得a=1.∴KD= √2a= √2.【解析】【分析】(1)在矩形ABCD中,AD∥BC,得到∠KDO=∠GBO,∠DKO=BGO,DO=BO,得到△DOK≌△BOG(AAS);(2)四边形ABCD是矩形,得到∠BAD=∠ABC=90°,AD∥BC,又AF平分∠BAD,得到∠BAF=∠BFA=45°,AB=BF,由OK∥AF,AK∥FG,得到四边形AFGK 是平行四边形,得到AK=FG,BG=BF+FG,即BG=AB+AK;(3)四边形AFGK是平行四边形,得到AK=FG,AF=KG,又△DOK≌△BOG,且KD=KG,得到AF=KG=KD=BG,设AB=a,则AF=KG=KD=BG=√2a,得到AK=2√2﹣1-√2a,FG=BG﹣BF=√2a﹣a,解得a=1,得到KD=√2a=√2.5.综合题(1)感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.(2)探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为________ .【答案】(1)证明:∵四边形ABCD、四边形CEFG均为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG,在△BCE和△DCG中,{CB=CD∠BCE=∠DCGCE=CG,∴△BCE≌△DCG,∴BE=DG.(2)∵四边形ABCD、四边形CEFG均为菱形,∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,∵∠A=∠F,∴∠BCD=∠ECG,∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG,∴△BCE≌△DCG.,∴BE=DG.(3)20【解析】【解答】解:应用:∵四边形ABCD是菱形,S△EBC=8,∴S△AEB+S△EDC=8,∵AE=3DE,∴S△AEB=3S△EDC,∴S△EDC=6,S△EDC=2,∵△BCE≌△DCG,∴S△DGC=S△EBC=8,∴S△ECG=8+2=10,∴菱形CEFG的面积=2•S△EGC=20,故答案为20.【分析】感知:根据正方形的性质,得到BC=CD,CE=CG,∠BCD=∠ECG=90°,得到∠BCE=∠DCG,得到△BCE≌△DCG,BE=DG;探究:由四边形ABCD、四边形CEFG均为菱形,得到BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,由∠A=∠F,得到∠BCE=∠DCG,△BCE≌△DCG,BE=DG;应用:由四边形ABCD是菱形,△EBC的面积为8,AE=3DE,得到S△AEB=3S△EDC,得到S△EDC=6,S△EDC=2,由△BCE≌△DCG,得到S△DGC=S△EBC=8,S△ECG=8+2=10,所以菱形CEFG的面积=2•S△EGC=20.6.如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(3,4),一次函x+b的图象与边OC、AB分别交于点D、E,并且满足OD=BE.点M是线段DE 数y=23上的一个动点.(1)求b的值;(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N 的坐标.【答案】(1)解:y=23x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,∵OD=BE,∴BE=b,则E的坐标是(3,4﹣b),把E的坐标代入y=23x+b得4﹣b=﹣2+b,解得:b=3(2)解:S四边形OAED= 12(OD+AE)•OA= 12×(3+1)×3=6,∵三角形ODM的面积与四边形OAEM的面积之比为1:3,∴S△ODM=1.5.设M的横坐标是a,则12×3a=1.5,解得:a=1,把x=a=1代入y=﹣23x+3得y=﹣23× 43+3= 73.则M的坐标是(1,73)(3)解:当四边形OMDN是菱形时,如图(1),M的纵坐标是32,把y= 32代入y=﹣23x+3,得﹣23x+3= 32,解得:x= 94,则M的坐标是(94,32),则N的坐标是(﹣94,32);当四边形OMND是菱形时,如图(2)OM=OD=3,设M的横坐标是m,则纵坐标是﹣23m+3,则m2+(﹣23m+3)2=9,解得:m= 3613或0(舍去).则M的坐标是(3613,1513).则DM的中点是(1813,2713).则N的坐标是(3613,5413).故N的坐标是(﹣94,32)或(3613,5413).【解析】【分析】(1)首先在一次函数的解析式中令x=0,即可求得D的坐标,则OD的长度即可求得,OD=b,则E的坐标即可利用b表示出来,然后代入一次函数解析式即可得到关于b的方程,求得b的值;(2)首先求得四边形OAED的面积,则△ODM的面积即可求得,设出M的横坐标,根据三角形的面积公式即可求得M的横坐标,进而求得M的坐标;(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论,四边形OMDN 是菱形时,M是OD的中垂线与DE的交点,M关于OD的对称点就是N;四边形OMND是菱形,OM=OD,M在直角DE上,设出M的坐标,根据OM=OD即可求得M的坐标,则根据ON和DM的中点重合,即可求得N的坐标.7.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2.(1)若DG=6,求AE的长;(2)若DG=2,求证:四边形EFGH是正方形.【答案】(1)解:∵AD=6,AH=2∴DH=AD﹣AH=4∵四边形ABCD是矩形∴∠A=∠D=90°∴在Rt△DHG中,HG2=DH2+DG2在Rt△AEH中,HE2=AH2+AE2∵四边形EFGH是菱形∴HG=HE∴DH2+DG2=AH2+AE2即42+62=22+AE2∴AE= =4(2)证明:∵AH=2,DG=2,∴AH=DG,∵四边形EFGH是菱形,∴HG=HE,在Rt△DHG和Rt△AEH中,,∴Rt△DHG≌Rt△AEH(HL),∴∠DHG=∠AEH,∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∵四边形EFGH是菱形,∴四边形EFGH是正方形【解析】【分析】(1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2,HE2=AH2+AE2,再根据菱形的性质,得到等式DH2+DG2=AH2+AE2,最后计算AE的长;(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,因为∠AEH+∠AHE=90°,∠DHG+∠AHE=90°,可得菱形的一个角为90°,进而判定该菱形为正方形.8.如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD 于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.(1)AM=________,AP=________.(用含t的代数式表示)(2)当四边形ANCP为平行四边形时,求t的值(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由②使四边形AQMK为正方形,则AC等于.【答案】(1)8﹣2t;2+t(2)解:∵四边形ANCP为平行四边形时,CN=AP,∴6﹣t=8﹣(6﹣t),解得t=2(3)解:①存在时刻t=1,使四边形AQMK为菱形.理由如下:∵NP⊥AD,QP=PK,∴当PM=PA时有四边形AQMK为菱形,∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,②要使四边形AQMK为正方形.∵∠ADC=90°,∴∠CAD=45°.∴四边形AQMK为正方形,则CD=AD,∵AD=8,∴CD=8,∴AC=8 √2.【解析】【解答】解:(1)如图1.∵DM=2t,∴AM=AD﹣DM=8﹣2t.∵在直角梯形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P,∴四边形CNPD为矩形,∴DP=CN=BC﹣BN=6﹣t,∴AP=AD﹣DP=8﹣(6﹣t)=2+t;故答案为:8﹣2t,2+t.【分析】(1)由DM=2t,根据AM=AD﹣DM即可求出AM=8﹣2t;先证明四边形CNPD为矩形,得出DP=CN=6﹣t,则AP=AD﹣DP=2+t;(2)根据四边形ANCP为平行四边形时,可得6﹣t=8﹣(6﹣t),解方程即可;(3)①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6﹣t﹣2t=8﹣(6﹣t),求解即可,②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.9.已知▱OABC的顶点A、C分别在直线x=2和x=4上,O为坐标原点,直线x=2分别与x轴和OC边交于D、E,直线x=4分别与x轴和AB边的交于点F、G.(1)如图,在点A、C移动的过程中,若点B在x轴上,①直线AC是否会经过一个定点,若是,请直接写出定点的坐标;若否,请说明理由.②▱OABC是否可以形成矩形?如果可以,请求出矩形OABC的面积;若否,请说明理由.③四边形AECG是否可以形成菱形?如果可以,请求出菱形AECG的面积;若否,请说明理由.(2)在点A 、C 移动的过程中,若点B 不在x 轴上,且当▱OABC 为正方形时,直接写出点C 的坐标.【答案】(1)解:①是,经过定点(3,0).理由如下:如图1中,连接AC 交OB 于K .∵四边形OABC 是平行四边形,∴OK=KB ,BC ∥OA ,BC=OA ,∴∠CBF=∠AOD ,在△DOA 和△FBC 中,{∠ODA =∠CFB =90°∠AOD =∠CBF OA =BC,∴△DOA ≌△FBC ,∴OD=FB=2,∴OB=6,∵OK=KB ,∴OK=3,∴K (3,0),∴直线AC 经过定点K (3,0).②可以.利用如下:当∠OCB=90°时,四边形OABC 是矩形,由(1)可知△DOA ≌△FBC ,∴OD=BF=2,∵∠OCF+∠FCB=90°,∠FCB+∠CBF=90°,∴∠OCF=∠CBF,∵∠CFO=∠CFB,∴△CFO∽△BFC,∴CFBF = OFCF,∴CF2= 4CF,∴CF=2 √2,∴S矩形OABC=2•S△OBC=2× 12× 6×2√2=12 √2.③可以.理由如下:如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,∴AD=CF,∵DE= 12CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,∵OE2=OD2+DE2,∴9x2=x2+4,∴x= √22,∴AE= 3√22,∴S菱形AECG=AE•DF= 3√22×2=3 √2(2)解:如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,∴OD=CF=2,∴点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.综上所述,点C坐标为(4,2)或(4,﹣2)【解析】【分析】(1)①是,经过定点(3,0).如图1中,连接AC交OB于K,只要证明OD=FB=2,推出OB=6,即可解决问题.②当∠OCB=90°时,四边形OABC是矩形,由(1)可知△DOA≌△FBC,推出OD=BF=2,由△CFO∽△BFC,可得CFBF = OFCF,由此即可解决问题.③可以.如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,推出AD=CF,易知DE= 12CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,根据OE2=OD2+DE2,列出方程即可解决问题.(2)如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,推出OD=CF=2,推出点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.10.如图1,在平面直角坐标系中,正方形ABCO的顶点C、A分别在x、y轴上,A(0,6)、E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH(1)当H(﹣2,6)时,求证:四边形EFGH为正方形(2)若F(﹣5,0),求点G的坐标(3)如图2,点Q为对角线BO上一动点,D为边OA上一点,DQ⊥CQ,点Q从点B出发,沿BO方向移动.若移动的路径长为3,直接写出CD的中点M移动的路径长为________.【答案】(1)证明:如图1中,∵E(0,2),H(﹣2,6),∴OE=AH=2,∵四边形ABCO是正方形,∴∠HAE=∠EOF=90°,∵四边形EFGH是菱形,∴EH=EF,在Rt△AHE和Rt△OEF中,{AH=EOHE=EF,∴Rt△AHE≌△Rt△OEF,∴∠AEH=∠EFO,∵∠EFO+∠FEO=90°,∴∠AEH+∠FEO=90°,∴∠HEF=90°,∴四边形EFGH是正方形(2)解:如图1中,连接GE、FH交于点K.∵F(﹣5,0),E(0,2),∴OF=5,OE=2,EA=4,∵HE=EF,∴52+22=42+AH2,∴AH= √13,∴H(﹣√13,6),∵四边形EFGH是菱形,∴HK=KF,KE=KG,设G(m,n),则有m+02= −5−√132,n+22= 6+02,∴m=﹣5﹣√13,n=4,∴G(﹣5﹣√13,4)(3)3√22【解析】【解答】(3)解:如图2中,如图2中,作MN⊥CO于M.∵MN∥OD,CM=MD,∴CN=ON,∴MN垂直平分线段CO,∴点M在线段OC的垂直平分线上运动,如图3中,易知当点Q与B重合时,点M与BD的中点N重合,当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),∵QC=QD,∠CEQ=∠QFD,易证∠ECQ=∠FQD,∴△EQC≌△FDQ,∴EQ=DF=BE= 3√22,CE=OF=6﹣3√22,∴DO=6﹣3 √2,∵CM=DM,∠CMH=∠OMD,∠CHM=∠DOM,∴△HMC≌△OMD,∴OM=HM,CH=OD=6﹣3 √2,BH=3 √2,∵ON=NB,∴MN= 12BH= 3√22,∴点M的运动的路径的长为3√22.故答案为3√2.2【分析】(1)只要证明Rt△AHE≌△Rt△OEF,推出∠AEH=∠EFO,由∠EFO+∠FEO=90°,推出∠AEH+∠FEO=90°,推出∠HEF=90°,即可解决问题.(2)如图1中,连接GE、FH交于点K.首先求出点H的坐标,设G(m,n),根据中点坐标公式,列出方程组即可解决问题.(3)如图2中,作MN⊥CO于M.由MN∥OD,CM=MD,推出CN=ON,推出MN 垂直平分线段CO,推出点M在线段OC的垂直平分线上运动,如图3中,易知当点Q与B 重合时,点M与BD的中点N重合,当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),想办法求出BH 的长,即可利用三角形的中位线定理解决问题.11.如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB, AC上的一动点,且满足BP=AQ,D 是BC的中点.(1)求证:△PDQ是等腰直角三角形.(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.【答案】(1)证明:连接AD.∵△ABC是等腰直角三角形,D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,又∵BP=AQ,∴△BPD≌△AQD,∴PD=QD,∠BDP=∠ADQ,∵∠BDP+∠ADP=90°,∴∠ADP+∠ADQ=∠PDQ=90°,∴△PDQ为等腰直角三角形(2)解:当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:由(1)知△ABD为等腰直角三角形,当P为AB的中点时,DP⊥AB,即∠APD=90°,又∵∠BAC=90°,∠PDQ=90°,∴四边形APDQ为矩形,AB,∴四边形APDQ为正方形又∵DP=AP= 12【解析】【分析】连接AD,根据直角三角形的性质可得AD=BD=DC,从而证明△BPD≌△AQD,得到PD=QD,∠ADQ=∠BDP,则△PDQ是等腰三角形;由∠BDP+∠ADP=90°,得出∠ADP+∠ADQ=90°,得到△PDQ是直角三角形,从而证出△PDQ是等腰直角三角形;若四边形APDQ是正方形,则DP⊥AB,得到P点是AB的中点.12.如图,在等边三角形ABC中,点D是BC边的中点,以AD为边作等边三角形ADE.(1)求∠CAE的度数;(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.【答案】(1)解:在等边三角形ABC中,∵点D是BC边的中点,∴∠DAC=30°.又∵△ADE为等边三角形,∴∠DAE=60°.∴∠CAE=∠DAE-∠DAC=30°(2)解:由(1)知,∠EAF=90°,由F为AB的中点知,∠CFA=90°,∴CF∥EA.在等边三角形ABC中,CF=AD.在等边三角形ADE中,AD=EA.∴CF=EA.∴四边形AFCE为平行四边形.又∵∠CFA=90°,∴四边形AFCE为矩形.【解析】【分析】根据等边三角形三线合一的特点,易求得∠DAC=30°,则∠CAE=∠DAE-∠DAC.先证明四边形AECF是平行四边形,然后根据∠CFA=∠FAE=90°,由矩形的定义判定四边形AFCE是矩形.13.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:(1)四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?【答案】(1)解:四边形ADEF是平行四边形.理由:∵△ABD,△EBC都是等边三角形.∴AD=BD=AB,BC=BE=EC∠DBA=∠EBC=60°∴∠DBE+∠EBA=∠ABC+∠EBA.∴∠DBE=∠ABC.在△DBE和△ABC中∵BD=BA∠DBE=∠ABCBE=BC,∴△DBE≌△ABC.∴DE=AC.又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.同理可证:AD=EF,∴四边形ADEF平行四边形(2)解:∵四边形ADEF是矩形,∴∠FAD=90°.∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°.∴∠BAC=150°时,四边形ADEF是矩形(3)解:当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.理由如下:若∠BAC=60°,则∠DAF=360°﹣∠BAC﹣∠DAB﹣∠FAC=360°﹣60°﹣60°﹣60°=180°.此时,点A、D、E、F四点共线,∴以A、D、E、F为顶点的四边形不存在【解析】【分析】可先证明△DBE≌△ABC ,又∵△ACF是等边三角形,∴AC=AF.∴DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;若四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;根据∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,A,D,E,F为顶点的四边形就不存在.14.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;(2)证明:如图1,当点G和点M、C不重合时,求证:DG=DN.【答案】(1)证明:如图2中,∵AM=ME.AD=DB,∴DM∥BE,∴∠GDN+∠DNE=180°,∵∠GDN=∠AEB,∴∠AEB+∠DNE=180°,∴AE∥DN,∴四边形DMEN是平行四边形,∵DM== BE,EM== AE,AE=BE,∴DM=EM,∴四边形DMEN是菱形(2)证明:如图1中,取BE的中点F,连接DM、DF.由(1)可知四边形EMDF是菱形,∴∠AEB=∠MDF,DM=DF,∴∠GDN=∠AEB,∴∠MDF=∠GDN,∴∠MDG=∠FDN,∵∠DFN=∠AEB=∠MCE+∠CME,∠GMD=∠EMD+∠CME,、在Rt△ACE中,∵AM=ME,∴CM=ME,∴∠MCE=∠CEM=∠EMD,∴∠DMG=∠DFN,∴△DMG≌△DFN,∴DG=DN【解析】【分析】(1)如图2中,首先证明四边形DMEN是平行四边形,再证明ME=MD 即可证明.(2)如图1中,取BE的中点F,连接DM、DF.只要证明△DMG≌△DFN即可.15.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,分别延长OB,OD到点E,F,使BE=DF,顺次连接A、E、C、F各点.(1)求证:∠FAD=∠EAB.(2)若∠ADC=130°,要使四边形AECF是正方形,求∠FAD的度数.【答案】(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,∴AD=AB,∠ADB=∠ABD,∴∠ADF=∠ABE,在△FAD与△EAB中,∴△FAD≌△EAB(SAS),∴∠FAD=∠EAB;(2)解:∵四边形AECF对角线互相垂直平分,∴只要∠EAF=90°即得四边形BFDE是正方形,∵∠ADC=130°,∴∠DAB=180°﹣130°=50°∴∠FAD+∠EAB=40°,∵∠FAD=∠EAB,∴∠FAD= ×40°=20°【解析】【分析】(1)由题意易证∠ADF=∠ABE,又因为DF=EB,AD=AB,于是可△FAD≌△EAB,;(2)由已知可得四边形AECF对角线互相垂直平分,只要∠EAF=90°即得四边形AECF是正方形,由∠FAD=∠EAB,再证得∠DAB=50°,可得∠FAD+∠EAB=40°,于是∠FAD= 1×40°=20°.216.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD 为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:________,②BC,DC,CF之间的数量关系为:________;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请直接写出GE的长.【答案】(1)垂直;BC=CF+CD(2)解:CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.理由如下:∵正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,在△DAB与△FAC中,{AD=AF∠BAD=∠CAFAB=AC,∴△DAB≌△FAC(SAS),∴∠ABD=∠ACF,∵∠BAC=90°,AB=AC,∴∠ACB=∠ABC=45°.∴∠ABD=180°﹣45°=135°,∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°,∴CF⊥BC.∵CD=DB+BC,DB=CF,∴CD=CF+BC .(3)解:过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于N ,如图3所示:∵∠BAC=90°,AB=AC ,∴BC= √2 AB=2 √2 ,AH= 12 BC= √2 ,∴CD= 14 BC= √22 ,CH= 12 BC= √2 ,∴DH= 3√22 ,由(2)证得BC ⊥CF ,CF=BD= 5√22 ,∵四边形ADEF 是正方形,∴AD=DE ,∠ADE=90°,∵BC ⊥CF ,EM ⊥BD ,EN ⊥CF ,∴四边形CMEN 是矩形,∴NE=CM ,EM=CN ,∵∠AHD=∠ADC=∠EMD=90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM ,在△ADH 与△DEM 中, {∠ADH =∠DEM∠AHD =∠DMEAD =DE, ∴△ADH ≌△DEM (AAS ),∴EM=DH= 3√22 ,DM=AH= √2 ,∴CN=EM= 3√22 ,EN=CM= 3√22 ,∵∠ABC=45°,∴∠BGC=45°,∴△BCG 是等腰直角三角形,∴CG=BC=2 √2 ,∴GN=CG ﹣CN= √22 , ∴EG= √GN 2+EN 2 = (√22)(3√22)= √5 . 【解析】【解答】解:(1)①正方形ADEF 中,AD=AF ,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF ,在△DAB 与△FAC 中, {AD =AF∠BAD =∠CAFAB =AC,∴△DAB ≌△FAC (SAS ),∴∠B=∠ACF ,∴∠ACB+∠ACF=90°,即BC ⊥CF ;故答案为:垂直;②△DAB ≌△FAC ,∴CF=BD ,∵BC=BD+CD ,∴BC=CF+CD ;故答案为:BC=CF+CD ;【分析】(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB ≌△FAC ,根据全等三角形的性质即可得到结论;②由正方形ADEF 的性质可推出△DAB ≌△FAC ,根据全等三角形的性质得到CF=BD ,∠ACF=∠ABD ,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB ≌△FAC ,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.(3)根据等腰直角三角形的性质得到BC= √2 AB=2 √2 ,AH= 12 BC= √2 ,求得DH= 3√22 ,根据正方形的性质得到AD=DE ,∠ADE=90°,根据矩形的性质得到NE=CM ,EM=CN ,由角的性质得到∠ADH=∠DEM ,根据全等三角形的性质得到EM=DH= 3√22 ,DM=AH= √2 ,等量代换得到CN=EM= 3√22 ,EN=CM= 3√22,根据等腰直角三角形的性质得到CG=BC=2 √2 ,根据勾股定理即可得到结论.17.如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO=CO ,BO=DO ,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD 是矩形.(2)DF ⊥AC ,若∠ADF :∠FDC=3:2,则∠BDF 的度数是多少?【答案】(1)证明:∵AO=CO ,BO=DO ,∴四边形ABCD 是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴CO=OD,∴∠ODC=∠DCO=54°,∴∠BDF=∠ODC﹣∠FDC=18°.【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,【解析】根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.18.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.(1)求证:PC=PE;(2)求∠CPE的度数;(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=________度.【答案】(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,{AB=BC∠ABP=∠CBPPB=PB,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE(2)解:由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∵PA=PE,∴∠PAE=∠PEA,∴∠CPB=∠AEP,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°,∵∠ABC=90°,∴∠EPC=90°(3)115°【解析】【解答】(3)∠EPC=115°,理由:在菱形ABCD中,AB=BC,∠ABP=∠CBP,在△ABP和△CBP中,{AB=BC∠ABP=∠CBPPB=PB,∴△ABP≌△CBP(SAS),∴∠BAP=∠BCP,∵PA=PE,∴∠DAP=∠DCP,∴∠PAE=∠PEA,∴∠CPB=∠AEP,∵∠AEP+∠PEB=180°,∴∠PEB+∠PCB=180°,∴∠ABC+∠EPC=180°.∴∠CPE=180°-∠ABC=180°-65°=115°【分析】(1)根据正方形的性质得到△ABP≌△CBP,得到对应边相等,得到PC=PE;(2)由(1)知△ABP≌△CBP,得到对应边对应角相等,根据等边对等角和两直线平行同旁内角互补,求出∠CPE的度数;(3)根据菱形的性质,得到△ABP≌△CBP,得到得到对应边对应角相等,根据等边对等角和两直线平行同旁内角互补,求出∠CPE的度数.19.实践探究,解决问题如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD.(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=________;(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD 之间满足的关系式为________;(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.解决问题:(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).【答案】(1)16(2)S阴影=12S平行四边形ABCD(3)解:满足(2)中的关系式,理由如下:连接BD,由图1得S△EBD= 12 S△ABD同理S△BDF= 12S△BDC∴S四边形EBFD=S△EBD+S△BDF= 12S四边形ABCD(4)解:设四边形的空白区域分别为a,b,c,d 由上述性质可以得出:a+S2+S3= 12S△ACD①,c+S1+S4= 12S△ACB②,b+S2+S1= 12S△ABD③,d+S4+S3= 12S△ACD④,①+②+③+④得,a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四边形ABCD⑤而S四边形ABCD=a+b+c+d+S1+S2+S3+S4+S阴影⑥所以联立⑤⑥得S1+S2+S3+S4=S阴影=20平方米.【解析】【解答】解:(1)∵E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,∴S阴影= 12×8×4=16,故答案为:16;(2)∵E、F分别为平行四边形ABCD的边AD、BC的中点,∴S阴影= 12S平行四边形ABCD;故答案为:S阴影= 12S平行四边形ABCD;【分析】(1)由矩形的性质容易得出结果;(2)由平行四边形的性质容易得出结果;(3)连接BD,由题意得出S△EBD= 12 S△ABD同理S△BDF= 12S△BDC,即可得出结论;(4)设四边形的空白区域分别为a,b,c,d,由(3)可以得出:a+S2+S3= 12S△ACD①,c+S1+S4= 12S△ACB②,b+S2+S1= 12S△ABD③,d+S4+S3= 12S△ACD④,进一步得出结论即可.20.如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形.(2)解:∵四边形AECF是菱形,如图所示:∴AE=EC,∴∠1=∠2,∵∠3=90°﹣∠2,∠4=90°﹣∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE= 12BC=5.【解析】【分析】(1)利用平行四边形的性质得出对边平行且相等,结合已知,可证出AECF是平行四边形;(2)利用菱形的邻边相等的性质,可证出BE=AE=CE= 12BC=5.。
菱形的判定方法

四条边相等的四边形是菱形.
A
在四边形ABCD中
∵AB=AD=BC=CD B
D
∴四边形ABCD是菱形
C
活动: 我们知道,当平移一个平行四边形成菱形时 ,它的两条对角线互相垂直,反过来,对角线互 垂直的平行四边形是菱形吗?
A
B
O
D
C
菱形的判别方法3:
对角线互相垂直的平行四边形是菱形.A在□ABCD中
拓展与延伸:
将两张等宽的矩形纸片重叠在一起(如 图),你知道重叠的部分即四边形ABCD是 什么图形?
A
D
B C
作业:
F.分别连结AF和CE.
(1)说明四边形AFCE是菱形;
(2)若AB=4cm,BC=8cm,求BF的长.
A
E
D
O
B
F
C
例题选讲:
例2 如图,在梯形ABCD中,AB∥CD, BC=CD,AD⊥BD,E为AB中点. 四边 形BCDE是菱形吗?为什么?
D
C
A
E
B
练习:
1.在四边形ABCD中,AB//DC,AD//BC.请再 添加一个条件,使四边形ABCD是菱形.你添 加的条件是____A_B__=_A_D____.(写出一种即可)
9.4.4 菱形的判别方法
数学问题:
一 个四边形满足什么条件,它就是菱形 呢? 定义:
有一组邻边相等的平行四边形叫做菱形.
A
在□ABCD中
∵AB=BC
B
D
∴□ABCD是菱形
C
活动:
我们知道,菱形的四条边相等,反过来, 四边相等的四边形是菱形吗?
四条边相等的四边形是菱形.请你说 明理由.
A
苏科版八年级数学下册9.4.3菱形的性质课件

操作
如图,BO是等腰△ABC的底边AC上的 中线,画出△ABC关于点O对称的图形.
A
B
O
D
C
四边形ABCD是平行四边形吗?
它与一般的平行四边形有什么不同?
9.4 矩形、菱形、正方形(3)
仔细看一看
上面的图片中有你熟悉的图形吗?
平行四边形
一组邻 边相等
菱形
1. 菱形的定义:
有一组邻边相等的平行四边形是菱形.
A
B
D
C
思考: 菱形具有哪些性质?
菱形具有平行四边形的所有性质. 那么菱形还有哪些特殊的性质?
合作探究
请你从对称性、边、角、对角线四 个方面进行考虑,你能发现菱形有什么 特有的性质吗?请讨论总结.
A
B
O
D
C
菱形的对角线互相垂直,. 并且每一条对 角线平分一组对角.
菱形的性质2:
菱形的对角线互相垂直,每一条对角 线平分一组对角.
A
B
O
D
C
菱形的性质:
从边看: 菱形的四边都相等; 从角看: 菱形的对角相等;
从对角线看:菱形的两条对角线互相垂直 且平分;(每一条对角线平分 一组对角)
从对称性看:菱形既是轴对称图形,又是 中心对称图形.
是12cm和16cm,求菱形的周长和面积。
分析: S菱形ABCD 4SAOB
D
4 1 OA OB A
O
C
2
4 1 1 AC 1 BD B
22
2
S菱形ABCD
1 2
AC BD
你有什么发现?
D
A
O
E B
S菱形ABCD AB DE
9.4菱形的性质
★自学中的遗留问题是哪些?在小组交流时一定要大胆的提问。
★用几何语言表述矩形的定义和性质。
★
要求:
导学案上错误的部分记得用红色笔订正,补充哦
一.自主先学
◆学法指导:课前参照学习任务独学学案,完成自主学习部分内容。没弄明白的地方用红笔打上“?”以待“小组合作”时讨论解决。
(一)预习任务
1.预习课本第78,79页所有内容。(★按要求完成课本“思考”“交流”)
二.小组合作
1.菱形是的平行四边形。在对称性方面,菱形与一般平行四边形相比较,相同之处是:二者都是_____对称图形.不同之处是:只有_______是_______对称图形,它有条对称轴。
2.下面性质中,矩形不一定具有的是().
(A)对角线相等(B)四条边相等(C)是轴对称图形(D)对角线垂直.
3.例1:如图,在菱形ABCD中,对角线AC、BD的长分别为a、b, AC、BD相交于点O.(1)用含a、b的代数式表示菱形ABCD的面积S;(2)若a=3cm,b=4cm菱形ABCD的面积和周长边形的定义:。
(2)平行四边形的性质:,,
(3)平行四边形的判定条件:
★的四边形是平行四边形。(定义)
★的四边形是平行四边形。
★的四边形是平行四边形。
2.新知
(1)菱形的定义:
(2)菱形的性质:
★菱形是特殊的平行四边形。它对称图形;
★菱形的
★菱形的对角
★菱形的对角线且
四.小结反思
1.我的错误:
2.我的收获:
五.检测反馈(5分钟)
第79页,第1题
4.知识运用
(1)在菱形ABCD中,AE⊥BC,AF⊥CD,且垂足E、F分别为BC、CD的中点,那么∠EAF =().
9.4 菱形的性质与判定习题课 (学案)
9.4 矩形、菱形、正方形——菱形的性质与判定习题课(学案)主备人:李婷婷 审核人:朱国华 班级 姓名 学号 【基础练习】 1、菱形具有平行四边形不具有的性质是 ( )A .对边相等B .对角线互相平分C .对角相等D .对角线互相垂直2、下列条件中,不能判定四边形ABCD 为菱形的是 ( )A .AC ⊥BD ,AC 与BD 互相平分B .AB =BC ,AD =CD ,且AC ⊥BDC . AB =BC =CD =DA D .AB =CD ,AD =BC ,AC ⊥BD3、如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,DH ⊥AB 于H ,连接OH ,∠DHO =30°,则∠CAD 的度数是 ( )A .20°B .25°C .30°D .40°4、将矩形纸片ABCD ,按如图所示的方式折叠,点A 、点C 恰好落在对角线BD 上,得到菱形BEDF ,若BC =3,则AB 的长为 ( )A .1B .2C .3D .325、如图,矩形ABCD 的对角线AC 、BD 相交于点O ,CE ∥BD ,DE ∥AC ,若AC =6,则四边形CODE的周长 cm .6、已知,菱形的周长为20㎝,其中一条对角线的长为6㎝,那么它的另一条对角线的长为 cm ;该菱形的面积为 cm 2.7、如图,将两条宽度都是为1的纸条重叠在一起,则四边形ABCD 是 形,若∠ABC=45°,四边形ABCD 的面积为 .8、如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AB =5,AC =6,过点D 作DE ∥AC 交BC 的延长线于点E .求△BDE 的周长.9、已知:如图,在□ABCD 中,点E 为BC 边上的一点,连结AE 、BD 且AE =AB ,∠AEB =2∠ADB , AB C E D O A B C D A B C D FE 第4题 第3题 第5题 A B C ED O 第7题求证:四边形ABCD 是菱形.【拓展提升】10、如图,点A 是∠NOM 边OM 上一点,AE ∥ON ,(1)在图中作∠NOM 的角平分线OB ,交AE 于点B ;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)中,过点A 画OB 的垂线,垂足为点D ,交ON 于点C ,连接CB ,将图形补充完整,并证明四边形OABC 是菱形.11、已知:如图,□ABCD 中,AB =4,AD =2,∠ADC =60°,将□ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D ′处,折痕交CD 边于点E .(1)求证:四边形BCED ′是菱形.(2)若点P 是直线l 上的一个动点,请计算PD ′+PB 的最小值.A OE N M 完成时间家长签字A D CE B。
9.4菱形判定教案
沭阳如东实验学校初二数学教学设计 9.4菱形的判定 主备人:殷佳佳 审核人:孟庆栋 日期:2014-3-28 教学目标: 1. 掌握菱形的判别条件并能应用于菱形的判定 2. 在操作和观察、分析过程中发展主动探究习惯和初步的审美意识 3. 进一步了解和体会说理的基本方法 教学重点:菱形的判定定理的综合应用 教学难点:菱形的判定定理的综合应用 作业布置:课本84页9,10,
一、复习巩固: 菱形的性质:边: 角: 对角线: 对称性: 二、合作探究: 1、一 个四边形满足什么条件,它就是菱形呢? 定义法: 有一组邻边相等的平行四边形叫做菱形. 几何语言: 在□ABCD中 ∵AB=BC ∴□ABCD是菱形 2、四边形的边满足什么条件,它就是菱形呢? 定理: 几何语言: 3、四边形的对角线满足什么条件,它就是菱形呢? 定理: 几何语言: 归纳总结:菱形的判别方法有哪些?
三、个性展示: 1、如图,矩形ABCD(AD>AB),对角线AC的垂直平分线与边AD、BC分别相交于点E、 F.分别连结AF和CE.
(1)说明四边形AFCE是菱形; (2)若AB=4cm,BC=8cm,求BF的长.
A B C D E
F O 2、如图,在梯形ABCD中,AB∥CD,BC=CD,AD⊥BD,E为AB中点. 四边形BCDE是菱形吗?为什么?
四、整合提升: 1、将两张等宽的矩形纸片重叠在一起(如图),你知道重叠的部分即四边形是 什么图形?
五、这节课你学到了什么? 六、反馈训练: 1、在四边形ABCD中,AB//DC,AD//BC.请再添加一个条件,使四边形ABCD是菱形.你添加的条件是_____________.(写出一种即可) 2、下列关于菱形的说法中正确的是( ) A.对角线相等的四边形是菱形 B.对角线互相垂直且平分的四边形是菱形 C.菱形的对角线互相垂直且相等 D.菱形的对角线相等且互相平分 3、如图,两条笔直的公路l1、l2相交于点A,村庄C的村民在公路的旁边建三个加工厂 A、B、D,已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是?
菱形的性质
§9.4.3菱形的性质学习目标:1.理解菱形的定义,探索菱形的特征;2.能简单运用菱形的特征解决问题. 学习重点:菱形的性质;学习难点:菱形性质和直角三角形的知识的综合应用. 教学过程:Ⅰ.创设情境,引入课题如图,BO 是等腰三角形ABC 的底边AC 上的中线,画出△ABC 关于点O 对称的图形.思考:图中的四边形有什么特点?归纳: 的平行四边形.....叫做菱形.菱形是一种特殊的平行四边形,它具有平行四边形的一切性质.另外它还具有哪些特殊性质?(1) 图中有哪些相等的线段相等?哪些角相等? (2) 菱形的对角线有什么特殊的位置关系? 归纳:1.菱形既是 对称图形又是 对称图形;2.菱形的 都相等;3.菱形的对角线 ,且 . 尝试练习:①在菱形ABCD 中,若AD =5,OA =3,则AC = ,BD = ,菱形周长= ;若∠ADC =60°,则∠OAB = °.②设菱形的对角线AC =a ,BD =b ,用含a 、b 的代数式表示菱形的面积为 . 一般地:对角线互相垂直的四边形的面积等于 . ③菱形具有而一般平行四边形不具有的性质是 ( ) A .对角线相等 B .对角线互相平分 C .对角相等 D .对角线互相垂直④菱形的两条对角线长分别为10cm 和24cm ,则它的周长是________,面积是________.(请画草图说明)Ⅱ.例题讲解,熟练应用1. 如图,在菱形ABCD 中,点E 、F 分别是CB 、CD 上的点,且CE =CF ,求证:AE =AF .FD CBA E2.在菱形ABCD 中,∠B ∶∠BAD =1∶2,周长为20cm ,试求菱形ABCD 的对角线AC 和BD 的长.归纳:有一个内角为60°的菱形,短的对角线等于 ;长的对角线等于 . 拓展1:如图,在菱形ABCD 中,E 是AB 的中点,且DE ⊥AB .①求∠ABD 的度数;②若菱形的边长为2,求菱形面积.拓展2:如图,在菱形ABCD 中,点E 、F 分别为BC 、CD 上的点,且∠B =∠F AE =60°∠BAE =20°(1)说明△AEF 是等边三角形;(2)求∠CEF 的度数.思考 1:假设点E 和点F 能在边BC 和CD 上滑动,且保持∠EAF =60°,上诉结论是否成立?2:在滑动的过程中,四边形AECF 的面积是否会发生变化?课时训练一、选择题1. 下列性质中,菱形具有而矩形不一定具有的( )A .对角线平分一组对角B .对角相等C .对角线互相平分D .对边平行且相等 2. 已知菱形ABCD 的对角线AC 、BD 的长度是6和8,则这个菱形的周长是( )A .20B . 14C . 28D . 24 3. 已知一个菱形的周长是20cm ,两条对角线的比是4∶3,则这个菱形的面积是( )A .12cm 2B . 24 cm 2C . 48 cm 2D . 96 cm 2 4. 已知菱形ABCD 中,∠BAD =120°,AC =4,则该菱形的面积是 ( )A .16 3B . 16C . 8 3D . 8E D C B A5. 在菱形ABCD 中,∠BAD =80°,AB 的垂直平分线交对角线AC 于点F ,垂足为E ,连接DF ,则∠CDF 的度数为 ( ) A .60° B .65° C .70° D .80°6. 如图,菱形ABCD 中,E 是AD 的中点,将△CDE 沿CE 折叠后,点A 和点D 恰好重合.若AB =4,则菱形ABCD 的面积为 ( ) A .2 3 B . 4 3 C . 8 2 D . 8 3 二、填空题7. 如图所示,在菱形ABCD 中,两条对角线AC =6,BD =8,则:①此菱形的边长为 ;周长为 .②此菱形的面积为 ;菱形的高为 . ③此菱形对角线的交点O 到AB 的距离为 .8. 己知:如图,菱形ABCD 中,∠B =60°,AB =4,则以AC 为边长的正方形ACEF 的周长为 . 9. 如图,菱形ABCD 的边长是2cm ,E 是AB 中点,且DE ⊥AB ,则S 菱形ABCD = cm 2.10.如图,菱形ABCD 中,∠B =60°,AB =2cm ,E 、F 分别是BC 、CD 的中点,连结AE 、EF 、AF ,则△AEF 的周长为 cm .11.如图所示,已知菱形ABCD 的对角线AC ,BD 的长分别为12cm ,16cm ,AE ⊥BC 于点E ,则AE 的长是 .12.如图,菱形ABCD 的边长为4,∠B =120°,M 为DC 的中点,点N 在AC 上.(1)若DC =NC ,则∠NDC = °;(2)若N 是AC 上动点,则DN +MN13.将矩形纸片ABCD 按如图所示的方式折叠.恰好得到菱形AECF .若AD =3,则菱形AECF 的面积为 .第5题第6题第7题 第8题 第9题第10题第11题 第12题 第13题三、解答题14.如图,已知四边形ABCD 是菱形,点E 、F 分别是边CD ,AD 的中点.求证:AE =CF .15.如图,菱形ABCD 中,CE ⊥AB ,交AB 的延长线于点E ,CF ⊥AD ,交AD 的延长线于点F . 请你猜猜CE 和CF 的关系,并证明你的猜想.16.已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B 、C 重合), 以AD 为边作菱形ADEF (A 、D 、E 、F 按逆时针排列),使∠DAF =60°,连接CF . (1)如图1,当点D 在边BC 上时,求证:①BD =CF ;②AC =CF +CD ;(2)如图2,当点D 在边BC 的延长线上且其他条件不变时,结论AC =CF +CD 是否成立?若不成立,请写出AC 、CF 、CD 之间存在的数量关系,并说明理由; (3)如图3,当点D 在边CB 的延长线上且其他条件不变时,补全图形,并直接写出AC 、CF 、CD 之间存在的数量关系.17.已知,△ABC 为等边三角形,点D 为直线BC 上一动点(点D 不与B 、C 重合). 以AD 为边作菱形ADEF ,使∠DAF =60°,连接CF . (1)如图1,当点D 在边BC 上时,①求证:∠ADB =∠AFC ;②请直接判断结论∠AFC =∠ACB +∠DAC 是否成立;(2)如图2,当点D 在边BC 的延长线上时,其他条件不变,结论∠AFC =∠ACB +∠DAC 是否成立?请写出∠AFC 、∠ACB 、∠DAC 之间存在的数量关系,并写出证明过程;(3)如图3,当点D 在边CB 的延长线上时,且点A 、F 分别在直线BC 的异侧,其他条件不变,请补全图形, 并直接写出∠AFC 、∠ACB 、∠DAC 之间存在的等量关系.图1 图2 图3AB C DEFAB C D EFDBA图1 图2 图3AB C DEF AB C D EFDBA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在□ABCD中 ∵AC⊥BD,
∴ □ ABCD是菱形
菱形的判别方法
一组邻边相等的平行四边形是菱形. 四边都相等的四边形是菱形. 对角线互相垂直的平行四边形是菱形.
明辨是非
⒈对角线互相垂直的四边形是菱形. ⒉对角线互相垂直的平行四边形是菱 形. ⒊对角线相等的平行四边形是菱形.
⒋对角线互相垂直平分的四边形是菱 形.
几何语言: ∵AB=BC=CD=AD, ∴四边形ABCD是菱形
合作学习
当平移一个平行四边形活动框架的一边,使这个平行 四边形成菱形时,它的两条对角线互相垂直。反过来, 对角线互相垂直的平行四边形是菱形吗?
在□ABCD中,AC⊥BD, □ABCD是 菱形吗?为什么?
B
A
D
C
菱形的判定定理2:对角线互相垂直的平行四边 形是菱形.
A F D
B
E
C
一展身手
在□ABCD中,E、G、F、H分别是AD、 AB、BC和CD边上的点,且EF⊥GH, AE=CF,DH=BG,试说明EGFH是菱形.
A G O B F C H E D
课堂小结:
1、一组邻边相等的 平行四边形 是菱形. 2、四边相等的 四边形 是菱形. 平行四边形 3、对角线互相垂直的 是菱形.
明辨是非
• 下列条件中,能判定四边形是菱形的是( ) A、对角线垂直 B、两对角线相等 C、两对线互相平分 D、两对角线互相垂直平分
例题精讲
1、平行四边形ABCD的两条对角线AC,BD相交 于点O,OA=3,OB=4,AB=5, (1)AC,BD互相垂直吗?为什么? (2)四边形ABCD是菱形吗?为什么?
9.4菱形(2)
菱形的定义:
菱形的判 定定理1
有一组邻边相等的 平行四边形是菱形.
A 符号语言: B C D
∵四边形ABCD是平行四边形
且AB=BC
∴四边形ABCD是菱形
合作学习
1、命题“菱形的四条边相等”的逆命题是什么? 逆命题:四边相等的四边形是菱形。
真命题
A D
请大家自己进行证明
B
C
菱形的判定定理1:四边都相等的四边形是菱形.
例题精讲
2、在四边形ABCD中,AD∥BC,对角 线AC的垂直平分线与边AD、BC相交于 点E、F.四边形AFCE是菱形吗?
A 1 O B 2 F C E D
一展身手
已知:如图,点E、F、G、H分别是矩形ABCD四 条边的中点,四边形EFGH是菱形吗?证明你的 结论。
A E B H D G
F
C
一展身手
作业:书P84 9 10
课外思考
小明在布置教室时,把两种宽度相同但颜色不 同的彩带粘贴在一起,发现重叠部分是一个菱 形(如图),他任意转动,发现重叠部分仍是 一个菱形,你知道这是为什么吗?
ADA B源自DFB E C C
课外思考
如图,在△ABC中,AD是角平分线,点E在 AB上,且AE=AC,EF∥BC,分别交AC、AD 于点F、G,CE交AD于点O.求证:四边形 CDEG是菱形. A
如图,在△ABC中,AD⊥BC,垂足为D,点 E、F分别是AB、AC的中点.当△ABC满足 什么条件时,四边形AEDF是菱形?请说明 A 理由.
E
F
B
D
C
一展身手
如图,四边形ABCD的对角线AC、BD相交于O,且
AD∥BC,AD=BC.请补充一个条件:
四边形ABCD为菱形.
A
O
使
D
B
C
一展身手
如图,□ABCD中,AE平分∠BAD 交BC于E,BF平分∠ABC交AD于F, 求证:四边形ABEF是菱形.
E B
G O D
F C
