结构力学 几何组成分析习题课
考研专业课复习 东南大学结构力学习题集及答案
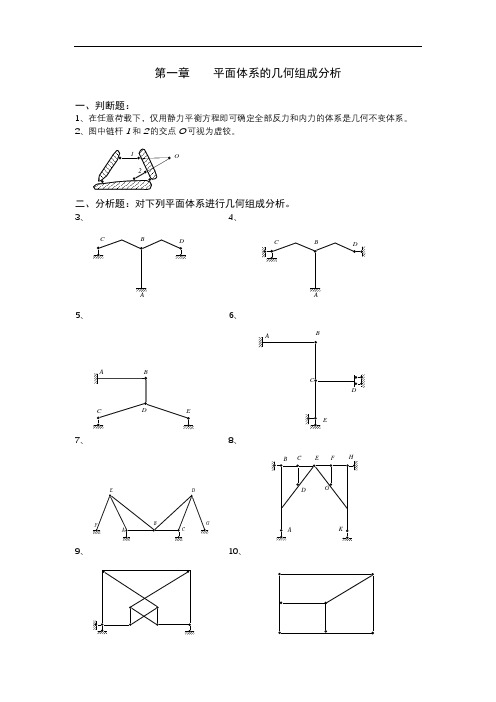
第一章 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBACDB5、 6、A CD BEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、123456781234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、BA CFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二章 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
aa(a)BCa aAϕ2a2(b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0, R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2()↑。
(d)9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:N1=N2=N3= 0。
13、图(h)所示桁架DE杆的内力为零。
a a(h)(i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
15、图(j)所示桁架共有三根零杆。
结构力学第2章平面几何组成分析

几何组成作业题
2-3, 2-5 2-7, 2-8 2-10, 2-12 2-16, 2-21 交作业时间:周 3
§2. 几何组成分析
补充作业:(不做) 2-1 (b)试计算图示体系的计算自由度
解:
或:
W 8 3 11 2 3 1 W 1 3 5 2 2 2 10 1
方法1: 若基础与其它部分三杆相连,去掉基础只分 析其它部分 方法2: 利用规则将小刚片变成大刚片.
例4: 对图示体系作几何组成分析
解: 该体系为瞬变体系. 方法3: 将只有两个铰与其它 部分相连的刚片看成链杆. 书上例题2-1、2-3同。
方法1: 若基础与其它部分三杆相连,去掉基础只分 析其它部分 方法2: 利用规则将小刚片变成大刚片. 方法3: 将只有两个铰与其它部分相连的刚片看成链杆.
计算自由度大于零一定可变; 若等于零则一定不变吗? 五. 计算自由度 六. 多余约束 必要约束 计算自由度小于零一定不变吗? 计算自由度小于零一定有多余约束
§2.1 基本概念
§2-1 基本概念 一. 几何不变体系 几何可变体系 二. 刚片 三. 自由度 四. 约束(联系) 链杆 单铰 复铰 虚铰 实铰 五. 计算自由度 六. 多余约束 必要约束
练习: 对图示体系作几何组成分析
方法1: 若基础与其它部分三杆相连,去掉基础只分 析其它部分 方法2: 利用规则将小刚片变成大刚片. 方法3: 将只有两个铰与其它部分相连的刚片看成链杆. 方法4: 去掉二元体. 方法5: 从基础部分(几何不变部分)依次添加.
练习: 对图示体系作几何组成分析
无多余约束的几何不变体系。
三杆不平行不变 平行且等长常变 平行不等长瞬变
§1. 几何组成分析
结构力学几何组成分析共36页

60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
结构力学几何组成分析
26、机遇对于有准备的头脑有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一, 也是成 功的利 器之一 。没有 它,天 才也会 在矛盾 无定的 迷径中 ,徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿.丘吉 尔。 30、我奋斗,所以我快乐。--格林斯 潘。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
结构力学

二、几何组成分析的目的
(1)判别体系是否几何不变; (2)按什么规律组成一个几何不变体系; (3)区分结构是静定的还是超静定的。
返回
§2-2 刚片、约束、体系自由度 和计算自由度
一、体系自由度的定义:
体系自由度:体系的独立运动方式数,或确定体系位置所需的独立坐标数。 例如:平面内一个点有2个自由度,一个刚片有3个自由度。
在某一瞬间可以产生微小运动的体系,称为瞬变体系,它是可变体系 的一种特殊情况。
FN
瞬变体系在工程中不能采用。
FP 2 Sin
如果一个几何可变体系可以发生大位移,则称为常变体系。
法则Ⅱ: 两刚片法则,两刚片用不完全 相交于一点且不完全平行的三 根连杆连接而成的体系,是几 何不变而无多余约束的。
两刚片以一铰及不通过该铰的一个链杆相联,构成几何不变体系。
法则Ⅲ:三刚片六连杆法则,三刚片之间用六连杆彼 此两两相连接,六连杆所组成的三个铰不在 同一条直线上,则所组成的体系是几何不变 而无多余约束的。
讨论
虚铰在无穷远的情形
二元体的概念
二元体的定义:从任意基础上用不共线的两根连杆形成一个 新结点的装置。
2.结论:给定体系为几何不变无多余约束体系。
返回
例六
试分析图示体系是否为几何不变系
解:1.几何组成分析 去除二元体 刚片Ⅰ、Ⅱ、Ⅲ符合三刚片法则。
2.结论:给定体系为几何不变无多余约束体系
返回
例七 试分析图示体系是否为几何不变体系
解:1.几何组成分析 ABEF与基础之间符合两刚片法则,组成新刚片Ⅲ 在刚片Ⅲ上增加一个二元体形成新节点G,由二元体的性质知 体系仍为几何不变,看作刚片Ⅳ CDHI看作刚片Ⅴ,刚片Ⅳ、Ⅴ之间三根连杆交于点D。 2.结论:该体系为几何瞬变体系。
结构力学:自由度及几何分析

实例分析:
B
C
A
F
E
F
例1
1
2
3
D
E
G C
A
B
例2
B C DE F
J
L
I
H
K
例3
5 4
6
例4
A
BC
D
EF例5FGHC
A
B
D
E
例6
实例分析 1
W=3×8-2×10-4=0 0 W=2×6-8-4=0
可能为几何不变体系。 利用二元体,不可主观臆测,认为平行
(将三刚片规则中的一个刚片换成链杆, 即为二刚片规则)
两个刚片用一个铰和一根不通过此铰的 链杆相连,几何不变。
不通过此铰:通过此铰为瞬变。 铰:可以是两根链杆组成的虚铰。 两个刚片用三根不平行、也不交于一点
的链杆相连,几何不变。
图示为一无多余约束的几何不变体系
将杆AC、BC均看成刚片, 就成为两 刚片组成的无多余约束几何不变体系
2.2.4自由度
O.
. O’
A
B
C D
虚铰
联结两刚片的两 根不共线的
链杆相当于一个 单铰即瞬铰。
2.2.4体系的自由度计算
1.定义 W=各部件的自由度总和-全部约束数 2. W=3m-2n - r [例1] m——刚片数(不计基础); n——单铰数(一个单铰、定向支座相当于两
个约束); r——支座链杆数(固定铰支座相当于2个链杆,
原体系的几何构造性质。
引申、两刚片以不互相平行,也不相交于一点的三根链杆相 联,组成无多余约束的几何不变体系。
2006典型例题解析--第1章 几何组成分析

第1章几何组成分析§1 – 1 基本概念1-1-1 名词解释●几何不变体系——结构(静定或超静定)在不考虑材料变形情况下,几何形状和位置不变的体系,称为几何不变体系。
●几何可变体系在不考虑材料变形情况下,形状或位置可变的体系,称为几何可变体系。
●刚片在平面上的几何不变部分。
●自由度确定体系位置所需的独立坐标数目。
●约束(联系)能够减少自由度的装置。
减少自由度的个数为约束个数。
①链杆——相当1个约束②铰——相当2个约束③虚铰——相当2个约束④复铰——相当n-1个单铰的作用●多余联系不能减少自由度的联系,称Array为多余联系。
●必要联系去掉时能够增加自由度(或维持体系不变性必须)的联系。
●瞬变体系几何特征:几何可变体系经过微小位移后成为几何不变体系。
静力特征:受很小的力将产生无穷大内力,因此不能作结构。
1-1-2 分析规则在不考虑材料应变所产生变形的条件下,构成无多余约束几何不变体系(静定结构)的基本规则如下:●三刚片规则三个刚片用不在同一条直线上的三个铰(或虚铰)两两相联。
●二刚片规则2结构力学典型例题解析两个刚片用不交于一点也不全平行的三根链杆相联;或:两个刚片用一个铰和不通过该铰心的链杆相联。
●二元体规则什么是二元体(二杆结点):两根不在同一条直线上的链杆联接一个新结点的装置,称为二元体。
在一个体系上增加或减少二元体不影响其几何不变性。
1-1-3 几何组成分析一般方法(步骤)(1)去二元体(二杆结点)。
(2)分析地基情况:上部体系与地基之间●当有满足二刚片规则的三个联系时,去掉地基,仅分析上部体系;●当少于三个联系时,必为几何常变体系;●当多于三个联系时,将地基当作一个刚片进行分析。
(3)利用规则找大刚片(最简单情况为:三个铰接杆件为刚片)。
(4)使用几何组成规则进行分析。
利用三刚片规则分析时:首先找出三个刚片,(满足三刚片规则的连接条件,即每两个刚片间有一个铰(或虚铰),然后再标出虚铰位置,最后看三个铰是否构成三角形。
02-2结构力学第二章 平面体系的几何组成分析-作业答案汇总
38 3 2 29 3 3
3个单铰结点, 3个折算为2个单铰结点的复铰结点
支杆
b3
11/73
(II III) 刚片II
(I II)
刚片III
几何不变且无多余约束
j9 单链杆:12根 复链杆:2根 折算为6根单链杆
W 2 j b 29 12 6 0
5/73
【作业1】分析图示体系的几何构造
图3
【作业1】分析图示体系的几何构造
图4
先考察如图所示结构
∞(II III)
9/73
【作业2】求图示系统的计算自由度
刚片 m 1 单刚结点 g 4 铰结点 h 0 支杆 b 3
内部无多余约束刚片
W 3m 3g 2h b
31 3 4 3 12
10/73
【作业2】求图示系统的计算自由度
刚片 m 8
单刚结点 g 2
W 3m 3g 2h b
铰结点 h 9
刚片 m 14 单铰链结点 h 18
刚片II
刚片III
(I II)
(I III) 刚片I
瞬变体系
其中折算为2个单铰结点的 复铰结点有6个
∞(II III)
其中折算为3个单铰结点的 复铰结点有2个 单刚结点 2个 g 2 和基础相连的支杆 0个 b 0
W 3m 3g 2h b
314 3 2 218 0
∞(II III)
刚片II (I II) (I III) 刚片III
刚片I
几何不变且无多余约束
(I II) 刚片II (I III) 刚片III
刚片I
几何不变且无多余约束
7/73
【作业2】求图示系统的计算自由度
图1 并进行几何构造分析
结构力学第二章几何组成分析
jy = 3x3-2x2-5 = 017 = 3x2-1-5-0几何不变体系,且无多余约束[例题2-2-2 ]对图示体系进行几何组成分析。
两刚片规则解:(a)厂-―一:J -:i^ = 3x5-3x2-2x2-5-0几何不变体系,无多余约束(b)— I 辽—HJ7 = 3x32-2x46-3 = l17-2x18-32-3=1几何可变体系[例题2-1-5 ]计算图示体系得自由度。
刚架自由体。
^ = 3x5-3x6-3 = -6J7 = 3x7-3x8-3=-6几何不变体系,有6个多余约束[例题2-2-1 ]对图示体系进行几何组成分析。
两刚片规则几何可变体系[例题2-1-2 ]计算图示体系得自由度。
桁架几何不变体系,有多余约束。
jy = 3xl5-2x22-3 = -2FF=2x8-15-3 = -2几何不变体系,有两个多余约束[例题2-1-3 ]计算图示体系得自由度。
桁架自由体。
jy = 3xll-2xl5-3 = 0FF=2x7-ll-3=0几何不变体系,无多余约束[例题2-1-4 ]几何不变体系,且无多余约束[例题2-2-3 ]对图示体系进行几何组成分析。
两刚片规则17=2x12-21-3 = 0几何不变体系,且无多余约束[例题2-2-4 ]对图示体系进行几何组成分析。
两刚片规则计算图示体系得自由度。
「厂 ' -,几何可变体系。
iy=2x9-15-3=0 几何不变体系,且无多余约束[例题2-3-1 ]对图示体系进行几何组成分析。
两刚片规则iy = 3xl0-2xl4-3=-l FF=2x«-10-3 = -l 几何不变体系,有一个多余约束[例题2-2-5 ]对图示体系进行几何组成分析。
二元体规则^ = 3x19-2x27-3=0iy= 2x11-19-3 = 0几何不变体系,且无多余约束[例题2-2-6 ]对图示体系进行几何组成分析。
两刚片规则,三刚片规则iy = 3x4- 2x3-3- 3= 0几何不变体系,且无多余约束[例题2-2-7 ]对图示体系进行几何组成分析。
结构力学 第二章 结构的几何构造分析.
A
B
C
Ⅲ
如图示,三刚片用三个不共线的 铰相连,故:该体系为无多余约 束的几何不变体系。
结构力学
36
(Ⅰ,Ⅱ)
Ⅰ (Ⅰ,Ⅲ) Ⅱ
Ⅲ
Ⅰ Ⅱ
Ⅲ
(Ⅰ,Ⅲ)
三刚片以三个无穷远处虚铰相连 组成瞬变体系
(Ⅱ,Ⅲ)
(Ⅰ,Ⅱ)
(Ⅱ,Ⅲ)
如图示,三刚片以共线三铰相连几何瞬变体系
2019/9/6
结构力学
② 在结构计算时,可根据其几何组成情况,选择适 当的计算方法;分析其组成顺序,寻找简便的解 题途径。
由若干杆件用各种结点连接而成的杆件体系,当 能承受一定范围内任意荷载时,称为杆件结构。不能 承受任意荷载的体系称为机构。
2019/9/6
结构力学
5
2-1-2 体系的分类
在忽略变形的前提下,体系可分为两类:
静定结构 — 几何特征为无多余约束几何不变。
2019/9/6
结构力学
21
2-2-1 静定结构组成规则
规则1 一刚片规则(二元体规则)
一个刚片与一个 点用两根链杆相连, 且三个铰不在一直线 上,则组成几何不变 的整体,并且没有多 余约束。
2019/9/6
图2-8
结构力学
A C
1 A2
22
在体系上用两个不共线杆件或刚片连接一个新
掌握: 体系的计算自由度的概念及计算,无多余 约束的几何不变体系的几何组成规则,及 常见体系的几何组成分析。
了解: 结构的几何特性与静力特性的关系。
2019/9/6
结构力学
4
§2-1 几何构造分析的几个概念
2-1-1 几何构造分析的目的
① 研究结构正确的连接方式,确保所设计的结构能 承受荷载,维持平衡,不至于发生刚体运动。
几何构造分析练习题
) )
4、在工程中,瞬变体系不能作为结构的原因是( A.会发生微小位移 B.约束的数量不足 C.正常荷载作用下,可能产生很大的内力 D.会产生较大的位移 5、下图中链杆 1 和链杆 2 的交点可视为虚铰。 (
1
) 。 (福州大学 2012)
) (河北工业大学 2012)
2
6、下图所示体系虽有 3 个多余约束,但未保证其几何不变,哪两根链杆是不能同时去掉的。 ( (中国矿业大学 2012) A.a 和 e B. a 和 b
B 1 A 2 C
瞬变体系与常变体系的两个判定规则: 1) 微小变形规则 让体系发生微小变形,如果三个铰还在同一直线上,则是常变体系,不在同一直线上,则是瞬 变体系。 2) 平行等长规则(特别注意平行等长的对象是谁) 组成无穷远铰的两根平行链杆与另外两铰的连线平行且等长,则为常变体系,否则为瞬变体系。 【例题】图示体系的计算自由度 W 1 ,是几何_________变体系;若在 A 点加一竖向链杆支座,则 称为几何_____________变体系;若在 A 点加一固定铰支座,则称为______变体系。 (哈尔滨工业大 学 2010 年)
J
C
D
E
F
A
B
【练习题】试对图示体系作几何组成分析。 (东南大学 2015,湖南大学 2
J
E A B C
F D
【练习题】试对图示体系作几何组成分析。(东南大学 2013)
D E G H
F
A
B
C
9 / 19
§1-4 计算自由度
所有体系都是由部件加约束组成的。但约束可分为必要约束和多余约束。 体系所有的部件自由度之和减去所有的约束,就是体系的计算自由度。之所以叫计算自由度,是为 了与体系的真实自由度区分开来。体系的真实自由度等于所有部件自由度之和减去必要约束。 1. 单约束与复约束 约束可以分为单约束和复约束,两个刚片间的结合为单结合,三个刚片间的结合相当于两个单 结合。一般说来,n 个刚片间的复结合相当于(n-1)个单结合。 举例说明:用 1 个铰连接 5 个链杆,相当于(5-1)个单铰约束。因为 5 个独立的链杆共有(5×3) 个自由度,用一个铰连接起来后,整体有 2 个平动自由度,外加每根杆有 1 个转动自由度,共有 7 个自由度,因此体系获得了(15-7)=8 个约束,即(5-1)=4 个单铰约束。满足 n 个刚片间的复结 合相当于(n-1)个单结合这一结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E 1 b 3 A a c 2
D
B
C
1、去除基础; 2、去除二元体; 3、剩下部分为大三角形CDE、 小三角形abc由链杆1、2、 3相联; 4、故原体系为无多余约束的 几何不变体系。
O13 O23 O12
1、去除二元体; 2、找三刚片、三个铰; 3、三铰 4、故原体系为 瞬变体系。
Ⅰ
Ⅱ
Ⅲ
④
②
③
规则 连接对象 必要约束数 一 二 三 四 两刚片
一点一刚片
对约束的布置要求 三铰(实或虚)不共线 链杆不过铰
瞬变体系
三刚片
六个 三个 两个
三种 一种 两种 一种
三链杆不平行也不交于一点
两链杆不共线
射影几何中关于无穷远点和无穷远线的四点结论
•每个方向有一个无穷远点(即该方向各平行线的交点)。 •不同方向有不同的无穷远点。 •各无穷远点都在同一直线上,此直线称为无穷远线。 •各有限远点都不在无穷远线上。
C
Ⅰ
Ⅱ Ⅲ/
O13
O23
Ⅲ/ Ⅰ/
O12
Ⅱ/
A
B
Ⅲ
(Ⅰ,Ⅲ)
Ⅰ
•每个方向有一个无穷远点(即 该方向各平行线的交点)。 •不同方向有不同的无穷远点。 Ⅲ •各无穷远点都在同一直线上, 此直线称为无穷远线。 Ⅱ (ห้องสมุดไป่ตู้,Ⅲ) •各有限远点都不在无穷远线上。
图示三刚片用三个不共线的铰相联,故该体 系为无多余约束的几何不变体系。
故该体系为由两个多余约束的几何不变体系。
1、抛开基础,只分析上部。 2、图示两刚片用三根链杆相 联; 3、无多余约束的几何不变 体系。
1、刚片等效代换。 2、图示三刚片用三个不共线 的瞬铰相联; 3、无多余约束的几何不变 体系。
A
1、支座等效平移; 2、去除二元体; 3、大地与刚片A用三根交于一点的支杆相联; 4、故体系为瞬变体系。
无多余约束几何不变体系的组成规则
一、三刚片以不在一条直 线上的三铰相联,组成无 多余约束的几何不变体系。 C 三铰共线瞬变体系 A
B
两平行链杆于两铰连线 平行, 瞬变体系
三刚片以三对平行 链杆相联瞬变体系
A
二、两刚片以一铰及不通过该 铰的一根链杆相联组成无多余约束 的几何不变体系 。 三、两刚片以不互相平行,也 不相交于一点的三根链杆相联,组 成无多余约束的几何不变体系。
几种常用的分析途径 1、去掉二元体,将体系化简单,然后再分析。 2、如上部体系与基础用满足要求的三个约束相联可去掉 基础,只分析上部。 3、当体系杆件数较多时,将刚片选得分散些,用链杆组 成的虚铰相连,而不用单铰相连。
4、由一基本刚片开始,逐步增加二元体,扩大刚片的范 围,将体系归结为两个刚片或三个刚片相连,再用规则判定。 5、由基础开始逐件组装。 6、刚片的等效代换:在不改变刚片与周围的连结方式的 前提下,可以改变它的大小、形状及内部组成。即用一个等效 (与外部连结等效)刚片代替它。
A a
C
B
B 杆通过铰 瞬 变 体 系 瞬变体系
瞬 变 体 系
常 变 体 系
四、一点与一刚片用两根不 共线的链杆相联,组成无多余约 束的几何不变体系。
1
A
A
2
B
C
两根共线的链杆联一点 瞬变体系
两根不共线的链杆联 结一点称为二元体。
在一体系上增加(或减去)二元体不改变 原体系的机动性,也不改变原体系的自由度。
①
E A F B D G
1、分别由一根杆添加两个 二元体得到图示两个刚片; 2、图示两个刚片由四根链 杆相联; 3、该体系是有一多余约束 的内部几何不变体系。
E G C B
C
A
依次组装梁AB、BC、两杆结点E、G,链杆EG是多余约束。 该体系是有一多余约束的几何不变体系。
1、大地作一刚片Ⅲ,体系内找 出两个刚片Ⅰ、Ⅱ,按三刚片组 成法则组成一新刚片Ⅲ´; 2、体系内在找出两个刚片Ⅰ´、 Ⅱ´,三个新刚片以共线的三铰 O13、O12、O23相联,组成瞬变 体系。
