流体的平衡微分方程及其积分
工程流体力学2

§2-1 流体静压强及其特性
静压强:当流体处于平衡或者相对平衡状态时, 作用在流体单位面积上的力。
p lim Fn
A 0
A
pn
特性一:
流体静压强的作用方向沿着
作用面的内法线方向。
静止流体对容器的作用一定垂直于固体壁面。
§2-1 流体静压强及其特性
特性二:
静止流体中的任一点上,来自任意方向上的静压强都是相等的。
三、流体静压强的测量和液柱式测压计
常见的测压仪器有:液柱式测压计;金属式压强计(利用
金属的变形来测量压强);电测式仪表(将压强变化转化
为电信号的变化)等。
液柱式测压计的测量原理是以流体静力学基本方程 为依据的。
§2-3 重力场中流体的平衡
1、测压管
p pa
p p a gh
p pa
计。通常采用双U形管或三U形管测压计。
§2-3 重力场中流体的平衡
3. U形管差压计 用于测量两个容器或管 道流体中不同位置两点 的压强差。
p p A p B 2 gh 1 gh 2 1 gh 1 2 1 gh
§2-3 重力场中流体的平衡
§2-3 重力场中流体的平衡
水头:单位重量流体所具有的能量用液柱高度来表示。 静水头:位置水头和压强水头之和。
方程的几何意义:
在重力作用下,静止的不可压缩流体中各点的静水头都相等。
§2-3 重力场中流体的平衡
有自由液面的静压强公式: p0 p z z h g g
p p 0 gh
h 为任意点在自由液面下的深
度,即淹深。
流体内部的静压强包含两部分:
第2章 流体静力学2012

↑
标准大气压——最初规定在摄氏温度0℃、纬度45°、晴天时海平 面上的大气压强为标准大气压,其值大约相当于76厘米汞柱高。 工程大气压——工程上为了使用和换算方便,将1kgf/cm2作为一 个大气压称为工程大气压,简称气压 (at)。 ↓
2.5 静止液体对壁面的作用力的计算
↑
2.5.1 静止液体对平面 壁的压力 如图2.13所示,AB 为任意形状的平面,倾 斜放置于水中,与水面 成α 角,浸水面积为A, 其形心C的坐标为xc,yc, 形心C在水面下的深度为 h c。 1. 微小面积dA的作用力:
↑
(2.12)
p dx p dx (p )dydz ( p )dydz Xdxdydz 0 (2.13) x 2 x 2 1 p 化简得 X 0 x 1 p Y 0 (2.14 ) y 1 p Z 0 z
A
P sin ydA sin yC A hC A pC A
结论:潜没于液体中的任意形状平面的静水总压力P, 大小等于受压面面积A与其形心点的静水压强pc之积。 方向为受压面的内法线方向。 2. 总压力作用点(压心) 压力P的作用点称为压力中心,设为D点。由理论 力学知,合力对任一轴的力矩等于其分力对同一轴的 力矩和(合力矩定理),则 (对Ox轴求矩):
Py D ydP y (y sin dA) sin y 2 dA (2.37)
A A A
↓
式中 y 2 dA 是浸水面积A对x轴的惯性矩Jx,因此可得
↑
2 由惯性矩平行移轴定理知 J x J C yC A ,式中Jc为浸 水面积对通过形心C且与x轴平行的轴的惯性矩,故
第2章
流体静力学
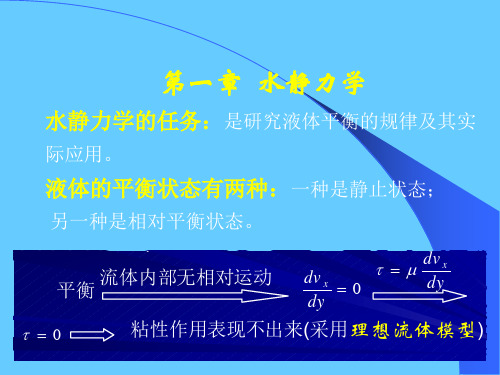
《水力学》第一章 水静力学
理论证明静水压力具有各项同性
四面体体积:V 1 xyz
6
总质量力在三个坐标
方向的投影为:
Fpx
1 6
xyzf x
Fpy
1 6
xyzf y
按照平衡条件,所有
Fpz
1 6
xyzf z
作用于微小四面体上
的外力在各坐标轴上
投影的代数和应分别 为零。
即在绕中心轴作等角速旋转的液体中有:只有r值相同的 那些点,即位于同心圆柱面上的各点 z p 才保持不变。
g
29
例1-1 有一圆柱形容器,内径为R,原
盛水深度为H,将容器以等角速度
绕中心轴oz旋转,试求运动稳定后容器 中心及边壁处的水深。
30
解 : 在 容 器 边 壁 处 r = R , Zs=Zw ,
1-3 等压面
等压面:静水压强值相等的点连接成的面(可
能是平面也可能是曲面)。
等压面性质:
1.在平衡液体中等压面即是等势面。 2.等压面与质量力正交。
15
1-3 等压面
等压面性质: dp ( U dx U dy U dz) dU
x
y
dz
1.在平衡液体中等压面即是等势面。
17
等压面性质2:等压面与质量力正交。
力 F 沿 ds 移动所做的功可写作矢量F与ds的数性积:
W F ds ( fxdx f ydy fzdz)dm W dUdm
因等压面上 dU=0 ,所以W=F*ds=0。也即质量力必 须与等压面正交。
注意: (1) 静止液体质量力仅为重力时,等压面必定 是水平面;
以 p' 表示绝对压强,p表示相对压强,pa 则表示当地
流体静力学

1 ∂p 1 ∂p 1 ∂p (X − ) dx + (Y − )dy + ( Z − )dz = 0 ρ ∂x ρ ∂y ρ ∂z ∂p ∂p ∂p ⇒ dx + dy + dz = ρ ( Xdx + Ydy + Zdz ) ∂x ∂y ∂z
静止流体中, 只是坐标的函数: ),所以 静止流体中,静压强 p 只是坐标的函数:p=f(x,y,z),所以 ),
–质量力 质量力——重力、惯性力,用单位质量 重力、 质量力 重力 惯性力,
py
C dz dx o A x pz m
px pn dy B y
– 表面力——仅有压力作用:px、py、pz、 图2-2 表面力——仅有压力作用: ——仅有压力作用 pn(n为任意方向)分别表示作用在垂 为任意方向) 为任意方向 直于x、 、 直于 、y、z 轴的坐标面和斜面 质量力 上的静压强, △ABC 上的静压强,Px、Py、Pz、Pn 表示总压力。 表示总压力。
略去二阶以上高阶小量后, 略去二阶以上高阶小量后,得:
z dz 1 ∂p p− dx A1 A 2 ∂x p dy y dx
1 ∂p p1 = p − dx 2 ∂x
1 ∂p p2 = p + dx 2 ∂x
A2
p+
1 ∂p dx 2 ∂x
x
图2-3 静止流体中六面体微元
第二章 流体静力学
3. 导出关系: 导出关系: 根据流体平衡的充要条件:静止流体所受的所有外力在各个坐标轴方 根据流体平衡的充要条件 静止流体所受的所有外力在各个坐标轴方 向上的投影之和为零, 向上的投影之和为零,即 方向为例: 方向为例 ∑F = 0。以x方向为例:
说明: 以上特性不仅适用于流体内部,而且也适用于 说明: 以上特性不仅适用于流体内部, 流体与固体接触的表面。 流体与固体接触的表面。
工程流体力学22流体平衡微分方程

2
1 6
3 p x 3
dx 2
3
p
p x
dx 2
1 2
2 p x 2
dx 2
2
1 6
3 p x 3
dx 2
3
略去二阶以上无穷小量后,分别等于
p 1 p dx 2 x
p 1 p dx 2 x
第二节 流体平衡微分方程
一、流体平衡微分方程式(推导)
垂直于x轴的左、右两微元面上的总压力分别为
第二节 流体平衡微分方程
静压强是空间坐标的连续函数
p p(x, y, z)
求静压强分布规律 研究平衡状态的一般情况 推导平衡微分方程式
流体静力学基本方程
第二节 流体平衡微分方程
一、流体平衡微分方程式(推导)
在静止流体中任取一平行六面体的流体微团, 边长为 dx,dy,dz的微元,中心点静压强为p(x,y,z)
1 p
f x x 0
第二节 流体平衡微分方程
一、流体平衡微分方程式(推导)
同理得
fx
1
p x
0
1 p
f y y 0
fz
1
p z
0
写成矢量形式
f
1
p
0
流体平衡微分方程式 欧拉平衡微分方程式
第二节 流体平衡微分方程
f
1
p
0
物理意义
在静止流体中,某点单位质量流体的质量力
与静压强的合力相平衡。
第二节 流体平衡微分方程
四、等压面 1. 定义
在流体中,压强相等的各点所组成的面称为等压面
等压面可以用p(x,y,z)=常数来表示。 dp=0
几点说明 对不同的等压面,其常数值是不同的 流体中任意一点只能有一个等压面通过。
第2章流体静力学1

P A
dP dA
B
A pn p
N
N'
p
1、静止流体表面应力只能是压应力或压 强,且静水压强方向与作用面的内法 线方向重合。
2、作用于静止流体同一点压强的大 小各向相等,与作用面的方位无关。
即有:
p x p y p z pn
证明:由于液体处于平衡状态,则有 F 0 ,即各向分力投影之和亦为
测压管水头( Z + p/ ρg ):单位重量液体的总势能。
p1/ρ
g
注意:位置水头和压强 水头都属于比能。 水头计算是对被研究流 体而言的,测量压强时 的工作流体可能与被测 流体不同。 (2) (1)
h
p2/ρg
Z1
Z2
o
o
• 重力作用下静水压强的分布规律
静水力学基本方程又可写为:
p g
zc
第2章 流体静力学
第一节 静止流体中应力的特性 第二节 流体平衡微分方程 第三节 重力场中流体静压强的分布规律 第四节 流体静力学基本方程讨论 第五节 作用在平面壁上的静水总压力 第六节 作用在曲面壁上的静水总压力
第一节 静止流体中应力的特性
一、静水压强的定义:
p lim
二、静水压强的特性:
A 0
p p 0 U U 0
第三节 重力场中流体静压强的分布规律
• 流体静力学的基本方程:反映静止流体中某一点的静水 压强的大小与该点空间坐标的关系。
质量力:
X Y 0,Z g
z p0
h
H A
流体平衡微分方程的全微分式
dp ( Xdx Ydy Zdz )
压强
真空度pv
工程流体力学
2.3.4 水头、液柱高度和能量守恒(略)
2.3.5 压强的计量单位
法定单位:
帕斯卡,简称帕。1Pa = 1 N/m2。1MPa = 106 Pa
2 流体静力学
2.1 静止流体中压强的特性
2.1.1 静压强定义
静止流体中的压强。平衡状态 F 2(Pa) p lim N/m A 0 A
2.2.2 静压强特性
a.静压强方向沿作用面的内法线方向 b.任一点静压强的大小与作用面的方位无关
从平衡状态下的流体中 取一微元四面体OABC,如 图所示取坐标轴。
绕铅垂轴等速旋转流体特点: 等压面为旋转抛物面,在同一水平面上,轴心 处压强最低,边缘处压强最高。
其它单位:
1atm(标准大气压)=101325 Pa = 1.034kgf/cm 2 = 760 mmHg 1at(工程大气压)=1kgf/cm2=98070 Pa 1mH2O(米水柱)=9807 Pa 1bar(巴) = 105 Pa≈1.02kgf/cm2
2.4 流体的相对平衡
相对平衡:指各流体质点彼此之间及流体与 器皿之间无相对运动的相对静止或相对平衡 状态。 相对平衡流体中,质量力除重力外,还受到 惯性力的作用。
帕斯卡(Pascal,Blaise 1623—1662),是法国著 名的数学家、物理学家、 哲学家和散文家。在物理 学方面作出的突出贡献是, 于1653年首次提出了著名 的帕斯卡定律,为此写成 了《液体平衡的论述》的 著名论文,详细论述了液 体压强的传递问题。应用 这个定律制造的各式各样 的液压机械,为人类创造 了无数的奇迹,他建立的 直觉主义原则对于后来一 些哲学家,如卢梭和柏格 森等都有影响。
重力场中流体的平衡微分方程
重力场中流体的平衡微分方程
在重力场中,流体的平衡微分方程可以通过质量守恒和动量守恒方程来描述。
1. 质量守恒方程:
质量守恒方程描述了流体质量在空间和时间上的变化。
根据质量守恒原理,流体在单位时间内进入一个控制体的质量应该等于离开该控制体的质量减去在控制体内积累的质量。
在重力场中,质量守恒方程可以表示为:
∂ρ/∂t + ∇·(ρv) = 0
其中,ρ是流体的密度,t是时间,v是流体的速度矢量,∇是梯度算子,·表示向量的点乘。
2. 动量守恒方程:
动量守恒方程描述了流体运动的力学行为。
根据牛顿第二定律,流体在单位时间内受到的外力等于流体动量的变化率。
在重力场中,动量守恒方程可以表示为:
ρ(∂v/∂t + v·∇v) = -∇P + ρg
其中,P是流体的压力,g是重力加速度。
综合以上两个方程,就可以得到重力场中流体的平衡微分方程。
需要注意的是,这是一个非线性偏微分方程组,求解方法较为复杂,通常需要结合适当的边界条件和物质特性方程进行求解。
流体力学理论基础
3.2.2 伯努利方程
3.3 流动阻力基本概念
流体旳平衡—流体静力学基础
3.1.1 平衡状态下流体中旳应力特征
1、流体静压力方向必然重叠于受力面旳内法向方向
n
A
c
b
B
P
a
2、平衡流体中任意点旳静压强只能由该点旳坐标位置
决定,而与该压强作用方向无关。
z
c
pn
dz py
px dy O dx b
a
pz
x
PyD g sin J x
PyD ghc AyD gyc sin AyD
gyc sin AyD g sin J x
根据面积二次力矩平行移轴定理
J x Jc yc2 A
yD
yC
JC yC A
常见图形旳几何特征量
常见截面旳惯性矩
y
z h
b
Jc
bh3 12
y
dz
Jc
d4
64
0
0'
p0=p=pa+ρgh0
h0=(p-pa) /ρg =(119.6-100)×103/(1000×9.81)=2.0m
3.1.5 均质流体作用在平面上旳液体总压力
p0
O
C点为平面壁旳形心,
a
hD
hc h dp P
y
yc
D点为总压力P旳作用点 取微元面积dA,设形
bα
yD
dA
心位于液面下列h深处
T
A hE
hc
HP
D
B 60
解:闸门形心
hc 1.5m
总压力
P hc A
98001.5 ( 3 1) sin 60
第二章.流体静力学
p0
14
水静力学基本方程:
p p0 gh
结论:重力作用下的均质流体有 1)静水压强随深度按线性规律增加。
A
1 2
A h
h
2)静水压强等于表面压强加上流体的g与该点淹没深度的乘积。
3)自由表面下深度h相等的各点压强均相等——只有重力作用下的 同一连续连通的静止流体的等压面是水平面。(例A—A) 4)推广:已知某点的压强和两点间的深度差,即可求另外一点的 压强值。
三、面积力
1、面积力(Surface Force):又称表面力,是相邻流体或其它物体 在隔离体表面上的直接施加的接触力。它的大小与作用面面 积成正比。 表面力按作用方向可分为:
5
压力:垂直于作用面。
切力:平行于作用面。
2、应力:单位面积上的表面力,单位: N/m2 或 Pa
压应力 切应力
p lim P A0 A
c.真空(Vacuum):是指绝对压强小于一个大气压的受压状态。 真空值pv
P
1
pν pa pabs
真空高度
( pabs pa )
0'
p1
p2
pabs1
0' 相对压强基准
2
hv
pv g
pa pabs g
pa
0
pabs2
绝对压强基准 0
注意:计算时无特殊说明时均采用相对压强计算。
pn py F
A
B
px O pz
D
C
x
类似地有:
y
n为斜面ABC的法线方向
质量力:
px p y pz pn
故与作用面的方位无关。
由∑X=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体的平衡微分方程及其积分
一、流体平衡微分方程——欧拉平衡方程
如图所示,在平衡流体中取一微元六面体,边长分别为d x ,d y ,d z ,设中心点的压强为p (x,y,z )=p ,对其进行受力分析:
根据平衡条件,在x 方向有0F x
=∑,即: 0zX y z y x
p 21z y )21=+)+-((d dxd d d dx p d d dx x p p ρ∂∂∂∂- 01X =-x
p ∂∂ρ 式中:X ——单位质量力在x 轴的投影
流体平衡微分方程(即欧拉平衡微分方程): ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂-=∂∂-=∂∂-
010101z p Z y p Y x p X ρρρ 物理意义:处于平衡状态的流体,单位质量流体所受的表面力分量与质量力分量彼此相等。
压强沿轴向的变化率(z
p y p x p ∂∂∂∂∂∂,,)等于轴向单位体积上的质量力的分量(ρX ,ρY ,
ρZ )。
二、平衡微分方程的积分
将欧拉平衡微分方程中各式,分别乘以dx 、dy 、dz ,整理: Zdz)Y dy (Xdx dz z
p dy y p x ++=∂∂+∂∂+∂∂ρdx p 因为p = p (x,y,z )
∴ Zdz)Ydy (Xdx dp ++=ρ ρ为常量;
Xdx +Ydy +Zdz 应为某函数W =F (x ,y ,z )的全微分: dz z
W dy y W dx x W dz dy dx d ∂∂+∂∂+∂∂=++=)Z Y (X W dW dp =ρ 平衡流体中压强p 的全微分方程 积分得:p=ρW +c
假定平衡液体自由面上某点(x 0,y 0,z 0)处的压强p 0及W 0为已知,则: c =p 0-ρW 0
∴ p=p 0+ρ(W-W 0) 欧拉平衡微分方程的积分
三、帕斯卡定律
处于平衡状态下的不可压缩流体中,任意点M 处的压强变化值△p 0,将等值地传递到此平衡流体的其它各点上去。
说明:只适用于不可压缩的平衡流体;
盛装液体的容器是密封的、开口的均可。
四、等压面
平衡流体中压强相等的各点所组成的面。
等压面:dp =ρ(Xdx +Ydy +Zdz )=0
ρ为常量,则:Xdx +Ydy +Zdz =0
即:质量力在等压面内移动微元长度所作的功为零。
等压面的特征:平衡流体的等压面垂直于质量力的方向 只有重力作用下的等压面应满足的条件:
1.静止;
2.连通;
3.连通的介质为同一均质流体;
4.质量力仅有重力;
5.同一水平面。
提问:如图所示中哪个断面为等压面? 答案: B-B’断面。
