(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 同步练习册_24
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_10
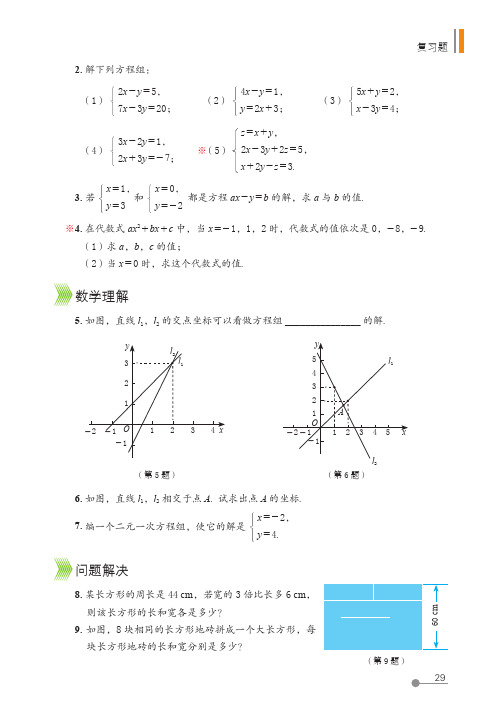
复习题2. 解下列方程组:(1)2x - y = 5,7x - 3y = 20; (2)4x - y = 1,y = 2x + 3; (3)5x + y = 2,x - 3y = 4;(4)3x - 2y = 1,2x + 3y = - 7; ※(5)z = x + y ,2x - 3y + 2z = 5,x + 2y - z = 3.3. 若x = 1,y = 3和x = 0,y = - 2都是方程 ax - y = b 的解,求 a 与 b 的值.※4. 在代数式 ax 2 + bx + c 中,当 x = - 1,1,2 时,代数式的值依次是 0,- 8,- 9.(1)求 a ,b ,c 的值;(2)当 x = 0 时,求这个代数式的值.5. 如图,直线 l 1,l 2 的交点坐标可以看做方程组 _______________ 的解.数学理解(第 5 题)(第 6 题)26. 如图,直线 l 1,l 2 相交于点 A. 试求出点 A 的坐标. 7. 编一个二元一次方程组,使它的解是x = - 2,y = 4.问题解决8. 某长方形的周长是 44 cm ,若宽的 3 倍比长多 6 cm ,则该长方形的长和宽各是多少?9. 如图,8 块相同的长方形地砖拼成一个大长方形,每块长方形地砖的长和宽分别是多少?(第 9 题)第七章二元一次方程组联系拓广(第10题)D CBEA10.如图,梯形 ABCD 中,AB∥CD,E 在 AB 上,CE∥AD,且 BE = CE,∠B -∠A = 30°,求∠A,∠B 的度数.11.某厂的甲、乙两个小组共同生产某种产品. 若甲组先生产1天,然后两组又一起生产了5天,则两组产量一样多. 若甲组先生产了300个产品,然后两组同时生产4天,则乙组比甲组多生产100个产品. 两组一天各生产多少个产品?12. A,B 两地相距80km. 一艘船从 A 出发,顺水航行4h到 B,而从 B 出发逆水航行5h到 A. 已知船顺水航行、逆水航行的速度分别是船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流速度.13.某粮食生产专业户去年计划生产水稻和小麦共15t,实际生产了17t,其中水稻超产15%,小麦超产10%. 该专业户去年实际生产水稻、小麦各多少吨?14.某商场按定价销售某种商品时,每件可获利45元;按定价的八五折销售该商品8件与将定价降低35元销售该商品12件所获利润相等. 该商品进价、定价分别是多少?15.某商场购进商品后,加价40% 作为销售价. 商场搞优惠促销,决定由顾客抽奖确定折扣. 某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,两种商品原销售价之和为490元. 甲、乙两种商品进价分别为多少元?16.列方程组解古算题:“今有甲、乙二人持钱不知其数. 甲得乙半而钱五十,乙得甲太半而亦钱五十.甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱. 如果甲得到乙所有钱的一半,那么甲共有钱50. 如果乙得到甲所有钱的23,那么乙也共有钱50. 甲、乙两人各带了多少钱?17.某景点的门票价格规定如下表:某校七年级一班和二班共102人去该景点游览,其中一班人数较少,不到50人,二班人数较多,有50多人. 如果两个班都以班级为单位分别购票,则一共应付1118元;如果两班联合起来作为一个团体购票,则可以节省不少钱. 两班各有多少名学生?联合起来购票能省多少钱?※18.方程组- 2x + y = 3,4x - 2y = - 6的解是什么?两个方程对应的两个一次函数的图象有怎样的位置关系?你能从中悟出些什么?哪一款“套餐”更合适哪一款“套餐”更合适手机是人与人沟通的重要工具,它给人们的生活带来了许多方便. 你了解哪些与手机资费相关的专业术语?你知道有哪些手机资费套餐?它们的收费标准是怎样的?假如你家刚刚添置了一部手机,下表是家长获得的一份手机资费宣传单,选择其中哪一款手机资费的“套餐”更合适?你能给你的家长出出主意吗?做一做以小组为单位合作完成下列任务.(1)分析资费宣传单,思考每月的资费受哪些因素影响,影响资费的通话。
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_18

定理 三角形的一个外角等于和它不相邻的两个内角的和. 定理 三角形的一个外角大于任何一个和它不相邻的内角.
上面这两个定理是由三角形内角和定理直接推导出来的. 像这样,由 一个基本事实或定理直接推出的真命题,叫做这个基本事实或定理的推论 (corollary). 推论可以当作定理使用.
例 2 已知:如图 8-15,在△ABC 中,∠B =∠C,AD 平分外角∠EAC.
求证:AD∥BC.
分析:要证明 AD∥BC,只需证明“同位角相等”,或“内错角相等”,或 “同旁内角互补”.
证明:∵∠E A C =∠B +∠C(三角形的一个外角等于和它不相邻的两个内 角的和),
∠B =∠C(已知), ∴∠C = 12 ∠EAC(等式的基本性质). ∵AD 平分∠EAC(已知), ∴∠DAC = 12 ∠EAC(角平分线的定义). ∴∠DAC =∠C(等量代换). ∴AD∥BC(内错角相等,两直线平行).
∵∠B = 38°,∠BAD = 40°,
∴∠ADB = 102°.
随堂练习
1. 证明:直角三角形的两个锐角互余. 2. 已知:如图,在△ABC 中,DE∥BC,∠A = 60°,∠C = 70°.
求证:∠ADE = 50°.
A
D
E
B
C
(第 2 题)
53
第八章 平行线的有关证明
习题 8.7
知识技能
6
三角形内角和定理
议一议
(1)在证明三角形内角和定理时,小明的想 P 法是把三个角“凑”到顶点 A 处,他过点 A 作直
A
Q
线 PQ∥BC(如图 8-12). 他的想法可行吗?如果可
行,你能写出证明过程吗?
(2)你还能用其他方法证明三角形内角和 B
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_12

1定义与命题(2)对顶角相等;(3)如果 a ,b ,c 是三角形的三条边的长,并且 a 2 + b 2 = c 2,那么这个三角形是直角三角形;(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.上面给出的语句都是对某件事情进行判断的句子. 判断一件事情的句子,叫做命题(statement ).反之,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题. 例如,下列句子都不是命题:(1)平行用符号“∥”表示;(2)作线段 AB = CD ;(3)∠A = 90°吗?随堂练习1. 说出它们的定义:(1)角; (2)角的平分线; (3)数轴; (4)一元一次方程.2. 分别说出两个语句,其中一个是命题,另一个不是命题.习题 8.1数学理解1. 根据线段的垂直平分线的定义,说一说:(1)线段的垂直平分线的一种判定方法;(2)线段的垂直平分线的两个性质.2. 下列语句中,哪些是命题?(1)三个角分别相等的两个三角形一定全等;(2)锐角都小于直角;(3)你的作业做完了吗?(4)所有的质数都是奇数;(5)过直线 l 外一点 P 作 l 的平行线;(6)如果明天是星期五,那么后天是星期六.第八章平行线的有关证明议一议观察下列命题:(A)如果两个三角形的三条边分别相等,那么这两个三角形全等;(B)如果 a = b,那么 a2 = b2;(C)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;(D)如果两个三角形中有两边和一个角分别相等,那么这两个三角形全等;(E)如果两个角是内错角,那么它们相等.(1)你发现这些命题的结构有什么共同特征?与同伴进行交流.(2)这些命题中,哪些命题是正确的?哪些命题是不正确的?命题通常由条件(condition)和结论(conclusion)两部分组成. 条件是已知的事项,结论是由已知事项推断出的事项. 一般地,命题都可以写成“如果……那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.在上面的命题中,(A),(B),(C)都是正确的. 正确的命题叫做真命题(true statement). 对于真命题来说,当条件成立时,结论一定成立. 命题(D)和(E)都是不正确的. 不正确的命题叫做假命题(false statement). 对于假命题来说,当条件成立时,不能保证结论一定成立.要判断一个命题是假命题,只要能够举出一个例子,使之具备命题的条件,而不具有命题的结论,就可以说明这一命题是假命题,这种例子通常称为反例(counter example).想一想你能举出一个反例,说明“相等的角是对顶角”是假命题吗?试试看.例 说出下列命题的条件和结论,指出它是真命题还是假命题:(1)面积相等的两个三角形全等;1定义与命题(2)同角的补角相等;(3)两角分别相等且其中一组等角的对边相等的两个三角形全等.解:(1)先把这个命题写成“如果……那么……”的形式:如果两个三角形的面积相等,那么这两个三角形全等.条件:两个三角形的面积相等;结论:这两个三角形全等.它是假命题.(2)原命题可以写成:如果两个角是同一个角的补角,那么这两个角相等. 条件:两个角是同一个角的补角;结论:这两个角相等.它是真命题.(3)原命题可以写成:如果两个三角形有两角分别相等且其中一组等角的对边相等,那么这两个三角形全等.条件:两个三角形有两角分别相等且其中一组等角的对边相等;结论:这两个三角形全等. 它是真命题.随堂练习1. 将下列命题写成“如果……那么……”的形式,分别说出它的条件和结论,并指出它是真命题还是假命题:(1)在同一平面内,垂直于同一直线的两条直线平行;(2)两个锐角的和是钝角;(3)同旁内角互补,两直线平行;(4)负数小于0.2. 下列命题中哪些是假命题?为什么?(1)如果 x - 52 = 3 - x 3,那么 x = 4;(2)各边分别相等的两个多边形一定全等;(3)如果 a ≠0,b ≠0,那么 a 2 + ab + b 2 =(a + b )2 .。
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_26

3等可能事件的概率前面我们用事件发生的频率来估计该事件发生的概率,但得到的往往只是概率的估计值. 那么,还有没有其他求概率的方法呢?3等可能事件的概率议一议1. 一个袋中装有 5 个球,分别标有 1,2,3,4,5 这五个号码,这些球除号码外都相同,搅匀后任意摸出一个球.(1)会出现哪些可能的结果?(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少.2. 前面我们提到的抛硬币、掷骰子和摸球的游戏有什么共同的特点?设一个试验的所有可能的结果有 n 个,每次试验有且只有其中的一个结果出现. 如果每个结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.想一想你能找一些结果是等可能的试验吗?一般地,如果一个试验有 n 个等可能的结果,事件 A 包含其中的 m 个结果,那么事件 A 发生的概率为:P (A )= m n .例 1 任意掷一枚均匀的骰子.(1)掷出的点数大于 4 的概率是多少?(2)掷出的点数是偶数的概率是多少?解:任意掷一枚均匀的骰子,所有可能的结果有 6 种:掷出的点数分别是第九章概率初步问题解决4. 小明所在的班有 40 名同学,从中选出一名同学为家长会做准备工作. 请你设计一种方案,使每一名同学被选中的概率都相同.1,2,3,4,5,6. 因为骰子是均匀的,所以每种结果出现的可能性相等.(1)掷出的点数大于 4 的结果只有 2 种:掷出的点数分别是 5,6,所以P (掷出的点数大于 4)= 26 = 13;(2)掷出的点数是偶数的结果有 3 种:掷出的点数分别是 2,4,6,所以P (掷出的点数是偶数)= 36 = 12 .你还能求哪些事件的概率?1. 一副扑克牌,任意抽取其中的一张,抽到大王的概率是多少?抽到 3 的概率是多少?抽到方块的概率是多少?请你解释一下:打牌的时候,你摸到大王的机会比摸到 3 的机会小.2. 一道单项选择题有 A ,B ,C ,D 四个备选答案,当你不会做的时候,从中随机地选一个答案,你答对的概率为多少?随堂练习习题 9.4知识技能1. 将 A ,B ,C ,D ,E 这五个字母分别写在 5 张同样的纸条上,并将这些纸条放在一个盒子中. 搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?2. 任意掷一枚均匀的骰子.(1)掷出的点数小于 4 的概率是多少?(2)掷出的点数是奇数的概率是多少?(3)掷出的点数是 7 的概率是多少?(4)掷出的点数小于 7 的概率是多少?3. 有 7 张纸签,分别标有数字 1,1,2,2,3,4,5,从中随机地抽出一张,求:(1)抽出标有数字 3 的纸签的概率;(2)抽出标有数字 1 的纸签的概率;(3)抽出标有数字为奇数的纸签的概率.3等可能事件的概率议一议1. 一个袋中装有2个红球和3个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?摸出的球不是红球就是白球,所以摸到红球和摸到白球的可能性相同,也就是,P(摸到红球)= 12.红球有2个,而白球有3个,如果将每一个球都编上号码,1号球(红色)、2号球(红色)、3号球(白色)、4号球(白色)、5号球(白色),摸出每一个球的可能性相同,共有5种等可能的结果. 摸到红球可能出现的结果有:摸出1号球或2号球,共有2种等可能的结果. 所以,P(摸到红球)= 25.你认为谁说的有道理?2. 小明和小凡一起做游戏. 在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一个球,摸到红球小明获胜,摸到白球小凡获胜. 这个游戏对双方公平吗?在一个双人游戏中,你是怎样理解游戏对双方公平的?选取4个除颜色外完全相同的球设计一个摸球游戏.(1)使得摸到红球的概率是12,摸到白球的概率也是12;(2)使得摸到红球的概率是12,摸到白球和黄球的概率都是14.做一做。
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_31

C
B
图 10-2
∴△OAC ≌△ODB(SAS).
∴AC = BD,∠A =∠D(全等三角形的定义).
根据全等三角形的定义, 我们可以得到全等三角形的对 应边相等、对应角相等.
93
第十章 三角形的有关证明
随堂练习
1. 完成下面的证明过程.
已知:如图,AB 与 CD 相交于点 O,△AOC ≌△DOB.
第十章 三角形的有关证明
1 全等三角形
在《平行线的有关证明》一章中,我们给出了八条基本事实,并从其中的 几条基本事实出发证明了有关平行线的一些结论. 运用这些基本事实和已经学 习过的定理,我们还可以证明有关三角形的一些结论.
想一想
有关全等三角形的基本事实有哪些?
基本事实:_________________________ 的两个三角形全等.(SAS) 基本事实:_________________________ 的两个三角形全等.(ASA) 基本事实:_________________________ 的两个三角形全等.(SSS)
).
2. 已知:如图,M 是线段 AB 的中点,∠C =∠D,∠1 =∠2.
求证:△AMC ≌△BMD.
A
D
O
C
B
(第 1 题)
12 (第 2 题)
习题 10.1
知识技能
1. 已知:如图,∠ACB =∠DBC,AC = DB. 求证:∠A =∠D,AB = DC.
A
D
O
C
B
(第 1 题)
2. 已知:如图,在四边形 ABCD 中,AC 平分∠BAD,AB = AD. 求证:AC 平分∠BCD.
92
∴∠A = 180°-∠B -∠C, ∠A′= 180°-∠B′-∠C′. ∵∠B =∠B′,∠C =∠C′, ∴∠A =∠A′. 在△ABC 和△A′B′C′中, ∵∠A =∠A′,AB = A′B′,∠B =∠B′, ∴△ABC ≌△A′B′C′(ASA).
三元一次方程组(同步练习)鲁教版(五四制)数学七年级下册

第七章二元一次方程组5 三元一次方程组夯基础1.下列方程组中,不是三元一次方程组的是( )A.{x=5,x+y=7,x+y+z=6B.{x+y+z=2,x−y+z=0,x−z=4C.{x+y=3,y+z=5,x+z=4D.{x+y+3z=5,x−3y=4z,xy+yz=12.一个三位数,百位上的数与十位上的数之差是2,如果交换十位数字与个位数字的位置,那么所得的数就比原来小36,则百位上的数与个位上的数之差为( )A.5B.6C.7D.83.已知{x=1,y=2,z=3是方程组{ax+by=2,by+cz=3,cx+az=7的解,则a+b+c的值为( )A.3B.2C.1D.04.如果{x+2y=3,y+2z=5,2x+z=4,则x+y+z的值为 .5.如果x+2y+3z=54,3x+y+2z=47,2x+y+z=31,那么代数式x+y+ z的值是 .6.解方程组{y=2x−7,5x+3y+2z=2, 3x−4z=4.7.学校的篮球数比排球数的2倍少3个,足球数与排球数的比是2:3,三种球共41个,求三种球各有多少个?练能力1.将三元一次方程组{5x+4y+z=0, ①3x+y−4z=11,②x+y+z=−2 ③经过①-③和③×4+②消去未知数z后,得到的二元一次方程组是( )A.{4x+3y=2,7x+5y=3B.{4x+3y=2,23x+17y=11C.{3x+4y=2,23x+17y=11D.{3x+4y=2,7x+5y=32.桌面上有甲、乙、丙三个杯子,三杯内原本均装有一些水,先将甲杯的水全部倒入丙杯,此时丙杯的水量为原本甲杯内水量的2倍多40毫升;再将乙杯的水全部倒入丙杯,此时丙杯的水量为原本乙杯内水量的3倍少180毫升.若过程中水没有溢出,则原本甲、乙两杯内的水量相差多少毫升( )A.80B.110C.140D.2203.如果三元一次方程组为{x+y=5,y+z=6,x+z=7,那么x+y+z= .4.已知关于x的代数式ax²+bx+c,且x=-1时,代数式的值为-1;x=0时,代数式的值为2;x=1时,代数式的值为3.则a,b,c的值分别为 .5.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需64元,若购甲4件,乙10件,丙1件,共需79元.现购甲、乙、丙各一件,共需元.6.盲盒为消费市场注入了活力,既能够营造消费者购物过程中的趣味体验,也为商家实现销售额提升拓展了途径.某商家将蓝牙耳机、多接口优盘、迷你音箱共22个,搭配为A,B,C三种盲盒各一个,其中A 盒中有2个蓝牙耳机,3个多接口优盘,1个迷你音箱;B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量,蓝牙耳机与迷你音箱的数量之比为3:2;C盒中有1个蓝牙耳机,3个多接口优盘,2个迷你音箱.经核算,A盒的成本为145元,B盒的成本为245元(每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和),则C盒的成本为元.7.解方程组{x+2y=4,2x+5y−2z=11, 3x−5y+2z=−1.8.有一场足球比赛,共有九支球队参加,采取单循环赛,其记分和奖励方案如下表:甲队参加完了全部8场比赛,共得积分16分.(1)求甲队胜负的所有可能情况;(2)若每一场比赛,每一个参赛队员均可得出场费500元,求甲队参加了所有8场比赛的队员的个人总收入(奖金加上出场费).参考答案夯基础1.D2.B3.A4.45.256.解{y=2x−7, ①5x+3y+2z=2,②3x−4z=4, ③把①代入②,得5x+6x−21+2x=2,即11x+2z=23,④④×2+③,得25x=50,即x=2,把x=2代入①,得y=-3,把x=2代入③,得z=12.所以方程组的解为{x=2,y=−3,z=12.7.解:设篮球有x个,排球有y个,足球有z个.依题意,得{x+y+z=41,x−2y=−3,2y−3z=0.解这个方程组,得{x=21,y=12,z=8.答:篮球有21个,排球有12个,足球有8个.练能力1.A2.B3.94.-1.2,25.346.155 解析:因为蓝牙耳机、多接口优盘、迷你音箱共22个,A盒中有2个蓝牙耳机,3个多接口优盘,1个迷你音箱;C盒中有1个蓝牙耳机,3个多接口优盘,2个迷你音箱;所以B盒中蓝牙耳机、多接口优盘、迷你音箱共22-2-3-1-1-3-2=10(个).因为B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量,蓝牙耳机与迷你音箱的数量之比为3:2,所以B盒中有多接口优盘10×12=5 (个),蓝牙耳机有5×33+2=3(个),迷你音箱有10-5-3=2(个).设蓝牙耳机、多接口优盘、迷你音箱的成本价分别为a元,b元,c元,由题意,知{2a+3b+c=145,①3a+5b+2c=245,②因为①×2-②,得a+b=45,②×2-①×3,得b+c=55,所以C盒的成本为a+3b+2c=(a+b)+(2b+2c)=45+55×2=155(元). 故答案为:155.7.解{x+2y=4,①2x+5y−2z=11,3x−5y+2z=−1,③②②+③,得5x=10④,解得x=2,把x=2代入①,得y=1,把x=2,y=1代入②得2×2+5×1-2z=11,解得z=-1,所以原方程组得解为{x=2, y=1, z=−1.8.解:(1)设甲队胜x场,平y场,负z场.根据题意,得{3x+y=16,x+y+z=8,解得{x=4+z2,y=4−32z,得整数解{x=4,y=4,z=0,或{x=5,y=1,z=2.即甲队胜负的所有可能情况有:“4胜4平”或者“5胜1平2负”.(2)若是4胜4平,甲队参加了所有8场比赛的队员的个人总收入为2000×4+800×4+500×8=15200(元),若是5胜1平2负,甲队参加了所有8场比赛的队员的总收入为2000×5+800+500×8=14800(元).答:若是4胜4平,总收入为15200元;若是5胜1平2负,总收入为14800元.。
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_42
角平分线
5 角平分线ቤተ መጻሕፍቲ ባይዱ
还记得角平分线上的点有什么性质吗?你是怎样得到的?你能证明它吗?
已知:如图 10-27,OC 是∠AOB 的平分线,点 P 在 OC 上,PD ⊥ OA,
PE ⊥ OB,垂足分别为点 D,E. 求证:PD = PE. 证明:∵∠1 =∠2,OP = OP,
O
1 2
D
A
PC
∠PDO =∠PEO = 90°, ∴△PDO ≌△PEO(AAS).
E
B
图 10-27
∴PD = PE(全等三角形的对应边相等).
定理 角平分线上的点到这个角的两边的距离相等.
议一议
你能写出这个定理的逆命题吗?它是真命题吗?如果是,请你证明它.
定理 在一个角的内部,并且到角的两边距离相等的点,在这个角的平 分线上.
已知:如图 10-28,点 P 为∠AOB 内一点,PD ⊥ OA,PE ⊥ OB,垂足分 别为 D,E,且 PD = PE.
DA
1 O2
PC
EB 图 10-28
例 1 如图 10-29,在 △ABC 中,∠BAC = 60°,点 D 在 BC 上,AD = 10,
DE ⊥ AB,DF ⊥ AC,垂足分别为点 E,F,且 DE = DF,求 DE 的长.
解:∵ DE ⊥ AB,DF ⊥ AC,垂足分别为点 E,F,且 DE = DF,
求证:OP 平分∠AOB. 证明:∵ PD ⊥ OA,PE ⊥ OB,垂足分别为点 D,E, ∴ ∠ODP =∠OEP = 90°.
125
第十章 三角形的有关证明
∵ PD = PE,OP = OP, ∴ Rt△DOP ≌ Rt△EOP(HL). ∴ ∠1 =∠2(全等三角形的对应角相等). ∴ OP 平分∠AOB.
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_9
复习题
知识技能
3x - 2y = 3,
1. 二元一次方程组
的解是 _________ .
x + 2y =5
x = 1, (1)
y = 0; 28
(2)
x
=
3 2
,
y = 2;
x=2,
(3)
y
=
3 2
;
x = 7, (4)
y = - 1.
知识技能
1. 解下列方程组: x + 2z = 3,
(1) 2y + z = 7, 2x - y - z = - 5;
(2)
2x - y + 2z = 8, y + 2z = - 2, 3x + y - 4z = 1.
2. 解方程组:
x + y + z = 10, 2x + 3y + z = 17, 3x + 2y - z = 8.
问题解决
3. 某校七、八、九年级共有 651 人,八年级的学生比九年级的学生人数多 10%,七 年级的学生比八年级的学生人数多 5%. 求三个年级各有多少学生.
4. 一个三位数,十位数字比个位数字大 2,百位数字是十位数字的 2 倍. 如果把百 位数字与个位数字对调,那么得到的三位数比原来的三位数小 495. 求原来的三 位数.
做一做
用不同的方法解下面的方程组: x + y = 15, y + z = 5, x + z = 20.
26
再对这些方法进行比较.
*5
三元一次方程组
例 已知等式 y = ax2 + bx + c,当 x = 1 时,y = 0;当 x = 2 时,y = 3;当 x = - 3 时,y = 28.
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_17
明∠ECD =∠B. 由此说明上述猜想是正确的.
A
B
C
图 8-10
E
1
2
B
C
D
图 8-11
这里的 CD,CE 称 为辅助线. 辅助线通常 画成虚线.
证明:作 BC 的延长线 CD,在△ABC 的外部,以 CA 为一边,作∠ACE = ∠A(如图 8-11). 于是,CE∥BA(内错角相等,两直线平行).
2 b
图 8-8
议一议
你能说说命题证明的一般步骤吗?
随堂练习
1. 已知:如图,直线 a,b 被直线 c 所截,且 a∥b. 求证:∠1 =∠3.
c 1
a 2
b 3
(第 1 题)
A
1
2
D 87
3 4
B
6 5
C
(第 2 题)
2. 如图,按照题目中给出的条件,补全结论,并给出证明: (1)已知 AD∥BC,可以推出哪些角相等? (2)已知 AB∥DC,可以推出哪些角的和是 180°?
b 1
2 C
用比较简洁的语言写出这一证明过程吗?与同伴
图 8-9
进行交流.
已知:如图 8-10,△ABC 是任意一个三角形.
求证:∠A +∠B +∠C = 180°.
分析:受图 8-9 的启发,我们可以以点 C 为顶
A
点,以 CA 为一边在三角形外部作∠1 =∠A,再作
BC 的延长线,得到平角∠BCD(如图 8-11). 可以证
50
6
三角形内角和定理
习题 8.6
知识技能
1. 探照灯以及其他很多灯具都与抛物线有关. 如图,从点O 照射到抛物线上的光 线 OB,OC 等反射以后沿着与 POQ 平行的方向射出. 图中如果∠BOP = 45°, ∠QOC = 88°,那么∠ABO 和∠DCO 各是多少度?
(五四制) 鲁教版数学 7年级下册 配套练习册 一课一练 基本功训练_53
x > m
(A)m ≥ 3
(B)m ≤ 3
(C)m = 3
(D)m < 3
问题解决
11. 暑假期间,两名家长计划带领若干名学生去旅游,他们联系了报价均为每人 500 元 的两家旅行社. 经协商,甲旅行社的优惠条件是:两名家长全额收费,学生都按 七折收费;乙旅行社的优惠条件是:家长、学生都按八折收费. 假设这两位家长带 领 x 名学生去旅游,他们选择哪家旅行社更优惠?
x.
6. 已知函数 y = 3x + 5.
(1)当 x 取何值时,y > 0?
(2)当 x 取何值时,y = 0?
(3)当 x 取何值时,y < 0?
7. 求不等式 5(x - 2)≤ 28 + 2x 的正整数解.
复习题
数学理解
8. 判断正误:
(1)由
2a
>
3,得
a
>
3 2
;
(2)由 2 - a < 0,得 2 < a;
用“<”或“>”填空: (1)a _____ b; (3)a + b _____ 0; (5)a + b _____ a - b;
(2)| a | _____ | b |; (4)a - b _____ 0; (6)ab _____ a.
x + 8 < 4x - 1,
※10. 如果不等式组
的解集是 x > 3,那么 m 的取值范围是( ).
联系拓广
15.(1)用“>”“<”或“ = ”填空: 52 + 32 _______ 2×5×3; 32 + 32 _______ 2×3×3; (- 3)2 + 22 _______ 2×(- 3)×2; (- 4)2 +(- 4)2 _______ 2×(- 4)×(- 4).
