工程力学轴向拉伸与压缩
工程力学16 轴向拉伸与压缩杆的变形

伸长量;(2)C截面相对B截面的位移
(相对位移)和C截面的绝对位移。 解:(2) 位移:指物体上的一些点、
B
B
B′
l2=200
线、面在空间位置上的改变。 显然,两个截面的相对位移,
C
C
C′
在数值上等于两个截面之间的
F=40 kN
那段杆件的伸长(或缩短)。 因A截面固定,所以C截面
因此,C截面与B 截面的
掌握:胡克定律表达式的应用 ; 轴向变形— —伸长量的计算 ——难点+重点
谢 谢!
解:(1) 变形:物体受力以后 发生尺寸和形状的改变。
B
B
B′
l2=200
l1
FN l1 EA1
40 103 N 210 109 Pa
300 103 m 400 106 m2
0.143103m=0.143mm(伸长)
C
C
C′
F=40 kN
l2
FN l2 EA2
40 103 N 210 109 Pa
实验表明,在材料正应力没有超过比例极限时,横向线应变与纵 向线应变之比为常数,用绝对值表示为
v
或写成
v
v称为横向变形因数或泊松比
无量纲,由实验测定
例1 已知: AB段:A1 =400mm2
A
BC段:A2 =250mm2 ,E=210GPa
l1=300
求:(1)AB、BC段的伸长量及杆 的总伸长量;(2)C截面相对B截面 的位移和C截面的绝对位移。
200 103 m 250 102 0.143mm+0.152mm
0.152103m=0.152mm(伸长) 0.295mm(伸长)
例1 已知: AB段:A1 =400mm2
工程力学轴向拉伸与压缩答案
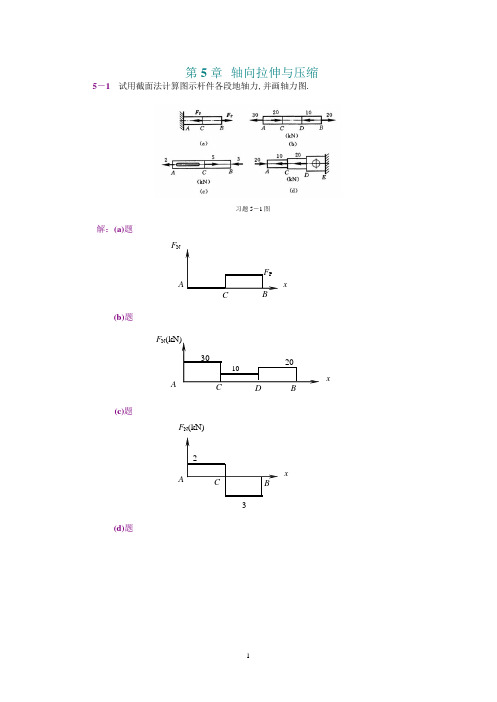
第5 章轴向拉伸与压缩5-1 试用截面法计算图示杆件各段地轴力,并画轴力图.习题5-1 图解:(a)题F Nx(b)题F NxA(c)题F N(kN)x-3(d)题F N-10x5-2 图示之等截面直杆由钢杆 ABC 与铜杆 CD 在 C 处粘接而成.直杆各部分地直径均为 d =36 mm ,受力如图所示.若不考虑杆地自重,试求 AC 段和 AD 段杆地轴向变形量 Δl AC和 Δl AD习题 5-2 图(F N ) l AB (F N ) l BC解: Δl AC =AB πd 2E s4+BC πd 2 E s 4 150 ×103 × 2000 +100 ×103 ×3000 4 = × = 2.947 mm(F N ) 200 ×103 l π ×362100 ×103 × 2500 × 4 Δl = Δl + CD CD = 2.947 + = 5.286 mm AD AC πd 2 E c4105 ×103 × π ×3625-3 长度 l =1.2 m 、横截面面积为 1.10×l0-3m 2 地铝制圆筒放置在固定地刚性块上;刚性板mC B −6 B 直径 d =15.0mm 地钢杆 BC 悬挂在铝筒顶端地刚性板上;铝制圆筒地轴线与钢杆地轴线重 合.若在钢杆地 C 端施加轴向拉力 F P ,且已知钢和铝地弹性模量分别为 E s =200GPa ,E a =70GPa ;轴向载荷 F P =60kN ,试求钢杆 C 端向下移动地距离.解:u A− u B −F l = P AB E a A a 3(其中 u A = 0)3∴ u =60 ×10 ×1.2 ×10= 0.935 mm B 70 ×10 3 ×1.10 ×10 −3 ×10 6钢杆 C 端地位移为F l60 ×103 × 2.1×103u = u + P BC = 0.935 + = 4.50 m m E s A s200 ×103 × π ×15245-4 螺旋压紧装置如图所示.现已知工件所受地压紧力为 F =4 kN .装置中旋紧螺栓 螺纹地内径 d 1=13.8 mm ;固定螺栓内径 d 2=17.3 mm .两根螺栓材料相同,其许用应力[σ ] =53.0 MPa .试校核各螺栓地强度是否安全.解:∑ M B = 0 ,F A = 2kN ∑ F y = 0 ,F B = 6kN习题 5-4 解图习题 5-4 图 σ = F A = 2000 = A π2000 × 42= 13.37 MPa < [σ ] ,安全. A A d 2 π ×13.8 ×104 σ = F B = 16000= 25.53 MPa <[σ ] ,安全. A B π ×17.32 ×10−645-5 现场施工所用起重机吊环由两根侧臂组成.每一侧臂 AB 和 BC 都由两根矩形截面 杆所组成,A 、B 、C 三处均为铰链连接,如图所示.已知起重载荷 F P =1200 kN ,每根矩形 杆截面尺寸比例 b/h =0.3,材料地许用应力[σ ]=78.5MPa .试设计矩形杆地截面尺寸 b 和 h .4⋅2FF N习题 5-5 图解:由对称性得受力图如习题 5-5 解图所示.∑ F y = 0 ,4F N cos α = F P 习题 5-5 解图F = F P = N 4 cos α 1200 ×103960 = 3.275 ×105 Nσ = F N A= F N 0.3h 2≤ [σ ]9602 + 42025h ≥ F N =0.3[σ ]3.275 ×100.3 × 78.5 ×106= 0.118m b = 0.3h ≥ 0.3 × 0.118 = 0.0354m = 35.4mmh = 118mm ,b = 35.4mm5-6 图示结构中 BC 和 AC 都是圆截面直杆,直径均为 d =20mm ,材料都是 Q235 钢, 其许用应力[σ ]=157MP .试求该结构地许用载荷.B习题 5-6 图习题 5-6 解图∑ F x = 0 , F B = 2F A (1)∑ F y= 0 ,2 F A + 23F B − F P = 0 2(2)1 + 3 F P = F B2(3)F ≤ [σ ] ⋅πd2B43 mdWs由式(1)、(2)得:F ≤ 1 + P2 = 1 + 23 ⋅π d 2 [σ ] 43 ⋅π × 202 ×10−4 ×157 ×106 = 67.4kN 4` (4)F P =2 (1 + 23 ) F A = 2 (1 + 2 3 ) ⋅[σ ]π 24= 90.28kN (5)比较(4)、(5)式,得 [F P ] = 67.4 kN5-7 图示地杆件结构中 1、2 杆为木制,3、4 杆为钢制.已知 1、2 杆地横截面面积A 1=A 2=4000 mm 2,3、4 杆地横截面面积 A 3=A 4=800 mm 2;1、2 杆地许用应力[σ]=20MPa , 3、4 杆地许用应力[σ ]=120 MPa .试求结构地许用载荷[F P ].习题 5-7 图P(a)3(b)解:1. 受力分析:由图(a )有5∑ F y = 0 , F 3 =F P 3 4 4由图(b )由∑ F x = 0 , F 1 = − 5 F 3 = − 3 F P∑ F x = 0 , F 4 = 4 F 3 = 5 43 F P2. 强度计算:5∑ F y = 0 , F 2= − 3F 3 = −F P| F 1 |>| F 2 || F 1 |≤ [σ w ] A 14 F ≤ A [σ ] 3P 1 w F ≤ 3 A [σ ] = 3 × 4000 ×10 −6 × 20 ×10 6 = 60 kN P 4 1 w4F 35F 3 > F 4 , ≤ [σ s ] , A 3F P ≤ [σ ]A 3 3F ≤3 [σ] A 3 ×120 ×10 6 × 800 ×10 −6= 57.6 kN[F P] = 57.6 kNa*5-8 由铝板和钢板组成地复合柱,通过刚性板承受纵向载 荷 F P =38 kN ,其作用线沿着复合柱地轴线方向.试确定:铝板和 钢板横截面上地正应力. 解:此为超静定问题.1. 平衡方程2. 变形协调方程:3. 物性关系方程:F Ns + F Na = F P Δl s = Δl a(1)(2)联立解得⎧F F Ns E s A sE s A s= FNaE a A a(3)习题 5-8 图⎪ Ns = E A E A F P ⎪ ⎨ ⎪F = s s + a E a A a a(压) F NaE A + E A P s s a aσ =F Ns =−E s F P = −E s F P s A E b h + E⋅ 2b h b hE + 2b hE s s 0 a 1 0 s 1 a9 3σ = − 200 ×10 ×385 ×10175MPa (压)= − s 0.03 × 0.05 × 200 ×109 + 2 × 0.02 × 0.05 × 70 ×109σa = F Na A = −b hE E a F P+ 2b hEa 0 s 1 aσ = −175E a E s = −17570 200= −61.25MPa (压)*5-9 铜芯与铝壳组成地复合棒材如图所示,轴向载荷通过两端刚性板加在棒材上. 现已知结构总长减少了 0.24 mm .试求:1.所加轴向载荷地大小; 2. 铜芯横截面上地正应力.习题 5-9 图F NcE A =F NaE A(1)E A E A σ aF = ΔlE c A c , F= ΔlE a A aF Nc + F Na = F P(2)Nc l NalF = F + F = ΔlE c A c + ΔlE a A aP Nc Nal l = Δl E A + E A( c c a a) l= 0.24 ×10−3 ⎧ π 2 =π ⎡ 2 2 ⎤⎫ = ⎨105 ×106 × ×(25 ×10−3 ) + 75 ×106 × × (60 ×10−3 ) − (25 ×10−3 ) ⎬ 30 ×10−3⎩ 4 4 ⎭ = 171 kNF =E c A cNc c c F P + E a A aF =E a A a Na c cF P + E a A a⎧ F Nc E c F P E c F P ⎪σ c = ⎪ A c ⎪ ∴ ⎨= E c A c + E a A a = E c ⋅ πd 2 4 + E a π 2 2 ⋅ (D− d ) 4 ⎪ = F Na ⎪ A a ⎪⎩ = πd 2E c 4E aF Pπ(D 2 − d 2 ) + E a 4 9 32. σ =4 ×105 ×10 ×171×1083.5MPa = c105 ×109 × π × 0.0252 + 70 ×109 × π × (0.062 − 0.025)2σa = σcE a = 83.5 × 70= 55.6MPa E c 105*5-10 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 地正方形,钢和铸铁 各占横截面地一半(b ×2b ).载荷 F P ,通过刚性板沿铅垂方向加在组合柱上.已知钢和铸铁 地弹性模量分别为 E s =196GPa ,E i =98.0GPa .今欲使刚性板保持水平位置,试求加力点地 位置 x =?解:∑ M 0 = 0 , (b ⋅ 2b σ 习题 5-10 图) ⋅( x − b ) = (b ⋅ 2b )σs i( 3 b − x )23∴σ σ s =iE sE i2 x − b = σ i3b − 2 x σ s(1)(2)代入(1)得σ i σ s4 x − 2b = 3b − 2 x5= 98 = 1196 2(2)∴ x = b 65-11 电线杆由钢缆通过旋紧张紧器螺杆稳固.已知钢缆地横截面面积为1×103 mm 2 ,E =200GPa ,[σ ] = 300MPa .欲使电杆有稳固力F R =100kN ,张紧器地螺杆需相对移动多少? 并校核此时钢缆地强度是否安全.F R习题 5-11 图解:(1)设钢缆所受拉力为 F N ,由平衡条件F N cos30°=F RF N =100/ cos30°=115.5kNΔl = F N l = 115.5 ×103 ×10 ×103= 6.67mm EA 200 ×103 ×103× 3 / 2张紧器地螺杆需相对移动 6.67mm .(2)钢缆地应力与强度σ = F N A = 115.5 ×10 103= 115.5MP a < [σ ]所以,强度安全.5-12 图示小车上作用着力 F P =15kN ,它可以在悬架地 AC 梁上移动,设小车对 AC梁地作用可简化为集中力.斜杆 AB 地横截面为圆形(直径 d =20mm),钢质,许用应力 [σ]=160MPa .试校核 AB 杆是否安全.3习题 5-12 图F N ABαF N ACF P习题 5-12 解图解:当小车开到 A 点时,AB 杆地受力最大,此时轴力为 F N A B .(1) 受力分析,确定 AB 杆地轴力 F N A B ,受力图如图 5-12 解图所示, 由平衡方程∑Fy= 0 ,F N AB sin α − F P = 0sin α =解得轴力大小为:0.8 0.82 +1.92F N AB = 38.7kN(2)计算应力σ = F N AB = F N AB = 4 × 38.7 ×10 =123 ×106Pa = 123MPa < [σ ] AB强度安全.A AB πd 2 4π × 202 ×10−65-13 桁架受力及尺寸如图所示.F P =30kN ,材料地抗拉许用应力[σ]+=120MPa , 抗压许用应力[σ]-=60MPa .试设计AC 及AD 杆所需之等边角钢钢号.(提示:利用附录B 型钢表.)F N AC45DAF N ADF PF RA习题 5-13 图习题 5-13 解图解:(1)受力分析,确定 AC 杆和 AD 杆地轴力 F N AC 、 F N AD ,对整体受力分析可得, F R A= F R B = F P 2= 15kN再取节点 A ,受力分析,受力图如图 5-13 解图所示,建立平衡方程D D 3 3 2 4 ∑F y = 0 , − F N AC sin 45 + F R A = 0解得 AC 杆轴力大小为:F N AC = 21.2kN(压)∑ F x = 0 , − F N AC cos 45 + F N AD = 0解得 AD 杆轴力大小为: F N AD = 15kN(拉)(2)强度条件拉杆:A AD = F N AD [σ ]+ = 15 ×10 120 = 125mm 2 压杆:(3)选择钢号A AC = F N AC [σ ]− = 21.2 ×10 60 = 353.3mm 2 拉杆: 20 × 20 × 4压杆: 40 × 40 × 55-14 蒸汽机地气缸如图所示.气缸内径D =560mm ,内压强p =2.5MPa ,活塞杆直径 d =100mm .所有材料地屈服极限σs =300MPa . (1)试求活塞杆地正应力及工作安全系数.(2)若连接气缸和气缸盖地螺栓直径为30mm ,其许用应力[σ]=60MPa ,求连接每个气缸盖 所需地螺栓数.习题 5-14 图解:(1)活塞杆受到地轴力为:⎡π (D 2 F = pA = p − d 2 ) ⎤ = 2.5⎡π (560 −1002 ) ⎤ = 596.12kN N ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ 4 ⎦活塞杆地正应力:σ =F N A 杆596.12 ×103 ) = = 75.9MPa π ×102 / 4 工作安全系数: (2)螺栓数mn = σ s σ= 300 = 3.95 75.93x 3 x y xm = F N = 596.12 ×10 = 14.1 个 A 栓 [σ ]栓 π × 302 / 4 × 60由于圆对称,取m =16个.5-15 图示为硬铝试件,h =200mm ,b =20mm .试验段长度l 0=70mm .在轴向拉力 F P =6kN 作用下,测得试验段伸长Δl 0=0.15mm ,板宽缩短Δb =0.014mm .试计算硬铝地弹 性模量E 和泊松比ν .习题 5-15 图解:(1)计算弹性模量Eε = Δl 0 l 0= 0.15 = 2.143 ×10−3 70σ = F P = 6 ×10 = 150MPa AE = σ = 20 × 2 150 ×106 = 70GPa ε 2.143 ×10−3 (2) 计算泊松比νε = Δb 0 b 0= − 0.014 = −7 ×10−4 20ε ν = y = − 7 ×10−4 = 0.327 ε 2.143 ×10−3上一章返回总目录下一章。
工程力学(杆件的轴向拉伸压缩问题)

教学设计一杆件轴向拉伸压缩问题问题一,杆件简单受力问题的分析与描述在学习了材料力学的基本泄理和假设后,接下来学习一下杆件的简单受力问题,即杆件 的轴向拉伸与压缩问题。
轴向拉伸或压缩变形是杆件的基本变形之一,轴向拉力一般用P 表示,轴向压力一般用N 表示。
【例1】如图1」所示直杆受轴向的外力作用,杆件A 端受拉力,D 端受压力,B 截面受拉力, C 裁面受拉力,对于杆件中1・1、2・2、3・3截面上的轴力大小是多少,它们的受力是压力还 是拉力,我们该如何判断呢?A 1B 1C 1 D1 23囹1.1杆件內力分析简囹在材料力学中我们通常采用受力分析图来描述杆件或是受力物体的受力问题,在杆件轴 向拉伸压缩问题中,我们采用轴力图N 来描述杆件的轴力变化和受力大小。
我们用大写字母N 来表示轴力图,用一条直线表示杆件的中轴线,并代表杆件,我们 以拉力为正,画在轴线上方,压力为负,画在轴线下侧,图形为矩形,矩形的髙度代表受力 的大小,并标注正负号,在图形上侧或下侧标注受力大小。
画出图示1・1的受力分析图 例题分析讲解对杆件进行分段分析AB 段,1“截面N 「3kN (拉) BC 段,2-2 <面 N 2=5-3=2kN (压)CD 段,3-3 <面 N3=4+2=6kN (压) 杆件受力分析图NN问题二,杆件简单受力问题的计算杆件截面应力计算问题,杆件上截而分为正截而和任意截而,我们把垂直与杆件轴线的 截而成为杆件的正截面,其他截面成为任意截而。
杆件的正截而应力我们用字母/表示,任意截面正应力我们用6表示,截而剪应力用r Q 表示。
横截面正应力计算大小我们用轴力除以正截而而积,如公式1」所示。
Nb A(公式 1.1)任意斜截面上的正应力和剪应力计算,我们将轴力沿斜截面的垂直方向和水平方向分解, 然后分别除以斜截而面积,得到斜截而正应力计算式1.2和剪应力1.3所示,其中a 角为横 截面与斜截面的夹角。
a (公式12)r=竺a~ A a(公式 1.3)例题分析讲解 【例2】图1.2所示,变截面杆件,已知P=25kN,横截面面积A 1=2000mm 2, A 2=1000mm 2,试 作轴力图,并计算各截面上的正应力。
工程力学课件 第6章 轴向拉伸与压缩

工程力学
12
二、拉压杆横截面上的正应力
在应力超过比例极限以后,图形出现了一段近似水平的小锯齿
形线段bc,说明此阶段的应力虽有波动,但几乎没有增加,却发生
了较大的变形。这种应力变化不大、应变显著增加的现象称为材料
的屈服。屈服阶段除第一次下降的最小应力外的最低应力称为屈服
极限,以σs表示。
4.强度极限
经过了屈服极限阶段,图形变为上升的曲线,说明材料恢复了
工程力学
4
1.1.1 电路的组成
列出左段杆的平衡方程得 Nhomakorabea工程力学
5
若以右段杆为研究对象,如图(c)所示,同样可得
1.1.1 电路的组成
实际上,FN与F′N是一对作用力与反作用力。因此,对同一截面, 如果选取不同的研究对象,所求得的内力必然数值相等、方向相反。
这种假想地用一个截面把杆件截为两部分,取其中一部分作为 研究对象,建立平衡方程,以确定截面上内力的方法,称为截面法。 截面法求解杆件内力的步骤可以归纳如下:
1.1.1 电路的组成
(1)计算AB段杆的轴力。沿截面1-1将杆件截开,取左段杆为研 究对象,以轴力FN1代替右段杆件对左段的作用,如图(b)所示
列平衡方程
得
工程力学
7
若以右段杆为研究对象,如图(c)所示
1.1.1 电路的组成
同样可得
(2)计算BC段杆的轴力,沿截面2-2将杆件截开,取左段杆为研 究对象,如图(d)所示
工程力学轴向拉伸与压缩教案

工程力学轴向拉伸与压缩教案教案标题:工程力学轴向拉伸与压缩教案教学目标:1. 理解轴向拉伸和压缩的基本概念和原理;2. 掌握计算轴向拉伸和压缩应力、应变以及变形的方法;3. 能够应用所学知识解决实际工程问题。
教学内容:1. 轴向拉伸和压缩的概念和特点;2. 应力、应变和变形的定义和计算公式;3. 杨氏模量和泊松比的概念和计算方法;4. 应用轴向拉伸和压缩原理解决实际工程问题的例子。
教学步骤:步骤一:导入(5分钟)引导学生回顾材料力学的基本概念,如应力、应变和变形的定义,并提问学生对轴向拉伸和压缩的理解。
步骤二:讲解轴向拉伸和压缩的概念和特点(10分钟)通过图示和实例,详细介绍轴向拉伸和压缩的概念、特点以及在工程中的应用。
步骤三:讲解应力、应变和变形的计算方法(15分钟)解释应力、应变和变形的定义,并引导学生掌握计算轴向拉伸和压缩应力、应变以及变形的公式和方法。
步骤四:讲解杨氏模量和泊松比的概念和计算方法(10分钟)介绍杨氏模量和泊松比的定义和计算方法,并与轴向拉伸和压缩的应力、应变关系进行关联。
步骤五:应用案例分析(15分钟)通过实际工程案例,引导学生应用所学知识解决轴向拉伸和压缩相关问题,如杆件的变形计算、应力分布分析等。
步骤六:小结与讨论(5分钟)对本节课的重点内容进行小结,并与学生进行互动讨论,解答学生提出的问题。
步骤七:作业布置(5分钟)布置相关作业,要求学生进一步巩固所学知识,如计算练习题、实际工程问题的解答等。
教学评估:1. 课堂互动:观察学生在课堂上的回答和提问情况,评估学生对轴向拉伸和压缩的理解程度。
2. 作业完成情况:评估学生通过作业完成情况,检验学生对所学知识的掌握程度。
3. 实际案例分析:通过学生在实际工程案例中的应用表现,评估学生能否将所学知识应用于解决实际问题。
教学资源:1. PowerPoint演示文稿;2. 实际工程案例材料;3. 计算器。
备注:以上教案仅供参考,具体教学内容和步骤可根据实际情况进行调整和修改。
轴向拉伸和压缩—轴向拉伸和压缩的概念与实例(建筑力学)

第七章 轴向拉伸与压缩
Hale Waihona Puke 轴向拉伸与压缩学习目标:
1. 弄清轴向拉(压)杆的受力特点和变形特点。 2. 应用截面法熟练计算轴向拉(压)杆的内力;并能正确 绘出轴力图。 3. 熟练掌握轴向拉(压)杆横截面上的正应力计算公式, 并能计算拉(压)杆的变形。 4.了解低碳钢和铸铁的σ-ε曲线,明确塑性材料和脆性材料 的力学性质及差别。 5. 会根据轴向拉(压)杆的强度条件进行强度计算。
重点:
轴向拉(压)杆的内力计算;轴向拉(压)杆横截面上的 应力计算及其强度条件在工程实际中的应用。
轴向拉伸与压缩
第一节 轴向拉伸和压缩的概念
在工程实际中经常遇到承受轴向拉伸和压缩的杆件。
轴向拉伸与压缩
受力特点:作用杆件上的外力(或外力合力)的作用线与 杆轴线重合。
变形特点:是纵向伸长或缩短。 这种变形形式称为轴向拉伸或压缩。 这类构件称为轴向拉(压)杆。
工程力学第八章
l-试验段原长(标距) -试验段原长(标距) ∆l0-试验段残余变形
28
断面收缩率
A A − 1 100 × 00 ψ= A
A -试验段横截面原面积 A1-断口的横截面面积 塑性与脆性材料 塑性材料: δ ≥ 5 % 例如结构钢与硬铝等 塑性材料: 脆性材料: δ <5 % 例如灰口铸铁与陶瓷等 脆性材料: 5
第8章 轴向拉伸与压缩
本章主要研究: :
拉压杆的内力、应力与强度计算 材料在拉伸与压缩时的力学性能 轴向拉压变形分析 简单拉压静不定问题分析 连接部分的强度计算
1
§1 引 言
轴向拉压实例 轴向拉压实例 轴向拉压及其特点 轴向拉压及其特点
2
轴向拉压实例 轴向拉压实例
3
轴向拉压及其特点
外力特征:外力或其合力作用线沿杆件轴线 : 变形特征:轴向伸长或缩短,轴线仍为直线 :轴向伸长或缩短, 轴向拉压: 以轴向伸长或缩短为主要特征的变形形式 : 拉 压 杆: 以轴向拉压为主要变形的杆件 :
37
应力集中对构件强度的影响
对于脆性材料构件, 对于脆性材料构件,当 σmax=σb 时,构件断裂
对于塑性材料构件, 后再增加载荷, 对于塑性材料构件,当σmax达到σs 后再增加载荷, σ 分布趋于均匀化,不影响构件静强度 分布趋于均匀化, 应力集中促使疲劳裂纹的形成与扩展, 对构件( 应力集中促使疲劳裂纹的形成与扩展 对构件(塑 性与脆性材料) 性与脆性材料)的疲劳强度影响极大
33
应力集中与应力集中因数
应力集中
由于截面急剧变化引起应力局部增大现象-应力集中 由于截面急剧变化引起应力局部增大现象-
34
应力集中因数
σmax K= σn
工程力学第7章++轴向拉伸与压缩
一、材料力学的任务 1、研究构件的承载能力 构件:组成结构或机械的部件。 构件:组成结构或机械的部件。 (1)衡量构件承载能力的强度要求: )衡量构件承载能力的强度要求: 强度:构件抵抗破坏的能力。 强度:构件抵抗破坏的能力。不因发生断裂或过量 的塑性变形而失效。 的塑性变形而失效。 破坏——断裂或过量的塑性变形 断裂或过量的塑性变形 破坏 变形——构件尺寸与形状的变化。 构件尺寸与形状的变化。 变形 构件尺寸与形状的变化 弹性变形——外力解除以后可消失的变形。 外力解除以后可消失的变形。 弹性变形 外力解除以后可消失的变形 塑性变形——外力解除以后不能消失的变形。 外力解除以后不能消失的变形。 塑性变形 外力解除以后不能消失的变形
F
FN (-)FN
F
3、轴力图:轴力沿轴线变化的图形 轴力图:
F FN + F
4、轴力图的意义
① ② 直观反映轴力与截面位置变化关系; 直观反映轴力与截面位置变化关系;
x
确定出最大轴力的数值及其所在位置, 确定出最大轴力的数值及其所在位置,即确定危险截
面位置,为强度计算提供依据。 面位置,为强度计算提供依据。
7.2 截面法 轴力 轴力图: 轴力图: 一、内力
F1 物体内部某一部分与相邻部分间的 相互作用力。必须截开物体, 相互作用力。必须截开物体,内力才能 B C A M F2 显示。 显示。 处于平衡状态的物体, 处于平衡状态的物体,其任一部分 F3 也必然处于平衡状态。 也必然处于平衡状态 截面将物体截开, 沿C截面将物体截开,A部分在外力 F1 Fy My 作用下能保持平衡,是因为受到B 作用下能保持平衡,是因为受到B部分的 约束。 限制了A 约束。B限制了A部分物体在空间中相对 Mx A C 于 B的任何运动(截面有三个反力、三个 的任何运动(截面有三个反力、 F2 Fx 反力偶) 反力偶)。 Fz Mz
《工程力学II》拉伸与压缩实验指导书
《工程力学II 》拉伸与压缩实验指导书§1 拉伸实验指导书1、概述常温、静载作用下的轴向拉伸实验是测量材料力学性能中最基本、应用最广泛的实验。
通过拉伸实验,可以全面地测定材料的力学性能,如弹性、塑性、强度、断裂等力学性能指标。
这些性能指标对材料力学的分析计算、工程设计、选择材料和新材料开发都有极其重要的作用。
2、实验目的2.1 测定低碳钢的下列性能指标:两个强度指标:流动极限s σ、强度极限b σ; 两个塑性指标:断后伸长率δ、断面收缩率ϕ;测定铸铁的强度极限b σ。
2.2观察上述两种材料在拉伸过程的各种实验现象,并绘制拉伸实验的F -l ∆曲线。
2.3分析比较低碳钢(典型塑性材料)和铸铁(典型脆性材料)的力学性能特点与试样破坏特征。
2.4了解实验设备的构造和工作原理,掌握其使用方法。
2.5了解名义应力应变曲线与真实应力应变曲线的区别,并估算试件断裂时的应力k σ。
3、实验原理对一确定形状试件两端施加轴向拉力,使有效部分为单轴拉伸状态,直至试件拉断,在实验过程中通过测量试件所受荷载及变形的关系曲线并观察试件的破坏特征,依据一定的计算及判定准则,可以得到反映材料拉伸试验的力学指标,并以此指标来判定材料的性质。
为便于比较,选用直径为10mm 的典型的塑性材料低碳钢Q235及典型的脆性材料灰铸铁HT150标准试件进行对比实验。
常用的试件形状如图1.1所示,实验前在试件标距范围内有均匀的等分线。
典型的低碳钢(Q235)的L F ∆-曲线和灰口铸铁(HT150)的L F ∆-曲线如图1.2、图1.3所示。
图1.2 低碳钢拉伸L F ∆-曲线 图1.3 铸铁拉伸L F ∆-曲线 F p -比例伸长荷载;F e -弹性伸长荷载;F su -上屈服荷载; F b -极限荷载F sl -下屈服荷载;F b -极限荷载;F k -断裂荷载图1.1常用拉伸试件形状低碳钢Q235试件的断口形状如图1.4所示,铸铁HT150试件的断口形状如图1.5所示,观察低碳钢的L F ∆-曲线,并结合受力过程中试件的变形,可明显地将其分为四个阶段:弹性阶段、屈服阶段、强化阶段、局部变形阶段。
工程力学(材料力学)1_3轴向拉伸与压缩
BC
D
PB PC N3 C
PC N4
5P +
–
PD D
PD D
PD
P
x
P8-9 例题
A 3F
1
2
B
C
F
2F
1
2
1
2
3F
F
1
2
3.应力
应力的表示:
(1)平均应力
(A上平均内力集度)
p平均
ΔP ΔA
P
M
A
(2)实际应力 (M点内力集度)
lim p
ΔP dP
ΔA0 ΔA dA
应力分解
垂直于截面的应力称为“正应力” (Normal Stress);
平杆BC为2杆)用截面法取节点B为研究对象
Fx 0 Fy 0
N1 cos 45 N2 0 N1sin 45 P 0
N1 28.3kN (拉力) N2 20kN (压力)
45° B C
p
N1
y
N2 45° B x
P
(2)计算各杆件的应力
1
N1 A1
28.3103 202 106
轴力的正负规定: N 与外法线同向,为正轴力(拉力); N
N与外法线反向,为负轴力(压力)。 N
轴力图—— N (x) 的图象表示。
N N>0 N
N<0
意 (1)轴力与截面位置的变化关系,较直观;
义
(2)最大轴力的数值及其所在面的位置,即危险截面位
置,为强度计算提供依据。 N
P
+
x
例1 图示杆的A、B、C、D点分别作用着大小为5P、8P、4P、 1P 的力,方向如图,试画出杆的轴力图。
