线性规划的应用
运筹学应用例题
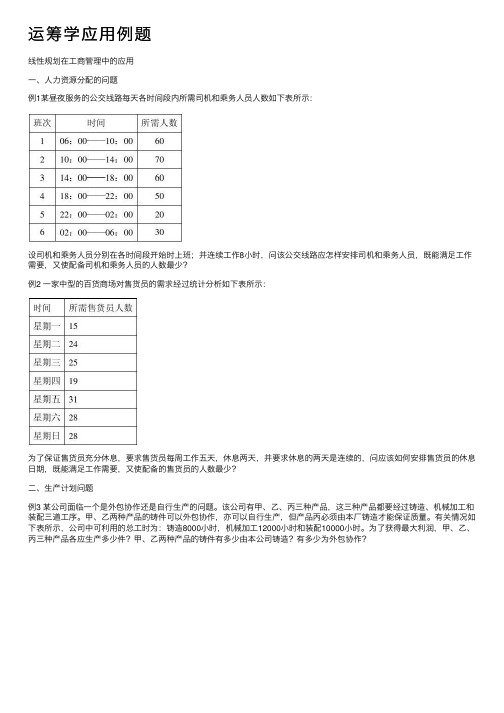
运筹学应⽤例题线性规划在⼯商管理中的应⽤⼀、⼈⼒资源分配的问题例1某昼夜服务的公交线路每天各时间段内所需司机和乘务⼈员⼈数如下表所⽰:设司机和乘务⼈员分别在各时间段开始时上班;并连续⼯作8⼩时,问该公交线路应怎样安排司机和乘务⼈员,既能满⾜⼯作需要,⼜使配备司机和乘务⼈员的⼈数最少?例2 ⼀家中型的百货商场对售货员的需求经过统计分析如下表所⽰:为了保证售货员充分休息,要求售货员每周⼯作五天,休息两天,并要求休息的两天是连续的,问应该如何安排售货员的休息⽇期,既能满⾜⼯作需要,⼜使配备的售货员的⼈数最少?⼆、⽣产计划问题例3 某公司⾯临⼀个是外包协作还是⾃⾏⽣产的问题。
该公司有甲、⼄、丙三种产品,这三种产品都要经过铸造、机械加⼯和装配三道⼯序。
甲、⼄两种产品的铸件可以外包协作,亦可以⾃⾏⽣产,但产品丙必须由本⼚铸造才能保证质量。
有关情况如下表所⽰,公司中可利⽤的总⼯时为:铸造8000⼩时,机械加⼯12000⼩时和装配10000⼩时。
为了获得最⼤利润,甲、⼄、丙三种产品各应⽣产多少件?甲、⼄两种产品的铸件有多少由本公司铸造?有多少为外包协作?三、套裁下料问题例4 某⼯⼚要做100套钢架,每套钢架需要长度分别为2.9⽶、2.1⽶、和1.5⽶的圆钢各⼀根。
已知原料每根长7.4⽶,问应如何下料,可使所⽤原料最省?四、配料问题例5某⼯⼚要⽤三种原料1、2、3混合调配出三种不同规格的产品甲、⼄、丙,产品的规格要求、产品的单价、每天能供应的原材料数量及原材料单价如下表所⽰:问该⼚应如何安排⽣产,才能使利润最⼤?五、投资问题例6 某部门现有资⾦200万元,今后五年内考虑给以下的项⽬投资:项⽬A :从第⼀年到第五年每年年初都可以投资,当年末能收回本利110%;项⽬B :从第⼀年到第四年每年年初都可以投资,次年末能收回本利125%,但规定每年最⼤投资额不能超过30万元;项⽬C :第三年初需要投资,到第五年末能收回本利140%,但规定每年最⼤投资额不能超过80万元;项⽬D :第⼆年初需要投资,到第五年末能收回本利155%,但规定每年最⼤投资额不能超过100万元。
线性规划模型的应用分析

第3章线性规划模型的应用1.某企业制造三种仪器,甲种仪器需要17小时加工装配,8小时检测,售价300元。
乙种仪器需要10小时加工装配,4小时检测,售价200元。
丙种仪器需要2小时加工装配,2小时检测,售价100元。
三种仪器所用的元件和材料基本一样,可供利用的加工装配时间为1000小时,检测时间为500小时。
又根据市场预测表明,对上述三种仪器的要求不超过50台、80台、150台。
试求企业的最优生产计划。
解:首先将问题中的数据表示到如下表格:imaxZ=300x1+200x2+100x317x1+10x2+2x3≤10008x1+4x2+2x3≤500x1≤50x2≤80x3≤150x1,x2,x3≥02. 某铸造厂要生产某种铸件共10吨,其成分要求:锰的含量至少达到0.45%,硅的允许范围是3.25%~5.5%。
目前工厂有数量充足的锰和三种生铁可作为炉料使用。
这些炉料的价格是:锰为15元/公斤,生铁A为340元/吨,生铁B为380元/吨,生铁C为280元/吨。
这三种生铁含锰和含硅量(%)如表3.22所示,问工厂怎样选择炉料使成本最低。
表3.22成分锰有部分是纯锰,部分是从生铁中提炼出来的,所以改进表格如下:设铸件中含有三种生铁和锰的量分别为xi(i=1,2,3,4)吨,则数学模型如下:maxZ=340x1+380x2+280x3+15000x4x1+x2+x3+x4=100.45%x1+0.5%x2+0.35%x3+x4≥0.45%*104%x1+1%x2+0. 5%x3≥3.25%*104%x1+1%x2+0. 5%x3≤5.5%*10xi≥0(i=1,2,3,4)3. 某工厂要做100套钢架,每套用长为2.9m,2.1m和1.5m的圆钢各一根。
已知原料每根长7.4m,问应如何下料,可使所用原料最省。
解:4. 绿色饲料公司生产雏鸡、蛋鸡、肉鸡三种饲料。
这三种饲料是由A、B、C三种原料混合而成。
产品的规格要求、产品单价、日销售量、原料单价见表3.23、表3.24。
线性规划:建模与应用

什么是线性规划模型
线性规划模型的一般形式
4
线性规划问题的分类
资源分配问题(resource-allocation):资源 约束。伟恩德玻璃制品公司产品组合问题
成本收益平衡问题(cost-benefit-trade-off): 收益约束。利博公司广告组合问题,大沼 泽地金色年代公司的现金流问题
网络配送问题(distribution-network):确 定需求约束。
混合问题(mix):多种约束。
5
主要内容
Super Grain Corp. Advertising-Mix Problem (Section 4.1)(超级食品公司的广告 组合问题)
Resource Allocation Problems & Think-Big Capital Budgeting (Section 4.2)(资源分配问 题和梦大发展公司的资金预算问题)
Question: At what level should they advertise Crunchy Start in each of the three media?
确定各种媒介的广
告力度以获得最有 效的广告组合?
11
Algebraic Formulation (数学模型)
Let (设定) TV = Number of commercials for separate spots on television (电视上的广告时段数目) M = Number of advertisements in magazines. (杂志上的广告数目) SS = Number of advertisements in Sunday supplements. (星期天增刊上的广告数目)
线性规划论文 (5)

线性规划论文简介线性规划是数学规划领域的一种重要方法,用于优化线性目标函数在一系列线性约束条件下的取值。
由于其广泛的应用性和高效的计算方法,线性规划在工程、经济、物流等领域中被广泛应用。
背景线性规划的出现与发展源于对优化问题的研究。
在过去的几十年中,随着计算机技术的进步和算法的优化,线性规划在实践中得到了广泛的应用。
线性规划的主要优点是能够处理大规模的问题,并且提供了一种可行的方式来解决复杂的决策问题。
定义和模型线性规划问题的一般形式可以表示为:最大化(或最小化)目标函数:Z = c₁x₁+ c₂x₂ + ... + cₙxₙ在约束条件下:a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ ≤ b₁a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ ≤ b₂...aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ ≤ bₙx₁, x₂, ..., xₙ ≥ 0其中,x₁, x₂, ..., xₙ是决策变量,c₁, c₂, ..., cₙ是目标函数的系数,a₁₁, a₁₂, ..., aₙₙ是约束条件的系数,b₁, b₂, ..., bₙ是约束条件的右侧常数。
算法和求解线性规划问题的求解可以使用多种算法,包括单纯形法、内点法等。
这些算法基于不同的思想和技巧,通过迭代计算来逼近最优解。
其中,单纯形法是最常用的算法之一,它通过不断地改变基变量和非基变量的组合来寻找最优解。
内点法则是近年来发展起来的一种新的算法,通过在可行域内部搜索最优解。
应用领域线性规划在众多领域中都有广泛的应用。
以下是线性规划常见的应用领域:生产计划与调度通过线性规划,可以优化生产计划和调度问题。
通过设置合理的约束条件和目标函数,可以最大程度地提高生产效率,减少生产成本。
运输与物流规划线性规划在运输和物流规划中也得到了广泛应用。
通过优化物流路径和运输计划,可以降低运输成本,提高物流效率。
金融与投资管理在金融领域中,线性规划可以用于优化投资组合和资产配置,以最大化收益或降低风险。
高三线性规划知识点

高三线性规划知识点线性规划是高中数学中的一个重要知识点,它在实际生活中有着广泛的应用。
本文将全面介绍高三线性规划的相关知识,包括定义、基本概念、解题步骤以及一些典型例题。
一、线性规划的定义线性规划是一种数学模型,用于求解一个线性函数在一组线性约束条件下的最优值。
在实际生活中,我们常常需要在一定的条件下寻找最优解,例如:生产成本最小、收益最大、资源利用最佳等等。
线性规划通过建立数学模型,帮助我们找到最优解。
二、线性规划的基本概念1. 目标函数:线性规划的目标通常是最大化或最小化一个线性函数。
这个函数被称为目标函数,记作Z。
2. 线性约束条件:线性规划的约束条件是一组线性不等式或等式,限制了变量的取值范围。
3. 变量:线性规划的变量是我们要求解的未知数,可以用任意字母表示。
4. 可行解:满足所有约束条件的解称为可行解。
可行解的集合称为可行域。
5. 最优解:在所有可行解中,使目标函数取到最大值或最小值的解称为最优解。
三、线性规划的解题步骤1. 建立数学模型:根据问题的描述,将目标函数和约束条件用代数式表示出来。
2. 确定可行域:将约束条件化为不等式形式,并将它们表示在坐标系中,找出它们的交集,确定可行域的范围。
3. 确定最优解:在可行域内寻找目标函数的极值点,得出最优解。
4. 检验最优解:将最优解代入原问题中,检验是否满足所有约束条件。
四、典型例题例题1:某工厂生产甲、乙两种产品,甲产品每吨利润为1000元,乙产品每吨利润为1200元。
已知生产一吨甲产品需要材料A 30千克,材料B 10千克;生产一吨乙产品需要材料A 20千克,材料B 40千克。
工厂每天可以使用材料A 600千克,材料B 200千克。
问如何安排生产,使得利润最大化?解:首先,我们定义两个变量x和y,分别表示甲、乙产品的生产量(吨)。
目标函数Z表示利润的最大值,即Z=1000x+1200y。
约束条件如下:30x+20y ≤ 60010x+40y ≤ 200x,y ≥ 0我们可以将该问题转化为图形解法,将约束条件绘制在坐标系中,确定可行域的范围。
线性规划知识点总结

线性规划知识点总结引言概述:线性规划是一种数学优化方法,用于在给定的约束条件下最大化或者最小化线性目标函数。
它在各种领域中都有广泛的应用,包括经济学、管理学、工程学等。
本文将对线性规划的基本概念、模型构建、求解方法和应用进行详细阐述。
一、线性规划的基本概念1.1 目标函数:线性规划的目标函数是一个线性函数,用于表示需要最大化或者最小化的目标。
1.2 约束条件:线性规划的约束条件是一组线性等式或者不等式,用于限制变量的取值范围。
1.3 可行解与最优解:线性规划问题存在无穷多个可行解,但惟独一个最优解,即使满足所有约束条件且使目标函数取得最大(或者最小)值的解。
二、线性规划模型构建2.1 决策变量:线性规划模型中的决策变量是需要优化的变量,可以是实数、整数或者二进制数。
2.2 目标函数的构建:根据问题的具体要求,将目标转化为线性函数的形式,并确定是最大化还是最小化。
2.3 约束条件的建立:根据问题的限制条件,将其转化为线性等式或者不等式的形式,并确定约束条件的数学表达式。
三、线性规划的求解方法3.1 图形法:对于二维线性规划问题,可以使用图形法进行求解。
通过绘制约束条件的直线或者曲线,找到目标函数的最优解点。
3.2 单纯形法:单纯形法是一种常用的求解线性规划问题的方法。
通过迭代计算,不断改变基变量和非基变量的取值,直到找到最优解。
3.3 整数规划法:当决策变量需要取整数值时,可以使用整数规划法进行求解。
该方法将线性规划问题转化为整数规划问题,并采用分支定界等算法求解最优解。
四、线性规划的应用4.1 生产计划:线性规划可以用于确定最佳的生产计划,以最大化产量或者最小化成本。
4.2 资源分配:线性规划可以用于优化资源的分配,如确定最佳的人力资源配置、物资采购策略等。
4.3 运输问题:线性规划可以用于解决运输问题,如确定最佳的货物运输路线和运输量,以降低运输成本。
4.4 金融投资:线性规划可以用于优化金融投资组合,以最大化收益或者最小化风险。
线性规划知识点

线性规划知识点一、概述线性规划是一种数学优化方法,用于解决线性目标函数和线性约束条件下的最优化问题。
它在各个领域都有广泛的应用,包括生产计划、资源分配、运输问题等。
本文将介绍线性规划的基本概念、模型建立、求解方法以及应用案例。
二、基本概念1. 目标函数:线性规划的目标是最大化或最小化一个线性函数,称为目标函数。
目标函数通常表示为Z=c1x1+c2x2+...+cnxn,其中ci为系数,xi为决策变量。
2. 约束条件:线性规划的决策变量需要满足一系列线性约束条件,通常表示为a1x1+a2x2+...+anxn≤b,其中ai为系数,b为常数。
3. 可行解:满足所有约束条件的解称为可行解。
4. 最优解:在所有可行解中,使目标函数达到最大或最小值的解称为最优解。
三、模型建立1. 决策变量:根据实际问题确定需要优化的变量,例如生产数量、销售数量等。
2. 目标函数:根据问题要求确定目标函数的形式,并确定系数。
3. 约束条件:根据问题要求确定约束条件的形式,并确定系数和常数。
4. 非负约束:线性规划中的决策变量通常要求非负,即xi≥0。
四、求解方法1. 图形法:对于二维线性规划问题,可以通过绘制约束条件的直线和目标函数的等高线来求解最优解。
2. 单纯形法:对于高维线性规划问题,可以使用单纯形法进行求解。
单纯形法是一种迭代算法,通过不断调整基变量和非基变量的取值,逐步接近最优解。
3. 整数规划:当决策变量需要为整数时,可以使用整数规划方法进行求解。
整数规划通常比线性规划更加复杂,求解时间也更长。
五、应用案例1. 生产计划:某公司有两种产品A和B,每单位产品A需要2小时加工时间和3小时装配时间,每单位产品B需要1小时加工时间和2小时装配时间。
公司每天有8小时的加工时间和10小时的装配时间可用。
产品A的利润为100元,产品B 的利润为80元。
如何安排生产计划,使利润最大化?2. 资源分配:某公司有三个项目需要分配资源,每个项目需要的资源量不同。
高中数学人教A版必修5课件线性规划

,
汇报人:
目录
CONTENTS
01 添加目录标题 02 线性规划的基本概念 03 线性规划的求解方法 04 线性规划的软件实现 05 线性规划的案例分析
06 线性规划的扩展知识
单击添加章节标题
第一章
线性规划的基本概念
第二章
线性用于求解线性目 标函数在满足一 组线性约束条件 下的最大值或最 小值。
运输问题
问题描述:某公司需要在多个城市之间运输货物,如何安排运输路线以最小化运输成本? 线性规划模型:建立线性规划模型,包括目标函数和约束条件 求解方法:使用单纯形法或其他优化算法求解模型 案例分析:分析某公司实际运输问题,计算最优运输方案,并比较不同方案的成本差异
资源分配问题
问题背景:某公司需要分配资源给多个项目,以实现最大收益 目标函数:最大化总收益 约束条件:资源有限,每个项目所需的资源数量不同 线性规划模型:通过建立线性规划模型,求解最优资源分配方案
线性规划的几何意义
线性规划是一种数学方法,用于解决线性约束条件下的优化问题
线性规划的目标是找到一组最优解,使得目标函数值最大或最小
线性规划的几何意义在于,它可以将线性规划问题转化为几何问题,通过图形直观地表示和解 决
线性规划的几何意义可以帮助我们更好地理解和解决线性规划问题,提高解决问题的效率和准 确性
投资优化问题
案例背景:某公 司计划投资多个 项目,但资金有 限,需要优化投 资方案
目标函数:最大 化投资回报率
约束条件:投资 总额不超过预算, 每个项目的投资 额不低于最小投 资额
线性规划模型: 通过建立线性规 划模型,求解最 优投资方案
线性规划的扩展知识
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性规划的应用
一、引言
线性规划是一种数学优化方法,可以用于解决各种实际问题。
本文将介绍线性规划的基本概念和应用领域,并通过一个实例详细说明线性规划的应用过程。
二、线性规划的基本概念
1. 目标函数:线性规划的目标是最大化或最小化一个线性函数,该函数被称为目标函数。
2. 约束条件:线性规划的解必须满足一系列线性约束条件,这些条件可以用一组线性不等式或等式表示。
3. 决策变量:线性规划中需要决策的变量被称为决策变量,它们的取值将影响目标函数的值。
三、线性规划的应用领域
线性规划广泛应用于各个领域,包括生产计划、资源分配、运输问题、投资组合等。
以下是其中几个常见的应用领域:
1. 生产计划:线性规划可以帮助企业确定最佳的生产计划,以最大化利润或最小化成本。
通过考虑资源限制、销售需求和生产能力等因素,可以确定最优的生产数量和产品组合。
2. 资源分配:线性规划可以帮助机构或组织合理分配有限的资源,以满足各种需求。
例如,一个学校可以使用线性规划确定最佳的课程安排,以最大化学生的满意度和资源利用率。
3. 运输问题:线性规划可以解决运输问题,如货物的最佳调度和运输路径的选择。
通过考虑运输成本、运输能力和需求量等因素,可以确定最优的运输方案,以降低成本并提高效率。
4. 投资组合:线性规划可以帮助投资者确定最佳的投资组合,以最大化回报并控制风险。
通过考虑不同投资资产的预期收益率、风险和相关性等因素,可以确定最优的投资权重。
四、线性规划应用实例:生产计划问题
假设某公司有两种产品A和B,每个产品的生产需要消耗不同的资源,并且有一定的市场需求和利润。
公司希望确定每种产品的生产数量,以最大化总利润。
1. 建立数学模型
设产品A的生产数量为x,产品B的生产数量为y。
根据题目描述,我们可以得到以下信息:
目标函数:最大化总利润,即maximize Z = 3x + 5y。
约束条件:
- 资源1的消耗:2x + 3y ≤ 10
- 资源2的消耗:4x + y ≤ 8
- 产品A的市场需求:x ≥ 0
- 产品B的市场需求:y ≥ 0
2. 解决线性规划问题
通过线性规划求解器或图形法,我们可以找到最优解。
最优解为x = 1.6,y = 2.8,总利润为19.6。
3. 结果解释
根据最优解,公司应该生产1.6个产品A和2.8个产品B,以最大化总利润。
此时总利润为19.6。
五、总结
本文介绍了线性规划的基本概念和应用领域,并通过一个生产计划问题的实例详细说明了线性规划的应用过程。
线性规划可以帮助解决各种实际问题,优化决策并达到最优解。
在实际应用中,我们需要根据具体问题建立数学模型,并使用适当的求解方法找到最优解。
通过合理应用线性规划,可以提高效率、降低成本,并取得良好的经济效益。
