理论力学2010.11.24
《理论力学(Ⅰ)》PPT 第11章
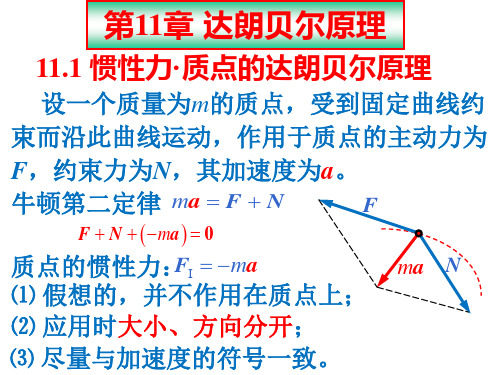
11.1 惯性力·质点的达朗贝尔原理
设一个质量为m的质点,受到固定曲线约
束而沿此曲线运动,作用于质点的主动力为
F,约束力为N,其加速度为a。
牛顿第二定律 ma F N
F
F N ma 0
质点的惯性力:FI ma
ma N
⑴ 假想的,并不作用在质点上;
⑵ 应用时大小、方向分开;
FAy
l aC1 2 α1
ml FIC1 maC1 2 α1
M IC1
ml 2 12 α1
A
FIC1
FAx αM1
IC1
l aC2 lα1 2 α2
ml 2 M IC2 12 α2
FIC2
maC2
mlα1
ml 2
α2
Fmg C1aC1
B α FIC2
2
M IC2
mg C2aC2
Fix 0
ωα O aC ain
MO
MO JOα
Fi M O Fit α miri2 M
负号表示矩的转向与α相反
IO
x
C
FIO FIit
y
ait FIin
结论:⑴ 定轴转动刚体惯性力系向轴心简
化,结果为通过轴心的一个惯性力和一个惯
性力偶。 FIO MaC,M IO JOα ⑵ 定轴转动刚体惯性力系向质心简化,结
ae P
FIAe
ar
P sin 2φ
aB ae 2 Q P sin2 φ
B Q FIB
φ
N
例11-6 长为l、质量为m的两均质细杆AB和 BD,用光滑铰链B相连接,并自由地挂在铅 直位置。今以水平力F作用于AB杆的中点, 求此瞬时两杆的角加速度及A点的约束力。
《理论力学》课件 第11章

因此,力F的元功又可表示为 δW F cosds F cos Rd
由静力学可知, F cosR 即为力 F 对轴 Oz 的力矩 Mz (F) ,于是有
δW Mz (F )d
(11-16)
即作用于定轴转动刚体上力的元功,等于该力对转轴的矩(简称 转矩)和微转角的乘积。
图11-5
当刚体在力 F 的作用下,绕轴转过 角时,力 F 所做的功为
v2 v1
d
1 2
mv2
M2 F dr
M1
或
1 2
mv22
1 2
mv12
W12
(11-22)
这就是质点动能定理的积分形式,即质点在某运动过程中动能的改 变,等于作用于质点上的力在同一过程中所做的功。
质点动能定理建立了质点动能和力的功之间的关系,它把质点的速度、作 用力和质点的路程联系在一起,对于需要求解这三个物理量的动力学问题, 应用动能定理是方便的。此外,通过动能定理对时间求导,式中将出现加 速度,因此动能定理也常用来求解质点的加速度。
则这种约束力所做功的总和为零。
图11-8
4.无重刚杆
如图 11-9 所示,无重刚杆 AB 连接两个物体,由于刚杆重量不计,因此其约束 力 FN 与 FN 应是一对大小相等、方向相反,作用线相同的平衡力。设 A,B 两点的 微小位移分别是 drA 和 drB ,则 FN 与 FN 元功之和为
δW FN drA FN drB FN | drA | cosA FN | drB | cosB FN (| drA | cosA | drB | cosB )
当力偶矩 M 常量时,上式可写为
(11-19)
W M
五、约束力的功与理想约束
2010.11动力学1—动力学基本方程

质点运动微分方程 应用
例三:求雨点下落时的末速度。设空气阻力为:R=kv2。
o m
解:
& m&& = mg − mkx x t =0 x =0
2
2
& x =0
R m mg
& 1 dx && = & x = g − kx2 2 dx g g 2 2 −2kx & & = + ce x = (1− e−2kx ) x k k
具有一定质量的几何点。 点:具有一定质量的几何点。
质点系:由许多(有限多或无限多) 质点系:由许多(有限多或无限多)相互联系着的 质点所组成的系统。 质点所组成的系统。 不变质点系:任意两质点之间的距离不变的质点系。 不变质点系:任意两质点之间的距离不变的质点系。 可变质点系:任意两质点之间的距离可变的质点系。 可变质点系:任意两质点之间的距离可变的质点系。
动力学基本定律:牛顿三定律 动力学基本定律:
第二定律
r r ma = F
注: (1) 上式称为—动力学基本方程
(2) 力与运动的关系的定量描述; (3)力是产生加速度的原因, 合力与加速度同时、同向。
动力学基本定律:牛顿三定律 动力学基本定律:
第三定律 (作用与反作用定律): 两个物体间的作用力与反作用力总是大小相等, 两个物体间的作用力与反作用力总是大小相等,方向 相反,沿着同一直线,且同时分别作用在这两个物体上。 相反,沿着同一直线,且同时分别作用在这两个物体上。
0
时
已知:匀速转动。 时小球掉下。 已知 匀速转动。 θ =θ 时小球掉下。 匀速转动 0 转速n. 求:转速 转速 解:研究铁球
其中 v =
理论力学第二版习题答案

理论力学第二版习题答案理论力学是物理学中研究物体运动规律的基础学科,它包括经典力学、相对论力学和量子力学等。
在经典力学中,牛顿运动定律是核心内容,而理论力学则进一步发展了这些定律,提供了更深入的分析和理解。
第二版的理论力学教材通常会包含更丰富的习题和更详尽的解答,以帮助学生更好地掌握力学的基本概念和方法。
习题1:牛顿运动定律的应用题目:一个质量为m的物体在水平面上受到一个恒定的力F作用,求物体的加速度。
解答:根据牛顿第二定律,力F等于物体质量m与加速度a的乘积,即F=ma。
因此,物体的加速度a等于力F除以质量m,即a=F/m。
习题2:动能和势能的计算题目:一个质量为m的物体从高度h自由落体,求落地时的动能。
解答:物体在自由落体过程中,重力势能转化为动能。
落地时的动能E_k等于重力势能的减少量,即E_k=mgh。
习题3:圆周运动的动力学分析题目:一个质量为m的物体以角速度ω在半径为R的圆周上做匀速圆周运动,求物体所受的向心力。
解答:匀速圆周运动的向心力F_c由公式F_c=mω^2R给出,其中m是物体的质量,ω是角速度,R是圆周的半径。
习题4:简谐振动的周期计算题目:一个质量为m的弹簧振子,弹簧的劲度系数为k,求其振动周期。
解答:简谐振动的周期T可以通过公式T=2π√(m/k)计算,其中m是振子的质量,k是弹簧的劲度系数。
习题5:刚体转动的动力学分析题目:一个均匀分布质量的刚体,其转动惯量为I,角速度为ω,求其转动动能。
解答:刚体的转动动能E_r可以通过公式E_r=0.5Iω^2计算,其中I是转动惯量,ω是角速度。
习题6:相对论效应的讨论题目:一个质量为m的物体以接近光速的速度v运动,求其相对论质量。
解答:在相对论中,物体的相对论质量m_r可以通过洛伦兹变换公式m_r=m/√(1-v^2/c^2)计算,其中m是静止质量,v是物体速度,c是光速。
习题7:量子力学的初步介绍题目:简述量子力学与经典力学的主要区别。
理论力学——精选推荐

理论⼒学理论⼒学总复习⼀、填空题1. 谐振⼦的向⼼⼒运动平均动能与势能的关系:V T =2. 物体向上抛科⽒⼒向东,向下落科⽒⼒向西。
3. α粒⼦运动轨道是双曲线,地球运动轨道是椭圆。
4. 惯量主轴上与转动轴存在夹⾓时转动轴上附加压⼒很⼤。
【动⼒反作⽤⼒与静⼒反作⽤⼒不相等时转动轴上附加压⼒很⼤。
】5. 枪膛为什么有来复线?⼦弹运动不会在出壳⽅偏离的太远6. 转动参考系中,泊松定理的推⼴:G dtG d dt G ?+=ω*d 7. 经典⼒学分为:⽜顿⼒学和分析⼒学。
8. ⽜顿定律适⽤范围:宏观、低速、惯性系中。
9. L —R —L ⽮量及其意义: rr mk J P A -?= 、得出物体的运动轨迹:θcos 2A GM m L r += 。
10. 极坐标系和⾃然(本征)坐标系单位⽮量:c o s s i n s i n c o s r e i j e i jθθθθθ→→→→→→=+=-+极坐标系:径向,横向; t r n r d d e e e e e e dr dr θθθθ==⾃然坐标系:切向+,法向- 。
11. 约束分类:约束⽅程中是否不显含时间t 不稳定约束稳定约束质点是否始终不能脱离约束可解约束不可解约束⼏何约束(完整约束):只限制质点在空间的位置。
运动约束(微分约束):除了限制质点的坐标,还要限制质点速度的投影。
不完整约束:①不能积分变为⼏何约束的微分约束。
②不能⽤等式表⽰的可解约束。
12.哈—雅⽅程:0),,,;,,,;(2121=+??s s q S q S q S q q q t H t S 。
13.理想约束:01=?∑=n i i i r R δ。
14.拉格朗⽇⽅程:(保守⼒系)0)(=-ααdq dL q d dL dt d 、(基本形式)αααQ dq dT q d dT dt d =-)( 15.虚功原理: 01=?=∑=n i i i r F W δδ。
16.哈密顿原理:积分形式:021=?t t Ldt δ。
理论力学第10章质点动力学的基本方程

动力学是研究物体运动与作用力之间的关系。
动力学中物体的抽象模型有质点和质点系。 质点是具有一定质量而几何形状和尺寸大小可以 忽略不计的物体。质点系是由几个或无限个相互 有联系的质点所组成的系统。刚体是特殊的质点 系。
动力学分为质点动力学和质点系动力学。
第十章 质点动力学的基本方程
重点:建立质点运动微分方程,质点动力学中“已知 运动求力”问题的解法。
eA
vy
0
dv y
m
eA mk
t
cos ktdt
0
得
vx
dy dt
dx dt
v0
sin kt
vy
由 t 0时
x y 0, 积分
v0dt ,
x
dx
0
t
0
y
dy
0
mk
2
eA
t
sin ktdt
0
得运动方程 x v t , 0 消去t, 得轨迹方程
F eE , 不计重力
作用。
已知常数A,k,忽略质点的重力,试求质点的运动轨迹。
求:质点的运动轨迹。
解:
m
d x dt
vx
2
2
m
dvx dt
0,
m
d y dt
2
2
m
dv y dt
eA cos kt
由 t 0时 v v , v 0, x 0 y 积分
v0
dv x 0
ab 0, 2 v m Fni ,
0 Fbi
3 、质点动力学的两类基本问题 第一类问题:已知运动求力(求导)。 第二类问题:已知力求运动(积分)。
2010江苏大学硕士研究生入学考试-理论力学(附答案)
江苏大学2010硕士研究生入学考试 理论力学(附答案)1、(10分)F 力作用于物体的A 点(如图),大小已知。
试求F 对x 、y 、z 轴之矩。
2、(20分)图示构件中不计各杆件重量,力1000P N ,杆ABC 与杆DEF 平行,尺寸如图,求A 、D 处的约束反力。
3、(10分)已知长为l 的AB 杆,其A 端放在水平面上,B 端放在斜面上,A 、B 处的摩擦系数都是0.25,试求能够支承重载荷W 的最大距离a ,杆自重不计。
3mBF4、(15分)图示直角弯杆OAB 绕O 轴转动,使套在其上的小环M 沿固定直杆CD 滑动。
已知:OA 与AB 垂直,1()OA m =,0.5()rad s ω=,在图瞬时OA 平行于CD且AM=,求此时小环M的速度;并求出小环M 的科氏加速度的大小和方向。
5、(20分)如图机构,圆盘以等角速度0ω顺时针转动。
试求在图示瞬时,AB 杆和BC 杆的角速度和角加速度。
6、(20分)重120()N 的均质杆AB ,长为0.8()m ,重心在C 点,A 、B 端的滚轮重量不计。
AB 杆在自重作用下在铅垂平面内运动,杆的两端限制在水平和垂直的光滑导槽内运动。
开始运动时,AB 杆处于铅垂位置,而B 点具有初始速度03()v m s =。
试求AB 杆达到水平位置时,A 端的速度;同时求出当AB 杆与水平线成任意角θ时(2πθ≤),连杆的角速度。
7、(20分)匀质杆AB 长l ,质量为M ;杆的一端在绳索BD 上另一端搁在光滑水平面上。
当绳铅直而静止时杆对水平面的倾角45ϕ=。
现在绳索突然断掉,求在刚断后的瞬时杆端A 的约束反力。
8、(10分)图示一滑道连杆机构,已知OA r =,滑道倾角为045β=,机构重量和各处摩擦均不计。
当030θ=时机构平衡,试求作用在曲柄OA 上的力偶M 与在滑道连杆上作用的水平力F 之间的关系(用虚位移原理求解)。
9、(10分)振动系统如图所示,杆的质量不计,在杆上端有一质量为m 的摆球。
(完整版)《理论力学》试题库
《理论力学》试题库第一部分填空题:第一类:1,已知某质点运动方程为x=2bcoskt,y=2bsinkt,其中b、k均为常量,则其运动轨迹方程为-—————-———--,速度的大小为——-—————-———,加速度的大小为—————————-—-。
2、已知某质点运动方程为x=2cos3t,y=2sin3t,z=4t则其运动速度的大小为,加速度的大小为 .3、已知某质点运动方程为r=e ct,θ=bt,其中b、c是常数,则其运动轨道方程为——-———-—-——-———-————--,其运动速度的大小为--———————-,加速度的大小为———-————————。
4、已知某质点的运动方程为x=2bcos2kt,y=bsin2kt,则其运动轨道方程为;速度大小为 ;加速度大小为。
5、已知质点运动的参数方程为y=bt,θ=at,其中a、b为常数,则此质点在极坐标系中的轨道方程式为,在直角坐标系中的轨道方程式为。
6、已知某质点的运动方程为r=at,θ=bt,其中a、b是常数,则其运动轨道方程为—-———-——-——-——————————,其运动速度的大小为——-———————,加速度的大小为—-—-———-————。
7、已知某质点运动方程为r=at,θ=b/t,其中a、b是常数,则其运动轨道方程为---—-———--————-,其运动速度的大小为—-—-—--———,加速度的大小为———-—————.8、已知某质点的运动方程为x=at,y=a(e t-e-t)/2,其中a为常数,则其运动轨道方程为—-—-——-—---—————---———,曲率半径为——-———————。
第二类:9、质点在有心力作用下,其————————————-—-—-———均守恒,其运动轨道的微分方程为—--——-——-——————--—————,通常称此轨道微分方程为比耐公式。
10、柯尼希定理的表达式为—-——-——————--————-—-,其中等式右边第一项和第二项分别为——————————————————————---—-—————-——————-——-——-———。
理论力学10章.ppt
(m1 m2 ) s ks m2e2 sin t
• 齐次解:
s
k
s 0,p2
k
m1 m2
m1 m2
s Asin pt
2020/1/29
理论力学第10章
16
• 令s=l-l1,它表示从静止平衡位置起算的位 移。则得到振动方程:
m1 m2 ) s ks m2e2 sin t
t0
t0
• 质点的动量定理:质点的动量在某时段的 增量等于作用在质点上的外力对时间的积 分(冲量)。
• 质点的动量守恒定理:如果作用在质点的 外力和为零,则质点的动量保持不变。
2020/1/29
理论力学第10章
4
• 质点系的动量定理
• 质点系的每个质点,除了受到系统外部的 作用力(如重力)外,还受到相邻质点的 作用力。
n
理论力学第10章 mivi mvc
1
i 1
• 动量的质心定理:
n mivi
i 1
n
mi
i 1
dri dt
d dt
n
mi ri
i 1
n
miri
rc
i 1
m
n
mivi mvc i 1
• 2.冲量:作用力与作用时间的乘积。
t
I 0 Fdt
J z M z (F) 0
J z const
2020/1/29
理论力学第10章
30
• 例10.5 复摆的质量为m,对摆轴O的转动惯量为J, 质心C到转轴O距离为a,求微小摆动的周期T。
• 解:对摆应用动量矩定理
哈工大第七版理论力学课件
FE1y F
FBy
P
50
[题1-2(i)] (P25) 画出下列各物体和整′体的受力图
A
F
F
CE
D
FOx
O
B
FBx
FOy
FBy FAx
FAy
A
FCx C
FC′ x C
E
D
FC′ y
FE
A
FA′ x
FA′y
E
FOx
FCy
O
FOy
F′E FBx
B
51 FBy
[例6] 画各物体的受力图和整体的受力图。
7 、正确判断二力构件。
45
[例5] 画出下列各构件的受力图和整体的受力图
FD
F FAx
FD
F
FBy
FBx
FH
FAy
FC
FD
F 'H
FAx
F'By
F'C
F FAx
FAy
F'Bx
FAy
46
[例6] 画出下列各构件的受力图和整体的受力图
[整体]
C
B 60º
A
FAx FAy
[AC杆]
FCy
C
[CE杆] F'Cx C
FN FN
FNA
FNB
23
渐开线 FN
—压力角 FN
节圆
24
2.由柔软的绳索、链条或皮带构成的约束
T
绳索类只能受拉,所以它们的约束力是
P
P
作用在接触点,方向沿绳索背离物体。
F
F1 F'1 F2 F'2
FA' FB'
