船模自航试验及实船性能预估船舶阻力与推进
船舶阻力船模阻力试验
第13页/共27页
§4-3 几何相似船模组试验
集合相似船模组试验是指几何相似而大小不 等的一系列船模的总称。作用有
1、验证傅汝德假定的正确性 2、确定形状因子 3、研究推进效率中各成分的尺度作用
13
第14页/共27页
一、验证傅汝德假定的正确性
14
第15页/共27页
2、确定形状因子(1+ k )
,在相同 的条件下才 能准确地判 别船型的优 劣。
1、傅汝德表达法比较阻力性能
23
第24页/共27页
24
第25页/共27页
2、泰洛表达法比较阻力性能
由于
表达法只要换算到相同
船长情况下的对应曲线,就可以比较不 同船型的阻力性能。这样在相同的傅汝
德数时的阻力性能的比较,实际上就是 在相同速度下对不同船型阻力性能的比 较。若在设计时船长和速度已知,则在 相应的傅汝德数处绘一垂线,即可得对 应的优良阻力性能船型。
注意:二因次法虽有不足之处,但由于误差 较小,尚能比较准确的满足工程实际需要, 故此方法具有工程应用价值,曾被广泛采用 ,现在仍被一些试验池继续采用。
9
第10页/共27页
二、三因次换算法
1、基本思想
1)粘压阻力和摩擦阻力合并为粘性阻力并 与雷诺数有关。 2)兴波阻力与傅汝德数有关。 3)根据船模试验结果,认为粘压阻力系数 与摩擦阻力系数之比是一常数k,则有:
§4-2 船模与实船的阻力换算
一、二因次换算法
1、假定
1)假定船体总阻力可以分为摩擦阻力和剩余阻 力两部分,且摩擦阻力和剩余阻力相互独立。
6
第7页/共27页
2)相当平板假定:假定船体的摩擦阻力等于同 速度、同长度、同湿面积的平板摩擦阻力。 2、二因次换算关系
2015-船舶阻力(7)-阻力的近似估算方法1

③ ④ ⑤Байду номын сангаас
根据
s
S C r 如果Cp>0.8且L/B≠6.5,由图7-6对 Am 进行修正。
计算Cr—Rr——Rt B/T≠2.4 修正 △Rt=±10(B/T-2.4)×0.5%Rt 2.4<B/T<3.0 取正;其他取负。 总阻力=Rt+ △Rt
S Cr C p L 的值,查 Am
7.3 母型船数据估算法
• 早期的泰勒系列试验图谱:单位排水量剩余阻力等值线的形式,英制单位。 • 1954年盖特勒对泰勒标准阻力数据进行了重新分析整理: 无量纲的剩余阻力系数图表。(不同排水体积系数(∨/L3),Cr—V/L0.5关 系曲线)——设计船的剩余阻力系数; 无量纲的湿表面积系数图谱——船体湿表面积,并记入一定的粗糙度补贴, 桑海公式——摩擦阻力系数。该系列图谱亦称为泰勒-盖特勒系列图谱。
2.泰勒-盖特勒系列阻力估算的具体步骤
e、计算总阻力Rt、有效功率Pe值。
总阻力系数:Cts=Cr`+Cf+ △Cf
总阻力 : Rts=Cts*0.5v 2S`
有效功率:Pe=Rts v/1000
(N)
(kw)
不同V—重复上述计算—v-Pe曲线
母型—巡洋舰 —适用航速较高船型较瘦(双桨) —普通货船结果偏低
扩展的泰勒系列图谱估算法
剩余比阻力Rr/△图谱的函数关系:
B Rr / f1 , C , C p , Fr T
当B/T、C▽一定时,该函数关系可表示为:
Rr / f 2 C p , Fr
图谱形式是:对每一组B/T,以不同的C▽给出不同的图谱,每张图谱中以
无型线图 — 查Cs图谱 — 插值计算得Cs
船舶性能试验技术报告

螺旋桨敞水试验
1.试验目的
(1)对于某一具体的螺旋桨,通过模型试验可以确定实际螺旋桨的水动力性能。 (2)通过多方案的试验研究,可以分析螺旋桨的各种几何要素对水动力性能的影 响。 (3)检验理论设计的正确性,不断完善理论设计的方法。 (4)通过对螺旋桨模型的系列试验,可以绘制成专用图谱,供设计螺旋桨使用。 现时广泛使用的楚思德 B 系列图谱和 MAU 系列图谱等都是螺旋桨模型系列敞水试 验的结果。
Ctm/Cfm=(1+k)+yFrn/Cfm (1+k)、A 及 n 等数值均由最小二乘法确定,指数 n 的范围为 2.0~6.0。 船的总阻力可以写为: Rt R f Re Rw
3. 试验设备和仪器 水池及控制系统、电机及调速仪、压力传感器、拉压传感器、多分力 天平、自航仪(推扭传感器)等。
图 2.1 六分力天平实物图
图 2.2 数据采集窗口
3. 试验船模
试验船模如图 3.1 所示,采用较为简单的箱型船体,其总长为 1350mm, 型宽为 240mm,型深为 240mm,最大吃水为 120mm,排水量为 10kg。
图 3.1 试验船模实物图
4. 试验过程与结果
为保证试验结果的可信性,选取多组位移 A 和频率 f 进行试验,如表 4.1 所示,试验如图 4.1 所示。数据采集软件测得的数据如表 4.2~4.7 所示。将 每组实验结果与相应的加速度绘制成如图 1.1 所示图像,即可求出相应的附 连水质量。
拖曳水池拖车
7. 试验步骤及数据记录
实验准备 • 制作船模,缩尺比依据水池长度、拖车 高速度以及实船尺度和航速确定 • 安装人工激流装置 • 称重,准确称量船模重量和压载重量,达到按船模缩尺比要求的实船相应排
演示文稿-船模阻力试验

C R CTm C Fm
其中CFS和CFm是实船和船模的摩擦阻力系数, 按1957年国际船池会议建议的公式计算,△CF 是摩擦阻力附加补贴值(或称相关因子),习 3 惯上取: CF 0.4 10
实船的总阻力和有效功率:
RTS 0 CTS 0 1 2 s SV s 2
(N)
4、检查水温测量装置工作是否正常,并记 录水池水温(在水深方向的温差应小于2℃); 5、调整船模的排水量、浮态,使其符合试 验要求,同时船模在水下部分的表面上应无气 泡;
6、导向器的安装应灵活可靠,激流丝的安 装要正确,参见图1; 7、拖点的位置以及拖力的方向要与实船一 致,对于一般的排水量船,通常拖点高度就取 在水线面上。
ν m:池水的运动粘性系数,
(m2/s);
可根据船模在低弗劳德数(Fr=0.1-0.2)范围的 试验结果按下式算出:
CTm Fr n (1 K ) A C Fm C Fm 式中(1+K)、A、n等数值由最小二乘法确定,
指数n的范围一般为2~6。也可采用普鲁哈斯卡方法进 行计算确定。 (注:为了获得最小的标准误差,应对船模阻力试验结 果作出曲线,经光顺后重新选取航速与阻力值对应点 再进行(1+K)等值的计算。)
1、1978年15届国际船模水池会议(ITTC) 推荐的三因次换算方法;
2、我国习惯使用的二因次换算方法
三因次换算方法:
C Tm RTm 1 2 m S mV m 2
CTm :船模总阻力系数;
RTm :船模总阻力(N);
m :池水密度(kg/m3);
S m :船模湿表面积(m2);
Vm :船模速度(m/s);
4、试验过程中,将每个速度所对应的 船模阻力值点绘在坐标纸上,以便随时检查 阻力曲线的光顺程度,判断试验结果是否可 信。对于有疑问的试验点应及时重做,或在 其附近增加试验点; 5、记录水池水温。
船模阻力

院系工学院理论与应用力学专业班级理论与应用力学12级实验课程流体力学实验姓名:梁彦豪指导教师苏炜船模阻力实验报告书目录一、实验摘要 (3)二、实验背景及工程应用 (3)三、实验目的要求 (3)四、实验装置 (3)五、实验原理 (4)六、实验方法与步骤 (6)七、实验数据处理与分析 (6)八、实验原始数据 (10)实验日期:2015年6月12日原创申明:我保证实验数据和实验报告是本人亲自完成。
签名:一、实验摘要本实验通过测量等比缩小的船模型的航行阻力,再与船模航行速度进行比较以得到船模阻力与速度之间的关系;再通过船模试验结果换算到实船阻力和实船航速之间的关系。
二、实验背景及工程应用船舶在水面上航行时,会遭受水的阻力作用。
如何预测船舶在航行时所遭受的阻力?船型和阻力之间的关系如何?这是船舶设计研究需要解决的重要问题。
迄今为止,船模阻力实验是确定船舶阻力的最有效的方法。
近年来,根据流体力学基本理论研究船舶阻力问题有很大进展,加上电子计算机的广泛应用,使得船舶阻力的理论计算方法有很大发展。
但是,由于船舶阻力问题比较复杂,在理论计算时常需作某些简化假定,故所得结果与实际到底存在多大差别,需要用船模实验结果进行检验,或进行适当的修正。
综上所述,船模阻力实验是目前研究船舶阻力最基本有效的方法。
三、实验目的要求本教学试验的目的是使学生初步掌握船模阻力试验的基本方法和根据船模试验结果换算到实船阻力的基本方法,借以培养学生进行科学试验研究的工作能力。
根据上述目的,本教学试验包括两个方面的内容: 1. 测定船模阻力与速度之间的关系。
2. 求出实船阻力(有效功率)与航速之间的关系。
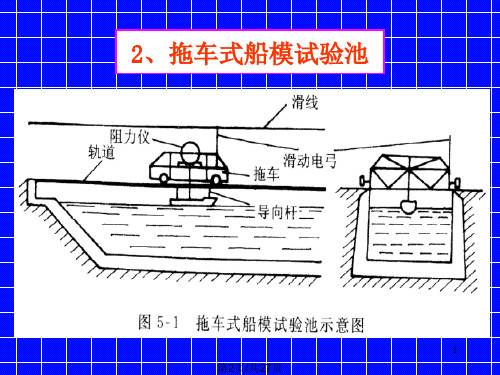
四、实验装置图1为我校试验水池简图。
拖车可沿水池两旁的轨道上行走;拖车上装置有控制、驱动系统及有关测量仪器,并载若干名试验人员。
图2表示船模与拖车连接的情况,拖曳船模的钢丝通过导轮与阻力仪连接。
图1 图2五、实验原理由船舶阻力理论已知,船舶在航行时遭受的总阻力可分为摩擦阻力、形状阻力和兴波阻力。
大工17秋《船模性能实验》实验报告答案

网络教育学院《船模性能实验》实验报告学习中心:层次:专业:学号:学生:完成日期:实验报告一一、实验名称:船模阻力实验二、实验目的: 主要研究船模在水中匀速直线运动时所受到的作用力及其航行状态。
三、实验原理:1.简述水面船舶模型阻力实验相似准则。
(1)船模与实船保持几何相似(2)船模实验的雷诺数e R 达到临界雷诺数以上。
(3)船模与实船傅汝德数相等2.分别说出实验中安装激流丝和称重工作的作用。
答:安装激流丝的作用,用1=Φmm 金属丝缚在船模的19站处使其在金属丝以后的边界层中产生紊流。
称重工作的作用,准确称量船模重量和压载重量,以达到按船模缩尺比要求的实船相应的排水量。
3.船模阻力实验结果换算方法有哪些?答:常用的船模阻力实验结构换算方法有两种,即二因次方法和三因次方法。
二因次方法亦称傅汝德方法;三因此方法为1978年ITTC 性能委员会推荐的换算方法。
4.简述傅汝德假定的内容,并写出傅汝德换算关系式。
答:傅汝德假定的内容是:①假定船体的总阻力可以分为独立的两部分,一为摩擦阻力f R ,只与雷诺数有关,另一个为粘压阻力pv R 和兴波阻力w R 合并后的剩余阻力r R ,只与傅汝德数有关,且适用比较定律。
②假定船体的摩擦阻力等于同速度、同长度、同湿面积的平板摩擦阻力。
因此,可以用平板摩擦阻力公式计算船体的摩擦阻力,通常称为相当平板摩擦。
傅汝德换算关系式:3)(αρρm s fm tm fs ts R R R R -+=四、实验内容: (一)填写实验主要设备表(表格可以追加)(二)实验步骤: 答:一.船模阻力实验准备(1)船模制作:船模缩尺比依据水池的长度和航速决定的,船模线型要与实船保持几何相似,表面必须光洁,满足一定的加工精度。
船模使用的材料通常是木模,木模不易变形,蜡模成本低。
(2)安装激流丝:用1=Φmm 金属丝缚在船模的19站处使其在金属丝以后的边界层中产生紊流。
(3)画水线:按首尾吃水、平均吃水画水线。
船舶阻力推进计算题及答案

船舶阻力与推进典型例题详解1.1.FroudeFroude 比较定律和Froude 假定及其相关一些概念例题1:某万吨船的船长=wl L 167m,排水量=∆25000t,航速kn V s 16=,对应船模缩尺比33=α,试着求船模的长度、排水量及其相应的速度。
解:根据流体力学中相似定律,可以知道有以下规律:α=VmVsα=m sL L 3αρρsm m s =∆∆因此求解结果如下表所示:参数Lwl(m)∆(t)Vs 实船1672500016船模5.0606060610.6956618532.7852425例题2:设有五艘尺度、船型、航速各不相同的船舶如下表:船类船长(m)航速(kn/h)货船12012客货船16023高速客船8523鱼雷艇2632拖轮46127分别计算它们的Froude 数Fn 和速长比LV s,并判断它们属于何种速度范围?解:注意计算Froude 数中各个量单位,gLV Fr s=,其中速度使用m/s 单位,g 为9.8m/s^2,L 单位为m ,而在速长比中,v 的单位为kn ,L 的单位为ft ,两者关系:L V F sr 2977.0=Fr LVs355.3=计算结果如下:L (m )航速(kn/h )Vs(km/h)Fr 船长(ft )速长比货船120.0012.00 6.170.18393.700.60客货船160.0023.0011.830.30524.93 1.00高速客船85.0023.0011.830.41278.87 1.38鱼雷艇26.0032.0016.46 1.0385.30 3.46拖轮(单放)46.0012.00 6.170.29150.920.98拖轮(拖带)46.007.003.600.17150.920.57例题3:某海船m L wl 100=,m B 14=,m T 5=,排水体积34200m =∇,航速为17kn,(1)试求缩尺比为20、25、30、35时船模的相当速度和重量;(2)当缩尺比为25,在相当速度时测得兴波阻力为1公斤,实验水池温度为12度,求其他船模在相当速度时的兴波阻力;(3)所有船模对应的实船在水温15度的海水中兴波阻力为多少吨?解:第一问考查相似定律,第二问考查Froude 比较定律,计算结果如下:α实船排水体积船模排水体积(m3)实船航速(m/s)船模速度(m/s )船模相当重量kg 船模Rw (kg )实船(kg )204200.000.538.74 1.96524.50 1.9516049.77254200.000.278.74 1.75268.54 1.0016049.77304200.000.168.74 1.60155.410.5816049.77354200.000.108.741.4897.870.3616049.772.二因次法解决船舶阻力问题(62)(B)例题4:某海船的水线长m L wl 100=,宽度m B 14=,吃水m T 5=,排水体积34200m =∇,中央剖面面积269m A M =,航速17kn,试求尺度比为25=α的船模相应速度。
船舶阻力1(修改稿)

兴波阻力:由兴波引起的压力分布改变所产生的阻力。 摩擦阻力:由于水存在粘性在船体周围形成边界层,使船体运动过程中
受到粘性切应力作用,表现为船体表面产生了摩擦力,其在运动方向的 合力为摩擦阻力。 粘压阻力:由于水的粘性和船体曲度变化,会产生旋涡、边界层等情况 改变了沿船体表面压力分布,引起船体前后压力不平衡而产生的阻力为 粘压阻力。
船舶阻力——第一章绪论 ——船舶快速性及研究方法
三、研究方法
1、理论方法 理论分析 CFD :STARCD、FLOW-3D、CFX、FLUENT 2、试验方法 船模试验和实船试验
江苏科技大学船舶与海洋工程学院
张瑞瑞
3
§1.2船舶阻力的分类及阻力曲线
一、概述
静水阻力 水阻力
船舶阻力
船舶阻力——第一章绪论—— 船舶阻力的分类及阻力曲线
裸船体阻力 附体阻力 汹涛阻力 空气阻力
船体阻力
附加阻力
二、船体阻力的成因及分类
1、船体阻力的成因 现象
波浪 边界层(粘性) 旋涡(曲度骤变处)
兴波阻力 Rw 摩擦阻力 Rf 粘压阻力(旋涡阻力)Rpv
江苏科技大学船舶与海洋工程学院
张瑞瑞
4
§1.2船舶阻力的分类及阻力曲线
船舶阻力——第一章绪论—— 船舶阻力的分类及阻力曲线
作业和思考题: (1)船舶阻力和船体阻力的划分图; (2)船体阻力中各阻力成分定义; (3)船体阻力的各相似定律; (4)傅汝德假定及其作用和存在的问题。
船舶阻力——第一章绪论 ——傅汝德假定
江苏科技大学船舶与海洋工程学院
张瑞瑞
18
江苏科技大学船舶与海洋工程学院 张瑞瑞
11
§1.3阻力相似定律
船舶阻力——第一章绪论 ——阻力相似定律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 船模自航试验及实船性能预估为了获得螺旋桨与船体之间的相互作用诸因素,如伴流分数、推力减额分数以及其他相互作用系数,应进行三种试验:船模阻力试验、螺旋桨敞水试验及有附体的船模自航试验。
船模自航试验是分析研究各种推进效率成分的重要手段。
对于给定的船舶来说,通过自航试验应解决两个问题:① 预估实船性能,即给出主机马力、转速和船速之间的关系,从而给出实船的预估航速,验证设计的船舶是否满足任务书中所要求的航速。
② 判断螺旋桨、主机、船体之间的配合是否良好。
如果配合不佳,则需考虑重新设计螺旋桨。
此外,根据实船试航结果与相应的船模自航试验数据,可以进行船模及实船的相关分析,积累资料以便改进换算办法,使船模试验预报实船的性能更正确可靠。
§ 6-1 自航试验的相似条件及摩擦阻力修正值一、相似定律在船模阻力试验时,我们只满足了傅氏数相同的条件,对于船模的雷诺数只要求超过临界数值。
因此,上式中,下标带m 者表示模型数值,带s 者表示实船数值(以下相同)。
在螺旋桨敞水试验时,只满足进速系数相同的条件,对于螺旋桨模型的雷诺数也只要求超过临界数值,因此,在进行船模的自航试验时,两者都要求满足,根据几何相似,有: 则满足傅氏数相等时有: λV V /s m = (6-1) 满足进速系数相等时有:λn V n V mAms As = 由于 ()s s As 1V ωV -=,()m m Am 1V ωV -= 故()()λn Vωn Vωmmmsss11-=-或 ⎪⎪⎭⎫⎝⎛--=s ms m 11ωω λn n 假定伴流无尺度作用,则m s ωω=,因此,可得:λn n s m = (6-2)(6-1)及(6-2)两式是船模自航试验应满足相似定律的条件,由于船后螺旋桨满足了进速系数相等的条件,因此在不考虑尺度作用的情况下,螺旋桨实桨及其模型在推力、转矩及收到马力方面存在下列关系:⎪⎪⎪⎭⎪⎪⎪⎬⎫===5.3ms Dm Ds 4ms m s 3ms ms λρρP P λρρQ Q λρρT T (6-3)(6-3)式只对螺旋桨说来是正确的,但自航试验是把螺旋桨与船体联系起来统盘考虑的。
因此推力与阻力之间必然有:对于实船 ()s s s 1R t T =-对于船模 ()m m m 1R t T =- 如果将(6-3)、(6-4)两式联系起来分析,发现两者是不一致的。
从推进的角度出发,当满足傅氏数和进速系数相同的条件时,模型与实桨的推力之间确实存在缩尺比三次方的关系。
假定推力减额无尺度作用,即t s = t m ,则从(6-4)式看来,实船与船模的阻力之间也应与缩尺比三次方有关才能使两者一致。
但是,在《船舶阻力》课程中我们已知,当船模与实船在傅氏数相同时,两者的总阻力并不存在缩尺比三次方的关系,即为了克服这个矛盾,需要在船模自航试验中作适当处理后才能进行实船的换算。
二、摩擦阻力的修正-实船自航点的确定在船模自航试验中,当满足傅氏数Fr 及进速系数J 相同的条件时,则模型与实船之间的各种力基本上是缩尺比的三次方关系,唯阻力之间不存在这种关系。
在阻力中,剩余阻力部分实际上也是满足这种关系的,因为在Fr 相同时实船和船模的剩余阻力系数相等,故两者总阻力之间不存在缩尺比三次方关系主要是摩擦阻力部分造成的。
为了使试验中各种力都存在缩尺比三次方的关系,需对阻力进行修正(实际上是对摩擦阻力修正),人为地将其硬凑成三次方关系。
设船模在速度V m 时的阻力为R m ,实船在相当速度m s V λV =时的阻力为R s ,则摩擦阻力修正值F D 为:或 ()D m 3m s s F R λρρR -= (6-5)这样,在船模自航试验中,当船模速度为V m 时,我们设法预先对船模加一个拖曳力F D ,则螺旋桨模型发出的推力T m 仅需克服阻力(R m -F D ),此点称为实船自航点即相当于实际螺旋桨发出推力T s 克服实船的总阻力R s 。
经过这样处理以后,船模自航试验系统中各种力便都存在λ3的关系。
假定t m = t s ,则(6-5)式可写作:或 3m s m s λρρT T =从上面的分析可知,进行摩擦修正(或称为决定实船自航点)的目的,是使模型桨的载荷与实船螺旋桨相当,只有在这种情况下,才能根据船模自航试验的结果预估实船推进性能。
§ 6-2 自航试验方法及数据表达一、自航试验概述(6-4)船模自航试验,一般是在阻力试验和敞水试验之后进行的,据此可以分析推进效率的各种成分。
图6-1是船模自航试验布置的示意图,借以说明试验中测量有关数据。
船模在速度V m 时的阻力R m 已自阻力试验中求得,在自航试验中,螺旋桨模型的转速n 、推力T及转矩Q B 由动力仪2测得,强制力z 由阻力仪1测得,船模速度V m 即为拖车的前进速度。
由于试验时要求保持等速直线前进,故力的平衡必然是:()m m 1R z t T =+- (6-6)自航试验的方法有所谓大陆法(即纯粹自航法)和英国法(即强制自航法)两种。
纯粹自航法根据船模速度V m 时的F D 值,事先在船模上予以扣除(即图6-1中时z 应等于F D ),然后调节螺旋桨的转速,使其发出的推力恰能克服阻力(R m -F D ),保持船模速度与拖车速度V m 相等。
由于F D 在试验中不能改变,因此调节比较困难。
在我国各水池中,基本上都采用强制自航法。
强制自航法是船模在螺旋桨推力T 和强制力z 的共同作用下,其前进速度和拖车速度V m保持相等。
对某一选定的船模试验速度V m ,一般需要外加五个强制力,即z 1、z 2、z 3、z 4、z 5。
对不同的强制力,为维持船模速度V m 而要求螺旋桨模型发出的推力T ,转速n 及转矩Q B 是不同的。
因此对于一个速度一般需要试五次,各次尽可能保持同一速度V m 。
测量记录数据有V m 、z 、T 、Q B 及n 五项。
五个强制力的范围大致是:z 1 = 0,相应于船模的自航点,即螺旋桨模型发出的推力克服船模的阻力;z 3=F D ,相应于实船的自航点。
z 2 = 0.5F D ,z 4、z 5一般大于F D ,总之使试验点子能合理布置。
为了正确预估实船性能,一般需要四个船模自航速度,即V 1,V 2,V 3,V 4,其中V 3约相当于实船试航速度,V 4则高于实船试航速度,以保证预估之实船性能在试验范围之内。
在对某一速度V m 进行试验时,由于很难保证相应于五个强制力的各次试验速度都相同,在有小量偏离的情况下,可以用下列办法进行修正。
如某次试验量得之船模速度为mV ',其相应的数值为T ′,BQ ',n ′,z ′,现在要化至标准的速度V m ,及其对应的数值T ,Q B ,n ,z ,其间之关系为:nn'V V ='m m(6-7) 2m m B B⎪⎪⎭⎫ ⎝⎛'=='=V V z z'Q Q T T' (6-8) 自航试验的测量结果通常应绘制成如图6-2所示之船模自航试验曲线。
据此可以进行各种推进效率成分的分析及实船性能预估。
图 6-1Q B zT 图 6-2二、试验结果的数据处理根据船模阻力曲线、螺旋桨模型敞水性征曲线及船模自航试验曲线,大体按下列步骤进行推进效率成分的分析处理,以便求得船体与螺旋桨相互影响的诸因素及推算出实船在相当速度时的推进性能。
1.相当于实船自航点的推进效率分析2.推进效率成分的分析上述表中分析所得的各种效率成分都是对应于船模的数值。
此外,两种表中分析所得之推进效率在数值上应基本一致,其误差应不超过0.001。
§ 6-3 实船推进性能预估所谓实船性能预估,是指根据船模自航试验结果给出实船航速、螺旋桨转速及收到马力之间的关系。
在20世纪50年代前,常用模型自航试验数据按相似定律和缩尺比直接算出实船的有关数据,由于忽略了所有的尺度作用,不可能得到正确的预报结果。
自50年代末开始,各国水池十分重视实船性能的预估问题,同时实船试航的资料积累也日渐增多,有可能对尺度作用进行经验统计的修正。
例如英国船池会议BTTP 于1965年采用的(1+ x )、K 2作为标准方法,1966年ITTC 也曾给以推荐,(1+x )、K 2统称为实船船模相关因子,前者主要是对阻力估算的相关因子,后者是照顾伴流尺度作用的相关因子。
由于该方法在分析中物理意义不清晰,后被废弃不用。
本节主要介绍实船性能预估的T ΔC 、ωΔ方法及1978 ITTC 的标准方法。
一、T ΔC 、ωΔ法在20世纪60、70年代,日本以及北欧的一些国家喜欢采用这种方法预估实船性能。
T ΔC 、ωΔ也称为相关因子,是根据经验统计资料而得出的修正数据。
这种方法认为:在船模实船的换算中,造成预估不正确的主要问题在于阻力和伴流二项,由于粘性不相似及摩擦阻力计算的外插等问题,致使阻力换算结果与实际有差别,因此需要用相关因子T ΔC 予以补救。
伴流受粘性的影响较大,船模试验得到的伴流数值偏高,应由相关因子ωΔ予以修正。
至于相对旋转效率ηR ,推力减额分数t 则认为尺度作用影响较小,可直接采用船模试验数据。
螺旋桨的敞水性征曲线有修正与不修正两种意见。
这类预估方法的大体步骤是:表中2T /J K 对于一定的船速是一常数,表示从阻力角度对螺旋桨的要求。
在螺旋桨的敞水性征图上可事先另设一个纵坐标2T /J K ,并绘制该桨的2T /J K J 曲线,从该曲线上可以读出表中2T /J K =常数的点子,该点表示了实船螺旋桨的工作点,由此可以读出η0、J 、K Q 等,并可按下表计算转速及马力。
据上述表中的计算结果,同样可以绘制如图6-3所示之N s -V s 及P Ds -V s 曲线。
二、1978 ITTC 单桨船实船性能预估的标准方法近二十年来关于实船性能预估问题的研究十分活跃,在历届ITTC 会议上都有相当的资料公布和有关这方面的讨论。
十五届ITTC 性能委员会企图总结出一个标准方法,经过三年的准备,在1978年十五届ITTC 会议上提出了一个《1978 ITTC 单桨船实船性能的预估方法》,并被大会通过作为暂行标准方法,要求各成员组织按此进行实船性能预估。
原先十五届ITTC 性能委员会准备给出统一的标准,但实际上无法做到,因而采取折衷的办法,将暂行标准分为两部分。
第一部分是1978 ITTC 标准预估,一切照其规定办法进行计算,第二部分是结合各水池自己积累的资料给予经验性修正,并据以得出实船航速、螺旋桨转速及收到马力之间的关系。
这个方法基本上与T ΔC 、ωΔ法相类同,唯对许多因素规定得更加明确具体而已。
现简述如下:第一部分:1978 ITTC 标准预估① 阻力采用三因次的(1+K )方法进行换算,故船模的总阻力系数应写作:()Rm Fm Tm 1C C K C ++= (6-9)式中,C Fm 为按1957ITTC 公式计算之摩擦阻力系数,C Rm 为剩余阻力系数,(1+K )为形状因子,可根据傅氏数Fr = 0.1~0.2范围内的试验结果按下式决定:()⎪⎪⎭⎫⎝⎛++=Fmm FmTm1C Fr A K C C(6-10) 其中,(1+K )、A 、m 等数值由最小二乘方确定。
