离散数学练习的题目(含详解2)(1)
离散数学习题答案及解析_2

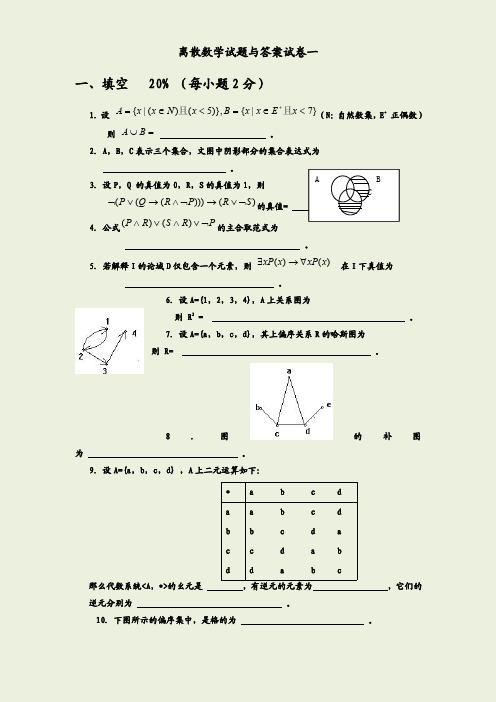
离散数学习题答案习题一1、利用逻辑联结词把下列命题翻译成符号逻辑形式(1)他既是本片的编剧,又是导演--- P∧ Q(2)银行利率一降低,股价随之上扬--- P→ Q(3)尽管银行利率降低,股价却没有上扬--- P∧ Q(4)占据空间的、有质量而且不断变化的对象称为物质--- M ←→<S∧P∧T> (5)他今天不是乘火车去北京,就是随旅行团去了九寨沟 --- P▽ Q(6)小张身体单薄,但是极少生病,并且头脑好使--- P∧ Q ∧ R(7)不识庐山真面目,只缘身在此山中--- P→ Q〔解释:因为身在此山中,所以不识庐山真面目(8)两个三角形相似,当且仅当他们的对应角相等或者对应边成比例--- S ←→<E∨T>(9)如果一个整数能被6整除,那么它就能被2和3整除。
如果一个整数能被3整除,那么它的各位数字之和也能被3整除解:设 P –一个整数能被6整除Q –一个整数能被2整除 R –一个整数能被3整除S –一个整数各位数字之和能被3整除翻译为:〔P→〔Q ∧ R∧〔R→ S2、判别下面各语句是否命题,如果是命题,说出它的真值〔1BASIC语言是最完美的程序设计语言--- Y,T/F〔2这件事大概是小王干的--- N〔3x2 = 64 --- N〔4可导的实函数都是连续函数--- Y,T/F〔5我们要发扬连续作战的作风,再接再厉,争取更大的胜利--- N〔6客观规律是不以人们意志为转移的--- Y,T〔7到2020年,中国的国民生产总值将赶上和超过美国--- Y,N/A〔8凡事都有例外--- Y,F3、构造下列公式的真值表,并由此判别哪些公式是永真式、矛盾式或可满足式〔1〔P∨〔~P∧ Q→ Q〔2~〔4表略:〔2可满足式、〔3永真式、〔4可满足式4、利用真值表方法验证下列各式为永真式〔1~〔8略5、证明下列各等价式〔3P→〔Q∨ R⇔〔P→ Q∨〔P→ R证明:左式⇔~P∨Q∨ R⇔~P∨Q∨~P∨ R⇔〔~P∨Q∨〔~P∨ R⇔〔P→ Q∨〔P→ R⇔右式〔4〔P∧ Q∨〔R∧ Q∨〔R∧ P⇔〔P∨ Q∧〔R∨ Q∧〔R∨ P证明:左式⇔<〔P∨R∧ Q∨〔R∧ P⇔<〔P∨R∨R>>∧<〔P∨R∨P>>∧〔Q∨R∧〔Q∨P⇔〔P∨ Q∧〔R∨ Q∧〔R∨ P⇔右式6、如果P∨ Q ⇔ Q∨R,能否断定 P ⇔ R ?如果P∧ Q ⇔ Q∧R,能否断定 P ⇔ R?如果~P ⇔~R,能否断定 P ⇔ R?解:〔1如果P∨ Q ⇔ Q∨R,不能判断P ⇔ R,因为如果 Q = P∨ R, 那么P∨ Q⇔P ∨P∨ R ⇔ Q∨R,但P可以不等价于R.〔2如果P∧ Q ⇔ Q∧R,不能判断P ⇔ R,因为如果 Q = P∧ R, 那么P∧ Q⇔P ∧P∧ R ⇔ Q∧R,但P可以不等价于R.〔3如果~P ⇔~R,那么有P ⇔ R,因为~P ⇔~R,则~P <-> ~R为永真式,及有P <-> R为永真式,所以P ⇔ R.8、把下列各式用↑等价表示出来〔1<P∧Q>∨~P解:原式⇔ <<P↑Q>↑<P↑Q>>∨<P↑P>⇔ <<<P↑Q>↑<P↑Q>>↑<<P↑Q>↑<P↑Q>>>↑<<P↑P>↑<P↑P>>9、证明:{ ~→}是最小功能完备集合证明: 因为{~,∨}是最小功能完备集合,所以,如果{ ~→}能表示出∨,则其是功能完备集合。
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学练习题(含答案)

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。
离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.二、简答题(共6道题,共32分)1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A B)-C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)三、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x)),x R(x) x P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠ 且B≠ ,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
离散数学练习题(含答案)

离散数学练习题(含答案)离散数学试题第一部分选择题1.下列命题变元p,q的小项是(C)。
A。
p∧┐p∧qB。
┐p∨qC。
┐p∧qD。
┐p∨p∨q2.命题“虽然今天下雪了,但是路不滑”可符号化为(D)。
A。
p→┐qB。
p∨┐qC。
p∧qD。
p∧┐q3.只有语句“1+1=10”是命题(A)。
A。
1+1=10B。
x+y=10___<0D。
x mod 3=24.下列等值式不正确的是(C)。
A。
┐(x)A(x)┐AB。
(x)(B→A(x))B→(x)A(x)C。
(x)(A(x)∧B(x))(x)A(x)∧(x)B(x)D。
(x)(y)(A(x)→B(y))(x)A(x)→(y)B(y) 5.量词x的辖域是“Q(x,z)→(x)(y)R(x,y,z)”(C)。
A。
(x)Q(x,z)→(x)(y)R(x,y,z))B。
Q(x,z)→(y)R(x,y,z)C。
Q(x,z)→(x)(y)R(x,y,z)D。
Q(x,z)6.设A={a,b,c,d},A上的等价关系R={。
}∪IA则对应于R的A的划分是(D)。
A。
{{a},{b,c},{d}}B。
{{a,b},{c},{d}}C。
{{a},{b},{c},{d}}D。
{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是(A)。
A。
{Ø,{Ø}}∈BB。
{{Ø,Ø}}∈BC。
{{Ø},{{Ø}}}∈BD。
{Ø,{{Ø}}}∈B8.集合相对补运算中,不正确的等式是(A)。
A。
(X-Y)-Z=X-(Y∩Z)B。
(X-Y)-Z=(X-Z)-YC。
(X-Y)-Z=(X-Z)-(Y-Z)D。
(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,不可结合的定义的运算是(D)。
A。
a*b=min(a,b)B。
a*b=a+bC。
a*b=GCD(a,b) (a,b的最大公约数)D。
离散数学试题十五套
度结点。
A.1; B.2; C.3; D.4 。
三、证明 26%
1、 R 是集合 X 上的一个自反关系,求证:R 是对称和传递的,当且仅当
< a, b> 和<a , c>在 R 中有<.b , c>在 R 中。(8 分)
2、 f 和 g 都是群<G1 ,★>到< G2, *>的同态映射,证明<C , ★>是<G1, ★>的一个
;是否有幂等 。
群或
。
9、n 个结点的无向完全图 Kn 的边数为
,欧拉图的充要条件是 。
10、公式 (P (P Q)) ((P Q) R 的根树表示为
。
二、选择 20% (每小题 2 分)
1、在下述公式中是重言式为(
)
A. (P Q) (P Q) ;B. (P Q) ((P Q) (Q P)) ;
)。
A.群; B.独异点; C.半群 。
三、证明 46%
1、 设 R 是 A 上一个二元关系,
10、
S { a,b | (a,b A) (对于某一个c A, 有 a, c R且 c,b R)} 试 证
子群。其中 C={x | x G1且f (x) g(x)} (8 分)
3、 G=<V, E> (|V| = v,|E|=e ) 是每一个面至少由 k(k 3)条边围成的连通
e k(v 2)
平面图,则
k 2 , 由此证明彼得森图(Peterson)图是非平面图。(11
分)
四、逻辑推演 16%
2、论域 D={1,2},指定谓词 P
P (1,1) P (1,2)
离散数学试题及解答

离散数学2^m*n一、选择题(2*10)1.令P:今天下雨了,Q:我没带伞,则命题“虽然今天下雨了,但是我没带伞”可符号化为()。
(A)P→⌝Q (B)P∨⌝Q(C)P∧Q (D)P∧⌝Q2.下列命题公式为永真蕴含式的是()。
(A)Q→(P∧Q)(B)P→(P∧Q)(C)(P∧Q)→P (D)(P∨Q)→Q3、命题“存在一些人是大学生”的否定是(A),而命题“所有的人都是要死的”的否定是()。
(A)所有人都不是大学生,有些人不会死(B)所有人不都是大学生,所有人都不会死(C)存在一些人不是大学生,有些人不会死(D)所有人都不是大学生,所有人都不会死4、永真式的否定是()。
(A)永真式(B)永假式(C)可满足式(D)以上均有可能5、以下选项中正确的是()。
(A)0= Ø(B)0 ⊆Ø(C)0∈Ø(D)0∉Ø6、以下哪个不是集合A上的等价关系的性质?()(A)自反性(B)有限性(C)对称性(D)传递性7、集合A={1,2,…,10}上的关系R={<x,y>|x+y=10,x,y∈A},则R的性质为()。
(A)自反的(B)对称的(C)传递的,对称的(D)传递的8.设D=<V, E>为有向图,V={a, b, c, d, e, f}, E={<a, b>, <b, c>, <a, d>, <d, e>, <f, e>}是()。
(A)强连通图(B)单向连通图(C)弱连通图(D)不连通图9、具有6个顶点,12条边的连通简单平面图中,每个面都是由()条边围成?(A)2(B)4 (C)3(D)5 10.连通图G是一棵树,当且仅当G中()。
(A)有些边不是割边(B)每条边都是割边(C)无割边集(D)每条边都不是割边二、填空题(2*10)1、命题“2是偶数或-3是负数”的否定是________。
离散数学考试题目及答案

离散数学考试题目及答案1. 试述命题逻辑中的等价关系和蕴含关系。
答案:命题逻辑中的等价关系是指两个命题在所有可能的真值赋值下都具有相同的真值。
若命题P和Q等价,则记作P⇔Q。
蕴含关系是指如果命题P为真,则命题Q也为真,但Q为真时P不一定为真。
若命题P蕴含Q,则记作P→Q。
2. 证明:若集合A和B的交集非空,则它们的并集包含A和B。
答案:设x属于A∩B,即x同时属于A和B。
根据并集的定义,若元素属于A或B,则它属于A∪B。
因此,x属于A∪B。
由于x是任意属于A∩B的元素,所以A∩B≠∅意味着A∪B至少包含A∩B中的所有元素,即A∪B包含A和B。
3. 给定一个有向图G,如何判断G中是否存在环?答案:判断有向图G中是否存在环,可以采用深度优先搜索(DFS)算法。
在DFS过程中,记录每个顶点的访问状态,如果遇到一个已访问过的顶点,且该顶点不是当前路径的直接前驱,则表示存在环。
4. 描述有限自动机的组成部分及其功能。
答案:有限自动机由以下几部分组成:输入字母表、状态集合、转移函数、初始状态和接受状态集合。
输入字母表定义了自动机可以接收的符号集合;状态集合包含了自动机所有可能的状态;转移函数定义了在给定输入符号和当前状态的情况下,自动机如何转移到下一个状态;初始状态是自动机开始工作时的状态;接受状态集合包含了所有使自动机接受输入字符串的状态。
5. 什么是图的连通分量?如何确定一个无向图的连通分量?答案:图的连通分量是指图中最大的连通子图。
在一个无向图中,如果两个顶点之间存在路径,则称这两个顶点是连通的。
确定无向图的连通分量可以通过深度优先搜索(DFS)或广度优先搜索(BFS)算法。
从任一顶点开始搜索,搜索过程中访问的所有顶点构成一个连通分量。
重复此过程,直到所有顶点都被访问过,即可确定图中所有连通分量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学试题
第一部分选择题
一、单项选择题
1.下列是两个命题变元p,q的小项是(C )
A.p∧┐p∧q B.┐p∨q
C.┐p∧q D.┐p∨p∨q
2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( D )A.p→┐q B.p∨┐q
C.p∧q D.p∧┐q
3.下列语句中是命题的只有( A )
A.1+1=10 B.x+y=10
C.sinx+siny<0 D.x mod 3=2
4.下列等值式不正确的是( D )
A.┐(∀x)A⇔(∃x)┐A
B.(∀x)(B→A(x))⇔B→(∀x)A(x)
C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)
D.(∀x)(∀y)(A(x)→B(y))⇔(∀x)A(x)→(∀y)B(y)
5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是(C )A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))
精彩文档
B.Q(x,z)→(∀y)R(x,y,z)
C.Q(x,z)→(∃x)(∀y)R(x,y,z)
D.Q(x,z)
6.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是( D )
A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}
C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}
7.设A={Ø},B=P(P(A)),以下正确的式子是(A )
A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈B
C.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B
8.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是(A )
A.(X-Y)-Z=X-(Y∩Z)
B.(X-Y)-Z=(X-Z)-Y
C.(X-Y)-Z=(X-Z)-(Y-Z)
D.(X-Y)-Z=X-(Y∪Z)
9.在自然数集N上,下列定义的运算中不可结合的只有( D )
A.a*b=min(a,b)
B.a*b=a+b
C.a*b=GCD(a,b)(a,b的最大公约数)
精彩文档
D.a*b=a(mod b)
10.设R和S是集合A上的关系,R∩S必为反对称关系的是( )
A.当R是偏序关系,S是等价关系; B.当R和S都是自反关系;
C.当R和S都是等价关系; D.当R和S都是传递关系
11.设R是A上的二元关系,且R·R⊆R,可以肯定R应是( D )
A.对称关系; B.全序关系; C.自反关系; D.传递关系
12.设R为实数集,函数f:R→R,f(x)=2x,则f是()
A.满射函数B.单射函数
C.双射函数D.非单射非满射
CDACCDAADADB
第二部分非选择题
二、填空题
1.设论域是{a,b,c},则(∀x)S(x)等价于命题公式S(a)∧S(b)∧S(c) ;(x∃)S(x)等价于命题公式S(a)∨S(b) ∨S(c) 。
2.设R为A上的关系,则R的自反闭包r(R)= _R∪A I_,对称闭包s(R)= _R∪R~。
3.某集合A上的二元关系R具有对称性,反对称性,自反性和传递性,此关系R是
I_,
A 其关系矩阵是只有主对角线上元素为1 。
三、计算题
精彩文档
精彩文档
1.(4分)如果论域是集合{a,b,c},试消去给定公式中的量词:)0y x )(x )(
y (=+∀∃。
2.用等值演算求下面公式的主析取范式。
)()(P Q Q P ∨⌝→→⌝
3.用等值演算法求公式)()(Q P Q P ⌝→↔→⌝的主合取范式。
精彩文档
4.(6分)在偏序集<Z,≤>中,其中Z={1,2,3,4,6,8,12,14}
,≤是Z 中的整除关系,求集合
D={2,3,4,6}的极大元,极小元,最大元,最小元,最小上界和最大下界。
5.设集合A={1,2,3,4,5},A 上的划分为π={{1,2,3},{4,5}},试求:
1) 写出划分π诱导的等价关系R ; 2) 写出关系矩阵R M ; 3) 画出关系图。
精彩文档
6. 设A ={a ,b ,c ,d },R 是A 上的二元关系,且R ={<a ,b >,<b ,a >,<b ,c >,<c ,
d >},求r (R )、s (R )和t (R )。
解 r (R )=R ∪I A ={<a ,b >,<b ,a >,<b ,c >,<c ,d >,<a ,a >,<b ,b >,<c ,
c >,<
d ,d >}
s (R )=R ∪R -1={<a ,b >,<b ,a >,<b ,c >,<c ,d >,<c ,b >,<d ,c >} R 2={<a ,a >,<a ,c >,<b ,b >,<b ,d >} R 3={<a ,b >,<a ,d >,<b ,a >,<b ,c >} R 4={<a ,a >,<a ,c >,<b ,b >,<b ,d >}=R 2
t (R )=i i R ∞
=1Y ={<a ,b >,<b ,a >,<b ,c >,<c ,d >,<a ,a >,<a ,c >,<b ,b >,
<b ,d >,<a ,d >}
7.已知集合A 和B 且|A|=n ,|B|=m ,求A 到B 的二元关系数是多少?A 到B 的函数数是多少?
精彩文档
解:因为|P(A ×B)|=2|A ×B|=2|A||B|=2mn ,所以A 到B 的二元关系有2mn 个。
因为|BA|=|B||A|=mn ,所以A 到B 的函数mn 个。
四、证明题
1.设R 和S 是二元关系,证明111
)
(---=S R S R Y Y
2.设A={a,b,c},R={(a,a),(a,b),(b,c)},验证rs(R)=sr(R)。
3.设R 是A 上的二元关系,试证:R 是传递的当且仅当
R R ⊆2,其中2R 表示R R •。
4.证明下列结论:
(1)R
∧
⇒
→
P→
∨
Q
P
R
Q
(2)D
→),
∧
⌝
(
)
∧
(
(
),
→
C
D
A
∨
B
C
B
A⇒
A
解:(1)1 P∧Q P附加前提
2 P T,1,I2
3 P∨Q T,2,I1
4 P∨Q→R P
5 R T,3,4,I3
6 P∧Q→R CP
(2)1 ⌝D P假设前提
2 D∨A P
3 A T,1,2,I5
4 (A→B)∧(A→C) P
5 A→B T,4,I2
6 B T,3,5,I3
7 A→C T,4,I2
8 C T,3,7,I3
9 B∧C T,6,8 ,合取式
10 ⌝(B∧C)P
精彩文档
11 (B∧C)∧⌝(B∧C)T,9,10,合取式,矛盾
5. 已知R和S是非空集合A上的等价关系,试证:1)R∩S是A上的等价关系;2)对a ∈A,[a]R∩S=[a]R∩[a]S。
解:∀x∈A,因为R和S是自反关系,所以<x,x>∈R、<x,x>∈S,因而<x,x>∈R∩S,故R∩S是自反的。
∀x、y∈A,若<x,y>∈R∩S,则<x,y>∈R、<x,y>∈S,因为R和S是对称关系,所以因<y,x>∈R、<y,x>∈S,因而<y,x>∈R∩S,故R∩S是对称的。
∀x、y、z∈A,若<x,y>∈R∩S且<y,z>∈R∩S,则<x,y>∈R、<x,y>∈S且<y,z>∈R、<y,z>∈S,因为R和S是传递的,所以因<x,z>∈R、<x,z>∈S,因而<x,z>∈R∩S,故R ∩S是传递的。
总之R∩S是等价关系。
2)因为x∈[a]R∩S⇔<x,a>∈R∩S⇔
<x,a>∈R∧<x,a>∈S⇔ x∈[a]R∧x∈[a]S⇔ x∈[a]R∩[a]S
所以[a]R∩S=[a]R∩[a]S。
五、应用题
1.所有的主持人都很有风度。
李明是个学生并且是个节目主持人。
因此有些学生很有风度。
请用谓词逻辑中的推理理论证明上述推理。
(论述域:所有人的集合)
精彩文档
精彩文档。
