正方体的截面图PPT课件

合集下载

高一下学期数学人教A版2019必修第二册8.1.3多面体的截面作法与正方体的截面形状课件.pptx

2、此平面与几何体的棱的交集(交点)叫做截点
探究与讨论Βιβλιοθήκη 现在用一个平面来截正方体，
D1
截面怎么作图，可能有哪些形状？
A1
G
例1如图，正方体ABCD―A1B1C1D1中， E、F、G分别在AB、BC、DD1上，求作过E、F、G三点的截面．
D
A
E
C1
B1
C F B
方法(交线法)：
该作图关键在于确定截点，有了位于多面体同一表面上的两个截点即可连结成截线，从而求得截面．
请数学课代表和6个小组长组织大家组内合作，将大家能找出的截面草图画出来，然后我会随机点一位组员分享每个组的学习成果！
注意：每组只有4分钟的时间交流，1-2分钟的时间分享！
各数学学习小组分享结果汇总ing
第一种情况：截面为三角形
第二种情况：截面为四边形
第三种情况：截面为五边形
第四种情况：截面为六边形
作法： (1)在底面AC内，过E、F作直线EF分别与DA、DC的延长线交于L、M．
D1
G A1
(2)在侧面A1D内，连结LG交AA1于K．
(3)在侧面D1C内，连结GM交CC1于H．
K
D
(4)连结KE、FH．则五边形EFHFK即为所求的截面． L A
E
C1
B1 H CM
F B
合作与交流
例1告诉咱们正方体的截面可以是五边形，那么还有哪些形状呢？
教师评价与归纳
课堂小结：
作业布置：
• 做完课时作业中关于截面的习题； • 回家找现有的水箱、水桶、纸箱、大碗等适量盛水移动部分顶点，观察水面图形的变化；
感谢聆听！
观察与思考
1、将一个西瓜或橘子切成两半，你能想象切面大致是什么形状吗？

正方体截面的三视图

正方体截面的三视图1、打开一个“新绘图”，建立直角坐标系。

2、用[画圆]工具画单位圆。

作出单位圆与y轴正半轴的交点C、负半轴交点D。

3、[标记]向量AB，依向量AB平移点B到B’；[标记]向量AC，依向量AC平移点C到C’；[标记]向量AD，依向量AD平移点D到D’。

4、[标记]原点A为“旋转中心”，把点D绕A旋转-45度，得到D’,用[文本编辑]工具把D’的标签改为D”。

5、用[画点]工具在屏幕上任意画三点E、F、G，用[画线段]工具连结AE、AF、AG。

6、用[选择]工具先后选择点E、点A，并选择[编辑]菜单中的[操作类按钮]、[移动]，选择“慢速地”后产生“→移动E->A按钮”。

用[文本编辑]工具把“→移动E->A按钮”改为“主视”。

7、用[选择]工具先后选择点E、B’、F、A，并选择[编辑]菜单中的[操作类按钮]、[移动]，选择“慢速地”后产生“移动”。

用[文本编辑]工具把“移动”改为“左视”。

8、用[选择]工具先后选择点E、D’、G、A，并选择[编辑]菜单中的[操作类按钮]、[移动]，选择“慢速地”后产生“→移动”。

用[文本编辑]工具把“→移动”改为“俯视”。

9、用[选择]工具先后选择点E、D”、F、B、G、C，并选择[编辑]菜单中的[操作类按钮]、[移动]，选择“中速”后产生“→移动”。

用[文本编辑]工具把“→移动”改为“还原”。

10、用[画点]工具在平面上任画一点H。

11、依向量AE平移点H，得到H’，立即把H’的标签改为I；依向量AF两次平移点H，得到H”，立即把H”的标签改为J；依向量AG两次平移点H，得到H”，立即把H”的标签改为K.12、以HI、HJ、HK为从一点出发的三条棱，完成平行六面体。

用[文本编辑]工具改写一些点的标签。

13、用[画线段]工具连结IK、LJ’,作出它们的中点，用[文本编辑]工具把标签分别改为M、N。

14、用[选择]工具先后选择K、M、L、N，并选择[作图]菜单中的[多边形内部]，给多边形填充。

正方体中截面的形状

A
。 ,
而截面
P
—
一
B
E A C
,
底面
C
AC
,
侧面
E
DC
C
I
,
己知两条交线的交点
,
一
图
1
I C
E
和
D
,
,
那么 C I 和底面
E
与
I
D
必在
,
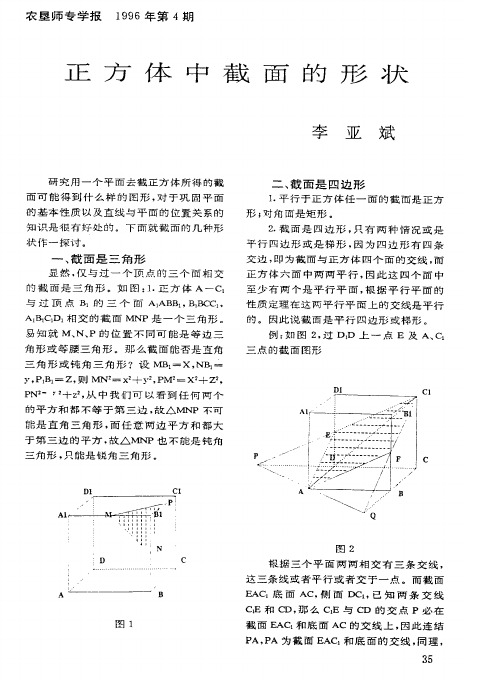
截面
P A
,
E A C
A C
的交线上因此连结
,
P A
为截面
A C
和底面的交线同理
35
P
A
的延长线与
B C
C B
I
的延长线交点 Q 必在
一
一一寸
硬
一
泛;
、
亡
二
户截面是六边形在图
中点图
3
,
5
中只需
I
E
、
H
为
,
A
A
I
和
E
c c
,
的
G
、
I D
L
L
~ D K ~
E F
B F
~
B G
且小于棱长的
, 、
一半截面一
1 H
、
,
G HK L
为六边形当
F
、
K
、
这六个点分别是六条棱的中点时
,
C 的截面都是五边形但是截面不可能是 ) 正五边形
, 。

正方体的截面形状

①截面可以是三角形：等边三角形、等腰三角形、一般三角形；
②截面三角形是锐角三角形；截面三角形不能是直角三角形、钝角三角形；
③截面可以是四边形：平行四边形、矩形、菱形、正方形、梯形、等腰梯形；截面为四边形时，这个四边形中至少有一组对边平行；
④截面不能是直角梯形；
⑤截面可以是五边形；截面五边形必有两组分别平行的边，同时有两个角相等；截面五边形不可能是正五边形；
⑥截面可以是六边形；截面六边形必有分别平行的边，同时有两个角相等；
⑦截面六边形可以是等角(均为120°)的六边形，特别地可以是正六边形．
对应截面图形如下图中各图形所示．。

初一数学截一个几何体教学课件.

1、用平面去截一个几何体，如果截面的形状是长方形，则原来的几何体不可能是（） A、正方体 B、棱柱体 C、圆柱 D、圆锥 2、用平面去截一个正方体，截面的形状不可能是（） A、四边形 B、五边形 C、六边形 D、七边形 3、下列说法上正确的是（） A、长方体的截面一定是长方形 B正方体的截面一定是正方形； C、圆锥的截面一定是三角形 D、球体的截面一定是圆 4、用一个平面去截五棱柱，边数最多的截面是_______形． 5.如果用一个平面去截一个几何体，如果截面是圆，那么原来的几何体可能是什么？
总结：正方体的截面可能是那些图形？
下列立体图形，可以截出什么样的截面？
五棱柱
圆柱体
圆锥体
用一个平面去截圆柱，得到的截面形状是什么图形？
小结
截面是认识世界的窗口、追溯历史的线索； 2、正方体的截面可以是三角形、四边形（正方形、长方形、梯形）五边形、六边形.
1、几何体的截面由平面与几何体各表面交线构成；
要得到四边形的截面，截取时应经过几个面？
试一试：正方体的截面能是五边形吗？如果能是五边形，截取时应经过几个面？
我们可以看到截面的形状是五边形
截过正方体六个面的截面一定是
六边形吗？
我们可以看到截面的形状是六边形
用平面去截正方体，能截出七边形截面吗？
点拨：
由前面的知识我们知道“面与面相交得到线”，而用平面去截几何体，所得的截面就是这个平面与几何体每个面相交的线所围成的图形．正方体只有六个面，所以截面最多有六条边，即截面边数最多的图形是六边形．
几何体的截面
截面
用一个平面去截一个几何体，截出的面叫做截面。
截一截：
用一个平面去截一个正方体，截面 (section)会是什么形状？

正方体的截面图(共27张PPT)

条边，而正方体只有六个面，所
以截面最多只能有六条边。
最大面积的截面：
有两个图形〔长方形跟正六边形〕比较可能，來比较看看吧。
可是用看的实在看不出哪个大
那就用来算算吧！
先算长方形面积
长方形比较好算，只要长乘以高
宽就是正方体边长n了那长就依照华氏定理两股为n，斜边长即对角线长
n2n2 2n2 2n
而这三边比就是直角三角形30度.60度.90度只要把它当成一长方体对角线
直角三角形、等腰三角形、钝角三角形…
面积就是的底乘以组高除以合二，所以角Ｂ的一半为60度。
所以角Ｂ就是120度啦！
因此这六边形是正六边形。
大于四边之其它形状截面：
六边形以上的多边形无法切出來，为什么？
因为正方体每个面只能有一个图形的边，才是一个直的截面，才能切成一直线，每个面只能有一
算就好了〔见右图〕
依长方体对角线公式：
X Y Z 2
2
2〔ＸＹＺ各代表长方体的长、宽、高。〕
所以：
BC ( 1 n ) 2 ( 1 n ) 2 n 2
2
2
3 n2 2
2
三角形就完成边长了（右上图）
算ＡＣ到Ｂ之高
( 2 n)2 ( 6 n)2
2
4
但有人想如果我这样切〔下面二图〕
不就可切出直角跟钝角吗？
ＯＯ
答案是：沒有这种切法。
因为你看看，此两图虽然两条边都在正方体
之一面上，但是有一条边是存在于正方体內，而这样就不是截面了。所以这是不可能出
現直角或钝角三角形。
面积最大的三角形截面：
四边形截面：
正方形：
长方形：
四边形截面：
梯形：

第八章多面体的截面作法和正方体的截面形状课件高一下学期数学人教A版

即可连结成截线，从而求得截面．
D1
C1
作法：(1)在底面AC内，过E、F作直线EF分别
G
与DA、DC的延长线交于L、M．
A1
B1
(2)在侧面A1D内，连结LG交AA1于K．
(3)在侧面D1C内，连结GM交CC1于H．
K
D
LA
E
(4)连结KE、FH．则五边形EFHFK即为所求的截面．
H CM
F B
探究新知
E
H CM
F B
探究新知
第一种情况：截面为三角形
第二种情况：截面为四边形
探究新知
第三种情况：截面为五边形第四种情况：截面为六边形
归纳总结
正方体的截面图形
截面为三角形：
截面为五边形
截面为四边形
截面为六边形
归纳总结
正方体的截面图形
探究新知
课堂练习
固学案：P59 第6，9，10，11.
例1：如图，正方体ABCD―A1B1C1D1中，E、F、G分别在AB、BC、DD1上，求作过E、F、G三点的截面．
问题2：例1告诉咱们正方体的截面可以是五边形，那么还有哪些形状呢？
D1
C1
请每组小组长组织大家组内合作，
G
A1
B1
将大家能找出的截面草图画出来，请一位组员分享每个组的学习成果！
K
D
LA
A a α
b αa P
b a α
温故知新基本事实2 如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内.
l
•
B
•
α
ቤተ መጻሕፍቲ ባይዱ
A
基本事实3 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.

《正方体的截面图》课件

是指通过切割正方体所得的图形。它展示了正方体在特定位置被截断的样子。
正方体的截面图的种类及解析图
1
底面截面图
正方体在底面被截断后的图形。
2
平行截面图
正方体在两个平行面之间被截断后的图形。
3
对角截面图
正方体在两个对角面之间被截断后的图形。
正方体的截面图的应用举例
建筑设计
在建筑设计中，截面图可以展示建筑物内部结构和布局。
数学几何研究
在数学几何研究中，截面图可以用于研究几何体的性质和特征。
工程制图
在工程制图中，截面图可以用于展示机械零件的内部结构和细节。
工艺制作
在工艺制作中，截面图可以用于设计和制作模具、雕塑等工艺品。
《正方体的截面图》PPT 课件
正方体是一种具有六个面都是正方形的立体图形。本课件将带您了解正方体的定义、特征以及截面图的各个方面，让您全面了解这个有趣的几何形体。
正方体的定义和特征
正方体是具有六个面都是正方形的立体图形。它拥有六个面、八个顶点和十二条棱。正方体的特征包括所有面都是相等的正方形，所有的顶点和棱都是相等的。
左视图
从正方体的左侧向右看的视图，展示了正方体的左侧面。
前视图
从正方体的前方向后看的视图，展示了正方体的前面。
正方体的可视部分和不可视部分
1 可视部分
正方体的可视部分是指在特定视角下可以看到的面和棱。
2 不可视部分
正方体的不可视部分是指在特定视角下无法看到的面和棱。
3 视角影响
正方体的可视部分和不可视部分的界定取决于观察者的视角。
正方体的展开图
展开图的概念
正方体的展开图是将正方体的各个面解剖并打开后得到的图形。

截一个几何体（课件）

用平面截正方体，当平面经过正方体六个面时，所得截面是六边形。
注意：用一平面去截正方体，由于正方体共有六个面，所以截面不可能是七边形。
新知讲解
图1-16的中的样的截面呢？
拓展提高
练习一：用一个平面去截一个圆柱体，不可能的截面是( D )。
拓展提高
练习六：图1是一个正六面体，把它按图2中所示方法切割，可以得到一个正六边形的截面，则下列展开图中正确画出所有的切割线的是( C )。
A、
B、
C、
D、
图1
图2
课堂总结
（1）用一个平面去截正方体，当平面经过正方体的三个面时，所得截面的形状是三角形。锐角三角形或等腰三角形或等边三角形。其中等边三角形的三个顶点是正方形的顶点。
图六
图七
图八
用一个平面去截正方体，当平面经过正方体的三个面时，所得截面的形状是三角形。如图六的锐角三角形、图七的等腰三角形、图八的等边三角形。其中等边三角形的三个顶点是正方形的顶点。
新知讲解
截面的形状还可能是几边形呢？
图九
用平面截正方体，当平面经过正方体五个面时，所得截面是五边形。
图十
图一
新知讲解
按图二、图三、图四的方式切截，那么得到的截面是长方形。
图二
图三
图四
新知讲解
按图五的方式切截，那么得到的截面是梯形。
图五
新知讲解
正方体各种截面动态图
新知讲解
用一个平面去截正方体，当平面经过正方体的四个面时，所得截面可能是正方形，长方形或梯形。
图一
图二
图三
图四
图五
新知讲解
截面的形状可能是三角形吗？
A、
B、

正方体的截面

正方体的截面
若正方体的截面按照截面的边数来分类可分为四类。

分别是截面为三角形，四边形，五边形和六边形。

（1）截面为三角形
（2）截面为四边形
（3）截面为五边形
（4）截面为六边形
1.当截面为三角形时，分为两种情况。

①
②
2.当截面为四边形时，分为七种情况. ①
②
③
④
⑤
⑥
⑦
结论：正方体的截面若按照其截面的边数来分类，可主要分为四种情况。

分别是三角形，四边形，五边形和六边形。

当截面为五边形和六边形时，只有一种情况。

当截面为三角形时分为两种情况，分别是截面为等边三角形和等腰三角形。

当截面为四边形时分为七种情况，分别为平行四边形，矩形，正方形和梯形。

相关主题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

CHENLI
8
面积最大的三角形截面：
2021/3/7
CHENLI
9
四边形截面：
正方形：
长方形：
2021/3/7
CHENLI
10
四边形截面：
梯形：
等腰梯形：
2021/3/7
CHENLI
11
这样來做个说明：为什么ＡＢ会平行ＣＤ？因为：正方体ＣＤ那一面和ＡＢ那一面是相对的面，因为截面不会弯曲，所以只要切到之两面是平行的，此两边就会平行。
4 2021/3/7
CHENLI
24
面积就是底乘以高除以二
即是
2 n 6 n 2 4
3 n2
2
8
33
再乘以6（六三角形）則正六边形面积即为 4
比较两个面积大小
长方形面积是
2n2，而正六边形面积为 3
3 4
n
2
由於 3和 2
不能直接比较，所以取近似值
最后近似值长方形面积就是1.414n2，
正六边形面积近似值就是1.299n2
2021/3/7
CHENLI
12
四边形截面：
菱形：
面积最大的四边形截面：
2021/3/7
CHENLI
13
此四边形两点位于正方体顶点，两点位于正方体边长之中点，所以此四边形四条边都是
5 n ，而四角不相等，所2以此四边形为菱形。
2021/3/7
CHENLI
14
大于四边其它的截面：
五边形：
2021/3/7
CHENLI
1
什么是截面？
截面就跟他名字一样，就是像用刀子切
出來的面。虽然有很多种切法，但在这里只讨论切平面而不讨论曲面。
2021/3/7
CHENLI
2
截面：
现在要讨论正方体的截面先把正方体的截面形状分成几个部分讨论：一、三角形：锐角三角形三角形、正三角形、直角三角形、等腰三角形、钝角三角形… 二、四边形：正方形、长方形、平行四边形
2021/3/7
CHENLI
26
结论与感想：
这次研究因为有模型的帮助而使研究更容易进行，当然，老師对我的帮助也很大，再加上同学们和父母帮我解決了很多问题，排除万难完成了此报告，不然研究可能就作不成了，谢谢各位帮助我的人！
2021/3/7
CHENLI
27
2021/3/7
CHENLI
16
依长方体对角线公式：
X2Y2Z2（ＸＹＺ各代表长方体的长、宽、高。）
所以：
BC ( 1 n ) 2 ( 1 n ) 2 n 2
2
2
3 n2 2
6n 2
再算出 AB.BC
长为 2 n
2
三角形就完成边长了（右上图）
2021/3/7
CHENLI
17
算ＡＣ到Ｂ之高
( 2 n)2 ( 6 n)2
2
4
1n 8
8n 8
接着把ＢＣ、ＡＣ的一半和
ＡＣ上的高比起來
2 n: 8n: 6 n 284 4 2 :2 2 :2 6
2 2: 2: 6
20221/3: /17 : 3
CHENLI
18
而这三边比就是直角三角形30度.60度.90度的组合，所以角Ｂ的一半为60度。所以角Ｂ就是120度啦！因此这六边形是正六边形。
2021/3/7
CHENLI
6
但有人想如果我这样切（下面二图）不就可切出直角跟钝角吗？
ＯＯ
2021/3/7
CHENLI
7
答案是：沒有这种切法。因为你看看，此两图虽然两条边都在正方体之一面上，但是有一条边是存在于正方体內，而这样就不是截面了。所以这是不可能出現直角或钝角三角形。
2021/3/7可是用看的Fra bibliotek在看不出哪个大
那就用来算算吧！
2021/3/7
CHENLI
21
先算长方形面积长方形比较好算，只要长乘以高宽就是正方体边长n了那长就依照华氏定理两股为n，斜边长即对角线长
n2n2 2n2 2n
再乘以n，面积就是
2n 2
2021/3/7
CHENLI
22
正六边形面积就比较麻烦了先把它切成六个正三角形如右图则其一正三角形边长AB即为
2021/3/7
CHENLI
19
大于四边之其它形状截面：
六边形以上的多边形无法切出來，为什么？因为正方体每个面只能有一个图形的边，才是一个直的截面，才能切成一直线，每个面只能有一条边，而正方体只有六个面，所以截面最多只能有六条边。
2021/3/7
CHENLI
20
最大面积的截面：
有两个图形（长方形跟正六边形）比较可能，來比较看看吧。
(1n)2(1n)2 1n 2n
22
22
右图即为ＡＢＯ之放大图。要求面积就得先知道此三角形的高，來求吧
2021/3/7
CHENLI
23
斜变为 2 n ，底面一半 2 n 就當一股
2
4
運用商高定理
( 2 n)2 ( 2 n)2
2
4
1 n2 1 n2 28
3n 8
24 n 8
6 n ←这就是ＡＢＯ的高啦！
、菱形、梯形、等腰梯形… 三、其他：正五边形、
正六边形、正七边形…
2021/3/7
CHENLI
3
我们先设一正方体边长为n，如下图：
2021/3/7
开始讨论CHEN截LI 面吧！
4
三角形截面：
正三角形：
等腰三角形：
2021/3/7
CHENLI
5
其他直角三角形、钝角三角形…都无法截出
因为三角形至少其中一个顶点必须要在正方体的顶点上，而一顶点在正方体顶点上之最大角度即为最大之正三角形的６０度，否则如果图形沒有任一点在正方体頂点上而在边上图形变数最少即为四边形；所以不可能出现直角或钝角三角形（角度小于９０度）。
所以正方体最大截面是长方形，
面202积1/3/7是1.414n2！
CHENLI
25
结论：１正方体的三角形的截面只有锐角三角形而
不会有钝角或直角三角形。２正方体面积最大的三角形截面是正三角形。３正方体面积最大的四边形截面是长方形。４正方体截面最少边是三角形，最大边是六边形。５正方体截面最大为长方形。
正六边形：
2021/3/7
CHENLI
15
可是这样又不能确定是正六边形虽然我们知道它每一边都是 2n 但是它每个角得120度才行來确认吧！首先取六边形中一三角形（如右图蓝色部分），只要确定Ｂ的度数是120就好了，首先要先算出ＡＣ的长度。要怎么算呢？
只要把它当成一长方体对角线算就好了（见右图）