物理化学相变过程熵变
2.6熵变的计算(物理化学)
S
T2
Qr
TT1T2来自T1CV dT T2 CV ln T T1
若T2>T1，则S >0，S高温>S低温
六、变温过程中熵变的计算
计算n摩尔的理想气体由始态A(P1,V1,T1) 到 终态B(P2,V2,T2)的熵变
解决方法(1) 设计可逆过程，如先经等温可逆过程到达中间态C，再经等容可 逆过程到达终态B.
p
A(P1,V1,T1) B(P2,V2,T2) D(P2,V3,T1)
A D B
等温过程 等压过程
' S S1' S2 T2 P1 dT nR ln nC p ,m P2 T1 T
' S1
' S2
V
p1 V2 两种方法的结果是等同的(自证, 提示因为T1T2, 所以 p V ) 2 1
1
四、可逆相变化过程中熵变的计算
正常相变是指在对应压力的相变温度时发生的等温等压过程. 如:液体在饱和蒸气压下的恒温蒸发或沸腾，固体在 熔点时的熔化或晶体在饱和浓度时的溶解等。 用等温等压可逆过程来计算熵变
Qr Q p H S T T T
固 液 气
因熔化和汽化都是吸热,所以
S
再见！
Qr
T
这是一个不可逆过程五理想气体混合过程的熵变计算变温过程中无相变低温六变温过程中熵变的计算解决方法1设计可逆过程如先经等温可逆过程到达中间态c再经等容可逆过程到达终态b
T 第六节 熵变的计算
S
Qr
一、系统 熵变的计算基本公式
计算系统熵变的基本公式为：
S系统 SB S A (
终态混合气中各物质的分压 pA(终) p xA
物理化学课件第6讲-熵变的计算
He (g) n, T, V1
等T, R
He (g) n, T, V2
nRT ln V2
S 2 δQR QR WR 1T T T
V1 T
S nR ln V2 V1
S nR ln p1 p2
对理想气体等T，IR过程，亦可直接套用。
2. 简单变温过程(等V变温或等p变温过程)
➢ 等压变温
S T
p
δQ / T T
p
nC p,m dT dT
T
p
nC p,m T
意义：T ↑ S ↑，且每升温1K，S 增加 nCp,m/T
则：
dS nCp,m dT T
dS S dT S dP T P P T
S T2 nCp,m dT
T T1
(1) 条件：等p简单变温
(2)
HⅡ H (373 .2K)
(33 75)dT
3 7 3.2 K
(Kirchoff’s Law)
(40.60 103 42 75) J 43.75 kJ
SⅡ
43.75 103 298 .2
146 .7
J K 1
Hale Waihona Puke SⅢ8.314ln
3160 101325
28.8
J K1
∴ S SⅠ SⅡ SⅢ 118 J K1
U
U
* A
U
* B
U
* C
H
H
* A
H
* B
H
* C
S
SA*
S
* B
SC*
∴ S SB
B
② 等T，p下不同理想气体的混合熵
T，nAp T，nBp T，nCp
《物理化学第4版》第二章2.5 熵变的计算ppt课件
p
和物质的体积膨胀系数 1 V ，可得：
S p
T
V
V
T
p
所以，纯凝聚态物质等温过程的熵变计算：
S pB-V dp pA
6
对溶液和固溶体, 熵 S =f ( T, p , wB ) 组成
7
3、变温过程
（1）等压变温:（无论过程是否可逆，都按 可逆过程计算） dH = Qp＝ nCp,mdT
S T2 δQr T 2 nCp, mdT
T1 T
T1
T
若Cp,m视为常数，则
S
nC p ,m ห้องสมุดไป่ตู้n
T2 T1
8
（2）等容变温（不论过程是否可逆，都按等 容可逆过程计算） QV＝ dU＝nCV,mdT
所以
S T 2 δQr T2 nCV ,mdT
T1 T
T1
T
若CV,m视为常数，则
S
nCV ,mln
T2 T1
9
例2：1 mol Ag(s) 在等容下，由273 K加热到 303 K，求这一过程的熵变。[已知在该温度区 间内，Ag(s)的CV,m为24.48 JK-1mol-1 ]
解：
S T 2 δQr T2 nCV ,mdT
T1
nCV
T
,mln
T2 T1
T1
T
= 1 mol24.48 JK-1mol-1 ln(303/273)=2.55 JK-1
18
[例3]：0.5 molO2气体从293 K冷却到193 K， 同时压力从100 kPa升高到 6 MPa，求系统熵 变ΔS。已知Cp,m(O2)=29.36 J·K-1·mol-1。
S p V T T V
物理化学：2.08熵变的计算
对于非理想气体，也有类似公式，但 Cp、Cv 不是常数，要会推导（选择 适当的可逆途径）。
四、相变过程的熵变
体系的熵变量不仅与温度、压力、 体积的变化有关，还与物质发生熔 融、蒸发、升华等相变化过程有关；
因为物质在发生这些相变化时，有 热量的吸收或放出，故也应有熵的 变化。
潜热：
若相变过程是在恒温和恒压的平衡状 态下可逆地进行的，同时有热量的吸 收或放出，这种热量称为“潜热”。
vHm：摩尔气化热； Tb：正常沸点，P下沸点。
3） P下升华过程：
SSm = SHm / T
SHm：摩尔升化热； T：固、气可逆相变时的平衡温度。
说明：
1）熔化和气化时都需吸收热量，故熔化过 程和蒸发过程的熵都增加，即物质的液 态熵值比固态的要大，气态熵值比液态
的大：S气 S液 S固
T = 10.83C = 283.98 K
1kg 雪 水： S1 = 2.09 ln ( 273.15 / 263.15 ) + ( 334.4 / 273.15 ) + 4.18 ln ( 283.98 / 273.15 ) = 1.465 kJ/K
5 kg 水降温： S2 = 4.18 ln ( 283.98 / 303.15 ) = 1.365 kJ/K
解：Sm = S1 + S2 + S3 = Cp, m( l ) ln (T2/T1) – fHm/ Tf + Cp, m(s) ln (T1/T2) = – 35.45 J/Kmol
• 结果表明此自发过程之体系熵变为
– 35.45 J/Kmol < 0 体系熵变小于零，不能说其和自发过程矛盾，需 再计算相应的环境的熵变 Sm, 环。
物理化学简明教程(重点内容)
第一章【理想气体的内能与焓只是温度的函数，与体积或压力的变化无关，所以对理想气体定温过程：dU=0，dH=0，△U=0，△H=0变温过程：△U=nC v,m △T ；△H=nC p,m △T节流膨胀：（特点）绝热、定焓，∴Q=0，△H=0，无论是理想气体还是实际气体均成立】1.理想气体的状态方程可表示为： pV=nRT2.能量守恒定律：自然界的一切物质都具有能量，能量有各种不同形式，能够从一种形式转化为另一种形式，但在转化过程中，能量的总值不变。
3.第一定律的数学表达式：△U=Q+W ；对微小变化：dU=δQ +δW （因为热力学能是状态函数，数学上具有全微分性质，微小变化可用dU 表示；Q 和W 不是状态函数，微小变化用δ表示，以示区别。
）4.膨胀作功：①自由膨胀：W=0；②等外压膨胀：W=-P 外(V 2-V 1)=P 2（V 1-V 2）； ③可逆膨胀：W=nRT ln 21V V =nRT ln 12P P ；④多次等外压膨胀，做的功越多。
5.①功与变化的途径有关。
不是状态函数。
②可逆膨胀，体系对环境作最大功；可逆压缩，环境对体系作最小功。
6.恒温恒压的可逆相变 W=RT V P dV dP P dV P i V V i V Ve n )(2121-=-=--=-⎰⎰△(恒温恒压的可逆相变,气体符合理想气体方程)7.焓的定义式：H=U+PV ，等压效应H =Q p △，焓是容量性质。
8.理想气体的热力学能和焓仅是温度的函数：在恒温时，改变体积或压力，理想气体的热力学能和焓保持不变。
还可以推广为理想气体的Cv,Cp 也仅为温度的函数。
9.①等压热容Cp ：p pp THdTQ C )(∂∂==δ，T C Q H p d p ⎰==△②等容热容Cv ：T C Q U TUdTQ C V vvd )(v v ⎰==∂∂==，△δ; ③RTQ Q vn p △=-10.理想气体的Cp 与Cv 之差：nR C C VP =- 或 R C C m v m p =-,,;单原子分子系统：R C m v 23,=，双原子分子系统：R C m v 25,=T nC H m p △△,= , T nC U m v △△,=11.绝热过程的特点：绝热压缩，使体系温度升高，而绝热膨胀，可获得低温。
物理化学03章_热力学第二定律(二)
Ssys = 19.14 J K
Ssur = 0
1
(系统未吸热,也未做功)
Siso = Ssys + Ssur = 19.14 J K 1 > 0
(2)为不可逆过程.
例2:在273 K时,将一个 22.4 dm3 的盒子用隔板一分为二,
0.5 mol 0.5 mol O2 (g) N2 (g)
p1 V1 p2 V2 T2 p2 V2 ∵ = ∴ = T1 T2 T1 p1V1
V2 p2V2 ∴ S = nR ln + nCV ,m ln V1 p1V1
V2 p2 V2 = nR ln + nC V ,m ln + nC V ,m ln V1 p1 V1
p2 V2 ∴ S = nCV ,m ln + nC p ,m ln p1 V1
因为在可逆相变中压力恒定,所以可逆热即为相 因为在可逆相变中压力恒定, 变焓.又由于温度一定,所以, 变焓.又由于温度一定,所以,物质 B 由 α 相态 转化为 β 相态
p ,T B (α ) → B ( β )
的相变熵为: 的相变熵为:
β α H β α S = T
用上式,可计算正常熔点下的熔化熵, 用上式,可计算正常熔点下的熔化熵,正常 沸点下的蒸发熵等等. 沸点下的蒸发熵等等.
= TC S > 0
Q W
热源
R2
TC
1
W2
Q W2
TB热源做功能力低于TA
TB热源做功能力低于TA
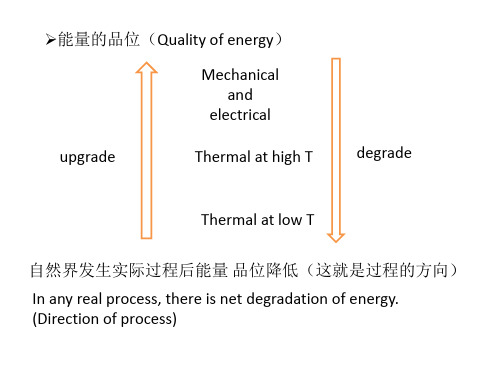
其原因是经过了一个不可逆的热传导过程 功变为热是无条件的,而热不能无条件 地全变为功. 热和功即使数量相同,但"质量"不等, 功是"高质量"的能量. 高温热源的热与低温热源的热即使数量相 同,但"质量"也不等,高温热源的热"质量" 较高,做功能力强. 从高"质量"的能贬值为低"质量"的能 是自发过程.
第3章 熵变的计算
等温，等压，可逆
1mol H 2 O g 373.15 K，p o
S SⅠ SⅡ SⅢ 373.15 40.60 103 298.15 33 ln 298.15 373.15 373.15 118 J K 1 75 ln
等压 可逆
1mol H 2 O l 373.15 K，p o
S
理想气体混合物 A(g) + B(g) + C(g) + …
* * * U UA UB UC * * * H HA HB HC
S B nB R ln
p nB R ln xB n xB R ln xB nR xB ln xB pB
思考：因为 S > 0，该过程为自发过程；此推理正确吗？
3. 环境熵变的计算
环 境 系 统
环境通常由不发生相变及化学变化的物质 组成，即使环境与系统有功与热的交换，其 温度、压力并没有发生可觉察的变化。所以 认为 环境内部过程都是可逆过程
Samb
Qamb Tamb
Qsys Tamb
Qsys 为系统实际从环境得到的热； Qamb为环境实际由系统得到的热 两者绝对值相等，符号相反
O
3. 先恒压后恒容
V p S nC p ,m ln 2 nCV ,m ln 2 V1 p1
前提：设定理想气体的 CV,m和 Cp,m 均为常数
V1
V2
V
(4) 混合或传热过程 (理想气体/凝聚态物质)
混合过程：种类很多，都不可逆；所以，需要设计可逆过程； 总的原则：分别计算各个组分的熵变，然后加和
(1) 可逆相变 (恒温恒压可逆相变)
大学课程《物理化学》第二章(热力学第二定律)知识点汇总
VB ,m
V nB T , p ,n jB
H nB T , p ,n jB G nB T , p ,n jB
U B ,m
U nB T , p ,n jB
S nB T , p ,n jB
T2 p1 dT S S '1 S '2 nR ln C p p2 T1 T
dU TdS pdV
T p V S S V
dH TdS Vdp
( U )V T S
T V p S S p
S系统 S B S A
Qr
T
S孤立＝S系统 S环境 0
A
熵变的计算
总则
S环境
Q实际 T环境
理想气体等温过程的熵变
S S B S A
B
Qr
A
Q ( )r T T
Wmax Qr S T T
可逆相变过程的熵变
V2
V1
dG SdT Vdp B dnB
B
dU TdS pdV B dnB
B
U dU TdS pdV dnB nB S ,V ,n j B
B
U H F G nB S ,V ,n j B nB S , p ,n j B nB T ,V ,n j B B nB T , p ,n j B
B
dG SdT Vdp B dnB
B
纯理想气体的化学势
Gm Vm p T p T
物理化学02章_热力学第二定律02
S体系
Qr Qsurr Qsys Q Δ S环 = = = Tsurr Tsurr Tsurr T
Δ S 总 =Δ S 体 + Δ S 环 ≥ 0
上一讲回顾
(1) 熵变的计算： 可逆过程，直接计算过程的热温商 不可逆过程，设计可逆过程计算。 (2) 等温过程,变温过程及相变过程熵变的计算 (3) 利用熵变判断过程的方向
a）恒 T 可逆 b）恒 T 不可逆 V2 V2 V2 Δ S 总 = nRTLn +(-nRLn ） Δ S 总 = nRTLn + 0 V1 V1 V1
= 0
V2 = nRTLn > 0 V1
等温过程的熵变
例： 1mol理想气体在等温下通过：(1)可逆膨胀，(2)真 空膨胀，体积增加到10倍，分别求其熵变。 解：（1）可逆膨胀
简化：
V2 P2 等 T：Δ S= nRLn =- nRLn V1 P1 T2 等 P：Δ S= CP Ln T1
T2 等 V：Δ S= CV Ln T1
变温过程的熵变
1. 先等温后等容 2. 先等温后等压 3. 先等压后等容
T2 nCV ,m dT V2 S nR ln( ) T1 V1 T T2 nC p ,m dT p1 S nR ln( ) T1 p2 T V2 p2 S nC p ,m ln( ) nCV ,m ln( ) V1 p1
S T
T2
1
nCV ,m dT T
(2) 物质的量一定的等压变温过程
S T
T2
1
nC p ,m dT T
等 P 过程：
W`=0， QP = dH = CPdT = QR
QR QP C P dT dS = = = T T T CP S )P 或 ( T T
物理化学 03-03相变过程熵变
将环境看作一个巨大的热源： 将环境看作一个巨大的热源： T(环)=常数；Qr(环)＝∆H(环) ； Q(环)＝－ 系) 常数； 环 ＝ ＝－Q(系 环 常数 环 环 ＝－
P121 例3.5.1
Q(系) ∆S (环境 )＝－ T (环)
∆H ( 263 K ) = ∆H ( 273 K ) + m ∆ C p ∆T＝－311.46kJ = Q( 系 )
-
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程 恒温恒压且无限接近平衡条件下进行的相变过程
∆H 相变 Qr ∆ S＝ ＝ T相变 T相变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
1
H2O(l) 263K 100kPa ∆1S
不可逆相变 ∆S(263K) ∆2S 可逆相变 ∆S(273K)
B
T δQ T δQ δQ r r = [S AB (0 K ) − S A (0 K ) − S B (0 K )] + ∫ −∫ −∫ r 0K T AB 0 K T A 0 K T B T
7
2.热力学第三定律
=
∫
Tf
C o--,m (s ) p T T
0K Tb
o ∆ fus H mdT + Tf
+∫ +∫
C o-,m ( l ) p
Tf T
dT +
o ∆ vap H m-
Tb
C o-,m ( g ) p
Tb
T
dT + ∆ pg S o- (T ) g m
4.标准摩尔反应熵的计算 4.标准摩尔反应熵的计算
《物理化学》教学提要 第五讲 熵变的计算
《物理化学》教学提要第五讲熵变的计算熵变是指热力学系统在定常过程中发生的熵的变化，即Δ
S=Sf-Si，其中Sf为终态熵，Si为初态熵。
2. 熵变的计算方法
(1) 对于理想气体的等温、等容和等压过程，熵变的计算公式分别为：
ΔS=q/T
ΔS=Cvln(Tf/Ti)
ΔS=Cpln(Tf/Ti)-Rln(Vf/Vi)
其中q为吸热量，T为热力学温度，Cv为定容热容，Cp为定压热容，R为气体常数，V为体积。
(2) 对于化学反应，熵变的计算公式为：
ΔS=∑nSf-∑mSi
其中n为生成物的系数，m为反应物的系数，S为标准熵。
(3) 对于固体和液体的物质状态变化，熵变的计算公式为：
ΔS=Cpln(Tf/Ti)
其中Cp为定压热容，T为热力学温度，f和i分别表示终态和初态。
3. 熵变的影响因素
熵变受到温度、压力、物质状态和化学反应等因素的影响。
一般来说，温度越高，熵变越大；压力越大，熵变越小；物质状态从固体到液体再到气体，熵变越大；而化学反应的熵变则与反应类型和反应
条件有关。
4. 熵定律
熵定律是指在孤立系统中，熵的增加是不可避免的。
这一定律对于热力学系统的稳定性和可逆性具有重要的理论和实际意义。
10-4 熵变的计算
S体系
V2 nR ln( ) V1
(2) 可逆膨胀：Q可 = W可＝ nRT ln(V2/V1)
S环 = －（Q实/T) = － nR ln(V2/V1) S 孤 = S 体 + S 环 ＝ 0
2016/11/1
物理化学II
5
热力学第二定律和第三定律
熵变的计算
（二）变温过程的熵变
体系：设计可逆（逐步加热）
热力学第二定律和第三定律
熵变的计算
物理化学
熵变的计算
2016/11/1
物理化学II
1
热力学第二定律和第三定律
熵变的计算
§4
熵变的计算
原则：S大孤立体系＝ S环＋ S体
S体：S = f (状态），所以， 无论过程如何，设计可逆过程 S体= 始终态 (Q/T)可
S环：假定环境热容无限大，
Q可= Qp − W电
S体 = Q可/T, S环 = －Qp/T
物理化学II
S体＝－15.13 J/K
S环＝727.18 J/K
17
热力学第二定律和第三定律
熵变的计算
一般化学反应的熵变计算： S体 = S 终 － S始 化学反应： rSm = (Sm )产－ (Sm )反
S (C p / T )dT
0
40
阴影下的面积， 就是所要求的该物质 的规定熵。
物理化学II
14
热力学第二定律和第三定律
熵变的计算
如要求某物质在沸点以上某温度 T 时的熵，则积分 不连续，要加上在熔点（Tf）和沸点（Tb）时的相应 熵，其积分公式可表示为：
S (T ) S (0)
S孤 = S体 + S环 = 0
物理化学热力学第二定律总结
热二定律总结一、热力学第二定律克劳修斯说法：热不能自动从低温物体传给高温物体而不产生其他变化开尔文说法：不可能从单一热源吸热使之全部对外做功而不产生其他变化典型例题：判断：1、某体系从单一热源吸收100 kJ热量，对外做功100 kJ，该过程不符合热力学第二定律。
（X）2、某循环过程，体系从环境吸收100 kJ热量，对外做功100 kJ，该过程不符合热力学第二定律。
（X）3、某过程体系从环境吸收100 kJ热量，对外做功100 kJ，同时，系统复原，该过程不符合热力学第二定律。
（X）二、热机和卡诺循环任意热机效率：η = -W/Q1 = (Q1+Q2)/Q1卡诺循环：1、等温可逆膨胀；2、绝热可逆膨胀（等熵膨胀）；3、等温可逆压缩；4、绝热可逆压缩（等熵压缩）可逆热机（卡诺热机）效率：η = 1-T2/T1对可逆热机，有Q1/T1 + Q2/T2 = 0卡诺定理：在两个不同温度的热源之间工作的所有热机，以可逆热机效率最大。
推论：所有卡诺热机的效率都相等。
典型例题：1、理想气体卡诺循环的图为下列四种情况中的哪一种?2、 判断：真实气体做为热机工质，经卡诺循环后，其热机效率低于以理想气体做为工质的可逆热机的效率。
三、 熵与克劳修斯不等式熵的定义：注意：熵是可逆热温商的积分，熵和热没有直接关系！克劳修斯不等式：（>，不可逆，=，可逆）如果是绝热过程： ΔS ≥0 （>，不可逆，=，可逆）(熵增原理)如果把系统及其相连的环境看成一个整体，则：ΔS iso =ΔS sys +ΔS amb ≥ 0（>，不可逆，=，可逆）（熵判据：判断过程是否自发）注意此公式的应用条件：绝热系统，或把系统和与之相连环境看成一个大的孤立系统。
不可只计算环境熵变，并以此判断过程自发与否。
典型例题：1、 判断：冰在0℃，101.325 kPa 下转变为液态水，其熵变>0，所以该过程为自发过程。
2、 判断：相变过程的熵变可由 计算。
物理化学1.12-4 熵变的计算
T1
T
V1
(5)理想气体定温、定压混合
1 V
( V T
)p
mixS = －R (n1lny1＋n2 lny2)
(6)在平衡温度、压力下的相变
（正常相变，可逆相变）
Qr
Qp＝H相变= n ·ΔHm
S Qr nHm(相变焓)
T
T
fusHm＞0， vapHm＞0
同一物质在一定T 、p下 : Sm(s) ＜ Sm(l),
H2O（l,90℃,101 325Pa）
H2O（g,90℃,101 325Pa)
不可逆相变
定压可逆升温 S1
S3
定压可逆降温
H2O（l,100℃,101 325Pa）
S2 可逆相变
H2O（g,100℃,101 325Pa）
T eq
S1 T1 nCp,m (H2O, l)dT/T
S2
系统熵变的计算
(1)定容变温过程
S δQV T
(2) 定压变温过程 S δQp
(3) 定温变压过程
T
S
p2 S p1 ( p )T dp
p2 ( V p1 T
) pdp
(4) 理想气体 p、V、T 、变化过程
S T2 nCV ,mdT nR ln V2
Sm(l) ＜ Sm(g)
(7)非平p1) S1
B(,Teq, peq)
S=? 不可逆相变
S2 可逆相变
p1=p2=psu×
B(, T2, p2) S3
B(, Teq, peq)
则 S＝S１＋S２＋S３
S =?
S隔离 Ssy Ssu 0自可发逆
物理化学熵变的计算
理想气体等温等压
2012-8-30
上一内容
下一内容
回主目录
返回
10
2. 环境ΔS的计算
amb S dSamb
1 2
Qr T amb 1
2
一般环境常为大气 般环境常为大气
Tamb b A, Qamb b amb bH Qamb Qamb是环境与系统实际交换的热=-Qsys amb S Tamb
1mol He(g) 1mol H2(g) 300K 200K 101 3kPa 101 3kPa 101.3kPa 101.3kPa
解：求末态 过程特点：孤立系统， U = 0
U U ( He ) U ( H 2 )
3 5 n R T2 200 K n R T2 300 K 0 2 2
T， r， S (1)1 ( ) mol , 理气， 气 V1 1mol , 理气， 气 10V1 T，真空，S (2)1mol , 理气，V1 1mol , 理气， 10V1
解：(1)可逆膨胀 (此过程为可逆过程)
Wmax V2 Q 1 S1 ( ) R nR R ln l 19.14 19 14 J K T T V1
1
(此过程为 逆过程) (2) 真空膨胀 真空膨 (此过程为不可逆过程)
S2 19.14 J K
2012-8-30
上一内容
下一内容
回主目录
返回
13
例2：10mol理想气体，25℃时由1.000MPa 膨胀到 0.100MPa, 计算S, Q/T。假定过程为： (a)可逆膨胀； (b)自由膨胀； (c)抗恒外压0.100 0.100MPa MPa膨胀。 解 题中三个过程的始终态相同，故 解：题中三个过程的始终态相同，故 解： 题中三个过程的始终态相同 故S相同 S= nRln ln( (p1 / p2) = 191 JK-1 热不是状态函数，要分别计算三个过程的热： 理想气体定温过程 U=0，Q= -W W 理想气体定温过程，
《物理化学》第2章
实际过程的热温商：
2．热由高温物体传向低温物体:
高温热源T2 Q’=Q1+W Q=W 做功W 吸热Q1 低温热源T1 冷冻机做功后，系统(两个热源)恢复原状，… 传热Q1
结果环境失去功W，得到热Q ，环境是否能恢复原状， 决定于热Q能否全部转化为功W而不引起任何其它变化 ?
3．化学反应:
Cd(s)+PbCl2(aq)=CdCl2(aq)+Pb(s)
用一闭合曲线代表任意可逆循环。在曲线上任 意取A，B两点，把循环分成AB和BA两个可逆过 程,即： A B A
根据任意可逆循环热温商的公式：
B
Qr
Qr Qr 0 T T B T A
B A
p T
Qr
热力学第二定律的提出
19世纪初,资本主义工业生产已经很发达,迫切需要解
决动力问题。当时人们已经认识到能量守恒原理,试图制
造第一类永动机已宣告失败,然而人们也认识到能量是可 以转换的。于是,人们就想到空气和大海都含有大量的能
量，应该是取之不尽的。有人计算若从大海中取热做功，
使大海温度下降1℃，其能量可供全世界使用100年…。于 是人们围绕这一设想，设计种种机器，结果都失败了。这 个问题的实质可归结为热只能从高温物体自动传向低温物 体，没有温差就取不出热来(即从单一热源吸热)。
环境中吸热全部变为功，但体积变大了，压力变小了。
3.“第二类永动机不可能造成”可用来判断过程的方
向。
热力学第二定律的提出是起源于热功转化的研究，寻找相
应的热力学函数需从进一步分析热功转化入手(热机效率)。
物理化学解析化学反应的熵变与自由能变化
物理化学解析化学反应的熵变与自由能变化在物理化学领域中，解析化学反应的熵变与自由能变化是一项重要的研究内容。
熵变（ΔS）和自由能变化（ΔG）是描述化学反应中系统混乱程度和能量变化的重要物理量。
本文将对熵变和自由能变化的概念进行解析，并探讨它们与化学反应的关系。
1. 熵变的概念及含义熵（S）是描述系统无序程度的物理量，即系统的混乱程度。
熵变（ΔS）表示在化学反应中系统熵的增加或减少。
根据热力学第二定律，一个孤立系统的熵不断增加，因此熵变通常表示为正值。
熵变的计算可以通过以下公式求得：ΔS = S产物 - S反应物其中，S产物和S反应物分别表示反应产物和反应物的熵值。
2. 自由能变化的概念及计算自由能（G）是描述系统可逆过程中能量的物理量，是系统的稳定性指标。
自由能变化（ΔG）表示在化学反应中系统自由能的增加或减少。
自由能变化可以通过以下公式计算：ΔG = ΔH - TΔS其中，ΔH表示反应焓变，T表示绝对温度（Kelvin），ΔS表示熵变。
3. 熵变与自由能变化的关系熵变和自由能变化之间存在着密切的关系。
根据ΔG的计算公式，可以得知当ΔG<0时，化学反应是自发进行的；当ΔG>0时，化学反应是不可逆进行的；当ΔG=0时，化学反应处于平衡状态。
根据ΔG的公式，我们可以得出以下结论：- 当ΔH<0且ΔS>0时，自由能变化ΔG<0，反应是自发进行的。
- 当ΔH>0且ΔS<0时，自由能变化ΔG>0，反应是不可逆进行的。
- 当ΔH<0且ΔS<0时，自由能变化ΔG的正负取决于温度的影响。
4. 熵变与自由能变化在化学反应中的应用熵变和自由能变化是描述化学反应方向和速率的重要指标，具有广泛的应用：- 在工业生产中，通过熵变和自由能变化的计算，可以优化反应条件，提高反应产率和选择性。
- 在生物化学中，熵变和自由能变化对于描述酶催化反应的速率和选择性也具有重要作用。
南开大学22春“药学”《物理化学》作业考核题库高频考点版(参考答案)试题号1
南开大学22春“药学”《物理化学》作业考核题库高频考点版（参考答案）一.综合考核(共50题)1.25℃及标准压力下，NaCl(s)与其水溶液平衡共存，体系的组分数、相数和自由度分别为()。
A.K=1，Φ=2，f=1B.K=2，Φ=2，f=1C.K=2，Φ=2，f=0D.K=4，Φ=2，f=1参考答案：C2.相变过程熵变变等于相变焓除以相变温度。
()A.错误B.正确参考答案：A3.某绝热封闭体系在接受了环境所作的功之后，温度()。
A.一定升高B.一定降低C.一定不变D.随接受功多少而定参考答案：A4.25℃时，将11.2升O₂与11.2升N₂混合成11.2升的混合气体，该过程：()。
A.∆S>0，∆GB.∆SC.∆S=0，∆G=0D.∆S=0，∆G<0参考答案：C电池对外做电功时，其电功可表示为W'=-zEF。
()A.错误B.正确参考答案：A6.今有298K，p的N₂(状态Ⅰ)和323K，p的N₂(状态Ⅱ)各一瓶，问哪瓶N₂的化学势大?()A.μ(Ⅰ)>μ(Ⅱ)B.μ(Ⅰ)C.μ(Ⅰ)=μ(Ⅱ)D.不可比较参考答案：B7.零级反应速率常数的量纲是()。
A.(浓度)-1·(时间)-1B.(浓度)·(时间)1C.(浓度)-2·(时间)-1D.(浓度)2·(时间)-1参考答案：B8.100℃、101325Pa的1mol水与100℃大热源接触，使其向真空容器中蒸发成100℃、101325Pa的水蒸气，为判断过程的方向可用()。
A.∆UB.∆S体C.∆AD.∆G参考答案：C9.胶束的出现标志着()。
A.表面活性剂的溶解度已达到饱和状态B.表面活性剂分子间的作用超过它与溶剂的作用参考答案：C10.下列哪些是容量性质状态函数?()A.温度B.考压力C.气体常数RD.体积参考答案：D11.实际气体经过某条件下节流膨胀，温度降低，则该条件下其焦耳-汤姆逊系数()。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s
dT
fus
H o-m
0K T
Tf
Tb
C
o-p ,m
(
l
) dT
vap
H
o-m
Tf
T
Tb
T
C
o-p ,m
(
g
) dT
Tb
T
pg g
S
o-m
T
4.标准摩尔反应熵的计算
r Sm（ T） B Sm（ B）
B
10
5.标准摩尔反应熵随温度的变化
例:分别计算298K和423K时甲醇合成反应的标准摩尔反应熵,
熵是度量系统无序度的函数
6
1. Nernst（1906）热定理
凝聚系统在恒温过程中的熵变，随温度趋于 0 K 而趋于零
lim T S 0（凝聚系统）
T 0 K
对于任意反应 A＋B→AB
在0K时 ΔrS(0K)=SAB(0K) －SA(0K) － SB(0K)=0 在温度为T时
r ST S AB T S A T SB T
423K,100kPa
423K,100kPa
r Sm 423K S1 S2 r Sm 298K S1
S 2
S1 S2
C 423K r p ,m
dT
CO(g)+2H2(g)
r
S
m
298K
CH3OH(g)
T 298 K
298K,100kPa
298K,100kPa
r
S
m
T
r
Q T
r
2、对于可逆过程，利用各种基础热力学数据计算其热温商
3、对于不可逆过程，则须在始末态之间设计一条可逆途径
求其ΔS
4、由多组分物质组成的理想气体系统，可分别求出每种组分
之ΔS，则系统总的ΔS等于各组分ΔS之和 5、利用ΔS判断过程的方向及限度有两种方法：
B Q ir 不可逆过程
S A T r 可逆过程
S(系)＋[H / T(环)] 0
ir r
T(环)S H 0
ir r
T (环)( S2 S1 ) (H 2 H1 ) (T2 S2 T1 S1 ) (H 2 H1 )
H－（TS）＝( H TS ) 0
ir r
14
G def H TS ＝U＋pV TS ＝A pV
H－（TS）＝(H TS) 0
nC-
p
,m
ln
T2 T1
nRln
p1 p2
nC-
p
,m
ln
V2 V1
nC-V,m ln
p2 p1
0
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程
S＝ Qr ＝ H相变
T相 变
T相 变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
1
H2O(l) 263K
ir r
S(系)＋[U / T(环)] 0
ir r
T(环)S U 0
ir r
T (环)( S2 S1 ) (U 2 U1 ) (T2 S2 T1 S1 ) (U 2 U1 )
U－（TS）＝(U TS) 0
ir r
12
A def U TS
U－（TS）＝(U TS) 0
ir r
上次课主要内容
1.熵
S SB SA
d=e=f
B Q r
AT
2.克劳修斯不等式 S B Q
AT
3.熵增原理
>0可能发生的不可逆过程
dS(隔离) =0平衡（可逆）过程
<0不可能发生的过程
4. 单纯pVT变化的熵变 理想气体
S
nCV,m
ln
T2 T1
nRlnV2 V1
凝聚系统
S
nC
p ,m
ln T2 T1
p1=25.664kPa
H n vap H m 0 2.5104kJ
dV 0 W 0
Q U H ( pVg pVl ) H pVg H nRT
2.5104kJ 0.1 8.314 308.66 103 kJ 2.2538kJ
S H nR ln p1 9.275J K 1
T
p2
5
§3.6 热力学第三定律和 化学变过程熵变的计算
熵的物理意义
理想气体恒压过程:
S
nC
p,m
ln
T2 T1
T , S 即S高温 S低温
理想气体恒温过程: S nR ln p1 p , S 即S低压 S高压
p2
理想气体恒温混合 : S＝
RnB
ln
yB
0
S混合后
S混合前
相变过程: 由计算知 : Sg Sl S s
SB SB ( T ) SB ( 0 K ) SB ( T )
Smo (B,T)
T C p,m dT 0K T
条件:纯固体（完美晶体），po 100 kPa，0 K T 间无相变
9
求某气体在温度为T时的标准熵
S o-m
(T
)
S o-m
( 0K
)
S
o-m
( 0K
T
)
Tf
C o-p ,m
S
m
298K
T rC p ,m dT T 298 K
11
§3.7 亥姆霍兹函数和吉布斯函数
1.Helmholtz函数及Gibbs函数 (1)Helmholtz函数
对恒T、恒V、W’＝0 的过程
T环 T1＝T2＝T , W ' 0, Q(系）＝U
Q(环) Q(系）＝ U
S(系)＋S(环) 0
ir r
G 0
ir 自发过程 r 平衡过程
dG 0
ir r
在恒温、恒压且非体积功为0的封闭系统中 发生的不可逆过程，总是向着G减小的方向进行。
15
A 0
ir r
自发过程 平衡过程
dA 0
ir r
在恒温、恒容且非体积功为0的封闭系统中 发生的不可逆过程，总是向着A减小的方向进行。
13
(2)Gibbs函数
对恒T、恒p、W’＝0 的过程
T环 T1＝T2＝T , W ' 0, Q(系）＝H
Q(环) Q(系）＝ H
S(系)＋S(环) 0
ir r
>0可能发生的不可逆过程
dS(隔离) =0平衡（可逆）过程
<0不可能发生的过程
4
ex3.28 解:设乙醚全部蒸发
(1)
P2
nRT V
0.1
8.314 308.66 10 103
Pa
25.664kPa
P2<101.325kPa 说明假设合理
(2)
B(l)
恒温恒压
B(g)
恒温变压
B(g)
p1=101kPa 可逆相变 p1=101kPa
S
(环境)＝－
Q(系) T (环)
H ( 263K ) H ( 273K ) mC pT＝－311.46kJ Q( 系 )
S
(环境)＝－
Q(系) T (环)
＝1.184kJ
K
1
S(隔离)＝S(系统)＋S(环境)＝45J K 1 0
3
ΔS的计算及利用其判断过程的方向与限度
1、 计 算S的 基 本 公 式 为 ：S＝
＝
fus
H (273K 273K
)
m[C
p
(
s)
C
p
(l
)]ln
263＝ 273
－1.139kJ
K
1
2
环境的熵变
S(隔离)＝S(系统)＋S(环境)
S(环境)＝
2 1
Qr (环) T (环)
将环境看作一个巨大的热源：
T(环)=常数；Qr(环)＝ΔH(环) ； Q(环)＝－Q(系)
P121
例3.5.1
S AB
0K
T 0K
Qr T
AB
S
A
0
K
T 0K
Qr T
A
SB
0K
T 0K
Qr T
B
SAB 0K SA 0K SB 0K
T Qr 0K T AB
T Qr 0K T A
T Qr 0K T B
7
2.热力学第三定律
反应方程式为: CO(g)+2H2(g) →CH3OH(g) CO(g) 、2H2(g) 、CH3OH(g)的Cp,m分别为:29.04、29.29、 51.25J·K-1·mol-1
解: (1) r Smo（298K） B Smo（B）
B
(2)
CO(g)+2H2(g)
r
S
m
423K
CH3OH(g)
planck说法: 0K时纯物质凝聚态熵值为零。
修正的planck说法:0K时纯物质完美晶体的熵值为零。
S
* m
完美晶体,OK
0
完美晶体:所有质点均 处于最低能级,规则地排列在
点阵结构中,形成一种唯一的排布状态.
COCOCOCOCO…
COCOOCCOCO…
8
3.规定熵和标准熵
以热力学第三定律为基础,我们可以求得任何状 态下纯物质的相对熵,称为该物质在指定状态下的 规定熵.如果指定状态为标准状态,则其规定熵称为 该物质的标准熵
100kPa
不可逆相变 ΔS(263K)
H2O(s) 263K
100kPa
Δ1S 可逆升温
Δ2S 可逆降温
H2O(l) 273K