理论力学:2动力学5-A
理论力学答案第5章点的复合运动分析
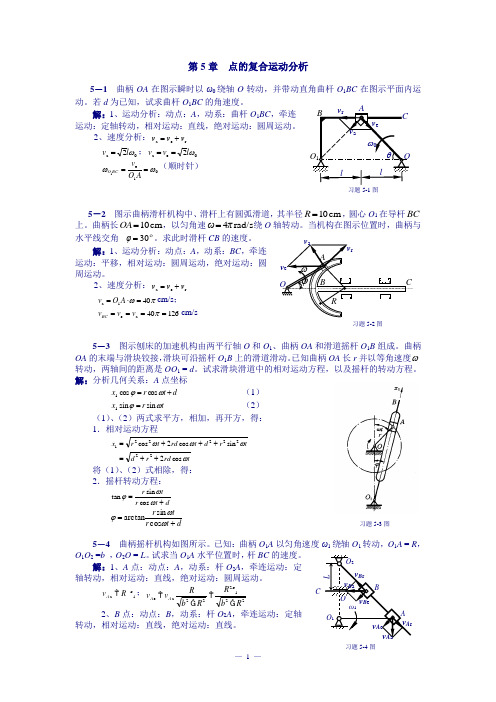
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
理论力学动力学部分5达朗伯原理
③当刚体作匀速转动且转轴通过质心C时, r FIR = 0,M IC = 0 ,惯性力系自成平衡力系。
五 达朗贝尔原理
23
3)平面运动
具有质量对称平面的刚体作平面运动,并且运 动平面与质量对称平面互相平行。
对于这种情形,先将刚体的空间惯性力系向质 量对称平面内简化,得到这一平面内的平面惯性力 系,然后再对平面惯性力系作进一步简化。
F1 FI1 FNam2m121FIiFmN1iFNFi ai
合力和外约束反力的合力,于是得
F2 a2
i
å
Mår OFr(i
+ Fi
å FrNi )+å
M+r
å FrIi O (FNi
=0 )+å
Mr O
( FIi
)
=
0
即:在质点系运动的任一瞬时,作用于质点系上的所
有主动力系,约束反力系和惯性力系构成形式上的平
五 达朗贝尔原理
24
解法1:利用达朗伯原理
取系统为研究对象,受力分析及 运动分析如图示:
运动分析:
以轮B为对象,vC = vD + wBr = wAr + wBr 求导得:aC = e Ar + e Br 由达朗伯原理:
åMO(F)
=
0,
1 2
×
P g
×r2
×eA
+
1 2
×
P g
×r2
×eB
-
P ×2r
衡力系。这就是质点系的达朗伯原理。
五 达朗贝尔原理
11
质点系达朗贝尔原理的投影形式
å Fix + FNix + FIix = Fx = 0 i
5.理论力学(2020版)
中国海洋大学本科生课程大纲一、课程介绍1•课程描述(中英文):理论力学是高等工科院校开设的一门重要的学科基础课,是一门理论性、逻辑性、实践性都很强的课程。
它是其他力学课程(例如:材料力学、结构力学、弹性力学、流体力学等)的基础,并在诸多工程技术领域有着广泛的应用。
该课程研究物体机械运动的一般规律,主要内容包括静力学、运动学和动力学。
本课程的任务是使学生掌握质点、质点系、刚体和刚体系机械运动(包括平衡)的基本规律及其研究方法,初步学会使用理论力学的理论和方法去分析、解决工程实际问题(包括把一些简单的工程实际问题抽象为理论力学模型),为学习一系列的后继课程打好必要的基础,并为将来学习和掌握新科学技术创造条件。
同时,结合本课程的特点,培养学生的思维能力、抽象化能力、表达能力、计算能力和自学能力。
Theoretical mechanics is an important basic course offered by engineering colleges and universities, and it is a course with strong theoretical, logical and practical nature. It is the foundation of other mechanics courses (such as material mechanics, stmctural mechanics, elasticity, fluid mechanics, etc.), and has a wide range of applications in many engineering and technical fields. This course studies the general laws of mechanical motion of objects, and the main content includes statics, kinematics and dynamics. The task of this course is to enable students to master the basiclaws and research methods of the mechanical motion (including equilibrium) of particle, system of particles, rigid body and rigid system, and to preliminarily learn to use the theories and methods to analyze and solve engineering problems, including abstracting some simple practical problems into mechanical models, which may lay a necessary foundation for learning a series of follow-up courses and create conditions for future learning and mastering of new science and technology. At the same time, taking into account the characteristics of this course, students* abilities of thinking, abstraction, expression, calculation and self-study can be cultivated through course-study.2. 设计思路:根据理论力学课程的特点,本课程以课堂讲授、例题讨论和课下作业为主,通过学习引导同学们将掌握的理论力学知识应用于解决工程实际问题。
第二篇动力学第五章 刚体动力学的基本概念

第二篇动力学第五章刚体动力学的基本概念一、目的要求1.深入地理解力、刚体、平衡和约束等重要概念。
2.静力学公理(或力的基本性质)是静力学的理论基础,要求深入理解。
3.能正确地将力沿坐标轴分解和求力在坐标轴上的投影,对合力投影定理有清晰的理解。
4. 理解力对点之矩的概念,并能熟练地计算。
5.深入理解力偶和力偶矩的概念,明确力偶的性质和力偶的等效条件。
6.明确和掌握约束的基本特征及约束反力的画法。
7.熟练而正确地对单个物体与物体系统进行受力分析,画出受力图。
二、基本内容1.重要概念1)平衡:物体机械运动的一种特殊状态。
在静力学中,若物体相对于地面保持静止或作匀速直线平动,则称物体处于平衡。
2)刚体:在力作用下不变形的物体。
刚体是静力学中的理想化力学模型。
3)约束:对非自由体的运动所加的限制条件。
在刚体静力学中指限制研究对象运动的物体。
约束对非自由体施加的力称为约束反力。
约束反力的方向总是与约束所能阻碍的物体的运动或运动趋势的方向相反。
4)力:物体之间的相互机械作用。
其作用效果可使物体的运动状态发生改变和使物体产生变形。
前者称为力的运动效应或外效应,后者称为力的变形效应或内效应,理论力学只研究力的外效应。
力对物体作用的效应取决于力的大小、方向、作用点这三个要素,且满足平行四边形法则,故力是定位矢量。
5)力的分类:集中力、分布力;主动力、约束反力6)力系:同时作用于物体上的一群力称为力系。
按其作用线所在的位置,力系可以分为平面力系和空间力系,按其作用线的相互关系,力系分为共线力系、平行力系、汇交力系和任意力系等等。
7)等效力系:分别作用于同一刚体上的两组力系,如果它们对该刚体的作用效果完全相同,则此两组力系互为等效力系。
8)平衡力系:若物体在某力系作用下保持平衡,则称此力系为平衡力系。
9)力的合成与分解:若力系与一个力FR 等效,则力FR 称为力系的合力,而力系中的各力称为合力FR 的分力。
力系用其合力FR 代替,称为力的合成;反之,一个力FR 用其分力代替,称为力的分解。
《理论力学》

中国海洋大学本科生课程大纲课程属性:公共基础/通识教育/学科基础/专业知识/工作技能,课程性质:必修、选修一、课程介绍1.课程描述:理论力学是一门关于刚体静力学、运动学及动力学的科学,是轮机工程专业的一门核心专业基础课程,是后续几门重要专业课程的基础。
本课程的内容主要包括刚体静力学中的力系简化及平衡、平面桁架、重心和摩擦等;运动学中点的运动合成及刚体的平面运动;动力学中的动量定理、动量矩定理、动能定理、达朗贝尔原理及虚位移原理,培养和建立学生的工程观点及理论联系实际解决工程实际问题的意识和能力,并为后续的专业课程提供必要的理论基础支撑。
2.设计思路:本课程知识面广、理论性强、系统性强,重点学习刚体的受力分析方法、运动分析方法及动力学研究知识,培养学生抽象思维的能力,掌握解决工程问题的理论分析方法,是后续机械原理、机械设计等课程的重要基础课程之一。
本课程使学生掌握刚体静力学、运动学和动力学中的基本原理及计算方法,并能用相关知识进行分析、设计工程中实际问题。
课程的主要内容包括以下三大模块。
(1)刚体静力学使学生重点掌握本门课中所用的静力学公理、平面系里中力矩和力偶(矩)的定义、性质及计算方法、力系的简化和平衡分析方法,了解空间力系中力矩、力偶、力系的简化及平衡的分析方法,并会用静力学的相关知识对平面桁架进行力的分析及求解,会计算物体系统的重心,会分析考虑摩擦情况下的物体系统平衡。
通过静力学的学习,使学生能用相关知识解决本专业中常见结构的力学分析及设计问题。
(2)刚体运动学使学生掌握点的运动学描述的三种方法及其关系、刚体的平行移动及定轴转动、定轴转动刚体上点的速度及加速度的解法,了解轮系的传动比计算方法、速度及加速度的矢量表示方法。
通过运动学的学习,使学生能使用相关知识解决本专业中常见机构的的运动分析问题,并能进行相关的运动设计。
(3)刚体动力学使学生理解牛顿三大定律及质点运动微分方程,重点掌握动量定理、动量矩定理和动能定理的内容及其应用;理解并会应用大朗贝尔原理及虚位移原理求解相关问题。
理论力学中的动力学分析与加速度的计算

理论力学中的动力学分析与加速度的计算动力学是理论力学中重要的一个分支,研究物体在受到力作用下的运动规律。
在动力学的分析中,计算加速度是非常重要的,它能揭示物体的速度变化情况以及力对物体运动的影响。
本文将介绍动力学分析中的基本概念以及计算加速度的方法。
一、运动物体的描述动力学研究的是物体在受力作用下的运动情况,为了描述运动物体的状态,我们需要引入一些基本概念。
1. 位移:物体在运动过程中,由于位置的变化而引起的变量称为位移。
通常用符号Δx表示。
2. 速度:速度是位移随时间的变化率,即单位时间内位移的大小。
用符号v表示。
3. 加速度:加速度是速度随时间的变化率,即单位时间内速度的变化量。
用符号a表示。
根据以上基本概念,我们可以推导出物体在匀变速运动的情况下,速度和加速度的计算方法。
二、匀变速运动中加速度的计算匀变速运动指的是物体的加速度保持恒定,速度按照一定规律变化的运动。
在这种情况下,我们可以通过已知的物理量来计算加速度。
假设一个物体的初速度为v0,末速度为v,时间为t,加速度为a。
根据物体运动的基本关系式可以得到以下等式:v = v0 + at (1)v = Δx / t (2)将式(1)代入式(2),可得:Δx / t = v0 + at通过变形,可以得到加速度a的计算公式:a = (v - v0) / t以上公式表明,当已知物体在运动过程中的初速度、末速度以及所用时间时,我们可以通过公式计算出加速度。
三、实际应用中的动力学分析与加速度计算动力学分析和加速度计算在实际应用中有着广泛的应用,下面以一个常见的例子来说明。
假设一个小球从高处自由落下,我们想要计算小球下落过程中的加速度。
首先,我们需要测量小球下落的时间,并记录为t。
同时,我们需要测量小球下落的距离,记录为Δx。
根据自由落体运动的特点,小球在自由落下过程中的加速度近似为地球的重力加速度g,约等于9.8 m/s^2。
根据公式a = Δx / t,我们可以计算出小球下落过程中的加速度。
理论力学

一、理论力学的研究对象和内容理论力学是研究物体机械运动一般规律的科学。
机械运动是指物体在空间的位置随时间的变化。
它是宇宙一切物质运动形式中最简单、最基本的一种。
平衡是机械运动的特殊情况。
由于物体之间相互的机械作用,即力的作用,使物体的运动状态发生改变。
具体地说理论力学就是研究力与机械运动改变之间的关系。
本课程所研究的内容是以伽利略、牛顿所建立的基本定律为基础,研究速度远小于光速的宏观物体的机械运动,因此属于古典力学的范畴。
理论力学的研究内容主要包括:静力学:研究物体在力系作用下的平衡规律,同时也研究力的一般性质和力系的简化方法等。
运动学:研究物体运动的几何性质,而不研究引起物体运动的原因。
动力学:研究受力物体的运动变化与作用力之间的关系。
二、理论力学的研究方法是从实践出发,经过抽象化、综合、归纳、建立公理,再应用数学演绎和逻辑推理而得到定理和结论,形成理论体系,然后再通过实践来验证理论的正确性。
三、学习理论力学的目的直接应用本课程理论或者与其它专业知识共同应用来解决工程中一些问题;其次为后继课程如材料力学、结构力学、机械原理、机械设计、弹塑性力学、流体力学、振动理论、断裂力学、飞行力学等许多课程的学习打下重要基础;同时通过理论力学的学习有助于培养辩证唯物主义世界观,培养正确的分析问题和解决问题的能力,为以后解决生产实践问题、从事科学研究工作打下基础。
静力学引言静力学是研究物体在力系作用下的平衡条件的科学。
理论力学所研究的物体大都是刚体。
所谓刚体是指物体在力的作用下,其内部任意两点距离始终保持不变。
但这是一个理想化的力学模型。
在静力学研究的物体只限于刚体。
力,是物体间相互的机械作用,这种作用使物体的机械运动状态发生变化(力的运动效应或外效应)和使物体产生变形(力的变形效应或内效应)。
因理论力学研究对象是刚体,所以主要研究力的运动效应即外效应。
力对物体的作用效果决定于三个要素:(1)力的大小;(2)力的方向(方位和指向);(3)力的作用点。
理论力学中的动力学原理及其在工程中的应用

理论力学中的动力学原理及其在工程中的应用动力学原理是理论力学的重要组成部分,它研究物体运动的原因和规律。
在工程领域中,动力学原理被广泛应用于设计和分析各种机械系统的运动行为。
本文将探讨动力学原理的基本概念以及其在工程中的应用。
动力学原理的基本概念可以追溯到牛顿的运动定律。
牛顿第一定律指出,一个物体如果没有外力作用,将保持静止或匀速直线运动。
这一定律为动力学原理奠定了基础。
牛顿第二定律则给出了物体运动的加速度与作用力之间的关系,即F=ma,其中F是作用力,m是物体的质量,a是物体的加速度。
牛顿第三定律则描述了作用力和反作用力的相互作用,即每个作用力都有一个等大反向的反作用力。
在工程中,动力学原理被广泛应用于机械系统的设计和分析。
例如,在汽车工程中,动力学原理可以用于研究车辆的加速度和制动距离。
根据牛顿第二定律,车辆的加速度与引擎输出的动力和车辆质量有关。
通过对动力学原理的应用,工程师可以优化车辆的动力系统,提高加速性能和燃油效率。
另一个应用动力学原理的例子是建筑物的结构设计。
在建筑物的设计过程中,工程师需要考虑地震和风力等外部力对建筑物的影响。
动力学原理可以用于分析建筑物在外部力作用下的应力和变形情况,以确保建筑物的结构安全可靠。
通过计算建筑物的固有频率和振动模态,工程师可以选择合适的结构材料和设计方案,以抵御外部力的影响。
除了机械系统和建筑物设计,动力学原理还在其他工程领域中发挥着重要作用。
在航空航天工程中,动力学原理被用于研究飞机和火箭的飞行特性。
通过对飞行器的动力学行为进行建模和仿真,工程师可以预测飞行器的性能和稳定性,从而指导设计和改进。
此外,动力学原理还在机器人技术、交通工程、能源系统等领域中得到广泛应用。
在机器人技术中,动力学原理可以用于控制机器人的运动和姿态。
在交通工程中,动力学原理可以用于研究交通流的行为和优化交通信号控制。
在能源系统中,动力学原理可以用于分析能源转换和传输过程中的效率和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可靠性与系统工程学院 学生会整理
Joseph Louis Lagrange (1736 - 1813) French mathematician and mathematical physicist The greatest mathematician of the eighteenth century
可靠性与系统工程学院 学生会整理
达朗伯原理 Jean Le Rond D'Alembert
一个新的质点和刚体动力学原理于1758 年由达 朗伯(Jean Le Rond D'Alembert)在其专著《动力学》 (《Traitéde Dynamique》)中提出. 他将虚位移原 理从静力学推广至动力学. 拉格朗日在达朗伯原理 的基础上,引入约束及广义坐标的概念,导出了拉 格朗日运动方程. 出现在《分析力学》 (《Mé canique Analytique》) (1788年)一书中的达 朗伯原理及拉格朗日方程现在仍被认为是力学基本 原理之一.
可靠性与系统工程学院 学生会整理
刚体的运动、以及刚体之间相互作用
自牛顿以来,物体被看作一个由多个质点组 成的质点系,但两质点或相连两刚体之间相互作 用的内力的性质并不清楚. 1757 年,欧拉在一篇 名为《Dé couverte d'un Nouveau Principle de la Mé canque》的论文中,通过刚体角动量定律对这 一问题作出了回答. 因而人们清楚了牛顿方程描 述刚体质心平动、欧拉方程则描述刚体转动 .
可靠性与系统工程学院 学生会整理
力学的两大理论体系
虚位移原理告诉了我们什么? 达朗贝尔原理告诉了我们什么? 到18 世纪晚期,已经确立了力学的两大理 论体系,分别是以牛顿定律为核心的牛顿力学体 系和欧拉方程、达朗伯原理和拉格朗日方程为核 心的分析力学体系. 每一体系都能完全详尽刻划 质点及刚体的运动.
His work Mécanique Analytique (Analytical Mechanics) (1788) was a mathematical masterpiece. It contained clear, symmetrical notation and covered almost every area of pure mathematics. It was the first book of mechanics published without the use of a single diagram. Lagrange succeeded Euler as the director of the Berlin Academy.
F1 F2 tan 3
可靠性与系统工程学院 学生会整理
问题:两种体系都能够求解问题, 为什么虚位移原理更为简洁方便?
直接的解释是:在应用虚位移原理原理计算虚 功时,由于约束力做虚功之和为零,因此约束力不 出现在平衡条件中。那么,更进一步的问题是:各 铰接处的约束明显对维持系统平衡起作用,而在应 用虚位移原理时,约束的作用—约束力不出现在平 衡条件中。那么,虚位移方程又是怎样刻画出约束 的作用呢?
可靠性与系统工程学院 学生会整理
The first fruit of Lagrange's labours here was his letter, written when he was still only nineteen, to Euler, in which he solved the isoperimetrical problem which for more than half a century had been a subject of discussion. Lagrange developed the calculus of variations which was later expanded by Weierstrass. Lagrange also established the theory of differential equations, and provided many new solutions and theorems in number theory, including Wilson's theorem. Lagrange's classic Théorie des fonctions analytiques laid some of the foundations of group theory, anticipating Galois. Lagrange also invented the method of solving differential equations known as variation of parameters. Lagrange commented that "I have always observed that the pretensions of all people are in exact inverse ratio to their merits; this is one of the axioms of morals".
经典力学的发展
——从虚位移与达朗贝尔原理谈起
虚位移原理告诉了我们什么?
达朗贝尔原理告诉了我们什么?
可靠性与系统工程学院 学生会整理
虚位移原理
17 世纪末,质点动力学理论已经完善. 此时, 伯努利家族的雅各布和约翰两兄弟将牛顿和莱布尼兹 创建的无穷小微积分加以扩展,创立了变分法. 1717 年,约翰提出了虚位移原理. 欧拉(Leonard Euler)师 承约翰.伯努利(Johann Bernoulli),在数学、力学的 众多领域都有突出贡献. 他对力学的两个主要贡献是 刚体转动的欧拉方程和流体力学中的欧拉方程.
可靠性与系统工程学院 方法
F1
F2
l
F2
F1
我们有两个途径求解此问题时,一是应用牛顿力学的静 力学平衡条件;二是应用分析力学中的虚位移原理。对于这类 问题(特征是什么?)我们通常的考虑是应用虚位移原理。
Fl 1 sin 3F 2l cos 0
