有限元分析与应用详细例题
CATIA有限元分析计算实例 完整版

CATIA有限元分析计算实例CATIA有限元分析计算实例11.1例题1 受扭矩作用的圆筒11.1-1划分四面体网格的计算(1)进入【零部件设计】工作台启动CATIA软件。
单击【开始】→【机械设计】→【零部件设计】选项,如图11-1所示,进入【零部件设计】工作台。
图11-1单击【开始】→【机械设计】→【零部件设计】选项单击后弹出【新建零部件】对话框,如图11-2所示。
在对话框内输入新的零件名称,在本例题中,使用默认的零件名称【Part1】。
点击对话框内的【确定】按钮,关闭对话框,进入【零部件设计】工作台。
(2)进入【草图绘制器】工作台在左边的模型树中单击选中【xy平面】, 如图11-3所示。
单击【草图编辑器】工具栏内的【草图】按钮,如图11-4所示。
这时进入【草图绘制器】工作台。
图11-2【新建零部件】对话框图11-3单击选中【xy平面】(3)绘制两个同心圆草图点击【轮廓】工具栏内的【圆】按钮,如图11-5所示。
在原点点击一点,作为圆草图的圆心位置,然后移动鼠标,绘制一个圆。
用同样分方法再绘制一个同心圆,如图11-6所示。
图11-4【草图编辑器】工具栏图11-5【轮廓】工具栏下面标注圆的尺寸。
点击【约束】工具栏内的【约束】按钮,如图11-7所示。
点击选择圆,就标注出圆的直径尺寸。
用同样分方法标注另外一个圆的直径,如图11-8所示。
图11-6两个同心圆草图图11-7【约束】工具栏双击一个尺寸线,弹出【约束定义】对话框,如图11-9所示。
在【直径】数值栏内输入100mm,点击对话框内的【确定】按钮,关闭对话框,同时圆的直径尺寸被修改为100mm。
用同样的方法修改第二个圆的直径尺寸为50mm。
修改尺寸后的圆如图11-10所示。
图11-8标注直径尺寸的圆草图图11-9【约束定义】对话框(4)离开【草图绘制器】工作台点击【工作台】工具栏内的【退出工作台】按钮,如图11-11所示。
退出【草图绘制器】工作台,进入【零部件设计】工作台。
有限元分析习题
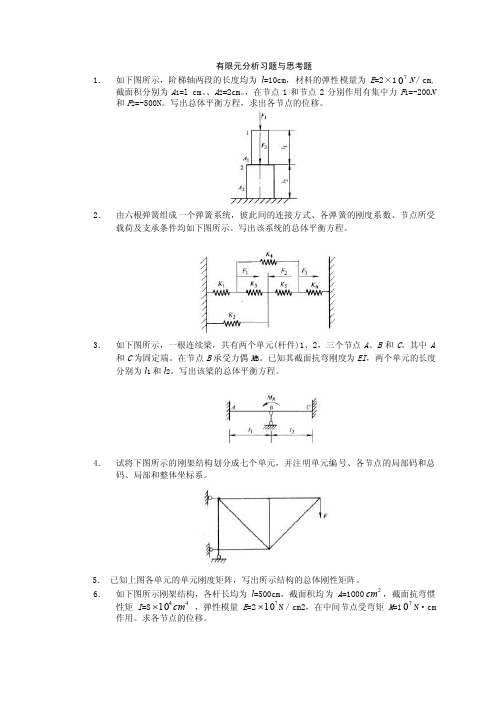
有限元分析习题与思考题1. 如下图所示,阶梯轴两段的长度均为l =10cm ,材料的弹性模量为E =2×170N /cm,截面积分别为A 1=l cm 。
、A 2=2cm 。
,在节点1和节点2分别作用有集中力F 1=-200N 和F 2=-500N 。
写出总体平衡方程,求出各节点的位移。
2. 由六根弹簧组成一个弹簧系统,彼此间的连接方式、各弹簧的刚度系数、节点所受载荷及支承条件均如下图所示。
写出该系统的总体平衡方程。
3. 如下图所示,一根连续梁,共有两个单元(杆件)1、2,三个节点A 、B 和C 。
其中A和C 为固定端。
在节点B 承受力偶M B 。
已知其截面抗弯刚度为EI ,两个单元的长度分别为l 1和l 2。
写出该梁的总体平衡方程。
4. 试将下图所示的刚架结构划分成七个单元,并注明单元编号、各节点的局部码和总码、局部和整体坐标系。
5. 已知上图各单元的单元刚度矩阵,写出所示结构的总体刚性矩阵。
6. 如下图所示刚架结构,各杆长均为l =500cm ,截面积均为A =1O002cm ,截面抗弯惯性矩I =84410cm ⨯ ,弹性模量E =2710⨯N /cm2,在中间节点受弯矩M =170N·cm作用。
求各节点的位移。
7.如下图所示,试对已划分好单元的圆环进行总码编号,以保证所获得的总刚度矩阵的带宽最窄。
8.什么叫结构离散化?结构离散化要完成那些工作?9.决定单元类型和数量应该考虑那些因数?10.怎样合理地进行节点编号?11.单元刚度矩阵与总单元刚度矩阵各有什么特点?12.什么叫单元节点位移向量和(有限元方程中的)节点位移向量?两者有什么不同?13.位移边界条件的处理通常采用什么方法?手算与计算机计算有什么不同?14.什么叫载荷移置?15.矩阵装配时为什么要进行坐标转换?16.何谓有限元的前处理?何谓有限元的后处理?17.对于每个节点具有两个位移分量的杆单元,两节点局部码为1,2,对应总码为4,6,其单元刚度矩阵中的元素k41应放入总体刚度矩阵[K]的【】A.第4行第1列上 B.第4行第6列上c.第8行第2列上 D.第12行第7列上18.图示平面应力问题的结构中,单元刚度矩阵【】A.[K I]=[K II],[K II]=[K IV],但[K I]≠[K II]B.[K I]=[K II],[K III]=[K IV],但[K I]≠[K III]c.[K I]≠[K II]≠[K III]≠ [K IV]D.[K I]=[K II]=[K III]= [K IV]19. 在一平面刚架中,支撑节点4的水平方向位移为已知,若用置大数法引入支撑条件,则应将总体刚度矩阵中的【】A.第4行和第4列上的元素换为大数AB.第4行和第4列上的所有元素换为大数AC.第10行、第10列上的元素换为大数AD.第10行、第lO列上的所有元素换为大数A.20.在有限元分析中,划分单元时,在应力变化大的区域应该【】A.单元数量应多一些,单元尺寸小一些 B.单元数量应少一些,单元尺寸大一些C.单元数量应多一些,单元尺寸大一些 D.单元尺寸和数量随便确定21.图示的四根杆组成的平面刚架结构,用杆单元进行有限元分析,单元和节点的划分如图示,则总体刚度矩阵的大小为【】A.8×8阶矩阵 B.10×10阶矩阵 C.12×12阶矩阵 D.16×16阶矩阵。
有限元例题

【1】图示弹性力学平面问题,采用三角形常应变元,网格划分及单元、节点编号如图1所示。
试求:(1) 计算系统刚度矩阵的最大带宽;(2) 根据图中结构的边界约束状态,给出约束节点位移值。
【解】(1) 相邻节点号的最大差为d = 4;所以,半带宽为B = 2 ⨯ (4 + 1) = 10。
(2) u1 = 0,v1 = 0,u4 = 0,v4 = 0。
【2】弹性力学平面问题4节点等参元,其单元自由度是多少?单元刚度矩阵是多少阶的?单元刚度矩阵有多少个元素?【解】平面问题4节点等参元,其单元自由度是4 ⨯2 = 8个;单元刚度矩阵是8 ⨯ 8 阶的,单元刚度矩阵有64个元素。
【3】平面刚架结构梁单元(考虑轴向和横向变形)的自由度是多少?单元刚度矩阵是多少阶的?单元刚度矩阵有多少个元素?【解】平面刚架结构梁单元(考虑轴向和横向变形)的自由度是2 ⨯ 3 = 6个;单元刚度矩阵是6 ⨯ 6阶的;单元刚度矩阵有36个元素。
【4】已知一等截面直杆中某一微段的起始点坐标为0.5m,终点坐标为0.6m,起始点的位移为0.2mm,终点的位移为0.3mm。
假定直杆内的位移是线性分布的。
求该微段等截面直杆的位移表达式f(x)。
【解】已知:x i = 0.5m, x j= 0.6m, u i = 0.2mm = 0.2⨯10-3m, u j= 0.3mm = 0.3⨯10-3m。
即【5】已知4节点一维问题中单元①(1, 2)的应力矩阵为结构总体位移列阵为求单元①的应力(用矩阵计算)。
【解】由总体结构位移列阵知,单元①的位移列阵为由{σ} = [C] {∆}e可求得单元①的应力【6】某结构中单元③的单元应力矩阵,节点位移列阵为,求单元3的应力{σ }。
【解】由{σ} = [C] {∆}e可求得单元③的应力【7】已知某结构中三角形常应变单元的单元③的应力矩阵与应变矩阵分别为,单元厚度t = 1,单元面积A = 0.5,求单元③的刚度矩阵[K]3。
有限元分析与应用大作业

有限元分析及应用大作业课程名称: 有限元分析及应用班级:姓名:试题2:图示薄板左边固定,右边受均布压力P=100Kn/m作用,板厚度为0.3cm;试采用如下方案,对其进行有限元分析,并对结果进行比较。
1)三节点常应变单元;(2个和200个单元)2)四节点矩形单元;(1个和50个单元)3)八节点等参单元。
(1个和20个单元)图2-1 薄板结构及受力图一、建模由图2-1可知,此薄板长和宽分别为2m和1.5m,厚度仅为0.3cm,本题所研究问题为平面应力问题。
经计算,平板右边受均匀载荷P=33.33MPa,而左边被固定,所以要完全约束个方向的自由度,如图2-2所示。
取弹性模量E=2.1×11Pa,泊松比μ=0.3。
P=33.33MPa图2-2 数学模型二、第一问三节点常应变单元(2个和200个单元)三节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用2个单元的网格划分后的结果如图2-3,200个单元的网格划分图如图2-6所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-4、7所示,应力云图如图2-5、8所示。
图2-3 2个三角形单元的网格划分图图2-4 2个三角形单元的位移云图图2-5 2个三角形单元的应力云图图2-7 200个三角形单元的位移云图三、第二问四节点矩形单元的计算四节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用1个单元的网格划分后的结果如图2-9,50个单元的网格划分图如图2-12所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-10、11所示,应力云图如图2-13、14所示。
图2-9 1个四边形单元的网格划分图图2-11 1个四边形单元的应力云图图2-12 50个四边形单元的网格划分图图2-13 50个四边形单元的位移云图图2-14 50个四边形单元的应力云图四、第三问八节点等参单元的计算四节点单元类型为PLANE82,设置好单元类型后,实常数设置板厚为0.3M。
有限元分析及应用习题

1.悬臂梁如图示,在自由端面作用分布剪力,其合力为P ,采用图示网格求结点位移及单元应力。
设梁厚 11/3t μ== ,。
解 :平面三角形单元划分及节点分布如上图:①(1,2,6);②(2,5,6);③(2,3,5);④(3,4,5)。
对于单元①,由于1,6结点为全位移约束,因此有:11660,0;0,0u v u v ====11111111121621111111222122262111166616266111111121611111121222622111616266660000F K K K u F F K K K K v F K K K K K K F K K K F K K K F δδδδδδδ⎧⎫⎪⎪⎪⎪⎧⎫⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪====⎨⎬⎨⎬⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎩⎭⎪⎪⎪⎪⎩⎭⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭单元平衡方程为1⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭对于单元②对于③单元对于④单元222222222225265222222255525556522226662656622222225262222252555655222626566600u v F K K K u F F K K K K v F K K K K K K F K K K F K K K δδδδδδδ⎧⎫⎪⎪⎪⎪⎧⎫⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪====⎨⎬⎨⎬⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎩⎭⎪⎪⎪⎪⎩⎭⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭ 单元平衡方程为:226F ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭223333222223253333333333323335333335552535555333222325233332333533335253555u v F K K K u F F K K K K v F K K K u v K K K K K K K K K δδδδδδδ⎧⎫⎪⎪⎪⎪⎧⎫⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪====⎨⎬⎨⎬⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭⎧⎫⎧⎫⎪⎪⎪⎪⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭ 单元平衡方程为:323335F F F ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭334444333334354444444444434445444445553545555444333435344443444544445354555u v F K K K u F F K K K K v F K K K u v K K K KK K K K K δδδδδδδ⎧⎫⎪⎪⎪⎪⎧⎫⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪====⎨⎬⎨⎬⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭ 单元平衡方程为434445F F F ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭{}223344551166000000000022Tu v u v u v u v P PF X Y X Y δ=⎧⎫=--⎨⎬⎩⎭节点位移矩阵:节点载荷矩阵: []211031091211010*********23E E A D μμμμ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦单元①26111162161222612116661210101111,1,[]010*********0101111,0,[]00001120101001110,1,[]0111210x y b c B x y A y x b c B y x Ay x b c B y x A --⎡⎤⎡⎤⎢⎥⎢⎥==-==-=-=-⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥======⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢=====⎢⎢⎣ 1111126000110101000010001110110B B B B ⎡⎤⎥⎢⎥=⎥⎢⎥⎥⎢⎥⎦⎣⎦-⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥--⎣⎦1111421111333332411113333311110093311111600333311110033331110013342111133333241111333311110033111100333391611033T E K tAB DB E K ⎡⎤----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥--⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦------------=--单元刚度矩阵:扩展为:1103311100133⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦单元②65222256262555622526665210,1,[]0101 11210101010 1111,1,[]0101 1121111101111,0,[]0011201b c By x Ay xb c By x Axyb c Bxy A⎢⎥⎢⎥====-=-=-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥======⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎢⎥==-===⎢⎥⎢-⎣⎦2222256100001001010010100101101B B B B-⎡⎤⎢⎥=⎢⎥⎥⎢⎥-⎣⎦-⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥--⎣⎦2222111100333311011033114211933333124111613333311011033111100333311110033331101103391611421133333124111333331013TEK tAB DBEK⎡⎤--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥----⎢⎥==⎢⎥⎢⎥----⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦----=----------单元刚度矩阵:扩展为:11031111003333⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦单元③53322235253333522335553211,1,[]0101 11211111010 1111,0,[]0000 1120101001110,1,[]0111210b c By x Ay xb c By x Axyb c Bxy A⎢⎥⎢⎥==-==-=-=-⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥======⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎢=====⎣3333235000110101000010001110110B B B B⎤⎡⎤⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎦⎣⎦-⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥--⎣⎦3333421111333332411113333311110093311111600333311110033331110013342111133333241111333331111003311119003333161133TEK tAB DBEK⎡⎤----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥--⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦------------=--单元刚度矩阵:扩展为:11003311100133⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦单元④45433354354444534345553410,1,[]010111210101010 1111,1,[]0101 1121111101111,0,[]0011201b c Bxy Ay xb c By x Ay xb c By x A⎢⎥⎢⎥====-=-=-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥======⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎢==-===⎢⎢-⎣⎦4444345100001001010010100101101B B B B-⎡⎤⎥⎢⎥=⎥⎢⎥⎥⎢⎥-⎣⎦-⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥--⎣⎦444411110033331101103311421193333312411161333331101103311110033331111003333110110339114211163333312411133333110133TEK tAB DBEK⎡⎤--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥----⎢⎥==⎢⎥⎢⎥----⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦----=----------刚度矩阵:扩展为:101111003333⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦122442111100000033333241110000133333182122211000333333311281122002033333333141120010*******3114120001000933333=1142116000010033333124110000133333E K K K K K ----------------------------+++=--------整体刚度矩阵:002221821000113333333221128110020333333331121400000103333312114133333⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥------⎢⎥⎢⎥------⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎣⎦引进边界条件求节点位移:代入42111100000033333241110000133333182122211000333333311281122002033333333141120010*******3114120001000933333114211600001003333312411000010033333222182000133333E ----------------------------------------22334455001013302211281100203333333311214000001033333121141033333u vu v u v u v ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎣⎦⎢⎥------⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎣⎦116600020200X Y P P X Y ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎥⎢⎥⎣⎦8212210033333281120023333314112100333331141201093333311421160013333312411001333332221820133333322112820333333E ⎡⎤⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥----⎢⎢⎢⎢⎣⎦即:2233445500020200u v u P v u v P u v ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⋅=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎥⎥⎥⎥求得节点位移如下:[][]223344552.0404 4.5453 2.546512.1179 3.036412.6170 2.2022 5.0306TT u v u v u v u v P E=------求得支反力1221226255625591()2163911() 1.2351633921()216339211()0.23516333E X u v PE Y u v PE X v u v PE Y u u v P=--==--==--=-=--=-由单元划分模型可知,上述支反力与外载荷构成一个平衡力系。
第一讲有限元例题
方法:代入已知位移。
1
1 2
Q1,
Q2
,
Q3
0
0
因为 Q1 0
0 6.0 105 2.0105
0 2.0105 2.0 105
QQ12 Q3
K 的第一行与第一列均与0相乘,可以在方程中将其划去。
K 简化成
6.0105 2.0105
2.0105
2.0 105
方程可以降阶为
10
5
QQ12
2.0 105 Q3
Q —— 结构整体节点位移向量
结构外力虚功
Wp
P • Q3
Q1
,
Q2
,
Q3
P1 P2
P3
P1 —未知 P2 0
P3 100 N
结构势能可以表示为
4.0 105
p
1 2
Q1
,
Q2
,
Q3
4.0 0
10
5
4.0 105 6.0 105 2.0 105
1 2
Q1,
Q2
4.0 105 4.0 105
4.0 105 Q1
4.0 105
Q2
1 2
Q2 ,Q3
2.0 105 2.0 105
2.0 105 2.0 105
QQ23
4.0 105
1 2
Q1,
Q2
,
Q3
4.0 0
10
5
4.0 105 4.0 105
0
0 0
QQ12
1
x Le
Q1e
x Le
Q2e
进一步写成矩阵形式有
ux
1
x Le
,
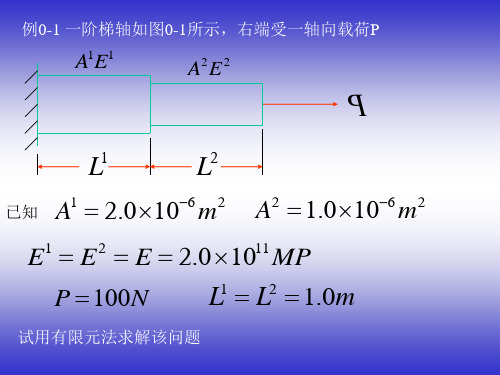
有限元分析实例
有限元分析实例引言有限元分析(Finite Element Analysis,简称FEA)是一种工程分析方法,能够将连续体结构分割成有限个小单元,通过在每个小单元内建立方程模型,最终求解整个结构的力学行为。
本文将以一个实例来介绍有限元分析的基本过程和步骤。
实例背景我们将以一个简单的杆件弯曲问题为例来进行有限元分析。
假设有一根长度为L、截面积为A的杆件,材料的弹性模量为E,截面的转动惯性矩为I。
我们希望通过有限元分析来计算杆件在一定加载条件下的弯曲变形。
有限元网格的划分首先,我们需要将杆件划分成有限个小单元,即有限元网格。
常用的网格划分方法有三角形划分、四边形单元划分等。
根据具体问题的要求和复杂度,选择合适的划分方法。
单元的建立划分好网格后,我们需要在每个小单元内建立方程模型。
在弯曲问题中,常见的单元模型有梁单元、壳单元等。
在本实例中,我们选择梁单元作为杆件的单元模型。
对于梁单元,我们需要定义每个节点的位移和约束条件。
根据杆件的几何尺寸和材料属性,可以利用应变能量原理和几何相似原理,得到每个节点的位移和约束条件。
材料特性和加载条件的定义在进行有限元分析之前,我们需要定义材料的特性和加载条件。
对于本实例中的杆件,我们需要定义弹性模量E、截面积A和转动惯性矩I。
加载条件可以包括集中力、均布力、弯矩等。
在本实例中,假设杆件受到均布力,即沿杆件轴向的受力分布是均匀的。
单元方程的建立和求解在定义了材料特性和加载条件之后,我们可以根据每个梁单元的位移和约束条件,建立每个单元的方程模型。
常见的方程模型有刚度矩阵方法、位移法等。
根据所选的单元模型,选择合适的方程模型进行计算。
通过对每个单元的方程模型进行组装,我们可以得到整个结构的方程模型。
将加载条件带入,可以求解出整个结构在给定加载条件下的位移、应力等参数。
结果分析根据求解得到的位移信息,我们可以绘制出结构的变形图。
通过变形图,可以直观地观察到结构在弯曲条件下的变形情况。
有限元分析及应用+homework+I
《有限元分析及应用》习题I要求:(1) 每位同学独立完成;(2) 请手写书面完成,交手写稿,不要打印稿;(3) 跟随课堂进度完成相应的习题,在课程结束时一并上交,具体时间见通知。
1.如图所示的1D 杆结构,试用取微单元体的方法建立起全部基本方程和边界条件,并求出它的所有解答。
注意:它的弹性模量为E ,横截面积为A第1题图2.设平面问题中的应力为123456789xx yy xy a a x a ya a x a y a a x a yσστ=++=++=++ 其中a i (i=1,2,…,9)为常数,令所有体积力为零,对下列特殊情况说明平衡是否满足?为什么?或者在a i 之间有什么关系才满足平衡。
(1)除a 1 、a 4 、a 7外,其余a i 为零。
(2)a 3=a 5=a 8=a 9=0 (3)a 2=a 6=a 8=a 9=0 (4)所有a i 均为非零。
3.如图所示,已知平面应力问题的应力状态为,,xx yy xy σστ, 求: (1)斜面上应力σN ,τN 的表达式。
(2)最大主应力、最小主应力及此时斜面的方向余弦。
第3题图4.分别就以下情形,写出所有基本方程及边界条件(分量形式、指标形式)、各基本变量(分量形式、指标形式以及对应关系)。
(1)1D 情形 (2)2D 情形 (3)3D 情形5 设有应变分量的表达式为22440122440122012()()()()()xx yy xy A A x y x y B B x y x y C C xy x y C εεγ=++++=++++=+++ 其中0101012,,,,,,A A B B C C C 为常数,试问这些常数需要满足何种关系时,以上的应变分量才能成为一种真正的应变状态。
6. 分别给出平面应力和平面应变状态下的前提条件及表达式,推导两种情况下的物理方程,以及它们之间的转换关系。
7. 一个立方块的弹性体放在同样大小的刚性盒内,其上面用刚性盖密闭后加均匀压力q , 方块与盒盖之间无摩擦力,设加压方向为z 轴,盒的侧面法向为x 轴和y 轴,求弹性体的应力,,xx yy zz σσσ和应变,,xx yy zz εεε8. 某一长方体的位移分量为321132213(12)(,,)(12)(,,)(12)(,,)P u x y z x b y b z a E P v x y z y b z b x a E P w x y z z b x b y a Eμμμ−=−+−+−=−+−+−=−+−+其中123123,,,,,a a a b b b 为常数。
有限元分析报告与应用大作业
有限元分析及应用大作业课程名称: 有限元分析及应用班级:姓名:试题2:图示薄板左边固定,右边受均布压力P=100Kn/m作用,板厚度为0.3cm;试采用如下方案,对其进行有限元分析,并对结果进行比较。
1)三节点常应变单元;(2个和200个单元)2)四节点矩形单元;(1个和50个单元)3)八节点等参单元。
(1个和20个单元)图2-1 薄板结构及受力图一、建模由图2-1可知,此薄板长和宽分别为2m和1.5m,厚度仅为0.3cm,本题所研究问题为平面应力问题。
经计算,平板右边受均匀载荷P=33.33MPa,而左边被固定,所以要完全约束个方向的自由度,如图2-2所示。
取弹性模量E=2.1×11Pa,泊松比μ=0.3。
P=33.33MPa图2-2 数学模型二、第一问三节点常应变单元(2个和200个单元)三节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用2个单元的网格划分后的结果如图2-3,200个单元的网格划分图如图2-6所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-4、7所示,应力云图如图2-5、8所示。
图2-3 2个三角形单元的网格划分图图2-4 2个三角形单元的位移云图图2-5 2个三角形单元的应力云图图2-6 200个三角形单元的网格划分图图2-7 200个三角形单元的位移云图图2-8 200个三角形单元的应力云图三、第二问四节点矩形单元的计算四节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用1个单元的网格划分后的结果如图2-9,50个单元的网格划分图如图2-12所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-10、11所示,应力云图如图2-13、14所示。
图2-9 1个四边形单元的网格划分图图2-10 1个四边形单元的位移云图图2-11 1个四边形单元的应力云图图2-12 50个四边形单元的网格划分图图2-13 50个四边形单元的位移云图图2-14 50个四边形单元的应力云图四、第三问八节点等参单元的计算四节点单元类型为PLANE82,设置好单元类型后,实常数设置板厚为0.3M。
有限元分析实例2
29 9
VM144, BENDING OF A COMPOSITE BEAM
分析结果比较
SHELL99 model Displacement, in StressxTOP , psi StressxBOT , psi SHELL99 model (with node offset) Displacement, in StressxTOP , psi StressxBOT , psi SOLID46 model Displacement, in StressxTOP , psi StressxBOT , psi Target 0.832 2258. 1731. Target 0.832 2258. 1731. Target 0.832 2258. 1731. Analysis 0.832 2258. 1731. Analysis 0.832 2258. 1731. Analysis 0.832 2258. 1731. Ratio 1.000 1.000 1.000 Ratio 1.000 1.000 1.000 Ratio 1.000 1.000 1.000
80°F
0.014 Btu/(hr-in2°F) 80°F
建模、划分网格、加载边界条件和初始条件
铸件凝固过程中的热焓变化
1 ENTH FOR MATERIAL 2
200 180 160 140 120
ENTH
ENTH
100 80 60 40 20 0 0 250 500 750 1000 1250 1500 1750 2000 2250 2500 2750 3000 3250
(边界上给定温度) (边界上给定热流密度) (边界上给定对流换热)
微元升温所需热量应与传入微元的热量和微体内 部产生的热量平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《有限元分析与应用》详细例题试题1:图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;2)分别采用不同数量的三节点常应变单元计算;3)当选常应变三角单元时,分别采用不同划分方案计算。
一.问题描述及数学建模无限长的刚性地基上的三角形大坝受齐顶的水压作用可看作一个平面问题,简化为平面三角形受力问题,把无限长的地基看着平面三角形的底边受固定支座约束的作用,受力面的受力简化为受均布载荷的作用。
二.建模及计算过程1. 分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算下面简述三节点常应变单元有限元建模过程(其他类型的建模过程类似):1.1进入ANSYS【开始】→【程序】→ANSYS 10.0→ANSYS Product Launcher →change the working directory →Job Name: shiti1→Run1.2设置计算类型ANSYS Main Menu: Preferences →select Structural →OK1.3选择单元类型单元是三节点常应变单元,可以用4节点退化表示。
ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete →Add →select Solid Quad 4 node 42 →OK (back to Element Types window)→Options… →select K3: Plane Strain→OK→Close (the Element Type window)1.4定义材料参数材料为钢,可查找钢的参数并在有限元中定义,其中弹性模量E=210Gpa,泊松比v=0.3。
ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear →Elastic→Isotropic→input EX:2.1e11, PRXY:0.3→OK1.5生成几何模型✓生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS→依次输入四个点的坐标:input:1(0,0),2(3,0),3(6,0),4(3,5),5(0,10),6(0,5)→OK✓生成坝体截面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS →依次连接1,2,6;2,3,4;2,4,6;4,5,6这三个特征点→OK1.6网格划分ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) Global: Set →input NDIV: 1→OK →(back to the mesh tool window)Mesh: Areas, Shape: Tri, Free →Mesh →Pick All (in Picking Menu) →Close( the Mesh Tool window)1.7模型施加约束✓分别给下底边和竖直的纵边施加x和y方向的约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→On lines→选择底边→OK→select:ALL DOF →OK✓给斜边施加x方向的分布载荷ANSYS 命令菜单栏: Parameters→Functions →Define/Edit→1) 在下方的下拉列表框内选择x ,作为设置的变量;2) 在Result窗口中出现{X},写入所施加的载荷函数:1000*{X};3) File>Save(文件扩展名:func) →返回:Parameters→Functions →Read from file:将需要的.func 文件打开,任给一个参数名,它表示随之将施加的载荷→OK →ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Pressure →On Lines →拾取斜边;OK →在下拉列表框中,选择:Existing table (来自用户定义的变量)→OK →选择需要的载荷参数名→OK1.8 分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →OK1.9 结果显示确定当前数据为最后时间步的数据ANSYS Main Menu: General Postproc →Read Result→Last Set查看在外力作用下的变形ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape→select Def + Undeformed→OK查看节点位移分布情况Contour Plot→Nodal Solu…→select: DOF solution→Displacement vctor sum→Def + Undeformed →OK查看节点应力分布情况Contour Plot→Nodal Solu…→select: Stress→XY shear stress→Def + Undeformed→OK 1.10 退出系统ANSYS Utility Menu: File→Exit…→Save Everything→OK三.结果分析三节点常应变单元(6个节点,4个单元)几何模型图变形图,节点位移图,节点应力图,节点应变图六节点常应变单元(6个节点,4个单元)几何模型图变形图,节点位移图,节点应力图,节点应变图分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算结果比较相符。
分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算结果比较可知,三节点常应变单元的结果好些。
2.分别采用不同数量的三节点常应变单元计算三节点常应变单元(13个节点,14个单元) 几何模型图单元划分方案变形大小应力大小 应变大小 值的比较分析 三节点三角形单元 DMX:0.109E-05 SMX:0.109E-05DMX:0.109E-05 SMN:2778 SMX:8749 DMX:0.109E-05 SMN: 0.344E-07 SMX: 0.108E-06 1.最大变形值小; 2.最大应力值小; 3.最大应变值小。
六节点三角形单元 DMX:0.289E-05 SMX:0.289E-05DMX:0.289E-05 SMN:-976.202 SMX:11598DMX:0.289E-05 SMN: -0.121E-07 SMX: 0.144E-061.最大变形值大;2.最大应力值大;3.最大应变值小。
变形图,节点位移图,节点应力图,节点应变图分别采用不同数量的三节点常应变单元计算结果相符。
分别采用不同数量的三节点常应变单元计算结果比较可得,节点多的比节点少的精确。
单元划分方案 位移大小应力大小 应变大小 值的比较分析 三节点三角形单元 (6节点4单元) DMX:0.109E-05 SMX:0.109E-05DMX:0.109E-05 SMN:2778 SMX:8749 DMX:0.109E-05 SMN: 0.344E-07 SMX: 0.108E-06 1.最大变形值小; 2.最大应力值大; 3.最大应变值大。
三节点三角形单元(13节点14单元)DMX:0.178E-05SMX:0.178E-05DMX:0.178E-05 SMN:990.156 SMX:8000DMX:0.178E-05 SMN: 0.123E-07 SMX: 0.990E-071.最大变形值大;2.最大应力值小;3.最大应变值小。
3.当选常应变三角单元时,分别采用不同划分方案三节点常应变单元(6个节点,4个单元)(另一种方案)几何模型图变形图,节点位移图,节点应力图,节点应变图当选常应变三角单元时,分别采用不同划分方案结果比较相符。
分别采用不同方案相同节点相同单元的三节点常应变单元计算结果比较可得,第二种划分的方案精确。
试题2:图示为带方孔(边长为80mm)的悬臂梁,其上受部分均布载荷(p=10Kn/m)作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置(即方位)进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为1mm,材料为钢)一.问题描述及数学建模悬臂梁受集中载荷以及均布载荷的作用可看作一个平面问题,简化为平面四边形受力问题,悬臂梁固定在墙上的部分看作是受全约束的作用,悬臂梁受力面的受集中载荷以及均布载荷的作用。
二.建模及计算过程有限元建模选用Solid单元的8节点82单元建模,材料为钢,可查找钢的参数并在有限元中定义,其中弹性模量E=210Gpa,泊松比v=0.3。
悬臂梁的左侧受全约束作用,同时梁上受集中载荷以及均布载荷的作用。
三.结果分析带斜方孔的悬臂梁(450节点130单元)几何模型图变形图,节点位移图,节点应力图,节点应变图带正方孔的悬臂梁(441节点127单元)几何模型图带圆形孔的悬臂梁(423节点121单元)几何模型图将三种方案进行比较相符。
根据以上分别采用不同方案的计算结果比较可得,带圆孔的悬臂梁的变形应力应变都最小,可得出先用圆孔设计最合理。
模型方案位移大小应力大小 应变大小 值的比较分析 带方孔(斜置)的悬臂梁 DMX:0.003182 SMX:0.003182DMX:0.003182 SMN:-127762 SMX:16794 DMX:0.003182 SMN: -0.158E-05 SMX: 0.208E-06 1.最大变形值中; 2.最大应力值中; 3.最大应变值中。
带方孔(正置)的悬臂梁 DMX:0.003193 SMX:0.003193DMX:0.003193 SMN:-144314 SMX:56804 DMX:0.003193 SMN: -0.179E-06 SMX: 0.703E-06 1.最大变形值大; 2.最大应力值大; 3.最大应变值大。
带圆孔的悬臂梁 DMX:0.003163 SMX:0.003163DMX:0.003163 SMN:-167003 SMX:16617DMX:0.003163 SMN: -0.207E-05 SMX: 0.206E-061.最大变形值小;2.最大应力值小;3.最大应变值小。
