2016-2017年江苏省无锡市天一中学高一上学期数学期末试卷与解析PDF
江苏省无锡市天一中学高一数学理月考试卷含解析

江苏省无锡市天一中学高一数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 等差数列{a n}的公差,且,则数列{a n}的前n项和S n取得最大值时的项数n是()A. 9B. 10C. 10和11D. 11和12参考答案:C【分析】利用等差数列性质得到,再判断或是最大值.【详解】等差数列的公差,且,根据正负关系:或是最大值故答案选C【点睛】本题考查了等差数列的性质,的最大值,将的最大值转化为中项的正负是解题的关键.2. 已知,,,则,,的大小关系为()A B C D参考答案:B略3. (5分)函数f(x)=|x|﹣cosx在(﹣∞,+∞)内()A.没有零点B.有且仅有一个零点C.有且仅有两个零点D.有无究多个零点参考答案:C考点:函数的零点.专题:函数的性质及应用.分析:函数f(x)=|x|﹣cosx的零点个数可转化为函数y=|x|与y=cosx的图象交点的个数.结合它们的图象特征即可作出判断.解答:函数f(x)=|x|﹣cosx的零点个数,即方程|x|﹣cosx=0的根的个数,也即函数y=|x|与y=cosx的图象交点的个数.当0≤x≤时,y=|x|=x从0递增到,y=cosx从1递减到0,所以两函数图象在上只有一个交点,当x>时,y=|x|=x>>1,y=cosx≤1,所以两函数图象在(,+∞)上没有交点,所以y=|x|与y=cosx的图象在上也只有一个交点,综上,函数y=|x|与y=cosx的图象交点的个数是2,故函数f(x)=|x|﹣cosx的零点个数为2.故选C.点评:本题考查函数的零点问题,即相应方程根的问题,注意体会转化思想与数形结合思想在本题中的运用.4. 函数的部分图象如图所示,若,且,则()A. B. C. D.1参考答案:C根据题意,函数中,,周期,所以,又函数图像过点,即,又,所以,所以,所以,即图中最高点的坐标为,又且,所以,所以.5. 若直线与曲线有两个公共点,则实数m的取值范围是()A. B.C. D.参考答案:B【分析】由于曲线表示原点为圆心,半径为2的半圆,根据题意画出图形,找出两个特殊的位置:1.直线y=x+m与半圆相切;2.直线y=x+m过点(2,0),当直线与半圆相切时,利用点到直线的距离公式表示圆心到直线的距离d,让d等于半径列出关于m的方程,求出m的值,写出满足题意的m的范围即可.【详解】由,得到,如图,当直线与圆相切时,因此:若直线与圆有两个公共点,则实数的取值范围是:.故选:B【点睛】本题考查了直线和半圆的位置关系,考查了学生转化与划归,数形结合的能力,属于中档题.6. 若函数在处取最小值,则等于()A. 3B.C.D. 4参考答案:A【分析】将函数的解析式配凑为,再利用基本不等式求出该函数的最小值,利用等号成立得出相应的值,可得出的值.【详解】当时,,则,当且仅当时,即当时,等号成立,因此,,故选:A.【点睛】本题考查基本不等式等号成立的条件,利用基本不等式要对代数式进行配凑,注意“一正、二定、三相等”这三个条件的应用,考查计算能力,属于中等题.7. 设全集,,,则( )A. B. C. D.参考答案:B略8. 已知直线m、n与平面、,给出下列三个命题:①若m∥,n∥,则m∥n;②若m∥,n⊥,则n⊥m;③若m⊥,m∥,则⊥.其中真命题的个数是()A.0 B.1 C.2D.3参考答案:C9. 已知点,点E是圆上的动点,点F是圆上的动点,则的最大值为()A. 2B.C. 3D. 4参考答案:D【分析】由于两圆不在直线的同侧,先做出圆关于直线对称的圆,把转化为,若最大,必须最大,最小.【详解】如图:依题意得点在直线上,点关于直线对称的点,点在圆关于直线对称的圆上,则,设圆的圆心为,因为,,所以,当五点共线,在线段上,在线段上时“=”成立.因此,的最大值为4.【点睛】本题主要考查圆与圆的位置关系,直线与圆的位置关系,距离和差的最值问题对称变换是常采用的方法.10. 已知等差数列的公差为,若,和成等比数列,则可以等于().A.B.C.D.参考答案:C【考点】8F:等差数列的性质.【分析】依题意,,可求得.【解答】解:∵等差数列的公差,,和成等比数列,∴, ∴,∴,故选:.二、 填空题:本大题共7小题,每小题4分,共28分11. 对于任意实数,符号[]表示的整数部分,即[]是不超过的最大整数,例如[2]=2;[]=2;[]=, 这个函数[]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
江苏省无锡市2016-2017学年高一上学期期末考试 数学 Word版含答案

2016年秋学期无锡市普通高中期末考试试卷高一数学 2017.01一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1.设全集{}0,1,2,3,U =集合{}{}1,2,2,3A B ==,则()U C A B = .2.函数()sin 3f x x π⎛⎫=-⎪⎝⎭的最小正周期为 . 3.若函数()22,0,1,0,x x f x x x +>⎧=⎨-≤⎩则()()2f f -= . 4.在平面直角坐标系xoy 中,300 角终边上一点P 的坐标为()1,m ,则实数m 的值为 .5.已知幂函数()y f x =的图象过点13⎫⎪⎭,则12f ⎛⎫= ⎪⎝⎭ .6.已知向量,a b 满足2,3a b == ,且3a b ⋅=- ,则a 与b 的夹角为 .7.若()1sin 3πα+=,则sin 22πα⎛⎫+= ⎪⎝⎭ . 8.函数()2log 3cos 1,,22y x x ππ⎡⎤=+∈-⎢⎥⎣⎦的值域为 . 9.在ABC ∆中,E 是边AC 的中点,4BC BD = 若DE xAB yAC =+ ,则x y +=为 .10.将函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象先向左平移3π个单位,再将图象上各点的横坐标变为原来的12倍(纵坐标不变),那么所得图象的解析式为 .11.若函数()224f x x ax a =-+-的一个零点在()2,0-区间内,另一个零点在()1,3区间内,则实数a 的取值范围为 .12.若()sin cos 11,tan 1cos 23αααβα=-=-,则tan β= . 13.已知()f x 是定义在(),-∞+∞上的奇函数,当0x >时,()24f x x x =-若函数()f x 在区间[],4t 上的值域为[]4,4-,则实数t 的取值范围为 .14.若函数()()sin 13f x x πωω⎛⎫=+> ⎪⎝⎭在区间5,4ππ⎡⎤⎢⎥⎣⎦上单调递减,则实数ω的取值范围为 .二、填空题:本大题共4小题,每小题5分,共20分.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程. 15.已知向量()()()3,1,1,2,.a b m a kb k R =-=-=+∈ (1)若m 与向量2a b - 垂直,求实数k 的值; (2)若向量()1,1c =- ,且m 与向量kb c + 平行,求实数k 的值.16.设0,3πα⎛⎫∈ ⎪⎝⎭cos 2αα+= (1)求cos 6πα⎛⎫+ ⎪⎝⎭的值;(2)求7cos 212πα⎛⎫+ ⎪⎝⎭的值.17.某机构通过对某企业2016年的生产经营情况的调查,得到每月利润y (单位:万元)与相应月份数x 的部分数据如下表:(1)根据上表数据,请从下列三个函数中选取一个恰当的函数描述y 与x 的变化关系,并说明理由:22,,x y ax b y x ax b y a b =+=-++=⋅;(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.20.已知函数()12.2x x f x ⎛⎫=- ⎪⎝⎭(1)若()154f x =,求x 的值; (2)若不等式()()()2cos 1cos 0f m m f f θθ-+--=对所有0,2πθ⎡⎤∈⎢⎥⎣⎦都成立,求实数m 的取值范围.21.已知t 为实数,函数()()()2log 22,log a a f x x t g x x =--=,其中0 1.a <<(1)若函数()()1x f x g a kx =+-是偶函数,求实数k 的值; (2)当[]1,4x ∈时,()f x 的图象始终在()g x 的图象的下方,求t 的取值范围;(3)设4t =,当[](),x m n m n ∈<时,函数()y f x =的值域为[]0,2,若n m -的最小值为16,求实数a 的值.22.已知向量33cos ,sin ,cos ,sin 2222x x x x a b ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭ ,函数()1,,,.34f x a b m a b x m R ππ⎡⎤=⋅-++∈-∈⎢⎥⎣⎦(1)当0m =时,求6f π⎛⎫ ⎪⎝⎭的值; (2)若()f x 的最小值为1-,求实数m 的值;(3)是否存在实数m ,使函数()()224,,4934g x f x m x ππ⎡⎤=+∈-⎢⎥⎣⎦有四个不同的零点?若存在,求出m 的取值范围;若不存在,请说明理由.。
(完整word版)江苏省无锡市天一中学2016-2017学年高一(上)期末数学试卷(解析版)
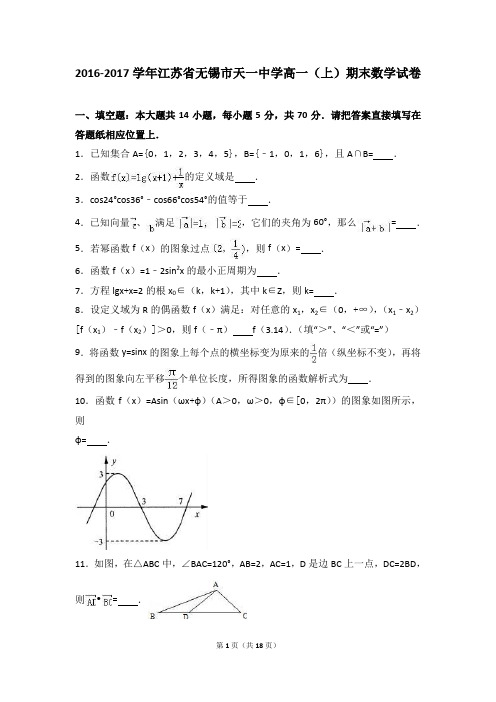
2016-2017学年江苏省无锡市天一中学高一(上)期末数学试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题纸相应位置上.1.已知集合A={0,1,2,3,4,5},B={﹣1,0,1,6},且A∩B=.2.函数的定义域是.3.cos24°cos36°﹣cos66°cos54°的值等于.4.已知向量、满足,它们的夹角为60°,那么=.5.若幂函数f(x)的图象过点,则f(x)=.6.函数f(x)=1﹣2sin2x的最小正周期为.7.方程lgx+x=2的根x0∈(k,k+1),其中k∈Z,则k=.8.设定义域为R的偶函数f(x)满足:对任意的x1,x2∈(0,+∞),(x1﹣x2)[f(x1)﹣f(x2)]>0,则f(﹣π)f(3.14).(填“>”、“<”或“=”)9.将函数y=sinx的图象上每个点的横坐标变为原来的倍(纵坐标不变),再将得到的图象向左平移个单位长度,所得图象的函数解析式为.10.函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象如图所示,则φ=.11.如图,在△ABC中,∠BAC=120°,AB=2,AC=1,D是边BC上一点,DC=2BD,则•=.12.已知角α、β的顶点在坐标原点,始边与x轴的正半轴重合,α、β∈(0,π),角β的终边与单位圆交点的横坐标是,角α+β的终边与单位圆交点的纵坐标是,则cosα=.13.若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f (cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是.14.已知△ABC的边长为2的等边三角形,动点P满足,则的取值范围是.二、解答题:本大题共6小题,共90分,解答应写出文字说明、证明过程或演算步骤.15.已知(1)求tanθ的值;(2)求的值.16.已知向量,向量,向量满足.(1)若,且,求的值;(2)若与共线,求实数k的值.17.已知函数(1)求函数f(x)的单调增区间;(2)若,求cos2α的值.18.某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.19.在平面直角坐标系中,O为坐标原点,已知向量=(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t),θ∈R.(1)若⊥,且,求向量;(2)若向量与向量共线,常数k>0,求f(θ)=tsinθ的值域.20.对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=a•f1(x)+b•f2(x),那么称h(x)为f1(x),f2(x)的生成函数.(1)给出函数,h(x)是否为f1(x),f2(x)的生成函数?并说明理由;(2)设,生成函数h(x).若不等式3h2(x)+2h(x)+t>0在x∈[2,4]上恒成立,求实数t的取值范围;(3)设,取a>0,b>0,生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1,x2且x1+x2=1.试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m 的值;如果不存在,请说明理由.2016-2017学年江苏省无锡市天一中学高一(上)期末数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题纸相应位置上.1.已知集合A={0,1,2,3,4,5},B={﹣1,0,1,6},且A∩B={0,1} .【考点】交集及其运算.【分析】利用交集定义直接求解.【解答】解:∵集合A={0,1,2,3,4,5},B={﹣1,0,1,6},∴A∩B={0,1}.故答案为:{0,1}.2.函数的定义域是(﹣1,0)∪(0,+∞).【考点】函数的定义域及其求法.【分析】由对数式的真数大于0,分式的分母不为0联立不等式组求解.【解答】解:要使原函数有意义,则,得x>﹣1且x≠0.∴函数的定义域是:(﹣1,0)∪(0,+∞).故答案为:(﹣1,0)∪(0,+∞).3.cos24°cos36°﹣cos66°cos54°的值等于.【考点】两角和与差的余弦函数.【分析】利用互余两角的诱导公式,算出cos66°=sin24°、cos54°=sin36°.将此代入题中式子并利用两角和的余弦公式加以计算,可得所要求的值.【解答】解:∵24°+66°=90°,∴cos66°=sin24°,同理可得cos54°=sin36°.由此可得cos24°cos36°﹣cos66°cos54°=cos24°cos36°﹣sin24°sin36°=cos(24°+36°)=cos60°=.故答案为:4.已知向量、满足,它们的夹角为60°,那么=.【考点】平面向量数量积的运算.【分析】根据平面向量的数量积与模长公式,计算即可.【解答】解:向量、满足,它们的夹角为60°,∴=+2•+=12+2×1×2×cos60°+22=7∴=.故答案为:.5.若幂函数f(x)的图象过点,则f(x)=x﹣2.【考点】幂函数的概念、解析式、定义域、值域.【分析】设出幂函数的解析式,然后把点的坐标代入求出幂指数即可.【解答】解:设幂函数为y=xα,因为图象过点,则,所以,α=﹣2.所以f(x)=x﹣2.故答案为x﹣2.6.函数f(x)=1﹣2sin2x的最小正周期为π.【考点】三角函数的周期性及其求法;二倍角的余弦.【分析】先利用二倍角公式对函数解析式进行化简整理,进而利用三角函数最小正周期的公式求得函数的最小正周期.【解答】解:f(x)=1﹣2sin2x=cos2x∴函数最小正周期T==π故答案为:π.7.方程lgx+x=2的根x0∈(k,k+1),其中k∈Z,则k=1.【考点】对数函数的图象与性质.【分析】设f(x)=lgx+x﹣2,求出函数f(x)的定义域,并判断出函数的单调性,验证f(1)<0和f(2)>0,可确定函数f(x)在(0,+∞)上有一个零点,再转化为方程lgx+x=2的一个根x0∈(1,2),即可求出k的值.【解答】解:由题意设f(x)=lgx+x﹣2,则函数f(x)的定义域是(0,+∞),所以函数f(x)在(0,+∞)是单调增函数,因为f(1)=0+1﹣2=﹣1<0,f(2)=lg2+2﹣2=lg2>0,所以函数f(x)在(0,+∞)上有一个零点,即方程lgx+x=2的一个根x0∈(1,2),因为x0∈(k,k+1),k∈Z,所以k=1,故答案为:1.8.设定义域为R的偶函数f(x)满足:对任意的x1,x2∈(0,+∞),(x1﹣x2)[f(x1)﹣f(x2)]>0,则f(﹣π)>f(3.14).(填“>”、“<”或“=”)【考点】抽象函数及其应用.【分析】根据已知分析出函数的单调性,结合函数f(x)是定义域为R的偶函数,可得答案.【解答】解:∵函数f(x)满足:对任意的x1,x2∈(0,+∞),(x1﹣x2)[f(x1)﹣f(x2)]>0,∴函数f(x)在(0,+∞)上为增函数,又由函数f(x)是定义域为R的偶函数,故f(﹣π)=f(π)>f(3.14).故答案为:>.9.将函数y=sinx的图象上每个点的横坐标变为原来的倍(纵坐标不变),再将得到的图象向左平移个单位长度,所得图象的函数解析式为y=sin(2x+).【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.【解答】解:将函数y=sinx的图象上每个点的横坐标变为原来的倍(纵坐标不变),可得y=sin2x的图象;再将得到的图象向左平移个单位长度,可得y=sin2(x+)=sin(2x+)的图象,故答案为:y=sin(2x+).10.函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象如图所示,则φ=.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】通过函数的图象求出A,T然后求出ω,通过函数经过(3,0),求出φ的值.【解答】解:由题意可知A=3,T=8,所以ω==,因为函数经过(3,0),所以═3sin(),φ∈[0,2π),所以φ=.故答案为:.11.如图,在△ABC中,∠BAC=120°,AB=2,AC=1,D是边BC上一点,DC=2BD,则•= .【考点】平面向量数量积的运算.【分析】法一:选定基向量,将两向量,用基向量表示出来,再进行数量积运算,求出的值.法二:由余弦定理得可得分别求得,又夹角大小为∠ADB,,所以=.【解答】解:法一:选定基向量,,由图及题意得,=∴=()()=+==法二:由题意可得BC 2=AB 2+AC 2﹣2AB•ACcosA=4+1+2=7,∴BC=,∴cosB===AD==,∵,∴=.故答案为:﹣.12.已知角α、β的顶点在坐标原点,始边与x轴的正半轴重合,α、β∈(0,π),角β的终边与单位圆交点的横坐标是,角α+β的终边与单位圆交点的纵坐标是,则cosα=.【考点】任意角的三角函数的定义.【分析】根据角的范围及同角三角函数的基本关系求出sinβ,根据α+β 的范围及cos(α+β)的值求出sin (α+β)的值,利用两角差的余弦公式计算cosα=cos[(α+β)﹣β]的值.【解答】解:由题意得α、β∈(0,π),cosβ=﹣,∴sinβ=,故<β<π.∵sin(α+β)=,∴<α+β<π,∴cos(α+β)=﹣,∴cosα=cos[(α+β)﹣β]=cos(α+β)cosβ+sin(α+β)sinβ=,故答案为.13.若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f (cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是﹣3.【考点】二倍角的余弦;奇偶性与单调性的综合;复合三角函数的单调性.【分析】根据函数是奇函数且在R上是减函数,将原不等式变形为cos2x+2sinx ≥a恒成立,结合二倍角的三角函数公式和二次函数在闭区间上求最值的方法,即可得到a的最大值.【解答】解:不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,即f(cos2x+sinx)≤﹣f(sinx﹣a)恒成立又∵f(x)是奇函数,﹣f(sinx﹣a)=f(﹣sinx+a)∴不等式f(cos2x+sinx)≤f(﹣sinx+a)在R上恒成立∵函数f(x)在其定义域R上是减函数,∴cos2x+sinx≥﹣sinx+a,即cos2x+2sinx≥a∵cos2x=1﹣2sin2x,∴cos2x+2sinx=﹣2sin2x+2sinx+1,当sinx=﹣1时cos2x+2sinx有最小值﹣3.因此a≤﹣3,a的最大值是﹣3故答案为:﹣314.已知△ABC的边长为2的等边三角形,动点P满足,则的取值范围是[﹣,0] .【考点】平面向量数量积的运算.【分析】根据题意,画出图形,结合图形化简,得出=cos2θ•,O为BC的中点,P在线段OA上,再设||=t,t∈[0,],计算(+)•的最大最小值即可.【解答】解:如图所示,△ABC中,设BC的中点为O,则=2,∵=sin2θ•+cos2θ•=sin2θ•+cos2θ•=(1﹣cos2θ)•+cos2θ•=+cos2θ•(﹣),即﹣=cos2θ•(﹣),可得=cos2θ•,又∵cos2θ∈[0,1],∴P在线段OA上,由于BC边上的中线OA=2×sin60°=,因此(+)•=2•,设||=t,t∈[0,],可得(+)•=﹣2t(﹣t)=2t2﹣2t=2(t﹣)2﹣,∴当t=时,( +)•取得最小值为﹣;当t=0或时,( +)•取得最大值为0;∴的取值范围是[﹣,0].故答案为:[﹣,0].二、解答题:本大题共6小题,共90分,解答应写出文字说明、证明过程或演算步骤.15.已知(1)求tanθ的值;(2)求的值.【考点】同角三角函数基本关系的运用.【分析】(1)根据角的范围,利用二倍角的正切公式,求得tanθ的值.(2)利用二倍角的余弦公式、同角三角函数的基本关系,求得tanθ的值.【解答】解:(1)∵,∴,∵π<θ<2π,∴<θ<π,∴tanθ=﹣2.(2)=.16.已知向量,向量,向量满足.(1)若,且,求的值;(2)若与共线,求实数k的值.【考点】平面向量数量积的运算.【分析】(1)由已知求得及,再由且列式求得k值,进一步得到的坐标,代入向量模的公式求的值;(2)由已知可得,则,由与共线可得,由此求得k值.【解答】解:(1)∵,∴,又,∴,而,且,∴,得k=﹣,∴=,则||=;(2)由,得,∴,∵与共线,∴,解得:k=1.17.已知函数(1)求函数f(x)的单调增区间;(2)若,求cos2α的值.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(1)化简函数f(x)为正弦型函数,根据正弦函数的单调性写出它的单调增区间;(2)根据f(x)的解析式,结合α的取值范围,利用三角函数关系即可求出cos2α的值.【解答】解:(1)函数=sin2x+2•﹣=sin2x+cos2x+=sin(2x+)+,令﹣+2kπ≤2x+≤+2kπ,k∈Z,解得﹣+kπ≤x≤+kπ,k∈Z,∴函数f(x)的单调增区间为[kπ﹣,kπ+],k∈Z;(2)∵f(α)=sin(2α+)+=2,∴sin(2α+)=,又α∈[,],∴≤2α+≤,∴2α+=,∴2α=,∴cos2α=.18.某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.【考点】解三角形的实际应用;函数的值域;二次函数的性质.【分析】(1)当MN和AB之间的距离为1米时,MN应位于DC上方,且此时△EMN中MN边上的高为0.5米,从而可求MN的长,由三角形面积公式求面积(2)当MN在矩形区域内滑动,即时,由三角形面积公式建立面积模型.当MN在半圆形区域内滑动,即时,由三角形面积公式建立面积模型.(3)根据分段函数,分别求得每段上的最大值,最后取它们当中最大的,即为原函数的最大值,并明确取值的状态,从而得到实际问题的建设方案.【解答】解:(1)由题意,当MN和AB之间的距离为1米时,MN应位于DC上方,且此时△EMN中MN边上的高为0.5米,又因为EM=EN=1米,所以MN=米,所以,即三角通风窗EMN的通风面积为(2)当MN在矩形区域内滑动,即时,△EMN的面积;当MN在半圆形区域内滑动,即时,△EMN的面积综上可得;(3)当MN在矩形区域内滑动时,f(x)在区间上单调递减,则f(x)<f(0)=;当MN在半圆形区域内滑动,等号成立时,因此当(米)时,每个三角形得到最大通风面积为平方米.19.在平面直角坐标系中,O为坐标原点,已知向量=(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t),θ∈R.(1)若⊥,且,求向量;(2)若向量与向量共线,常数k>0,求f(θ)=tsinθ的值域.【考点】平面向量的坐标运算.【分析】(1)=(n﹣8,t),由⊥,且,可得﹣(n﹣8)+2t=0,=8,联立解出即可得出.(2)=(ksinθ﹣8,t),由向量与向量共线,常数k>0,可得t=﹣2ksinθ+16,f(θ)=tsinθ=﹣2ksin2θ+16sinθ=﹣2k+.对k分类讨论,利用三角函数的值域、二次函数的单调性即可得出.【解答】解:(1)=(n﹣8,t),∵⊥,且,∴﹣(n﹣8)+2t=0,=8,解得t=±8,t=8时,n=24;t=﹣8时,n=﹣8.∴向量=(24,8),(﹣8,﹣8).(2)=(ksinθ﹣8,t),(2)∵向量与向量共线,常数k>0,∴t=﹣2ksinθ+16,∴f(θ)=tsinθ=﹣2ksin2θ+16sinθ=﹣2k+.①k>4时,,∴sinθ=时,f(θ)=tsinθ取得最大值,sinθ=﹣1时,f(θ)=tsinθ取得最小值﹣2k﹣16,此时函数f(θ)的值域为.②4>k>0时,>1.∴sinθ=1时,f(θ)=tsinθ取得最大值﹣2k+16,sinθ=﹣1时,f(θ)=tsinθ取得最小值﹣2k﹣16,此时函数f(θ)的值域为[﹣2k﹣16,﹣2k+16].20.对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=a•f1(x)+b•f2(x),那么称h(x)为f1(x),f2(x)的生成函数.(1)给出函数,h(x)是否为f1(x),f2(x)的生成函数?并说明理由;(2)设,生成函数h(x).若不等式3h2(x)+2h(x)+t>0在x∈[2,4]上恒成立,求实数t的取值范围;(3)设,取a>0,b>0,生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1,x2且x1+x2=1.试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m 的值;如果不存在,请说明理由.【考点】函数恒成立问题.【分析】(1)根据新定义h(x)=a•f1(x)+b•f2(x),判断即可.(2)根据新定义生成函数h(x),化简,讨论其单调性,利用换元法转化为二次函数问题求解最值,解决恒成立的问题.(3)根据新定义生成函数h(x),利用基本不等式与生成函数h(x)图象的最低点坐标为(2,8).求解出ab.假设最大的常数m,使h(x1)h(x2)≥m恒成立,带入化简,利用换元法与基本不等式判断其最大值是否存在即可求解.【解答】解:(1)函数,若h(x)是af1(x)+bf2(x)的生成函数,则有:lgx=,由:,解得:,存在实数a,b满足题意.∴h(x)是f1(x),f2(x)的生成函数.(2)由题意,,生成函数h(x).则h(x)=2•f1(x)+f2(x)=∴h(x)是定义域内的增函数.若3h2(x)+2h(x)+t>0在x∈[2,4]上恒成立,即.设S=log2x,则S∈[1,2],那么有:y=﹣3S2﹣2S,其对称轴S=.∴﹣16≤y≤﹣5,故得t>﹣5.(3)由题意,得h(x)=a•f1(x)+b•f2(x)=ax,则h(x)=ax≥2∴,解得:a=2,b=8.∴h(x)=2x+,(x>0)假设最大的常数m,使h(x1)h(x2)≥m恒成立,令u=h(x1)h(x2)==∵x1+x2=1,∴u=,令t=x1x2,则t=x1x2≤,即,那么:u=4t,在上是单调递减,∴u≥u()=289.故最大的常数m=289.2017年3月9日。
江苏无锡市2016-2017高一数学上学期期末试题含答案

江苏无锡市2016-2017高一数学上学期期末试题(含答案)2016年秋学期无锡市普通高中期末考试试卷高一数学2017.01一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1.设全集集合,则.2.函数的最小正周期为.3.若函数则.4.在平面直角坐标系中,角终边上一点P的坐标为,则实数的值为.5.已知幂函数的图象过点,则.6.已知向量满足,且,则与的夹角为.7.若,则.8.函数的值域为.9.在中,E是边AC的中点,若,则为.10.将函数的图象先向左平移个单位,再将图象上各点的横坐标变为原来的倍(纵坐标不变),那么所得图象的解析式为.11.若函数的一个零点在区间内,另一个零点在区间内,则实数a的取值范围为.12.若,则.13.已知是定义在上的奇函数,当时,若函数在区间上的值域为,则实数t的取值范围为.14.若函数在区间上单调递减,则实数的取值范围为.二、填空题:本大题共4小题,每小题5分,共20分. 二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.已知向量(1)若与向量垂直,求实数的值;(2)若向量,且与向量平行,求实数的值.16.设,满足(1)求的值;(2)求的值.17.某机构通过对某企业2016年的生产经营情况的调查,得到每月利润y(单位:万元)与相应月份数x的部分数据如下表:14712229244241196(1)根据上表数据,请从下列三个函数中选取一个恰当的函数描述y与x的变化关系,并说明理由:;(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.20.已知函数(1)若,求的值;(2)若不等式对所有都成立,求实数m的取值范围.21.已知t为实数,函数,其中(1)若函数是偶函数,求实数的值;(2)当时,的图象始终在的图象的下方,求t的取值范围;(3)设,当时,函数的值域为,若的最小值为,求实数a的值.22.已知向量,函数(1)当时,求的值;(2)若的最小值为,求实数的值;(3)是否存在实数m,使函数有四个不同的零点?若存在,求出m的取值范围;若不存在,请说明理由.。
江苏省无锡市2016-2017学年高一(上)期末数学试卷(解析版)

2016-2017学年江苏省无锡市高一(上)期末数学试卷一、填空题:本大题共14小题,每小题5分,共70分).1.设全集U={0,1,2,3},集合A={1,2},B={2,3},则(∁U A)∪B=.2.函数的最小正周期为.3.若函数f(x)=,则f(f(﹣2))=.4.在平面直角坐标系xOy中,300°角终边上一点P的坐标为(1,m),则实数m的值为.5.已知幂函数y=f(x)的图象过点(,),则f()=.6.已知向量与满足||=2,||=3,且•=﹣3,则与的夹角为.7.已知sin(α+π)=﹣,则sin(2α+)=.8.函数y=log2(3cosx+1),x∈[﹣,]的值域为.9.在△ABC中,E是边AC的中点,=4,若=x+y,则x+y=.10.将函数y=sin(2x﹣)的图象先向左平移个单位,再将图象上各点的横坐标变为原来的倍(纵坐标不变),那么所得图象的解析式为y=.11.若函数f(x)=x2﹣ax+2a﹣4的一个零点在区间(﹣2,0)内,另一个零点在区间(1,3)内,则实数a的取值范围是.12.若=1,tan(α﹣β)=,则tanβ=.13.已知f(x)是定义在(﹣∞,+∞)上的奇函数,当x>0时,f(x)=4x﹣x2,若函数f(x)在区间[t,4]上的值域为[﹣4,4],则实数t的取值范围是.14.若函数f(x)=|sin(ωx+)|(ω>1)在区间[π,π]上单调递减,则实数ω的取值范围是.二、解答题:本大题共6小题,共90分.解答写出文字说明、证明过程或演算过程.15.已知向量=(﹣3,1),=(1,﹣2),=+k(k∈R).(1)若与向量2﹣垂直,求实数k的值;(2)若向量=(1,﹣1),且与向量k+平行,求实数k的值.16.设α∈(0,),满足sinα+cosα=.(1)求cos(α+)的值;(2)求cos(2α+π)的值.17.某机构通过对某企业2016年的生产经营情况的调查,得到每月利润y(单位:万元)与相应月份数x的部分数据如表:(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述y与x的变化关系,并说明理由,y=ax3+b,y=﹣x2+ax+b,y=a•b x.(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.18.已知函数f(x)=()x﹣2x.(1)若f(x)=,求x的值;(2)若不等式f(2m﹣mcosθ)+f(﹣1﹣cosθ)<f(0)对所有θ∈[0,]都成立,求实数m的取值范围.19.已知t为实数,函数f(x)=2log a(2x+t﹣2),g(x)=log a x,其中0<a<1.(1)若函数y=g(a x+1)﹣kx是偶函数,求实数k的值;(2)当x∈[1,4]时,f(x)的图象始终在g(x)的图象的下方,求t的取值范围;(3)设t=4,当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],若n﹣m的最小值为,求实数a的值.20.已知向量=(cos,sin),=(cos,﹣sin),函数f(x)=•﹣m|+|+1,x∈[﹣,],m∈R.(1)当m=0时,求f()的值;(2)若f(x)的最小值为﹣1,求实数m的值;(3)是否存在实数m,使函数g(x)=f(x)+m2,x∈[﹣,]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.2016-2017学年江苏省无锡市高一(上)期末数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分).1.设全集U={0,1,2,3},集合A={1,2},B={2,3},则(∁U A)∪B={0,2,3} .【考点】交、并、补集的混合运算.【分析】根据补集与并集的定义,写出运算结果即可.【解答】解:全集U={0,1,2,3},集合A={1,2},B={2,3},则∁U A={0,3},所以(∁U A)∪B={0,2,3}.故答案为:{0,2,3}.2.函数的最小正周期为π.【考点】三角函数的周期性及其求法.【分析】由函数解析式找出ω的值,代入周期公式T=即可求出函数的最小正周期.【解答】解:函数,∵ω=2,∴T==π.故答案为:π3.若函数f(x)=,则f(f(﹣2))=5.【考点】函数的值.【分析】先求出f(﹣2)=(﹣2)2﹣1=3,从而f(f(﹣2))=f(3),由此能求出结果.【解答】解:∵函数f(x)=,∴f(﹣2)=(﹣2)2﹣1=3,f(f(﹣2))=f(3)=3+2=5.故答案为:5.4.在平面直角坐标系xOy中,300°角终边上一点P的坐标为(1,m),则实数m的值为﹣.【考点】任意角的三角函数的定义.【分析】由条件利用任意角的三角函数的定义、诱导公式,可得tan300°=﹣=,从而求得m的值.【解答】解:在平面直角坐标系xOy中,∵300°角终边上一点P的坐标为(1,m),∴tan300°=tan=﹣tan60°=﹣=,∴m=﹣,故答案为:﹣.5.已知幂函数y=f(x)的图象过点(,),则f()=4.【考点】幂函数的概念、解析式、定义域、值域.【分析】在解答时可以先设出幂函数的解析式,由于过定点,从而可解得函数的解析式,故而获得问题的解答.【解答】解:∵幂函数y=f(x)=xα的图象过点(,),∴=,解得:α=﹣2,故f(x)=x﹣2,f()==4,故答案为:4.6.已知向量与满足||=2,||=3,且•=﹣3,则与的夹角为.【考点】平面向量数量积的运算.【分析】由条件利用两个向量的数量积的定义求得cosθ的值,可得与的夹角θ 的值.【解答】解:∵向量与满足||=2,||=3,且•=﹣3,设与的夹角为θ,则cosθ===﹣,∴θ=,故答案为:.7.已知sin(α+π)=﹣,则sin(2α+)=.【考点】两角和与差的正弦函数.【分析】根据诱导公式和二倍角公式计算即可.【解答】解:∵sin(α+π)=﹣,∴sinα=,∴sin(2α+)=cos2α=1﹣2sin2α=1﹣=,故答案为:.8.函数y=log2(3cosx+1),x∈[﹣,]的值域为[0,2] .【考点】对数函数的图象与性质.【分析】根据x∈[﹣,],得出1≤3cosx+1≤4,利用对数函数的性质,即可得出结论.【解答】解:∵x∈[﹣,],∴0≤cosx≤1,∴1≤3cosx+1≤4,∴0≤log2(3cosx+1)≤2,故答案为[0,2].9.在△ABC中,E是边AC的中点,=4,若=x+y,则x+y=﹣.【考点】平面向量的基本定理及其意义.【分析】由E是边AC的中点,=4,可得=,所以x=﹣,y=,x+y=﹣.【解答】解:∵E是边AC的中点,=4,∴=,所以x=﹣,y=,x+y=﹣.故答案为:﹣.10.将函数y=sin(2x﹣)的图象先向左平移个单位,再将图象上各点的横坐标变为原来的倍(纵坐标不变),那么所得图象的解析式为y=sin(4x+).【考点】函数y=Asin(ωx+φ)的图象变换.【分析】先求函数y=sin(2x﹣)的图象先向左平移,图象的函数表达式,再求图象上所有的点的横坐标变为原来的倍(纵坐标不变),则所得到的图象对应的函数解析式.【解答】解:将函数y=sin(2x﹣)的图象先向左平移,得到函数y=sin[2(x+)﹣]=sin(2x+)的图象,将所得图象上所有的点的横坐标变为原来的倍(纵坐标不变),则所得到的图象对应的函数解析式为:y=sin(4x+)故答案为:sin(4x+).11.若函数f(x)=x2﹣ax+2a﹣4的一个零点在区间(﹣2,0)内,另一个零点在区间(1,3)内,则实数a的取值范围是(0,2).【考点】一元二次方程的根的分布与系数的关系.【分析】由条件利用二次函数的性质可得,由此求得a的范围.【解答】解:∵函数f(x)=x2﹣ax+2a﹣4的一个零点在区间(﹣2,0)内,另一个零点在区间(1,3)内,∴,求得0<a<2,故答案为:(0,2).12.若=1,tan(α﹣β)=,则tanβ=.【考点】两角和与差的正切函数.【分析】由条件利用同角三角函数的基本关系求得tanα的值,再利用两角差的正切公式求得tanβ=tan[α﹣(α﹣β)]的值.【解答】解:∵═==,∴tanα=,又tan(α﹣β)=,则tanβ=tan[α﹣(α﹣β)]===,故答案为:.13.已知f(x)是定义在(﹣∞,+∞)上的奇函数,当x>0时,f(x)=4x﹣x2,若函数f(x)在区间[t,4]上的值域为[﹣4,4],则实数t的取值范围是[﹣2﹣2,﹣2] .【考点】函数奇偶性的性质.【分析】根据函数奇偶性的性质求出函数的解析式,利用数形结合以及一元二次函数的性质进行求解即可.【解答】解:如x<0,则﹣x>0,∵当x>0时,f(x)=4x﹣x2,∴当﹣x>0时,f(﹣x)=﹣4x+x2,∵函数f(x)是奇函数,∴f(0)=0,且f(﹣x)=﹣4x+x2=﹣f(x),则f(x)=4x+x2,x<0,则函数f(x)=,则当x>0,f(x)=4x﹣x2=﹣(x﹣2)2+4≤4,当x<0,f(x)=4x+x2=(x+2)2﹣4≥﹣4,当x<0时,由4x+x2=4,即x2+4x﹣4=0得x==﹣2﹣2,(正值舍掉),若函数f(x)在区间[t,4]上的值域为[﹣4,4],则﹣2﹣2≤t≤﹣2,即实数t的取值范围是[﹣2﹣2,﹣2],故答案为:[﹣2﹣2,﹣2]14.若函数f(x)=|sin(ωx+)|(ω>1)在区间[π,π]上单调递减,则实数ω的取值范围是[,] .【考点】正弦函数的图象.【分析】由题意求得ω≤2,区间[π,]内的x值满足kπ+≤ωx+≤kπ+π,k∈z,求得k+≤ω≤(k+),k∈z,再给k取值,进一步确定ω的范围.【解答】解:∵函数f(x)=|sin(ωx+)|(ω>0)在[π,π]上单调递减,∴T=≥,即ω≤2.∵ω>0,根据函数y=|sinx|的周期为π,减区间为[kπ+,kπ+π],k∈z,由题意可得区间[π,]内的x值满足kπ+≤ωx+≤kπ+π,k∈z,即ω•π+≥kπ+,且ω•+≤kπ+π,k∈z.解得k+≤ω≤(k+),k∈z.求得:当k=0时,≤ω≤,不符合题意;当k=1时,≤ω≤;当k=2时,≤ω≤,不符合题意.综上可得,≤ω≤,故答案为:[,].二、解答题:本大题共6小题,共90分.解答写出文字说明、证明过程或演算过程.15.已知向量=(﹣3,1),=(1,﹣2),=+k(k∈R).(1)若与向量2﹣垂直,求实数k的值;(2)若向量=(1,﹣1),且与向量k+平行,求实数k的值.【考点】平面向量共线(平行)的坐标表示;平面向量数量积的运算.【分析】(1)由与向量2﹣垂直,可得•(2﹣)=0,解得k.(2)利用向量共线定理即可得出.【解答】解:(1)=+k=(﹣3+k,1﹣2k),2﹣=(﹣7,4).∵与向量2﹣垂直,∴•(2﹣)=﹣7(﹣3+k)+4(1﹣2k)=0,解得k=.(2)k+=(k+1,﹣2k﹣1),∵与向量k+平行,∴(﹣2k﹣1)(﹣3+k)﹣(1﹣2k)(k+1)=0,解得k=.16.设α∈(0,),满足sinα+cosα=.(1)求cos(α+)的值;(2)求cos(2α+π)的值.【考点】三角函数的化简求值.【分析】(1)利用两角和的正弦公式求得sin(α+)的值,再利用同角三角函数的基本关系求得cos(α+)的值.(2)利用二倍角公式求得cos(2α+)的值,可得sin(2α+)的值,从而求得cos(2α+π)=cos[(2α+)+]的值.【解答】解:(1)∵α∈(0,),满足sinα+cosα==2sin(α+),∴sin(α+)=.∴cos(α+)==.(2)∵cos(2α+)=2﹣1=,sin(2α+)=2sin(α+)cos(α+)=2••=,∴cos(2α+π)=cos[(2α+)+]=cos(2α+)cos﹣sin(2α+)sin=﹣=.17.某机构通过对某企业2016年的生产经营情况的调查,得到每月利润y(单位:万元)与相应月份数x的部分数据如表:(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述y与x的变化关系,并说明理由,y=ax3+b,y=﹣x2+ax+b,y=a•b x.(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.【考点】函数模型的选择与应用.【分析】(1)由题意知,描述每月利润y(单位:万元)与相应月份数x的变化关系函数不可能是常数函数,也不是单调函数,排除另2个函数,选二次函数模型进行描述;(2)由二次函数的图象与性质,求出函数y=﹣x2+10x+220在x取何值时有最小值.【解答】解:(1)由题目中的数据知,描述每月利润y(单位:万元)与相应月份数x的变化关系函数不可能是常数函数,也不是单调函数;所以,应选取二次函数y=﹣x2+ax+b进行描述;(2)将(1,229),(4,244)代入y=﹣x2+ax+b,解得a=10,b=220,∴y=﹣x2+10x+220,1≤x≤12,x∈N,+y=﹣(x﹣5)2+245,∴x=5,y max=245万元.18.已知函数f(x)=()x﹣2x.(1)若f(x)=,求x的值;(2)若不等式f(2m﹣mcosθ)+f(﹣1﹣cosθ)<f(0)对所有θ∈[0,]都成立,求实数m的取值范围.【考点】函数恒成立问题;函数的值.【分析】(1)由f(x)=()x﹣2x=可求得2x=,从而可求得x的值;(2)由f(x)=()x﹣2x可判断f(x)为奇函数,且为减函数,不等式f(2m﹣mcosθ)+f(﹣1﹣cosθ)<f(0)⇔2m﹣mcosθ>1+cosθ对所有θ∈[0,]都成立,分离参数m,利用函数的单调性可求实数m的取值范围.【解答】解:(1)令t=2x>0,则﹣t=,解得t=﹣4(舍)或t=,…3分,即2x=,所以x=﹣2…6分(2)因为f(﹣x)=﹣2﹣x=2x﹣=﹣f(x),所以f(x)是定义在R上的奇函数,…7故f(0)=0,由f(2m﹣mcosθ)+f(﹣1﹣cosθ)<f(0)=0得:f(2m﹣mcosθ)<f(1+cosθ) (8)分,又f(x)=()x﹣2x在R上单调递减,…9分,所以2m﹣mcosθ>1+cosθ对所有θ∈[0,]都成立,…10分,所以m>,θ∈[0,],…12分,令μ=cosθ,θ∈[0,],则μ∈[0,1],y==﹣1+,μ∈[0,1]的最大值为2,所以m的取值范围是m>2 (16)分19.已知t为实数,函数f(x)=2log a(2x+t﹣2),g(x)=log a x,其中0<a<1.(1)若函数y=g(a x+1)﹣kx是偶函数,求实数k的值;(2)当x∈[1,4]时,f(x)的图象始终在g(x)的图象的下方,求t的取值范围;(3)设t=4,当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],若n﹣m的最小值为,求实数a的值.【考点】函数单调性的判断与证明;对数函数的图象与性质.【分析】(1)根据偶函数的定义可得k的值;(2)构造函数h(x)=f(x)﹣g(x),根据对数函数的图象和性质可得,只需要t>﹣2x++2恒成立,根据二次函数的性质求出t的取值范围即可;(3)先判断函数y=|f(x)|的单调性,令|2log a(2x+2)|=2,得到x=或,即可得到n﹣m的最小值为(﹣)﹣=,求出a即可.【解答】解:(1)∵函数y=g(a x+1)﹣kx是偶函数,∴log a(a﹣x+1)+kx=log a(a x+1)﹣kx,对任意x∈R恒成立,∴2kx=log a(a x+1)﹣log a(a﹣x+1)=log a()=x∴k=,(2)由题意设h (x )=f (x )﹣g (x )=2log a (2x +t ﹣2)﹣log a x <0在x ∈[1,4]恒成立,∴2log a (2x +t ﹣2)<log a x , ∵0<a <1,x ∈[1,4],∴只需要2x +t ﹣2>恒成立,即t >﹣2x ++2恒成立,∴t >(﹣2x ++2)max ,令y=﹣2x ++2=﹣2()2++2=﹣2(﹣)2+,x ∈[1,4],∴(﹣2x ++2)max =1,∴t 的取值范围是t >1, (3)∵t=4,0<a <1,∴函数y=|f (x )|=|2log a (2x +2)|在(﹣1,﹣)上单调递减,在(﹣,+∞)上单调递增,∵当x ∈[m ,n ]时,函数y=|f (x )|的值域为[0,2],且f (﹣)=0,∴﹣1<m ≤≤n (等号不同时取到),令|2log a (2x +2)|=2,得x=或,又[﹣(﹣)]﹣[(﹣)﹣]=>0,∴﹣(﹣)>(﹣)﹣,∴n ﹣m 的最小值为(﹣)﹣=,∴a=.20.已知向量=(cos ,sin),=(cos ,﹣sin ),函数f (x )=•﹣m |+|+1,x ∈[﹣,],m ∈R .(1)当m=0时,求f ()的值;(2)若f (x )的最小值为﹣1,求实数m 的值;(3)是否存在实数m,使函数g(x)=f(x)+m2,x∈[﹣,]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.【考点】函数零点的判定定理;三角函数中的恒等变换应用;正弦函数的图象.【分析】(1)利用向量数量积的公式化简函数f(x)即可.(2)求出函数f(x)的表达式,利用换元法结合一元二次函数的最值性质进行讨论求解即可.(3)由g(x)=0得到方程的根,利用三角函数的性质进行求解即可.【解答】解:(1)•=(cos,sin)•(cos,﹣sin)=cos cos﹣sinsin=cos(+)=cos2x,当m=0时,f(x)=•+1=cos2x+1,则f()=cos(2×)+1=cos+1=;(2)∵x∈[﹣,],∴|+|===2cosx,则f(x)=•﹣m|+|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,令t=cosx,则≤t≤1,则y=2t2﹣2mt,对称轴t=,①当<,即m<1时,当t=时,函数取得最小值此时最小值y=﹣m=﹣1,得m=(舍),②当≤≤1,即m<1时,当t=时,函数取得最小值此时最小值y=﹣=﹣1,得m=,③当>1,即m>2时,当t=1时,函数取得最小值此时最小值y=2﹣2m=﹣1,得m=(舍),综上若f(x)的最小值为﹣1,则实数m=.(3)令g(x)=2cos2x﹣2mcosx+m2=0,得cosx=或,∴方程cosx=或在x∈[﹣,]上有四个不同的实根,则,得,则≤m<,即实数m的取值范围是≤m<.2017年1月25日。
易错汇总江苏省无锡市高一上学期期末数学试卷和答案

故答案为:﹣ .
10.( 5.00 分)将函数 y=sin(2x﹣ )的图象先向左平移 个单位,再将图象 上各点的横坐标变为原来的 倍(纵坐标不变),那么所得图象的解析式为 y= sin ( 4x+ ) . 【分析】 先求函数 y=sin(2x﹣ )的图象先向左平移 ,图象的函数表达式, 再求图象上所有的点的横坐标变为原来的 倍(纵坐标不变) ,则所得到的图象 对应的函数解析式. 【解答】 解:将函数 y=sin(2x﹣ )的图象先向左平移 , 得到函数 y=sin[ 2(x+ )﹣ ] =sin( 2x+ )的图象, 将所得图象上所有的点的横坐标变为原来的 倍(纵坐标不变), 则所得到的图象对应的函数解析式为: y=sin( 4x+ ) 故答案为: sin( 4x+ ).
的最小正周期为
.
3.(5.00 分)若函数 f(x)=
,则 f (f (﹣ 2))=
.
4.( 5.00 分)在平面直角坐标系 xOy 中,300°角终边上一点 P 的坐标为 (1,m),
则实数 m 的值为
.
5.(5.00 分)已知幂函数 y=f(x)的图象过点( , ),则 f( )=
.
6.( 5.00 分)已知向量 与 满足 | | =2, | | =3,且 ? =﹣3,则 与 的夹角
=4,
故答案为: 4.
6.(5.00 分)已知向量 与 满足 | | =2,| | =3,且 ? =﹣3,则 与 的夹角为 .
【分析】 由条件利用两个向量的数量积的定义求得 cosθ的值,可得 与 的夹角 θ 的值. 【解答】 解:∵向量 与 满足 | | =2,| | =3,且 ? =﹣ 3,设 与 的夹角为 θ,
无锡市高一上学期苏教版数学期末试卷(附答案)

.
7. 已知 sin (α + π)
=
−
1
,则
sin
( 2α
+
π
) =
.
3
2
8. 函数
y
=
log2 (3 cos x + 1),x
∈
[ −
π 2
,
π 2
] 的值域为
.
9. 在 △ABC 中,E 是边 AC 的中点,−B−→C = 4−B−→D,若 −D−→E = x−A−→B + y−A→C,则 x + y =
π
] 都成立,求实数
m
的取值范围.
2
20. 已知向量
−→a
=
( cos
3x
, sin
3x
),−→b
[ −
π 3
,
π 4
] ,m
∈
R.
(1) 当 m = 0 时,求
2 f
(
π
)
2 的值;
=
( cos
x 2
, − sin
x
) ,函数
f
(x)
2
=
−→a
·
−→ b
−
m
−→a
+
−→ b
+ 1,x
∈
6
(2) 若 f (x) 的最小值为 −1,求实数 m 的值;
(2) 利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
19. 已知函数 f (x) = ( 1 )x − 2x.
2
(1) 若 f (x) = 15 ,求 x 的值;
(2) 若不等式 f
4 (2m − m cos θ) + f
2016-2017学年江苏省高一上学期期末考试数学试题word版含答案

2016-2017学年江苏省高一上学期期末考试数学试题第Ⅰ卷(共60分)一、填空题:本大题共14个小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题纸上.1.函数y =的定义域为 .2.函数cos 43y x π⎛⎫=+ ⎪⎝⎭的最小正周期为 . 3.已知函数()2,0,0x x f x x x ⎧>=⎨≤⎩ ,()()11f f +- .4.已知幂函数()y f x =的图象过点1,82⎛⎫⎪⎝⎭,则()2f = . 5.把函数sin y x =的图象向左平移6π个单位长度,所得到的图象的函数表达式为 . 6.1234log 9+= .7.函数sin cos y x x =+的单调递增区间为 . 8.若函数()sin y x πϕ=+过点1,16⎛⎫⎪⎝⎭,则()0f = .9.若,a b r r 的夹角为060,1a =r ,2b =r ,则a b +=r r . 10.在ABC ∆ 中,D 为边BC 上一点,且AD BC ⊥,若1AD =,2BD =,3CD =,则BAC ∠的度数为 .11.若1tan tan θθ+=,则sin 2θ= . 12.若锐角,αβ满足22cos cos 1αβ+=,则cos 2αβ+= . 13.若方程20x a a --=有四个不同的实根,则实数a 的取值范围为 .14.已知函数()31f x x x =++,若对任意的x ,都有()()22f x a f ax ++>,则实数a 的取值范围是 .二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15. 已知集合{}216x A x =≥,{}2log B x x a =≥ .(1)当1a =时,求A B I ;(2)若A 是B 的子集,求实数a 的取值范围.16.已知向量()1,2a x =-r ,()1,2b x =+r .(1)若//a b r r ,求x 的值;(2)当[]0,2x ∈时,求()a a b ⋅-r r r 的取值范围.17.如图,某儿童公园设计一个直角三角形游乐滑梯,AO 为滑道,OBA ∠为直角,20OB =米,设AOB rad θ∠=,一个小朋友从点A 沿滑道往下滑,记小朋友下滑的时间为t 秒,已知小朋友下滑的长度s 与2t 和sin θ的积成正比,当6πθ=时,小朋友下滑2秒时的长度恰好为10米.(1)求s 关于时间t 的函数的表达式;(2)请确定θ的值,使小朋友从点A 滑到O 所需的时间最短.18.已知函数()()cos 3sin cos f x x x x =+,x R ∈. (1)求函数()f x 的最大值;(2)若324f θ⎛⎫=⎪⎝⎭,R θ∈,求3f πθ⎛⎫+ ⎪⎝⎭的值.19.如图,在ABC ∆中,2BF FC =u u u r u u u r ,AM MF FN ==u u u u r u u u r u u u r .(1)用AB u u u r ,AC u u u r 表示AF u u u r ;(2)若AB AC ⊥u u u r u u u r ,2AB AC =u u u r u u u r ,求证:AN BC ⊥u u u r u u u r ;(3)若1BM BC MF ⋅==u u u u r u u u r u u u r ,求BA BN ⋅u u u r u u u r 的值.20.已知函数()22f x x x a =-+-,x R ∈. (1)若函数()f x 为偶函数,求实数a 的值;(2)当1x =-时,函数()f x 在取得最大值,求实数a 的取值范围.(3)若函数()f x 有三个零点,求实数a 的取值范围.2016-2017学年江苏省高一上学期期末考试数学试题答案一、填空题1.[)1,+∞2.2π 3.1 4.18 5.sin 6y x π⎛⎫=+ ⎪⎝⎭ 6. 4 7.()32,24k k k Z πππ⎡⎤-∈⎢⎥⎣⎦013513.()1,+∞ 14.04a <<二、解答题15.解:(1)当1a =时,由216x ≥得4x ≥,所以{}4A x x =≥,由2log 1x ≥得2x ≥,所以{}2A x x =≥, 所以{}4A B x x =≥I ;(2){}{}2log 2a B x x a x x =≥=≥,因为A 是B 的子集,所以24a ≤,所以实数a 的取值范围2a ≤.16.解:(1)因为//a b r r ,所以()()2112x x -+=⨯,解得0x =或1x =,(2)因为()1,2a x =-r ,()1,2b x =+r ,所以(),a b x x -=--r r ,所以()()()22392324a a b x x x x x x ⎛⎫⋅-=-+--=-=-- ⎪⎝⎭r r r ,因为[]0,2x ∈,所以()a a b ⋅-r r r 的取值范围9,04⎡⎤-⎢⎥⎣⎦.17.解:(1)由题意,设2sin ,0s kt t θ=>,2102sin 6k π∴=⨯ ,5k ∴= ,25sin ,0s t t θ∴=> ;(2)20cos OA θ=Q , 2205sin cos t θθ∴= ,t ∴== , ∴当4πθ=时,时间t 最短.18.解:(1)())21cos 2cos cos cos cos 22x f x x x x x x x x +=+=+=+ 1sin 262x π⎛⎫=++ ⎪⎝⎭ , ∴当()6x k k Z ππ=+∈时,()max 13122f x =+=; (2)324f θ⎛⎫= ⎪⎝⎭Q ,13sin 624πθ⎛⎫∴++= ⎪⎝⎭,即1sin 64πθ⎛⎫+= ⎪⎝⎭ , 25sin 2sin 212sin 36326f πππππθθθθ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=+=++=-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 2171248⎛⎫=-⨯= ⎪⎝⎭. 19.因为2BF FC =u u u r u u u r ,所以()2AF AB AC AF -=-u u u r u u u r u u u r u u u r , 所以1233AF AB AC =+u u u r u u u r u u u r , (2)因为AB AC ⊥u u u r u u u r ,所以0AB AC ⋅=u u u r u u u r ,即()()0AF FB AF FC +⋅+=u u u r u u u r u u u r u u u r ,即2220AF AF FC FC -⋅-=u u u r u u u r u u u r u u u r ,又因为AB =u u u r 所以()()222AF FB AF FC +=+u u u r u u u r u u u r u u u r ,即22280AF FC AF FC --⋅=u u u r u u u r u u u r u u u r . 所以0AF FC ⋅=u u u r u u u r ,所以AN BC ⊥u u u r u u u r ,(3)因为AM MF FN ==u u u u r u u u r u u u r ,所以2AM MN =u u u u r u u u u r ,即()2BM BA BN BM -=-u u u u r u u u r u u u r u u u u r ,因此2133BM BA BN =+u u u u r u u u r u u u r , 同理1233BF BA BN =+u u u r u u u r u u u r ,又2BF FC =u u u r u u u r ,所以31212332BC BA BN BA BN ⎛⎫=+=+ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r , 因为1BM BC ⋅=u u u u r u u u r ,所以2111332BA BN BA BN ⎛⎫⎛⎫+⋅+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r , 即()22256BA BN BA BN ++⋅=u u u r u u u r u u u r u u u r ① 又因为1MF =u u u r ,AM MF FN ==u u u u r u u u r u u u r ,所以3AN =u u u r ,所以()29BN BA -=u u u r u u u r ,即2229BN BA BN BA +-⋅=u u u r u u u r u u u r u u u r ② 由①②得43BA BN ⋅=-u u u r u u u r . 20.解:(1)任取x R ∈,则()()f x f x -=恒成立,即()2222x x a x x a --+--=-+-恒成立, x a x a ∴-=+恒成立,两边平方得:222222x ax a x ax a -+=++,0a ∴= ;(2)()2222,22,x x a x a f x x x a x a⎧-+-≥⎪=⎨--+<⎪⎩ ,因为函数()y f x =在1x =-时取得最大值, 当1a ≥时,必须()()1f f a -≥,即21222a a a a +≥-+-,即()210a +≥,所以1a ≥适合题意; 当11a -<<时,必须()()11f f -≥,即1212a a +≥-,即0a ≥,所以01a ≤<适合题意; 当1a ≤-时,因为()()11f f -<,不合题意,综上,实数a 的取值范围是[)0,+∞.(3)()2222,22,x x a x a f x x x a x a⎧-+-≥⎪=⎨--+<⎪⎩, ()()21241248a a ∆=---=- ,()()()22241248a a ∆=---=+, 当10∆=时,12a =,此时函数()22121,2121,2x x x f x x x x ⎧-+->⎪⎪=⎨⎪--+<⎪⎩ 有三个零点1,1-±当20∆=时,12a =-,此时函数()22121,2121,2x x x f x x x x ⎧-++≥-⎪⎪=⎨⎪---<-⎪⎩有三个零点1,1-± ; 当120,0∆>∆>时,即1122a -<<时,方程2220x x a -+-=的两根为1x =±, 方程2220x x a --+=的两根为1x =-,因为11a -<-<,所以1a ≥且1a -+≥,解得0a = ,或者1a <且1a -+<,此时无解, 综上得12a =±或0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的伸缩横杆(MN 和 AB、DC 不重合) . (1)当 MN 和 AB 之间的距离为 1 米时,求此时三角通风窗 EMN 的通风面积; (2)设 MN 与 AB 之间的距离为 x 米,试将三角通风窗 EMN 的通风面积 S(平 方米)表示成关于 x 的函数 S=f(x) ; (3)当 MN 与 AB 之间的距离为多少米时,三角通风窗 EMN 的通风面积最大? 并求出这个最大面积.
2016-2017 学年江苏省无锡市天一中学高一(上)期末数 学试卷
参考答案与试题解析
一、填空题:本大题共 14 小题,每小题 5 分,共 70 分.请把答案直接填写在 答题纸相应位置上. 1. (5 分)已知集合 A={0,1,2,3,4,5},B={﹣1,0,1,6},且 A∩B= 1} . 【解答】解:∵集合 A={0,1,2,3,4,5}, B={﹣1,0,1,6}, ∴A∩B={0,1}. 故答案为:{0,1}. {0,
19. (16 分)在平面直角坐标系中,O 为坐标原点,已知向量 =(﹣1,2) ,又 点 A(8,0) ,B(n,t) ,C(ksinθ,t) ,θ∈R. (1)若 ⊥ ,且 ,求向量 ;
(2)若向量
与向量 共线,常数 k>0,求 f(θ)=tsinθ 的值域.
20. (16 分)对于函数 f1(x) ,f2(x) ,h(x) ,如果存在实数 a,b 使得 h(x) =a•f1(x)+b•f2(x) ,那么称 h(x)为 f1(x) ,f2(x)的生成函数. (1 )给出函数 (x) ,f2(x)的生成函数?并说明理由; (2)设 ,生成函数 h(x) .若 , h ( x)是否为 f1
.
8. (5 分)设定义域为 R 的偶函数 f(x)满足:对任意的 x1,x2∈(0,+∞) , (x1 ﹣x2)[f(x1)﹣f(x2)]>0,则 f(﹣π) f(3.14) . (填“>”、“<”或“=”)
9. (5 分) 将函数 y=sinx 的图象上每个点的横坐标变为原来的 倍 (纵坐标不变) , 再将得到的图象向左平移 个单位长度,所得图象的函数解析式为 .
不等式 3h2(x)+2h(x)+t>0 在 x∈[2,4]上恒成立,求实数 t 的取值范围; (3)设 ,取 a>0,b>0,生成函数
h(x)图象的最低点坐标为(2,8) .若对于任意正实数 x1,x2 且 x1+x2=1.试问 是否存在最大的常数 m,使 h(x1)h(x2)≥m 恒成立?如果存在,求出这个 m 的值;如果不存在,请说明理由.
13. (5 分)若奇函数 f(x)在其定义域 R 上是减函数,且对任意的 x∈R,不等 式 f(cos2x+sinx)+f(sinx﹣a)≤0 恒成立,则 a 的最大值是 .
14 . ( 5 分 ) 已 知 △ ABC 的 边 长 为 2 的 等 边 三 角 形 , 动 点 P 满 足 ,则 的取值范围是 .
18. (16 分)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自 动通风设施.该设施的下部 ABCD 是矩形,其中 AB=2 米,BC=0.5 米.上部 CmD 是个半圆,固定点 E 为 CD 的中点.△EMN 是由电脑控制其形状变化的三角通风 窗(阴影部分均不通风) ,MN 是可以沿设施边框上下滑动且始终保持和 AB 平行
2. (5 分)函数
的定义域是
(﹣1,0)∪(0,+∞) ,得 x>﹣1 且 x≠0.
.
【解答】解:要使原函数有意义,则 ∴函数
的定义域是: (﹣1,0)∪(0,+∞) .
故答案为: (﹣1,0)∪(0,+∞) .
3. (5 分)cos24°cos36°﹣cos66°cos54°的值等于
.
【解答】解:∵24°+66°=90°,∴cos66°=sin24°,同理可得 cos54°=sin36°. 由此可得 cos24°cos36°﹣cos66°cos54°=cos24°cos36°﹣sin24°sin36°=cos(24°+36°) =cos60°= . 故答案为:
2016-2017 学年江苏省无锡市天一中学高一(上)期末数学试卷
一、填空题:本大题共 14 小题,每小题 5 分,共 70 分.请把答案直接填写在 答题纸相应位置上. 1. (5 分) 已知集合 A={0, 1, 2, 3, 4, 5}, B={﹣1, 0, 1, 6}, 且 A∩B= 2. (5 分)函数 的定义域是 . . ,它们的夹角为 60°,那么 .
4. (5 分)已知向量 、 满足
,它们的夹角为 60°,那么
=
. 【解答】解:向量 、 满足 ∴ = +2 • + ,它们的夹角为 60°,
3. (5 分)cos24°cos36°﹣cos66°cos54°的值等于 4. ( 5 分)已知向量 、 = . 满足
5. (5 分)若幂函数 f(x)的图象过点f(x)=1﹣2sin2x 的最小正周期为
7. (5 分)方程 lgx+x=2 的根 x0∈(k,k+1) ,其中 k∈Z,则 k=
二、解答题:本大题共 6 小题,共 90 分,解答应写出文字说明、证明过程或演 算步骤. 15. (14 分)已知 (1)求 tanθ 的值; (2)求 16. (14 分)已知向量 (1)若 (2)若 与 ,且 ,求 的值. ,向量 的值; ,向量 满足 .
共线,求实数 k 的值.
17. (14 分)已知函数 (1)求函数 f(x)的单调增区间; (2)若 ,求 cos2α 的值.
10. (5 分)函数 f(x)=Asin(ωx+φ) (A>0,ω>0,φ∈[0,2π) )的图象如图 所示,则 φ= .
11. (5 分)如图,在△ABC 中,∠BAC=120°,AB=2,AC=1,D 是边 BC 上一点,
DC=2BD,则
•
=
.
12. (5 分)已知角 α、β 的顶点在坐标原点,始边与 x 轴的正半轴重合,α、β ∈(0,π) ,角 β 的终边与单位圆交点的横坐标是 交点的纵坐标是 ,则 cosα= . ,角 α+β 的终边与单位圆
