(完整版)全等三角形竞赛试题精选及答案
全等三角形经典题型50题(含答案)
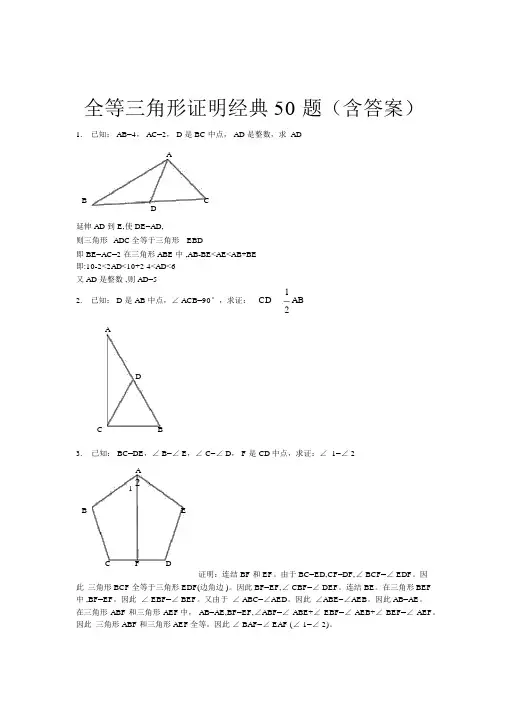
全等三角形证明经典50 题（含答案）1. 已知： AB=4， AC=2， D 是 BC 中点， AD 是整数，求ADAB CD延伸 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知： D 是 AB 中点，∠ ACB=90°，求证：CD AB2ADC B3.已知： BC=DE，∠ B=∠ E，∠ C=∠ D， F 是 CD中点，求证：∠ 1=∠ 2A21B EC F D证明：连结 BF 和 EF。
由于 BC=ED,CF=DF,∠ BCF=∠ EDF。
因此三角形 BCF 全等于三角形 EDF(边角边 )。
因此 BF=EF,∠ CBF=∠ DEF。
连结 BE。
在三角形BEF 中 ,BF=EF。
因此∠ EBF=∠ BEF。
又由于∠ ABC=∠AED。
因此∠ABE=∠AEB。
因此 AB=AE。
在三角形 ABF 和三角形 AEF中， AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
因此三角形 ABF 和三角形 AEF全等。
因此∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知：∠ 1=∠ 2， CD=DE， EF//AB，求证： EF=AC 1 2证明：过 E 点，作 EG//AC，交 AD 延伸线于 G 则∠ DEG=∠ DCA，F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE（AAS）∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知：AD均分∠ BAC，AC=AB+BD，求证：∠B=2∠C ACB D证明：在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB，连结（SASED∵ AD）均分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB，，DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知： AC 均分∠ BAD，CE⊥ AB，∠ B+∠ D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连结 CF 由于 CE⊥AB 因此∠CEB＝∠ CEF＝ 90 °由于 EB＝ EF， CE＝ CE，所以△CEB≌△CEF 所以∠B ＝∠ CFE 由于∠ B＋∠ D＝ 180 ，°∠CFE＋∠ CFA＝ 180°因此∠ D＝∠ CFA 由于AC 均分∠ BAD 因此∠ DAC＝∠ FAC 又由于AC＝ AC因此△ ADC≌ △ AFC（ SAS）因此 AD＝ AF 因此 AE＝ AF＋ FE＝ AD＋ BE12.如图，四边形 ABCD 中， AB∥ DC， BE、 CE 分别均分∠ ABC、∠ BCD，且点 E 在 AD 上。
全等三角形经典50题(含答案)
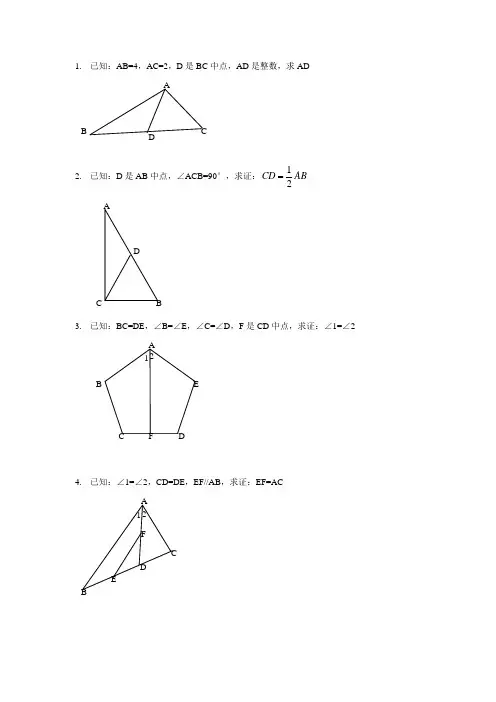
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=ACAD BC BACDF21E5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠ C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD8. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB AD BC A9.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。
∵BC=ED,CF=DF,∠BCF=∠EDF。
∴三角形BCF全等于三角形EDF(边角边)。
∴BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
∴ ∠EBF=∠BEF 。
又∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
10. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CG∠CGD ＝∠EFD又EF ∥AB∴∠EFD ＝∠1∠1=∠2∴∠CGD ＝∠2∴△AGC 为等腰三角形，AC ＝CG又 EF ＝CG∴EF ＝AC11. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CB ACDF21 E证明：延长AB 取点E ，使AE ＝AC ，连接DE∵AD 平分∠BAC∴∠EAD ＝∠CAD∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ）∴∠E ＝∠C∵AC ＝AB+BD∴AE ＝AB+BD∵AE ＝AB+BE∴BD ＝BE∴∠BDE ＝∠E∵∠ABC ＝∠E+∠BDE∴∠ABC ＝2∠E∴∠ABC ＝2∠C12. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC又∵AC ＝AC∴△ADC ≌△AFC （SAS ）CD B A∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
全等三角形经典题型50题(含答案)
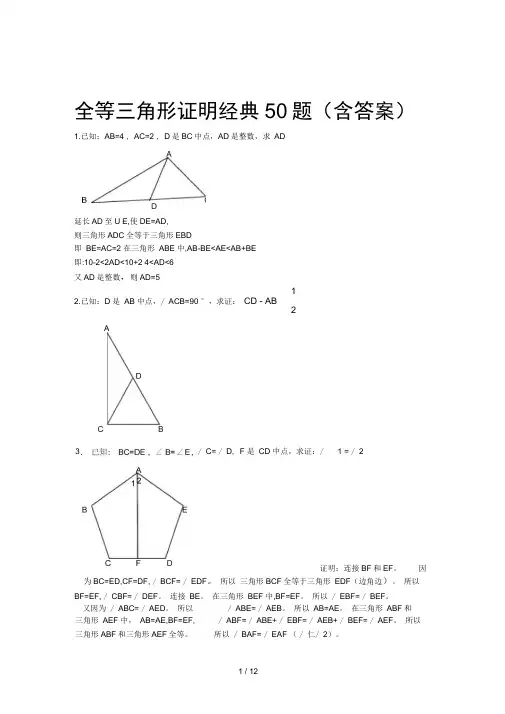
全等三角形证明经典50题（含答案）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数，则AD=512.已知：D 是 AB 中点，/ ACB=90 °，求证： CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF （边角边）。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点，求证：/ 1 = / 2证明：连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中， AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF （ / 仁/ 2）。
A3因为 EB = EF ,CE = CE ， 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图，四边形 ABCD 中，AB // DC ，BE 、CE 分别平分/ ABC 、/ BCD ，且点 E 在AD 上。
全等三角形经典题型50题(含答案)
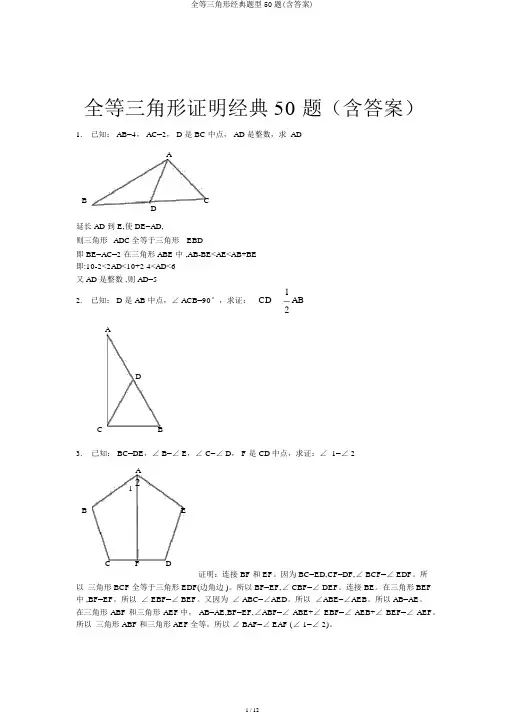
全等三角形证明经典50 题（含答案）1. 已知： AB=4， AC=2， D 是 BC 中点， AD 是整数，求ADAB CD延长 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知： D 是 AB 中点，∠ ACB=90°，求证：CD AB2ADC B3.已知： BC=DE，∠ B=∠ E，∠ C=∠ D， F 是 CD中点，求证：∠ 1=∠ 2A21B EC F D证明：连接 BF 和 EF。
因为 BC=ED,CF=DF,∠ BCF=∠ EDF。
所以三角形 BCF 全等于三角形 EDF(边角边 )。
所以 BF=EF,∠ CBF=∠ DEF。
连接 BE。
在三角形BEF 中 ,BF=EF。
所以∠ EBF=∠ BEF。
又因为∠ ABC=∠AED。
所以∠ABE=∠AEB。
所以 AB=AE。
在三角形 ABF 和三角形 AEF中， AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
所以三角形 ABF 和三角形 AEF全等。
所以∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知：∠ 1=∠ 2， CD=DE， EF//AB，求证： EF=AC 1 2证明：过 E 点，作 EG//AC，交 AD 延长线于 G 则∠ DEG=∠ DCA，F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE（AAS）∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知：AD平分∠ BAC，AC=AB+BD，求证：∠B=2∠C ACB D证明：在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB，连接（SASED∵ AD）平分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB，，DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知： AC 平分∠ BAD，CE⊥ AB，∠ B+∠ D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接 CF 因为 CE⊥AB 所以∠CEB＝∠ CEF＝ 90 °因为 EB＝ EF， CE＝ CE，所以△CEB≌△CEF 所以∠B ＝∠ CFE 因为∠ B＋∠ D＝ 180 ，°∠CFE＋∠ CFA＝ 180°所以∠ D＝∠ CFA 因为AC 平分∠ BAD 所以∠ DAC＝∠ FAC 又因为AC＝ AC所以△ ADC≌ △ AFC（ SAS）所以 AD＝ AF 所以 AE＝ AF＋ FE＝ AD＋ BE12.如图，四边形 ABCD 中， AB∥ DC， BE、 CE 分别平分∠ ABC、∠ BCD，且点 E 在 AD 上。
全等三角形测试题及答案
全等三角形测试题及答案一、选择题（每题5分，共20分）1. 若两个三角形的对应角相等，对应边成比例，则这两个三角形是：A. 相似三角形B. 全等三角形C. 等腰三角形D. 直角三角形答案：B2. 在全等三角形中，对应边的长度关系是：A. 不相等B. 相等C. 互为相反数D. 无法确定答案：B3. 以下哪个条件不能判定两个三角形全等？A. SSS（三边相等）B. SAS（两边及其夹角相等）C. ASA（两角及其夹边相等）D. SSA（两边及其中一边的对角相等）答案：D4. 如果两个三角形的两边和一角对应相等，且这角是两边的夹角，则这两个三角形：A. 一定全等B. 不一定全等C. 一定不全等D. 无法确定答案：A二、填空题（每题5分，共20分）1. 如果两个三角形的三边对应相等，根据______判定这两个三角形全等。
答案：SSS2. 两个三角形的两角和一边对应相等，根据______判定这两个三角形全等。
答案：ASA3. 如果两个三角形的两角和其中一角的对边对应相等，根据______判定这两个三角形全等。
答案：AAS4. 两个三角形的两边和其中一边的对角对应相等，根据______判定这两个三角形全等。
答案：HL（直角三角形的斜边和一条直角边对应相等）三、解答题（每题15分，共40分）1. 已知三角形ABC和三角形DEF，AB=DE=5cm，BC=EF=7cm，∠A=∠D=60°，求证：△ABC≌△DEF。
证明：在△ABC和△DEF中，AB=DE，BC=EF，∠A=∠D，∴由SAS判定，△ABC≌△DEF。
2. 若△ABC≌△DEF，且AB=DE，AC=DF，∠B=∠E，求证：BC=EF。
证明：由于△ABC≌△D EF，∴AB=DE，AC=DF，∠B=∠E，∴BC=EF（全等三角形的对应边相等）。
结束语：以上是全等三角形的测试题及答案，希望同学们通过这些题目能够更好地理解和掌握全等三角形的判定方法和性质。
八年级奥数全等三角形试题及答案
【导语】奥林匹克数学竞赛或数学奥林匹克竞赛，简称奥数。
奥数体现了数学与奥林匹克体育运动精神的共通性：更快、更⾼、更强。
国际数学奥林匹克作为⼀项国际性赛事，由国际数学教育专家命题，出题范围超出了所有国家的义务教育⽔平，难度⼤⼤超过⼤学⼊学考试。
下⾯是为⼤家带来的⼋年级奥数全等三⾓形试题及答案，欢迎⼤家阅读。
1．如图，∠D=∠C=90°，E是DC的中点，AE平分∠DAB，∠DEA=28°，则∠ABE的度数是（）A. 62°B. 31°C. 28°D. 25° 2．如图，△ABC中，∠C=90°，AD平分∠BAC，过点D作DE⊥AB于E，测得BC=9，BE=3，则△BDE的周长是 ( )A. 6B. 9C. 12D. 15 3．如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（）A. 30°B. 40°C. 20°D. 35° 4．如图，△ABC≌△BAD，A和B、C和D是对应顶点，如果AB＝5，BD＝6，AD＝4，那么BC等于（ ）A. 4B. 5C. 6D. ⽆法确定 5．如图，在和中，，若添加条件后使得≌，则在下列条件中，不能添加的是（）．A. ，B. ，C. ，D. ， 6．如图，某同学把⼀块三⾓形的玻璃打碎成了三块，现在要到玻璃店去配⼀块完全⼀样的玻璃，那么最省事的办法是（ ）A. 带①去B. 带②去C. 带③去D. 带①和②去 7．如图，在四边形ABCD中，M、N分别是CD、BC的中点，且AM⊥CD，AN⊥BC，已知∠MAN = 74°，∠DBC = 41°，则∠ADC的度数为（）．A. 49°B. 47°C. 45°D. 43° 8．如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是（ ）A. 30°B. 45°C. 60°D. 75° 9．如图，AD是△ABC中∠BAC的⾓平分线，DE⊥AB于点E，DF⊥AC于点F，S△ABC=7，DE=2，AB=4，则AC长是 ． 10．如图，已知OC平分∠AOB，CD//OB，若OD=3cm，则CD=___________cm. 11．如图，已知在△ABC中，CD是AB边上的⾼，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的⾯积等于_____． 12．如图，△ABC≌△DEF，已知∠A＝50°，∠B＝60°，则∠F＝____度. 13．如图，△ABC中，BA=BC，∠ABC=40°，∠ABC的平分线与BC的垂直平分线交于点O，E在BC边上，F在AC边上，将∠A沿直线EF翻折，使点A与点O恰好重合，则∠OEF的度数是_____． 14．如图，在△ABC中，AB=AC，BF=CD，BD=CE．若∠A=40°，则∠FDE=__________°． 15．如图，点C、D在BE上，BC=DE，∠1=∠2，要使得△ABD≌△AEC，还需要添加⼀个边或⾓的条件，你添加的条件是__________． 16．如图，直线l上有三个正⽅形a，b，c，若a，c的边长分别为5和12，则b的⾯积为_________________. 17．如图，在 ABC中，∠ABC=45°，AD,BE是 ABC的⾼，AD,BE相交于点F.求证：BF=AC． 18．⑴已知：如图1，等腰直⾓三⾓形ABC中，∠B=90°，AD是∠BAC的外⾓平分线，交CB边的延长线于点D．求证：BD=AB+AC ⑵对于任意三⾓形ABC，∠ABC=2∠C，AD是∠BAC的外⾓平分线，交CB边的延长线于点D，如图2，请你写出线段AC、AB、BD之间的数量关系并加以证明． 图1 图2 19．如图，校园有两条路OA、OB，在交叉⼝附近有两块宣传牌C、D，学校准备在这⾥安装⼀盏路灯，要求灯柱的位置P离两块宣传牌⼀样远，并且到两条路的距离也⼀样远，请你⽤尺规作出灯柱的位置点P。
全等三角形测试题及答案
全等三角形测试题及答案一、选择题（每题5分，共20分）1. 若两个三角形的对应角相等，则这两个三角形一定是全等三角形。
A. 正确B. 错误答案：B2. 根据SAS（边-角-边）公理，如果两个三角形的两边和夹角相等，则这两个三角形全等。
A. 正确B. 错误答案：A3. 已知三角形ABC和三角形DEF，若AB=DE，BC=EF，且∠A=∠D，则三角形ABC≌三角形DEF。
A. 正确B. 错误答案：A4. 如果两个三角形的对应边成比例，并且对应角相等，则这两个三角形全等。
A. 正确B. 错误答案：B二、填空题（每题5分，共20分）1. 根据AAS（角-角-边）公理，如果两个三角形的两个角和其中一个角的对边相等，则这两个三角形______。
答案：全等2. 在全等三角形中，对应边______。
答案：相等3. 如果两个三角形的三边对应相等，则这两个三角形______。
答案：全等4. 根据HL（斜边-直角边）公理，如果两个直角三角形的斜边和一条直角边相等，则这两个三角形______。
答案：全等三、解答题（每题15分，共40分）1. 已知三角形ABC和三角形DEF，AB=DE=5cm，BC=EF=7cm，∠A=∠D=90°，求证：三角形ABC≌三角形DEF。
证明：∵AB=DE，BC=EF，∠A=∠D∴根据HL公理，三角形ABC≌三角形DEF。
2. 已知三角形ABC和三角形DEF，∠A=∠D=60°，AC=DF=6cm，AB=3cm，DE=3cm，求证：三角形ABC≌三角形DEF。
证明：∵∠A=∠D，AC=DF∴∠B=∠E（等角的补角相等）∵AB=DE∴根据ASA（角-边-角）公理，三角形ABC≌三角形DEF。
四、证明题（每题20分，共20分）1. 已知三角形ABC和三角形DEF，AB=DE=5cm，∠B=∠E，∠A=∠D，求证：三角形ABC≌三角形DEF。
证明：∵∠A=∠D，∠B=∠E∴∠C=∠F（三角形内角和定理）∵AB=DE∴根据ASA公理，三角形ABC≌三角形DEF。
全等三角形测试题及答案
全等三角形测试题及答案一、选择题1. 下列选项中，哪两个三角形是全等的？A. ∠A=∠B，AB=BCB. ∠A=∠B，AC=BDC. ∠A=∠C，AB=ACD. ∠A=∠B，AB=BC，AC=BD2. 如果两个三角形的对应边成比例，且夹角相等，这两个三角形是：A. 相似但不全等B. 必然全等C. 不一定全等D. 无法判断二、填空题3. 根据全等三角形的性质，如果两个三角形的对应角相等，且对应边成比例，那么这两个三角形是_________。
4. SAS全等条件指的是_________。
三、判断题5. 如果两个三角形的三边对应相等，那么这两个三角形一定全等。
（）6. 根据HL全等条件，直角三角形中，如果斜边和一条直角边对应相等，那么这两个直角三角形全等。
（）四、解答题7. 已知三角形ABC和三角形DEF，其中∠A=∠D=90°，AB=DE，AC=DF，求证：三角形ABC全等于三角形DEF。
8. 如图所示，三角形ABC和三角形DEF在平面直角坐标系中，点A(2,3)，B(4,5)，C(1,1)，点D(-1,-2)，E(1,-1)，F(-2,-4)。
若AB=DE，AC=DF，∠BAC=∠EDF，请证明三角形ABC全等于三角形DEF。
五、综合题9. 在三角形ABC中，点D在BC上，若AD平分∠BAC，且BD=DC，求证：AB=AC。
10. 已知三角形ABC和三角形DEF，其中AB=DE，∠B=∠D，∠C=∠E，求证：三角形ABC全等于三角形DEF。
答案：一、选择题1. 答案：D2. 答案：A二、填空题3. 答案：相似4. 答案：边角边三、判断题5. 答案：正确6. 答案：正确四、解答题7. 解：由于∠A=∠D=90°，AB=DE，AC=DF，根据直角三角形的HL全等条件，我们可以得出三角形ABC全等于三角形DEF。
8. 解：由于AB=DE，AC=DF，∠BAC=∠EDF，根据SAS全等条件，我们可以得出三角形ABC全等于三角形DEF。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
八年级数学《全等三角形》竞赛试题精选
注: 此卷试题有一定难度,可能每题都不会轻松做下来,你需要提高能力,而且要学会思考难题,这样你才能在
考试中得心应手,一定要认真思考,并学会总结,把一类题型掌握透彻,望认真做.
一.选择题与填空题:
1. 如图，已知AB∥CD,AD∥BC，AC与BD交于O，AE⊥BD于E，CF⊥BD于F，那
么图中全等的三角形有【 】
A.5对 B.6对 C.7对 D.8对
2. 在△ABC和ABC中, ABAB,BB,补充件后仍不一定能保证
ABC
≌ABC,则补充的条件是【 】
A.BCBC B.AA C.ACAC
D.CC
3. 如图,在等边△ABC中,AD＝BE＝CF,D、E、F不是中点,连结AE、BF、CD,构成
一些三角形.如果三个全等的三角形组成一组,那么图中全等的三角形的组数
是【 】
A.3个 B.4个 C.5个 D.6个
4. 若在ABC中,∠ABC的平分线交AC于D,BC＝AB＋AD,∠C＝300，则∠B的度数
为【 】
A.450 B.600 C.750 D.900
5. 如图，AD是ΔABC的中线，E、F分别在AB、AC上且DE⊥DF，则（ ）
A．BE+CF＞EF B.BE+CF=EF
C．BE+CF＜EF D.EF与BE+CF大小关系无法确定
6. (黄冈市中考题)在△ABC和ABC中, ABAB,BB,补充条件后仍不一定能保证
ABC
≌ABC,则补充的条件是( )
A.BCBC B.AA C.ACAC D.CC
7. (2001,北京市初二竞赛题)下面四个命题:①两个三角形有两边及一角对应相等,则这两个三角形全等;②
两个三角形有两角及一边对应相等,则这两个三角形全等; ③两个三角形的三
条边分别对应相等,则这两个三角形全等;④ 两个三角形的三个角分别对应相
等,则这两个三角形全等.其中真命题是( )
A. ② ③ B. ① ③ C. ③ ④ D. ② ④
8. (第十五届江苏初二竞赛题)已知三角形的每条边长是整数,且小于等于4,这样的互
不全等的三角形有( )
A.10个 B.12个 C.13个 D.14
9. 如图,D是△ABC的边AB上一点,DF交AC于点E,给出3个论断:①DE＝FE;②AE
＝CE;③FC∥AB. 以其中一个论断为结论,其余两个论断为条件,可作出3个命
题.其中正确的命题个数是_______.
10. 如图,如果正方形ABCD中,CE＝MN,∠MCE＝350,那么∠ANM的度数是________.
11. 如图,在ABC中,过A点分别作AD⊥AB,AE⊥AC,且使AD＝AB,AE＝AC,BE和CD
相交于O,则∠DOE的度数是_____.
二.证明题:
1. 如图，在ΔABC中，∠BAC=90°，AB=AC，BE平分∠ABC，CE⊥BE。求证：BD=2CE
2. 已知：ΔABC为等边三角形，点D、E、F分别在AB、BC、CA上，且ΔDEF也是等边三角形，求证： Δ
O
F
E
D
C
BA
C'
B
'
A
'
F
EDCB
A
A
F
E
D
C
B
N
M
A
E
D
C
B
A
O
E
D
C
B
D
B
A
C
E
F
2
ADF,ΔCFE,ΔDBE三个三角形互相全等.
3. 如图, ABC与ABC中, AD,AD分别是高, ACAC,BCBC,ADAD,求证:
BB
.
4. 如图, ABC中,∠ACB＝900, A,以C为中心将ABC旋转角到∠A’B’C’的位置,(旋
转过程中保持ABC的形状大小不变)B恰好落在上A’B’,求旋转角 (用表示).
5. 如图,在ABC中,AB＝AC,直线l过A且l∥BC,∠B的平分线与AC和l分别交于D、E,∠C的平分
线与AB和l分别交于F、G.求证:DE＝FG
6. 如图,已知DO⊥AB,OA＝OD,OB＝OC,求∠OCE＋∠B的度数.
7. 如图，△ABC的两条高BD、CE相交于点P，且PD＝PE。求证：AC＝AB。
8. 如图，AC＝BC，∠ACB＝90°，∠A的平分线AD交BC于点D，过点B作BE⊥AD于点E。求证：BE＝21AD。
9. 如图2-2所示．△ABC是等腰三角形，D，E分别是腰AB及AC延长线上的一点，且BD=CE，连接DE交
底BC于G．求证：GD=GE．
(1)过D作DF∥AC，交BC于F．可用同样方法证明△GFD≌△GCE(图2-3)．
(2)过D作DF⊥BC于F；过E作EH⊥BC于BC延长线于H，可证明△GFD≌△GEH(图2-4)．
10. 如图2-5所示．在等边三角形ABC中，AE=CD，AD，BE交于P点，BQ⊥AD于Q．求证：BP=2PQ．
l
GDFECBA
O
D
E
C
BA
3
1
2
D
E
BCA
F
第8题图 第7题图 31221DEBPBACAFCED第5题图 第6题图
第1题图 ADCBD'C'B'A'B A D E C 第3题图 第4题图 B'A'CBA_ F_ E_ C _ D _ B_ A第2题图