知识点例题精讲 第2讲整式与因式分解
2022年中考数学总复习第一部分考点指导 第2节整式与因式分解

返回目录
续表
幂运算
①同底数幂的乘法:am·an = am+n (m,n 都是整数)
②幂的乘方:(am)n = amn (m,n 都是整数) ③积的乘方:(ab)m= ambm (m,n 都是整数) ④同底数幂的除法:am÷an = am-n (a ≠ 0,m,n 都是整数)
⑤负指数幂:a-p= ⑥零指数幂:a0=
返回目录
考点
近5年考情
1. 代数式 2. 整式 3. 因式分解
2021年 / 第4题 / 3分 2020年 / 第 11、12、14、18题 / 16分 2019年 / 第4、14题 / 7分 2018年 / 第12题 / 4分 2017年 / 第 8、11、15 题 /11分
中考专家解读:整式与因式分解为中考必考内容,属于一般性轮换考点,一般以计 算为主,考查形式灵活多样
返回目录
阅读理解:已知 x3 - 8有一个因式 x - 2,我们可以用如下 方法对 x3 - 8进行因式分解 . 解:设 x3 - 8 =(x - 2)(x2 + ax + b), 因为(x - 2)(x2 + ax + b)= x3 +(a - 2)x2+(b - 2a)x 2b,所以a - 2 = 0,且b - 2a = 0,且 -2b = -8, 所以 a = 2,且 b = 4,所以 x3 - 8 =(x - 2)(x2 + 2x + 4). 这种分解因式的方法叫做待定系数法 .
公式法 a2 ± 2ab + b2 = (a ± b)2 . *十字相乘法: x2 +(p + q)x + pq = (x + p)(x + q) .
第2讲 整式与因式分解

第2讲整式与因式分解1.下列代数式中,是整式的是( A )A.x+1B.1x+1C.√x2+1D.x+1x2.(2021河北)下列不一定相等的一组是( D )A.a+b与b+aB.3a与a+a+aC.a3与a·a·aD.3(a+b)与3a+b3.下列说法中,正确的是( C )A.m 2n4不是整式B.-3abc2的系数是-3,次数是1C.-3与a都是单项式D.多项式2x2y-xy是五次二项式4.对于①x-3xy=x(1-3y),②(x+3)(x-1)=x2+2x-3,从左到右的变形,表述正确的是( C )A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解5.(2022东营三模)下列运算正确的是( C )A.x2+x3=x5B.(x-y)2=x2-y2C.(x2)3=x6D.x6÷x3=x26.(2022聊城)下列运算正确的是( D )A.(-3xy)2=3x2y2B.3x2+4x2=7x4C.t(3t2-t+1)=3t3-t2+1D.(-a3)4÷(-a4)3=-17.(2021玉林)下列计算正确的是( D )A.a5+a5=a10B.-3(a-b)=-3a-3bC.(ab)-3=ab-3D.a6÷a2=a48.(2022重庆)把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形……按此规律排列下去,则第⑥个图案中菱形的个数为( C )A.15B.13C.11D.99.(2022赤峰)已知(x+2)(x-2)-2x=1,则2x2-4x+3的值为( A )A.13B.8C.-3D.510.(2022台州)一个垃圾填埋场,它在地面上的形状为长80 m,宽60 m 的矩形,有污水从该矩形的四周边界向外渗透了3 m,则该垃圾填埋场外围受污染土地的面积为( B )A.(840+6π)m2B.(840+9π)m2C.840 m2D.876 m211.若7a x b2与-a3b y的和为单项式,则y x= 8 .12.计算:(1)(-6x2)2+(-3x)3·x= 9x4;(2)(-5)16×0.2×(-2)15= -1015.13.(2022河口二模)因式分解:-3am2+12an2= -3a(m+2n)(m-2n) .14.(2022广安)已知a+b=1,则代数式a2-b2+2b+9的值为10 .15.(2021广安)若x,y满足{x-2y=-2,x+2y=3,则代数式x2-4y2的值为-6 .16.若多项式x y|m-n|+(n-2)x2y2+1是关于x,y的三次多项式,则mn的值为0或8 .17.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:-3x=x2-5x+1.(1)求所捂的二次三项式;(2)若x=√6+1,求所捂二次三项式的值.解:(1)设所捂的二次三项式为A,则A=x2-5x+1+3x=x2-2x+1.(2)若x=√6+1,则A=(x-1)2=(√6+1-1)2=6.18.分解因式:(1)(2021齐齐哈尔)-3xy3+12xy;(2)(2021河池模拟)(x-1)2+2(x-5).解:(1)原式=-3xy(y2-4)=-3xy(y+2)(y-2).(2)原式=x2-2x+1+2x-10=x2-9=(x+3)(x-3).19.(2022南充)先化简,再求值:(x+2)(3x-2)-2x(x+2),其中x=√3-1. 解:原式=(x+2)(3x-2-2x)=(x+2)(x-2)=x2-4.当x=√3-1时,原式=(√3-1)2-4=-2√3.)的值.20.(2022苏州)已知3x2-2x-3=0,求(x-1)2+x(x+23x解:原式=x2-2x+1+x2+23x+1.=2x2-43∵3x2-2x-3=0,x=1,∴x2-23x)+1∴原式=2(x2-23=2×1+1=3.21.按一定规律排列的单项式:a,-2a,4a,-8a,16a,-32a,…,第n个单项式是( A )A.(-2)n-1aB.(-2)n aC.2n-1aD.2n a22.已知3m=4,32m-4n=2.若9n=x(x>0),则x的值为( C )A.8B.4C.2√2D.√223.南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将其称为“杨辉三角”.(a+b)0=1(a+b)1=a+b(a+b)2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b3(a+b)4=a4+4a3b+6a2b2+4ab3+b4(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5…则(a+b)9展开式中所有项的系数和是( C )A.128B.256C.512D.1 02424.分解因式:(2a+b)2-(a+2b)2= 3(a+b)(a-b) .25.若x2+2(m-3)x+16是关于x的完全平方式,则m的值为-1或7 .26.(2022乐山)已知m2+n2+10=6m-2n,则m-n= 4 .27.(2020山西)如图所示是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形……按此规律摆下去,第n个图案有(3n+1) 个三角形.(用含n的代数式表示)28.(2022十堰)如图所示,某链条每节长为2.8 cm,每两节链条相连接部分重叠的圆的直径为1 cm,按这种连接方式,50节链条总长度为91 cm.1节2节50节29.(2022金华)如图①所示,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图②所示),得到大、小两个正方形.(1)用含a的代数式表示图②中小正方形的边长;(2)当a=3时,该小正方形的面积是多少?①②解:(1)∵直角三角形较短的直角边=1×2a=a,2较长的直角边=2a+3,∴小正方形的边长=2a+3-a=a+3.(2)小正方形的面积=(a+3)2.当a=3时,小正方形的面积=(3+3)2=36.30.(2022宁波)将两张全等的矩形纸片和另两张全等的正方形纸片按如图所示方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( C )A.正方形纸片的面积B.四边形EFGH的面积C.△BEF的面积D.△AEH的面积。
人教版2021中考数学总复习 第2讲 整式与因式分解

=12mn+10n
11. (2019·广州)分解因式: x2y+2xy+y=____y_(__x_+_1_)__2__________________. 12. (2019·深圳)分解因式: ab2-a=________a_(__b_+_1_)__(__b_-_1_)_____________. 13.(2020·广东)分解因式: xy-x=_________x_(_y_-__1_)____________________.
14.(2020·长春)长春市净月潭国家森林公园门票的价格为成
人票每张30元,儿童票每张15元.若购买m张成人票和n张儿童
票,则共需花费___(__3_0_m_+_12+2m=1,则4m2+8m-3的值是( D )
A.4
B.3
C.2
D.1
分层训练
变式诊断
9. (2019·深圳)下列运算正确的是( C )
A. a2+a2=a4
B. a3·a4=a12
C. (a3)4=a12
D. (ab)2=ab2
10.(2020·南通)计算:
(2m+3n)2-(2m+n)(2m-n).
解:原式=4m2+12mn+9n2-(4m2-n2)
=4m2+12mn+9n2-4m2+n2
续表 4. 因式分解的步骤(概括为“一提,二套,三检查”): (1)提公因式法:ma+mb+mc=m(a+b+c). (2)套公式:a2-b2=(a+b)(a-b),a2±2ab+b2=(a±b)2(乘法公式 的逆运算). (3)检查:分解因式要分解到每一个多项式都不能再分解为止.
浙江专版中考数学第一章数与式第2讲整式与因式分解精讲本课件

a(1±x%)
每天工作量为a,完成工作量m所需时间
商品单价为a元,共有m个,总价
am
两y个种,商总品费单用价分别为a,b,两种商品分别购买x,ax+by
商品单价a元,共有m元,购买n个,剩余金额 m-an
2.代数式求值的两种方法 (1)直接代入法:把已知字母的值代入代数式求值; (2)整体代入法:①观察已知条件和所求代数式的关系;②将所 求代数式变形成含有已知等式或部分项的形式,一般会用到提 公因式、平方差公式、完全平方公式;③把已知等式或部分项 之和看成一个整式代入所求代数式中求值.
1.(2021·温州)某地居民生活用水收费标准:每月用水量不
超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元
.该地区某用户上月用水量为20立方米,则应缴水费为( D)
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
2.(2021·杭州二模)已知a=1,则a2+4a+4=__9__.
A.a2
B.-a2
C.a4
D.-a4
9.(2021·衡阳)下列运算结果为 a6 的是( C )
A.a2·a3
B.a12÷a2
C.(a3)2
D.(12 a3)2
10.(2021·营口)下列计算正确的是( D )
A.2a+3b=5ab B.5a3b÷ab=5a2b C.(2a+b)2=4a2+b2 D.(-2a2b3)3=-8a6b9
11.(2021·常州)计算:2a2-(a2+2)= a2-2 .
12.(2021·宁波)计算:(1+a)(1-a)+(a+3)2. 解:原式=1-a2+a2+6a+9
=6a+10.
第2讲 整式与因式分解-2021年中考数学一轮复习知识考点习题课件(22张)
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为__7__.
上一页 下一页
20.(2020·常德)阅读理解:对于x3-(n2+1)x+n这类特殊的代数式,可以按下
面的方法分解因式.
解: x3-(n2+1)x+n
=x3-n2x-x+n
上一页 下一页
9.(2020·枣庄)图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线
(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那
样拼成一个正方形,则中间空余部分的面积是( C ) A.ab
B.(a+b)2
C.(a-b)2
D.a2-b2
上一页 下一页
10.(2020·新疆)分解因式:am2-an2=___a_(_m_+__n_)_·_(m__-__n_)_____. 11.(2020·哈尔滨)把多项式m2n+6mn+9n分解因式的结果是___n_(_m__+__3_)2___. 12.(2020·成都)已知a=7-3b,则代数式a2+6ab+9b2的值为___4_9____. 13(2020·衢州)定义a※b=a(b+1),例如:2※3=2×(3+1)=2×4=8,则(x
=x(x2-n2)-(x-n)
=x(x-n)(x+n)-(x-n)
=(x-n)(x2+nx-1).
上一页 下一页
理解运用:如果x3-(n2+1)x+n=0,那么(x-n)(x2+nx-1)=0,即有x-n =0或x2+nx-1=0.因此,方程x-n=0和x2+nx-1=0的所有解就是方程x3 -(n2+1)x+n=0的解.
第一章 数与式
第2讲 整式与因式分解
第2讲 整式及因式分解(精练)(解析版)

第2讲整式及因式分解(精练)(解析版)A基础训练B能力提升A基础训练一、单选题1.(2022•山东枣庄•中考真题)下列运算正确的是()A. 3屋一次=3 B. a3-ra2=a C. ( - 3ab2) 2= - 6a2h4 D. (a+h) 2=a2+ab+b2【答案】B【详解】A、3/-。
2=2〃2,故A错误,不符合题意;B、a3-ra2=ch故B正确,符合题意;C、( - 3ab2) 2 = 9612b4,故c错误,不符合题意;D、(6f+Z?) 2 = a2+2ah+h29故D不正确,不符合题意;故选:B.2.(2022•江苏泰州,中考真题)下列计算正确的是()A. 3ab + 2ab = 5ab B. 5y2 -2y2 = 3C. 7a + a = 7。
2D. /rTn — Imn2 = —mn2【答案】A【详解】解:A、3ab+lab - 5ab,故选项正确,符合题意;B、5/-2/=3/,故选项错误,不符合题意;C、Ja + a = Sa,故选项错误,不符合题意;D、和22不是同类项,不能合并,故选项错误,不符合题意;故选:A.3.(2022•广西河池・中考真题)多项式/一以+ 4因式分解的结果是()A. x (% - 4) +4 B. (x+2) (x- 2) C. (x+2) 2D. (%- 2) 2【答案】D【详解】解:d-4x+4 = (%-2)2.故选:D.4.(2022・湖南永州•中考真题)下列因式分解正确的是()A. 6+冲= i(x+y) + lB. 3Q +3Z?=3(Q+Z7)C. Q?+4Q +4=S+4『D. a2 -^b = a(a+b)【答案】B【详解】解:A、ax+ay=a(x+y),故选项计算错误;B、3a+3b=3(a+b)9选项计算正确;C> (a+b)2=a2^2ab+b2,故原选项错误;D、由A项解答可得a2-9b2=(a+3b)(a-3b),故原选项正确;故选D.2.(2022,江苏・顾山中学九年级阶段练习)直角三角形两直角边是方程%2一8%+ 14 = 0的两根,则它的斜边为()A. 8B. 7C. 6D. 2、/7【答案】C【详解】解:设直角三角形的斜边为J两直角边分别为〃与b,・・・直角三角形两直角边是方程8x + 14 = 0的两根,:,a + b = S,勿? = 14,根据勾股定理可得:=/+/=(〃 +与2—2^ = 64-28 = 36,• • c = 6 ♦故选:C.3.(2022・全国•七年级课时练习)若4 = /—2xy, 3 = J孙+ /,则A-23为()A. 3x2-2y2 -5xy^B. x2-2y2 -3xyC. —5xy — 2 y ~D . 3x~ + 2y~【答案】B【详解】解:A = £-2盯,8 = J孙+ y2,A — 2B = x~-2xy _ 2 _xy+y~] = x2 _2xy _ xy _ 2^~ =—2y——3xy ,故选:B.4.(2022 ・全国•八年级课时练习)对于多项式(1) d-y2;(2)-x2-y2; (3) 4x2-y ; (4)—4 + d中,能用平方差公式分解的是()A. (1) (2) B. (1) (3) C. (1) (4)D. (2) (4)【答案】C【详解】解:・・・平方差公式必须只有两项,并且是两个数平方差的形式,(1)—— y2两平方项符号相反,可以利用平方差公式;(2)-%2 - ,两平方项符号相同,不能运用平方差公式;(3)4/—y虽然是两项,并且是差的形式,但不是平方差的形式;(4)-4 + X2,两平方项符号相反,可以利用平方差公式.所以(1) (4)能用平方差公式分解.故选:C.5.(2022•辽宁•沈阳市南昌初级中学(沈阳市第二十三中学)八年级期中)小军是一位密码编译爱好者,在他的密码手册中,有这样一条信息:%-V, a—b, c , /_)/,《J工+了,分别对应下列六个字:抗,胜,必、,利,我,疫.现将y2户阳/_力因式分解,结果呈现的密码信息可能是() A.抗疫胜利B.抗疫必胜C.我必胜利D.我必抗疫【答案】B【详解】解:原式=(/一》2)(女—秘) = C(Q_〃)(X+・・・x-y, a-b,c, /_y2, 0 ,x+y,分别对应下列六个字:抗,胜,必,利,我,疫. 对应抗,x+y对应疫,。
整式与因式分解
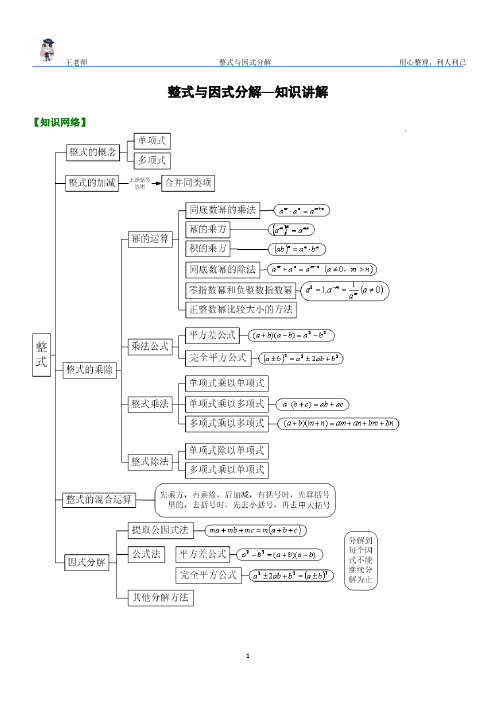
整式与因式分解—知识讲解【知识网络】【考点梳理】考点一、整式1.单项式数与字母的积的形式的代数式叫做单项式.单项式是代数式的一种特殊形式,它的特点是对字母来说只含有乘法的运算,不含有加减运算.在含有除法运算时,除数(分母)只能是一个具体的数,可以看成分数因数.单独一个数或一个字母也是单项式.要点诠释:(1)单项式的系数是指单项式中的数字因数.(2)单项式的次数是指单项式中所有字母的指数和.2.多项式几个单项式的代数和叫做多项式.也就是说,多项式是由单项式相加或相减组成的.要点诠释:(1)在多项式中,不含字母的项叫做常数项.(2)多项式中次数最高的项的次数,就是这个多项式的次数.(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.(4)把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.3.整式单项式和多项式统称整式.4.同类项所含字母相同,并且相同字母的指数也分别相同的项,叫做同类项.5.整式的加减整式的加减其实是去括号法则与合并同类项法则的综合运用.把多项式中的同类项合并成一项,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.整式加减的运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.6.整式的乘除①幂的运算性质:②单项式相乘:两个单项式相乘,把系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.③单项式与多项式相乘:单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加.用式子表达:④多项式与多项式相乘:一般地,多项式乘以多项式,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.用式子表达:平方差公式:完全平方公式:在运用乘法公式计算时,有时要在式子中添括号,添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.⑤单项式相除:两个单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.⑥多项式除以单项式:多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.要点诠释:(1)同底数幂是指底数相同的幂,底数可以是任意的有理数,也可以是单项式、多项式.(2)三个或三个以上同底数幂相乘时,也具有这一性质,即m n p m n p a a a a ++⋅⋅=(,,m n p 都是正整数).(3)公式()=m n mn a a 的推广:(())=m n p mnp a a (0≠a ,,,m n p 均为正整数)(4)公式()=⋅n n n ab a b 的推广:()=⋅⋅n n n n abc a b c (n 为正整数).考点二、因式分解1.因式分解把一个多项式化成几个整式的积的形式,这样的式子变形叫做把这个多项式因式分解.2.因式分解常用的方法(1)提取公因式法:)(c b a m mc mb ma ++=++(2)运用公式法:平方差公式:))((22b a b a b a -+=-;完全平方公式:222)(2b a b ab a ±=+±(3)十字相乘法:))(()(2b x a x ab x b a x ++=+++3.因式分解的一般步骤(1)如果多项式的各项有公因式,那么先提公因式;(2)提出公因式或无公因式可提,再考虑可否运用公式或十字相乘法;(3)对二次三项式,应先尝试用十字相乘法分解,不行的再用求根公式法;(4)最后考虑用分组分解法及添、拆项法.要点诠释:(1)因式分解的对象是多项式;(2)最终把多项式化成乘积形式;(3)结果要彻底,即分解到每个因式都不能再分解为止.(4)十字相乘法分解思路为“看两端,凑中间”,二次项系数a 一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.【典型例题】类型一、整式的有关概念及运算1.若3x m+5y 2与x 3y n 的和是单项式,则n m = .【答案】14【解析】由3x m+5y 2与x 3y n 的和是单项式得3x m+5y 2与x 3y n 是同类项,∴532m n +=⎧⎨=⎩ 解得22m n =-⎧⎨=⎩ , n m =2-2=14 【点评】本题考查同类项定义结合求解二元一次方程组,负整数指数幂的计算.同类项的概念为:所含字母相同,并且相同字母的指数也相同的单项式.举一反三:【变式】若单项式是同类项,则的值是( )A 、-3B 、-1C 、D 、3【答案】由题意单项式是同类项, 所以,解得 ,,应选C.2.下列各式中正确的是( )A.B.a 2·a 3=a 6C.(-3a 2)3=-9a 6D.a 5+a 3=a 8【答案】A ;【解析】选项B 为同底数幂乘法,底数不变,指数相加,a 2·a 3=a 5,所以B 错;选项C 为积的乘方,应把每个因式分别乘方,再把所得的幂相乘,(-3a 2)3=-27a 6,所以C 错;选项D 为两个单项式的和,此两项不是同类项,不能合并,所以D 错;选项A 为负指数幂运算,一个数的负指数幂等于它的正指数幂的倒数,A 正确.答案选A.【点评】考查整数指数幂运算.举一反三:【变式1】下列运算正确的是 ( )A .B .C .D .【答案】A.2-3 =18;2= ;C.235a a a = 正确 ;D.325a a a +=. 故选C.【变式2】下列运算中,计算结果正确的个数是( ).(1)a 4·a 3=a 12; (2)a 6÷a 3=a 2; (3)a 5+a 5=a 10;(4)(a 3)2=a 9; (5)(-ab 2)2=ab 4; (6) A .无 B .1个 C .2个 D .3个【答案】A.3.利用乘法公式计算:(1)(a+b+c)2 (2)(2a 2-3b 2+2)(2-2a 2+3b 2)【答案与解析】(1)(a+b+c)2可以利用完全平方公式,将a+b 看成一项,则(a+b+c)2=[(a+b)2+2(a+b)c+c 2]=a 2+2ab+b 2+2ac+2bc+c 2=a 2+b 2+c 2+2ab+2ac+2bc.(2)(2a 2-3b 2+2)(2-2a 2+3b 2)两个多项式中,每一项都只有符号的区别,所以,我们考虑用平方差公 式,将符号相同的看作公式中的a ,将符号相反的项,看成公式中的b ,原式=[2+(2a 2-3b 2)][2-(2a 2-3b 2)]=4-(2a 2-3b 2)2=4-4a 4+12a 2b 2-9b 4.【点评】利用乘法公式去计算时,要特别注意公式的形式及符号特点,灵活地进行各种变形. 举一反三:【变式】如果a 2+ma+9是一个完全平方式,那么m=______.【答案】利用完全平方公式:(a ±3)2=a 2±6a+9. m=±6.类型二、因式分解4.(2015春•兴化市校级期末)因式分解(1)9x 2﹣81(2)(x 2+y 2)2﹣4x 2y 2(3)3x (a ﹣b )﹣6y (b ﹣a )(4)6mn 2﹣9m 2n ﹣n 3.⋅=-22212x x【思路点拨】(1)如果多项式的各项有公因式,那么先提公因式;(2)提出公因式或无公因式可提,再考虑可否运用公式或十字相乘法;(3)对二次三项式,应先尝试用十字相乘法分解,不行的再用求根公式法;(4)最后考虑用分组分解法及添、拆项法.【答案与解析】解:(1)原式=9(x 2﹣9)=9(x+3)(x ﹣3);(2)原式=(x 2+y 2+2xy )(x 2+y 2﹣2xy )=(x+y )2(x ﹣y )2;(3)原式=3(a ﹣b )(x+2y );(4)原式=﹣n (9m 2+n 2﹣6mn )=﹣n (3m ﹣n )2.【点评】把一个多项式进行因式分解,首先要看多项式是否有公因式,有公因式就要先提取公因式,再看是否还可以继续进行分解,是否可以利用公式法进行分解,直到不能进行分解为止.举一反三:【变式】(2015春•陕西校级期末)分解因式:(1)(2x+y )2﹣(x+2y )2(2)﹣8a 2b+2a 3+8ab 2.【答案】解:(1)原式=[(2x+y )+(x+2y )][(2x+y )﹣(x+2y )]=3(x+y )(x ﹣y );(2)原式=2a (a 2﹣4ab+4b 2)=2a (a ﹣2b )2.5.若x y mx y 2256-++-能分解为两个一次因式的积,则m 的值为( )A. 1B. -1C. ±1D. 2【思路点拨】对二元二次多项式分解因式时,要先观察其二次项能否分解成两个一次式乘积,再通过待定系数法确定其系数,这是一种常用的方法.【答案】C.【解析】解:()()x y mx y x y x y mx y 225656-++-=+-++--6可分解成()-⨯23或()-⨯32,因此,存在两种情况:(1)x+y -2 (2)x+y -3x-y 3 x-y 2由(1)可得:m =1,由(2)可得:m =-1.故选择C.【总结升华】十字相乘法分解思路为“看两端,凑中间”,二次项系数a 一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.举一反三:【变式】因式分解:6752x x --=_______________.【答案】()()67521352x x x x --=+-类型三、因式分解与其他知识的综合运用6.已知a 、b 、c 是△ABC 的三边的长,且满足: a 2+2b 2+c 2-2b(a+c)=0,试判断此三角形的形状.【思路点拨】式子a 2+2b 2+c 2-2b(a+c)=0体现了三角形三边长关系,从形式上看与完全平方式相仿,把2b 2写成b 2+b 2,故等式可变成2个完全平方式,从而得到结论.【答案与解析】解: a 2+2b 2+c 2-2b(a+c)=0a 2+b 2+ b 2+c 2-2ba-2bc=0(a-b) 2+(b-c) 2=0即: a-b=0 , b-c=0,所以a=b=c.所以△ABC 是等边三角形.【总结升华】通过对式子变化,化为平方和等于零的形式,从而求出三边长的关系.整式与因式分解—巩固练习(基础)【巩固练习】一、选择题1.下列计算中错误的是( )A.()2532242a b c a bc ab ÷-=B.()()2322243216a b a b a ab -÷-=C.214)21(4222-=÷-⋅y x y y x D.3658410221)()(a a a a a a =÷÷÷÷ 2. 已知537x y 与一个多项式之积是736555289821x y x y x y +-,则这个多项式是( )A. 2243x y -B.2243x y xy -C.2224314x y xy -+D.223437x y xy -+ 3.把代数式分解因式,下列结果中正确的是( ) A . B .C .D . 4.(2015•佛山)若(x+2)(x ﹣1)=x 2+mx+n ,则m+n=( )A .1B .﹣2C .﹣1D .25. 如果,则b 为 ( )A .5B .-6C .-5D .66.把2222a b c bc --+进行分组,其结果正确的是( )A. 222()(2)a c b bc ---B. 222()2a b c bc --+C. 222()(2)a b c bc ---D. 222(2)a b bc c --+二、填空题7.已知2220x +=,则2x 的值为 .8.(1)已知10m =3,10n =2,210m n -__________.(2)已知23m =6,9n =8,643m n -___________.9.分解因式:()()()()26121311x x x x x ----+=_________________.10.(2015秋•乌海校级期中)在边长为a 的正方形中挖去一个边长为b 的小正方形(a >b )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证 (填写序号).①(a+b )2=a 2+2ab+b 2 ②(a ﹣b )2=a 2﹣2ab+b 2③a 2﹣b 2=(a+b )(a ﹣b ) ④(a+2b )(a ﹣b )=a 2+ab ﹣2b 2.11.多项式可分解为()()5x x b --,则a ,b 的值分别为_________.12.分解因式:=__ ______.三、解答题13.将下列各式分解因式:(1)22355x x +-; (2)25166x x ++; (3)22616x xy y --; (4).14.(2015春•故城县期末)(1)实验与观察:(用“>”、“=”或“<”填空)当x=﹣5时,代数式x 2﹣2x+2 1;当x=1时,代数式x 2﹣2x+2 1;…(2)归纳与证明:换几个数再试试,你发现了什么?请写出来并证明它是正确的;(3)拓展与应用:求代数式a 2+b 2﹣6a ﹣8b+30的最小值.15. 已知 21x x =+,求下列代数式的值:(1)553x x -+; (2)221x x+.16.若三角形的三边长是a b c 、、,且满足2222220a b c ab bc ++--=,试判断三角形的形状. 小明是这样做的:解:∵2222220a b c ab bc ++--=,∴2222(2)(2)0a ab b c bc b -++-+=.即()()220a b b c -+-=321a a a +--∵()()220,0a b b c -≥-≥,∴,a b b c a b c ====即.∴该三角形是等边三角形.仿照小明的解法解答问题:已知: a b c 、、为三角形的三条边,且2220a b c ab bc ac ++---=,试判断三角形的形状.中考总复习:整式与因式分解—巩固练习(提高)【巩固练习】一、选择题1. 若4821-能被60或70之间的两个整数所整除,这两个数应当是( )A .61,63B .63,65C .61,65D .63,672.乘积22221111111123910⎛⎫⎛⎫⎛⎫⎛⎫--⋅⋅⋅-- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭应等于( ) A .512 B .12 C .23D .1120 3.(2015•十堰模拟)已知x 2﹣x ﹣1=0,则x 3﹣2x+1的值为( )A .﹣1B .2C .﹣1D .﹣24.93191993+的个位数字是( )A .2B .4C .6D .85.若x 为任意实数时,二次三项式26x x c -+的值都不小于0,则常数c 满足的条件是( )A.0c ≥B. 9c ≥C. 0c >D. 9c >6.如图,从边长为(a+1)cm 的正方形纸片中剪去一个边长为(a ﹣1)cm 的正方形(a >1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )A .2cm 2B . 2acm 2C . 4acm 2D . (a 2﹣1)cm 2二、填空题7. 已知999999=P ,909911=Q ,那么P ,Q 的大小关系是 . 8.已知322,3m m a b ==,则()()()36322mm m m a b a b b +-⋅= . 9.若n 是正整数,且210n a =,则3222()8()n n a a --=__________.10. (1)如果1ab =,那()()22_________n n n n a b a b --+=.(2)已知200080,200025==y x ,则=+yx 11 . 11.对于任意的正整数n ,能整除代数式()()()()313133n n n n +---+的最小正整数是_______.12.(2015秋•巴中期中)图1可以用来解释:(2a )2=4a 2,则图2可以用来解释: .三、解答题13.(2014秋•静宁县校级期中)若关于x 的多项式﹣5x 3+(2m ﹣1)x 2+(3n ﹣2)x ﹣1不含二次项和一次项,求m ,n 的值.14.将下列各式分解因式:(1)21136x x -+; (2)251124a a --; (3)10722+-xy y x ; (4)()()342++-+b a b a .15. 若二次三项式()232350kx x k +-≠能被 27x +整除,试求k 的值.16.已知:()26,90,a b ab c a -=+-+=求a b c ++的值.整式与因式分解—巩固练习(基础解析)一、选择题1.【答案】D ;【解析】10485631()()22a a a a a a -÷÷÷÷=. 2.【答案】C ;【解析】这个多项式为()7365555322228982174314x y x y x y x y x y xy +-÷=-+.3.【答案】D ;【解析】运用提取公因式法和公式法因式分解.4.【答案】C ;【解析】∵原式=x 2+x ﹣2=x 2+mx+n ,∴m=1,n=﹣2.∴m+n=1﹣2=﹣1.故选:C . 5.【答案】B ;【解析】由题意5306b b =-=-,.6.【答案】D ;【解析】原式=()()222(2)a b bc c a b c a b c --+=+--+.二、填空题7.【答案】5;【解析】由2220x +=得22220x ⋅=.∴ 25x =.8.【答案】(1)29;(2)827; 【解析】(1)()2291010102m n m n -=÷=;(2)()()332642262733988m n m n -=÷==. 9.【答案】()22661x x -+;【解析】原式()()()()26112131x x x x x =----+⎡⎤⎡⎤⎣⎦⎣⎦()()222671651x x x x x =-+-++令2671x x u -+=,()22222u u x x u ux x ++=++()()222661u x x x =+=-+. 10.【答案】 ③;【解析】∵图甲中阴影部分的面积=a 2﹣b 2,图乙中阴影部分的面积=(a+b )(a ﹣b ), 而两个图形中阴影部分的面积相等,∴a 2﹣b 2=(a+b )(a ﹣b ).故可以验证③.故答案为:③.11.【答案】10,2a b =-=-;【解析】()()()2555x x b x b x b --=-++,所以53,2b b +==-,5,10a b a ==-.12.【答案】()()211a a +-;【解析】()()()()221111a a a a a =+-+=+-.三、解答题13.【答案与解析】(1)22355x x +-=()315x x ⎛⎫+- ⎪⎝⎭;(2)251116623x x x x ⎛⎫⎛⎫++=++ ⎪⎪⎝⎭⎝⎭.(3)()()2261682x xy y x y x y --=-+;(4)因为()()()25242292x x x -+-+=-+所以:原式()()225522x x =+-+-⎡⎤⎡⎤⎣⎦⎣⎦()()2158x x =-+14.【答案与解析】解:(1)把x=﹣5代入x 2﹣2x+2中得:25+10﹣2=33>1;把x=1代入x 2﹣2x+2中得:1﹣2+1=1,故答案为:>,=;(2)∵x 2﹣2x+2=x 2﹣2x+1+1=(x ﹣1)2+1,X 为任何实数时,(x ﹣1)2≥0,∴(x ﹣1)2+1≥1;321a a a +--(3)a 2+b 2﹣6a ﹣8b+30=(a ﹣3)2+(b ﹣4)2+5.∵(a ﹣3)2≥0,(b ﹣4)2≥0,∴(a ﹣3)2+(b ﹣4)2+5≥5,∴代数式a 2+b 2﹣6a ﹣8b+30的最小值是5.15.【答案与解析】(1)()()()2523343111x x x x x x x x x x =⋅=+⋅=+=+++()2231213153x x x x x =++=+++=+∴55353536x x x x -+=+-+=. (2)已知两边同除以x ,得111,1x x x x=+-=即 ∴22211()21x x x x-=+-= ∴2213x x+=.16.【答案与解析】∵2222222220a b c ab bc ac ++---=∴()()()2222222220a ab b b bc c a ac c -++-++-+=()()()2220a b b c a c -+-+-= ∴000a b b c a c -=⎧⎪-=⎨⎪-=⎩∴a b c ==,该三角形是等边三角形.整式与因式分解—巩固练习(提高解析)1.【答案】B ;【解析】()()()()()482424241212212121212121-=+-=++-()()()()()()24126624122121212121216563=+++-=++⨯⨯2.【答案】D ; 【解析】22221111111123910⎛⎫⎛⎫⎛⎫⎛⎫--⋅⋅⋅-- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭111111111111......11112233991010314253108119 (223344991010)1111121020⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+-+-+- ⎪⎪⎪⎪ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=⨯= 3.【答案】B ;【解析】∵x 2+x ﹣1=0,∴x 2+x=1,∴x 3﹣2x+1=x (x 2﹣x )+x 2﹣2x+1=x+x 2﹣2x+1=(x 2﹣x )+1=1+1=2.故选:B . 4.【答案】C ;【解析】93191993+的个位数字等于931993+的个位数字.∵93246469(9)9819=⋅=⋅;1944343(3)3(81)27=⋅=⋅.∴931993+的个位数字等于9+7的个位数字.则 93191993+的个位数字是6. 5.【答案】B ;【解析】()()22639x x c x c -+=-+-,由题意得,90c -≥,所以9c ≥.6.【答案】C ;二、填空题7.【答案】P =Q ;【解析】∵999990991199P Q ÷=÷()9909999990999911991191191911⨯=⨯⨯⨯==⨯∴ P =Q.8.【答案】-5;【解析】原式()()()()23223232m m m m a b a b =+-⋅ ∵∴ 原式=23222323+-⨯=-5.9.【答案】200; 【解析】()()32322222()8()81000800200n n n n a a a a --=-=-=.10.【答案】(1)-4;(2)1;【解析】(1)原式()()()22n n n n n n n n n n a b a b a b a b a b =-++---=⋅-()444n n n a b ab =-=-=-.(2)∵252000,802000,20002580x y ===⨯ ∴()()2525200025802580252000y y x xy y y y y ===⨯=⨯=⨯;252525200025x y x y y +⋅==⨯∴2525xy x y +=;∴xy x y =+,111x y x y xy++==. 11.【答案】10;【解析】利用平方差公式化简得10()21n -,故能被10整除.12.【答案】(a+b )2=a 2+2ab+b 2;【解析】如图2:整体来看:可看做是边长为(a+b )的正方形,面积为:(a+b )2;从部分看,可看作是有四个不同的长方形构成的图形,其中两个带阴影的长方形面积是相同的, 面积为:a 2+2ab+b 2;∴a 2+2ab+b 2=(a+b )2.故答案为:(a+b )2=a 2+2ab+b 2三、解答题13.【答案与解析】解:∵多项式﹣5x 3+(2m ﹣1)x 2+(3n ﹣2)x ﹣1不含二次项和一次项,∴2m﹣1=0,3n ﹣2=0,解得m=,n=,∴m=,n=.14.【答案与解析】(1)22111121366332x x x x x x ⎛⎫⎛⎫-+=+-=+- ⎪⎪⎝⎭⎝⎭; (2)2513112443a a a a ⎛⎫⎛⎫--=-+ ⎪⎪⎝⎭⎝⎭; (3)()()2271025x y xy xy xy -+=--;(4)()()()()24313a b a b a b a b +-++=+-+-.15.【答案与解析】 因为()232352752k kx x x x ⎛⎫+-=+- ⎪⎝⎭所以710322k -=,解得12k =.16.【答案与解析】∵6,a b -=∴6a b =+∵()290,ab c a +-+=∴()()2690,b b c a ++-+=∴()()2230,b c a ++-=∴3,b c a =-=∴()363,3a c =-+==∴()3333a b c ++=+-+=.。
第二讲、代数式—整式与因式分解复习讲义

一、知识点归纳 ★整式部分 (1)代数式的分类⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧无理式分式多项式单项式整式有理式代数式 (2)概念:①代数式: 用______把数与表示数的字母连接而成的式子叫___________.注:单独一个_____或一个_____也是代数式.②代数式的值: 用_____代替代数式的字母计算后所得的_____,叫代数式的________. ③整式: 分母中不含有________的_______式叫整式. ④同类项:条件是 _______________,_____________________.⑤单项式:是数与字母的______.注:★不含_____运算,★★单独的一个_____或____也是单项式.⑥多项式:是几个单项式的______. (3)运算:整式的加减:(实质是去括号,合并同类项)①合并同类项:把同类项的系数相加,所得结果作为系数,字母及字母的指数不变; ②去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里面各项都不变;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都变号.③添括号法则:括号前面是“+”号,括到括号里的各项都不变;括号前面是“-”号,括到括号里的各项都变号. 整式的乘除:①单项式相乘:把它们的系数、相同字母分别相乘;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.②单项式与多项式相乘:就是根据分配律用单项式乘以多项式的每一项,在把所得的积相加.mc mb ma c b a m ++=++)(.③多项式与多项式相乘:方法★bn bm an am n m b a +++=++))((方法★★乘法公式(用于多项式乘法的简便运算) 平方差公式:__________))((=-+b a b a ;完全平方公式:___________)(2=+b a ;___________)(2=-b a .④单项式相除:把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的因式.⑤多项式除以单项式:先把这个多项式的每一项除以这个单项式,再把所得的商相加. ⑥幂的运算性质(m 、n 为正整数)____=⋅n m a a ; ____=÷n m a a (0≠a ); _____)(=n m a ;____)(=n ab .10=a )0(≠a ,)0(1≠=-a aa n n . ★分解因式部分:(1)概念:把一个多项式化成几个整式的积的形式,这种式子变形叫做把这个多项式因式分解. (2)常用分解因式方法: ①提取公因式法:_____________=++mc mb ma .其分解步骤为:★确定多项式的公因式:公因式=各项系数的最大公约数与相同字母的最低次幂的积;★★将多项式除以它的公因式从而得到多项式的另一个因式. ②运用公式法:__________22=-b a ;__________222=+±b ab a .注意:★如果多项式中各项含有公因式,应该先提取公因式,再考虑运用公式法;★★公式中的字母,即可以表示一个数,也可以表示一个单项式或者一个多项式. ③分组分解法.多项式四项及以上的考虑用这种方法.(3)分解因式的一般步骤:一提二套三分组,二次三项想十字. 注:必须进行到每一个多项式因式都不能再分解为止. (4)整式乘法与分解因式的区别和联系:互为逆变形 .多项式整式的积因式分解方法 1. 提取公因式法:例:将2x 3n -20x 2n y 3+50x n y 6分解因式. 解:原式=2x n (x 2n -10x n y 3+25y 6) =2x n (x n -5y 3)2 2. 公式法:a 2-b 2=(a -b )(a +b ) a 2±2ab +b 2=(a ±b )2 a 3+b 3=(a +b )(a 2-ab +b )2 a 3-b 3=(a -b )(a 2+ab +b 2)例:64x 6-y 12解:原式=(8x 3+y 6)(8x 3-y 6)=(2x +y 2)(4x 2-2xy 2+y 4)(2x -y 2)(4x 2+2xy 2+y 4) 3. 分组分解法:例:(am +bn )2+(an -bm )2+c 2m 2+c 2n 2解:原式=a 2m 2+b 2n 2+2abmn +a 2n 2+b 2m 2-2abmn +c 2m 2+c 2n 2=a 2m 2+b 2n 2+a 2n 2+b 2m 2+c 2(m 2+n 2) =(m 2+n 2)(a 2+b 2+c 2) 4.十字相乘法:例:12x 2+10xy -12x +5y -9 解:原式=12x 2+(10y -12)x +5y -9 2x 16x 5y -9∴ 原式=(2x +1)(6x +5y -9) 5.配方法:例:将x 4+y 4+z 4-2x 2y 2-2x 2z 2-2y 2z 2分解因式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年中考数学一轮复习----知识点例题精讲第一章数与式第2讲整式与因式分解【思维框图】
【知识点归纳】
一、代数式
1、代数式:用运算符号把数或表示数的字母连结而成的式子,叫代数式。
单独一个数或者一个字母也是代数式。
2、代数式的值:用数值代替代数里的字母,计算后得到的结果叫做代数式的值。
3、代数式的分类:
⎪⎪⎩
⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧无理式分式
多项式单项式整式有理式代数式 二、整式的有关概念及运算
1、概念
(1)单项式:像x 、7、y x 2
2,这种数与字母的积叫做单项式。
单独一个数或字母也是单项式。
单项式的次数:一个单项式中,所有字母的指数叫做这个单项式的次数。
单项式的系数:单项式中的数字因数叫单项式的系数。
(2)多项式:几个单项式的和叫做多项式。
多项式的项:多项式中每一个单项式都叫多项式的项。
一个多项式含有几项,就叫几项式。
多项式的次数:多项式里,次数最高的项的次数,就是这个多项式的次数。
不含字母的项叫常数项。
升(降)幂排列:把一个多项式按某一个字母的指数从小(大)到大(小)的顺序排列起来,叫做把多项式按这个字母升(降)幂排列。
(3)同类项:所含字母相同,并且相同字母的指数也分别相同的项叫做同类项。
2、运算
(1)整式的加减:
合并同类项:把同类项的系数相加,所得结果作为系数,字母及字母的指数不变。
去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变;括号前面是“–”号,把括号和它前面的“–”号去掉,括号里的各项都变号。
添括号法则:括号前面是“+”号,括到括号里的各项都不变;括号前面是“–”号,括到括号里的各项都变号。
整式的加减实际上就是合并同类项,在运算时,如果遇到括号,先去括号,再合并同类项。
(2)整式的乘除:
幂的运算法则:其中m 、n 都是正整数
同底数幂相乘:n m n m a a a +=⋅;同底数幂相除:n m n m a a a -=÷;幂的乘方:mn n m a a =)(积的乘
方:n n n b a ab =)(。
单项式乘以单项式:用它们系数的积作为积的系数,对于相同的字母,用它们的指数的和作为这个字母的指数;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
单项式乘以多项式:就是用单项式去乘多项式的每一项,再把所得的积相加。
多项式乘以多项式:先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
单项除单项式:把系数,同底数幂分别相除,作为商的因式,对于只在被除式里含有字母,则连同它的指数作为商的一个因式。
多项式除以单项式:把这个多项式的每一项除以这个单项,再把所得的商相加。
乘法公式:
平方差公式:22))((b a b a b a -=-+; 完全平方公式:2222)(b ab a b a ++=+,2
222)(b ab a b a +-=-
三、因式分解
1、因式分解概念:把一个多项式化成几个整式的积的形式,叫因式分解。
2、常用的因式分解方法:
(1)提取公因式法:)(c b a m mc mb ma ++=++
(2)运用公式法:
平方差公式:))((22b a b a b a -+=-;完全平方公式:222)(2b a b ab a ±=+± (3)十字相乘法:))(()(2
b x a x ab x b a x ++=+++
(4)分组分解法:将多项式的项适当分组后能提公因式或运用公式分解。
(5)运用求根公式法:若)0(02
≠=++a c bx ax 的两个根是1x 、2x ,则有: ))((212x x x x a c bx ax --=++
3、因式分解的一般步骤:
(1)如果多项式的各项有公因式,那么先提公因式;
(2)提出公因式或无公因式可提,再考虑可否运用公式或十字相乘法;
(3)对二次三项式,应先尝试用十字相乘法分解,不行的再用求根公式法。
(4)最后考虑用分组分解法。
【例题精讲】
考点1 列代数式及求代数式的值
例:1.下列代数式符合规范书写要求的是( )
A .﹣1x
B .1xy
C .0.3÷x
D .﹣a
2.若m 2+2m =3,则4m 2+8m ﹣1的值是( ) A .11 B .8 C .7 D .12
针对训练:
1. 如图,大圆半径为R ,小圆半径为大圆半径的,则阴影部分的面积是( )
A .πR 2
B .πR 2
C .πR 2
D .πR 2 2. 若x 2﹣3x ﹣2=0,则2x 2﹣6x +2020的值为( )
A .2021
B .2022
C .2023
D .2024
3. 已知2y 2+3y =6,则4y 2+6y ﹣3= .
考点2 整式的有关概念
例:1.已知:,,0,4x+1中,其中单项式有()个.A.1B.2C.3D.4
2. 若﹣2a m+1b3与5a3b2n﹣3是同类项,则mn的值是()
A.6B.5C.﹣5D.﹣6
:
1.下列各式﹣mn,m,8,,x2+2x+6,,,中,整式有()
A.3个B.4个C.6个D.7个
2.下列说法中,不正确的是()
A.﹣ab2c的系数是﹣1,次数是4
B.﹣1是整式
C.6x2﹣3x+1的项是6x2、﹣3x,1
D.2πR+πR2是三次二项式
3.下列说法正确的是()
A.若|a|=﹣a,则a<0
B.如果,那么a=b
C.3xy7﹣4x3y+12是七次三项式
D.当a<0时,a3=﹣a3
考点3 整式的运算
例:若m2+mn=﹣7,n2﹣5mn=﹣17,则m2+6mn﹣n2=.
针对训练:1.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如﹣2x2﹣2x+1=﹣x2+5x﹣3:则所捂住的多项式是.
2.计算:
(﹣2x)3(﹣xy2)=,(﹣a5b7)÷a5b5=.
3.计算:
(1)(2x)3(﹣5xy2);(2)4(x+1)2﹣(2x+5)(2x﹣5).
考点4 整式的化简求值
例:1.如果a和1﹣4b互为相反数,那么多项式2(b﹣2a+10)+7(a﹣2b﹣3)的值是()A.﹣4B.﹣2C.2D.4
2.先化简,再求值:2(a3﹣2b2)﹣(a﹣2b)﹣(a﹣3b2+2a3),其中:a=﹣1,b=1.
针对训练:
1.已知5x2﹣x﹣1=0,代数式(3x+2)(3x﹣2)+x(x﹣2)的值为.
2.(1)先化简,再求值:
x(x+1)+x(x+2),其中x=1;
(2)计算:(2x+3y)2﹣(2x+y)(2x﹣y).
3.已知2x2﹣7x=7,求代数式(2x﹣3)2﹣(x﹣3)(2x+1)的值.
考点5 因式分解
分解因式:2ax2﹣12axy+18ay2=.
针对训练:
1.下列各式因式分解正确的是()
A.m2+n2=(m+n)(m﹣n)B.﹣2x﹣8=﹣2(x﹣4)
C.a2﹣a=a(a﹣1)D.a2+2a+1=a(a+2)+1
2.已知x+y=1,则=()
A.1B.C.2D.1或2 3.下列各式中,正确分解因式的个数为()
①x3+2xy+x=x(x2+2y)
②x2+2xy+4y2=(x+2y)2
③﹣2x2+8y2=﹣(2x+4y)(x﹣2y)
④a3﹣abc+a2b﹣a2c=a(a﹣c)(a+b)
⑤(m﹣n)(2x﹣5y﹣7z)+(m﹣n)(3y﹣10x+3z)=﹣(m﹣n)(8x+2y+4z)
A.1B.2C.3D.4。
