第1章 位错的定义及柏氏矢量
位错理论1-位错的结构

把位错环分成几段,而每一段有它自己不
同的柏氏矢量。
48
Conservation of Burgers vector
柏氏矢量守恒性的推论3
描述:位错线不可能中断于晶体内部
中断于:dis. Ring; dis. node; surface of crystal
证明:
设位错AB的柏氏矢量为b,其中断于B点 I区——已滑移区;II区——未滑移区 所以:未涉及的III区只能是两情况之一:
Байду номын сангаас刃型位错的基本特点:
位错线(dislocation line)是多余半原子 面和滑移面的交线,但位错线不一定就是 直线
直线 折线 位错环
19
Edge Dislocation
刃型位错的基本特点:
刃位错的点阵畸变相对于多余半原子面是左右对 称的
对于正刃位错:滑移面上部位错线周围原子受压, 向外偏离平衡;滑移面下部位错线周围原子受拉, 向内偏离平衡。
20
Edge Dislocation
刃型位错的基本特点:
位错线垂直于滑移矢量
b
21
目录
位错理论之序 滑移和位错 刃型位错 螺型位错 柏氏矢量及其守恒性 混合位错
22
Screw Dislocation
螺型位错的结构
ABCD面为滑移面:在 t作用下发生滑移 EF:位错线
第1章 位错的定义及柏氏矢量

即 c
Gb G 2a 2
因为原子间的斥力的短程性,能量曲线不是正弦形的,所以上面 的估计是过高的,c的更合理值约为G/30。理论切变强度和切变 模量相差约1个数量级。但是,实验测定的切变强度比理论切变 强度低2~4个数量级。 一些金属的理论强度与实验强度的比较
晶体
Ag Al Cu Ni Fe
理论强度(G/30)GPa 实验强度/MPa
2.64 2.37 4.10 6.70 7.10 0.37 0.78 0.49 3.2~7.35 27.5
理论强度 /实验强度
~7103 ~3103 ~8103 ~2103 ~3102
Mo
Nb Cd Mg (柱面滑移)
在弹性介质产生位错的沃特拉过程的示意图。位错线平行于z轴。 (a)和(b)是刃位错,产生位错的割面位移分别平行于y轴和x轴;(c) 是螺位错,产生位错的割面位移平行于z轴
在弹性介质产生向错的沃特拉过程的示意图。向错线平行于z轴。 (a)是楔型向错,产生向错的割面位移是绕平行z轴的轴转动角; (b)是扭型向错,产生向错的割面位移是绕平行x轴的轴转动角; (c)也是扭型向错,产生向错的割面位移是绕平行y轴的轴转动角
晶体变形的宏观现象: ①形变的晶体学性(即晶体在固定的晶面和晶向滑移); ②形变的不均匀性和不连续性,即变形不是在整个晶体各处发生; ③形变滑移的传播性,形变时,观察到滑移线(带)是从无到有, 由浅到深,由短到长(即),数目由少到多; ④滑移服从临界分切应力定律(以后会介绍,对于体心立方晶体, 会发生例外) ⑤温度对临界分切应力有显著的影响,等等。 设想的这种缺陷结构及特性必需和上述观察到的宏观变形现象相 符。
设想的缺陷引入晶体必需要: ①它的晶体学要素不依赖于加力的大小,而由晶体学本 身确定。由它运动导致的变形不破坏晶体结构,只是原 子间的相对运动。所以引入的缺陷不是完全无规而是有 晶体学特性的; ②它能解释变形的不均匀性,即能说明它的结构敏感性; ③它能说明变形过程的传播性; ④引入的这种缺陷是易动的,能解释实验强度比理论强 度低的原因。但它又不能像空位那样易受热起伏的影响; ⑤它应有合理的增殖机制。 现在已经知道,这种缺陷就是这里要讨论的位错。
2.位错类型及柏氏矢量
柏振海 baizhai@
中南大学材料科学与工程学院
材料科学与工程基础
位错类型,柏氏矢量
螺型位错分类
按照螺旋面前进的方向与螺旋面旋转方向的关系分
• 左螺型位错 • 右螺型位错
• 符合右手定则(右手拇指代表螺旋面前进方向,其它四指代表螺旋面旋 转方向)的称为右螺型位错,符合左手定则的称为左螺型位错
中南大学材料科学与工程学院
材料科学与工程基础
位错类型,柏氏矢量
位错的基本类型及特征
工程材料理论切变强度与实际强度相差100~1000倍
晶体中位错的基本类型 1.刃型位错 2.螺型位错 3.混合位错
柏振海 baizhai@
中南大学材料科学与工程学院
材料科学与工程基础
位错类型,柏氏矢量
含有刃型位错的晶体结构示意图
柏振海 baizhai@
中南大学材料科学与工程学院
材料科学与工程基础
位错类型,柏氏矢量
刃型位错线周围的弹性畸变
• 位错线长度有数百个到数万个原子间距,与位错长度相比, 位错宽度非常小,所以把位错看作是线缺陷 刃位错周围原子不同程度地偏离平衡位臵,使周围点阵发生 弹性畸变
中南大学材料科学与工程学院
材料科学与工程基础
位错类型,柏氏矢量
3.柏氏矢量特征
1)柏氏矢量与回路起点选择无关,也与柏氏回路的具体路径, 大小无关
一条位错线只有一个柏氏矢量 2)几根位错相遇于一点,其方 向朝着节点的各位错线的柏氏 矢量 b之和等于离开节点之和 如有几根位错线的方向均指 向或离开节点,这些位错 线的柏氏矢量之和值为零
中南大学材料科学与工程学院
材料科学与工程基础
位错类型,柏氏矢量
刃型位错特征
位错基本知识

Fc
f b2
; f 是空位的形成能。
产生攀移的力:①外加正应力; ②过饱和空位产生的力——渗透力(化学力)F0。
如攀移力靠外加正应力 提供,则,Fc
b
f b2
;
=
f b3
已知 f
1 5
b3,
代入上式:
=
f b3
1 。可知,刃型位错要整体向上攀移, 5
第一节 直线位错的应力场
直线位错的应力场
⑴螺型位错
柱面坐标表示:
z
z
G z
Gb
2r
rr r rz 0
直角坐标表示:
式中,G为切变模量,b为柏氏矢量,r为距位错中心的距离
螺型位错应力场的特点: (1)只有切应力分量,正应力分量全为零,这表明螺型位错不引起晶体的膨胀和收缩。 (2)螺型位错所产生的切应力分量只与r有关(成反比),且螺型位错的应力场是轴对称
②位错的应变能与b2成正比。因此,从能量的观点来看,晶体中具有最小b的 位错应该是最稳定的,而b大的位错有可能分解为b小的位错,以降低系统的能量。 由此也可理解为滑移方向总是沿着原子的密排方向的。
③螺位错的弹性应变能约为刃位错的2/3。 ④位错的能量是以单位长度的能量来定义的,故位错的能量还与位错线的形 状有关。由于两点间以直线为最短,所以直线位错的应变能小于弯曲位错的,即 更稳定,因此,位错线有尽量变直和缩短其长度的趋势。 ⑤位错的存在均会使体系的内能升高,虽然位错的存在也会引起晶体中熵值 的增加,但相对来说,熵值增加有限。可以忽略不计。因此,位错的存在使晶体 处于高能的不稳定状态,可见位错是热力学上不稳定的晶体缺陷。
的,并随着与位错距离的增大,应力值减小。
(3)这里当r→0时,τθz→∞,显然与实际情况不符,这说明上述结果不适用位错中心的
实际晶体中的位错

Frank分位错的特点: (a) 位于{111}晶面上,可以是直线、曲线和封闭环,但是无论
是什么形状,它总是刃型的。因为b=1/3<111>和{111}晶面 垂直。 (b) 由于b不是FCC的滑移方向,所以Frank分位错不能滑移, 只能攀移(只能通过扩散扩大或缩小)。不再是已滑移区和 未滑移区的边界,而且是有层错区和无层错区的边界。 注意与Shockley分位错的特点进行比较。
n
m
1、几何条件: ∑b' j = ∑bi
j =1
i =1
即,新位错的柏氏矢量 之和应等于反应前位错 的柏氏矢量之和。
∑ ∑ 2、能量条件:
n
m
b'2j < bi2
j =1
i =1
即,新位错的总能量应 小于反应前位错的总能 量。
前面讲过位错的弹性能Eel=αGb2
例如,FCC的全位错分解为Shockley分位错:b→b1+b2
αβ = αA + Aβ = 1 [1 1 1] + 1 [1 12] = 1 [1 1 0] = 1 BA
3
6
6
3
同理可得:
αγ
=
1 [0 1 1] =
1 CA
6
3
αδ = 1 [101] = 1 DA
6
3
希-希向量就是FCC中 压杆位错的柏氏矢量。
βγ = 1 [1 01] = 1 CB
6
3
FCC中的位错反应,即 位错的合成与分解也可
⎤2 ⎥⎦
=
1 2
∑n
反应后:
j =1
b'2j
=
b12
+
b22
晶体缺陷-位错概念

混合位错
位错线上任一点的滑移矢量相同,但两者方向夹角呈任意 角度。 图为混合位错的产生
位错环
位错线不能终止于晶体内部,具有封闭性
有纯的刃型位错环,无纯的螺型位错环
柏氏矢量
柏氏矢量是描述位错性质的一个重要物理量,1939年Burgers 提出,故称该矢量为“柏格斯矢量”或“柏氏矢量”,用b 表 示 柏氏矢量的确定(方法与步骤) 1)人为假定位错线方向,一般是从纸背向纸面或由上向下为位 错线正向 2)用右手螺旋法则来确定柏格斯回路的旋转方向,使位错线的 正向与右螺旋的正向一致 3)将含有位错的实际晶体和理想的完整晶体相比较 在实际晶体中作一柏氏回路,在完整晶体中按其相同的路线和 步伐作回路,自路线终点向起点的矢量,即“柏氏矢量”。
位错线运动的方向始终和位错线方向垂直,二者决定了滑移面,由食指和中指决定滑 移面,大拇指决定滑移面法向的正方向,该方向指向顺着位错的柏氏矢量方向滑移的 那部分晶体 中指指向位错运动方向
食指指向位错线的正方向
位错的运动方向由位错的本身性质决定!
左右螺旋位错
图为螺型位错形成模型
螺型位错
螺型位错---特征:
几何特征:位错线与原子滑移方向相平行;位错线周围原子的配置是螺旋状的。 分类:有左、右旋之分.符合左手、右手螺旋定则。 位错线的方向与滑移矢量一致:右手螺旋 位错线的方向与滑移矢量相反:左手螺旋
右手法则:
确定位错滑移 面两侧的两部 分晶体的具体 滑移方向
拇指指向顺着位错的柏氏 矢量方向滑移的那部分晶体
1)螺型位错无额外半原子面,原子错排呈轴对称 2)螺型位错与滑移矢量平行,故一定是直线 3)包含螺位错的面必然包含滑移矢量,故螺位错可以有 无穷个滑移面,但实际上滑移通常是在原子密排面上进 行,故有限 4)螺位错周围的点阵也发生了弹性畸变,但只有平行于 位错线的切应变,无正应变(在垂直于位错线的平面投 影上,看不出缺陷) 5)位错线的移动方向与晶块滑移方向互相垂直
2.位错类型及柏氏矢量
位τ
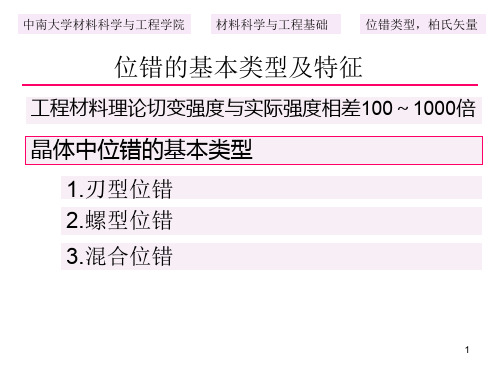
τ
受切应力作用原子面移动
7
中南大学材料科学与工程学院 材料科学与工程基础
位错类型,柏氏矢量
晶体局部滑移形成刃型位错
τ
τ
受切应力作用原子面移动
8
中南大学材料科学与工程学院 材料科学与工程基础
位错类型,柏氏矢量
晶体局部滑移形成刃型位错
τ
τ
出现多余半原子面,表面形成台阶
17
中南大学材料科学与工程学院 材料科学与工程基础
位错类型,柏氏矢量
Screw dislocation
18
中南大学材料科学与工程学院 材料科学与工程基础
螺型位错分类
位错类型,柏氏矢量
按照螺旋面前进的方向与螺旋面旋转方向的关系分
• 左螺型位错
• 右螺型位错
• 符合右手定则(右手拇指代表螺旋面前进方向,其它四指代表螺旋面旋 转方向)的称为右螺型位错,符合左手定则的称为左螺型位错
13
中南大学材料科学与工程学院 材料科学与工程基础
位错类型,柏氏矢量
螺型位错(Screw dislocation)
• 右侧晶体上下两部分发生晶格扭动 • 从俯视角度看,在滑移区上下两层原子发生了错动,晶体点阵畸变最严
重的区域内的两层原子平面变成螺旋面 • 畸变区的尺寸与长度相比小得多,在畸变区范围内称为螺型位错 • 已滑移区和未滑移区的交线BC则称之为螺型位错线
螺位错可以有无穷个滑移面 实际上滑移通常是在原子密排面上进行,故滑移面有限
4)螺位错周围的点阵也发生弹性畸变,但只有平行于位错 线的切应变,无正应变(在垂直于位错线的平面投影上, 看不出缺陷)
5)位错线的移动方向与晶块滑移方向、应力矢量互相垂直
20
hcp单位位错柏氏矢量

hcp单位位错柏氏矢量位错(Dislocation)是晶体中的一种缺陷,它是由晶体中原子或离子的位移引起的。
它可以被视为晶格错配的方式,因此会影响晶体的力学性能和变形行为。
位错对于晶体的变形起着关键的作用。
而柏氏矢量(Burgers vector)则是描述位错的重要参数之一。
本文将详细介绍位错的概念、柏氏矢量的定义,以及位错类型和位错模型等内容,旨在对读者对位错有一个全面的认识。
位错的概念位错是晶体中原子或离子的位移导致的晶体结构缺陷。
其概念最早由G. I. Taylor 在1934年引入。
当晶体中出现位错时,晶体结构就发生了错配,使得晶格的一部分位移相对于其他晶格部分。
由于位错所引起的晶格错配,晶格的形变能量也相应增加。
位错是晶体中原子运动的一种结果,它不仅影响晶体的力学行为,也影响晶体的物理、热学和电学性质等。
柏氏矢量的定义柏氏矢量是位错线的一种描述,它用来描述位错线所引起的晶格错配。
柏氏矢量通常用符号b表示,它是一个矢量,其方向平行于位错线的方向,其大小等于晶格间距乘以位错线密度。
柏氏矢量的大小与位错的类型有关,不同类型的位错具有不同的柏氏矢量。
位错类型根据位错线的性质,位错可以分为螺旋位错、边界位错和混合位错等几种类型。
1. 螺旋位错(Screw Dislocation):螺旋位错是一种具有线状结构的位错,其柏氏矢量沿位错线的方向,并且沿位错线方向是周期性的。
螺旋位错可以视为沿位错线旋转晶体结构一周所引起的错配。
2. 边界位错(Edge Dislocation):边界位错是一种具有线状结构的位错,其柏氏矢量垂直于位错线的方向,并且沿位错线方向是周期性的。
边界位错可以视为晶体结构的一部分被插入到另一部分中,导致晶体结构错位。
3. 混合位错(Mixed Dislocation):混合位错即同时具有边界位错和螺旋位错性质的位错。
混合位错的柏氏矢量既具有垂直于位错线方向的边界位错性质,也具有沿位错线方向的螺旋位错性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立方晶体中=90的几种假想的向错的示意图,其中图(a)是 +90楔型向错;图(b)是90楔型向错;图 (c)和(d)是90扭型 向错。
位错理论发展简史
1907年 Volterra解决了一类弹性体中的内应力不连续的弹性问题,
把它称为位错。 1934年 M.Polanyi,E.Orowan和G.1.Taylor差不多同时地独立提出有关 这类晶体缺陷(位错)的模型,特别是Taylor明确地把Volterra位 错引入晶体。 约菲用正交的尼科耳镜观察岩盐形变,看到岩盐形变时有亮线 从晶体一侧传播到另一侧,说明晶体形变滑移时局部地区有应 力集中,并说明滑移是从一侧传播到另一侧的。 Taylor注意到这种实验现象,根据设想的位错排列形状,计算了 位错运动所产生的晶体硬化曲线。 1939年 Burgers提出描述位错的一个重要特征量柏氏矢量,同时 引入了螺位错。 1940年 Peierls提出后来在1947年由Nabarro修正的位错点阵模型,它 突破了一般弹性力学范围,提出了位错宽度的概念,估算了位 错开动的应力,这一应力正是和实际晶体屈服应力的同一数量 级。
这一过程的原 子尺度的描述
理论切变强度的估算 假设能量曲线是正弦形式。 这样,要使原子面相对切开所需 要的切应力表达为
2x Csin b
在弹性变形范围,应力和应变服 从胡克定律:
G
式中G是切变模量,对于各向同 性弹性体,它等于拉梅系数, 是切应变。可以近似为x/a,a是2 个相对切动的面的面间距。上式 变成
位错的几何形态
刃型位错
刃位错的原子模型
产生刃位错的Volterra过程
半原子面在上侧,称正刃位错,“┻”;若半原子面在下侧,称负 刃位错,“┳”。
螺型位错
右螺位错的原子模型
产生右螺位错 的Volterra过程
右图的顶视投影图
柏氏回路及柏氏矢量
位错线在晶体中产生应力和应变场,从“制造”位错的Volterra 过程可知,割面的相对位移矢量b是位错的最根本特征,绕位错的 回路C的弹性位移u的线积分值应该等于b :
G x 2πx c a b
即 c
Gb G 2a 2
因为原子间的斥力的短程性,能量曲线不是正弦形的,所以上面 的估计是过高的,c的更合理值约为G/30。理论切变强度和切变 模量相差约1个数量级。但是,实验测定的切变强度比理论切变 强度低2~4个数量级。 一些金属的理论强度与实验强度的比较
两岸的相对位移D(r)一般能分解为一个平移分量b和一个转动 分量=wr,r是原点在割面上的矢径。如果D(r)只有平移分量, 则形成的位错称平移位错(Dislocation);如果D(r)只有旋转分量, 则形成的位错称旋转位错,简称为向错(Dislination)。 实在晶体并不是真正的连续介质,它存在各向异性及结构的 不连续,所以在Volterra过程中的D(r)不是任意的,只能根据晶体 的特点取有限的值。不论平移分量或旋转分量都必须符合晶体点 阵的对称性质。例如平移只能是晶体的点阵平移矢量,旋转角必 须是晶体的基转角。在以后我们会知道,由于能量的原因,真正 位错线的平移矢量也不可能是任意的点阵平移矢量,而是其中较 短的几个矢量。 对于向错,晶体的旋转对称性最多为六次对称,也就是说, 在晶体中产生向错最小的旋转角也要60,它会引起很大的畸变, 随着离开中心的距离加大畸变加大,所以旋错的能量很高,所以 在晶体中除了个别特殊情况,一般是不会出现向错。而在液晶中 向错却是常见的线缺陷。
b du
C
b称柏氏矢量。按照这样的概念,可以用简单的左图办法来定出位
错的柏氏矢量。其步骤如下∶ ①人为地规定位错线的正向,以表示位错线的切矢量; ②以位错线正向为轴环绕位错线在离开位错线附近的原子严重错 排的区域作右螺旋闭合回路,这回路称柏氏回路; ③用同样的方法在不含位错的完整晶体中作相同回路; ④比较这2个回路,绕位错线所作的回路是闭合的,而在完整晶体 中所作的相同回路是不闭合或是重叠的,从这个回路的终点向始 点连接所得的矢量,就是位错线的柏氏矢量b。
一个柏氏矢量b与位错线t夹角为的混位错,可以看成是柏氏矢量 为bsin的刃位错和柏氏矢量为bcos的螺位错的叠加。
b be bs
bs (b ) be [(b ) ]( )
其中 b
b
柏氏回路任意扩大、移动,只要在扩大和移动过程不和原位错 线或其它位错线相遇,由它确定的柏氏矢量也不会改变,这就是 柏氏矢量的守恒性。从这一点引伸,可以得到如下的重要概念: ①一根不分岔的位错线不论它的形状如何变化,它只有一个恒定 的柏氏矢量。 ②一根位错线不能终止在晶体内部,只能终止于晶体表面或晶界; 若它终止在晶体中部,它必和其他位错线相连接,相交于一个接 点,或者自成封闭的位错环。 ③汇聚在一点的各位错线,如果从汇聚点向外的方向定为正向, 则它们的柏氏矢量总和为零。
晶体
Ag Al Cu Ni Fe
理论强度(G/30)GPa 实验强度/MPa
2.64 2.37 4.10 6.70 7.10 0.37 0.78 0.49 3.2~7.35 27.5
理论强度 /实验强度
~7103 ~3103 ~8103 ~2103 ~3102
Mo
Nb Cd Mg (柱面滑移)
位错与向错的定义
单晶体滑移
滑移是指在外力作用下晶体沿某些特定的晶面和晶向相对滑 开的形变方式。
用扫描电镜观察到形变 钴单晶的表面形貌
用光学显微镜观察经7%形变的铝的 表面图象140
在变形时,如果晶体在滑移面两侧相对滑过,则在滑移面上所 有的键都要破断来产生永久的位移 。据此,可以估算滑移所需要的 临界分切应力。 这一过程的宏 观描述
bi
ui u u u d xk ( i d x1 i d x2 i d x3 ) xk x1 x2 x3 L L
如果以回路L为界作一曲面S,它把把位错终点P包含在曲面S内侧, 根据Stokes定理,对L的线积分可换成对S的面积分
早在知道有序介质材料中存在线缺陷之前,在20世纪初数学 家沃特拉(V.Volterra)就提出了线缺陷的概念和模型,他是研究 连续弹性介质中的一个半割面两侧变形后从新粘合后的数学奇异 性问题。“制造”沃特拉线缺陷的过程的步骤如下:
①在弹性体内割开一个以C为界的割面S。
②使割面两岸相对位移D(r)。在相对移动过程中两岸不发生歪曲 变形。 ③割面两侧位移后,如果产生空隙,在空隙中填满相同的物质; 如果产生重叠,把多余的物质去掉。 ④把割面的两岸重新粘合,并去 除操作过程所加的外力。 经这样的操作后就产生内应力场, 其内应力沿C环是不连续奇异性的, C环称为沃特拉线缺陷。
这个线缺陷的弹性性质显然取决于位错环C的位置以及产生位错 时割面两侧的相对位移D(r)。但是,无论割面两侧位移多大,周界 的应力是无限大的。为了避免周界这样的应力发散,一般沿周界 挖一个空心管道,这个非常小的空心管道区域就是介质中的线缺 陷。 线缺陷是晶体(有序介质)中原子(或分子)出现的严重错排 仅集中在线附近的小区域内,远离这条线只有弹性畸变,并且这 些畸变随着离开这条线的距离而急剧减小。可以把严重错排区域 用类似一个“管道”来描述,这个管道的直径通常仅有几个原子 间距,并贯穿于有序介质之中。在管道内,原子间的坐标与在完 整有序介质中很不同,而在管道之外的原子的坐标接近于完整有 序介质。这里的所谓管道“内部”和管道“外部”之间并无明确 界线,它们之间是逐渐过渡的,并且管道的截面也不一定是圆形。 管道“内部”这个定义不很精确的区域是线缺陷的核心 还要注意的是,“产生”线缺陷的沃特拉过程只是用以描述线 缺陷的奇异性本质,以及描述线缺陷的结构,而实际的线缺陷并 不是用沃特拉过程的方式产生的。
在弹性介质产生位错的沃特拉过程的示意图。位错线平行于z轴。 (a)和(b)是刃位错,产生位错的割面位移分别平行于y轴和x轴;(c) 是螺位错,产生位错的割面位移平行于z轴
在弹性介质产生向错的沃特拉过程的示意图。向错线平行于z轴。 (a)是楔型向错,产生向错的割面位移是绕平行z轴的轴转动角; (b)是扭型向错,产生向错的割面位移是绕平行x轴的轴转动角; (c)也是扭型向错,产生向错的割面位移是绕平行y轴的轴转动角
1947年 Cottrell阐明溶质原子和位错的交互作用并用以解释低碳纲的
屈服现象,第一次成功地利用位错理论解决金属机械性能的具体 问题。 同年 Shockley描绘了面心立方形成扩展位错的过程。 1950年 Frank和Read共同提出了位错的增殖机制。 上面所列出的是早期位错理论的发展的重要过程,到那时,对于 单个位错的运动规律,位错的交互作用等理论基本已经解决。 1953年Nye和1954年Bilby以及以后的krö 提出的无限小位错连续分 ner 布模型,为研究更复杂位错组态提供方法。 在解决任意形状的位错线的性质方面,由Burgers在1939年提出 的位移公式、Peach和krö 在1950年提出的应力场公式和位错受力 ner 公式及Blin在1955年提出的交互作用能公式等基本上能得到解决。 1956年 Menter直接在电镜观察了铂钛花青晶体中位错的存在,同年, Hirsch等应用相衬法在电镜观察到位错的运动,位错理论就在更坚 实的基础上发展了。 近几十年,随着实验设备和计算机的发展,研究位错核心的 组态以及在复杂结构中的位错方面取得很多很有成效的结果。
设想的缺陷引入晶体必需要: ①它的晶体学要素不依赖于加力的大小,而由晶体学本 身确定。由它运动导致的变形不破坏晶体结构,只是原 子间的相对运动。所以引入的缺陷不是完全无规而是有 晶体学特性的; ②它能解释变形的不均匀性,即能说明它的结构敏感性; ③它能说明变形过程的传播性; ④引入的这种缺陷是易动的,能解释实验强度比理论强 度低的原因。但它又不能像空位那样易受热起伏的影响; ⑤它应有合理的增殖机制。 现在已经知道,这种缺陷就是这里要讨论的位错。
