回溯法作业

算法设计与分析——批处理作业调度（回溯法）

算法设计与分析——批处理作业调度（回溯法）之前讲过⼀个相似的问题流⽔作业调度问题，那⼀道题最开始⽤动态规划，推到最后得到了⼀个Johnson法则，变成了⼀个排序问题，有兴趣的可以看⼀下本篇博客主要参考⾃⼀、问题描述给定n个作业的集合{J1,J2,…,Jn}。

每个作业必须先由机器1处理，然后由机器2处理。

作业Ji需要机器j的处理时间为t ji。

对于⼀个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。

所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。

批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度⽅案，使其完成时间和达到最⼩。

例：设n=3，考虑以下实例：看到这⾥可能会对这些完成时间和是怎么计算出来的会有疑问，这⾥我拿123和312的⽅案来说明⼀下。

对于调度⽅案（1,2,3）作业1在机器1上完成的时间是2，在机器2上完成的时间是3作业2在机器1上完成的时间是5，在机器2上完成的时间是6作业3在机器1上完成的时间是7，在机器2上完成的时间是10所以，作业调度的完成时间和= 3 + 6 + 10这⾥我们可以思考⼀下作业i在机器2上完成的时间应该怎么去求？作业i在机器1上完成的时间是连续的，所以是直接累加就可以。

但对于机器2就会产⽣两种情况，这两种情况其实就是上图的两种情况，对于（1,2,3）的调度⽅案，在求作业2在机器2上完成的时间时，由于作业2在机器1上还没有完成，这就需要先等待机器1处理完；⽽对于（3,1,2）的调度⽅案，在求作业2在机器2上完成的时间时，作业2在机器1早已完成，⽆需等待，直接在作业1被机器1处理之后就能接着被处理。

综上，我们可以得到如下表达式if(F2[i-1] > F1[i])F2[i] = F2[i-1] + t[2][i]elseF2[i] = F1[i] + t[2][i]⼆、算法设计类Flowshop的数据成员记录解空间的结点信息，M输⼊作业时间，bestf记录当前最⼩完成时间和，数组bestx记录相应的当前最佳作业调度。

第一章回溯法(习题三)

1.8 售货员的难题(salesman.pas)【问题描述】某乡有n个村庄（1<n<15），有一个售货员，他要到各个村庄去售货，各村庄之间的路程s（0<s<1000）是已知的，且A村到B村与B村到A村的路大多不同。

为了提高效率，他从商店出发到每个村庄一次，然后返回商店所在的村，假设商店所在的村庄为1，他不知道选择什么样的路线才能使所走的路程最短。

请你帮他选择一条最短的路。

【输入】村庄数n和各村之间的路程（均是整数）。

【输出】最短的路程。

【样例】salesman,in3 {村庄数}0 2 1 {村庄1到各村的路程}1 02 {村庄2到各村的路程}2 1 0 {村庄3到各村的路程}salesman.out31.9 驾车旅行(tour.pas)【问题描述】如今许多普通百姓家有了私家车，一些人喜爱自己驾车从一个城市到另一个城市旅游。

自己驾车旅游时总会碰到加油和吃饭的问题，在出发之前，驾车人总要想方设法得到从一个城市到另一个城市路线上的加油站的列表，列表中包括了所有加油站的位置及其每升的油价（如3.25元/L）。

驾车者一般都有以下的习惯：⑴除非汽车无法用油箱里的汽油达到下一个加油站或目的地，在油箱里还有不少于最大容量一半的汽油时，驾驶员从不在加油站停下来；(2)在每个停下的加油站总是将油箱加满；(3)在加油站加油的同时，买快餐等吃的东西花去20元。

(4)从起始城市出发时油箱总是满的。

(5)加油站付钱总是精确到0.1元（四舍五入）。

(6)驾车者都知道自己的汽车每升汽油能够行驶的里程数。

现在要你帮忙做的就是编写一个程序，计算出驾车从一个城市到另一个城市的旅游在加油和吃饭方面最少的费用。

【输入】第一行是一个实数，是从出发地到目的地的距离（单位：km）。

第二行是三个实数和一个整数，其中第一个实数是汽车油箱的最大容量（单位：L）；第二个实数是汽车每升油能行驶的公里数；第三个实数是汽车在出发地加满油箱时的费用（单位：元），一个整数是1到50间的数，表示从出发地到目的地线路上加油站的数目。

回溯法练习1

火柴游戏• 有红，绿，蓝三种颜色的火柴，所有火柴长度一样。

用它们可以组成一些数字，如下图所示：•• 为了让组成的火柴好看一些，我们规定：有公共点的火柴必须不同色。

例如，用红火柴4根和蓝火柴3根可以组成数12，21，7等。

而且有些方案虽然数字和它们的排列顺序都相同，但是有颜色之分。

问：一共可以组成多少个数（可以包含多个数字，但至少包含一个数字）？同一个数用不同颜色表示算作不同的数，火柴可以有剩余。

• 输入• 三个整数n1， n2， n3 (0 ≤ n1，n2，n3 ≤ 15)，即三种颜色的火柴的数目。

• 输出• 仅一个数，即可以组成的数的数目。

结果保证不超过1016。

骑士游历问题设有一个n*m 的棋盘(2≤n ≤50，2≤m ≤50)，如下图。

在棋盘上任一点有一个中国象棋马，马走的规则为：1.马走日字2.马只能向右走。

即左图所示：当n ，m 给出之后，同时给出马起始的位置和终点的位置，试找出从起点到终点的所有路径的数目。

例如：(n=10，m=10)，(1，5)(起点)，(3，5)(终点)。

应输出2(即由(1，5)到(3，5)共有2条路径，如下图)：输入：n ，m ，x1，y1，x2，y2(分别表示n ，m ，起点坐标，终点坐标) 输出：路径数目(若不存在从起点到终点的路径，输出0)过河卒如图，A点有一个过河卒，需要走到目标B点。

卒行走的规则：可以向下、或者向右。

••同时在棋盘上的任一点有一个对方的马（如上图的C点）,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。

例如上图C点上的马可以控制8个点（图中的P1，P2….P8）。

卒不能通过对方马的控制点。

•棋盘用坐标表示，A点（0，0）、B点（n，m）(n,m为不超过20的整数,并由键盘输入)，同样马的位置坐标是需要给出的（约定：C≠A，同时C≠B）。

现在要求你计算出卒从A点能够到达B点的路径的条数。

•输入：•键盘输入B点的坐标(n,m)以及对方马的坐标（X，Y）输出：•屏幕输出一个整数（路径的条数）。

回溯法习题汇总

回溯法习题汇总1.1 马拦过河卒源程序名knight.???（pas, c, cpp）可执行文件名knight.exe输入文件名knight.in输出文件名knight.out【问题描述】棋盘上A点有一个过河卒，需要走到目标B点。

卒行走的规则：可以向下、或者向右。

同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。

因此称之为“马拦过河卒”。

棋盘用坐标表示，A点(0, 0)、B点(n, m)(n, m为不超过15的整数)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

【输入】一行四个数据，分别表示B点坐标和马的坐标。

【输出】一个数据，表示所有的路径条数。

【样例】knight.in knight.out6 6 3 3 6【算法分析】从起点开始往下走(只有两个方向可以走)，如果某个方向可以走再继续下一步，直到终点，此时计数。

最后输出所有的路径数。

这种方法可以找出所有可能走法，如果要输出这些走法的话这种方法最合适了，但是本题只要求输出总的路径的条数，当棋盘比较大时，本程序执行会超时，此时最好能找出相应的递推公式更合适，详见后面的递推章节。

1.2 出栈序列统计源程序名stack1.???（pas, c, cpp）可执行文件名stack1.exe输入文件名stack1.in输出文件名stack1.out【问题描述】栈是常用的一种数据结构，有n令元素在栈顶端一侧等待进栈，栈顶端另一侧是出栈序列。

你已经知道栈的操作有两·种：push和pop，前者是将一个元素进栈，后者是将栈顶元素弹出。

现在要使用这两种操作，由一个操作序列可以得到一系列的输出序列。

请你编程求出对于给定的n，计算并输出由操作数序列1，2，…，n，经过一系列操作可能得到的输出序列总数。

【输入】一个整数n（1<=n<=15）【输出】一个整数，即可能输出序列的总数目。

第5章-回溯法-习题

9
运动员最佳匹配问题
编程任务：
设计一个算法，对于给定的男女运动员竞赛优势，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。
数据输入：
第一行有1 个正整数n (1≤n≤20)。接下来的2n 行，每行n 个数。前n 行是p，后n 行是q。
结果输出: 男女双方竞赛优势的总和的最大值。输入示例：
}
//第lev位
//lev的前k位坐标x[0]~x[k-1] //下标必须大于0 //是相同的
//每隔i个位置
23
5-30 离散01串问题
//判断是否相同
bool same() {
int len = x[0] - x[1];
//计算位置差
for (int i=0; i<len; i++)
//搜索每一位
只有一个下标是变化的
11
运动员最佳匹配问题算法
解空间是一棵排列树 void pref::Backtrack(int t) {
if (t>n) Compute(); else
for (int j=t; j<=n; j++) { swap(r[t], r[j]); Backtrack(t+1); swap(r[t], r[j]);
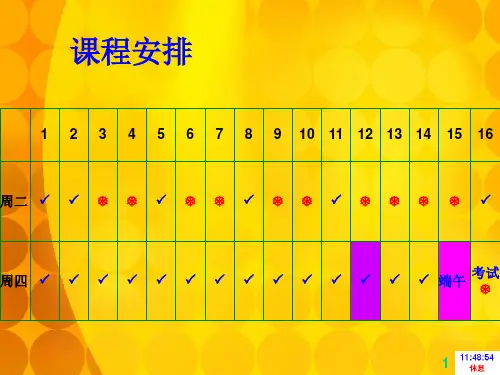
课程安排
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 周二 P P T T P T T P T T P T T T T P
周四 P
P
P
P
P
P
P
P
P
P
P
P
P
P
端午
考试 T
1
第5章回溯法习题课

算法习题回溯法

x[j] = 0;
}
}
main(){
ifstream fin("input.txt",ios::in);
fin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
fin>>c[i][j];
x[j] = 0;
}
cost+=c[i][i];
}
work(1,0);
void backtrack(int i){
if(i>n){
if(cw<sum)
sum = cw;
return ;
}
for(int j=1;j<=m;j++){
cw+=w[i][j];
cp+=c[i][j];
if(cw<sum && cp<=d)
backtrack(i+1);
cw-=w[i][j];
ofstream fout("output.txt",ios::out);
cout<<cost<<endl;
fout<<cost<<endl;
system("pause");
fout.close();
return 0;
}
cp-=c[i][j];
}
}
int main(){
ifstream fin("input.txt",ios::in);
fin>>n>>m>>d;

第5章回溯法(1-例子)

n; // 作业数};
8
} //end Backtrack
旅行售货员问题
9
旅行售货员问题
解空间树 —— 排列树剪枝函数：当搜索到第i 层，图G中存在从顶点1经i个顶点到某其他顶点的一条路径，且x[1:i]的费用和大于当前已获得的最优值时，剪去该子树的搜索。算法效率：
O((n-1)!)*O(n) =O(n!)
cleft -= w[i];
b += p[i];
i++;
} // 装满背包
if (i <= n) b += p[i]/w[i] * cleft;
return b;
4
}
0-1背包问题
例：n=4，c=7，p=[9，10，7，4]，w=[3，5，2，1] 解空间树如下：
物品 1 物品 2 物品 3 物品 4
class Flowshop { friend Flow(int**, int, int []);
f+=f2[i];
private:
if (f < bestf) {
void Backtrack(int i);
Swap(x[i], x[j]);
int **M, // 各作业所需的处理时间
Backtrack(i+1);
(2)将剩余的集装箱装上第二艘轮船。
将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，
使该子集中集装箱重量之和最接近c1。由此可知，装载问题等
价于以下特n殊的0-1背包问题。
max wi xi i 1
用回溯法设计解装载问题的O(2n)计
n
s.t. wi xi c1
算时间算法。

0028算法笔记——【回溯法】批作业调度问题和符号三角形问题

1、批作业调度问题(1)问题描述给定n个作业的集合{J1,J2,…,Jn}。

每个作业必须先由机器1处理，然后由机器2处理。

作业Ji需要机器j的处理时间为tji。

对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。

所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。

批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

例：设n=3，考虑以下实例：这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。

易见，最佳调度方案是1,3,2，其完成时间和为18。

(2)算法设计批处理作业调度问题要从n个作业的所有排列中找出具有最小完成时间和的作业调度，所以如图，批处理作业调度问题的解空间是一颗排列树。

按照回溯法搜索排列树的算法框架，设开始时x=[1,2,……n]是所给的n个作业，则相应的排列树由x[1:n]的所有排列构成。

算法具体代码如下：[cpp]view plain copy1.#include "stdafx.h"2.#include <iostream>ing namespace std;4.5.class Flowshop6.{7.friend int Flow(int **M,int n,int bestx[]);8.private:9.void Backtrack(int i);10.11.int **M, // 各作业所需的处理时间12. *x, // 当前作业调度13. *bestx, // 当前最优作业调度14.15. *f2, // 机器2完成处理时间16. f1, // 机器1完成处理时间17. f, // 完成时间和18.19. bestf, // 当前最优值20. n; // 作业数21. };22.23.int Flow(int **M,int n,int bestx[]);24.25.template <class Type>26.inline void Swap(Type &a, Type &b);27.28.int main()29.{30.int n=3,bf;31.int M1[4][3]={{0,0,0},{0,2,1},{0,3,1},{0,2,3}};32.33.int **M=new int*[n+1];34.35.for(int i=0;i<=n;i++)36. {37. M[i]=new int[3];38. }39. cout<<"M(i,j)值如下："<<endl;40.41.for(int i=0;i<=n;i++)42. {43.for(int j=0;j<3;j++)44. {45. M[i][j]=M1[i][j];46. }47. }48.49.int bestx[4];50.for(int i=1;i<=n;i++)51. {52. cout<<"(";53.for(int j=1;j<3;j++)54. cout<<M[i][j]<<" ";55. cout<<")";56. }57.58. bf=Flow(M,n,bestx);59.60.for(int i=0;i<=n;i++)61. {62.delete []M[i];63. }64.delete []M;65.66. M=0;67.68. cout<<endl<<"最优值是："<<bf<<endl;69. cout<<"最优调度是：";70.71.for(int i=1;i<=n;i++)72. {73. cout<<bestx[i]<<" ";74. }75. cout<<endl;76.return 0;77.}78.79.void Flowshop::Backtrack(int i)80.{81.if (i>n)82. {83.for (int j=1; j<=n; j++)84. {85. bestx[j] = x[j];86. }87. bestf = f;88. }89.else90. {91.for (int j = i; j <= n; j++)92. {93. f1+=M[x[j]][1];94.//机器2执行的是机器1已完成的作业，所以是i-195. f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2];96.97. f+=f2[i];98.if (f < bestf)//剪枝99. {100. Swap(x[i], x[j]); 101. Backtrack(i+1); 102. Swap(x[i], x[j]); 103. }104. f1-=M[x[j]][1];105. f-=f2[i];106. }107. }108.}109.110.int Flow(int **M,int n,int bestx[]) 111.{112.int ub=30000;113.114. Flowshop X;115. X.n=n;116. X.x=new int[n+1];117. X.f2=new int[n+1];118.119. X.M=M;120. X.bestx=bestx;121. X.bestf=ub;122.123. X.f1=0;124. X.f=0;125.126.for(int i=0;i<=n;i++)127. {128. X.f2[i]=0,X.x[i]=i;129. }130. X.Backtrack(1);131.delete []X.x;132.delete []X.f2;133.return X.bestf;134.}135.136.template <class Type>137.inline void Swap(Type &a, Type &b) 138.{139. Type temp=a;140. a=b;141. b=temp;142.}由于算法Backtrack在每一个节点处耗费O(1)计算时间，故在最坏情况下，整个算法计算时间复杂性为O(n!)。

acm回溯例题

Begin{主程序} readln(s); n:=length(s); fillchar(can,sizeof(can),0); count:=0; try(1);{开始生成第一个字符} end.
3、有重复元素的全排列
输入n（<=10）个小些字母（可能重复），输出n个字符的全部排列。样例：输入： abaab 输出： 1:aaabb 2:aabab 3:aabba 4:abaab 5:ababa 6:abbaa 7:baaab 8:baaba 9:babaa 10:bbaaa
procedure print; var i:integer; begin for i:=1 to n-1 do write(b[i],' '); writeln(B[N]); end;
procedure try(i:integer);{要搜索第i个人可以借的书} var j:integer; begin if i=n+1 then print; {得到一组解} for j:=1 to n do if book[j] and (a[i,j]=1) then begin b[i]:=j; book[j]:=false; try(i+1); book[j]:=true; {回溯} end; end; Begin init; try(1); end.
var n,k,i,count:integer; a:array[1..100] of integer;{记录分解项} Procedure print(x);{输出分解方案} var i:integer; begin inc(count); write(count,':',n,'='); for i:=1 to k do write(a[i],‘+’);writeln(x);{输出分解方案} End; procedure try(x:integer);{要分解x，前面已有k项} var i,j:integer; begin print(x)； for j:=a[k] to x div 2 do{分解x=j + （x-j）：保证非递减} if (j>=a[k])and(x-j>=j) then begin inc(k); a[k]:=j; try(x-j); dec(k); end; end;

回溯算法解决批处理作业

回溯算法---解决批处理作业调度问题1、问题的描述n个作业{1, 2, …, n}要在两台机器上处理，每个作业必须先由机器1处理，然后再由机器2处理，机器1处理作业i所需时间为ai，机器2处理作业i 所需时间为bi（1≤i≤n），批处理作业调度问题要求确定这n个作业的最优处理顺序，使得从第1个作业在机器1上处理开始，到最后一个作业在机器2上处理结束所需时间最少。

利用回溯法解决批作业最优调度问题。

算法思想：对于有n个不同的任务，搜索出其最佳排列，属于一棵排列树搜索问题。

采用回溯法，搜索到第t层时，当已经是叶子节点时，说明该路径就是当前情况下的最优解。

当t不是叶子节点时，依次按照一定的顺序执行当前剩下的任务，将剩下的任务全部遍历一遍。

计算执行当前任务后，各个时间点的变化。

如果该层某个节点的任务执行之后，依然符合剪枝函数，则将当前的策略顺序做出调整，将刚刚执行的那个节点的任务序号放置到当前，然后继续向下进行搜索。

剪枝函数：当当前节点的总时间已经大于已找到的最优时间，则该节点后面的节点都不用进行搜索。

直接回溯。

2、代码及注释#include <iostream>using namespace std;#define MAX 1111111111//宏定义设置一个在适当范围内足够大的数字，方便以后进行比较//定义全局变量，包含如下int* x1;//作业Ji在机器1上的工作时间；int* x2;//作业Ji在机器2上的工作时间；int number=0;//作业的数目；int* xOrder;//作业顺序；int* bestOrder;//最优的作业顺序；int bestValue=MAX;//最优的时间；int xValue=0;//当前完成用的时间；int f1=0;//机器1完成的处理时间；int* f2;//第i阶段机器2完成的时间；//定义一个递归调用函数，找出最优void BackTrace(int k){if (k>number)//算法搜索至叶子结点，{for (int i=1;i<=number;i++){bestOrder[i]=xOrder[i];//得到一个新的作业调度方案。

回溯法练习题

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意:只使用ANSI C/ANSI C++标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意:所有依赖的函数必须明确地在源文件中#include <xxx>，不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。
a[k]++;
if(a[k] < 30 && k == n-1)
{
s = 0;
for(i = 0;i < n;i++)
s = s + 1 / a[i];
if(s < 1.000001 && s > 0.999999)//满足条件就输出
{
for(i = 0;i < n;i++)
cout<<"1"<<"/"<<a[i]<<" ";
/*
形如：1/a的分数称为单位分数。
可以把1分解为若干个互不相同的单位分数之和。
例如：
1 = 1/2 + 1/3 + 1/9 + 1/18
1 = 1/2 + 1/3 + 1/10 + 1/15
1 = 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/15 + 1/35 + 1/45 + 1/231
1/2 1/4 1/9 1/12 1/18
1/2 1/4 1/10 1/12 1/15

算法实验四回溯法

n=nn;
sum=0;
x=newint[n+1];
//尝试第一行的所有位置
for(inti=0;i<=n;i++)
x[i]=0;
backtrack(1);
returnsum;
}
privatestaticvoidbacktrack(intt) {
if(t>n)sum++;
else
for(inti=1;i<=n;i++){//从第一行开始往下放置，放置陈功继续
xi @{0,1},1<=i<=n
用回溯法解装载问题时，用子集树表示其解空间显然是最合适的。可行性约束函数可剪去不满足约束条件（
(w1x1+w2x2+...+wixi)<= c1）的子树。在子集树的第j+1层的节点Z处，用cw记当前的装载重量，即cw=(w1x1+w2x2+...+wjxj)，当cw>c1时，以节点Z为根的子树中所有节点都不满足约束条件，因而该子树中解均为不可行解，故可将该子树剪去。
【算法描述】
importjava.util.Scanner;
publicclassNQueen {
staticintn;//皇后个数
staticintx[];//当前解，表示x[i]表示第i行皇后位置
staticlongsum;//当前已找到的可行方案数
publicstaticvoidmain(String[] args) {
1.首先将第一艘轮船尽可能装满。
2.将剩余的集装箱装上第二艘轮船。
将第一艘轮船尽可能的装满等价于选取全体集装箱的子集，使该子集中集装箱的重量之和最接近c1。因此，等价于一个特殊的0-1背包问题。因此是一棵子集树。

N皇后问题—回溯算法经典例题

N皇后问题—回溯算法经典例题题⽬描述: N 皇后是回溯算法经典问题之⼀。

问题如下：请在⼀个 n×n 的正⽅形盘⾯上布置 n 名皇后，因为每⼀名皇后都可以⾃上下左右斜⽅向攻击，所以需保证每⼀⾏、每⼀列和每⼀条斜线上都只有⼀名皇后。

题⽬分析：在 N 皇后问题中，回溯算法思路是每⼀次只布置⼀个皇后，如果盘⾯可⾏，就继续布置下⼀个皇后。

⼀旦盘⾯陷⼊死局，就返回⼀步，调整上⼀个皇后的位置。

重复以上步骤，如果解存在，我们⼀定能够找到它。

可以看到，我们在重复“前进—后退—前进—后退”这⼀过程。

问题是，我们不知道⼀共需要重复这个过程多少次，也不能提前知道 n 是多少，更不知道每⼀次后退时需要后退⼏⾏，因此我们不能利⽤ for 循环和 while 循环来实现这个算法。

因此我们需要利⽤递归来实现代码结构。

逻辑如下：当⽅法布置完当前⾏的皇后，就让⽅法调⽤⾃⼰去布置下⼀⾏的皇后。

当盘⾯变成绝境的时候，就从当前⽅法跳出来，返回到上⼀⾏，换掉上⼀⾏的皇后再继续。

我们定义 NQueens(n) ⽅法，它负责输出所有成⽴的 n×n 盘⾯。

其中 1 代表皇后，0 代表空格。

代码：def NQueens(n): #输出所有成⽴的n·n盘⾯cols = [0 for _ in range(n)] #每⼀⾏皇后的纵坐标res = [] #结果列表def checkBoard(rowIndex): #检查盘⾯是否成⽴,rowIndex是当前⾏数for i in range(rowIndex):if cols[i]==cols[rowIndex]: #检查竖线return Falseif abs(cols[i]-cols[rowIndex]) == rowIndex-i: #检查斜线return Falsereturn Truedef helper(rowIndex): #布置第rowIndex⾏到最后⼀⾏的皇后if rowIndex==n: #边界条件board = [[0 for _ in range(n)] for _ in range(n)]for i in range(n):board[i][cols[i]] = 1res.append(board) #把当前盘⾯加⼊结果列表return#返回for i in range(n): #依次尝试当前⾏的空格cols[rowIndex] = iif checkBoard(rowIndex): #检查当前盘⾯helper(rowIndex+1) #进⼊下⼀⾏helper(0) #从第1⾏开始return resprint(NQueens(4))代码分析：在 NQueens() ⽅法中，我们会定义 helper(x) ⽅法帮助实现递归结构。

回溯法实验(0-1背包问题)

算法分析与设计实验报告第五次附加实验cp += p[i];Backtrack(i+1); //回溯//回溯结束回到当前根结点cw -= w[i];cp -= p[i];}//进入右子树，条件是上界值比当前最优值大，否则就将右子树剪掉if(Bound(i+1)>bestp){Backtrack(i+1);}}测试结果当输入的数据有解时：当输入的数据无解时：当输入的数据稍微大点时：附录：完整代码（回溯法）//0-1背包问题回溯法求解 #include <iostream> using namespace std;template <class Typew,class Typep>class Knap //Knap 类记录解空间树的结点信息 {template <class Typew,class Typep>friend Typep Knapsack(Typep [],Typew [],Typew,int ); private :Typep Bound(int i); //计算上界的函数void Backtrack(int i); //回溯求最优解函数实验分析在实验中并没有生成多组数据，进行比较，也没有利用随机生成函数，因为在这种有实际有关联的问题中，利用随机生成函数生成的数据是十分的不合适的，在此我们只需要验证该程序是否正确即可。

0-1背包问题和之前的最优装载其实质上一样的，都是利用解空间树，通过深度优先搜索子集树，通过利用上界函数和一些剪枝策略，从而得到最优解。

由于数据较小，所以时间上并不能反映出什么东西。

实验心得在这一章的回溯算法中，我们用的比较多的就是；利用子集树来进行问题的探索，就例如上图是典型的一种子集树，在最优装载、0-1背包都是利用了这种满二叉树的子集树进行求解，然后通过深度优先的策略，利用约束函数和上界函数，将一些不符合条件或者不包含最优解的分支减掉，从而提高程序的效率。

回溯法——精选推荐

回溯法一、算法介绍：回溯是一种模拟人类思维过程的算法思想。

它的基本方法是：按照深度优先的顺序向下一层扩展结点；扩展到某一层时，若已无法继续扩展且仍未找到解，则退回到父结点，从父结点的下一个分支开始，按同样的策略继续扩展……，直到找到问题的解或证明无解。

代码框架：procedure try(i:integer);varbeginif i>nthen 输出结果else for j:=下界to 上界dobeginx[i]:=h[j];if 可行{满足限界函数和约束条件} thenbegin置值；try(i+1);{尝试下一个位置}对此位置还原；end;end;end;二、典型例题：1、n皇后：在一个n×n国际象棋盘上，有n个皇后，每个皇后占一格；要求皇后间不会出现相互“攻击”的现象，即不能有两个皇后处在同一行、同一列或同一对角线上。

问共有多少种不同的方法。

【思路】逐一对每行的n个位置进行尝试（横坐标记为i，纵坐标记为j）。

若此位置安全则占用，并表明此位置所在的两对角线、列不安全（由于是对每行进行尝试，故不需标注该行是否安全）。

若此位置不安全则尝试下一个位置。

找到本行的安全位置后，如果已经尝试n行则输出结果，否则对下一行进行同样的尝试。

无论是继续尝试还是输出结果，在进行操作后都要对所占位置进行释放（即返回，进行本行下一位置的尝试）。

【注】棋盘中，从左至右的对角线横纵坐标之和一定（如图），从右至左的对角线横纵坐标之差一定。

varn,i:longint;no:longint;{记录方案个数}ans:array[1..1000]of longint;｛储存答案｝ lr,rl,l:array[-1000..1000] of boolean; {储存左右对角线、右左对角线、列是否安全}procedure print; {输出答案}vari:longint;beginno:=no+1;write('NO.',no,':');for i:=1 to n do write(ans[i],' '); writeln;end;procedure try(j:longint);vari:longint;beginfor i:=1 to n doif l[i] and rl[i+j] and lr[j-i]thenbeginl[i]:=false;rl[i+j]:=false;lr[j-i]:=false;ans[j]:=i;if j<n then try(j+1)else print;l[i]:=true;{释放该位置}rl[i+j]:=true;lr[j-i]:=true;end;end;beginwriteln('How many queens?');read(n);no:=0;for i:=1 to n do l[i]:=true;for i:=2 to 2*n do rl[i]:=true;for i:=1-n to n-1 do lr[i]:=true;try(1);if no=0 then write('No way!');end.2、跳马：在5*5格的棋盘上，从（1,1）点出发，按日字跳马，要求不重复地跳经所有方格。

00算法笔记记录——回溯法批作业调度问题及符号三角形问题.doc

1、批作度(1)问题描述定 n 个作的集合 {J1,J2, ⋯,Jn}。

每个作必先由机器 1 理，然后由机器 2 理。

作 Ji 需要机器 j 的理 tji。

于一个确定的作度， Fji 是作 i 在机器 j 上完成理的。

所有作在机器 2 上完成理的和称作度的完成和。

批处理作业调度问题要求对于给定的 n 个作业，制定最佳作业调度方案，使其完成时间和达到最小。

例： n=3 ，考以下例：3 个作的 6 种可能的度方案是 1,2,3 ；1,3,2 ； 2,1,3 ；2,3,1 ；3,1,2 ；3,2,1 ；它所相的完成和分是19，18，20，21，19 ，19。

易，最佳度方案是1,3,2 ，其完成和18。

(2)算法设计批理作度要从 n 个作的所有排列中找出具有最小完成和的作度，所以如，批理作度的解空是一排列树。

按照回溯法搜索排列的算法框架，开始 x=[1,2, ⋯⋯n]是所的 n 个作，相的排列由 x[1:n] 的所有排列构成。

算法具体代如下：[cpp]view plain copy1.#include "stdafx.h"2.#include <iostream>ing namespace std;4.5.class Flowshop6.{7.friend int Flow( int **M, int n, int bestx[]);8.private :9. void Backtrack( int i);10.11. int **M, // 各作业所需的处理时间12. *x, // 当前作业调度13. *bestx, // 当前最优作业调度14.15. *f2, // 机器 2 完成处理时间16. f1, // 机器 1 完成处理时间17. f, // 完成时间和18.19. bestf, // 当前最优值20. n; // 作业数21.};22.23. int Flow( int **M, int n, int bestx[]);24.25. template < class Type>26. inline void S &a, Type &b);27.28.int main()29.{30.int n=3,bf;31.int M1[4][3]={{0,0,0},{0,2,1},{0,3,1},{0,2,3}};32.33.int **M= new int *[n+1];34.35.for ( int i=0;i<=n;i++)36.{37.M[i]=new int[3];38.}39.cout<<"M(i,j) 值如下： " <<endl;40.41.for ( int i=0;i<=n;i++)42.{43.for ( int j=0;j<3;j++)44.{45.M[i][j]=M1[i][j];46.}47.}48.49.int bestx[4];50.for ( int i=1;i<=n;i++)51.{52.53.54.55. cout<< "(" ;for ( int j=1;j<3;j++)cout<<M[i][j]<< " " ; cout<< ")" ;56.}57.58.bf=Flow(M,n,bestx);59.60.for ( int i=0;i<=n;i++)61.{62.delete[]M[i];63.}64.delete []M;65.66.M=0;67.68.cout<<endl<<" 最优值是： " <<bf<<endl;69.cout<<" 最优调度是： " ;70.71.for ( int i=1;i<=n;i++)72.{73.cout<<bestx[i]<<" " ;74.}75.cout<<endl;76.return 0;77.}78.79. void Flowshop::Backtrack(int i)80.{81.if (i>n)82.{83.for ( int j=1; j<=n; j++)84.{85.bestx[j] = x[j];86.}87.bestf = f;88.}89.else90.{91.for ( int j = i; j <= n; j++)92.{93.f1+=M[x[j]][1];94.// 机器 2 执行的是机器 1 已完成的作业，所以是i-195.f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2];96.97.f+=f2[i];98.if (f < bestf)// 剪枝99.{100. Swap(x[i], x[j]);101. Backtrack(i+1);102. Swap(x[i], x[j]);103.}104.f1-=M[x[j]][1];105.f-=f2[i];106.}107.}108.}109.110. int Flow( int **M, int n, int bestx[])111.{112.int ub=30000;113.114.Flowshop X;115.X.n=n;116. X.x= new int [n+1];117. X.f2= new int [n+1];118.119.X.M=M;120.X.bestx=bestx;121.X.bestf=ub;122.123.X.f1=0;124.X.f=0;125.126.for ( int i=0;i<=n;i++)127.{128.X.f2[i]=0,X.x[i]=i;129.}130.X.Backtrack(1);131.delete []X.x;132.delete []X.f2;133.return X.bestf;134.}135.136.template < class Type>137. inline void S &a, Type &b)138.{139.Type temp=a;140.a=b;141.b=temp;142.}由于算法 Backtrack 在每一个节点处耗费O(1) 计算时间，故在最坏情况下，整个算法计算时间复杂性为O(n!) 。

回溯法习题汇总

回溯法习题汇总1.1 马拦过河卒源程序名knight.???（pas, c, cpp）可执行文件名knight.exe输入文件名knight.in输出文件名knight.out【问题描述】棋盘上A点有一个过河卒，需要走到目标B点。

卒行走的规则：可以向下、或者向右。

同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。

因此称之为“马拦过河卒”。

棋盘用坐标表示，A点(0, 0)、B点(n, m)(n, m为不超过15的整数)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

【输入】一行四个数据，分别表示B点坐标和马的坐标。

【输出】一个数据，表示所有的路径条数。

【样例】knight.in knight.out6 6 3 3 6【算法分析】从起点开始往下走(只有两个方向可以走)，如果某个方向可以走再继续下一步，直到终点，此时计数。

最后输出所有的路径数。

这种方法可以找出所有可能走法，如果要输出这些走法的话这种方法最合适了，但是本题只要求输出总的路径的条数，当棋盘比较大时，本程序执行会超时，此时最好能找出相应的递推公式更合适，详见后面的递推章节。

1.2 出栈序列统计源程序名stack1.???（pas, c, cpp）可执行文件名stack1.exe输入文件名stack1.in输出文件名stack1.out【问题描述】栈是常用的一种数据结构，有n令元素在栈顶端一侧等待进栈，栈顶端另一侧是出栈序列。

你已经知道栈的操作有两·种：push和pop，前者是将一个元素进栈，后者是将栈顶元素弹出。

现在要使用这两种操作，由一个操作序列可以得到一系列的输出序列。

请你编程求出对于给定的n，计算并输出由操作数序列1，2，…，n，经过一系列操作可能得到的输出序列总数。

【输入】一个整数n（1<=n<=15）【输出】一个整数，即可能输出序列的总数目。

实验八.回溯算法

实验八回溯算法（4学时）一、实验目的与要求1、掌握装载问题的回溯算法；2、初步掌握回溯算法；二、实验题有一批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i 的重量为wi ，且装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。

如果有，找出一种装载方案。

三、实验提示装载问题↔ 问题描述有一批共n 个集装箱要装上2艘载重量分别为c 1和c 2的轮船，其中集装箱i 的重量为w i ，且，要求确定是否有一个合理的装载方案可将这n 个集装箱装上这2艘轮船。

如果有，请给出该方案。

↔ 编程任务利用回溯法试设计一个算法求出该装载问题的解。

↔ 数据输入由文件input.txt 提供输入数据。

文件的第1行中有2个正整数n 及c ，表示有n 个集装箱，第一艘船的载重量为c 。

接下来的一行为每个集装箱的重量。

↔ 结果输出程序运行结束时，将计算出的最优解输出到文件output.txt 中，如果某集装箱被装入船上，则对应的解为1，如果不能装入则为0。

输入文件示例输出文件示例input.txt output.txt3 30 16 15 150 1 1代码：#include<stdio.h>#include<stdlib.h>#include<fstream.h>int result;int nn,cc;int *ww,*superbestx,*superbestw;template<class Type>class Loading{friend Type Maxloading(Type[],Type,int,int[]);public:void Backtrack(int i);int n,////集装箱数*x,//当前解*bestx;//当前最优解 211c c w ni i +≤∑=Type* w,//集装箱重量数组c,//第一艘轮船的载重量cw,//当前载重量bestw,//当前最优载重量r;//剩余集装箱重量};template<class Type>void Loading<Type>::Backtrack(int i){//搜索第i层结点if(i>n){////到达叶结点if(cw>bestw){for(int j=1;j<=n;j++)bestx[j]=x[j];bestw =cw;}return;}//搜索子树r-=w[i];if((cw + w[i]) <= c)//{x[i]=1;cw+=w[i];Backtrack(i+1);cw -=w[i];}if(cw+r>bestw)//{x[i]=0;Backtrack(i+1);}r+=w[i];}template<class Type>Type Maxloading(Type w[],Type c, int n,int bestx[]) {//返回最优载重量Loading<Type> X;//X.x = new int[n+1];X.w = w;X.c = c;X.n = n;X.bestx = bestx;X.bestw = 0;X.cw = 0;//X.r = 0;for(int i=1;i<=n;i++)X.r+=w[i];//初始时r为全体物品的重量和//计算最优载重量X.Backtrack(1);delete [] X.x;for(int k=0;k<n;k++)superbestx[k] = X.bestx[k];result=X.bestw;// delete [] X.x;return result;}int main(int argc,int *argv){// Loading<int> X;ifstream in("input.txt");//打开输入文件ofstream out("output.txt");//打开输出文件in>>nn;//集装箱数in>>cc;//第一艘轮船的载重量ww = (int *)malloc(sizeof(int)*nn);superbestx = (int *)malloc(sizeof(int)*nn);// superbestw = (int *)malloc(sizeof(int)*nn);for(int i=0;i<nn;i++){in>>ww[i];//集装箱重量数组superbestx[i]=0;//初始当前化最优解}Maxloading(ww,cc,nn, superbestx);for(int kk=0;kk<nn;kk++)out<<superbestx[kk]<<'\t';//将最优解写入输出文件out<<endl;system("type output.txt");//显示输出文件in.close;//关闭输入文件out.close;//关闭输出文件system("pause");return 0;}。

回溯算法的一些例题

回溯算法搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。

回溯是搜索算法中的一种控制策略。

它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。

如迷宫问题:进入迷宫后,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已无路可走,这时,首先看其它方向是否还有路可走,如果有路可走,则沿该方向再向前试探;如果已无路可走,则返回一步,再看其它方向是否还有路可走;如果有路可走,则沿该方向再向前试探。

按此原则不断搜索回溯再搜索,直到找到新的出路或从原路返回入口处无解为止。

递归回溯法算法框架[一]procedure Try(k:integer);beginfor i:=1 to 算符种数 Doif 满足条件 thenbegin保存结果if 到目的地 then 输出解else Try(k+1);恢复:保存结果之前的状态{回溯一步}end;end;递归回溯法算法框架[二]procedure Try(k:integer);beginif 到目的地 then 输出解elsefor i:=1 to 算符种数 Doif 满足条件 thenbegin保存结果Try(k+1);end;end;例 1:素数环:把从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。

【算法分析】非常明显,这是一道回溯的题目。

从1 开始,每个空位有20(19)种可能,只要填进去的数合法:与前面的数不相同;与左边相邻的数的和是一个素数。

第 20个数还要判断和第1个数的和是否素数。

〖算法流程〗1、数据初始化; 2、递归填数:判断第J种可能是否合法;A、如果合法:填数;判断是否到达目标(20个已填完):是,打印结果;不是,递归填下一个;B、如果不合法:选择下一种可能;【参考程序】program z74;框架[一]var a:array[0..20]of byte;b:array[0..20]of boolean;total:integer;function pd(x,y:byte):boolean;var k,i:byte;begink:=2; i:=x+y; pd:=false;while (k<=trunc(sqrt(i)))and(i mod k<>0) do inc(k);if k>trunc(sqrt(i)) then pd:=true;end;procedure print;var j:byte;begininc(total);write('<',total,'>:');for j:=1 to 20 do write(a[j],' ');writeln;end;procedure try(t:byte);var i:byte;beginfor i:=1 to 20 doif pd(a[t-1],i)and b[i] thenbegina[t]:=i; b[i]:=false;if t=20 then begin if pd(a[20],a[1]) then print;end b[i]:=true;end;end;BEGINfillchar(b,sizeof(b),#1);total:=0;try(1);write('total:',total);END.通过观察,我们可以发现实现回溯算法的特性:在解决过程中首先必须要先为问题定义一个解的空间.这个空间必须包含问题的一个解。

《回溯法实验》实验报告

实验4、《回溯法实验》一、实验目的1. 掌握回溯算法思想2. 掌握回溯递归原理3. 了解回溯法典型问题二、实验内容1. 编写一个简单的程序，解决8皇后问题。

2. 批处理作业调度问题[问题描述]给定n个作业的集合J=(J1, J2, … , Jn)。

每一个作业Ji都有两项任务需要分别在2台机器上完成。

每一个作业必须先由机器1处理，然后再由机器2处理。

作业Ji需要机器i的处理时间为tji，i=1,2, … ,n; j=1,2。

对于一个确定的作业调度，设Fji是作业i在机器i上完成处理的时间。

则所有作业在机器2上完成处理的时间和成为该作业调度的完成时间和。

批处理作业调度问题要求对于给定的n个作业，制定一个最佳的作业调度方案，使其完成时间和达到最小。

要求输入：1）作业数 2）每个作业完成时间表：作业完成时间机器1 机器2作业1 2 1作业2 3 1作业3 2 3要求输出： 1）最佳完成时间 2）最佳调度方案提示：算法复杂度为O(n!),建议在测试的时候n值不要太大，可以考虑不要超过12。

3. 数字全排列问题任意给出从1到N的N个连续的自然数，求出这N个自然数的各种全排列。

如N=3时，共有以下6种排列方式：123，132，213，231，312，321。

注意：数字不能重复，N由键盘输入（N<=9）。

三、算法思想分析1.八皇后问题是典型的回溯问题，先从空格子起逐行放皇后，如果符合要求即安全则放置，否则返回上一行下一个位置继续，直至最后一行安全放置则为一种放置方式。

2.批处理作业调度的解空间为排列数，不断利用递归函数直至叶节点，剪枝函数为当前用时与最佳用时的比较。

关于时间的计算，每次选择作业后先将机器1用时累加，机器2上总用时需要先比较上一个作业完成时间与此时机器1上的总用时，如果机器1上总用时大于上一作业用时，那么机器2上用时则加上机器1上用时与此作业在机器2上的单独用时，反之，则代表此时机器2仍然在处理上一任务，那么机器2上用时则加上上一作业用时与此作业在机器2上的单独用时。

回溯法 作业

算法设计与分析——批处理作业调度（回溯法）

第一章回溯法(习题三)

回溯法练习1

回溯法习题汇总

第5章-回溯法-习题

算法习题回溯法

第5章 回溯法(1-例子)

0028算法笔记——【回溯法】批作业调度问题和符号三角形问题

acm回溯例题

回溯算法解决批处理作业

回溯法练习题

算法实验四 回溯法

N皇后问题—回溯算法经典例题

回溯法实验(0-1背包问题)

回溯法——精选推荐

00算法笔记记录——回溯法批作业调度问题及符号三角形问题.doc

回溯法习题汇总

实验八.回溯算法

回溯算法的一些例题

《回溯法实验》实验报告

第5章回溯法(1-例子)

算法实验四回溯法