自适应控制--第二讲 模型参考自适应控制的MIT法
第5章 模型参考自适应控制
设n1 ( s ) nm ( s ) ( s) nm ( s ) ( s ) n1 ( s )n p ( s ) nm ( s ) ( s)n p ( s) a ( s ) ( s )n p ( s )
d p ( s )d1 ( s ) k p n p ( s )n2 ( s ) d m ( s ) ( s ) d p ( s )d1 ( s ) k p n p ( s )n2 ( s ) d m ( s ) ( s )n p ( s ) d1 ( s ) d m ( s ) ( s ) d p ( s ) k p n2 ( s ) n p (s) q( s)d p ( s) p( s) p( s) d1 ( s ) q ( s )n p ( s ), n2 ( s ) kp
例题
x p a p x p bp u y p cp xp c p bp 1 G p ( s) , Gm s - ap s 1
设 ( s ) s a d m ( s ) ( s ) ( s 1)( s a ) d p (s) s - ap s 1 a a p a a p (1 a a p ) 1 C0 c pbp n1 ( s ) d 2 ( s ) s a d1 ( s ) n p ( s ) q ( s ) s 1 a a p a a p (1 a a p ) n2 ( s ) p ( s ) / k p c pbp
未知或 者缓慢 变化
nm ( s) n p ( s) n( s) d m ( s) d p ( s) d ( s) 求C0
对象参数未知或者部分参数未知 lime(t)=0
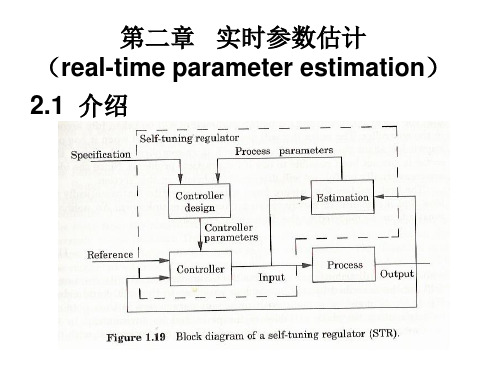
自适应控制的基本概念
2. 自适应控制提出 当不确定因素难以事先预知，又要设计满 意的控制系统，由此提出自适应控制思想。 自适应调节器就是期望修正自己的特性以 补偿过程和扰动的动力学变化。
四、自适应控制思想雏形
观测 运行指标 系统参数 再认识 系统 （不确定） 决策修正 控制器参数 控制器结构 控制作用
性能指标
2. 模型参考自适应控制系统 a. 线性模型跟随系统
参考模型给出 了期望闭环响 应特性
参考模型
es Gm 1 GcG p GcG p u s 1 GcG p G p G f
y p s GcG p GmG p G f u s 1 GcG p G p G f
二、控制问题的几种情况
1. 无扰动，系统模型确定
系统模型
属于确定性控制 可以采用开环控制 2. 有扰动，系统模型确定 属于随机控制 当扰动不确定采用闭环控制 扰动确定可以采用补偿控制 3. 可能有扰动，系统模型不确定
采用闭环控制？ 扰动√ 系统模型不确定×
扰动
系统模型
扰动
系统模型
ym
模型跟随 调节器
e
yp
+
u
－
控制器
＋
－
被控对象
已知被控对象的数学模型√ 未知被控对象的数学模型或变化×
b. 模型参考自适应控制系统
参考模型
+
－
e
u
－ －
前馈调节器
被控对象
反馈调节器
参数调整 信号综合
自适应机构
美国Minorsky研制船舶驾驶伺服结构，提出PID控制(1922)
美国MIT的Vannevar Bush研制成大型模拟计算机 (1928)
自适应控制课件
标量输入信号 (2.7)
标量输出信号
Dm ( p ) ami p i
i 0 n
微分算子 (2.8) (2.9)
N m ( p) bmi p i
i 0
m
参考模型的输入输出方程的常系数 在参数自适应方案中，可调系统的输入输出方程
Ds (t , p) ys N s (t , p)r
(2.16)
在参数自适应方案中，可调系统模型为
ys (k ) asi (e, k ) ys (k i ) bsi (e, k )r (k i) sT s (k 1)
i 1 i 0 n m
(2.19)
sT [as1 (e, k ), as 2 (e, k ), , asn (e, k ), bs 0 (e, k ), bs1 (e, k ), , bsn (e, k )]
信号向量
sT (k 1) [ y s (k 1),, y s (k n), r (k ),, r (k m)]
(2.21)
模型参考自适应系统状态方程描述对比
连续模型参考自适应系统 参考模型：
m Am x m Bm u, x m (0) x m0 x
(2.1)
(2.5)
信号综合自适应方案的系统模型
x (k 1) Ax(k ) Bu(k ) ua (e, k ) x (0) x 0 , ua (0) ua0
(2.6)
模型参考自适应系统输入输出方程描述对比
连续模型参考自适应系统 参考模型：
Dm ( p) ym N m ( p)r
Dm ( p ) ami p i
自适应控制
自适应控制什么是自适应控制自适应控制是一种控制系统设计方法，它通过实时监测和调整系统的参数来适应不确定的外部环境和内部系统变化。
自适应控制可以提高控制系统的性能和鲁棒性，使其能够快速、准确地响应不断变化的环境或系统参数。
在传统的控制系统中，通常假设系统的数学模型是已知和固定的。
然而，在实际应用中，系统的动态特性常常受到各种因素的影响，如外部扰动、参数变化、非线性效应等。
这些因素使得传统的控制方法往往无法满足系统的控制要求。
而自适应控制则能够通过不断地观测和在线调整系统参数，使系统能够适应这些变化，并实现良好的控制效果。
自适应控制的基本原理自适应控制的基本原理是根据系统的实时反馈信息来调整控制器的参数。
具体来说，自适应控制系统通常由以下几个部分组成：1.参考模型：参考模型是指描述所期望控制系统输出的理想模型，通常由一组差分方程来表示。
参考模型的作用是指导控制系统的输出，使其能够尽可能接近参考模型的输出。
2.系统模型：系统模型是指描述被控对象的数学模型，包括其输入、输出和动态特性。
系统模型是自适应控制的重要基础，它确定了控制系统需要调整的参数和控制策略。
3.控制器：控制器是自适应控制系统的核心部分，它根据系统输出和参考模型的误差来实时调整控制器的参数。
控制器可以通过不同的算法来实现，如模型参考自适应控制算法、最小二乘自适应控制算法等。
4.参数估计器：参数估计器是自适应控制系统的关键组件，它用于估计系统模型中的未知参数。
参数估计器可以通过不断地观测系统的输入和输出数据来更新参数估计值，从而实现对系统参数的实时估计和调整。
5.反馈环路：反馈环路是指通过测量系统输出并将其与参考模型的输出进行比较，从而产生误差信号并输入到控制器中进行处理。
反馈环路可以帮助控制系统实时调整控制器的参数，使系统能够适应外部环境和内部变化。
自适应控制的应用领域自适应控制在各个领域都有广泛的应用，特别是在复杂和变化的系统中，其优势更为突出。
自适应控制第2章.详解
1 2 n
(φ ) (Y φ θ1 φ θ2 φ θn ) 0, i 1,t
i T 1 2 n
最小二乘的统计解释（statistical interpretation）
y(i) φ (i)θ e(i)
T 0
（2.12）
ˆ(t ) θ ˆ(t 1) θ
φ(t ) T ˆ(t 1) y ( t ) φ ( t ) θ T φ (t )φ(t )
（2.23）
Kaczmarz算法
ˆ(t ) θ ˆ(t 1) θ γφ(t ) T ˆ(t 1) y ( t ) φ ( t ) θ φT (t )φ(t )
t
新的采样数据对参数估计的改进不再起作用， 这种现象称为数据饱和。
时变参数情形
1、参数突变但不频繁 重置（resetting）
2、参数连续变换但很缓慢
1 t i T V (θ , t ) λ y (i) φ (i)θ 2 i1
0 λ 1
t
2
（2.20）
遗忘因子（折扣因子） forgetting（discounting） factor
φn (1) ε (1) y (1) φ1 (1) φ ( 2) ε ( 2) y ( 2 ) φ ( 2 ) 1 θ1 n θn ε (t ) y (t ) φ1 (t ) φn (t )
T
1
ˆ θ (t ) P(t ) φ(i ) y (i ) i1
自适应控制--第二讲 模型参考自适应控制的MIT法
e（t）广义误
差
自适应机构
智能楼宇的综合布线系统
多元函数及其偏导数
z
z x1
z=f(x1,x2)
x1
x2
智能楼宇的综合布线系统
方向导数
z
z=f(x1,x2)
α
x1
l
x2
智能楼宇的综合布线系统
梯度的几何意义
grad z
智能楼宇的综合布线系统
只有当目标函数的等高线轮廓球形(或在二维空间中 的圆形时)，梯度法可以一步达到极小点，否则，该 方法不一定直接指向最小点
• （5）μ由人工设定，与梯度法的步长λ成正比 ，因此可以视为自适应调节的步长，或称为 自适应增益，其值影响自适应过程收敛的速 度和精度，需要通过实验来确定。
• （6）性能指标可以选择各种形式
智能楼宇的Байду номын сангаас合布线系统
一阶系统稳定性分析
• MIT方案中，调节Kc的目标是使广义误差 e(t)逐步趋近于零。
• （1）的变化速度远慢于的调节速度是一个必 要的条件，否则无法求出的导数；
• （2）系统动态响应速度要远快于调节速度； • （3）自适应机构包含积分环节，自适应调节
效果与ym有关，即与参考模型传递函数和输 入r(t)有关。
智能楼宇的综合布线系统
MIT法的特点
• （4）自适应过程不具智能性，整个系统是非 线性系统，且只能解决对象参数局部时变的 问题。
智能楼宇的综合布线系统
课后作业
用Matlab对MIT方案进行仿真，参考模 型分别为以下一阶和二阶形式：
Y (s) 10 R(s), Kv 4, Kc(0) 2 0.2s 1
Y
(s)
s2
1 2s
模型参考自适应控制—MIT法
一 原理及方法模型参考自适应系统，是用理想模型代表过程期望的动态特征，可使被控系统的特征与理想模型相一致。
一般模型参考自适应控制系统的结构如图1所示。
图1 一般的模型参考自适应控制系统其工作原理为，当外界条件发生变化或出现干扰时，被控对象的特征也会产生相应的变化，通过检测出实际系统与理想模型之间的误差，由自适应机构对可调系统的参数进行调整，补偿外界环境或其他干扰对系统的影响，逐步使性能指标达到最小值。
基于这种结构的模型参考自适应控制有很多种方案，其中由麻省理工学院科研人员首先利用局部参数最优化方法设计出世界上第一个真正意义上的自适应控制律，简称为MIT 自适应控制，其结构如图2所示。
图2 MIT 控制结构图系统中，理想模型Km 为常数，由期望动态特性所得，被控系统中的增益Kp 在外界环境发生变化或有其他干扰出现时可能会受到影响而产生变化，从而使其动态特征发生偏离。
而Kp 的变化是不可测量的，但这种特性的变化会体现在广义误差e 上，为了消除或降低由于Kp 的变化造成的影响，在系统中增加一个可调增益Kc ，来补偿Kp 的变化，自适应机构的任务即是依据误差最小指标及时调整Kc ，使得Kc 与Kp 的乘积始终与理想的Km 一致，这里使用的优化方法为最优梯度法，自适应律为：⎰⨯+=tm d y e B Kc t Kc 0)0()(τYp Yme+__+R参考模型调节器被控对象适应机构可调系统———kmq(s)p(s)KcKpq(s)-----p(s)适应律Rymype+-MIT 方法的优点在于理论简单，实施方便，动态过程总偏差小，偏差消除的速率快，而且用模拟元件就可以实现；缺点是不能保证过程的稳定性，换言之，被控对象可能会发散。
二 对象及参考模型该实验中我们使用的对象为：122)()()(2++==s s s p s q K s G pp 参考模型为：121)()()(2++==s s s p s q K s G mm 用局部参数最优化方法设计一个模型参考自适应系统，设可调增益的初值Kc(0)=0.2，给定值r(t)为单位阶跃信号，即r(t)=A ×1(t)。
自适应控制
• 只与 K 有* 关，而与 F无* 关
• 通常 P要靠解李雅普诺夫方程得到
最终得到 Vx 1 eTQe
2
26
结果分析
V x 1 eT Pe tr 1T
2
Vx
1
eT
Qe
2
• e , 时 V 所x,t得 到的结果是大范围
（全局）渐近稳定
• 渐近稳定 lim e， 0 lim e 0
t
统是平衡态大范围渐近稳定。
Vx,t 0
x V x,t
Barbalat引理
如果 f t : R R是一个 [0,) 上的一致连续函数，
同时
lim
t
t
0
f
d
存在而且有界，则当t
时，
f t 0
若定义在实数区间A（注意区间A可以是闭区间，亦可以是开区间甚至 是无穷区间）上的任意函数f(x)，对于任意给定的正数ε>0，总存在一 个与x无关的实数ζ>0，使得当区间A上的任意两点x1，x2，满足|x1x2|<ζ时，总有|f(x1)-f(x2)|<ε，则称f(x)在区间A上是一致连续的。
数学表示方法——传递函数表示
参考模型的输出
rt
ym
s
Gm
sRs
KN s Ds
Rs
可调系统输出
KC
yp
s
Gp
sRs
Kc Kv Ns Ds
Rs
定义广义误差 e ym yp
KN s Ds
Kv N s Ds
+ et 广义误差
-
自适应机构
2. 自适应律推导
取性能指标
IPRM
1 2
t e2 d
自适应控制课件
模型参考自适应控制系统结构图
2.2.1 模型参考自适应控制的数学描述
2.2.1.1 并联模型参考自适应系统的数学模型 并联模型参考自适应系统可以用状态方程和输入－输出方程进行描述。 并联模型参考自适应系统可以用状态方程和输入－输出方程进行描述。 状态方程 进行描述 一、用状态方程描述的模型参考自适应系统 对于连续模型参考自适应控制系统 对于连续模型参考自适应控制系统 连续模型 参考模型： 参考模型：
i
由广义误差 e = y m − y s 通过自适应规律进行自适 应调整
Ds (t , p) = N s (t , p) =
i =0 m
∑ a si (e, t ) p ∑ bsi (e, t ) p
n
(2.11) (2.12)
i
i =0
2.2.1.1 并联模型参考自适应系统的数学模型 二、用输入－输出方程描述的模型参考自适应系统 用输入－ 信号综合自适应方案中 在信号综合自适应方案中，可调系统的输入输出方程为
2.2 模型参考自适应控制
2.2.1 模型参考自适应控制的数学描述
不为0 广义误差向量 e 不为0时，自适应机构按照一定规律改变可调机构的结构或参 数或直接改变被控对象的输入信号， 数或直接改变被控对象的输入信号，以使得系统的性能指标达到或接近希望的性能 指标。 指标。 参数自适应方案：通过更新可调机构的参数来实现的模型参考自适应控制。 参数自适应方案：通过更新可调机构的参数来实现的模型参考自适应控制。 可调机构的参数来实现的模型参考自适应控制 信号综合自适应方案：通过改变施加到系统的输入端信号来实现的模型参考自适应 信号综合自适应方案：通过改变施加到系统的输入端信号来实现的模型参考自适应 系统的输入端信号 控制。 控制。
模型参考自适应控制—MIT法
一 原理及方法模型参考自适应系统，是用理想模型代表过程期望的动态特征，可使被控系统的特征与理想模型相一致。
一般模型参考自适应控制系统的结构如图1所示。
图1 一般的模型参考自适应控制系统其工作原理为，当外界条件发生变化或出现干扰时，被控对象的特征也会产生相应的变化，通过检测出实际系统与理想模型之间的误差，由自适应机构对可调系统的参数进行调整，补偿外界环境或其他干扰对系统的影响，逐步使性能指标达到最小值。
基于这种结构的模型参考自适应控制有很多种方案，其中由麻省理工学院科研人员首先利用局部参数最优化方法设计出世界上第一个真正意义上的自适应控制律，简称为MIT 自适应控制，其结构如图2所示。
图2 MIT 控制结构图系统中，理想模型Km 为常数，由期望动态特性所得，被控系统中的增益Kp 在外界环境发生变化或有其他干扰出现时可能会受到影响而产生变化，从而使其动态特征发生偏离。
而Kp 的变化是不可测量的，但这种特性的变化会体现在广义误差e 上，为了消除或降低由于Kp 的变化造成的影响，在系统中增加一个可调增益Kc ，来补偿Kp 的变化，自适应机构的任务即是依据误差最小指标及时调整Kc ，使得Kc 与Kp 的乘积始终与理想的Km 一致，这里使用的优化方法为最优梯度法，自适应律为：⎰⨯+=tm d y e B Kc t Kc 0)0()(τMIT 方法的优点在于理论简单，实施方便，动态过程总偏差小，偏差消除的速率快，而Yp Yme+__+R参考模型调节器被控对象适应机构可调系统———kmq(s)p(s)KcKpq(s)-----p(s)适应律Rymype+-且用模拟元件就可以实现；缺点是不能保证过程的稳定性，换言之，被控对象可能会发散。
二 对象及参考模型该实验中我们使用的对象为：122)()()(2++==s s s p s q K s G pp 参考模型为：121)()()(2++==s s s p s q K s G mm 用局部参数最优化方法设计一个模型参考自适应系统，设可调增益的初值Kc(0)=0.2，给定值r(t)为单位阶跃信号，即r(t)=A ×1(t)。
自适应控制的分类_自适应控制的主要类型
自适应控制的分类_自适应控制的主要类型什么是自适应控制1、自适应控制所讨论的对象，一般是指对象的结构已知，仅仅是参数未知，而且采用的控制方法仍是基于数学模型的方法。
2、但实践中我们还会遇到结构和参数都未知的对象，比如一些运行机理特别复杂，目前尚未被人们充分理解的对象，不可能建立有效的数学模型，因而无法沿用基于数学模型的方法解决其控制问题，这时需要借助人工智能学科，也就是智能控制。
3、自适应控制与常规的控制与最优控制一样，是一种基于数学模型的控制方法。
4、自适应控制所依据的关于模型的和扰动的先验知识比较少，需要在系统的运行过程中不断提取有关模型的信息，使模型愈来愈准确。
5、常规的反馈控制具有一定的鲁棒性，但是由于控制器参数是固定的，当不确定性很大时，系统的性能会大幅下降，甚至失稳。
自适应控制的原理框图自适应控制的分类自从50年代末由美国麻省理工学院提出第一个自适应控制系统以来，先后出现过许多不同形式的自适应控制系统。
比较成熟的自适应控制系统有下述几大类。
（1）可变增益自适应控制系统这类自适应控制系统结构简单，响应迅速，在许多方面都有应用。
其结构如图1所示，调节器按被控过程的参数的变化规律进行设计，也就是当被控对象（或控制过程）的参数因工作状态或环境情况的变化而变化时，通过能够测量到的某些变量，经过计算而按规定的程序来改变调节器的增益，以使系统保持较好的运行性能。
另外在某些具有非线性校正装置和变结构系统中，由于调节器本身对系统参数变化不灵敏。
采用此种自适应控制方案往往能去的较满意的效果。
（2）模型参考自适应控制系统（Model Reference Adaptive System，简称MRAS）模型参考自适应控制系统由以下几部分组成，即参考模型、被控对象、反馈控制器和调整控制器参数的自适应机构等部分组成，如图2所示。
模型参考自适应控制系统
“匹配”。 将 a*(s) , b*(s) 代入“可调系统”，则模型参数辨时器
(s) (s)
的结构图（P29图）变为Fig 2.（ 7 P37书）
r p(s) SI 1b
a0 aT
可调系统
yp (t)
SI 1b －
b0
bT
e1(t)
ym (t)
则kc
B'
J kc
B'
t 0
2e1
e1 kc
d
B
t 0
e1
e1 kc
d
kc
Be1
e1 kc
而开环传函：e (s)
(km
kck p )
z(s) R(s)
e1 ( s) r(s)
(1)
对应的微分方程为：R( p)e1 (km kck p )z( p)r
两边对kc求导：
R( p) e1 kc
(s)
b0*
b*T
(sI
)1b
w(2) (s) yp (s)
b、状态方程描述：w (1) w(1) b r
w (2) w(2) b y p
举例：以三阶前馈滤波器为例。( P36 )
n 1 3阶输输出入：：wr(1) 状态空间结构图见Fig 2.6
5、模型参考辨识器的结构：
定义回归向量w(t) : wT (t) r(t), w(1) (t), y p (t), w(2) (t) R2n 设标称参数向量： * a0*, a*T , b0*, b*T R2n
第一节 概述
3.1.1 模型参考自适应控制系统的结构 3.1.2 MRAC的设计问题
3.1.1 模型参考自适应控制系统的结构
模型参考自适应控制
针对不同的被控对象和工况，需要设计相应的调整策略，以快速响应系统变化并保持控制性能。这需 要对被控系统的特性和动态行为有深入了解。
模型参考自适应控制在复杂系统中的应用拓展
复杂系统控制
模型参考自适应控制适用于具有非线性、时变和不确定性的复杂系统。通过设计合适的 自适应律和控制器，可以实现对复杂系统的有效控制。
2
在模型参考自适应控制中，滑模控制可以用于设 计自适应控制器，使得被控系统的状态跟踪误差 收敛到零。
3
滑模控制具有鲁棒性强、对系统参数变化不敏感 等优点，因此在模型参考自适应控制中具有广泛 的应用前景。
基于模糊逻辑的模型参考自适应控制
模糊逻辑是一种处理不确定性和模糊信息的智能控制方法，通过将模糊集合和模糊推理规则应用于控 制系统，可以实现模型参考自适应控制。
系统稳定性
系统稳定性是确保控制过程平稳、可靠的关键因素。在模型参考自适应控制中，需要权衡控制精度和系统稳定在线优化
模型参考自适应控制需要在线优化控制参数，以适应系统状态的变化和外部扰动。优化算法的选择和 应用对于提高控制性能和系统适应性至关重要。
化工过程控制
在化工生产过程中，模型参考自适应控制用于实现反应过程的优化 和稳定控制，提高生产效率和产品质量。
智能制造系统
在智能制造领域，模型参考自适应控制用于自动化流水线和智能机 器人的精确控制，提高生产效率和降低能耗。
机器人领域的应用
移动机器人导航
模型参考自适应控制用于移动机器人的路径规划和避障，提高机 器人在复杂环境下的自主导航能力。
应用领域
模型参考自适应控制的应用领域广泛，包括航空航天、机器人、电力系统和化工过程等。 随着技术的不断发展，其在智能制造、新能源和生物医学等领域的应用前景也日益广阔。
自适应控制（研究生经典教材）
自适应控制Adaptive control1.关于控制2.关于自适应控制3.模型参考自适应控制4.自校正控制5.自适应替代方案6.预测控制参考文献主要章节内容说明：第一部分：第一章自适应律的设计§1.参数最优化方法§2.基于Lyapunov稳定性理论的方法§3.超稳定性理论在自适应控制中的应用第二章误差模型§1.Narendra误差模型§2.增广矩阵§3.线性误差模型第三章MRAC的设计和实现第四章小结第二部分：第一章模型辨识及控制器设计§1.系统模型：CARMA模型§2.参数估计：LS法§3.控制器的设计方法：利用传递函数模型§4.自校正第二章最小方差自校正控制§1.最小方差自校正调节器§2.广义最小方差自校正控制第三章极点配置自校正控制§1.间接自校正§2.直接自校正1.About control engineering education1)control curriculum basic concept(1)dynamic system●The processes and plants that are controlled have responses that evolvein time with memory of past responses●The most common mathematical tool used to describe dynamic system isthe ordinary differential equation (ODE).●First approximate the equation as linear and time-invariant. Thenextensions can be made from this foundation that are nonlinear 、time-varying、sampled-data、distributed parameter and so on.●Method of building model (or equation )a)Idea of writing equations of motion based on the physics andchemistry of the situation.b)That of system identification based on experimental data.●Part of understanding the dynamical system requires understanding theperformance limitations and expectation of the system.2.stabilityWith stability, the system can at least be used●Classical control design method, are based on a stability test.Root locus 根轨迹Bode‟s frequency response 波特图Nyquist stability criterion 奈奎斯特判据●Optimal control, especially linear-quadratic Gaussian (LQG) control (线性二次型高斯问题) was always haunted by the fact that method did notinclude a guarantee of margin of stability.The theory and techniques of robust (鲁棒)design have been developedas alternative to LQG●In the realm of nonlinear control, including adaptive control, it iscommon practice to base the design on Lyapunov function in order to beable to guarantee stability of final result.3.feedbackMany open-loop devices such as programmable logic controllers (PLC) are in use, their design and use are not part of control engineering.●The introduction of feedback brings costs as well as benefits. Among thecosts are need for both actuators and sensors, especially sensors.●Actuator defines the control authority and set the limits of speed indynamic response.●Sensor via their inevitable noise, limit the ultimate(最终) accuracy ofcontrol within these limits, feedback affords the benefit of improveddynamic response and stability margins, improved disturbancerejection(拒绝) ，and improved robustness to parameter variability.●The trade off between costs and benefits of feedback is at the center ofcontrol design.4.Dynamic compensation●In beginning there was PID compensation, today remaining a widely usedelement of control, especially in the process control.●Other compensation approaches : lead-and-log networks (超前-滞后)observer-based compensators include : pole placement, LQG designs.●Of increasing interest are designs capable of including trade-off amongstability, dynamic response and parameter robustness.Include: Q parameterization, adaptive schemes.Such as self-tuning regulators, neural-network-based-controllers.二、historical perspectives (透视)●Most of early control manifestations appear as simple on-off (bang-bang)controllers with empirical (实验；经验性的) setting much dependent uponexperience.●The following advances such as Routhis and Hurwitz stability analysis(1877).Lyapunov‟s state model and nonlinear stability criteria(判据) (1890) .Sperry‟s early work on gyroscope and autopilots (1910), and Sikorsky‟swork on ship steering (1923)Take differential equation, Heaviside operators and Laplace transform astheir tools.●电机工程(electrical engineering)The largely changed in the late 1920s and 1930s with Black‟s developmentof the feedback electronic amplifier, Bush‟s differential analyzer, Nyquist‟sstability criterion and Bode‟s frequency response methods.The electrical engineering problems faced usually had vary complex albeitmostly linear model and had arbitrary (独立的；随机的) and wide-ringingdynamics.●过程控制(process control in chemical engineering)Most of the progress controlled were complex and highly nonlinear, butusually had relatively docile (易于处理的) dynamics.One major outcome of this type of work was Ziegler-Nichols‟PIDthres-term controller. This control approach is still in use today, worldwidewith relatively minor modifications and upgrades (including sampled dataPID controllers with feed forward control, anti-integrator-windupcontrollers :抗积分饱和，and fuzzy logic implementations).●机械工程(mechanical engineering)The application of controls in mechanical engineering dealt mostly in thebeginning with mechanism controls, such as servomechanisms, governorsand robots.Some typical control application areas now include manufacturing processcontrols, vehicle dynamic and safety control, biomedical devices and geneticprocess research.Some early methodological outcomes were the olden burger-Kahenbugerdescribing function method of equivalent linearization, and minimum-time,bang-bang control.●航空工程（aeronautical engineering ）The problems were generally a hybrid (混合) of well-modeled mechanicsplus marginally understood fluid dynamics. The models were often weaklynonlinear, and the dynamics were sometimes unstable.Major contributions to framework of controls as discipline were Evan‟s rootlocus (1948) and gain-scheduling.●Additional major contributions to growth of the discipline of control over thelast 30-40 years have tended to be independent of traditional disciplines.Examples include:Pontryagin‟s maximum principle (1956) 庞特里金Bellman‟s dynamic programming (1957)贝尔曼Kalman‟s optimal estimation (1960)And the recent advances in robust control.三、Abstract thoughts on curriculum●The possibilities for topic to teach are sufficiently great. If one tries topresent proofs of all theoretical results. One is in danger of giving thestudents many mathematical details with little physical intuition orappreciation for the purposes for which the system is designed.●Control is based on two distinct streams of thought. One stream is physicaland discipline-based. Because one must always be controlling some thing.The other stream is mathematics-based, because the basis concepts ofstability and feedback are fundamentally abstract concepts best expressedmathematically. This duality(两重性) has raised, over the years, regularcomplaints about the …gap‟ between theory and practice.●The control curriculum typically begins with one or two courses designed topresent an overview of control based on linear, constant, ODE models,s-plane and Nyquist‟s stability ideas, SISO feedback and PID, lead-lay andpole-placement compensation.These introductory courses can then be followed by courses in linear systemtheory, digital of control, optimal control, advanced theory of feedback, andsystem identification.四、Main control courses●Introduction to controlLumped system theoryNonlinear controlOptimal controlAdaptive controlRobot controlDigital controlModeling and simulationAdvanced theoryStochastic processesLarge scale multivariable systemManufacturing systemFuzzy logic Neural Networks外文期刊：《Automatic》IFAC 国际自动控制联合会Computer and control abstractsIEEE translations on Automatic controlAutomation●Specialized \ experimental courses✓Intelligent controlApplication of Artificial IntelligenceSimulation and optimization of lager scale systems robust control ✓System identification✓Microcomputer-based control systemDiscrete-event systemsParallel and Distributed computationNumerical optimization methodsNumerical system theory●Top key works from 1963-1995 in IIACAdaptive control 305Optimal control 277Identification 255Parameter estimation 244Stability 217Linear system 184Non-linear systems 168Robust control 158Discrete-time systems 143Multivariable systems 140Robustness 140Multivariable systems control systems 110Optimization 110Computer control 104Large-scale systems 103Kalman filter 102Modeling 107为什么自适应 《Astrom 》chapter 1✓ 反馈可以消除扰动。
自适应控制课件
(2.1)
m维分段连续的输入向量 维分段连续的输入向量 n维状态向量 n维状态向量 相应维数常数矩阵 参考模型为稳定的，并且是完全可控和完全可观测的。 参考模型为稳定的，并且是完全可控和完全可观测的。 在可调参数模型参考自适应系统中，可调系统 可调参数模型参考自适应系统中， 模型参考自适应系统中
w(k )
u (k )
y (k )
自校正控制系统结构图
2.2 模型参考自适应控制
2.2.1 模型参考自适应控制的数学描述
模型参考自适应控制系统由参考模型、可调系统和自适应机构三部分组成. 模型参考自适应控制系统由参考模型、可调系统和自适应机构三部分组成 参考模型 三部分组成
参考模型 可调机构 自适应机构 根据系统广义误差 e (t ) , 按照 一定的规律改变可调系统的结构或参数。 一定的规律改变可调系统的结构或参数。 理想模型
ɺ x m = Am x m + Bm u, x m (0) = x m 0
(2.1)
在可调参数模型参考自适应系统中，可调系统 在可调参数模型参考自适应系统中， 参数模型参考自适应系统中
ɺ x = A(e, t ) x + B (e, t )u x (0) = x 0 , A(0) = A0 , B (0) = B0
模型参考自适应控制系统结构图
2.2.1 模型参考自适应控制的数学描述
2.2.1.1 并联模型参考自适应系统的数学模型 并联模型参考自适应系统可以用状态方程和输入－输出方程进行描述。 并联模型参考自适应系统可以用状态方程和输入－输出方程进行描述。 状态方程 进行描述 一、用状态方程描述的模型参考自适应系统 对于连续模型参考自适应控制系统 对于连续模型参考自适应控制系统 连续模型 参考模型： 参考模型：
现代控制理论_第17章_模型参考自适应控制
(17-31)
根据劳斯稳定性判据可知，当满足以下不等式时：
K M K s Bro2 a1 a2
(17-32)
系统将不稳定。
局部参数优化法除了前面介绍的M.I.T.可调增益方案外，还有反 馈补偿器，前置反馈补偿器等多个参数同时可调的方案，这里就不 一一介绍了。这类方案有共同的缺点，即不能保证自适应系统的稳 定性，最后均必须对整个的稳定性检验。另外，由于各种参数优化 方法都要求对参数进行搜索，这就需要一定的搜索时间，所以自适 应速度比较低。还要求参考模型应相当精确地反映受控系统的动态 特性，以使参数的误差不致过大以免造成系统过度扰动。
统的基本结构如图17－1所示。
图（17-1）模型参考自适应系统基 本结构图
模型参考自适应控制问题的提法可归纳：根据获得的有关受
控对象及参考模型的信息（状态、输出、误差、输入等）设 计一个自适应控制律，按照该控制律自动地调整控制器的可 调参数（参数自适应）或形成辅助输入信号（信号综合自适 应），使可调系统的动态特性尽量接近理想的参考模型的动
生相应变化，由自适应机构检测理想模型与实际系统之 间的误差，例如水箱液面控制系统。对系统的可调参数 进行调整，且寻求最优的参数，使性能指标处于超曲面 的最小值或其邻域内。
最常用的参数最优化方法有梯度法、共轭梯度法等。这种设
计方法最早是由M.I.T.在五十年代末提出来的，故M.I.T.法。
M.I.T.提出的自适应方案假定受控对象传递函数为：
WM s
KM a2 s 2 a1s 1
试按M.I.T.自适应方案设计自适应系统。
解:
系统数学模型为 输出误差： 模型输出： 自适应律：
模型参考自适应控制
e
c
(Km
'eym
K
p
Kc
)r
设在t=0时，输入r(t)=R(阶跃),假定ym的动态响应比e的自适应调
整过程快得多，则当时间充分长以后，ym取稳态值KmR,yp取稳态
值Kc(0)KpR,此时输出的广义误差e满足：
a2e a1e e -KmKp' R2e
a2e a1e e KmKp' R2e 0
r(t) Kc
自适应机构
KpQ(s) P(s)
e -
y
图 1 增益可调的参考模型自适应 控制系统
即e(t)所满足的微分方程为：P(D)e (Km KcK p )Q(D)r
微分算子：D
d dt
,
D2
d2 dt 2
.
.
.
.
两边对Kc求导：
P(D) e Kc
K pQ(D)r
ym
– 对实际控制系统来说,带有微分因素的控制规律对系统的环 境变化或扰动较敏感,容易引起系统的不稳定,而且实现纯 微分环节也较困难.
– 因此,该自适应规律在具体实现上有一定困难.
– 为此，可在选择P矩阵时使P满足PB=μCT =[μ 0 … 0]T，
– μ>0此时就有
K c
er,
K p
i0
i0
下面基于李氏稳定性理论,设计比例调节器的增益Kc的自适应 规律.
• 首先定义如下广义误差 e=ym-y • 因此,误差e的传递函数为
E(s) r(s)
(Km
-
Kc Kp )
N (s) D(s)
第二章 自适应控制
(PN 1 x(n N 1)xT (n N 1))1
为避免矩阵求逆，并使 N 1 与 N 具
有一个简单的关系，利用矩阵求逆定理
PN1 PN KN1xT (n N 1)PN
（8）
K N 1
1
xT
PN x(n N (n N 1)PN
1) x(n
N
1)
将（8）式带入（7）式，整理得到最小二乘的递推公式
可写成矩阵方程
y(n 1)
YN
y(n
2)
y(n
N
)
e(n 1)
N
e(n
2)
e(n N )
xT (n 1) y(n) y(1) u(n 1) u(1)
XN
xT
n
2
y(n 1)
y(2)
u(n 2)
u(2)
xT n N y(n N ) y(N ) u(n N ) u(N )
所以新的参数估计
N 1
是用新的观测值与基于老
模型预测得到的量xT (n N
数
N
加以修正得到。
K N 1
1为)修N 正之系偏数差.，对老参
因此，若知道前一时刻的
道
N 1
了，
N
PN
，我们就可以知
确定
o
Po
的初值的方法
（1）若已知参数的大致范围，可在此范围内确定初 值
（2）若完全不知道，参数范围可简单取
n 方程的阶数;e(k) 为不可测量的随机干扰
问题: 假设方程阶数n已知,如何由输入输出的 观测数
据 y(k) , u(k) 来估计模型的参数 a1,a2 an,b0,b1, bn
2模型参数的最小二乘估计方法
自适应控制技术
模型参考自适应控制系统模型参考自适应系统是比较常用的自适应系统，对于这类系统，人们已经提出了许多的设计方法，有的比较成熟，有的还正在发展，尚待完善。
从工程实施的观点出发，希望设计出的系统能在性能和复杂程度之间取得较好的权衡。
为了简化适应系统，希望所确定的自适应规律，无需直接求解线性或非线性方程。
因此，2模型参考自适应系统的设计问题看做是系统的参数或状态平衡位置而进行自动调整的问题。
1模型参考自适应控制系统典型结构模型参考自适应控制系统有参考模型、可调系统和自适应机构3部分组成，常见的一种典型结构如下图所示。
由四部分组成：◆带有未知参数的被控对象假设被控对象的结构已知。
对于线性系统，这意味着系统的极点数和零点数是已知的，但它们的位置是未知的。
◆参考模型（它描述控制系统的期望的输出）应当能反映控制任务中的指定的性能；规定的理想性态应当是自适应控制系统可以达到的，即当给定对象模型结构后，对参考模型的结构有一些特有的限制（如阶数和相对阶）。
◆带有可校正参数的反馈控制律可以得到一族控制器；应当具有“完全的跟踪能力”，达到跟踪收敛，即当被控对象的参数精确已知时，相应的控制律应当使系统的输出与参考模型的输出相等；现有的自适应控制设计通常要求控制器参数线性化。
如果控制规律中可调整的参数是线性的，则称控制器是参数线性化的。
◆ 校正参数的自适应机制能保证当参数变化时系统稳定并使得跟踪误差收敛到零； 设计方法有李雅普诺夫定理，超稳定性理论，耗散理论等。
2质量未知的模型参考自适应控制图1.2 一个非线性质量一阻尼—弹簧系统图1.2中的质量一阻尼—弹簧系统，其动力学方程为301||0mxbx x k x k x +++=其中，||bxx 表示非线性耗散式阻尼，而31()k x k x +代表非线性弹簧。
考查用电动机力u 控制一个质量为m 的质点在没有摩擦的表面上运动，其性态可以描述为x m = （1.1）假设给控制系统发出定位指令)(t r 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一阶系统的阶跃响应
自 适 应 控 制
µ=0.5
一阶系统的阶跃响应
自 适 应 控 制
µ=0.02
一阶系统的阶跃响应
自 适 应 控 制
µ=50
一阶系统的正弦响应
自 适 应 控 制
µ=5.5，r(t)=sin ωt， ω=4.5 rad/sec ， ，
一阶系统的正弦响应
自 适 应 控 制
µ=6，r(t)=sin ωt， ω=4.5 rad/sec ， ，
并联MRAS 并联MRAS
自 适 应 控 制 参考模型
r（t） yp（t） y m （ t）
＋
e（t）广义误差
－
可调系统
自适应机构
多元函数及其偏导数
自 适 应 控 制
z
∂z ∂ x1
z=f(x1,x2)
x1
x2
方向导数
自 适 应 控 制
z
z=f(x1,x2)
α
x1
l
x2
梯度的几何意义
自 适 应 控 制
自 适 单调递增； ）设定性能指标IP 单调递增 应 （1）设定性能指标 RM，使IPRM对| e(t)|单调递增； 控 制 （2）将IPRM表示为参数空间上的一个多元函数； 表示为参数空间上的一个多元函数 参数空间上的一个多元函数； ）
（3）寻找使 RM取得局部极小值的参数值； ）寻找使IP 取得局部极小值的参数值； （4）控制器参数寻优调节规律，就是适应律。 ）控制器参数寻优调节规律，就是适应律。 寻优调节规律
1 Y (s) = 2 R ( s ), Kv = 0.4, Kc(0) = 2 s + 2s + 1
MIT法的特点 MIT法的特点
自 适 • 应 控 制
从MIT法自适应律的推导过程可以看出几个 MIT法自适应律的推导过程可以看出几个 特点： 特点： （1）的变化速度远慢于的调节速度是一个必 要的条件，否则无法求出的导数； 要的条件，否则无法求出的导数； 系统动态响应速度要远快于调节速度； （2）系统动态响应速度要远快于调节速度； 自适应机构包含积分环节， （3）自适应机构包含积分环节，自适应调节 有关， 效果与ym有关，即与参考模型传递函数和输 有关。 入r(t)有关。
一阶系统的正弦响应
自 适 应 控 制
µ=80，r(t)=sin ωt， ω=2 rad/sec ， ，
二阶系统的阶跃响应
自 适 应 控 制
µ=2
二阶系统的阶跃响应
自 适 应 控 制
µ=5
二阶系统的阶跃响应
自 适 应 控 制
µ=5.5
•
•
一阶系统稳定性分析
自 适 应 控 制
• MIT方案中，调节Kc的目标是使广义误 MIT方案中，调节Kc的目标是使广义误 方案中 Kc 逐步趋近于零。 差e(t)逐步趋近于零。 • 因此MIT法自适应控制系统的稳定性应当 因此MIT MIT法自适应控制系统的稳定性应当 的动态特性进行分析。 以广义误差e(t)的动态特性进行分析。
• • •
MIT法的特点 MIT法的特点
自 适 • 应 控 制
（4）自适应过程不具智能性，整个系统是非 自适应过程不具智能性， 线性系统， 线性系统，且只能解决对象参数局部时变的 问题。 问题。 由人工设定， （5）µ由人工设定，与梯度法的步长λ成正 因此可以视为自适应调节的步长， 比，因此可以视为自适应调节的步长，或称 为自适应增益，其值影响自适应过程收敛的 为自适应增益， 速度和精度，需要通过实验来确定。 速度和精度，需要通过实验来确定。 （6）性能指标可以选择各种形式
自适应控制
第二讲 模型参考自适应控制 MIT法 的MIT法
预备知识 MIT法的基本原理 MIT法的基本原理 MIT法的仿真实验及其分析 MIT法的仿真实验及其分析
模式识别与智能系统研究所,6号教学楼703 ,6号教学楼 潘峰 模式识别与智能系统研究所,6号教学楼703 andropan@ 68913261
grad z
自 适 应 控 制
只有当目标函数的等高线轮廓球形(或在二维空间中 的圆形时)，梯度法可以一步达到极小点，否则，该 方法不一定直接指向最小点
非线性规划的梯度法
自 适 应 控 制
x*
x0
飞机自动驾驶仪
自 适 应 控 制
反馈控制器 自适应控制器
局部参数最优化设计MRAS 局部参数最优化设计MRAS
µ
s
－
yp（t）
自适应机构
课后作业
自 适 应 控 制
用Matlab对MIT方案进行仿真，参考模 Matlab对MIT方案进行仿真， 方案进行仿真 型分别为以下一阶和二阶形式： 型分别为以下一阶和二阶形式：
10 Y (s) = R ( s ), 0. 2 s + 1
Kv = 4, Kc(0) = 2
MIT法的系统模型 法的系统模型
自 适 应 控 制
N(s) K D(s)
r（t）
ym（t）ቤተ መጻሕፍቲ ባይዱ
＋
e（t）广义误差
Kc
N(s) Kv D(s)
－
yp（t）
自适应机构
MIT自适应控制方案 MIT自适应控制方案
自 适 应 控 制
N(s) K D(s)
r（t）
ym（t）
＋
e（t）
Kc
N(s) Kv D(s)