启智杯考前模拟训练题50题有答案 的
“启智杯”训练题(附答案)

1.一张三角形纸片,请你剪去一个角,还剩几个角?怎么剪?答案如图所示:2.规定四个碗可换一个炒饭,某小队28人来吃饭,问至少买多少碗炒饭才能保证每人一碗?答案:三个空碗=一炒饭(不含碗)所以只需花钱买21碗,然后21个碗可换4碗炒饭共28碗。
3.2011个碗,碗口朝下,每次翻动4个,能否经过若干次翻动,使所有碗口全部碗口朝上?每次五个呢?答案:2011个碗口全向下,需翻动奇数次,但4的倍数均为偶数,所以不行。
每次翻动5个,依次翻2011/5次即可。
1、一刀可将薄饼切成两块,2刀最多切成四块,7刀最多切成几块?答:2、有一堆小朋友,如果8人一组,多2人;如果9人一组,多3人;如果10人一组,多4人,求最少几个小朋友?答:每8人一组差6人,每9人一组差6人,每10人一组差6人,所以:[8,9,10]360-6=354(人)3、在一长方形纸上有2011个点,这些点任意三点都不在同一条直线上,现在以这20 11个点及长方形四个顶点为顶点,将长方形纸片剪开,最多剪出几个三角形?答:4+(2011-1)X2=40241、下面是一串打乱顺序的数字,请找出规律。
3 5 13 21 1 1 2 8答:1 1 2 3 5 8 13 212、有三封不同的信,四个信箱可供传递,共有多少种投信方式?答:4X4X4=64(种)3、 A、B不同,求A+B。
答:A=38 B=83A+B=38+83=1211、一根钢管锯成5段,用20分钟;锯成12段用多少时间?答:20/(5-1)=5(分)5X(12-1)=55(分)2、答:(7+4+2)X2=263、一群男生女生在一起游戏,一个女生说:“我看到的男同学比女同学多一人”,一男生说:“我们男生我能看到6人。
”问,共多少个学生?答:男:6+1=7(人)女:7-1=6(人)共:7+7=14(人)1、一猴子爬树,每爬上5米,下落4米,树高14米,爬几次能上到树顶?答:(14-5)/(5-4)=99+1=10(次)2、移动2根火柴,使4个正方形变6个。
第1~6届启智杯真题+答案
6.已知 a 1 1 1 23
1 ,b 1 2 4 5 7 8
672
369
2014 2015 .求 a b 的值,写出计算过程. 2016
7.下图左边是一个 4 4 的正方形去掉六个1 1的小正方形后剩下的“十字”形图形,右边的六个图形也是有 1 1的小正方形拼成的图形,这些图形中,选择两块可以在平面上移动(可转动,但不翻动)拼成左边“十 字”形图形,请把所有可能选出两块的拼法画在“十字”形图形上,并标出拼图组件所对应的字母.
7.在一个孤岛上生活着三种怪物:奇虎、奇狮、奇豹,数量分别为 2010、2015、2020 个.这些怪物有一种 古怪的习性:它们任何两种怪物一旦见面,就双方都变成第三种怪物(比如,一个奇虎和一个奇狮见面,就 都变成奇豹),见一种怪物见面则不会产生变化.问,如此下去,它们是否有可能到某种时刻全部变成同一 种怪物?请说明理由.
10.右边乘法算式中,只有四个位置源自的数已知,它们分别是 2,0,1,5,请你在空白位置填上数字,使 得算式能够成立,写出所有可能成立的算式.
3
11.如下图,在正方形 ABCD 的四个顶点 A 、 B 、 C 、 D 上按照顺时针方向依次进行如下标注:首先在顶 点 A 、 B 上分别标注数 1、2,之后将 AB 两点的标注数之和(1+2=3)标注在下一个顶点 C 处,再将 BC 两 点的标注数之和(2+3=5)标注在下一个顶点 D 处.接下来再把 A 点的标注数 1 擦去,将 CD 两点的标注数 之和(3+5=8)标注在 A 点,如此下去,请问:对 A 点进行第 2015 次标注的数被 3 除的余数是多少?说明 你的依据.
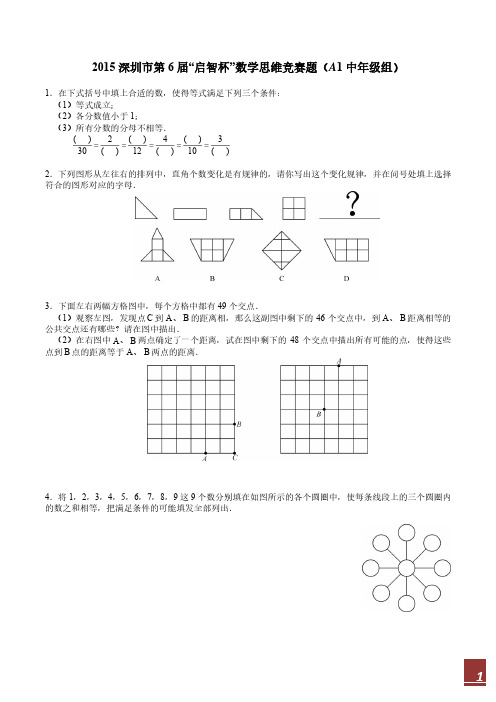
2015 深圳市第 6 届“启智杯”数学思维竞赛题(A1 中年级组)
启智杯考前模拟训练题50题有答案 的

启智杯考前模拟训练题50题1. 方兴超市购进一批食盐,第一个月售出这批食盐的40%,第二个月又售出420袋,这时已售出的和剩下的食盐的数量比是3:1,则方兴超市购进的这批食盐有 袋.【解析】 分百应用题,寻找量率对应,420所对应的率为140%25%35%--=,42035%1200÷=(袋)2. 已知甲乙两数的和是231,已知甲数的末位是0,如果把甲数末位0去掉,正好等于乙数,那么乙数是 ,甲数是 .【解析】 乙数:21;甲数:2103. 如图,三个图形的周长相等,则::a b c = .【解析】 45,:5:4b a b a ==,65,:5:6a c a c ==,得到::20:25:24a b c =4. 一瓶可乐2.5元,3个空瓶可以再换一瓶可乐.有30元,最多可以喝到 瓶可乐.【解析】 3个空瓶可以换一瓶,相当于买3瓶只花2瓶的钱(借一个空瓶还回去),30 2.52318÷÷⨯=(瓶)5. “12345678910111213…484950”是一个位数很多的多位数,从中划去80个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?最小为多少?【解析】 (1)这个数的位数是9+2×41=91,所以划去80个数字后是11个11位数.(2)为了使这个多位数最大,应使前面的9尽量多,所以这个多位数最大为99997484950.(3)为了使这个多位数最小,除了使第一位是1之外,还应使前面的0尽量多,这个多位数最小为10000123440.a 2a c c c c c 2a a2b2b a6. 在右边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++d W V ☆=_______. +dd WW W W W W V V☆☆ 【解析】 比较竖式中百位与十位的加法,如果十位上没有进位,那么百位上两个“□”相加等于一个“□”,得到“□”0=,这与“□”在首位不能为0矛盾,所以十位上的“□+□”肯定进位,那么百位上有“□+□110+=+□”,从而“□”9=,“☆”8=.再由个位的加法,推知“○+△8=”.从而“+++=d W V ☆98825++=”.7. 在1~100中任意取出两个不同的数相加,其和是偶数的共有多少种不同的取法?【解析】 两个数的和是偶数,通过前面刚刚学过的奇偶分析法,这两个数必然同是奇数或同是偶数,而取出的两个数与顺序无关,所以是组合问题.从50个偶数中取出2个,有2505049122521C ⨯==⨯(种)取法; 从50个奇数中取出2个,也有2505049122521C ⨯==⨯(种)取法. 根据加法原理,一共有122512252450+=(种)不同的取法.8. 正方形ABCD 的面积为9平方厘米,正方形EFGH 的面积为64平方厘米,如图所示,边BC 落在EH 上,已知三角形ACG 的面积为6.75平方厘米.则三角形ABE 的面积为 平方厘米【解析】 连接EG ,AG 与EG 平行,阴影部分面积=三角形AEC 的面积,AB =3cm ,所以EC =6.7523 4.5cm ⨯÷=,()24.5332 2.25ABE S cm =-⨯÷=V .也可以用三角形AEC 的面积减去三角形ABC 的面积得到ABE 的面积26.75 4.5 2.25cm =-=9. a 、b 、c 是整数,则(a -b )/2、(b -c )/2、(c -a )/2中( )整数.A 、至少有一个B 、仅有一个C 、仅有两个D 、没有【解析】 若均为偶数,则有三个整数,而当奇奇偶或偶偶奇时,最少整数有一个,选A10. a #b =a +b -1 ,a !b =a ×b -1(1)求3![(6#8)#(6!2)];(2)x #(x !8)=61,求x ;【解析】 (1)68(2)7x =11. 由数字0,1,3,9可以组成多少个无重复数字的自然数?【解析】 满足条件的数可以分为4类:一位、二位、三位、四位数.第一类,组成0和一位数,有4个(0不是一位数,最小的一位数是1);第二类,组成二位数,有339⨯=个;第三类,组成三位数,有33218⨯⨯=个;第四类,组成四位数,有332118⨯⨯⨯=个.由加法原理,一共可以组成49181849+++=个数.12. 如图,这是一个棋盘,将一个白子和一个黑子放在棋盘线的交叉点上,但不能在同一条棋盘线上,则有 种不同的放法.【解析】 2516400⨯=种13. 如果a ,b 均为质数,且3741a b +=,则a b +=______.【解析】 根据题意a ,b 中必然有一个偶质数2,,当2a =时,5b =,当2b =时不符合题意,所以257a b +=+=.14. 有甲、乙两堆棋子,其中甲堆棋子多于乙堆.现在按如下方法移动棋子:第一次从甲堆中拿出和乙堆一样多的棋子放到乙堆;第二次从乙堆中拿出和甲堆剩下的同样多的棋子放到甲堆;第三次又从甲堆中拿出和乙堆同样多的棋子放到乙堆.照此移法,移动三次后,甲、乙两堆棋子数恰好都是32个.问甲、乙两堆棋子原来各有多少个?【解析】 我们从最后一步倒着分析.因为第三次是从甲堆拿出棋子放到乙堆,这样做的结果是两堆棋子都是32个,因此,在未进行第三次移动之前,乙堆只有32216÷=(个)棋子,而甲堆的棋子数是321648+=(个),这样再逆推下去,逆推的过程可以用下表来表示,表中的箭头表示逆推的方向.所以,甲堆原有44个棋子;乙堆原有20个棋子.采用列表法非常清楚.【答案】甲乙两堆棋子原来各有44个和20个15. 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【解析】 所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米).16. 同学们,你玩过“扫雷”的游戏吗?在64个方格内一共有10个地雷,每格中至多有一个,对于填有数字的方格,其格内无地雷且与其相邻的所有方格中地雷的个数与该数字相等,你认为图中所标的数字_______是有雷的.【解析】 “扫雷”游戏主要考查观察能力和推理能力.先考虑标有①②的两个方格周边的情况.由于第六行有4个方格中的数字都是0,表示它们的周围没有雷,所以得到第五行前三列的3个方格都不是雷,而第四行第一列的方格中的数是1,表示它的周围有1个雷,所以标有①②的两个方格中恰好有1个雷,那么对于第三行第一列标有2的方格来说,它的周围有2个雷,其中一个在标有①②的两个方格中,另一个只能在第二行第二列的方格内.然后再看第二行第一列的方格,它的周围有1个雷,在第二行第二列的方格内,所以标有①的方格中没有雷,标有②的方格中有雷.再考虑标有③的方格的周边.由于第七行第一列的方格标有数字1,表示第八行第一、二列的两个方格中恰好有1个雷,而第七行第二列的方格标有数字2,说明它的周围有2个雷,那么一个雷在第八行第一、二列的两个方格中,另一个雷只能在标有③的方格中,所以标有③的方格中有雷.再看标有④⑤的方格的周边.由于第八行第七列的方格标有数字1,说明第八行第八列和第七行第八列的两个方格内恰有1个雷,而第七行第七列的方格也标有数字1,所以标有④的方格是没有雷的.而第六行第七列的方格标有数字3,说明它的周围有3个雷,所以标有⑤的方格是有雷的.所以图中所标数字为②、③、⑤的方格是有雷的.17. 如图3,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷.内部的小方块没有雷,数字表示所在小方块周围的雷数.图中共有 个雷.【解析】 1612113332313312111234图318.7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【解析】由图可知,长方形的长是宽的4倍,宽的6倍是24厘米,则长方形的宽是4厘米,故图中空白部分的面积是44232⨯⨯=(平方厘米).19.敌人欲从河岸B进攻对岸A,河上有13座桥,为阻止敌人进攻决定将桥炸坏.至少炸掉座桥可将敌人拦阻在河岸B.【解析】3座:5、9、1020.一班和二班的人数之比是8:7,如果将一班的8名同学调到二班去,则一班和二班的人数比变为4:5.求原来两班的人数.【解析】一班:二班=8:724:21⨯=和不变153一班:二班=4:520:25⨯=95一班向二班调了4份为8人,故每份842÷=(人),一班:24248⨯=(人)⨯=;二班:2124221.自然数N是一个两位数,它是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数有多少个?【解析】这样的自然数有4个:23,37,53,73.22.由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少.已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天.照此计算,可以供多少头牛吃10天?【解析】设1头牛1天的吃草量为“1”,那么每天自然减少的草量为:()()20105150+⨯=;10天吃完需要牛的⨯-⨯÷-=,原有草量为:()2051566510头数是:15010105÷-=(头).23.甲、乙两人同时从A点背向出发,沿400米的环形跑道行走,甲每分钟走80米,乙每分钟走50米,两人至少经过多长时间才能在A点相遇?【解析】甲、乙走一圈分别需要5分钟和8分钟,因此他们要是在A点再次相遇,两人都要走整圈数,所以所需的时间应是5和8的最小公倍数40分钟.24.长方形有四个角,剪掉一个角,还剩几个角?【解析】共有三种情况,如下图,分别剩下5、4、3个角.25.图中的三个图形都是由A、B、C、D(线段或圆)中的两个组合而成,记为A*B、C*D、A*D.请你画出表示A*C的图形.【解析】观察上图,第一个图形和第三个图形的共同之处是都有一条竖向线段,而它们共有的字母是A,因此A表示竖向线段;第二个图形与第三个图形的共同之处是都有一条横向线段,它们的共同字母是D,因此D表示横向线段.这样,由第一个图形可知B表示大圆,由第二个图形可知C表示小圆,从而A*C表示的图形应为竖向线段和小圆组合而成,即下图.26.用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上,每一个面只涂一种颜色.如图所示,现有涂色方式完全一样的四块小正方体拼成了一个长方体.试回答:每个小正方体中,红色面的对面涂的是什么色?黄色面的对面涂的是什么色?黑色面的对面是什么色?【解析】在能看见的9个面中红色出现的次数最多.观察图8—4中最上面的一个正方体,由于红色和黑色、黄色相邻,所以它的对面不可能是黑黄两色.同理,由第二个正方体可知,红色的对面不能是白色;由第三个正方体知,红色的对面不能是蓝色.所以红色的面的对面只可能是绿色.同理,黄色面的对面不可能是红色、黑色或白色,又已推知不可能是绿色,所以黄色面的对面只可能是蓝色.这样黑色面的对面就只可能是涂白色的了.27.图1是下面的表面展开图①甲正方体;②乙正方体;③丙正方体;④甲正方体或丙正方体.甲 乙 丙【解析】 从展开图可以看出,每个面上至少有一块阴影,从而排除丙;又每个面上没有相邻的两块阴影,从而排除乙.故选甲答案为①.28. 如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L 形区域乙和丙.甲的周长为4厘米,乙的边长是甲的周长的1.5倍,丙的周长是乙的周长的1.5倍,那么丙的周长为多少厘米?EF 长多少厘米?【解析】 乙的周长实际上是正方形AHJE 的周长(我们可将乙与甲重合的两条线段分别向左、向下平移),同样的,丙的周长也就是正方形ABCD 的周长.由于4 1.56AE =⨯=,6 1.59AD =⨯=,所以丙的周长为9436⨯=厘米,642EF AE AF =-=-=(厘米).29. 在一块长方形的地里有一正方形的水池(如下图).试画一条直线把除开水池外的这块地平分成两块.【解析】 用连对角线的办法找出这块长方形地的中心O 和正方形水池的中心A .过O 、A 画一条直线,这条直线正好能把除开水池外的这块地平分为两块(如右上图).FEH BA AO30. 试将任意一个矩形分成三块,然后拼成一个三角形.【解析】 方方法二:31. 900000-9=________×99999.【解析】 832. 多米诺骨牌是由塑料制成的1×2长方形,共28张,每张牌上的两个1×1正方形中刻有“点”,点的个数分别为0,1,2,…,6个不等,其中7张牌两端的点数一样,即两个0,两个1,…,两个6;其余21张牌两端的点数不一样,所谓连牌规则是指:每相邻两张牌必须有一端的点数相同,且以点数相同的端相连,例如:现将一付多米诺骨牌按连牌规则连成一条链,如果在链的一端为6点,那么在链的另一端为多少点?并简述你的理由.【解析】 由连牌规则可知,在链的内部各种点数均成对相连,即所有点都有偶数个,而6点的个数为8,所以在链的两端一定有偶数个点,所以链的另一端也应为6.33. 甲、乙两个哲人将正整数5至11分别写在7张卡片上.他们将卡片背面朝上,任意混合之后,甲取走三张,乙取走两张.剩下的两张卡片,他们谁也没看,就放到麻袋里去了.甲认真研究了自己手中的三张卡片之后,对乙说:“我知道你的两张卡片上的数的和是偶数.”试问:甲手中的三张卡片上都写了哪些数?答案是否唯一.【解析】 甲手中的8张卡片上分别写了6,8和10.甲知道其余4张卡片上分别写了哪些数,但不知道它们之中的哪两张落到了乙的手中.因此,只有在它们之中任何两张卡片上的数的和都是偶数时,甲才能说出自己的断言.而这就意味着,这4张卡片上所写的数的奇偶性相同,亦即或者都是偶数,或者都是奇数.但是由于一共只有3张卡片上写的是偶数,所以它们不可能都是偶数,从而只能都是奇数.于是3张写着偶数的卡片全都落入甲的手中.答案是唯一的.34. 三个人同时前往相距30千米的甲地,已知三人行走的速度相同,都是5千米每小时;现在还有一辆自行车,但只能一个人骑,已知骑车的速度为10千米每小时.现先让其…………中一人先骑车,到中途某地后放车放下,继续前进;第二个人到达后骑上再行驶一段后有放下让最后那人骑行,自己继续前进,这样三人同时到达甲地.问,三人花的时间各为多少?【解析】 由于每人的速度相同,所以每人行走的路程相同,骑车的路程也要相同,这样每人骑车的距离都是1/3,所以时间就是20÷5+10÷10=5小时35. 张师傅开汽车从A 到B 为平地(见下图),车速是36千米/时;从B 到C 为上山路,车速是28千米/时;从C 到D 为下山路,车速是42千米/时. 已知下山路是上山路的2倍,从A 到D 全程为72千米,张师傅开车从A 到D 共需要多少时间?【解析】 方法一:设BC 距离为:[]28,4284=(千米),所以CD 距离为842168⨯=(千米),那么B -C -D 的平均速度为:()()8416884281684236+÷÷+÷=(千米/小时),和平路的速度恰好相等,说明A -B -C -D 的平均速度为36千米/小时,所以从A -D 共需要的时间为:72362÷=(小时)方法二:设上山路为x 千米,下山路为2x 千米,则上下山的平均速度是:22824236x x x x +÷÷+÷=()()(千米/时),正好是平地的速度,所以行AD 总路程的平均速度就是36千米/时,与平地路程的长短无关.因此共需要72362÷=(小时).36. 右图是一个园林的规划图,其中,正方形的43是草地;圆的76是竹林;竹林比草地多占地450平方米. 问:水池占多少平方米?【解析】 正方形的43是草地,那如果水池占1份,草地的面积便是3份;圆的76是竹林,水池占1份,竹林的面积是6份.从而竹林比草地多出的面积是(6-3=)3份.3份的面积是450平方米,可见1份面积是450÷3=150(平方米),即水池面积是150平方米.37. 地球表面的陆地面积和海洋面积之比是29∶71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是( ).A . 284∶29B . 284∶87C . 87∶29D . 171∶113【解析】 解:设地球表面积为1,则北半球海洋面积为:0.5-0.29×34=1.134南半球海洋面积为:0.71-1.134=1.714南北半球海洋面积之比为:1.714∶1.134=171∶113 答案:D38. 对任意两个不同的自然数,将其中较大数换成这两数之差,称为一次变换.如对18和42可作这样的连续变换:18,42→18,24→18,6→12,6→6,6直到两数相同为止.问:对1234和4321作这样的连续变换最后得到的两个相同的数是 .【解析】 操作如下:1234,4321→1234,3087→1234,1853→1234,619→615,619→615,44714243前一数每次减少→…→,4→3,4→3,1→2,1→1,1实际上按此法操作最后所得两相同的数为开始两数的最大公约数.即1234与4321的最大公约数为1.此法也称为辗转相减法求最大公约数.39. 有一副扑克牌,一开始抓若干张(小于13张),然后进行下列操作:抓和手里现有的扑克牌数目相等的扑克牌,然后若扑克牌总数超过13张,则放回其中的13张,称为一次操作.进行了777次操作后,手里有7张牌,则一开始手里有多少张?【解析】 根据倒退法知道第777次操作后是7,那么第776次操作就是:()7132=10+÷,第775次操作就是102=5÷,找到规律是遇见奇数就是加13后除以2,遇见偶数就是直接除以2,所以操作后得到这样一串数为:7、10、5、9、11、12、6、3、8、4、2、1、7、10L L ,观察发现是12个一周期,所以77712=649÷L L ,所以第一次手里的数是8,一开始手里的数是4张扑克.40. 小华和爸爸分享“红、黑甜品”(红豆沙加芝麻糊).方法是:小华先将两勺红豆沙倒进盛载芝麻糊的碗中,搅匀后再取回两勺放入原先盛载红豆沙的碗中,混成后,爸爸问小华:“如果混合前红豆沙与芝麻糊的体积一样,那么混合后红豆沙含芝麻糊的分量与芝麻糊含红豆沙的分量比较,哪一个多?”.小华的正确答案是_____.【解析】 一样多41. 由于潮汐的长期作用,月球自转周期与绕地球公转周期恰好相同,这使得月球总是以相同的一面对着我们.在地球上最多能看到 50%的月球面积,从一张月球照片中最多能看到 50%的月球面积.(填“大于”、“小于”或“等于”)【解析】 小于; 小于方法一、一张静止的照片,能看到的球体面积的极限是一半,只有当距离球体无限远时才能看到球体表面积的一半.方法二、如果能看到一半,则能看到一半的直线为两条平行线,不可能相交.42. 刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【解析】 因为兄妹二人不许搭伴,所以题目条件表明:刘刚与小丽、李强与小英、李强与小红都不是兄妹.由第二盘看出,小红不是马辉的妹妹.将这些关系画在左下表中,由左下表可得右下表.刘刚与小红、马辉与小英、李强与小丽分别是兄妹.43. 甲、乙、丙、丁四个人的职业分别是教师、医生、律师、警察.已知:⑴教师不知道甲的职业;⑵医生曾给乙治过病;⑶律师是丙的法律顾问(经常见面);⑷丁不是律师;⑸乙和丙从未见过面.那么甲、乙、丙、丁的职业依次是: .【解析】 律师、教师、警察.由⑶可以知道丙不是律师,但是他见过律师,再由⑸知乙不是律师,又由⑷可知甲是律师.于是由⑴和⑶知丙不是教师,由⑵和⑸知丙不是医生,从而丙是警察.再由⑵知乙是教师,丁是医生.列表如下(列表的好处在于直观明了,不会犯错误):李强马辉刘刚小丽小红小英×√×××××√√44. 右边算式中,A 表示同一个数字,在各个□中填入适当的数字,使算式完整.那么两个乘数的差(大数减小数)是 ?11AA A ⨯【解析】 由11AA 能被11整除及只有11⨯,37⨯,99⨯的个位是1,所以A 可能为1,3,7或9,而且11AA 可分解成11与1个一位数和一个两位数的乘积.分别检验1111、1331、1771、1991,只有1771满足:177111723=⨯⨯,可知原式是77231771⨯=.所以两个乘数的差是772354-=.45. 电子数字0~9如图所示,右图是由电子数字组成的乘法算式,但有一些模糊不清,请将右图的电子数字恢复,并将它写成横式形式: .【解析】 ⑴可以看出乘积的百位可能是2或8,由于被乘数的十位和乘数都不能是9,最大可能为8,所以它们的乘积不超过898712⨯=,故乘积的首位不能为8,只能为2;⑵被乘数的十位和乘数要与图中相符,只能是0、2、6或8,0首先可以排除,所以可能为2、6或8;⑶如果被乘数的十位是6或8,那么乘数无论是2、6或8,都不可能乘出百位是2的三位数.所以被乘数的十位是2,相应得出乘数是8;⑷被乘数应大于200825÷=,可能为27、28或29,检验得到符合条件的答案:288224⨯=46. 有一道关于蜗牛爬墙的题:“日升六尺六,夜降三尺三,墙高一丈九,几日到顶端”.蜗牛第 天首次到顶端.【解析】 蜗牛一整天可升三尺三6.6 3.3 3.3-=,四天可升一丈三尺二,第五天白天即已经达到顶端.47. 现有5段铁链,每段上有4个封闭的铁环.现在要打开一些铁环,把这20个铁环焊接成一个一环套一环的圆圈.如果每打开一个铁环要2分钟,焊接上一个铁环要3分钟.那么焊成这个圆圈,至少需要________分钟.【解析】 把第一段的每个都打开之后用了428⨯=(分钟),下面用每个铁环把剩下的4 段铁链之间的两个相连,只需要4312⨯=(分钟).所以至少需要20分钟.48. 用数字1,1,2,2,3,3拼凑出一个六位数,使两个1之间有1个数字,两个2之间有2个数字,两个3之间有3个数字.【解析】 312132 23121349. 一城镇共有5000户居民,每户居民的小孩都不超过两个.其中一部分家庭每户有一个小孩,余下家庭的一半每户有两个小孩,则此城镇共有 个小孩.【解析】 5000户居民可以分为三部分:(1)只有1个小孩的;(2)有2个小孩的;(3)没有小孩的.其中(2)与(3)的居民相同,我们就可以将有2个小孩的家庭的其中1个孩子分给没有小孩的家庭,这样5000户居民每个家庭都有1个小孩,所以这城镇共有5000个小孩.50. 若干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了.小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下.小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子.问共有多少个盒子?【解析】 原来有个空的,说明现在也有个空的;现在空的说明原来这盒有1个,当然现在也必须有个盒子有1个;现在盒中有1个,说明原来是2个,当然现在也必须有个盒子有2个;……考虑50多,所以有0+1+2+3+4+5+6+7+8+9+10=55 共11个盒子.第8题。
第八届“启智杯”数学思维能力竞赛集训(一)代数--观察与归纳(含答案)

第八届“启智杯”数学思维能力竞赛集训(一)代数---观察与归纳【备注】一、考察的思维品质考察数学思维的广阔性、深刻性、灵活性、独创性与批判性。
二、考察的思维能力1.发散性思维能力:直觉思维——数学直觉和数学灵感;形象思维——数学表象和数学想象。
2.收敛性思维能力:逻辑思维——形式逻辑、数理逻辑、辩证逻辑。
3、从个别事例开始,先观察、研究这类问题的几个简单的、特殊的情况的共同特征,通过逆推、比较、分析,从中发现一般规律,找到解决问题的途径和方法,叫做归纳思维同步练习1.找规律填数(1)30、36、31、40、32、44、()、()(2)2, 6, 4, 12, 10, 30, 28,(),()【参考答案】(1)30、36、31、40、32、44、(33 )、(48 )(2)2, 6, 4, 12, 10, 30, 28,(84 ),(82 )乘3减22.根据规律填数。
43×101=4343 29×101=292951×101=()86×()=8686()×101=7272 ()×()=9494【参考答案】51×101=(5151 )86×(101 )=8686(72 )×101=7272 (94 )×(101 )=94943.根据规律填数。
67×67=4489667×667=4448896667×6667=()66......67× 66......67=44......488 (89)【参考答案】101个4,100个84.观察下面的几个算式,找出规律:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,……利用上面的规律,请你迅速算出:1+2+3+……+99+100+99+……+3+2+1=________.【参考答案】1002=100005. 一串分数按规律排列:11,12,21,13,22,31,14,23,32,41,15,24,33,42,51……,那么,第100个分数是多少? 2011是排列中的第 个分数。
第一届启智杯真题及答案详解

7. 解:不必问月球赤道的半径是多大,也用不着做计算,头顶只比脚底多走的路程还是只有 18.84 米。 因为在刚才解答环绕地球旅行的问题时,地球赤道的半径在计算过程中消去了,计算结果与脚底圆周 的半径无关。 8. 解:实验归纳:在 n 刀的基础上再增加一刀,就增加了 n 块。共 37 个
9. 解:如图,假定此人在 P 点遇到接他的汽车,也就 是说,与往常相比,汽车少车两个 PB(一个来回) , 结果少用 10 分钟, 说明走一个 PB 需 5 分钟.汽车到单 位应是 5 点钟,那么到 P 点是 4 点 55 分,也就是,此 人 4 点开始从办公室出来, 4 点 55 分在 P 点遇到汽车, 共走了 55 分钟。
6.商店规定 4 个空汽水瓶可换一瓶汽水,某班 28 位同学春游,他们至少买多少瓶汽水才能确保每人 有一瓶汽水喝?
1
理科教研部
7.一位 3 米高的巨人,沿赤道环绕地球步行一周。那么他的脚底沿赤道圆周移动了一圈,他的头顶画 出了一个比赤道更大的圆。已知地球赤道的半径是 6371 千米。在这次环球旅行中,这位巨人的头顶比 他的脚底多走了多少千米? 巨人的脚底走过的圆, 半径是 6371 千米。巨人的身高是 3 米,所以他的头顶走过的圆,半径增加 3 米。 都用千米做长度单位,半径增加的数量就是 0.003 千米。取圆周率的近似值为 3.14,那么两圆周长的 差=3.14×2×(6371+0.003)-3.14×2×6371=3.14×2×0.003=0.01884(千米)=18.84(米)。 结论是:环绕地球一周,巨人的头顶只比脚底多走 18.84 米。 如果这位巨人打算再环绕月球表面步行一圈,那样一圈走下来,他的头顶比脚底多走了________ 千米呢? 8.我们知道:1 刀可以把一个蛋糕切成两块,2 刀最多可以把一个蛋糕切成四块,那么 8 刀最多可以把 一个蛋糕切成________块。
第四届启智杯训练试题

39
70
2
27
976
823
-1
725
708
98
-5
983
36
32
37
-31
-40
60
12
8
180
47
1
34
46
3
8
9
867
231
-34
-629
571
5
1
792
35
21
78
41
891
9
62
167
8
28
-793
38
3
1
6
-45
125
380
81
-345
7
83
1
96
-352
98
6
101
69
-6
475
457
二六
二七
二八
二九
三十
658
7
5
6
4
82
7
9
78
48
5
56
63
7
74
9
57
3
43
83
8
24
3
40
-6
305
6
25
864
175
62
5
8
872
350
34
12
91
5
-85
3
865
781
-281
-89
71
261
7
-162
231
64
4
57
349
349
启智杯模拟练习精选30题答案[1]
![启智杯模拟练习精选30题答案[1]](https://img.taocdn.com/s3/m/3c9a7963a98271fe910ef999.png)
为杯口朝上;每次翻动 9 只水杯,经过若干次翻动,________使所有茶杯全变为杯口朝上.
【解析】由奇偶性可知:奇数个奇数之和还是奇数,偶数与偶数的和还是偶数,所以每次翻动 6 只水杯不能 使所有茶杯全变为杯口朝上;每次翻动 5 只水杯能使所有茶杯全变为杯口朝上.
13. 锴子、娟子、臻子、顺子四人,他们各自过一座桥所需要的时间分别是 1 分钟,2 分钟,8
蓝天数学 涂凡才老师
第 7 页 /共 10 页
A:“是 E” ; B:“是我”; C:“是 B” ; D:“不是 E”; E:“是 B 或 H”; F:“是 E”; G:“不是 B”; H:“不是 B 也不是我”; I:“H 所说的是事实”. 其中,说实话的只有 3 个人,那么请问合格的是 .
【解析】逻辑推理,假设法。假设 A 说实话,则 F、G、H、I 也是说实话,这“与说实话的只有 3 个人”不符,所以 A 说了假话,从而 E 不合格, F 说了假话, D 说了实话. 假设 B 说实话,则 C、D、E 也是说实话,这“与说实话的只有 3 个人”不符,所以 B 说了假话,从而 B 不合格,C 说了假话, G 说了实话. E 与 H 一定是一人说假话,一人说实话,从而 I 说假话,继而得出 H 说假话, E 说实话. 所以 H 是合格的.
,B=
。
A × B 1 1 3 0 4
B A 4
3 1 5 4 【解析】 两位数 AB 既是 114 的因数, 又是 304 的因数, 经过分解质因数可以看出。 两位数 AB=38。
24. 复旦大学某班 A、B、C、D、E、F、G、H、I 共 9 名同学参加 2010 年上海世博会志愿者
知识测试.测试合格者进入志愿者选拔范围.测试结果只有一人合格.向他们询问谁合格.他们 的回答如下:
50题智商测试题(3篇)

1. 以下哪个数字不是偶数?A. 2B. 3C. 4D. 5答案:B。
偶数是能被2整除的数,而3不能被2整除。
2. 下列哪个图形与其他三个不同?A. 正方形B. 长方形C. 三角形D. 梯形答案:A。
正方形是四边相等、四个角都是直角的四边形,而其他三个图形的边长和角度都不相等。
3. 以下哪个字母不是元音字母?A. AB. EC. ID. Z答案:D。
元音字母包括A、E、I、O、U,而Z不是元音字母。
4. 下列哪个数字在1到10之间?A. 11B. 10C. 9答案:B。
10是1到10之间的数字。
5. 以下哪个词语与其他三个不同?A. 狗B. 猫C. 老虎D. 鸟答案:D。
狗、猫、老虎都是哺乳动物,而鸟是鸟类。
6. 以下哪个词语表示“美丽”?A. 美丽B. 好看C. 漂亮D. 丑陋答案:A。
美丽、好看、漂亮都表示美丽,而丑陋表示不美丽。
7. 以下哪个词语表示“悲伤”?A. 悲伤B. 快乐C. 愉快D. 开心答案:A。
悲伤表示伤心、难过,而快乐、愉快、开心表示快乐。
8. 以下哪个词语表示“帮助”?A. 帮助B. 损害D. 阻碍答案:A。
帮助、协助都表示帮助,而损害、阻碍表示不帮助。
9. 以下哪个词语表示“善良”?A. 善良B. 恶毒C. 仁慈D. 凶恶答案:A。
善良、仁慈都表示善良,而恶毒、凶恶表示不善良。
10. 以下哪个词语表示“强大”?A. 强大B. 弱小C. 坚强D. 软弱答案:A。
强大、坚强都表示强大,而弱小、软弱表示不强大。
11. 以下哪个词语表示“聪明”?A. 聪明B. 愚笨C. 智慧D. 傻瓜答案:A。
聪明、智慧都表示聪明,而愚笨、傻瓜表示不聪明。
12. 以下哪个词语表示“勇敢”?A. 勇敢C. 勇敢D. 胆小答案:A。
勇敢、勇敢都表示勇敢,而懦弱、胆小表示不勇敢。
13. 以下哪个词语表示“诚实”?A. 诚实B. 欺骗C. 诚恳D. 虚伪答案:A。
诚实、诚恳都表示诚实,而欺骗、虚伪表示不诚实。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
启智杯考前模拟训练题50题1. 方兴超市购进一批食盐,第一个月售出这批食盐的40%,第二个月又售出420袋,这时已售出的和剩下的食盐的数量比是3:1,则方兴超市购进的这批食盐有 袋.【解析】 分百应用题,寻找量率对应,420所对应的率为140%25%35%--=,42035%1200÷=(袋)2. 已知甲乙两数的和是231,已知甲数的末位是0,如果把甲数末位0去掉,正好等于乙数,那么乙数是 ,甲数是 .【解析】 乙数:21;甲数:2103. 如图,三个图形的周长相等,则::a b c = .【解析】45,:5:4b a b a ==,65,:5:6a c a c ==,得到::20:25:24a b c =4. 一瓶可乐2.5元,3个空瓶可以再换一瓶可乐.有30元,最多可以喝到 瓶可乐.【解析】 3个空瓶可以换一瓶,相当于买3瓶只花2瓶的钱(借一个空瓶还回去),30 2.52318÷÷⨯=(瓶)5. “12345678910111213…484950”是一个位数很多的多位数,从中划去80个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?最小为多少?【解析】 (1)这个数的位数是9+2×41=91,所以划去80个数字后是11个11位数.(2)为了使这个多位数最大,应使前面的9尽量多,所以这个多位数最大为99997484950.(3)为了使这个多位数最小,除了使第一位是1之外,还应使前面的0尽量多,这个多位数最小为10000123440.6. 在右边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++☆=_______.+☆☆【解析】 比较竖式中百位与十位的加法,如果十位上没有进位,那么百位上两个“□”相加等于一个“□”,得到“□”0=,这与“□”在首位不能为0矛盾,所以十位上的“□+□”肯定进位,那么百位上有“□+□110+=+□”,从而“□”9=,“☆”8=.再由个位的加法,推知“○+△8=”.从而“+++=☆98825++=”.7. 在1~100中任意取出两个不同的数相加,其和是偶数的共有多少种不同的取法? a 2a c c c c c 2a a2b2b a【解析】 两个数的和是偶数,通过前面刚刚学过的奇偶分析法,这两个数必然同是奇数或同是偶数,而取出的两个数与顺序无关,所以是组合问题.从50个偶数中取出2个,有2505049122521C ⨯==⨯(种)取法; 从50个奇数中取出2个,也有2505049122521C ⨯==⨯(种)取法. 根据加法原理,一共有122512252450+=(种)不同的取法.8. 正方形ABCD 的面积为9平方厘米,正方形EFGH 的面积为64平方厘米,如图所示,边BC 落在EH 上,已知三角形ACG 的面积为6.75平方厘米.则三角形ABE 的面积为 平方厘米【解析】 连接EG ,AG 与EG 平行,阴影部分面积=三角形AEC 的面积,AB =3cm ,所以EC =6.7523 4.5cm ⨯÷=,()24.5332 2.25ABE S cm =-⨯÷=.也可以用三角形AEC 的面积减去三角形ABC 的面积得到ABE 的面积26.75 4.5 2.25cm =-=9. a 、b 、c 是整数,则(a -b )/2、(b -c )/2、(c -a )/2中( )整数.A 、至少有一个B 、仅有一个C 、仅有两个D 、没有【解析】 若均为偶数,则有三个整数,而当奇奇偶或偶偶奇时,最少整数有一个,选A10. a #b =a +b -1 ,a !b =a ×b -1(1)求3![(6#8)#(6!2)];(2)x #(x !8)=61,求x ;【解析】 (1)68(2)7x =11. 由数字0,1,3,9可以组成多少个无重复数字的自然数?【解析】 满足条件的数可以分为4类:一位、二位、三位、四位数.第一类,组成0和一位数,有4个(0不是一位数,最小的一位数是1);第二类,组成二位数,有339⨯=个;第三类,组成三位数,有33218⨯⨯=个;第四类,组成四位数,有332118⨯⨯⨯=个.由加法原理,一共可以组成49181849+++=个数.12. 如图,这是一个棋盘,将一个白子和一个黑子放在棋盘线的交叉点上,但不能在同一条棋盘线上,则有 种不同的放法.【解析】2516400⨯=种13. 如果a ,b 均为质数,且3741a b +=,则a b +=______.【解析】 根据题意a ,b 中必然有一个偶质数2,,当2a =时,5b =,当2b =时不符合题意,所以257a b +=+=.14. 有甲、乙两堆棋子,其中甲堆棋子多于乙堆.现在按如下方法移动棋子:第一次从甲堆中拿出和乙堆一样多的棋子放到乙堆;第二次从乙堆中拿出和甲堆剩下的同样多的棋子放到甲堆;第三次又从甲堆中拿出和乙堆同样多的棋子放到乙堆.照此移法,移动三次后,甲、乙两堆棋子数恰好都是32个.问甲、乙两堆棋子原来各有多少个?【解析】 我们从最后一步倒着分析.因为第三次是从甲堆拿出棋子放到乙堆,这样做的结果是两堆棋子都是32个,因此,在未进行第三次移动之前,乙堆只有32216÷=(个)棋子,而甲堆的棋子数是321648+=(个),这样再逆推下去,逆推的过程可以用下表来表示,表中的箭头表示逆推的方向.所以,甲堆原有44个棋子;乙堆原有20个棋子.采用列表法非常清楚.【答案】甲乙两堆棋子原来各有44个和20个15. 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【解析】 所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米).16. 同学们,你玩过“扫雷”的游戏吗?在64个方格内一共有10个地雷,每格中至多有一个,对于填有数字的方格,其格内无地雷且与其相邻的所有方格中地雷的个数与该数字相等,你认为图中所标的数字_______是有雷的.【解析】 “扫雷”游戏主要考查观察能力和推理能力.先考虑标有①②的两个方格周边的情况.由于第六行有4个方格中的数字都是0,表示它们的周围没有雷,所以得到第五行前三列的3个方格都不是雷,而第四行第一列的方格中的数是1,表示它的周围有1个雷,所以标有①②的两个方格中恰好有1个雷,那么对于第三行第一列标有2的方格来说,它的周围有2个雷,其中一个在标有①②的两个方格中,另一个只能在第二行第二列的方格内.然后再看第二行第一列的方格,它的周围有1个雷,在第二行第二列的方格内,所以标有①的方格中没有雷,标有②的方格中有雷.再考虑标有③的方格的周边.由于第七行第一列的方格标有数字1,表示第八行第一、二列的两个方格中恰好有1个雷,而第七行第二列的方格标有数字2,说明它的周围有2个雷,那么一个雷在第八行第一、二列的两个方格中,另一个雷只能在标有③的方格中,所以标有③的方格中有雷.再看标有④⑤的方格的周边.由于第八行第七列的方格标有数字1,说明第八行第八列和第七行第八列的两个方格内恰有1个雷,而第七行第七列的方格也标有数字1,所以标有④的方格是没有雷的.而第六行第七列的方格标有数字3,说明它的周围有3个雷,所以标有⑤的方格是有雷的.所以图中所标数字为②、③、⑤的方格是有雷的.17. 如图3,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷.内部的小方块没有雷,数字表示所在小方块周围的雷数.图中共有 个雷.【解析】 1612113332313312111234图318.7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【解析】由图可知,长方形的长是宽的4倍,宽的6倍是24厘米,则长方形的宽是4厘米,故图中空白部分的面积是44232⨯⨯=(平方厘米).19.敌人欲从河岸B进攻对岸A,河上有13座桥,为阻止敌人进攻决定将桥炸坏.至少炸掉座桥可将敌人拦阻在河岸B.【解析】3座:5、9、1020.一班和二班的人数之比是8:7,如果将一班的8名同学调到二班去,则一班和二班的人数比变为4:5.求原来两班的人数.【解析】一班:二班=8:724:21⨯=和不变153一班:二班=4:520:25⨯=95一班向二班调了4份为8人,故每份842÷=(人),一班:24248⨯=(人)⨯=;二班:2124221.自然数N是一个两位数,它是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数有多少个?【解析】这样的自然数有4个:23,37,53,73.22.由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少.已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天.照此计算,可以供多少头牛吃10天?【解析】设1头牛1天的吃草量为“1”,那么每天自然减少的草量为:()()20105150+⨯=;10天吃完需要牛的⨯-⨯÷-=,原有草量为:()2051566510头数是:15010105÷-=(头).23.甲、乙两人同时从A点背向出发,沿400米的环形跑道行走,甲每分钟走80米,乙每分钟走50米,两人至少经过多长时间才能在A点相遇?【解析】甲、乙走一圈分别需要5分钟和8分钟,因此他们要是在A点再次相遇,两人都要走整圈数,所以所需的时间应是5和8的最小公倍数40分钟.24.长方形有四个角,剪掉一个角,还剩几个角?【解析】共有三种情况,如下图,分别剩下5、4、3个角.25.图中的三个图形都是由A、B、C、D(线段或圆)中的两个组合而成,记为A*B、C*D、A*D.请你画出表示A*C的图形.【解析】观察上图,第一个图形和第三个图形的共同之处是都有一条竖向线段,而它们共有的字母是A,因此A表示竖向线段;第二个图形与第三个图形的共同之处是都有一条横向线段,它们的共同字母是D,因此D表示横向线段.这样,由第一个图形可知B表示大圆,由第二个图形可知C表示小圆,从而A*C表示的图形应为竖向线段和小圆组合而成,即下图.26.用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上,每一个面只涂一种颜色.如图所示,现有涂色方式完全一样的四块小正方体拼成了一个长方体.试回答:每个小正方体中,红色面的对面涂的是什么色?黄色面的对面涂的是什么色?黑色面的对面是什么色?【解析】在能看见的9个面中红色出现的次数最多.观察图8—4中最上面的一个正方体,由于红色和黑色、黄色相邻,所以它的对面不可能是黑黄两色.同理,由第二个正方体可知,红色的对面不能是白色;由第三个正方体知,红色的对面不能是蓝色.所以红色的面的对面只可能是绿色.同理,黄色面的对面不可能是红色、黑色或白色,又已推知不可能是绿色,所以黄色面的对面只可能是蓝色.这样黑色面的对面就只可能是涂白色的了.27. 图1是下面 的表面展开图①甲正方体;②乙正方体;③丙正方体;④甲正方体或丙正方体.甲 乙 丙【解析】 从展开图可以看出,每个面上至少有一块阴影,从而排除丙;又每个面上没有相邻的两块阴影,从而排除乙.故选甲答案为①.28. 如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L 形区域乙和丙.甲的周长为4厘米,乙的边长是甲的周长的1.5倍,丙的周长是乙的周长的1.5倍,那么丙的周长为多少厘米?EF 长多少厘米?【解析】 乙的周长实际上是正方形AHJE 的周长(我们可将乙与甲重合的两条线段分别向左、向下平移),同样的,丙的周长也就是正方形ABCD 的周长.由于4 1.56AE =⨯=,6 1.59AD =⨯=,所以丙的周长为9436⨯=厘米,642EF AE AF =-=-=(厘米).29. 在一块长方形的地里有一正方形的水池(如下图).试画一条直线把除开水池外的这块地平分成两块.【解析】 用连对角线的办法找出这块长方形地的中心O 和正方形水池的中心A .过O 、A 画一条直线,这条直线正好能把除开水池外的这块地平分为两块(如右上图).FEH BA AO30. 试将任意一个矩形分成三块,然后拼成一个三角形. 【解析】 方方法二:31. 900000-9=________×99999.【解析】 832. 多米诺骨牌是由塑料制成的1×2长方形,共28张,每张牌上的两个1×1正方形中刻有“点”,点的个数分别为0,1,2,…,6个不等,其中7张牌两端的点数一样,即两个0,两个1,…,两个6;其余21张牌两端的点数不一样,所谓连牌规则是指:每相邻两张牌必须有一端的点数相同,且以点数相同的端相连,例如:现将一付多米诺骨牌按连牌规则连成一条链,如果在链的一端为6点,那么在链的另一端为多少点?并简述你的理由.【解析】 由连牌规则可知,在链的内部各种点数均成对相连,即所有点都有偶数个,而6点的个数为8,所以在链的两端一定有偶数个点,所以链的另一端也应为6.33. 甲、乙两个哲人将正整数5至11分别写在7张卡片上.他们将卡片背面朝上,任意混合之后,甲取走三张,乙取走两张.剩下的两张卡片,他们谁也没看,就放到麻袋里去了.甲认真研究了自己手中的三张卡片之后,对乙说:“我知道你的两张卡片上的数的和是偶数.”试问:甲手中的三张卡片上都写了哪些数?答案是否唯一.【解析】 甲手中的8张卡片上分别写了6,8和10.甲知道其余4张卡片上分别写了哪些数,但不知道它们之中的哪两张落到了乙的手中.因此,只有在它们之中任何两张卡片上的数的和都是偶数时,甲才能说出自己的断言.而这就意味着,这4张卡片上所写的数的奇偶性相同,亦即或者都是偶数,或者都是奇数.但是由于一共只有3张卡片上写的是偶数,所以它们不可能都是偶数,从而只能都是奇数.于是3张写着偶数的卡片全都落入甲的手中.答案是唯一的.34. 三个人同时前往相距30千米的甲地,已知三人行走的速度相同,都是5千米每小时;现在还有一辆自行车,但只能一个人骑,已知骑车的速度为10千米每小时.现先让其中一人先骑车,到中途某地后放车放下,继续前进;第二个人到达后骑上再行驶一段后有放下让最后那人骑行,自己继续前进,这样三人同时到达甲地.问,三人花的时间各为多少?【解析】 由于每人的速度相同,所以每人行走的路程相同,骑车的路程也要相同,这样每人骑车的距离都是1/3,所以时间就是20÷5+10÷10=5小时…………35. 张师傅开汽车从A 到B 为平地(见下图),车速是36千米/时;从B 到C 为上山路,车速是28千米/时;从C 到D 为下山路,车速是42千米/时. 已知下山路是上山路的2倍,从A 到D 全程为72千米,张师傅开车从A 到D 共需要多少时间?【解析】 方法一:设BC 距离为:[]28,4284=(千米),所以CD 距离为842168⨯=(千米),那么B -C -D 的平均速度为:()()8416884281684236+÷÷+÷=(千米/小时),和平路的速度恰好相等,说明A -B -C -D 的平均速度为36千米/小时,所以从A -D 共需要的时间为:72362÷=(小时)方法二:设上山路为x 千米,下山路为2x 千米,则上下山的平均速度是:22824236x x x x +÷÷+÷=()()(千米/时),正好是平地的速度,所以行AD 总路程的平均速度就是36千米/时,与平地路程的长短无关.因此共需要72362÷=(小时).36. 右图是一个园林的规划图,其中,正方形的43是草地;圆的76是竹林;竹林比草地多占地450平方米. 问:水池占多少平方米?【解析】 正方形的43是草地,那如果水池占1份,草地的面积便是3份;圆的76是竹林,水池占1份,竹林的面积是6份.从而竹林比草地多出的面积是(6-3=)3份.3份的面积是450平方米,可见1份面积是450÷3=150(平方米),即水池面积是150平方米.37. 地球表面的陆地面积和海洋面积之比是29∶71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是( ).A . 284∶29B . 284∶87C . 87∶29D . 171∶113【解析】 解:设地球表面积为1,则北半球海洋面积为:0.5-0.29×34=1.134南半球海洋面积为:0.71-1.134=1.714南北半球海洋面积之比为:1.714∶1.134=171∶113 答案:D38. 对任意两个不同的自然数,将其中较大数换成这两数之差,称为一次变换.如对18和42可作这样的连续变换:18,42→18,24→18,6→12,6→6,6直到两数相同为止.问:对1234和4321作这样的连续变换最后得到的两个相同的数是 .【解析】 操作如下:1234,4321→1234,3087→1234,1853→1234,619→615,619→615,447前一数每次减少→…→,4→3,4→3,1→2,1→1,1实际上按此法操作最后所得两相同的数为开始两数的最大公约数.即1234与4321的最大公约数为1.此法也称为辗转相减法求最大公约数.39. 有一副扑克牌,一开始抓若干张(小于13张),然后进行下列操作:抓和手里现有的扑克牌数目相等的扑克牌,然后若扑克牌总数超过13张,则放回其中的13张,称为一次操作.进行了777次操作后,手里有7张牌,则一开始手里有多少张?【解析】 根据倒退法知道第777次操作后是7,那么第776次操作就是:()7132=10+÷,第775次操作就是102=5÷,找到规律是遇见奇数就是加13后除以2,遇见偶数就是直接除以2,所以操作后得到这样一串数为:7、10、5、9、11、12、6、3、8、4、2、1、7、10,观察发现是12个一周期,所以77712=649÷,所以第一次手里的数是8,一开始手里的数是4张扑克.40. 小华和爸爸分享“红、黑甜品”(红豆沙加芝麻糊).方法是:小华先将两勺红豆沙倒进盛载芝麻糊的碗中,搅匀后再取回两勺放入原先盛载红豆沙的碗中,混成后,爸爸问小华:“如果混合前红豆沙与芝麻糊的体积一样,那么混合后红豆沙含芝麻糊的分量与芝麻糊含红豆沙的分量比较,哪一个多?”.小华的正确答案是_____.【解析】 一样多41. 由于潮汐的长期作用,月球自转周期与绕地球公转周期恰好相同,这使得月球总是以相同的一面对着我们.在地球上最多能看到 50%的月球面积,从一张月球照片中最多能看到 50%的月球面积.(填“大于”、“小于”或“等于”)【解析】 小于; 小于方法一、一张静止的照片,能看到的球体面积的极限是一半,只有当距离球体无限远时才能看到球体表面积的一半.方法二、如果能看到一半,则能看到一半的直线为两条平行线,不可能相交.42. 刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【解析】 因为兄妹二人不许搭伴,所以题目条件表明:刘刚与小丽、李强与小英、李强与小红都不是兄妹.由第二盘看出,小红不是马辉的妹妹.将这些关系画在左下表中,由左下表可得右下表.刘刚与小红、马辉与小英、李强与小丽分别是兄妹.43. 甲、乙、丙、丁四个人的职业分别是教师、医生、律师、警察.已知:⑴教师不知道甲的职业;⑵医生曾给乙治过病; 李强马辉刘刚小丽小红小英×√×××××√√⑶律师是丙的法律顾问(经常见面);⑷丁不是律师;⑸乙和丙从未见过面.那么甲、乙、丙、丁的职业依次是: .【解析】 律师、教师、警察.由⑶可以知道丙不是律师,但是他见过律师,再由⑸知乙不是律师,又由⑷可知甲是律师.于是由⑴和⑶知丙不是教师,由⑵和⑸知丙不是医生,从而丙是警察.再由⑵知乙是教师,丁是医生.列表如下(列表的好处在于直观明了,不会犯错误):44. 右边算式中,A 表示同一个数字,在各个□中填入适当的数字,使算式完整.那么两个乘数的差(大数减小数)是 ?11AA A ⨯【解析】 由11AA 能被11整除及只有11⨯,37⨯,99⨯的个位是1,所以A 可能为1,3,7或9,而且11AA 可分解成11与1个一位数和一个两位数的乘积.分别检验1111、1331、1771、1991,只有1771满足:177111723=⨯⨯,可知原式是77231771⨯=.所以两个乘数的差是772354-=.45. 电子数字0~9如图所示,右图是由电子数字组成的乘法算式,但有一些模糊不清,请将右图的电子数字恢复,并将它写成横式形式: .【解析】 ⑴可以看出乘积的百位可能是2或8,由于被乘数的十位和乘数都不能是9,最大可能为8,所以它们的乘积不超过898712⨯=,故乘积的首位不能为8,只能为2;⑵被乘数的十位和乘数要与图中相符,只能是0、2、6或8,0首先可以排除,所以可能为2、6或8;⑶如果被乘数的十位是6或8,那么乘数无论是2、6或8,都不可能乘出百位是2的三位数.所以被乘数的十位是2,相应得出乘数是8;⑷被乘数应大于200825÷=,可能为27、28或29,检验得到符合条件的答案:288224⨯=46. 有一道关于蜗牛爬墙的题:“日升六尺六,夜降三尺三,墙高一丈九,几日到顶端”.蜗牛第 天首次到顶端.【解析】 蜗牛一整天可升三尺三6.6 3.3 3.3-=,四天可升一丈三尺二,第五天白天即已经达到顶端.47. 现有5段铁链,每段上有4个封闭的铁环.现在要打开一些铁环,把这20个铁环焊接成一个一环套一环的圆圈.如果每打开一个铁环要2分钟,焊接上一个铁环要3分钟.那么焊成这个圆圈,至少需要________分钟.【解析】 把第一段的每个都打开之后用了428⨯=(分钟),下面用每个铁环把剩下的4 段铁链之间的两个相连,只需要4312⨯=(分钟).所以至少需要20分钟.48. 用数字1,1,2,2,3,3拼凑出一个六位数,使两个1之间有1个数字,两个2之间有2个数字,两个3之间有3个数字.【解析】 312132 23121349. 一城镇共有5000户居民,每户居民的小孩都不超过两个.其中一部分家庭每户有一个小孩,余下家庭的一半每户有两个小孩,则此城镇共有 个小孩.【解析】 5000户居民可以分为三部分:(1)只有1个小孩的;(2)有2个小孩的;(3)没有小孩的.其中(2)与(3)的居民相同,我们就可以将有2个小孩的家庭的其中1个孩子分给没有小孩的家庭,这样5000户居民每个家庭都有1个小孩,所以这城镇共有5000个小孩.50. 若干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了.小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下.小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子.问共有多少个盒子?【解析】 原来有个空的,说明现在也有个空的;现在空的说明原来这盒有1个,当然现在也必须有个盒子有1个;现在盒中有1个,说明原来是2个,当然现在也必须有个盒子有2个;……考虑50多,所以有0+1+2+3+4+5+6+7+8+9+10=55 共11个盒子.第8题。
