3.1.2共线向量与共面向量2
空间向量的共线与共面问题

么条件?
bC
p
P
Aa B
O
结论:空间一点P位于平面ABC内
存在有序实数对x,y使 AP x AB y AC
或对空间任一点O,有 OP xOA yOB zOC (x y z 1)
可证明或判断四点共面
三.类似地,有空间向量基本定理:
如果三个向量 a 、b 、c 不共面,那么对于空间任一向
a
+
1 2
b+
1 2
c
A
C N
(C)
1 2
a
+
12b -
23 c
B
(D)
2 3
a
+
2 3
b
-
1 2
c
课外补充练习:
1.对于空间任意一点O,下列命题正确的是:A
(A)若 OP OA t AB ,则P、A、B共线
(B)若 3OP OA AB ,则P是AB的中点
(C)若 OP OA t AB ,则P、A、B不共线
向量规.规定定a 平:: oo行与与于任任b一一记向向作量量aaa/是/是b共.共线线向向量量..
2.共线向量定理:空间任意两个向量
a
、b(
b
≠
0
),
a // b 的充要条件是存在实数 ,使 a b .
练习.已知A、B、P三点共线,O为直线外
一点,且OP OA OB,求 的值.
那么 A 、B 、P 三点共线吗?
思考:如图, l 为经过已知点 A 且平行非零向量 a 的直线,
如何表示直线 l 上的任一点 P ?
A•
•• l
BP
a
O
注:我们把非零 向量 a 叫做直线 l 的方向向量.
原创1:3.1.2 空间向量的基本定理

典例分析
若{a,b,Ԧc}是空间的一个基底,判断{a+b,b+Ԧc,Ԧc+a}能否
作为该空间的一个基底.
是否共面
【解析】假设a+b,b+Ԧc,Ԧc+a共面,
则存在实数λ,μ使得
a+b=λ(b+Ԧc)+μ(Ԧc+a),
∴ a+b =μa+λb+(λ+μ)Ԧc.
答案
②③
典例分析
空间四边形OABC中,M,N是△ABC,△OBC的重心,设=a,
=b, =Ԧc,用向量a,b,Ԧc表示向量, , .
利用线性运算,结合图形,
【解析】如图,取BC中点P,
O
对向量进行分解
则A、M、P,O、N、P分别共线,
a
cԦ
连结AP,OP.
2
AM=OA+AM=a+ AP
= k =k( + )
跟踪训练
=k( − + − )
= − + −
= + .
所以E、F、G、H共面.
(2) = − =k( − )=k ,
且由第(1)问的证明中知=k,
于是EF∥AB,EG∥AC.且EF∩EG=E,AB∩AC=A,
已知平行四边形ABCD,从平面AC外一点O引向量
=k, =k , =k , =k =k,
求证:(1)四点E、F、G、H共面;
(2)平面EG∥平面AC.
证明:(1)因为四边形ABCD是平行四边形,
所以 = + ,
= − = k - k
第三章 空间向量与立体几何
§3.1.2
空间向量的基本定理
高中数学选修2-1·精品课件
引入课题
3.1.2共线与共面

OP xOA yOB zOC (其中x+y+z=1)
作 业: 教辅第23页~第26页,活页课时作业十一
教材31页练习:
1. 空间四边形ABCD中,连结AC、BD, M、G分别是BC、CD边的中点,化简:
A
() AB BC CD AD 1
A1
A2
A3 An
An1
A4
4. 平行六面体: 平行四边形ABCD(包括它的内部)平移向量 a到A1B1C1D1的轨迹所形成的几何体,叫做平行六面体.
D1 A1 a A B1 C1 A1 D A B
D1
B1
C1
D
B
C
C
AB AD AA1 AC1
记作ABCD—A1B1C1D1,它的六个面都是平行四边 形,每个面的边叫做平行六面体的棱.
于是点 P在平面MAB内,向量p // 平面MAB .
即向量 p 与 a 、 共面 . b
(3)共面向量定理: 如果两个向量a、b 不共线,则向量p与 向量a、b共面的充 要条件是存在实数 对x、y,使 B b p A A'
P
M
a
p = xa + yb.
ห้องสมุดไป่ตู้.O
推论:空间一点P 位于平面MAB内的充分必要条件是存在 有序实数对x、y,使 MP = xMA + yMB 或对空间任一定点O,有 OP = OM + xMA + yMB. 即 OP (1 x y )OM xOA yOB (平面MAB的向量表达式)
证明:( 2) EF OF OE
k (OB OA)
k AB
3.1.2空间向量共面定理

3.1.2空间向量共面定理教学目标:1.理解共线向量定理和共面向量定理及它们的推论;2.掌握空间直线、空间平面的向量参数方程和线段中点的向量公式.教学重、难点:共线、共面定理及其应用. 教学过程: (一)复习:1.空间向量的概念及表示:(二)阅读课本P 74~P 75,⑴怎样的向量叫做共线,共面向量?⑵两个向量共线,共面的充要条件是什么?1.共线(平行)向量:2.共线向量定理:推论:问题思考3.向量与平面平行:4.共面向量定理:如何证明?推论:()()1=020?a λ≠当实数时,表示什么意思?充要条件中,为什么规定(三)预习练习1、下列说法正确的是:A.在平面内共线的向量在空间不一定共线B.在空间共线的向量在平面内不一定共线C.在平面内共线的向量在空间一定不共线D.在空间共线的向量在平面内一定共线E.在平面内,任意两个向量一定共线2已知A 、B 、M 三点不共线,对于平面ABM 外的任一点O ,确定在下列各条件下,点P 是否与A 、B 、M 一定共面?3下列命题中正确的有______4.对于空间中的三个向量 它们一定是: A.共面向量 B.共线向量 C.不共面向量 D.既不共线又不共面向量5.已知点M 在平面ABC 内,并且对空间任意一点O , ,则x的值为:_____(四)典型例题例1、已知A 、B 、P 三点共线,O 为空间任意一点,且 ,求 的值.αβ=+OP OA OBαβ+(1)3=+-OB OM OP OA (2)4=--OP OA OB OM(1)=+⇒ 与、共面;p xa yb p a b (2)⇒=+与、共面 ;p a b p xa yb (3)=+⇒、、、共面;MP xMA yMB P M A B (4)⇒=+、、、共面;P M A B MP xMA yMB 2、、-MA MB MA MB=11++33OM xOA OB OC (1)λλ=≠-AP PB变式、设点P 在直线AB 上并且 ,O 为空间任意一点, 求证:方法一:方法二:11111111,,,1,,,ABCD AC O OA kOA OB kOB OC kOC OD kODA B C D ====11变式:如图平行四边形,从平面外一点引向量求证:()四点共面 (2)A C ||平面D'B'C'D ABC1λλ+=+OA OBOP 1,11,,,33ABCD ADEF M N BD AE BM BD AN AE MN CED ==例、如图,已知矩形与所在平面相互垂直,点分别在对角线上,且求证:平面五:课堂小结六,课后作业 P761,2,3强化训练:1.若对任意一点O , ,则x+y=1是P 、A 、B 三点共线的: ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2.已知两个非零向量21,e e 不共线,如果21AB e e =+,2128AC e e =+,2133AD e e =-,求证:,,,A B C D 共面.3.已知324,(1)82a m n p b x m n yp =--=+++,0a ≠,若//a b ,求实数,x y 的值。
课件1:3.1.2 空间向量的数乘运算(共线与共面向量)

∴EH ∥FG且|EH |=43|FG |≠|FG |.
又 F 不在直线 EH 上, ∴四边形 EFGH 是梯形.
规律方法 判断向量 a,b 共线的方法有两种: (1)定义法 即证明 a,b 所在基线平行或重合. (2)利用“a=xb⇒a∥b”判断 a,b 是空间图形中的有向线段,利用空间向量的运算性质, 结合具体图形,化简得出 a=xb,从而得 a∥b,即 a 与 b 共 线.
存在有序实数组{x,y,z},使得 p= xa+yb+zc
.
其中,表达式 xa+yb+zc 叫做向量 a,b,c 的线性表
达式或线性组合, a,b,c 叫做空间的一个基底,记 作 {a,b,c} ,a,b,c 都叫做基向量.
互动探究
题型一:共线向量的判定 例 1 如图 3-1-11 所示,已知四边形 ABCD 是空间四边形,E,H 分别是边 AB,AD 的中点,F, G 分别是边 CB,CD 上的点,且C→F=23C→B,C→G=23C→D. 求证:四边形 EFGH 是梯形.
图 3-1-11
【思路探究】 (1)E→H与F→G共线吗?怎样证明? (2)|E→H|与|F→G|相等吗? 【自主解答】 ∵E,H 分别是 AB、AD 的中点, ∴A→E=21A→B,A→H=12A→D, 则E→H=A→H-A→E=12A→D-12A→B=12B→D =21(C→D-C→B)=12(32C→G-32C→F) =43(C→G-C→F)=34F→G,
(2)由(1)知向量M→A,M→B,M→C共面,三个向量的基线又 过同一点 M,
∴M、A、B、C 四点共面, ∴M 在面 ABC 内.
规律方法 1.空间一点 P 位于平面 MAB 内的充分必要条件是存在有序 实数对(x,y),使 MP xMA yMB.满足这个关系式的点 P 都 在平面 MAB 内;反之,平面 MAB 内的任一点 P 都满足这个 关系式.这个充要条件常用于证明四点共面.
第3章 3.1.2 共面向量定理

→ → ②若AB=CD,则 A,B,C,D 四点共线;
③若a,b不共线,则空间任一向量p=λa+μb(λ,μ∈R). 解析 当a,b中有零向量时,①不正确;
→ → AB=CD时,A,B,C,D 四点共面不一定共线,故②不正确;
由p,a,b共面的充要条件知,当p,a,b共面时才满足p= λa+μb(λ,μ∈R),故③不正确.
→ → 此为空间共面向量定理,其实质就是平面向量基本定理,MA,MB实质 就是平面 MAB 内平面向量的一组基底.
D四点共面.
[思考辨析
判断正误] ) )
1.实数与向量之间可进行加法、减法运算 × .( 2.空间中任意三个向量一定是共面向量.( ×
→ → → 3.若 P,M,A,B 共面,则MP=xMA+yMB.( × )
题型探究
类型一 向量共面的判 定 例1 给出以下命题: ①用分别在两条异面直线上的两条有向线段表示两个向量,则 这两个向量一定不共面; ②已知空间四边形ABCD,则由四条线段AB,BC,CD,DA分
要条件是 存在有序实数组(x,y),使得p=xa+yb
_____________________________________,即向量p可以由 两个不共线的向量a,b线性表示.
知识点三 空间四点共面的 条件
若空间任意无三点共线的四点,对于空间任一点 O,存在实数 x,y,z 使 → → → → 得OA=xOB+yOC+zOD,且 x,y,z 满足 x+y+z=1,则 A,B,C,
解答
反思与感悟
利用向量法证明向量共面问题,关键是熟练的
进行向量的表示,恰当应用向量共面的充要条件,解题过程 中注意区分向量所在的直线的位置关系与向量的位置关系.
跟踪训练 2 如图,在正方体 ABCD-A1B1C1D1 中,E,F 分别为 BB1 ― → ― → → 和 A1D1 的中点.证明:向量 A1B , B1C ,EF是共面向量.
3.1.2空间向量的共线与共面
例. 如图,已知平行四边形ABCD,过平面AC外
一点O作射线OA,OB,OC,OD,在四条射线上
分别取点E,F,G,H,并且使
OE OF OG OH k, OA OB OC OD
O
求证: E,F,G,H四点共面.
DC
A
ห้องสมุดไป่ตู้
B
H
G
E
F
C
p
P
b
A aB
对空间任一点O,有OP OA xAB y AC ③
C
p
P
b
A aB
O 填空:OP (1__-_x_-_y)OA (_x___)OB (__y__)OC
③式称为空间平面ABC的向量表示式,空间中任意 平面由空 间一点及两个不共线的向量唯一确定.
由此可判断空间任意四点共面
P与A,B,C共面
AP xAB yAC
OP OA xAB y AC
OP xOA yOB zOC 0(x y z 1)
练习2.若对任一点O和不共线的三点A、B、C,
且有 OP xOA yOB zOC(x, y, z R), 则x+y+z=1 是四点P、A、B、C共面的( C )
A.必要不充分条件 C.充要条件
B
b
O
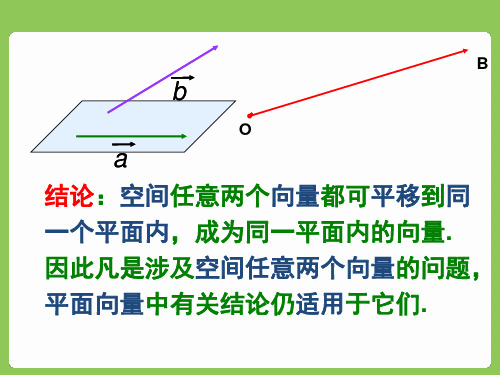
a 结论:空间任意两个向量都可平移到同 一个平面内,成为同一平面内的向量. 因此凡是涉及空间任意两个向量的问题, 平面向量中有关结论仍适用于它们.
1、共线向量:如果表示空间向量的有向
线段所在直线互相平行或重合,则这些向量
叫做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
思考:空间向量的平行满足传递性吗?
2.共线向量定理:对空间任意两个向量 a,b(b 0), a // b的充要条件是存在实数 使
【课件】高二数学选修2-1 第三章3.1.2共线向量与共面向量

空间中如果两个向量 a、b不共线,则向量 p与向量a、b共面的 充要条件是存在唯一 实数对x、y,使
P = xa + yb.
P Bp b M a A A'
平面向量的基本定理
如果e1, e2是同一平面内的两个不共线 向量,那么对于这一平面内的任一向
量 a,有且只有一对实数1, 2 ,使 a 1e1 2 e2
⑵平面EG//平面AC。
D
C
A
B
H G
E
F
练习1.对于空间中的三个向量 MA、MB 、2MA-MB
它们一定是:
A.共面向量
B.共线向量
C.不共面向量 D.既不共线又不共面向量
练习2. 已知A、B、M三点不共线,对于平面 ABM外的任一点O,确定在下列各条件下, 点P是否与A、B、M一定共面?
(1) OB+OM 3OP-OA
A. 1
B. 0
C. 3
D. 1
3
4.已知A、B、C三点不共线,对平面外一点 O,在下列条件下,点P是否与A、B、C共面?
(1) OP 2 OA 1 OB 2 OC ; 555
(2) OP 2OA 2OB OC ;
OP OA OB 1
二.空间共面向量
1.已知平面α与向量a,如果向
O
量a所在的直线OA平行于平
面α或向量a在平面α内,那么我
们就说向量a平行于平面α,记 α
作a//α.
2.共面向量:平行于同一平面的向量
思考:
空间任意两个向量一定共面,
B
空间任意三个向量呢?
a A
a
A D
C
3.空间共面向量定理:
结论: 已知P 、 A、B、C四点共面,O为空间任 意一点, OP xOA yOB zOC,( x y z 1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例5 如图,已知平行四边形ABCD,从平
面AC外一点O引向量 OE kOA, OF kOB,
OG kOC , OH kOD ,求证:
O
⑴四点E、F、G、H共面;
⑵平面EG//平面AC。
A
D B
C
D' A' B'
C'
1.下列命题中正确的有:
(1) p xa yb p与 a 、 b 共面 ;
D.在空间共线的向量在平面内一定共线
2.下列说法正确的是:
A.平面内的任意两个向量都共线
B.空间的任意三个向量都不共面 C.空间的任意两个向量都共面 D.空间的任意三个向量都共面
3.对于空间任意一点O,下列命题正确的 是:
A.若
OP OA t AB
,则P、A、B共线
B.若 3OP OA AB ,则P是AB的中点 C.若 OP OA t AB ,则P、A、B不共线 D.若 OP OA AB ,则P、A、B共线
ABM外的任一点O,确定在下列各条件下, 点P是否与A、B、M一定共面?
(1) OB+OM 3OP-OA
(2) OP 4OA OB OM
注意:
空间四点P、M、A、B共面 存在唯一实数对 (x , y ) , 使得MP xMA yMB
OP xOM yOA zOB(其中,x y z 1)
4.若对任意一点O,且 OP xOA y AB ,
则x+y=1是P、A、B三点共线的:
A.充分不必要条件
B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.设点P在直线AB上并且AP PB( 1)
,O为空间任意一点,求证:
OA OB OP 1
二.共面向量:
1.共面向量:平行于同一平面的向量,
叫做共面向量.
O
a a
A
注意:空间任意两个向量是共面的,但空间 任意三个向量就不一定共面的了。
2.共面向量定理:如果两个向量 a , b
不共线,则向量 p 与向量 a , b共面的充要
条件是存在实数对x, y 使P
xa yb
b
B
p
A
P
M a A
O
推论:空间一点P位于平面MAB内的充
要条件是存在有序实数对x,y使
MP xMA yMB
或对空间任一点O,有OP OM xMA yMB
例3 对空间任意一点O和不共线的三点
A、B、C,试问满足向量关系式
OP xOA yOB zOC
(其中 P、A、B、 x y z )的四点 1
C是否共面?
例4
已知A、B、M三点不共线,对于平面
C.不共面向量
B.共线向量
D.既不共线又不共面向量
3.已知点M在平面ABC内,并且对空间任 1 1 意一点O, OM xOA + OB + OC ,则x 3 3 的值为:
A. 1
B. 0
C. 3
1 D. 3
4.已知A、B、C三点不共线,对平面外一点 O,在下列条件下,点P是否与A、B、C共面?
已知非零向量 a 的直线,那么对任一点O, 点P在直线 l 上的充要条件是存在实数t, 满足等式OP=OA+t a 其中向量叫做直线的 方向向量. P
aபைடு நூலகம்
推论:如果 l 为经过已知点A且平行
若P为A,B中点, 则 1 OP OA OB 2
O
B A
例1 已知A、B、P三点共线,O为空间任
共线向量与共面向量
江苏如东马塘中学 张伟锋
一、共线向量: 1.共线向量:如果表示空间向量的
有向线段所在直线互相平行或重合,则这些 向量叫做共线向量(或平行向量),记作 a // b 零向量与任意向量共线.
2.共线向量定理:对空间任意两个 向量 a, b(b o), a // b 的充要条件是存在实 数使 a b
意一点,且OP OA OB,求 的值.
例2 用向量的方法证明:顺次连结空间 四边形各边中点所得的四边形为平行四 边形。
A E
H D F C G
B
1.下列说明正确的是:
A.在平面内共线的向量在空间不一定共 线 B.在空间共线的向量在平面内不一定共 线 C.在平面内共线的向量在空间一定不共 线
(2) p 与 a 、 b 共面 p xa yb ;
(3) MP xMA yMB P、M、A、B共面;
(4) P、M、A、B共面 MP xMA yMB ;
A.1个
B.2个
C.3个
D.4个
2 MA -MB 2.对于空间中的三个向量MA 、MB 、
它们一定是:
A.共面向量
2 1 2 (1) OP OA OB OC ; 5 5 5
(2) OP 2OA 2OB OC ;
5. 课本第31页
练习
1、 2 。
三、课堂小结:
1.共线向量的概念。
2.共线向量定理。
3.共面向量的概念。 4.共面向量定理。
