3.2.2 平面的法向量与平面的向量表示
高中数学-平面的法向量

14
例:(试用向量方法证明直线与平面垂直的判定定理)
已知直线m ,n是平面 内的两条相交直线,
如果 l⊥m, l ⊥n,求证: l ⊥ .
l
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可 知,就是要证明这条直线与平面内 的任意一条直线都垂直.
gl
m
m n mg
取已知平面内的任一条直线 g ,拿相关直线的方 向向量来分析,看条件可以转化为向量的什么条件?要 证的目标可以转化为向量的什么目标?怎样建立向量 的条件与向量的目标的联系?
l m 0, l n 0 ,
gl
m
l g 0,即l g.
m n ng
l g,即l垂直于平面内任一直线.l .
16
6.有关平面的斜线概念, 三垂线定理及其逆定理 P104
17
什么叫平面的斜线、垂线、射影?
P
oa
α
A
PO是平面α的斜线,
O为斜足; PA是平面α 的垂线, A为垂足; AO
12
(1, 2,2)或 ( 1,2, 2).
3 33
33 3
练习 1:已知 AB (2, 2,1), AC (4, 5, 3), 求平面 ABC 的
单位法向量.
解:设平面 ABC 的一个法向量为 n ( x, y, z)
则 n AB ,n AC .
∴
( (
x, x,
3 33
33 3
13
例 如图,已知矩形 ABCD和矩形 ADEF所在平面互相垂直,点
M , N 分别在对角线 BD, AE上,且 BM 1 BD, AN 1 AE,
求证:MN // 平面CDEபைடு நூலகம்
高二数学选修课件:3-2-2平面的法向量与平面的向量表示

人 教 B 版 数 学
第三章
空间向量与立体几何
[例 1]
如图, ABCD 是直角梯形, ∠ABC=90° SA⊥ ,
人 教 B 版 数 学
1 平面 ABCD,SA=AB=BC=1,AD=2,求平面 SCD 与平 面 SAB 的法向量.
第三章
空间向量与立体几何
[分析] 解答本题可先建立空间直角坐标系,写出每
个平面内两个不共线向量的坐标,再利用待定系数法求出 平面的法向量.
人 教 B 版 数 学
[解析]
∵AD、AB、AS 是三条两两垂直的线段,
→ → → ∴以 A 为原点,以AD、AB、AS的方向为 x 轴,y 轴, 1 z 轴的正方向建立坐标系, A(0,0,0), 2, 则 D( 0,0), C(1,1,0), → =(1,0,0),是平面 SAB 的法向量, S(0,0,1),AD 2 设平面 SCD 的法向量 n=(1,λ,μ),
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
1.知识与技能
掌握平面的法向量的概念及性质. 理解平面的向量表示. 2.过程与方法 用向量的观点认识平面、利用平面的法向量证明平行人ຫໍສະໝຸດ 教 B 版 数 学或垂直问题.
3.情感态度与价值观 培养学生转化的数学思想,增强应用意识.
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
重点:平面法向量的概念及性质. 难点:利用法向量法解决几何问题.
人 教 B 版 数 学
第三章
空间向量与立体几何
人 教 B 版 数 学
3.2.2平面的法向量与平面的向量表示
A' A'
B
二、概念形成
概念5.用法向量证明“三垂线定理”
三垂线定理: 如果在平面内的一条直线与平面的一条斜线在这个平面内 的射影垂直,则它也和这条斜线垂直。
的斜线, A' B 是 l 在平面 直线 a 且 a A ' B l 求证: a l A
已知 l 是平面
已知 l 是平面 直线
向量。那么 n DA y 0 n DB1 ,0),B 1(1,0,1)
z A1 B1 A B x
y 0 x z 0
A B C
D
令z=1,得 n (1,0,1)
n a 0, n b 0 n m 0 即 nm 所以 n m
因为 n 垂直于平面 内任意一条直 线,所以 n
因为 a , b ,由共面向量定理可知,存在唯一的数对(x,y),使
n
n
b
b
a
m a b m
设平面AMN的一个法向量为 n1 ( x1 , y1 , z1 ) A
D B
C
x
向量解法
A
利用法向量证明两个平面平行的基本思路是证明两个平面
的法向量平行(或共线)。
三、应用举例
例2.已知正方体ABCD-A1B1C1D1,求证: (1)AD1//平面BDC1 ; (2)AC1⊥平面BDC1 。
→ =OM → +OA → =(9,1,1).故选 B. ∴OB
2→ → 2.已知 A(3,-2,4),B(0,5,-1),若OC=3AB,则 C 的坐标是 14 10 A.(2,- 3 , 3 ) 14 10 C.(2,- ,- ) 3 3 ( )
高中数学平面的法向量与平面的向量表示题库

3.2.2 平面的法向量与平面的向量表示学习目标 1.理解平面的法向量的概念,会求平面的法向量.2.会用平面的法向量证明平面与平面平行、垂直.3.了解三垂线定理及其逆定理.知识点一 平面的法向量已知平面α,如果向量n 的基线与平面α垂直,则向量n 叫做平面α的法向量或说向量n 与平面α正交.知识点二 平面的向量表示设A 是空间任一点,n 为空间内任一非零向量,则适合条件AM →·n =0的点M 的集合构成的图形是过空间内一点A 并且与n 垂直的平面.这个式子称为一个平面的向量表示式. 知识点三 两平面平行或垂直的判定及三垂线定理 1.两平面平行或垂直的判定方法设n 1,n 2分别是平面α,β的法向量,则容易得到 α∥β或α与β重合⇔n 1∥n 2; α⊥β⇔n 1⊥n 2⇔n 1·n 2=0. 2.三垂线定理如果在平面内的一条直线与平面的一条斜线在这个平面内的射影垂直,则它也和这条斜线垂直.1.已知直线垂直于α,向量a 平行直线l ,则a 是平面α的法向量.( × )2.若向量n 1,n 2为平面的法向量,则以这两个向量为方向向量的直线一定平行.( × ) 3.若平面外的一条直线的方向向量与平面的法向量垂直,则该直线与平面平行.( √ ) 4.直线的方向向量与平面的法向量的方向相同或相反时,直线与平面垂直.( √ )题型一 求平面的法向量例1 如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点.AB =AP =1,AD =3,试建立恰当的空间直角坐标系,求平面ACE 的一个法向量.解 因为P A ⊥平面ABCD ,底面ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB 所在直线为x 轴建立空间直角坐标系Axyz ,则D (0,3,0),E ⎝⎛⎭⎫0,32,12,B (1,0,0),C (1,3,0), 于是AE →=⎝⎛⎭⎫0,32,12,AC →=(1,3,0).设n =(x ,y ,z )为平面ACE 的法向量, 则⎩⎪⎨⎪⎧n ·AC →=0,n ·AE →=0,即⎩⎪⎨⎪⎧x +3y =0,32y +12z =0,所以⎩⎪⎨⎪⎧x =-3y ,z =-3y ,令y =-1,则x =z = 3.所以平面ACE 的法向量为n =(3,-1,3). 引申探究若本例条件不变,试求直线PC 的一个方向向量和平面PCD 的一个法向量. 解 如图所示,建立空间直角坐标系Axyz ,则P (0,0,1),C (1,3,0),所以PC →=(1,3,-1)即为直线PC 的一个方向向量.设平面PCD 的法向量为n =(x ,y ,z ). 因为D (0,3,0),所以PD →=(0,3,-1). 由⎩⎪⎨⎪⎧n ·PC →=0,n ·PD →=0,即⎩⎪⎨⎪⎧x +3y -z =0,3y -z =0,所以⎩⎪⎨⎪⎧x =0,z =3y ,令y =1,则z = 3.所以平面PCD 的法向量为n =(0,1,3). 反思感悟 利用待定系数法求平面法向量的步骤 (1)设向量:设平面的法向量为n =(x ,y ,z ). (2)选向量:在平面内选取两个不共线向量AB →,AC →. (3)列方程组:由⎩⎪⎨⎪⎧ n ·AB →=0,n ·AC →=0列出方程组.(4)解方程组:⎩⎪⎨⎪⎧n ·AB →=0,n ·AC →=0.(5)赋非零值:取其中一个为非零值(常取±1). (6)得结论:得到平面的一个法向量.跟踪训练1 如图,在四棱锥P -ABCD 中,平面P AB ⊥平面ABCD ,△P AB 是边长为1的正三角形,ABCD 是菱形.∠ABC =60°,E 是PC 的中点,F 是AB 的中点,试建立恰当的空间直角坐标系,求平面DEF 的法向量.解 连接PF ,CF ,因为P A =PB ,F 为AB 的中点,所以PF ⊥AB , 又因为平面P AB ⊥平面ABCD ,平面P AB ∩平面ABCD =AB ,PF ⊂平面P AB . 所以PF ⊥平面ABCD ,因为AB =BC ,∠ABC =60°,所以△ABC 是等边三角形,所以CF ⊥AB .以F 为坐标原点,建立空间直角坐标系Fxyz (如图所示). 由题意得F (0,0,0),P ⎝⎛⎭⎫0,0,32,D ⎝⎛⎭⎫-1,32,0,C ⎝⎛⎭⎫0,32,0, E ⎝⎛⎭⎫0,34,34. 所以FE →=⎝⎛⎭⎫0,34,34,FD →=⎝⎛⎭⎫-1,32,0.设平面DEF 的法向量为m =(x ,y ,z ). 则⎩⎪⎨⎪⎧m ·FE →=0,m ·FD →=0,即⎩⎨⎧34y +34z =0,-x +32y =0.所以⎩⎪⎨⎪⎧z =-y ,x =32y ,令y =2,则x =3,z =-2.所以平面DEF 的法向量为m =(3,2,-2). 题型二 利用空间向量证明平行问题例2 已知正方体ABCDA 1B 1C 1D 1的棱长为2,E ,F 分别是BB 1,DD 1的中点,求证: (1)FC 1∥平面ADE ; (2)平面ADE ∥平面B 1C 1F .证明 (1)建立如图所示的空间直角坐标系Dxyz ,则有D (0,0,0),A (2,0,0),C (0,2,0),C 1(0,2,2),E (2,2,1),F (0,0,1),B 1(2,2,2),所以FC 1→=(0,2,1),DA →=(2,0,0),AE →=(0,2,1).设n 1=(x 1,y 1,z 1)是平面ADE 的法向量, 则n 1⊥DA →,n 1⊥AE →,即⎩⎪⎨⎪⎧n 1·DA →=2x 1=0,n 1·AE →=2y 1+z 1=0,得⎩⎪⎨⎪⎧x 1=0,z 1=-2y 1,令z 1=2,则y 1=-1,所以n 1=(0,-1,2). 因为FC 1→·n 1=-2+2=0,所以FC 1→⊥n 1. 又因为FC 1⊄平面ADE ,所以FC 1∥平面ADE .(2)因为C 1B 1—→=(2,0,0),设n 2=(x 2,y 2,z 2)是平面B 1C 1F 的法向量.由n 2⊥FC 1→,n 2⊥C 1B 1—→, 得⎩⎪⎨⎪⎧n 2·FC 1→=2y 2+z 2=0,n 2·C 1B 1—→=2x 2=0,得⎩⎪⎨⎪⎧x 2=0,z 2=-2y 2.令z 2=2,得y 2=-1,所以n 2=(0,-1,2), 因为n 1=n 2,所以平面ADE ∥平面B 1C 1F .反思感悟 利用向量证明平行问题,可以先建立空间直角坐标系,求出直线的方向向量和平面的法向量,然后根据向量之间的关系证明平行问题.跟踪训练2 如图,在四棱锥P-ABCD 中,P A ⊥平面ABCD ,PB 与底面所成的角为45°,底面ABCD 为直角梯形,∠ABC =∠BAD =90°,P A =BC =12AD =1,问在棱PD 上是否存在一点E ,使CE ∥平面P AB ?若存在,求出E 点的位置;若不存在,请说明理由.解 分别以AB ,AD ,AP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系Axyz ,∴P (0,0,1),C (1,1,0),D (0,2,0),设E (0,y ,z ),则PE →=(0,y ,z -1), PD →=(0,2,-1), ∵PE →∥PD →,∴(-1)×y -2(z -1)=0,①∵AD →=(0,2,0)是平面P AB 的法向量, 又CE →=(-1,y -1,z ),CE ∥平面P AB , ∴CE →⊥AD →,∴(-1,y -1,z )·(0,2,0)=0. ∴y =1,代入①得z =12,∴E 是PD 的中点,∴存在E 点,当点E 为PD 的中点时,CE ∥平面P AB . 题型三 利用空间向量证明垂直问题例3 三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC ,A 1A =3,AB =AC =2A 1C 1=2,D 为BC 的中点.证明:平面A 1AD ⊥平面BCC 1B 1.证明 方法一 如图,以点A 为坐标原点,AB ,AC ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (0,2,0),A 1(0,0,3),C 1(0,1,3). ∵D 为BC 的中点,∴D 点坐标为(1,1,0), ∴AD →=(1,1,0),AA 1→=(0,0,3),BC →=(-2,2,0), ∴AD →·BC →=1×(-2)+1×2+0×0=0,AA 1→·BC →=0×(-2)+0×2+3×0=0, ∴AD →⊥BC →,AA 1→⊥BC →, ∴BC ⊥AD ,BC ⊥AA 1.又A 1A ∩AD =A ,∴BC ⊥平面A 1AD .又BC ⊂平面BCC 1B 1,∴平面A 1AD ⊥平面BCC 1B 1. 方法二 同方法一建系后,得AA 1→=(0,0,3), AD →=(1,1,0),BC →=(-2,2,0),CC 1→=(0,-1,3). 设平面A 1AD 的法向量为n 1=(x 1,y 1,z 1), 平面BCC 1B 1的法向量为n 2=(x 2,y 2,z 2). 由⎩⎪⎨⎪⎧n 1·AA 1→=0,n 1·AD →=0,得⎩⎪⎨⎪⎧3z 1=0,x 1+y 1=0,令y 1=-1,则x 1=1,z 1=0, ∴n 1=(1,-1,0).由⎩⎪⎨⎪⎧n 2·BC →=0,n 2·CC 1→=0,得⎩⎪⎨⎪⎧-2x 2+2y 2=0,-y 2+3z 2=0,令y 2=1,则x 2=1,z 2=33, ∴n 2=⎝⎛⎭⎫1,1,33. ∵n 1·n 2=1-1+0=0,∴n 1⊥n 2, ∴平面A 1AD ⊥平面BCC 1B 1.反思感悟 利用空间向量证明面面垂直通常可以有两个途径,一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.跟踪训练3 在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点. (1)求证:平面AED ⊥平面A 1FD 1;(2)在直线AE 上求一点M ,使得A 1M ⊥平面AED . 考点 向量法求解平面与平面的位置关系 题点 向量法解决面面垂直(1)证明 以点D 为坐标原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系Dxyz .设正方体的棱长为2,则D (0,0,0),A (2,0,0),E (2,2,1),F (0,1,0),A 1(2,0,2),D 1(0,0,2), ∴DA →=D 1A 1—→=(2,0,0),DE →=(2,2,1),D 1F →=(0,1,-2). 设平面AED 的法向量为n 1=(x 1,y 1,z 1). 由⎩⎪⎨⎪⎧n 1·DA →=0,n 1·DE →=0,得⎩⎪⎨⎪⎧2x 1=0,2x 1+2y 1+z 1=0.令y 1=1,得n 1=(0,1,-2).同理,平面A 1FD 1的法向量为n 2=(0,2,1). ∵n 1·n 2=(0,1,-2)·(0,2,1)=0,∴n 1⊥n 2, ∴平面AED ⊥平面A 1FD 1. (2)解 由于点M 在直线AE 上, 因此可设AM →=λAE →=λ(0,2,1)=(0,2λ,λ), 则M (2,2λ,λ),∴A 1M →=(0,2λ,λ-2). 要使A 1M ⊥平面AED ,只需A 1M →∥n 1, 即2λ1=λ-2-2,解得λ=25.故当AM =25AE 时,A 1M ⊥平面AED .利用向量求解空间中的探索性问题典例 在正方体ABCD -A 1B 1C 1D 1中,E 是棱BC 的中点,试在棱CC 1上求一点P ,使得平面A 1B 1P ⊥平面C 1DE .考点 向量法求解平面与平面的位置关系 题点 向量法解决面面垂直解 如图,以D 为原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系.设正方体的棱长为1,P (0,1,a ),则A 1(1,0,1),B 1(1,1,1),E ⎝⎛⎭⎫12,1,0,C 1(0,1,1), A 1B 1—→=(0,1,0),A 1P →=(-1,1,a -1),DE →=⎝⎛⎭⎫12,1,0,DC 1→=(0,1,1). 设平面A 1B 1P 的一个法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n 1·A 1B 1—→=0,n 1·A 1P →=0,即⎩⎪⎨⎪⎧y 1=0,-x 1+y 1+(a -1)z 1=0,∴x 1=(a -1)z 1,y 1=0. 令z 1=1,得x 1=a -1, ∴n 1=(a -1,0,1).设平面C 1DE 的一个法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧ n 2·DE →=0,n 2·DC 1→=0,即⎩⎪⎨⎪⎧12x 2+y 2=0,y 2+z 2=0,∴⎩⎪⎨⎪⎧x 2=-2y 2,z 2=-y 2.令y 2=1,得x 2=-2,z 2=-1, ∴n 2=(-2,1,-1).∵平面A 1B 1P ⊥平面C 1DE ,∴n 1·n 2=0,即-2(a -1)-1=0,得a =12.∴当P 为CC 1的中点时,平面A 1B 1P ⊥平面C 1DE .[素养评析] 立体几何中探索性、存在性问题的思维层次较高,分析时应特别注意.本例由题意设出探求点的坐标,利用两平面垂直,法向量的位置关系及严密的逻辑推理,从而得出点P 的坐标.1.若直线l ∥α,且l 的方向向量为(2,m,1),平面α的法向量为⎝⎛⎭⎫1,12,2,则m 等于( ) A .-4 B .-6 C .-8 D .8 答案 C解析 ∵l ∥α,平面α的法向量为⎝⎛⎭⎫1,12,2, ∴(2,m,1)·⎝⎛⎭⎫1,12,2=0, 即2+12m +2=0,∴m =-8.2.若两个不同平面α,β的法向量分别为u =(1,2,-1),v =(-3,-6,3),则( ) A .α∥βB .α⊥βC .α,β相交但不垂直D .以上均不正确答案 A解析 ∵v =-3u ,∴v ∥u .故α∥β.3.若a =(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( ) A .(0,1,2) B .(3,6,9) C .(-1,-2,3) D .(3,6,8) 答案 B解析 向量(1,2,3)与向量(3,6,9)共线.4.已知平面α的法向量是(2,3,-1),平面β的法向量是(4,λ,-2),若α∥β,则λ的值是( )A .-103B .6C .-6 D.103答案 B解析 ∵α∥β,∴α的法向量与β的法向量也互相平行.∴24=3λ=-1-2.∴λ=6. 5.已知平面α与平面β垂直,若平面α与平面β的法向量分别为μ=(-1,0,5),v =(t,5,1),则t 的值为________.答案 5解析 ∵平面α与平面β垂直,∴平面α的法向量μ与平面β的法向量v 互相垂直,∴μ·v =0,即-1×t +0×5+5×1=0,解得t =5.1.用法向量来解决平面与平面的关系问题,思路清楚,不必考虑图形的位置关系,只需通过向量运算,就可得到要证明的结果.2.利用三垂线定理证明线线垂直,需先找到平面的一条垂线,有了垂线,才能作出斜线的射影,同时要注意定理中的“平面内的一条直线”这一条件,忽视这一条件,就会产生错误结果.一、选择题1.直线l 的方向向量s =(-1,1,1),平面α的一个法向量为n =(2,x 2+x ,-x ),若直线l ∥α,则x 的值为( )A .-2B .- 2 C. 2 D .±2答案 D解析 由题意知,-1×2+1×(x 2+x )+1×(-x )=0,解得x =±2.2.若平面α,β的法向量分别为u =(2,-3,5),v =(-3,1,-4),则( )A .α∥βB .α⊥βC .α,β相交但不垂直D .以上均不正确答案 C3.已知平面α内有一个点A (2,-1,2),α的一个法向量为n =(3,1,2),则下列点P 中,在平面α内的是( )A .(1,-1,1)B.⎝⎛⎭⎫1,3,32C.⎝⎛⎭⎫1,-3,32 D.⎝⎛⎭⎫-1,3,-32 答案 B解析 对于A ,P A →=(1,0,1),则P A →·n =(1,0,1)·(3,1,2)=5≠0,故排除A ;同理可排除C ,D ;对于B ,P A →=⎝⎛⎭⎫1,-4,12,则P A →·n =⎝⎛⎭⎫1,-4,12·(3,1,2)=0. 4.若n 1,n 2分别是平面α,β的法向量,且α⊥β,n 1=(1,2,x ),n 2=(x ,x +1,x ),则x 的值为( )A .1或2B .-1或-2C .-1D .-2 答案 B解析 由题意可知,n 1·n 2=(1,2,x )·(x ,x +1,x )=x +2x +2+x 2=x 2+3x +2=0,解得x =-1或x =-2.5.设直线l 的方向向量为a ,平面α的法向量为b ,若a ·b =0,则( )A .l ∥αB .l ⊂αC .l ⊥αD .l ⊂α或l ∥α 答案 D解析 当a ·b =0时,l ⊂α或l ∥α.6.已知平面α内两向量a =(1,1,1),b =(0,2,-1)且c =m a +n b +(4,-4,1).若c 为平面α的法向量,则m ,n 的值分别为( )A .-1,2B .1,-2C .1,2D .-1,-2答案 A解析 c =m a +n b +(4,-4,1)=(m ,m ,m )+(0,2n ,-n )+(4,-4,1)=(m +4,m +2n -4,m -n +1), 由c 为平面α的法向量,得⎩⎪⎨⎪⎧ c ·a =0,c ·b =0,得⎩⎪⎨⎪⎧m =-1,n =2.7.两平面α,β的法向量分别为μ=(3,-1,z ),v =(-2,-y ,1),若α⊥β,则y +z 的值是( )A .-3B .6C .-6D .-12答案 B解析 α⊥β⇒μ·v =0⇒-6+y +z =0,即y +z =6.8.已知A (1,0,0),B (0,1,0),C (0,0,1),则平面ABC 的一个单位法向量是( )A.⎝⎛⎭⎫33,33,-33 B.⎝⎛⎭⎫33,-33,33 C.⎝⎛⎭⎫-33,33,33 D.⎝⎛⎭⎫-33,-33,-33 答案 D解析 AB →=(-1,1,0),AC →=(-1,0,1).设平面ABC 的一个法向量为n =(x ,y ,z ).∵⎩⎪⎨⎪⎧ AB →·n =0,AC →·n =0, ∴⎩⎪⎨⎪⎧-x +y =0,-x +z =0. 令x =1,则y =1,z =1,∴n =(1,1,1),单位法向量为⎝⎛⎭⎫33,33,33或⎝⎛⎭⎫-33,-33,-33. 二、填空题9.已知A (4,1,3),B (2,3,1),C (3,7,-5),点P (x ,-1,3)在平面ABC 内,则x 的值为________. 答案 11解析 ∵点P 在平面ABC 内,∴存在实数k 1,k 2,使AP →=k 1AB →+k 2AC →,即(x -4,-2,0)=k 1(-2,2,-2)+k 2(-1,6,-8), ∴⎩⎪⎨⎪⎧ 2k 1+6k 2=-2,k 1+4k 2=0,解得⎩⎪⎨⎪⎧k 1=-4,k 2=1.∴x -4=-2k 1-k 2=8-1=7,即x =11.10.设平面α的法向量为m =(1,2,-2),平面β的法向量为n =(-2,-4,k ),若α∥β,则k =________.答案 4解析 由α∥β,得1-2=2-4=-2k (kD =/0),解得k =4. 11.在三棱锥S -ABC 中,∠SAB =∠SAC =∠ACB =90°,AC =2,BC =13,SB =29,则直线SC 与BC 是否垂直________.(填“是”“否”)答案 是解析 如图,以A 为坐标原点,AC ,AS 所在直线分别为y 轴,z 轴建立空间直角坐标系Axyz ,则由AC =2,BC =13,SB =29,得B (-13,2,0),S (0,0,23),C (0,2,0),SC →=(0,2,-23),CB →=(-13,0,0).因为SC →·CB →=0,所以SC ⊥BC .三、解答题12.已知平面α经过点A (1,2,3),B (2,0,-1),C (3,-2,0),试求平面α的一个法向量. 解 ∵A (1,2,3),B (2,0,-1),C (3,-2,0),∴AB →=(1,-2,-4),AC →=(2,-4,-3).设平面α的法向量为n =(x ,y ,z ),依题意有⎩⎪⎨⎪⎧ n ·AC →=0,n ·AB →=0,即⎩⎪⎨⎪⎧2x -4y -3z =0,x -2y -4z =0, 解得⎩⎪⎨⎪⎧z =0,x =2y ,令y =1,则x =2, ∴平面α的一个法向量为n =(2,1,0).13.如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,∠ABC =60°,P A =AB =BC ,AD =233AB ,E 是PC 的中点.求证:PD ⊥平面ABE .证明 ∵P A ⊥底面ABCD ,AB ⊥AD ,∴AB ,AD ,AP 两两垂直,建立如图所示的空间直角坐标系Axyz ,设P A =AB =BC =1,则P (0,0,1),A (0,0,0),B (1,0,0),D ⎝⎛⎭⎫0,233,0. ∵∠ABC =60°,∴△ABC 为正三角形.∴C ⎝⎛⎭⎫12,32,0,E ⎝⎛⎭⎫14,34,12. ∴AB →=(1,0,0),AE →=⎝⎛⎭⎫14,34,12, ∴设平面ABE 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧ n ·AB →=0,n ·AE →=0,即⎩⎪⎨⎪⎧ x =0,14x +34y +12z =0,令y =2,则z =-3,∴n =(0,2,-3).∵PD →=⎝⎛⎭⎫0,233,-1, 显然PD →=33n ,∴PD →∥n ,∴PD →⊥平面ABE ,即PD ⊥平面ABE .14.如图所示,△ABC 是一个正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE =CA =2BD ,M 是EA 的中点.求证:平面DEA ⊥平面ECA .证明 建立如图所示的空间直角坐标系Cxyz ,不妨设CA =2,则CE =2,BD =1,C (0,0,0),A (3,1,0),B (0,2,0),E (0,0,2),D (0,2,1).所以EA →=(3,1,-2),CE →=(0,0,2),ED →=(0,2,-1).分别设平面CEA 与平面DEA 的法向量为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧n 1·EA →=0,n 1·CE →=0, 即⎩⎪⎨⎪⎧3x 1+y 1-2z 1=0,2z 1=0.解得⎩⎪⎨⎪⎧ y 1=-3x 1,z 1=0.⎩⎪⎨⎪⎧ n 2·EA →=0,n 2·ED →=0, 即⎩⎪⎨⎪⎧ 3x 2+y 2-2z 2=0,2y 2-z 2=0.解得⎩⎪⎨⎪⎧x 2=3y 2,z 2=2y 2.不妨取n 1=(1,-3,0),n 2=(3,1,2),因为n 1·n 2=0,所以两个法向量相互垂直.所以平面DEA ⊥平面ECA .15.如图,已知ABCD -A 1B 1C 1D 1是棱长为3的正方体,点E 在AA 1上,点F 在CC 1上,且AE =FC 1=1.(1)求证:E ,B ,F ,D 1四点共面;(2)若点G 在BC 上,BG =23,点M 在BB 1上,GM ⊥BF ,垂足为H ,求证:ME ⊥平面BCC 1B 1. 考点 向量法求解直线与平面的位置关系题点 向量法解决线面垂直证明 (1)以点B 为坐标原点,BA ,BC ,BB 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Bxyz ,则BE →=(3,0,1),BF →=(0,3,2),BD 1→=(3,3,3),∴BD 1→=BE →+BF →,故BD 1→,BE →,BF →共面.又它们有公共点B ,∴E ,B ,F ,D 1四点共面.(2)设M (0,0,z ),则GM →=⎝⎛⎭⎫0,-23,z , 而BF →=(0,3,2),由题设得GM →·BF →=-23·3+z ·2=0,得z =1. ∵M (0,0,1),E (3,0,1),∴ME →=(3,0,0),又BB 1→=(0,0,3),BC →=(0,3,0),∴ME →·BB 1→=0,ME →·BC →=0,从而ME⊥BB1,ME⊥BC. 又BB1∩BC=B,故ME⊥平面BCC1B1.。
法向量与平面的向量表示
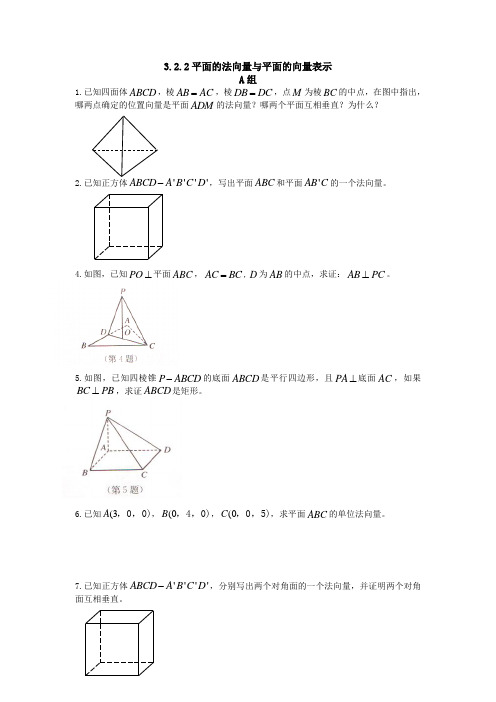
3.2.2平面的法向量与平面的向量表示
A 组
1.已知四面体ABCD ,棱AB AC =,棱DB DC =,点M 为棱BC 的中点,在图中指出,哪两点确定的位置向量是平面ADM 的法向量?哪两个平面互相垂直?为什么?
2.已知正方体''''ABCD A B C D -,写出平面ABC 和平面'AB C 的一个法向量。
4.如图,已知PO ⊥平面ABC ,AC BC =,D 为AB 的中点,求证:AB PC ⊥。
5.如图,已知四棱锥P ABCD -的底面ABCD 是平行四边形,且PA ⊥底面AC ,如果BC PB ⊥,求证ABCD 是矩形。
6.已知(3A ,0,0),(0B ,4,0),(0C ,0,5),求平面ABC 的单位法向量。
7.已知正方体''''ABCD A B C D -,分别写出两个对角面的一个法向量,并证明两个对角面互相垂直。
8.已知四面体ABCD 的棱AB CD ⊥,AC BD ⊥,求证:AD BC ⊥。
B 组
9.直四棱柱1111ABCD A BC D -中,底面ABCD 是矩形,121 3.AB AD AA ===,, M 是BC 的中点.在1DD 上是否存在一点N ,使1MN DC ⊥?。
3.2.2平面的法向量与平面的向量表示

3.2.2 平面的法向量与平面的向量表示峡山中学 高二数学组 2010-12-23【课标点击】(一)学习目标:1、掌握平面的法向量;2、利用平面的法向量判定平面的位置关系;3、平面的向量表示;4、线面垂直的判定定理;5、三垂线定理.(二)教学重、难点:平面的向量表示、线面垂直的判定,面面垂直的判定【课前准备】(一)知识连接:1、 空间直线的向量参数方程:a t OA OP +=或OB t OA t OP +-=)1(2、 设P 为AB 之中点则)(21OB OA OP +=3、 直线1l 与2l 的方向向量为1v 和2v ,则2121////v v l l ⇔,212121v v v v l l ⋅⇔⊥⇔⊥=04、 两直线成的角,与两直线的方向向量成角的关系5、 p 与a ,b 共面(a ,b 不共线)⇔R y x ∈∃,使b y a x p +=6、 点A 、B 、C 不共线,则点A 、B 、C 、P 共面⇔∃x 、y R ∈使AC y AB x AP += (二)问题导引:如何证明线面平行、线面垂直、面面平行、面面垂直?【学习探究】(一)自学引导:自主学习课本102页至103页部分. 1、平面的法向量2、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面(用向量方法证明)3、平面的向量表示:4、设1n 、2n分别是平面α、β的法向量,那么:α//β或α与β重合⇔ 21//n n αβ⊥⇔21n n ⊥5、三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直已知:,PO PA 分别是平面α的垂线和斜线,O A 是P A 在平面α内的射影,a α⊂,且a O A ⊥求证:a P A ⊥;证明:∵P O α⊥ ∴PO a ⊥,又∵,a OA PO OA O ⊥=∴a ⊥平面P O A ,∴a P A ⊥. 说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;(2)推理模式:,,PO O PA A a PA a a O A αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭6条斜线的射影垂直证明思路: ,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭.(二)思考与讨论:⑴三垂线指: (PA ,PO ,AO 都垂直α内的直线a )2)其实质是: ( 斜线和平面内一条直线垂直的判定和性质定理)注意:要考虑a 的位置,并注意两定理交替使用(三)典型例题:例1.在正方体111ABCD A B C D -中,求证:1D B是平面1AC D 的法向量.例2:已知正方体''''ABC D A B C D -.求证:平面''//A B D 平面'B D C .例3.如图,底面A B C D 是正方形,SA ⊥底面A B C D ,且SA AB =,E 是S C 中点. 求证:平面BD E ⊥平面A B C D .说明:一.证明垂直关系,可通过向量的数量积等于0来实现;二.要善于转化,即挖掘已知的垂直关系,将未知向已知转化(四)变式拓展:已知正方体1111ABC D A B C D -中,,E F 分别为1,BB C D 的中点, 求证:1D F ⊥平面A D E 。
3.2.2学案

3.2.2平面的法向量与平面的向量表示班级___姓名:__________时间2012.2.10 一、【教材知识梳理】1.已知平面α,如果向量n 的基线与平面α垂直,则向量n叫做____________________。
2.平面α的一个法向量垂直于与平面α共面的所有向量,同时,一个平面的所有法向量____________。
3.如果一条直线和平面内的两条___________直线垂直,那么这条直线_______于这个平面。
4.设12n n 、分别是平面αβ、的法向量,则容易得到:α∥β或(αβ、重合)⇔_________,12n n αβ⊥⇔⊥⇔_______________。
5.已知平面α和一点A ,过点A 作α的垂线l 与α相交于点'A ,则'A 就是点A 在平面α内的________,简称_________________。
6.如果一条直线AB 和平面α相交于点B ,但不和α垂直,那么直线AB 叫做这个平面的____________,斜线和平面的交点B 叫做____________,斜线上一点A 与斜足B 之间的线段叫做_____________。
7.如果在平面内的一条直线与平面的一条斜线在这个平面的____________重直,则它也和这条_________垂直。
8.如果________________的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在平面内的______垂直。
二、【课前检测】1.若平面αβ、的法向量分别为1n =(1,2,-2),2n =(-3,-6,6),则( ) A.α∥β B.αβ⊥ C.αβ,相交但不垂直 D.以上说法都不对2.已知==AB AC(2,2,1),(4,5,3),则平面ABC 的一个单位法向量为( )A.122333(-,-,-) B.122333(-,,-) C.122333(-,,) D. 122333(,,)3.设平面α的法向量为(1,2,-2),平面β的法向量为k (-2,-4,),若α∥β,则k =__________;若αβ⊥,则k =________________。
(完整版)平面的法向量

∴平面 ABC 的单位法向量为(1, 2,2)或( 1,2, 2).
3 33
33 3
例 如图,已知矩形 ABCD和矩形 ADEF所在平面互相垂直,点
M , N 分别在对角线 BD, AE上,且 BM 1 BD, AN 1 AE,
求证:MN // 平面CDE
3
3
简证:因为矩形ABCD和矩形ADEF 所在平面互相垂直u,uur所uuu以r uAuuBr,AD,
解: 在 内作不r与urm r,nu重r 合的任一直线g,在l, m, n, g
上取非零向量 l, m, n, g,因m与n相交,故向量m ,n
不平行,由共面向量定理,存在唯一实数(x, y),使
ur ur r r ur r ur r r
g xm yn , l g xl m yl n , l
3.
平面的向量表示:
AMgn
r
0
给定一点rA和一个向量 n,那么过点
l
r
A,以向量n 为法向量的平面是完全
确定的.
n
M
A
因为方向向量与法向量可以确定直线和 平面的位置,上节我们用直线的方向向量表 示了空间直线、平面间的平行
如何用平面的法向量表示空间两平面平 行、垂直的位置关系呢?
4. 两平面平行或重合、垂直的充要条件
则 n AB ,n AC .∵ AB (3, 4, 0) , AC (3, 0, 2)
∴
( x, ( x,
∴
yห้องสมุดไป่ตู้
z
y, z)
y, z)
3x 4
3x 2
(3, (3,
4, 0,
0) 2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2.2平面的法向量与平面的向量表示
(一)教学目标
1.知识与技能: 掌握平面的法向量,利用平面的法向量判定平面的位置关系,平面的向量表示,线面垂直的判定定理,三垂线定理。
2.过程与方法:通过实践演算掌握运用平面的法向量解。
3.情态与价值:通过学生对问题的探究思考,广泛参与,改变学生学习方式,提高学习质量。
(二)教学重、难点
重点:平面的向量表示、线面垂直的判定。
难点:平面的向量表示、线面垂直的判定。
(三)教学设想
(一)、复习:
1、 直线的位置向量
2、 直线l 的参数方程:a t AP =
3、 空间直线的向量参数方程:t +=或t t +-=)1(
4、 设P 为AB 之中点则)(2
1+= 5、 直线1l 与2l 的方向向量为1v 和2v ,则2121////v v l l ⇔,
212121v v v v l l ⋅⇔⊥⇔⊥
6、 两直线成的角,与两直线的方向向量成角的关系
7、 p 与,共面(,不共线)⇔R y x ∈∃,使b y a x p +=
8、 点A 、B 、C 不共线,则点A 、
B 、
C 、P 共面⇔∃x 、y R ∈使y x += (二)、引入新课
1、平面的法向量
2、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
(用向量方法证明)
3、平面的向量表示:0AM n =
4、设1n 、2n 分别是平面α、β的法向量,那么
α//β或α与β重合⇔1n //2n
αβ⊥⇔12n n ⊥⇔120n n =
5、三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直(向量证明见教材,这里补充传统证法)
已知:,PO PA 分别是平面α的垂线和斜线,OA 是
PA 在平面α内的射影,a α⊂,且a OA ⊥
求证:a PA ⊥;
证明:∵PO α⊥
∴PO a ⊥,又∵,a OA PO OA O ⊥=
∴a ⊥平面POA ,
∴a PA ⊥. 说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;
(2)推理模式:,,PO O PA A a PA a a OA αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭
6、三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那麽它也和这条斜线的射影垂直(向量证明见教材,这里补充传统证法思路)
证明思路: ,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭
.
注意:⑴三垂线指PA ,PO ,AO 都垂直α内的直线a 其实质是:斜线和平面内一条直线垂直的判定和性质定理 ⑵要考虑a 的位置,并注意两定理交替使用小结:本节课我们学习了直线的向量方程
课堂练习:第108页练习A 、B
课后作业:略。
