2013年初中数学中考模拟题集一合

合集下载

2013年中考数学模拟题(含答案)

2013年中考数学模拟题一、选择题（每小题3分，共15分）1.下列运算正确的是（）A. x 2·x 3=x 6B. –2x -2=- 14x 2 C.(-x 2)3=x 5 D.-x 2-2x 2=-3x 2 2.在平面直角坐标系中，点P （-1，-1）关于x 轴的对称点在（） A.第一象限 B. 第二象限C.第三象限D. 第四象限3.某班5位同学的身高（单位：厘米）分别155，160，160，161，169，这组数据中，下列说法错误的是（）A.众数是160B.中位数是160C.平均数是161D.方差是24.如图，PA 切⊙O 于A ，∠P=30°，OP =2，则⊙O 的半径的是（）A.21B.1C. 2D.45.已知圆锥的母线长为5cm ，底面半径为3cm ，则此圆锥的侧面积为（）A. 12πcm 2B. 15πcm 2C. 20πcm 2D. 30πcm 2二、填空题（每小题4分，共20分）6.已知代数式2x 2-x+1的值等于2，则代数式 4x 2-2x+5的值为___________.7.若反比例函数y=- x8的图象经过点（m ，-2m ），则m 的值为___________.8、十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是黄灯的概率是________.9.如图，CD⊥AB，BE⊥AC，请你再添加一个条件：________使ΔABE≌ΔACD。

10.如图，在 RtΔABC中，∠C=90°，AB=4cm，AC=23cm，以B为圆心，以BC为半径作弧交AB于D，则阴影部分的面积是 _____cm2。

三、解答题（每小题6分，共30分）11.有这样一道题：“计算x2-2x+1x2-1÷x-1x2+x-x 的值，其中x=2007”。

甲同学把“x=2007”错抄成“x=2070”，但他的计算结果也是正确的，你说这是怎么回事？12. ，并把解集在数轴上表示出来。

2013年中考数学模拟卷(一)(有答案)

2013年中考数学模拟卷(一)(时间:120分满分:120分)一、选择题（本大题共8小题，每小题3分，共24分） 1.下列实际问题中的数据是近似数的有【】①我国人口总数为:122389万人，②.某本书共有304页，③.九年级某班学生共有53人，④.圆周率 3.14π≈ ⑤.若干千克苹果平均分给若干个人,每人大约得3.33千克 A ．①④⑤ B.②⑤ C.③④ D.① ② 2．下列各式运算正确的是【】A. 235a a a +=B. 235a a a = C.235()a a = D .1025a a a ÷= 3. 把点1(23)P -，向右平移3个单位长度再向下平移2个单位长度到达点2P 处，则2P 的坐标是【】Ａ．(51)-，Ｂ．(15)--，Ｃ．(55)-，Ｄ．(11)--， 4. 已知线段a 、b 、c 并有a>b>c,则组成三角形满足的条件是【】A ．a+b>c B.a+c>b C.a-b<c D .b-c<a5．如图,为测楼房BC 的高,在距离楼房30米的A 处,测得楼顶的仰角为α,则楼高BC 的高为【】 A.30tan α米; B.30tan α米; C.30sin α米; D.30sin α米.6.下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小明从中抽出一张，则抽到偶数的概率是【】 A ．13 B ．12 C ．34 D ．237.形状相同、大小相等的两个小木块放置于桌面，其俯视图如下图所示，则其主视图是【】8．如图，一张矩形纸片，沿折痕CE 分别作两次不同情况的折叠，①顶点B 落在AD 边上（如图1）；②顶点B 落在矩形ABCD 的内部（如图2）.那么∠1+∠2与∠3+∠4的大小关系是【】A ．∠1+∠2=∠3+∠4 B.∠1+∠2＜∠3+∠4 C ．∠1+∠2＞∠3+∠4 D.不能确定二、填空题 (本大题共8小题,每小题3分,共24分)9. ( 在下面(Ⅰ)、(Ⅱ)两题中任选一题，若两题都做按第(Ⅰ)题计分)(Ⅰ).2sin60°·tan30°=(Ⅱ)．利用计算器计算：2sin42°≈ （保留4个有效数字） 10.不等式x －3＜0的最大整数解是11．如图,在△ABC 中，E 、F 分别是AB 、AC 上点，当∠1+∠2+∠B+∠C=300°时，∠A= 度.12.如图.AB 是⊙O 的切线，∠B=30°,则 OA ︰OB= 13. 写一个不等式(组),使它的整数解有且仅有:-1、-2，则这个不等式（组）可以是__________________.14. 观察下列各直角坐标系中的正方形ABCD ，点P(x,y)是四条边上的点，且x ,y 都是整数，由图中所包含的规律，可得第n 个图中满足条件的点P 个数是_____________(用含n 的代数式表示).15.如图：已知直线AB ∥y 轴，且直线AB 分别与函数2y x = (x>0)、ky x= (x>0)的图象交于A 、B 两点，并知△AOB 的面积2.5,则k=16．如图中，∠ABC=60,∠B DE=∠C=45,DF=1, AB=1+3,DE ⊥AB,分别交AB 于F,BC 于E,则下列结论: ①AF =EF ；②△ADF ≌△EBF ；③21=AE BD ； ④△DBE ∽△CEA 中,正确结论的序号．．．．．．．是 (多填或错填得0分,少填酌情给分) . 三、(本大题共3小题,第17题6分，第18、19均为7分，共20分）.17. 求代数式的值：)2422(4222+---÷--x x x x x x ，其中22+=x18．如图，在△ABC 中，AB=5，AD=4，BD=DC=3,且DE AB 于E ，DF ⊥AC 于F.（1）请你写出图中与A 点有关的三个不同类型的正确结论；（2）DE 与DF 在数量上有何关系？并证明之.19．某班同学上学期全部参加了捐款献爱心活动，个人捐款额见如下统计图，资助对象金额分配情况见如下统计表（1）补填统计表中的空白；（2）求该班学生个人捐款额的中位数和众数；（3）求捐款额多于15元的学生数占全班人数的百分数；（4）根据统计表中的数据画出扇形统计图.四、（本大题共2小题，每小题8分，共16分）20. 在平行四边形ABCD 中，对角线AC ，BD 交于O 点（BD>AC ）,E 、F 是BD 上的两点. (1) 当点E 、F 满足条件：时，四边形AECF 是平行四边形（不必证明）; （2）当点E 、F 满足条件：时，四边形AECF 是矩形，并加以证明.资助对象灾区民众重病学生孤老病者捐助金额（元）13518921.现有三个数：1、3、5，要添加一数，使得它们的平均数增大，平均数增大多少，只能通过如图所示的自由转盘来决定，你认为添加一个什么数可能性较大？五、（本大题共2小题，第22题8分，第23题9分，共17分）22.在⊙O中,AB是非直径弦,弦CD⊥AB,(1)当CD经过圆心时(如图1)∠AOC+∠DOB= 度;(2)当CD不经过圆心时(如图2), ∠AOC+∠DOB的度数与(1)的情况相同吗?试说明你的理由.23. 在购买课桌椅时，设购买套数为x（套），总费用为y（元）．现有两种购买方案：方案一：若学校赞助出售单位10000元，则该校所购课桌椅的价格为每套40元；（总费用=赞助费+课桌椅费）方案二：购买课桌椅方式如图所示．解答下列问题：（1）方案一中，y与x的函数关系式为；方案二中，当0≤x≤200时，y与x的函数关系式为；当x＞200时，y与x的函数关系式为；（2）如果购买课桌椅超过200套，你将选择哪一种方案，使总费用最省？请说明理由；（3）甲、乙两校分别采用方案一、方案二购买课桌椅共500套，花去总费用计40000元，求甲、乙两校各购买课桌椅多少套．六、（本大题共2小题，第24题9分，第25题10分，共19分）24.有一张梯形纸片ABCD，DC∥AB，∠DAB=90°，将△ADC沿AC折叠，点D恰好落在BC的中点E上（如图1）（1）求证：∠DAC=∠EAB；（2）当上底DC=10cm时，求梯形两腰AD、BC的长；（3）若过E作EF⊥AB于F，现将这张梯形纸片沿AE、EF剪成三块，然后按如图2所示拼成四边形HDAE（对应部分有相同的编号），那么四边形HDAE是什么特殊四边形（不证明）？并请你在图3中画出两条分割线（虚线），同样将梯形纸分成三块，然后拼成一个正六边形，要求仿图2方法画出拼图.25.在直角坐标系中，△ABC 的顶点坐标为A （4，6），B （2，3），C （5，3）.将△ABC 绕点C 顺时针旋转180°后得到△11CB A .(1)求A 1,B 1的坐标;(2)已知坐标系中有抛物线y=ax 2-10ax+24a (a ≠0) ①求该抛物线与x 轴的交点坐标,并说明这两交点分别与A 点有何位置关系（从对称角度来说明）?②当抛物线经过点B 时,能否确定一定经过点B 1,说说你的理由;③若点P 是该抛物线的顶点,是否存在一个实数a,使△BPB 1与△BAC 相似,若存在,求出P 点坐标,若不存在,说明其理由.2013年中考数学模拟卷(一)参考答案一、选择题（本大题共8小题，每小题3分，共24分）1. A,2. B,3. C4. C,5. A ,6. C7. D ,8. A 二、填空题 (本大题共8小题,每小题3分,共24分)9. (Ⅰ). 1,(Ⅱ) 1.338 10. 2 11. 30 12. 1︰2 13.如：10250x x +≤⎧⎨+>⎩14. 4n , 15. -3 16.①②④三、(本大题共3小题,第17题6分，第18、19均为7分，共20分）.17. 解: 原式=2242222+-÷--x xx x x x =错误！不能通过编辑域代码创建对象。

2013中考数学模拟测试卷

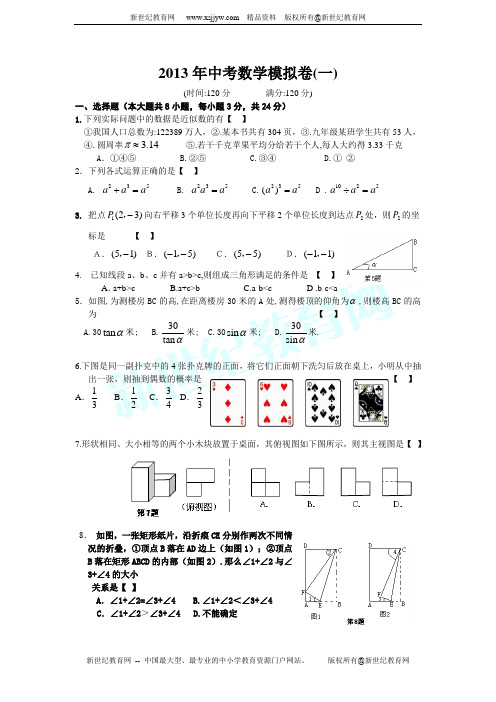
2013中考数学模拟测试卷一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在题．前括号内．．．．．【】1. －2的绝对值是A．2 B．－2 C．12- D．2±【】2. 下列计算正确的是A．3x2·4x2＝12x2 B．x3·x5＝x15 C．x4÷x＝x3 D．(x5)2＝x7【】3. 某同学在“百度”搜索引擎中输入“魅力南通”，能搜索到与之相关的结果个数约为3930000，这个数用科学记数法表示为A．0.393×107 B．393×104C．39.3×105 D．3.93×106【】4. 若一个多边形的内角和是900°，则这个多边形的边数是A．5 B．6 C．7 D．8【】5. 如图所示，△ABC的顶点是正方形网格的格点，则sin A的值为A．12B．5C．10D．25【】6. 如图，点A、C、B、D分别是⊙O上四点，OA⊥BC，∠AOB=50°则∠ADC的度数为A．20° B．25° C．40° D．50°【】7. 如图所示的工件的主视图是【】8. 某鞋店一天中卖出运动鞋11双，其中各种尺码的鞋的销售量如下表：则这11双鞋的尺码组成的一组数据中，众数和中位数分别是A．24.5，24.5 B．24.5，25 C．25，24.5 D．25，25尺码（cm）23.5 24 24.5 25 25.5销售量（双） 1 2 2 5 1A.B.C.D.（第5题）【】9. 下列轴对称图形中，只用一把无刻度的直尺不能．．画出对称轴的是 A ．菱形B ．矩形C ．等腰梯形D ．正五边形【】10. 如图，已知在Rt△ABC 中，AB =AC =2，在△ABC 内作第一个内接正方形DEFG ；然后取GF 的中点P ，连接PD 、PE ，在△PDE 内作第二个内接正方形HIKJ ；再取线段KJ 的中点Q ，在△QHI 内作第三个内接正方形……依次进行下去，则第n 个内接正方形的边长为A ．21()32n ⋅B ．221()2n ⋅C ．121()32n -⋅ D ． 1221()2n -⋅二、填空题：本大题共8小题，每小题3分，共24分．请把最后结果填在题中横线上． 11. 计算：327-＝．12. 将一直角三角板与两边平行的纸条如图所示放置，若∠1=53°，则∠2＝ °． 13. 已知分式21x x -+的值为0，那么x 的值为． 14. 一个圆锥的母线长为4，侧面积为12π，则这个圆锥的底面圆的半径是． 15. 如图，函数2y x =和5y ax =+的图象相交于A (m ，3)，则不等式25x ax <+的解集为．16. 设m ，n 是方程220120x x --=的两个实数根，则2m n +的值为． 17. 如图，已知正方形ABCD 的边长为2，对角线AC 、BD 相交于点O ，AE 平分∠BAC 交 BD 于点E ，则BE 的长为． 18. 如图，点A 是双曲线4y x=在第一象限上的一动点，连接AO 并延长交另一分支于点B ，以AB 为斜边作等腰Rt △ABC ，点C 在第二象限，随着点A 的运动，点C 的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为．A BCD EFGH I K J PQ （第10题）（第6题）OD C B12（第12题）三、解答题:本大题共10小题，共计96分．解答时应写出文字说明、证明过程或演算步骤.19．（本题满分10分）（1）计算：0(3)-＋12cos30°－11()5- （2）解方程组：38 53 4 x y x y +=⎧⎨-=⎩①②20．（本题满分8分）化简分式222421444a aa a a -÷--++，并选取一个你认为合适的整数a 代入求值.y AOx（第15题）xBAC（第18题）O y（第17题）OE小敏为了解本市的空气质量情况，从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．请你根据图中提供的信息，解答下列问题：（1）计算被抽取的天数；（2）请补全条形统计图，并求扇形统计图中表示优的扇形的圆心角度数；（3）请估计该市这一年（365天）达到优和良的总天数．22．（本题满分8分）如图，AB 与⊙O 相切于点C ，OA ＝OB .（1）如图①，若⊙O 的直径为8cm ，AB ＝10cm ，求OA 的长（结果保留根号）；（2）如图②，OA 、OB 与⊙O 分别交于点D 、E ，连接CD 、CE ，若四边形ODCE 为菱形，求ODOA的值．OA B C 图 ①ADCBOE图 ②本市若干天空气质量情况扇形统计图优良 64%轻微污染轻度污染中度污染重度污染轻微污染轻度污染天数（天）20 15105832311中度污染重度污染空气质如图，在边长为1的正方形组成的网格中，△ABC的顶点和O点均在格点上．（1）以点O为位似中心，在网格中将△ABC放大为原来的2倍，得到△A′B′C′；（2）△A′B′C′绕点B′顺时针旋转90°，画出旋转后得到的△A″B′C″，并求边A′B′在旋转过程中扫过的图形面积．24．（本题满分8分）如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF＝3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．DF甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标有的三个数值为－7，－1，3，乙袋中的三张卡片所标的数值为－2，1，6，先从甲袋中随机取出一张卡片，用x表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用y 表示取出卡片上的数值．把x、y分别作为点A的横坐标和纵坐标．（1）用列表或画树形图的方法写出点A（x，y）的所有情况；（2）求点A落在直线2上的概率．y x26．（本题满分10分）甲、乙两组同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示．（1）直接写出甲组加工零件的数量y与时间x之间的函数关系式▲；（2）求乙组加工零件总量a的值；（3）甲、乙两组加工出的零件合在一起装箱，每满300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t >0）秒．（1）当点Q从B点向A点运动时（未到达A点），若△APQ∽△ABC，求t的值；（2）伴随着P，Q两点的运动，线段PQ的垂直平分线为直线l．①当直线l经过点A时，射线QP交AD边于点E，求AE的长；②是否存在t的值，使得直线l经过点B？若存在，请求出所有t的值；若不存在，请说明理由．如图，二次函数212y x mx n =-++的图象与y 轴交于点N ，其顶点M 在直线32y x =-上运动，O 为坐标原点. （1）当m ＝－2时，求点N 的坐标；（2）当△MON 为直角三角形时，求m 、n 的值；（3）已知△ABC 的三个顶点的坐标分别为A (－4，2)，B (－4，－3)，C (－2，2)，当抛物线212y x mx n =-++在对称轴左侧的部分与△ABC 的三边有公共点时，求m的取值范围.（第2问图）。

2013年中考数学模拟试卷

2013年中考数学模拟试卷2013年中考数学模拟试卷一一、选择题(本题共12个小题，每小题3分，满分36分)每小题都给出标号为A，B，C，D四个备选答案，其中有且只有一个是正确的。

1、的值是 4A、4B、2C、-2D、?22A B C Dx-1?3 23、不等式组的解集在数轴上表示正确的是x,-1A B C D(第3题图)4、如图，所给图形中是中心对称图形但不是轴对称图形的是A B C D 5、过度包装既浪费资源又污染环境(据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为5657A、 B、 C、 D、 0.312，103.12，103.12，1031.2，106、在共有15人参加的“我爱祖国”演讲比赛中，参赛选手要想知道自己是否能进入前8名，只需要了解自己的成绩以及全部成绩的A、平均数B、众数C、中位数D、方差7、下列一元二次方程两实数根和为-4的是2222A、x+2x-4=0 B、x-4x+4=0 C、x+4x+10=0 D、x+4x-5=08、如图，在四边形ABCD中，DC?AB，CB?AB，AB=AD，1CD=AB，点E、F分别为AB，AD的中点，则?AEF与多边形2BCDFE的面积之比为1111 A、 B、C、D、7654川眉山，11，3分)圆锥底面圆的半径为1cm，母线长为6cm，则圆锥侧面展9、(2012四开图的圆心角是( )0000A(30 B(60 C(90 D(12010、一个由小菱形组成的装饰链，断去了一部分，剩下部分如图所示，则断去部分的小菱形的个数可能是A、3B、4C、5D、6yDDB C HF O AF Gx EC BAE4y,y,x，311、如图，一次函数的图象与轴，轴交于A，B两点，与反比例函数的yx xy图象相交于C，D两点，分别过C，D两点作轴，轴的垂线，垂足为E，F，连接CF，xDE(有下列四个结论:??CEF与?DEF的面积相等;??AOB??FOE;ACBD,??DCE??CDF;?。

2013年数学中考模拟试题及答案

2013年中考数学模拟试题一、选择题：本大题共8小题，在每小题给出的四个选项中，只有一项是正确的，请把正确选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分． 1．－ 13的倒数是A ．－3B ．3C ．－ 13D ．132．下列各式运算中，正确的是A ．222()a b a b +=+ B3=C ．3412a a a ⋅=D ．)0(6)3(22≠=a a a3．下列几何体中，主视图、左视图、俯视图完全相同的是 A. 圆柱 B. 圆锥 C. 球 D. 棱锥 4．下列说法正确的是A ．买一张福利彩票一定中奖，是必然事件．B ．买一张福利彩票一定中奖，是不可能事件．C ．抛掷一个正方体骰子，点数为奇数的概率是13． D ．一组数据：1，7，3，5，3的众数是3． 5．函数y =中自变量的取值范围在数轴上表示为6．在□ABCD 中，点E 为AD 的中点，连接BE ，交AC 于点F ，则=CFAFA ．1：2B ．1：3C ．2：3D ．2：5第7题图7．如图，在△ABC 中，AB = AC ，AB = 8，BC = 12以AB 、AC 为直径作半圆，则图中阴影部分的面积是A．64π-B ．1632π-C．16π-．16π-8．如图，点P 按A →B →C →M 的顺序在边长为1的正方形边上运动，M 是CD 边上的中点。

设点P 经过的路程x 为自变量，△APM 的面积为y ，则函数y 的大致图像是二、填空题：本大题共8小题，共32分，只要求填写最后结果，每小题填对得4分． 9．我国公安部交管局公布的数据显示，截至2012年初，全国机动私家车保有量达0.195亿辆，将0.195亿辆用科学记数法表示应是辆（结果保留2个有效数字） 10．分解因式：=+-y xy y x 22 。

11．= ． 12．如果圆锥的底面周长为20πcm ，侧面展开后所得的扇形的圆心角是120º，则该圆锥的侧面积是___________．（结果保留π） 13．如图，直线a ∥b ，l 与a 、b 交于E 、F 点，PF 平分∠EFD 交a 于P 点，若∠1 = 70︒，则∠2 = ． 14．已知n 是正整数，n P (n x ，n y )是反比例函数xky =图象上的一列点，其中1x 1=，21F E DblPa2x 2=，…，n x n =，记211y x T =，322y x T =，…，1099y x T =；若1T 1=，则921T T T ⋅⋅⋅⋅⋅⋅的值是_________；15．如图，在等边△ABC 中，9=AC ，点O 在AC 上，且3=AO ，点P 是AB 上一动点，连接OP ，以O 为圆心，OP 长为半径画弧交BC 于点D ，连接PD ，如果PD PO =，那么AP 的长是 .16．如图，n +1个边长为2的等边三角形有一条边在同一直线上，设211B D C ∆的面积为1S ，322B D C ∆的面积为2S ，……，1n n n B D C +∆的面积为n S ，则n S = （用含n 的式子表示）．三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤．17．化简求值 (本题满分6分) 。

2013年中考数学模拟试卷(一、二)(A3版)-----

2013年中考数学模拟试卷（一）（满分120分，考试时间100分钟）一、选择题（每小题3分，共24分）1．9的平方根是【】A．3 B．-3 C．±3 D．62．某种微粒子，测得它的质量为0.000 067 46克，这个质量用科学记数法表示（保留三个有效数字）应为【】A．6.75×10-5克B．6.74×10-5克C．6.74×10-6克D．6.75×10-6克3．下列图形中，既是轴对称图形又是中心对称图形的共有【】A．1个B．2个C．3个D．4个4．某市5月上旬前五天的最高气温如下（单位：°C）：28，29，31，29，33，对这组数据，下列说法错误的是【】A．平均数是30 B．众数是29 C．中位数是31 D．极差是55．如图，二次函数2y ax bx c=++的图象经过(-1，1)，(2，-1)两点，下列关于这个二次函数的叙述正确的是【】A．当x=0时，y的值大于1 B．当x=3时，y的值小于0C．当x=1时，y的值大于1 D．y的最大值小于水平面主视方向第5题图第6题图第7题图6．两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视图是【】A．两个外离的圆B．两个相交的圆C．两个外切的圆D．两个内切的圆A．30°B．45°C．60°D．90°FEDA第8题图第10题图第13题图二、填空题（每小题3分，共21分）∠AEC=_________．11．圆锥的底面圆直径和母线长均为80cm，则它的侧面展开图的圆心角是_________．12．某市初中毕业男生体育测试项目有四项，其中“立定跳远”、“1 000米跑”、“掷实心球”为必测项目，另一项从“篮球运动”或“一分钟跳绳”中选一项测试．小亮、小明和大刚从“篮球运动”或“一分钟跳绳”中选择同一个测试项目的概率是__________．16．（8分）先化简2111122xx x x⎛⎫-÷⎪-+-⎝⎭，然后从-2≤x≤2的范围内选择一个合适的整数作为x的值代入求值．17．（9分）为了更好地宣传吸烟的危害，某中学九年级一班数学兴趣小组设计了如下调查问卷，调查了部分吸烟人群，并将调查结果绘制成统计图．42%调查结果的扇形统计图调查结果的条形统计图ACBDE根据以上信息，解答下列问题：（1）本次接受调查的总人数是_________人，并把条形统计图补充完整．（2）在扇形统计图中，C选项的人数百分比是________，E选项所在扇形的圆心角的度数是________．（3）若某地区约有烟民14万人，试估计对吸烟有害持“无所谓”态度的约有多少人？M A E F D B C 18．（9分）已知：如图，四边形ABCD 是正方形，BD 是对角线，BE 平分∠DBC 交DC 于E 点，交DF 于M 点，F 是BC 延长线上一点，且CE =CF ．（1）求证：BM ⊥DF ；（2）若正方形ABCD 的边长为2，求ME ·MB 的值．19．（9分）甲、乙两地相距300km ，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA 表示货车离甲地的距离y （km ）与时间x （h ）之间的函数关系，折线BC -CD -DE 表示轿车离甲地的距离y （km ）与时间x （h ）之间的函数关系．请根据图象，解答下列问题：（1）线段CD 表示轿车在途中停留了________h ；（2）求线段DE 对应的函数解析式；（3）求轿车从甲地出发后经过多长时间追上货车．20．（9分）如图所示，当小华站立在镜子EF 前的A 处时，他看自己的脚在镜中的像的俯角为45°；如果小华向后退0.5米到B 处，这时他看自己的脚在镜中的像的俯角为30°．求小华的眼睛到地面的距离．（结果精确到0.1米，参考数据1.73）21．（10分）某商店为了抓住文化艺术节的商机，决定购进A ，B 两种艺术节纪念品．若购进A 种纪念品8件，B 种纪念品3件，需要950元；若购进 A 种纪念品5件，B 种纪念品6件，需要800元．（1）求购进A ，B 两种纪念品每件各需多少元．（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这 100件纪念品的资金不少于7 500元，但不超过7 650元，那么该商店共有几种进货方案？（3）若销售每件A 种纪念品可获利润20元，每件B 种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？22．（10分）在正方形ABCD 中，对角线AC ，BD 交于点O ，点P 在线段BC 上（不与点B 重合），∠BPE =12∠ACB ，PE 交BO 于点E ，过点B 作BF ⊥PE ，垂足为F ，交AC 于点G ．（1）当点P 与点C 重合时（如图1），求证：△BOG ≌△POE ；（2）通过观察、测量，猜想：BF PE=________，并结合图2证明你的猜想；（3）把正方形ABCD 改为菱形，其他条件不变（如图3），若∠ACB =α，求BF PE的值．（用含α的式子表示）（1）求过点A ，O ，B 的抛物线解析式．（2）在（1）中抛物线的对称轴上是否存在点M ，使△AOM 的周长最小？若存在，求出点M 的坐标；若不存在，请说明理由．（3）在x 轴下方的抛物线上是否存在一点P ，过点P 作x 轴的垂线，交直线AB 于点E ，线段OE 把△AOB 分成两个三角形，使其中一个三角形的面积与四边形BPOE 的面积之比为 2:3？若存在，求出点P 的坐标；若不存在，请说明理由．y11ACD E FG OAD E F G OOGF ED BCA2013年中考数学模拟试卷（二）（满分120分，考试时间100分钟）一、选择题（每小题3分，共24分）1. 某市1月份某天的最高气温是5℃，最低气温是-3℃，那么这天的温差（最高气温减最低气温）是【】A ．-2℃B ．8℃C ．-8℃D ．2℃2. 下列四个图形中，既是轴对称图形又是中心对称图形的有【】A ．4个B ．3个C ．2个D ．1个3. 某市对城区主干道进行绿化，计划把某一段公路的一侧全部栽上桂花树，要求路的两端各栽一棵，并且每两棵树的间隔相等．如果每隔5米栽1棵，则树苗缺21棵；如果每隔6米栽1棵，则树苗正好用完．设原有树苗x 棵，则根据题意列出方程正确的是【】 A ．5(211)6(1)x x +-=- B ．5(21)6(1)x x +=- C ．5(211)6x x +-=D ．5(21)6x x +=4. 一次函数|1|y mx m =+-的图象过点(0，2)，且y 随x 的增大而增大，则m =【】A ．-1B ．3C ．1D ．-1或35. 如图所示，把一张矩形纸片对折，折痕为AB ，再把以AB 的中点O 为顶点的平角∠AOB 三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O 为顶点的等腰三角形，那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是【】BOA BAAA ．正三角形B ．正方形C ．正五边形D ．正六边形6. 在平面直角坐标系中，对于平面内任意一点(x ，y )，若规定以下两种变换：①f (x ，y ) = (y ，x )，如f (2，3) = (3，2)；②g (x ，y ) = (-x ，-y )，如g (2，3) =(-2，-3)．按照以上变换有f (g (2，3)) =f (-2，-3) =(-3，-2)，那么 g (f (-6，7)) =【】A ．(7，6)B ．(7，-6)C ．(-7，6)D ．(-7，-6)7. 如图，等边△ABC 的周长为6π，半径为1的⊙O 从与AB 相切于点D 的位置出发，在△ABC 外部按顺时针方向沿三角形滚动，又回到与AB 相切于点D 的位置，则⊙O 自转了【】 A ．2周 B ．3周 C ．4周 D ．5周第7题图第8题图8. 如图，直角梯形AOCD 的边OC 在x 轴上，O 为坐标原点，CD 垂直于x 轴，点D 的坐标为(5，4)，AD =2．若动点E ，F 同时从点O 出发，点E 沿折线OA -AD -DC 运动，到达C 点时停止；点F 沿OC 运动，到达C 点时停止，它们运动的速度都是每秒1个单位长度．设点E 运动x 秒时，△EOF 的面积为y （平方单位），则y 关于x 的函数图象大致为【】二、填空题（每小题3分，共21分）9. x 的取值范围是_________．10. 如图，E ，F 分别是正方形ABCD 的边BC ，CD 上的点，BE =CF ，连接AE ，BF ．将△ABE 绕正方形的对角线交点O按顺时针方向旋转到△BCF ，则旋转角的度数为_________．F BN CO 第10题图第12题图11. 一个盒子里有完全相同的三个小球，球上分别标有数字-1，1，2．随机摸出一个小球（不放回），其数字记为p ，再随机摸出另一个小球，其数字记为q ，则满足关于x 的方程20x px q ++=有实数根的概率是_________．12. 如图，矩形OABC 内接于扇形MON ，当CN =CO 时，∠NMB 的度数是．13. 如图1，用8个同样大小的小立方体粘成一个大立方体，得到的几何体的三视图如图2所示，若小明从这8个小立方体中取走若干个，剩余小立方体保持原位置不动，并使得到的新几何体的三视图仍是图2，则他取走的小立方体最多可以是_____个．14. 如图，□ABCD 的顶点A ，C 在双曲线11y x =-上，B ，D 在双曲线22y x=上，122k k =（k 1＞0），AB ∥y 轴，S □ABCD =24，则k 1=_________．15. 已知：在△ABC 中，AC =a ，AB 与BC 所在直线成45°角，AC 与BC cosC=），则A C 边上的中线长是____________．三、解答题（本大题共8小题，满分75分）16. （8分）已知x 是一元二次方程x 2-2x +1=0的根，求代数式2352362x x x x x -⎛⎫÷+- ⎪--⎝⎭的值．17.（9分）九（1）班同学为了解某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理：请解答以下问题：（1）把上面频数分布直方图补充完整，并计算：a=_______，b=________；（2）求该小区用水量不超过15t的家庭占被调查家庭总数的百分比；（3）若该小区有1 000户家庭，根据调查数据估计，该小区月均用水量超过20t的家庭大约有多少户？18.（9分）如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与B C相交于点N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=4，AD=8，求MD的长．A B MODC19.（9分）如图，四边形ABCD是正方形，其中A(1，1)，B(3，1)，D(1，3)．反比例函数myx=（x>0）的图象经过对角线BD的中点M，与BC，CD的边分别交于点P，Q．（1）直接写出点M，C的坐标；（2）求直线BD的解析式；（3）线段PQ与BD是否平行？并说明理由．（10分）已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．根据以上信息，解答下列问题：（1）1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？（2）请你帮该物流公司设计租车方案；（3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．22.（10分）如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，点D在BC上，且CD=3cm．现有两个动点P，Q分别从点A和点B同时出发，其中点P以1厘米/秒的速度沿AC向终点C运动；点Q以1.25厘米/秒的速度沿BC向终点C运动．过点P作PE∥BC交AD于点E，连接EQ．设动点运动时间为t秒（t>0）．（1）连接PQ，在运动过程中，不论t取何值时，总有线段PQ与线段AB平行，为什么？（2）连接DP，当t为何值时，四边形EQDP能成为平行四边形？（3）当t为何值时，△EDQ为直角三角形？23.（11分）已知抛物线y=ax2+bx+c（a>0）的图象经过点B(12，0)和C(0，-6)，对称轴为直线x=2．（1）求该抛物线的解析式．（2）点D在线段AB上，且AD=AC，若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动，同时另一动点Q 以某一速度从C出发沿线段CB匀速运动，是否存在某一时刻，使线段PQ被直线CD垂直平分？若存在，请求出此时两点的运动时间t（秒）和点Q的运动速度；若不存在，请说明理由．（3）在（2）的结论下，直线x=1上是否存在点M，使△MPQ为等腰三角形？若存在，请求出所有点M的坐标；若不存在，请说明理由．。

2013年中考模拟数学试卷数学答案

（2）由全等及三线合一得AO⊥BC，（5分）
∴∠DBC=∠BAO，∵BD是直径，∴∠BCD=∠ABO=90°，
∴△BDC∽△AOB，（6分）∴ ，（7分）
22．（1）设A组的频数是x，那么B组的频数为5x，那么x+5x=12，x=2，（2分）
12÷(1-40%-28%-8%)=50（4分）
（2）（7分）（3）(28%+8%)×500=180（户）（9分）
（2）S1=4m-4(m-4)=16，（5分）
S2=S梯形AECD-S△CEEF= =16，∴S1=S2（8分）
（求S2时也可以将两个三角形的面积一一求出，再求差）
.（3）∵△AEG与△FDG面积和为24，差为16，∴△AEG的面积=20（10分）
∴ ，∴AG=10，∵△FDG∽△FCE，∴ ，
m1=12，m2=6（舍去），∴tan∠BAE= （12分）
∴ ，即
∴ 或．（14分）
19．解：原式= （4分）= （6分）
20． → （2分）→
→ （5分）→经检验，原方程的解是（7分）
21．解：（1）证明：连结OC，
∵OB=OC,AB=AC,OA=OA，∴△ABO≌△ACO，（2分）
∴∠ABO=∠ACO，∵AC是切线，∴∠ACO=90°，
∴∠ABO=90°，∴AB是⊙O的切线．（4分）
26．（1）第一条抛物线的解析式是（3分）
（2）第n个三角形的面积是，当n=1，2，5时为整数（6分）
（3）设第n条抛物线的解析式为，（7分）
又∵过点 ∴ ，设，∴
= ，∴
，n=2．（10分）
（4）作第m个三角形和第n个三角形底边上的高AmC和AnD，
∵顶角互补，∴底角互余．即△AmCBm-1∽△AnDBn-1．

2013 年中考数学模拟试卷参考答案

1 1 1 1 6( x 2) 2 x x(6 x) x 2 x 6 2 2 2 2 当 4 x 6 时，△EPQ 的面积等于梯形 ABPQ 的面积减去△AEQ 和△BEP 的面积 1 1 1 y 4( x 10 x) 2(10 x) 2 x 10 2 2 2 y
1 2
3 2
15． 4 3 3或4 3 3 三、解答题（本大题共 11 小题，共 88 分） 17(本题 6 分) 解：△= 62 4 7 8
16． 2 2 2或2 - 2 2
x1
6 8 6 8 3 2, x2 3 2 2 2
18（本题 9 分）
2013 年中考数学模拟试卷参考答案
一、选择题（每小题 2 分，共 12 分）题号答案 1 B 2 D 3 D 4 B 5 D 6 B
二、填空题（每小题 2 分，共 20 分） 7． 4 11．9.0 8．圆柱体（此题答案不唯一） 12．( 1,3 ) 9． 1或 1 13． 10. 6 14． m 1且m
4x 1 x 解不等式 3 4 x 6 x 6
得 3 x 1 满足条件的整数 a 的值为-2、-1、0、1 但由
a2 1 a 2 2a 1 1 知 a 1 a2 a a
a -1、0、1
所以满足条件的整数 a 的值只有-2
a2 1 a 2 2a 1 1 a 1 a2 a a (a 1) 2 1 (a 1)(a 1) a 1 a (a 1) a (a 1) 1 a 1 a (a 1) a 1 1 a 1 a a a 1 = 当a 2时，原式= 1
y1 950 250 x, y2 300( x 0.5)

2013年中考数学模拟试题和答案

数学试卷（一）*考试时间120分钟试卷满分150分一、选择题（下列各题的备选答案中，只有一个答案是正确的，将正确答案的序号填在题后的括号内，每小题3分，共24分） 1．|65-|＝（） A ．65+B ．65-C ．－65-D ．56-2．如果一个四边形ABCD 是中心对称图形，那么这个四边形一定是（） A ．等腰梯形 B ．矩形 C ．菱形 D ．平行四边形 3．下面四个数中，最大的是（）A ．35-B ．sin88°C ．tan46°D ．215- 4．如图，一个小圆沿着一个五边形的边滚动，如果五边形的各边长都和小圆的周长相等，那么当小圆滚动到原来位置时，小圆自身滚动的圈数是（） A ．4 B ．5 C ．6 D ．10 5．二次函数ｙ＝（2ｘ－1）2＋2的顶点的坐标是（） A ．（1，2） B ．（1，－2） C ．（21，2） D ．（－21，－2）6．足球比赛中，胜一场可以积3分，平一场可以积1分，负一场得0分，某足球队最后的积分是17分，他获胜的场次最多是（） A ．3场 B ．4场 C ．5场 D ．6场 7．如图，四边形ABCD 的对角线AC 和BD 相交于点E ，如果△CDE 的面积为3，△BCE 的面积为4，△AED 的面积为6，那么△ABE 的面积为（） A ．7 B ．8 C ．9 D ．108．如图，△ABC 内接于⊙O，AD 为⊙O 的直径，交BC 于点E ，若DE ＝2，OE ＝3，则tanC·tanB ＝（）A ．2B ．3C ．4D ．5 二、填空题（每小题3分，共24分）9．写出一条经过第一、二、四象限，且过点(1-，3)的直线解析式 . 10．一元二次方程ｘ2＝5ｘ的解为．11．凯恩数据是按照某一规律排列的一组数据，它的前五个数是：269,177,21,53,31，按照这样的规律，这个数列的第8项应该是． 12．一个四边形中，它的最大的内角不能小于． 13．二次函数x x y 2212+-=，当x 时，0<y ;且y 随x 的增大而减小.14．如图，△ABC 中，BD 和CE 是两条高，如果∠A ＝45°，则BC DE＝． 15．如图，已知A 、B 、C 、D 、E 均在⊙O 上，且AC 为⊙O 的直径，则∠A ＋∠B ＋∠C ＝__________度． 16．如图，矩形ABCD 的长AB ＝6cm ，宽AD ＝3cm. O 是AB 的中点，OP ⊥AB ，两半圆的直径分别为AO 与OB ．抛物线ｙ＝ａｘ2经过C 、D 两点，则图中阴影部分的面积是 cm 2.三、（第17小题6分，第18、19小题各8分，第20小题10分，共32分） 17．计算：01)32009(221245cos 4)21(8--⨯÷-︒-+-18．计算：22111211x x x x ⎛⎫-+÷ ⎪-+-⎝⎭19．已知：如图，梯形ABCD 中，A B ∥CD ，E 是BC 的中点，直线AE 交DC 的延长线于点F ．（1）求证：△ABE ≌△FCE ；（2）若BC ⊥AB ，且BC ＝16，AB ＝17，求AF 的长．CA20．观察下面方程的解法ｘ4－13ｘ2＋36＝0解：原方程可化为（ｘ2－4）（ｘ2－9）＝0∴（ｘ＋2）（ｘ－2）（ｘ＋3）（ｘ－3）＝0∴ｘ＋2＝0或ｘ－2＝0或ｘ＋3＝0或ｘ－3＝0∴ｘ1＝2，ｘ2＝－2，ｘ3＝3，ｘ4＝－3你能否求出方程ｘ2－3｜ｘ｜＋2＝0的解？四、（每小题10分，共20分）21．（１）顺次连接菱形的四条边的中点，得到的四边形是．（２）顺次连接矩形的四条边的中点，得到的四边形是．（３）顺次连接正方形的四条边的中点，得到的四边形是．（４）小青说：顺次连接一个四边形的各边的中点，得到的一个四边形如果是正方形，那么原来的四边形一定是正方形，这句话对吗？请说明理由．22．下面的表格是李刚同学一学期数学成绩的记录，根据表格提供的信息回答下面的问题（１）李刚同学6次成绩的极差是．（２）李刚同学6次成绩的中位数是．（３）李刚同学平时成绩的平均数是．（４）如果用右图的权重给李刚打分，他应该得多少分？（满分100分，写出解题过程）23．（本题12分）某射击运动员在一次比赛中，前6次射击已经得到52环，该项目的记录是89环（10次射击，每次射击环数只取1~10中的正整数）.（1）如果他要打破记录，第7次射击不能少于多少环？（2）如果他第7次射击成绩为8环，那么最后3次射击中要有几次命中10环才能打破记录？（3）如果他第7次射击成绩为10环，那么最后3次射击中是否必须至少有一次命中10环才有可能打破记录？24．（本题12分）甲、乙两条轮船同时从港口A出发，甲轮船以每小时30海里的速度沿着北偏东60°的方向航行，乙轮船以每小时15海里的速度沿着正东方向行进，1小时后，甲船接到命令要与乙船会和，于是甲船改变了行进的速度，沿着东南方向航行，结果在小岛C 处与乙船相遇．假设乙船的速度和航向保持不变，求：（１）港口A与小岛C之间的距离（２）甲轮船后来的速度．25．（本题12分）如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒． (1) 求直线AB 的解析式；(2) 当t 为何值时，△APQ 与△AOB 相似？(3) 当t 为何值时，△APQ 的面积为524个平方单位？26．（本题14分）如图，直线y= -x+3与x轴，y轴分别相交于点B、C，经过B、C两点的抛物线与x轴的另一交点为A，顶点为P，且对称轴为直线x=2．（1）求A点的坐标；（2）求该抛物线的函数表达式；（3）连结AC．请问在x轴上是否存在点Q，使得以点P、B、Q为顶点的三角形与△ABC 相似，若存在，请求出点Q的坐标；若不存在，请说明理由．2009年中考模拟题数学试题参考答案及评分标准一、选择题（每小题3分，共24分）1．Ｄ； 2．D ； 3．C ；4．Ｃ；5．Ｃ； 6．C ；7．Ｂ；8．C ．二、填空题（每小题3分，共24分）9．ｙ＝－ｘ＋2等； 10．ｘ1＝0，ｘ2＝5； 11．133； 12．90°； 13．227； 14．2115．90；16．π49三、（第17小题6分，第18、19小题各8分，第20小题10分，共32分） 17．解：原式＝222224222⨯⨯-⨯-+ －1 ．．．．．．．．．．．．．．．4分＝822222--+ －1＝－7 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分18．计算：22111211x x x x ⎛⎫-+÷ ⎪-+-⎝⎭解：原式＝)1(])1()1)(1(1[2-⨯--++x x x x ）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分 xx x x x x 211)1(]111[=++-=-⨯-++．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分19．（１）证明： ∵E 为BC 的中点 ∴BE ＝CE ∵AB ∥CD∴∠BAE ＝∠F ∠B ＝∠FCE∴△ABE ≌△FCE ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分解：由（１）可得：△ABE≌△FCE∴CE＝AB＝15，CE＝BE＝8，AE＝EF∵∠B＝∠BCF＝90°根据勾股定理得AE＝17∴AF＝34．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分20．解：原方程可化为｜ｘ｜2－3｜ｘ｜＋2＝0．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分∴（｜ｘ｜－1）（｜ｘ｜－2）＝0∴｜ｘ｜＝1或｜ｘ｜＝2∴ｘ＝1，ｘ＝－1，ｘ＝2，ｘ＝－2 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分四．（每小题10分，共20分）21．解：（１）矩形；（２）菱形，（３）正方形．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分（４）小青说的不正确如图，四边形ABCD中AC⊥BD，AC＝BD，BO≠DO，E、F、G、H分别为AD、AB、BC、CD的中点显然四边形ABCD不是正方形但我们可以证明四边形ABCD是正方形（证明略）所以，小青的说法是错误的．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分22．解：（１）10分．．．．．．．．．．．．．．．．．．．．．．．．．．．．．2分（２）90分．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分（３）89分．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分（４）89×10％＋90×30％＋96×60％＝93.5李刚的总评分应该是93.5分．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分23．小强和小亮的说法是错误的，小明的说法是正确的．．．．．．．．．．．．．．．．．．．．2分不妨设小明首先抽签，由树状图可知，共出现6种等可能的结果，其中小明、小亮、小强抽到A 签的情况都有两种，概率为31，同样，无论谁先抽签，他们三人抽到A 签的概率都是31．所以，小明的说法是正确的．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分24．解：（１）作BD ⊥AC 于点D由题意可知：AB ＝30×1＝30，∠BAC ＝30°，∠BCA ＝45° 在Rt △ABD 中∵AB ＝30，∠BAC ＝30°∴BD ＝15，AD ＝ABcos30°＝153 在Rt △BCD 中， ∵BD ＝15，∠BCD ＝45° ∴CD ＝15，BC ＝152 ∴AC ＝AD ＋CD ＝153＋15即A 、C 间的距离为（153＋15）海里．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分（２）∵AC ＝153＋15轮船乙从A 到C 的时间为1515315 ＝3＋1由B 到C 的时间为3＋1－1＝3 ∵BC ＝152∴轮船甲从B 到C 的速度为3215＝56（海里／小时）答：轮船甲从B到C的速度为56海里／小时．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分七、25．解：（１）老师说，三个同学中，只有一个同学的三句话都是错的，所以丙的第一句话和老师的话相矛盾，因此丙的第一句话是错的，同时也说明甲、乙两人中有一个人是全对的；．．．．．．．．．．．．．．．．．．．．．．．．．．．．2分（２）如果丙的第二句话是正确的，那么根据抛物线的对称性可知，此抛物线的对称轴是直线ｘ＝2，这样甲的第一句和乙的第一句就都错了，这样又和（１）中的判断相矛盾，所以乙的第二句话也是错的；根据老师的意见，丙的第三句也就是错的．也就是说，这条抛物线一定过点（－1，0）；．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分（３）由甲乙的第一句话可以断定，抛物线的对称轴是直线ｘ＝1，抛物线经过（－1，0），那么抛物线与ｘ轴的两个交点间的距离为4，所以乙的第三句话是错的；由上面的判断可知，此抛物线的顶点为（1，－8），且经过点（－1，0）设抛物线的解析式为：ｙ＝ａ（ｘ－1）2－8∵抛物线过点（－1，0）∴0＝ａ（－1－1）2－8解得：ａ＝2∴抛物线的解析式为ｙ＝2（ｘ－1）2－8即：ｙ＝2ｘ2－4ｘ－6．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分八、（本题14分）26．【探究】证明：过点F作GH∥AD，交AB于H，交DC的延长线于点G∵AH∥EF∥DG，AD∥GH∴四边形AHFE和四边形DEFG都是平行四边形∴FH＝AE，FG＝DE∵AE＝DE∴FG＝FH∵AB∥DG∴∠G＝∠FHB，∠GCF＝∠B∴△CFG≌△BFH2013年中考数学模拟试题和答案- 11 - / 11 ∴FC ＝FB ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分【知识应用】过点C 作CM ⊥ｘ轴于点M ，过点A 作AN ⊥ｘ轴于点N ，过点B 作BP ⊥ｘ轴于点P则点P 的坐标为（ｘ2，0），点N 的坐标为（ｘ1，0）由探究的结论可知，MN ＝MP∴点M 的坐标为（221x x +，0） ∴点C 的横坐标为221x x + 同理可求点C 的纵坐标为221y y + ∴点C 的坐标为（221x x +，221y y +）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分【知识拓展】当AB 是平行四边形一条边，且点C 在ｘ轴的正半轴时，AD 与BC 互相平分，设点C 的坐标为（ａ，0），点D 的坐标为（0，ｙ）由上面的结论可知：－6＋ａ＝4＋0，－1＋0＝5＋ｂ∴ａ＝10，ｂ＝－6∴此时点C 的坐标为（10，0），点D 的坐标为（0，－6）同理，当AB 是平行四边形一条边，且点C 在ｘ轴的负半轴时求得点C 的坐标为（－10，0），点D 的坐标为（0，6）当AB 是对角线时点C 的坐标为（－2，0），点D 的坐标为（0，4）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．14分。

2013年中考数学模拟试题及参考答案

2013年中考数学模拟考试数学试题一、选择题（本大题共有8小题，每小题2分，共16分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡．．．相应位置．．．．上） 1．-2的相反数是A.－2B.2C.－21 D.212．已知两圆的半径分别为6和4，圆心距为7，则两圆的位置关系是 A ．相交B ．内切C ．外切D ．内含3．下列计算中，正确的是（）A ．42232a a a =+ B ．()52322x x x -=-⋅ C ．()53282a a -=- D ．22326x x xm m=÷4．下列美丽的图案，既是轴对称图形又是中心对称图形的个数是A ．1个B ． 2个C ． 3个D ． 4个 5．下列说法正确的是A ．若甲组数据的方差20.01S =甲，乙组数据的方差20.1S =乙，则乙组数据比甲组数据稳定B ．为了解全国中学生的心理健康情况，应该采用普查的方式C ．一组数据6，8，7，8，8，9，10的众数和中位数都是8D ．一个游戏的中奖概率是110，则做10次这样的游戏一定会中奖 6．下面四个几何体中，左视图是四边形的几何体共有A. 1个B. 2个C. 3个D. 4个7．如图所示，在方格纸上建立的平面直角坐标系中，将△ABO 绕点O 按顺时针方向旋转90°，得A B O ''△ ，则点A '的坐标为A ．（3，1）B ．（3，2）C ．（2，3）D ．（1，3）y C 2C 1C y 24 3B8．在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于点A 2，作正方形A 2B 2C 2C 1…按这样的规律进行下去，第2011个正方形的面积为（） A ．201035()2⨯B ．201195()4⨯ C ． 200995()4⨯ D ．402035()2⨯二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 9．去年冬季的某一天，学校一室内温度是8℃，室外温度是2-℃，则室内外温度相差 ▲ ℃.10．国家游泳中心“水立方”是北京2008年奥运会场馆之一，它的外层膜的展开面积约为260 000平方米，将260 000用科学记数法表示应为 ▲ 平方米． 11．五边形的内角和为 ▲ 度．12．已知反比例函数的图象经过点A （6，-1），请你写出该函数的表达式 ▲ ． 13．已知二元一次方程组⎩⎨⎧=-=-52832y x y x ，则y x -的值为 ▲ ．14．不等式组30210x x -<⎧⎨-⎩≥的解集是 ▲ ．15．在如图的甲、乙两个转盘中，指针指向每一个数字的机会是均等的．当同时转动两个转盘，停止后指针所指的两个数字表示两条线段的长，如果第三条线段的长为5，那么这三条线段能构成三角形的概率为_____▲____．16．如图，点A 、B 、C 在⊙O 上，若∠BAC = 24°，则∠BOC = °．17．已知圆锥的底面半径是3cm ，母线长为6cm ，则这个圆锥的侧面积为_ ▲ ．cm 2．（结果保留π）B 题）yxO BCA （第18题）OAC（第16题）·（第15题）18．如图，A 、B 是双曲线 y = k x(k >0) 上的点， A 、B 两点的横坐标分别是a 、2a ，线段AB 的延长线交x 轴于点C ，若S △AOC =6．则k= ▲ ．三、解答题（本大题共有10小题，共74分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤） 19．（本题6分）计算：（1）200821(1)()162---+；（2）2311()11x x x x--⋅-+． 20．（本题6分）为了增强环境保护意识，6月5日“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，抽样调查了全市40个噪声测量点在某时刻的噪声声级（单位：dB ），将调查的数据进行处理（设所测数据是正整数），得频数分布表如下：组别噪声声级分组频数频率 1 44.5——59.5 4 0.1 2 59.5——74.5 a 0.2 3 74.5——89.5 10 0.25 4 89.5——104.5 bc 5 104.5——119.56 0.15 合计401.00根据表中提供的信息解答下列问题：（1）频数分布表中的a =________，b =________，c =_________；（2）补充完整频数分布直方图；（3）如果全市共有200个测量点，那么在这一时刻噪声声级小于75dB 的测量点约有多少个？21．（本题6分）小晶和小红玩掷骰子游戏，每人将一个各面分别标有1，2，3，4，5，6的正方体骰子掷一次，把两人掷得的点数相加，并约定：点数之和等于6，小晶赢；点数之和等于7．小红赢；点数之和是其它数，两人不分胜负．问他们两人谁获胜的概率大？请你用“画树状图”或“列表”的方法加以分析说明．22．（本题6分）某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2:1．在温室内，沿前侧内墙保留3m 宽的空地，其它三侧内墙各保留1m 宽的通道．当矩形温室的长与宽各为多少时，蔬菜种植区域的面积是2288m ？23．（本题8分）如图，点E 、F 是四边形ABCD 的对角线AC 上的两点，AF =CE ，DF =BE ，DF ∥BE ．（第24题）（第22题）蔬菜种植区域前侧空地F EDCBA（第23题）（1）求证：△AFD ≌△CEB（2）四边形ABCD 是平行四边形吗？请说明理由．24．（本题8分）如图15，河旁有一座小山，从山顶A 处测得河对岸点C 的俯角为30°，测得岸边点D 的俯角为45°，又知河宽CD 为50米.现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ，求缆绳AC 的长（结果精确到0.1m ）（参考数据：2 1.41≈，3 1.73≈） 25．（本题8分）如图，A （－1，0）、B （2，－3）两点在二次函数y 1＝ax 2+bx －3与一次函数y 2＝－x +m 图像上。

2013年中考数学模拟试题(第一组)

2013年中考数学模拟试题（第一组）数学本试卷分第Ⅰ卷和第Ⅱ卷，满分120分，考试时间120分钟．注意：答案一律填写在答题卡上，在试卷上作答无效．．．．．．．．．考试结束，将本试卷和答题卡一并交回．第Ⅰ卷（选择题，共36分）一、选择题（本大题共12小题，每小题3分，共36分）每小题都给出代号为（A ）、（B ）、（C ）、（D ）四个结论，其中只有一个是正确的．请考生用2B 铅笔在答题卡上将选定的答案标号涂黑． 1．－5的绝对值是：（A ）－5（B ）51 （C ）－51 （D ）52．某同学把如图1所示的几何体的三种视图画出如下（不考虑尺寸）：这三种视图正确的是：（A ）主视图和左视图（B ）主视图和俯视图（C ）左视图和俯视图（D ）全部正确 3．在学习党的十八大精神的知识竞赛中，全国有10.5万人参加，10.5万人用科学记数法表示为：（A ）10.5×310 （B ）1.05×410 （C ）1.05×510（D ）1.05×6104．下列计算中，正确的是：（A ）25 =±5 （B ）=（C ）325a a a ⋅= （D ）22x x x -= 5.在函数y =x 的取值范围是：（A ）x ≥ 3（B ）x ≤ 3 （C ）x ≥ - 3（D ）x ≤ - 36.把多项式22123x y －分解因式所得结果是：（A ）3（4 x 2－y 2）（B ）3（2x+y ）（2x －y ）（C ）3（4x+y ）（4x －y ）（D ）(12x+3y)（12x －3y) 7．函数x1y -=的图象上有两点A )y ,x (11，B )y ,x (22，若21x x 0<<，则：（A ） 21y y < （B ） 21y y > （C ） 21y y = （D ） 1y 、2y 的大小不确定8.如图2，⊙O 是等边三角形ABC 的外接圆，⊙O 的半径为2，则等边三角形ABC 的边长为：（A ）3 （B ）5 （C ）23 （D ）25A主视图左视图俯视图图19.某校九年级（1）班50名学生中有20名团员，他们都积极报名参加学校开展的“文明劝导活动”。

2013年中考数学模拟题

2013年中考数学模拟题（仿真卷）一、选择题（每小题3分，共15分）1.∣-3∣的相反数是（）A. -3B. 3C. -31D.312.一次课堂练习，小华做了如下4道因式分解题，你认为小华做得不够完整的一题是（）A. x 3-x =x(x 2-1)B. x 2-2xy+y 2=(x-y)2C. x 2y-xy 2=xy(x-y)D. x 2-y 2=(x+y)(x-y)3.如图所示的两个圆盘中，指针落在同一个圆盘的每一个区域的机会均等，则两个指针同时落在偶数区域的概率是（）A. 121B. 61C. 21D.654.如图，MB=ND ，∠MBA=∠NDC ，下列条件中，不能判定ΔABM ≌ΔCDN 的是（）A. ∠M=∠NB.AB=CDC. AM=CND. AM ∥CN5.如图，⊙O 的半径是5，弦AB 的长是8，M 为弦AB 上的动点，则线段OM 长的最小值是（）A. 2B. 3C. 4D. 5二、填空题（每小题4分，共20分）6.函数y=x 24 的自变量x 的取值范围是 ___________.7.0.00624用科学记数法表示为___________.8. 已知不等式组无解，则9.如图，两直线a、b 被第三条直线c所截，若a ∥b∠1=70°，则∠2 =_____度。

10.如图，圆锥的主视图是边长为6的正三角形ABC ，则这个圆锥侧面展开图的圆心角是_____度。

三、解答题（每小题6分，共30分）11. 先化简，再求值：a a 2-1 ÷(1+ 1a-1)，其中 a = 3-1 .12.已知ΔABC （如图）。

求作：（1）线段AB 的中点O ；（2）以O 为旋转中心，将ΔABC 旋转180°后的ΔA ′B ′C ′。

（要求用直尺圆规作图，用不用写画法，但要保留作图痕迹)。

13. 已知一次函数y=kx+k P （4，n ）。

（1）求n 的值；（214. 如图，在ΔABC 中，∠ACB=90°，CD ⊥AB 于D 。

2013年中考数学模拟卷含答案一

各位同学，考试开始请认真作答一．选择题(每小题3分，共30分)1．方程x －1＝1的解是（）．A 、x ＝－1B 、x ＝0C 、x ＝1D 、x ＝2 2．21的倒数（）．A 、2B 、－2C 、21D 、21-3．如图，直线a 、b 被直线c 所截，如果a ∥b ，那么（）． A 、∠1＞∠2 B 、∠1＝∠2 C 、∠1＜∠2 D 、∠1＋∠2＝180°4．近几年某地区义务教育普及率不断提高，据2006年末统计的数据显示，仅初中在校生就约有13万人．数据13万人用科学记数法表示为（）．A 、13×104人B 、1.3×106人C 、1.3×105人D 、0.13×106人 5．在正方形网格中，∠α的位置如图所示，则sin α的值为（）．A 、21B 、22C 、23D 、336．若顺次连接四边各边中点所得四边形是矩形，则原四边形一定是（）．A 、等腰梯形B 、对角线相等的四边形C 、平行四边形D 、对角线互相垂直的四边形 7．如图，CD 是⊙O 的直径，A 、B 是⊙O 上的两点，若∠ABD ＝20°，则∠ADC 的度数为（）．A 、40°B 、50°C 、60°D 、70° 8．当x ＜0时，反比例函数x31y -=（）．A 、图象在第二象限内，y 随x 的增大而减小B 、图象在第二象限内，y 随x 的增大而增大C 、图象在第三象限内，y 随x 的增大而减小 C 、图象在第三象限内，y 随x 的增大而增大 9．下面有关概率的叙述，正确的是（）．A 、投掷一枚图钉，钉尖朝上的概率和钉尖着地的概率不相同B 、因为购买彩票时有“中奖”与“不中奖”两种情形，所以购买彩票中奖的概率为21C 、投掷一枚均匀的正方体骰子，每一种点数出现的概率都是61，所以每投掷6次，肯定出现一次6点D 、某种彩票的中奖概率是1％，买100张这样的彩票一定中奖10．如图①是一个几何体的主视图和左视图．某班同学在探究它的俯视图时，画出了如图②的几个图形，其中，可能是该几何体俯视图的共有（）． A 、3个 B 、4个 C 、5个 D 、6个二．填空题(每小题2分，共20分) 11．计算：(－3)2的结果等于_______． 12．比较大小：－3___－2．(用“＞”、“＝”或“＜”填空)α (第05题图) (第07题图)(第10题图) a b c d 图① 图②左视图主视图第03题图) ab c1213．函数3x 1y -=的自变量x 的取值范围是___________． 14．分解因式：a 3＋a 2＝_____________．15．小亮的身高是1.6米，某一时刻他在水平地面上的影长是2米，若同一时刻测得附近一古塔在水平地面上的影长为18米，则古塔的高度是________米．16．如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB 的顶点都在格点上，请在网格中画出．．．．．△OAB 的一个位似图形，使两个图形以O 为位似中心，且所画图形与△OAB 的位似比为________．17．小明要用圆心角为120°，半径是27cm 的扇形纸片(如图)围成一个圆锥形纸帽，做成后这个纸帽的底面直径为____________cm ．(不计接缝部分，材料不剩余) 18．二次函数y ＝x 2＋bx ＋c 的图象经过点A(－1，0)、B(3，0)两点．其顶点坐标是_____________． 19．如图，正方形ABCD 的边长为216cm ，对角线AC 、BD 相交于点O ，过O作OD 1⊥AB 于D 1，过D 1作D 1D 2⊥BD 于点D 2，过D 2作D 2D 3⊥AB 于D 3，…，依次类推．其中的OD 1＋D 2D 3＋D 4D 5＋D 6D 7＝__________cm ．20．用长度分别为2、3、4、5、6(单位：cm)的5根细木棒摆成一个三角形(允许连接，但不允许折断)，在所有摆成的三角形中，面积最大的三角形的面积为____________cm 2．三．解答题(本大题含9个小题，共80分)21．(本小题满分7分)解不等式组：⎪⎩⎪⎨⎧-≤--x 2382x x6x 2＞，并把它的解集表示在数轴上．22．(本小题满分8分)先化简，再求值：4a 4a a 2)2a 12a 1(2+-÷++-，其中a ＝－4．23．(本小题满分8分)市政府为了解决老百姓看病贵的问题，决定下调一些药品的价格．某种药品原售价为125元/盒，连续两次降价后售价为80元/盒．假设每次降价的百分率相同，求这种药品每次降价的百分率．24．(本小题满分8分)如图①，在等腰梯形ABCD 中，AB ∥CD ，E 、F 是边AB 上的两点，且AE ＝BF ，DE 与CF 相交于梯形ABCD 内一点O ． (1)求证：OE ＝OF ；(2)如图②，当EF ＝CD 时，请你连接DF 、CE ，判断四边形DCEF 是什么样的四边形，并证明你的结论．AB O (第17题图)A (第19题图)BDCOD 1 D 3 D 2 D 4 …(第24题图)C DOC DO25．(本小题满分8分)某地区教育部门要了解初中学生阅读课外书籍的情况，随机调查了本地区500名初中学生一学期阅读课外书的本数，并绘制了如图的统计图．请根据统计图反映的信息回答问题． (1)这些课外书籍中，哪类书的阅读数量最大？(2)这500名学生一学期平均每人阅读课外书多少本？(精确到1本)(3)若该地区共有2万名初中学生，请估计他们一学期阅读课外书的总本数．26．(本小题满分9分)今年的全国助残日这天，某单位的青年志愿者到距单位6千米的福利院参加“爱心捐助活动”．一部分人步行，另一部分人骑自行车，他们沿相同的路线前往．如图，l 1、l 2分别表示步行和骑自行车的人前往目的地所走的路程y(千米)随时间x (分钟)变化的函数图象． (1)分别求l 1、l 2的函数表达式； (2)求骑车的人用多长时间追上步行的人．27．(本小题满分10分)如图，有两个可以自由转动的均匀转盘，转盘A 被分成面积相等的三个扇形，转盘B 被分成面积相等的四个扇形，每个扇形内都涂有颜色．同时转动两个转盘，停止转动后，若一个转盘的指针指向红色，另一个转盘的指针指向蓝色，则配成紫色；若其中一个指针指向分界线时，需重新转动两个转盘．(1)用列表或画树状图的方法，求同时转动一次转盘A 、B 配成紫色的概率； (2)小强和小丽要用这两个转盘做游戏，他们想出如下两种游戏规则： ①转动两个转盘，停止后配成紫色，小强获胜；否则小丽获胜；②转动两个转盘，停止后指针都指向红色，小强获胜；指针都指向蓝色，小丽获胜．判断以上两种规则的公平性，并说明理由．(第25题图) 术类技类记类说类它类漫类(第26题图) )(第27题图)转盘A 转盘B28．(本小题满分10分)数学课上，同学们探究下面命题的正确性：顶角为36°的等腰三角形具有一种特性，即经过它某一顶点的一条直线可把它分成两个小等腰三角形．为此，请你解答问题(1)．(1)已知：如图①，在△ABC 中，AB ＝AC ，∠A ＝36°，直线BD 平分∠ABC 交AC 于点D ．求证：△ABD 与△DBC 都是等腰三角形；(2)在证明了该命题后，小颖发现：下面两个等腰三角形如图②、③也具有这种特性．请你在图②、图③中分别画出一条直线，把它们分成两个小等腰三角形，并在图中标出所画等腰三角形两个底角的度数；(3)接着，小颖又发现：直角三角形和一些非等腰三角形也具有这样的特性，如：直角三角形斜边上的中线可把它分成两个小等腰三角形．请你画出两个具有这种特性的三角形的示意图，并在图中标出三角形各内角的度数．说明：要求画出的两个三角形不相似，而且既不是等腰三角形也不是直角三角形．29．(本小题满分12分)如图，在平面直角坐标系中，□ABCO 的顶点O 在原点，点A 的坐标为(－2，0)，点B 的坐标为(0，2)，点C 在第一象限． (1)直接写出点C 的坐标；(2)将□ABCO 绕点O 逆时针旋转，使OC 落在y 轴的正半轴上，如图②，得□DEFG(点D 与点O 重合)．FG 与边AB 、x 轴分别交于点Q 、点P ．设此时旋转前后两个平行四边形重叠部分的面积为S 0，求S 0的值；(3)若将(2)中得到的□DEFG 沿x 轴正方向平移，在移动的过程中，设动点D 的坐标为(t ，0)，□DEFG 与□ABCO 重叠部分的面积为S ．写出S 与t(0＜t ≤2)的函数关系式．(直接写出结果)(第29题图)A (第28题图)BC D图① 图② 图③36°123数学试题参考答案一．选择题(每小题3分，共30分)二．填空题(每小题2分，共20分)11．9 12．＜ 13．x ≠3 14．a 2(a ＋1) 15．144 16．2∶1 17．1818．(1，－4) 19．215 20．106三．解答题(本大题含9个小题，共80分)21．解：解不等式2x －6＞－x ，得x ＞2解不等式x 2382x -≤，得x ≤4 所以，原不等式组的解集伟2＜x ≤4在数轴上表示为22．解：原式＝2)2a (a2)2a )(2a (2a 2a -÷-+-++ ＝)2a )(2a (a2-+·a 2)2a (2-＝2a 2a +- 当a ＝－4时，原式＝323．解：设这种药品每次降价的百分率为x ，根据题意得125(1－x)2＝80解这个方程，得x 1＝0.2，x 2＝1.8 ∵x ＝1.8不合题意，舍去 ∴x ＝0.2＝20％答：这种药品每次降价的百分率为20％． 24．证明：(1)∵梯形ABCD 为等腰梯形，AB ∥CD∴AD ＝BC ，∠A ＝∠B ∵AE ＝BF∴△ADE ≌△BCF ∴∠DEA ＝∠CFB ∴OE ＝OF(2)∵DC ∥EF 且DC ＝EF∴四边形DCEF 是平行四边形又由(1)得△ADE ≌△BCF ∴CF ＝DE∴四边形DCEF 是矩形25．解：(1)这些类型得课外书籍中，小说类课外书阅读数量最大(2)(2.0＋3.5＋6.4＋8.4＋2.4＋5.5)×100÷500＝5.64≈6(本) 答：这500名学生一学期平均每人阅读课外书6本． (3)20000×6＝120000(本)或2×6＝12(万本)答：他们一学期阅读课外书得总数是12万本．26．解：(1)设l 1的表达式为y 1＝k 1x由图象知l 1过点(60，6)∴60k 1＝6，k 1＝101 ∴y 1＝101x 设l 2的表达式为y 2＝k 2x ＋b 2由图象知l 2过点(30，0)和(50，6)两点∴⎩⎨⎧=+=+6b k 500b k 302222解得⎪⎩⎪⎨⎧-==9b 103k 22 ∴y 2＝103x －9 (2)当骑车的人追上步行的人时， y 1＝y 2，即101x ＝103x －9 ∴x ＝4545－30＝15(分钟)答：骑车的人用15分钟追上步行的人．27．解：∴P (配成紫色)＝124＝31(2)由(1)可知，P (配不成紫色)＝128＝32≠P (配成紫色) ∴规则①不公平∵P (都指向红色)＝122＝61 P (都指向蓝色)＝122＝61∴规则②是公平的28．证明：(1)在△ABC 中，AB ＝AC∴∠ABC ＝∠C ∵∠A ＝36°∴∠ABC ＝∠C ＝21(180°－∠A)＝72° ∵BD 平分∠ABC ∴∠1＝∠2＝36°∴∠3＝∠1＋∠A ＝72° ∴∠1＝∠A ，∠3＝∠C ∴AD ＝BD ，BD ＝BC∴△ABD 与△BDC 都是等腰三角形 (2)如下图所示：(3)如下图所示：29．解：(1)C(2，2)；(2)∵A(－2，0)，B(0，2) ∴OA ＝OB ＝2∴∠BAO ＝∠ABO ＝45°∵□EFGD 由□ABCO 旋转而成∴DG ＝OA ＝2，∠G ＝∠BAO ＝45° ∵□EFGD ∴FG ∥DE∴∠FP A ＝∠EDA ＝90°或40°80°60°35°70°75°α 2α20°60°100° 80°25°75°35°105°45°α 3α…或…0°＜α＜45°，其中，α≠30°， α≠36°．0°＜α＜45°， α≠36°，a ≠7180．其中，α≠30°，∵∠AQP ＝90°－∠BAO ＝45° ∴PQ ＝AP ＝OA －OP ＝2－2 S 0＝21(PQ ＋OB)·OP ＝21(2－2＋2)·2＝22－1当□DEFG 运动到点F 在AB 上是，如图①，t ＝22－2 <1>当0＜t ≤22－2时，如图②，S ＝－t 2＋2t ＋22－1 <2>当22－2＜t ≤2时，如图③，S ＝－21t 2＋42－3<3>当2＜t ≤2时，如图④，S ＝－2t ＋42－2图①图② 图③图④。

2013年历年初三数学中考模拟试卷及答案

2013年中考数学模拟试卷一、选择题（本大题共有8小题，每小题3分，共计24分．在每小题所给出的四个选项中，只有一项是正确的，请将正确选项前的字母代号涂在答题卡相应位．．．．．．置．上） 1．51-的绝对值是（ ▲ ） A ．－5 B ．15 C ．15- D ． 52．下列图形是生活中常见的道路标识，其中不是．．轴对称图形的是( ▲ )A ．B ．C ．D ．3．下列运算正确的是( ▲ )A ．22a a a =+B ．4226)3(a a =C ．49)23)(23(2-=-+-a a aD ．ab ba ab 2=+4．两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的主视图是( ▲ )A ．两个外离的圆B ．两个相交的圆C ．两个外切的圆D ．两个内切的圆5. 将不等式组x 1x 3≥⎧⎨≤⎩的解集在数轴上表示出来，正确的是( ▲ ) Ａ．Ｂ．Ｃ．Ｄ．6．下列说法中正确的是( ▲ )A ．“打开电视，正在播放《新闻联播》”是必然事件B ．想了解某种饮料中含色素的情况，宜采用抽样调查C ．数据1，1，2，2，3的众数是3D ．一组数据的波动越大，方差越小7. 若直线y 3x m =+经过第一、三、四象限，则抛物线2y (x m)1=-+的顶点必在 ( ▲ )A ．第一象限B ．第二象限C ．第三象限D ．第四象限8. 下列图形都是由同样大小的五角星按一定的规律组成，其中第①个图形一共有2个五角星，第②个图形一共有8个五角星，第③个图形一共有18个五角星，…，则第⑥个图形中五角星的个数为( ▲ )二、填空题（本大题共有10小题，每小题3分，共计30分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 9. 4的算术平方根为 ▲ ．10.若代数式21-+x x 的值为零，则x = ▲ ． 11.分解因式：y xy -= ▲ ． 12.今年3月底在上海和安徽两地发现的H7N9型禽流感是一种新型禽流感．研究表明，禽流感病毒的颗粒呈球形,杆状或长丝状,其最小直径约为0.00000008m , 其最小直径用科学计数法表示约为 ▲ m .13.如图，过CDF ∠的一边DC 上的点E 作直线AB ∥DF ，若110AEC ∠=o，则CDF ∠的度数为 ▲ o .14. 已知关于x 的一元二次方程x 2+2x ﹣a=0有两个相等的实数根，则a 的值是 ▲ ．15.如图，AB 是⊙O 的直径，圆心O 到弦BC 的距离是1，则AC 的长是 ▲ ．第13题第15题第18题16. 某学校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶x 元，则可列出方程为 ▲ .17.将一个圆心角为120°，半径为6cm 的扇形围成一个圆锥的侧面，则所得圆锥的高为 ▲ cm ．18. 如图所示，点1A 、2A 、3A 在x 轴上，且11223OA A A A A ==，分别过点1A 、2A 、3A 作y 轴的平行线，与反比例函数()80y x x=>的图象分别交于点1B 、2B 、3B ，分别过点1B ，2B ，3B 作x 轴的平行线，分别与y 轴交于点1C ，2C ，3C ，连接1OB ，2OB ，3OB ，那么图中阴影部分的面积之和为 ▲ ．三、解答题（本大题共有10小题，共计96分．请在答题卡指定区域内作答．．．．．．．．．．，解答时应写出必要的文字说明、证明过程或演算步骤）19. （本题满分8分）（1）计算：()10230sin 3-︒-+-π；（2）化简：2242(1)44a a a a-÷-++．20．（本题满分8分）某班从2名男生和2名女生中随机抽取学生参加学校举行的“我的中国梦”演讲比赛，求下列事件的概率：（1）抽取1名，恰好是男生；（2）抽取2名，恰好是1名女生和1名男生．21（本题满分8分）小敏为了解我市的空气质量情况，从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．请你根据图中提供的信息，解答下列问题：（1）计算被抽取的天数；（2）请补全条形统计图，并求扇形统计图中表示优的扇形的圆心角度数；（3）请估计该市这一年（365天）达到优和良的总天数．如图，点E ，F 在平行四边形ABCD 的对角线AC上，AE =CF ．（1）证明：ABE ∆≌CDF ∆；（2）猜想：BE 与DF 平行吗？对你的猜想加以证明．23．（本题满分10分）如图，在我国钓鱼岛附近海域有两艘自西向东航行的海监船A 、B ，B 船在A 船的正东方向，且两船保持10海里的距离，某一时刻两海监船同时测得在A 的东北方向，B 的北偏东15°方向有一不明国籍的渔船C ，求此时渔船C 与海监船B 的距离是多少．（结果保留根号）24．（本题满分10分）如图， Rt ABC △中，90ABC ∠=°，以AB 为直径作半圆⊙O 交AC于点D ，点E 为BC 的中点，连结DE .（1）求证：DE 是半圆⊙O 的切线；（2）若︒=∠30BAC ，DE =2，求AD 的长．A B C D E F·先锋岛大润发超市进了一批成本为8元/个的文具盒. 调查发现：这种文具盒每个星期的销售量y（个）与它的定价x（元/个）的关系如图所示：（1）求这种文具盒每个星期的销售量y（个）与它的定价x（元/个）之间的函数关系式（不必写出自变量x的取值范围）；（2）每个文具盒的定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少？26．（本题满分10分）在直角坐标系中，点A是抛物线y=x2在第二象限上的点，连接OA，过点O 作OB⊥OA，交抛物线于点B，以OA、OB为边构造矩形AOBC．（1）如图1，当点A的横坐标为▲时，矩形AOBC是正方形；（2）如图2，当点A的横坐标为时，①求点B的坐标；②将抛物线y=x2作关于x轴的轴对称变换得到一个新抛物线，试判断新抛物线经过平移变换后，能否经过A，B，C三点？如果可以，说出变换的过程；如果不可以，请说明理由．定义：如图1，射线OP 与原点为圆心，半径为1的圆交于点P ，记xOP α∠=，则点P 的横坐标叫做角α的余弦值，记作cos α；点P 的纵坐标叫做角α的正弦值，记作sin α；纵坐标与横坐标的比值叫做角α的正切值，记作tan α．如：当ο45=α时, 点P 的横坐标为ο45cos =22, 纵坐标为ο45sin=22,即P (22,22)．又如：在图2中，α-=∠ο90xOQ (α为锐角), PN ⊥y 轴，QM ⊥x 轴，易证OPN OQM ∆≅∆，则Q 点的纵坐标)90sin(α-ο等于点P 的横坐标cos α，得)90sin(α-ο= cos α．解决以下四个问题：（1）当60α=o 时，求点P 的坐标；（2）当α是锐角时，则cos α+sin α ▲ 1（用>或<填空），（sin α）2 + （cos α）2= ▲ ；（3）求证：sin(90)cos αα+=o （α为锐角）；（4）求证：1cos tan2sin ααα-=（α为锐角）．图1 图2已知，把Rt△ABC和Rt△DEF按图1摆放（点C与E重合），点B，C，E，F始终在同一条直线上，∠ACB=∠EDF=90°，DE=DF,AC=8，BC=6，EF=10．如图2，△DEF从图1位置出发，以每秒1个单位的速度沿CB向△ABC匀速运动，同时，点P从点A出发，沿AB以每秒1个单位的速度向点B匀速运动，AC与△DEF 的直角边相交于点Q，当E到达终点B时，△DEF与点P同时停止运动，连接PQ，设移动的时间为t（s）．解答下列问题：（1）当D在AC上时，求t的值；（2）在P点运动过程中，是否存在点P，使△APQ为等腰三角形？若存在，求出t的值；若不存在，说明理由．（3）连接PE，设四边形APEQ的面积为y（cm2），求y与t之间的函数关系式，并写出自变量t的取值范围．参考答案1-8 BBDC ABBC9．2 10．-1 11．y(x-1) 12．8×10-8 13．70 14．-1 15．216．204205.0420=--xx 17．24 18．949 19．(1) 1 ; (2)2+a a 20．(1)21; (2)32 21．(1)50; (2)57.6度 (3)29222．(1)证明略；（2）平行，证明略23．21024．（1）证明略；（2）6 25．（1）y=-10x+300 ; (2)设超市每星期销售这种文具可获得利润为w 元，w=y(x-8)=-10(x-19)2+1210, 当x=19时，最高利润为1210元26．（1）-1；（2）①B （2，4）②过点C 作CG ⊥FB 的延长线于点G ，∵∠AOE+∠EAO=90°，∠FBO+∠CBG=90°，∠AOE=∠FBO ，∴∠EAO=∠CBG ，在△AEO 和△BGC 中，，∴△AEO ≌△BGC （AAS ）， ∴CG=OE=，BG=AE=．∴x c =2﹣=，y c =4+=，∴点C （，），设过A （﹣，）、B （2，4）两点的抛物线解析式为y=﹣x 2+bx+c ，由题意得，，解得，∴经过A 、B 两点的抛物线解析式为y=﹣x 2+3x+2，当x=时，y=﹣（）2+3×+2=，所以点C 也在此抛物线上，故经过A 、B 、C 三点的抛物线解析式为y=﹣x 2+3x+2=﹣（x ﹣）2+．平移方案：先将抛物线y=﹣x 2向右平移个单位，再向上平移个单位得到抛物线y=﹣（x。

2013届九年级数学中考模拟试题

2013届九年级数学中考模拟试题2013届九年级数学中考模拟试题一、选择题(每小题3分，满分24分)( )1. 是A. 的相反数B. 的相反数C. 的相反数D. 的相反数( )2.特庸海慧寺一年接待旅游者约876000人，这个数可以用科学记数法表示为A.0.876×106B. 876×103C. 8.76×106D.8.76×105( )3.下列运算中，计算正确的是A.3x2+2x2=5x 4B.(-x2)3=-x 6C.(2x2y)2=2x4y2D.(x+y2)2=x2+y4( )4.体育课上，体育委员记录了6位同学在25秒内连续垫排球的情况，6位同学连续垫球的个数分别为30、27、32、30、28、34，则这组数据的众数和极差分别是A.33，7B.32，4C.30，4D.30，7( )5.如右图所示的几何体是由一些小立方块搭成的，则这个几何体的左视图是( )6.已知 ,那么在数轴上与实数对应的点可能是A. B. C. 或 D. 或( )7.如图，已知□ABCD，ang;A=45deg;，AD=4，以AD为直径的半圆O与BC相切于点B，则图中阴影部分的面积为A.4B.pi;+2C.4D.2( )8.如图，在的正方形网格中，以AB为边画直角△ABC，使点C在格点上，满足这样条件的点C的个数A.6B.7C.8D.9二、填空(每小题3分，共30分)9.写出一个小于0的无理数_____________.10.函数y =- 中自变量x的取值范围_______________.11.分解因式： = _____________.12.已知等腰梯形的面积为24cm2，中位线长为6cm，则等腰梯形的高为_________cm.13、如图所示，数轴的一部分被墨水污染，被污染的部分内含有的整数为___________.14.如图，把一块直角三角板的直角顶点放在直尺的一边上，如果ang;1=35deg;，那么ang;215. 已知实数m是关于x的方程2x2-3x-1=0的一根，则代数式4m2-6m -2值为___ __.16.在一个不透明的袋子中装有2个白球，个红球，它们除了颜色不同外，其余均相同.若从中随机摸出一个球，摸到红球的概率是，则的值等于 .17.如图，△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上，将△ABC绕点B 顺时针旋转到△ABC的位置，则点A经过的路径长为 .(结果保留pi;).18.某中学在校内安放了几个圆柱形饮水桶的木制支架(如图①)，若不计木条的厚度，其俯视图如图②所示，已知AD垂直平分BC，AD=BC=40cm，则圆柱形饮水桶的底面半径的最大值是 cm.三、解答题：(96分)19.(1)计算： (2)解方程：20.某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表：型号 A B进价 1200元/部 1000元/部售价 1380元/部 1200元/部用36000元购进 A、B两种型号的手机，全部售完后获利6300元，求购进A、B两种型号手机的数量。