第四章 力 法
《船舶结构力学》第4章 力法
M 0l0 M1l0 1 q0l0 l02 0 3EI 0 6EI 0 16 2 EI 0 再列出支座 l 和支座2的转角连续方程式：
2 M 0l0 M1l0 1 q0l0 l0 M1l0 M 2l0 6EI 0 3EI 0 16 2 EI 0 3EI 0 6EI 0 3 M1l0 M 2l0 M 2l0 q0l0 6EI 0 3EI 0 3EI 0 24EI 0
式中δi j代表基本结构中力Xi 在Xj 位置处引起的位移； Δi q代表基本结构中外力在相应于力Xi 位置处引起的位移。
3、三弯矩方程
11 M 1 12 M 2 1q
21 M 1 22 M 2 23 M 3 2 q ... n1n M n1 nn M n nq
M 0l M 1l ql 3 0 3EI 6 EI 24 EI M 0l M 1l M 1l ql 3 ql 3 6 EI 3EI 24 EI 3EI 24 EI 1 将上面两式整理后得：2 M 0 M 1 ql 2 4 1 2 M 0 4 M 1 ql 2 3）解之，得： 1 3 2 M 0 ql 2 0.01714ql 2 , M 1 ql 0.107ql 2 14 28
Pre
Next
Exit
4、例题（第一题）
1.计算图4-6中的双跨梁,画出梁的弯矩图与剪力图
解：1)判断：此双跨梁为两次静不定结构，故需去掉两个多余约束
才能得到基本结构。 为此去掉左端的刚性固定约束并在中间支座切开，得到下图中 的基本结构。
第4章空间力系分解
合力的大小
FR ( Fx )2 ( Fy )2 ( Fz )2
Fx 方向余弦 cos( FR , i ) FR
Fy Fz cos( FR , j ) cos( FR , k ) FR FR
7
空间汇交力系的合力等于各分力的矢量和，合力的作用 线通过汇交点.
M 为合力偶矩矢，等于各分力偶矩矢的矢量和。
25
力偶系的合成（与汇交力系的计算完全相同）
合力偶矩矢
M Mi
M x Mix M y Miy Mz Miz
M M xi M y j Mzk
合矢量投影定理：Βιβλιοθήκη 合力偶矩矢的大小和方向余弦:
M
M M M
2 2 ix iy iz
2
M ix cos M
cos
M iy M
M iz cos M
26
空间力偶系平衡的充分必要条件是：合力偶矩矢等于零。
为代数量
z
即：力对轴之矩，等于力在垂直于
该轴的平面上的投影对轴与平面交 点之矩。 O x
y
特殊情况：
1、力与轴平行，矩为零。 2、力与轴相交，矩为零。
即： 力与轴位于同一平面内时，力对轴之矩为零。 16
合力矩定理
空间任意力系的合力对于任一轴的矩等于力系中所有各 力对于该轴的矩的代数和。（用于求力矩）
B
F
F
rBA rA
A
M rBA F
rB
O
23
2、空间力偶等效定理
作用在同一刚体上的两个力偶，如果力偶矩矢相等， 则它们彼此等效。
《结构力学习题集》(上)第四章超静定结构计算——力法
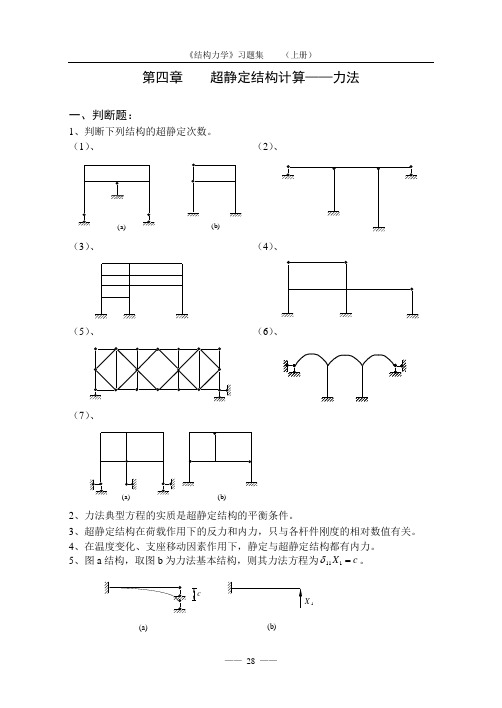
第四章 超静定结构计算——力法一、判断题：1、判断下列结构的超静定次数。
（1）、 （2）、(a )(b)（3）、 （4）、（5）、 （6）、（7）、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下，静定与超静定结构都有内力。
5、图a 结构，取图b 为力法基本结构，则其力法方程为δ111X c =。
(a)(b)X 16、图a 结构，取图b 为力法基本结构，h 为截面高度，α为线膨胀系数，典型方程中∆12122t a t t l h =--()/()。
t 21t l Ah(a)(b)X 17、图a 所示结构，取图b 为力法基本体系，其力法方程为。
(a)(b)1二、计算题：8、用力法作图示结构的M 图。
3mm9、用力法作图示排架的M 图。
已知 A = 0.2m 2，I = 0.05m 4，弹性模量为E 0。
qa a11、用力法计算并作图示结构的M 图。
ql /212、用力法计算并作图示结构的M 图。
q3 m4 m13、用力法计算图示结构并作出M 图。
E I 常数。
（采用右图基本结构。
）l 2/3l /3/3l/314、用力法计算图示结构并作M 图。
EI =常数。
3m 3m2m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l lql l17、用力法计算并作图示结构M 图。
E I =常数。
18、用力法计算图示结构并作弯矩图。
161kNmmmm19、已知EI = 常数，用力法计算并作图示对称结构的M 图。
ql lqa a21、用力法作图示结构的 M 图 。
EI = 常数。
2ql22、用力法作M 图。
各杆EI 相同，杆长均为 l 。
23、用力法计算图示结构并作M 图。
EI = 常数。
4m2kN24mmm24、用力法计算并作出图示结构的M 图。
E = 常数。
20kN3m 4m 3m26、用力法计算图示结构并作M 图。
第四章 运动和力的关系 连接体问题(课件)-高中物理课件(人教版2019必修第一册)
得T3－m1g＝m1a3，联立解得T3＝
F。综上分析可知，细线上拉力始终不变且
大小为
F，选项C正确。
+
+
【变式1】如果将【例题1】中的“拉力”改为“推力”，题目情景如下：将两质量不
同的物体P、Q放在倾角为θ的光滑斜面体上，如图甲所示，在物体P上施加沿斜面
向上的恒力F，使两物体沿斜面向上做匀加速直线运动；图乙为仅将图甲中的斜
在三个阶段的运动中，细线上拉力的大小 ( C )
A.由大变小
B.由小变大
C.始终不变且大小为
F
+
D.由大变小再变大
解析：在水平面上时，对整体由牛顿第二定律得F－μ(m1＋m2)g＝(m1＋m2)a1，对
m1由牛顿第二定律得T1－μm1g＝m1a1，联立解得T1＝
F；在斜面上时，对整
+
【例】相同材料的物块m和M用轻绳连接，在M上施加恒力 F，使两物块作匀加速
直线运动,求在下列各种情况下绳中张力。
(1)地面光滑，FT=?
mF/(m+M)
(2)地面粗糙， FT =？
m
m
M
F
F
M
mF/(m+M)
(3)竖直加速上升（不考虑阻力）， FT =?
mF/(m+M)
F
F
M
M
m
(4)斜面光滑，加速上升， FT =?
D.a乙＞a甲＞a丙，F甲＝F乙＝F丙
解析： 以P、Q为整体由牛顿第二定律可得：
甲图：F－(mP＋mQ)gsin θ＝(mP＋mQ)a甲，解得：a甲＝
乙图：F＝(mP＋mQ)a乙，解得：a乙＝
(＋)
2021_2022学年新教材高中物理第4章运动和力的关系2实验：探究加速度与力质量的关系课件新人教版
3．实验结论 (1)保持物体质量不变时，物体的加速度 a 与所受拉力 F 成正比。 (2)保持拉力 F 不变时，物体的加速度 a 与质量 m 成反比。
五、误差分析
偶然 误差
系统 误差
产生原因
减小方法
质量测量不准、计数点 多次测量求平均值
间距测量不准
①准确平衡摩擦力 小车所受拉力测量不准
②使细绳和纸带平行于木板
表 2 小车所受的拉力一定
四、数据分析 1．分析加速度 a 与力 F 的定量关系 由表 1 中记录的数据，以加速度 a 为纵坐标，力 F 为横坐标， 根据测量数据描点，然后作出 a-F 图像，如图甲所示，若图像是一 条通过原点的直线，就能说明 a 与 F 成正比。
甲
乙
2．分析加速度 a 与质量 m 的定量关系 由表 2 中记录的数据，以 a 为纵坐标，以m1 为横坐标，根据测量 数据描点，然后作出 a-m1 图像，如图乙所示。若 a-m1 图像是一条过原 点的直线，说明 a 与m1 成正比，即 a 与 m 成反比。
二、实验器材 小车、槽码、砝码、细绳、一端附有定滑轮的长木板、垫木、 打点计时器、交流电源、纸带、刻度尺、天平。
三、进行实验(以参考案例 1 为例) 1．用天平测出小车的质量 m，并把数值记录下来。 2．按如图所示的装置把实验器材安装好(小车上先不系细绳)。
3．补偿阻力：在长木板不带定滑轮的一端下面垫上垫木，反复 移动垫木位置，启动打点计时器，直到轻推小车使小车在斜面上运 动时可保持匀速直线运动为止(纸带上相邻点间距相等)，此时小车重 力沿斜面方向的分力等于打点计时器对小车的阻力和长木板的摩擦 阻力及其他阻力之和。
4．用细绳绕过定滑轮系在小车上，另一端挂上槽码，保持小车 质量不变，改变槽码的个数，以改变小车所受的拉力，处理纸带， 测出加速度，将结果填入表 1 中。
高中物理必修1第四章知识点归纳
高中物理必修1第四章知识点归纳高中物理必修1第四章主要是讲牛顿运动定律这部分内容，下面是店铺给大家带来的高中物理必修1第四章知识点归纳，希望对你有帮助。
高中物理必修1第四章知识点一、牛顿第一定律1、内容：(揭示物体不受力或合力为零的情形)2、两个概念：①、力②、惯性：(一切物体都具有惯性，质量是惯性大小的唯一量)二、牛顿第二定律1、内容：(不能从纯数学的角度表述)2、公式：F合=ma3、理解牛顿第二定律的要点：①、式中F是物体所受的一切外力的合力。
②、矢量性③、瞬时性④、独立性⑤、相对性三、牛顿第三定律作用力和反作用力的概念1、内容2、作用力和反作用力的特点：①等值、反向、共线、异点②瞬时对应③性质相同④各自产生其作用效果3、一对相互作用力与一对平衡力的异同点四、力学单位制1、力学基本物理量：长度(l) 质量(m) 时间(t) 力学基本单位：米(m) 千克(kg) 秒(s)2、应用：用单位判断结果表达式，能肯定错误(但不能肯定正确)五、动力学的两类问题。
1、已知物体的受力情况，求物体的运动情况(v0 v t x )2、已知物体的运动情况，求物体的受力情况( F合或某个分力)3、应用牛顿第二定律解决问题的一般思路(1)明确研究对象。
(2)对研究对象进行受力情况分析，画出受力示意图。
(3)建立直角坐标系，以初速度的方向或运动方向为正方向，与正方向相同的力为正，与正方向相反的力为负。
在Y轴和X轴分别列牛顿第二定律的方程。
(4)解方程时，所有物理量都应统一单位，一般统一为国际单位。
4、分析两类问题的基本方法(1)抓住受力情况和运动情况之间联系的桥梁——加速度。
(2)分析流程图六、平衡状态、平衡条件、推论1、处理方法：解三角形法(合成法、分解法、相似三角形法、封闭三角形法)和正交分解法2、若物体受三力平衡，封闭三角形法最简捷。
若物体受四力或四力以上平衡，用正交分解法七、超重和失重1、超重现象和失重现象2、超重指加速度向上(加速上升和减速下降)，超了ma;失重指加速度向下(加速下降和减速上升)，失ma。
第四章 第3节 牛顿第二定律
确定研 究对象
→
受力 分析
→求合力→
利用F＝ ma列方程
→
求加 速度
首页
上一页
下一页
末页
[解析] 方法一：合成法 (1)小球和车厢相对静止，它们的加速度相 同。以小球为研究对象，对小球进行受力分析如
结束
图所示，小球所受合力 F 合＝mgtan 37°， 由牛顿第二定律得小球的加速度为
上一页
下一页
末页
结束
1.(2018·全国卷Ⅰ)如图，轻弹簧的下端固定在水平桌面上，
上端放有物块 P，系统处于静止状态。现用一竖直向上
的力 F 作用在 P 上，使其向上做匀加速直线运动。以 x
表示 P 离开静止位置的位移，在弹簧恢复原长前，下列
表示 F 和 x 之间关系的图像可能正确的是
()
首页
上一页
(2)力与速度无因果关系：合外力方向与速度方向可以同向，
可以反向。合外力方向与速度方向同向时，物体做加速运动，
反向时物体做减速运动。
(3)两个加速度公式的区别
a＝ΔΔvt 是加速度的定义式，是比值定义法定义的物理量，a
与 v、Δv、Δt 均无关；a＝mF是加速度的决定式：加速度由物体 受到的合外力和质量决定。
a＝Fm合＝gtan 37°＝34g＝7.5 m/s2， 加速度方向水平向右。
车厢的加速度与小球相同，车厢做的是向右的匀加速运动
或向左的匀减速运动。
(2)由图可知，悬线对球的拉力大小为
F＝cosm3g7°＝12.5 N。
首页
上一页
下一页
末页
方法二：正交分解法
哈工大结构力学题库四章
第四章 力 法一 判 断 题1. 图示结构，据平衡条件求出B 点约束力，进而得图示弯矩图，即最后弯矩图。
（ ）（X ）题1图 题2图2. 图示结构用力法求解时，可选切断杆件2，4后的体系作为基本结构。
（ ）（X ）3. 图a 结构，支座B 下沉a 。
取图b 中力法基本结构，典型方程中1C a ∆=-。
（ ） （X ）题3图 题4图4. 图a 所示桁架结构可选用图b 所示的体系作为力法基本体系。
（ ）（√）5. 图a 结构，取图为力法基本结构，1C l θ∆=。
（ ） （X ）题5图 题6图6. 图a 结构的力法基本体系如图b ，主系数3311/(3)/()l EI l EA δ=+。
（ ）（X ）7. 图示结构用力法解时，可选切断1，2，3，4杆中任一杆件后的体系作为基本结构.（ ）（X ）题7图 题9图 8. 图示结构受温度变化作用，已知α，h ，选解除支杆B 为力法基本体系(设B X 向上为正)，典型方程中自由项2121()/(4)t a t t l h ∆=--。
（ ）（X ）9. 图a 结构，力法基本体系如图b ，自由项412/(8)P ql EI ∆=-。
（ ）（X ）题10图 题11图10.图示超静定梁在支座转动1A ϕ=时的杆端弯矩26.310AB M KN m =⨯⋅，22( 6.310)EI KN m =⨯⋅。
（ ）（√） 11. 图a 结构，取图b 为力法基本结构，h 为截面高度，α为线胀系数，典型方程中2121()/(2)t a t t l h ∆=--。
（ ）（X ）题12图 题13图 12. 图a 结构，取力法基本体系如图b 所示，则1/C l ∆=∆（ ）。
（X ）13. 超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
（ ）（√）14. 图示结构的超静定次数为4。
（ ）（X ）题15图 题16图15. 图示结构，选切断水平杆为力法基本体系时，其3112/(3)h EI δ=。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章力法一、是非题（“是”打√，“非”打）1、图（a）所示超静定结构，力法求解时，所有副系数全为零的基本结构如图（b）所示（除BC杆EI=∞外，其余各杆EI=C）。
（）2、图（a）所示超静定结构，AC杆端剪力可由图（b）所示脱离体用静力平衡条件直接求出。
（）3、图（a）所示超静定梁M图与图（b）所示静定梁M图相同。
（）4、图（a）所示超静定梁在均布荷载作用下的M图与图（b）所示静定梁M图图乘的结果不等于其与图（c）所示静定梁的M图的图乘结果。
（）5、图示结构中，去掉其中任意两根支座链杆后余下部分都可作为力法计算的基本体系。
（）6、图示结构中，去掉其中任意两根支座链杆后余下部分都可作为力法计算的基本体系。
（）7、图示两结构，对应点内力相同。
8、图示两结构，对应点内力相同。
9、图示两结构，对应点内力相同。
（）10、图示结构，其力法典型方程的自由项,。
（）11、图（a）所示结构，用力法求解时，可取图（b）做基本系。
（）12、图（a）所示结构，用力法求解时可取图（b）做基本系。
（）13、超静定结构在支座移动作用下一定会有内力产生。
（）14、图示结构在支座C垂直向下移动时结构的内力全为零。
（）15、对于超静定桁架，如果在结构外荷载及结构材料不变的情况下增加某些杆件的截面积，则指定处所的位移一定会减小（）。
16、某超静定梁，截面的高度为h，线膨胀系数为α，EA=常数，EI=常数。
图（a）中梁上、下面的温度均升高50℃，图（b）中梁上面的温升为30℃，梁下面的温升为70℃。
两种情况下梁的内力一样（）。
17、图（a）与图（b）所示结构在支座C处的反力关系为不超过。
( )18、图（a）所示结构（不计杆长变化）用力法求解时可采用图（b）所示结构进行计算。
（）19、图示对称结构受对称荷载（不计杆长变化），则B支座的约束反力0。
( )20、图示结构各杆刚度E I=常数,则其图示的弯矩图是正确，( ）21、图示对称结构受对称荷载，D支座的反力0。
（）22、对于温度改变作用下的等刚度闭合结构，可以根据最终弯矩图的面积的代数和为零这个条件，判断弯矩图是否正确。
（）23、结构只在荷载作用下的，力法典型方程中的系数与自由项，有的与结构的刚度有关，有的与结构的刚度无关。
（）二、选择题1、图示为结构及其力法基本系，则力法典型方程的自由项为：（）A、，B、，C、，D、，2、图（a）所示结构，EI=C，取图（b）为力法基本体系，则为：（）A、 B、 C、 D、3、图示结构EI=C，在给定荷载作用下，支座反力(向右为正)和(向上为正)，轴力(以拉为正)分别为：（）A ，，B ，，C ，，D ，，4、图（a）所示组合结构，取图（b）为其力法计算基本系，则，分别为：（）A、 ,B、 ,C、 ,D、 ,5、图A～图D所示结构均可作为图（a）所示结构的力法基本结构，使得力法计算最为简便的基本结构是：（）6、图示超静定结构，列出其力法计算典型方程，下述四个表述中不正确的是：（）A. BB.CC.D.7、图示超静定结构及其M图，要校核其正确性可采用下述哪种做法：（）计算E点位移计算D点水平位移及E点竖向位移计算E点位移计算C点位移8、图示超静定结构，其力法典型方程不正确的是：（）ABCD9、图示对称超静定结构，力法计算时基本未知值最少为：（）A 12B 9C 8D 310、图示对称结构，力法求解时，未知量最少为: ( )A 12B 8C 4D 211、图(a)所示结构，EI=常数，取图(b)为力法基本系，=A.；B. ；C. ；D.12、图示（a）、（b）两结构，当A支座顺时钟发生单位角位移时，（a）、（b）两图中,与的关系为 ( )(Ａ) ＝(Ｂ) > (C)< (D) = -13、结构在温度改变作用下，力法典型方程中的系数和自由项与结构刚度之间的关系是（）A、系数项和自由项均与结构刚度有关；B、系数项与结构刚度有关，自由项与结构刚度无关；C、系数项和自由项均与结构刚度无关；D、系数项与结构刚度无关，自由项与结构刚度有关；14、超静定结构在支座移动作用下，力法典型方程中的系数项和自由项与结构刚度之间的关系为（）A、系数项和自由项均与结构刚度无关；B、系数项和自由项均与结构刚度有关；C、系数项与结构刚度有关，自由项与结构刚度无关；D、系数项与结构刚度无关，自由项与结构刚度有关；15、图示超静定梁，截面的高度为h，线膨胀系数为α，ＥＡ＝常数，ＥＩ＝常数。
图（a）中梁的上、下面的温度均长高50℃，图（b）中梁上面的温度为30℃，而梁下面的温度为70℃，下面结论正确的是（）Ａ、图（a）、图（b）中梁的内力是一样的，只有轴力；Ｂ、图（a）所示梁中只有轴力，图（b）所示梁中只有弯矩；Ｃ、图（a）所示梁中有轴力和弯矩，图（b）所示梁中只有弯矩；Ｄ、图（a）所示梁中只有轴力，图（b）所示梁中有轴力和弯矩；16、如图所示结构，各杆刚度ＥＡ＝常数，某种荷载作用下的下列内力中，正确解答是（）Ａ、＝，＝，＝－，＝－，＝－，＝；Ｂ、＝，＝－，＝－，＝，＝，＝；Ｃ、＝，＝，＝，＝，＝－，＝；Ｄ、＝，＝，＝－，＝，＝－，＝；17、图示对称结构受对称荷载，则下面结论正确的是（）A、=0 ，=0 ，=0 ，=0 ，= —B、=，=，=，=，= 0；C、=，=，=，=，= —；D、= —，= —，= —，= —，= —2；18、图示对称结构受荷载作用，则D支座反力为（）A、=，方向向上；B、=，方向向下；C、=，方向向上；D、=，方向向下；19、图（a）所示结构，杆件刚度EI = 常数。
用力法求解时，取图（b）所示基本系，要使力法方程中的副系数全部为零，刚x、y应满足下列哪个条件（）A、x = a/3， y=b/3；B、x = a/2， y=b/2；C、x = a/3，y=b/2；D、x = a/2， y=b/3；20、图示对称结构受反对称荷载，其超静定次数为N，力法求解时的未知量个数最少为n，则正确答案为（）A、超静定次数为5，力法求解时的未知量个数最少为2 ；B、超静定次数为5，力法求解时的未知量个数最少为1；C、超静定次数为4，力法求解时的未知量个数最少为1；D、超静定次数为4，力法求解时的未知量个数最少为2；三、填空题1、图示体系的超静定次数为___________。
2、图示结构力法求解时未知量最少的基本系为____________。
3、已知图（a）所示静定梁的(顺时针为正)，利用该结论求解图（b）所示结构的＝____________。
4、已知图（a）所示静定梁的,(顺时针为正)，利用图（a）结论求图（b）所示结构的＝______________。
5、图（a）所示对称结构，若取图（b）所示基本系时，则力法典型方程为______________。
6、力法计算图示结构时，未知量最少的基本结构为_________________。
7、超静定结构在荷载作用下的M图如图所示，则A点的水平线位移为____________。
8、图（a）所示超静定结构，取图（b）所示基本系，则_________________，=______________。
9、图示对称结构，各杆EI相同，则C截面的弯矩为____________，____侧受拉。
10、图（a）所示结构，取图（b）为力法计算的基本系，则＝__________，＝__________，＝__________。
11、图（a）所示结构A支座的弯距大小为，则图（b）所示结构A支座的弯距大小为 .12、图（a）所示结构A支座的弯距大小为，则图（b）所示结构A支座的弯距大小为 .13、已知图（a）所示结构B支座的约束反力为，则图（b）所示结构杆件的内力与的关系为= 。
14、图（a）所示结构，各杆刚度EA=常数。
用力法求解时分别取图（b）和图（c）两种基本系，则两个力法方程分别为和，则柔度系数与关系为：。
15、图（a）所示结构当B支座顺时针转动θ角时的弯矩图如图（b）。
试求该结构E点的水平位移____________，方向____________。
16、图（a）所示结构，MBA =________，MBD=__________。
17、图示对称结构，超静定次数为，力法未知量个数最少为。
18、性中心法适用于三次超静定的闭合结构。
当把结构基本未知量的作用点用刚臂引到结构的“弹性中心”处时，不仅保证了弹性中心处的位移与处的位移相等，还可使力法典型方程中为0。
19、图示对称结构，在图示参考坐标系下，如采用弹性中心法求解，弹性中心的位置坐标为x= , y= 。
20、图示对称结构，在图示参考坐标系下，如采用弹性中心法求解，弹性中心的位置坐标为x= , y= 。
21、对于荷载作用下的等刚度闭合结构，若最终弯矩图的面积的代数和为零，则弯矩图是正确的。
那么，这个条件表示的位移条件是。
22、图示等截面无铰拱的拱轴半径为R，中心角为2φ，如采用弹性中心法求解，弹性中心的位置坐标为x= , y= 。
一、是非题1、√。
2、√，AC杆剪力静定。
（铰支座A处水平链杆为绝对必须约束，其反力是静定的）3、√，对图（b）所示悬臂梁，在均布荷载及集中力作用下悬臂梁自由端竖向位移为零，故两结构满足相同的平衡条件和位移条件。
4、×，两图乘结果都是图（a）所示超静定梁跨中挠度。
5、×，例如，去掉铰支座A，则体系成为几何瞬变。
去掉铰支座A和铰支座C处水平连杆，则体系成为几何可变体系。
6、×，例如，去掉两根水平连杆，则体系成为几何可变体系。
7、√，刚度相对比值不变。
8、×，杆件弯曲刚度的绝对值不同。
9、×，杆件弯曲刚度的绝对值不同。
10、×，图正对称，图正对称，图反对称，故,。
11、×，AB杆是受弯杆件。
12、√，力法基本结构可以是超静定结构。
13、×，不一定，例如，结构内部超静定，而外部静定。
14、√，结构外部静定。
15、×，，，当第j杆的两套内力异号时Aj 增加，减小。
16、√，只有轴力（压），大小为50αEA。
17、√，,（a）中支座反力不超过（b）中支座反力。
18、√，对称结构受正对称荷载作用，不计轴向变形，则B处相当于固定端。
19、√，外荷载F只引起CD杆轴向内力。
20、×，显然，铰C两侧相对转角不为零。
（而图示弯矩内、外侧面积相等）21、√，结构对称，荷载正对称，荷载通过竖柱（产生轴力）传至基础，竖柱无弯矩和侧移。
22、×，在温度改变作用下，某一截面两侧的相对转角。
（前一项表示切口处基本未知力引起的转角，后一项表示温度改变引起切口处的相对转角）。
23、×，在荷载作用下,力法典型方程中的系数和自由项均为基本结构在外力作用下的位移.二、选择题1、B，正对称，反对称,反对称。