第1章多自由度体系自由振动分析
合集下载
振动分析_精品文档
振动分析1. 引言振动分析是一种研究和分析物体振动行为的方法。
振动是指物体在固有频率下的周期性运动。
振动分析可以应用于各个领域，如工程、物理学、机械等，以帮助我们理解和掌握物体的振动特性。
本文将介绍振动分析的基本概念、方法和应用。
2. 振动分析方法2.1 自由振动自由振动是指物体在无外力作用下以自身固有频率振动的现象。
自由振动可以用简谐振动模型来描述。
简谐振动是指物体在恢复力作用下按正弦或余弦函数的规律周期性振动。
2.2 强迫振动强迫振动是指物体在外力作用下振动的现象。
外力作用会改变物体原来的振动特性，使振动频率改变。
强迫振动可以通过叠加法和复合振动模型来描述。
2.3 阻尼振动阻尼振动是指物体在有耗散力的情况下振动的现象。
耗散力会使振动逐渐减弱，最终停止。
阻尼振动可以通过阻尼振动模型来描述。
2.4 频域分析频域分析是指将振动信号转换到频域进行分析的方法。
频域分析可以通过傅里叶变换将时域信号转换成频谱图，以研究振动信号中的频率成分和幅度。
频域分析常用于诊断和解决振动问题。
2.5 时域分析时域分析是指在时间轴上分析振动信号的方法。
时域分析可以通过绘制波形图、自相关函数和互相关函数来分析振动信号中的时间特性。
时域分析常用于振动信号的处理和特征提取。
2.6 模态分析模态分析是指通过确定物体的振动模态和固有频率来分析其振动特性的方法。
模态分析可以通过模态测试和有限元法进行，以确定物体的振动模态和模态参数。
模态分析可以帮助我们了解和设计物体的振动特性。
3. 振动分析应用振动分析在各个领域都有广泛的应用。
以下是一些常见的振动分析应用：3.1 结构健康监测振动分析可以用于结构健康监测，以检测和评估结构的损伤和变形情况。
例如在桥梁和建筑物中安装振动传感器，通过实时监测结构的振动信号，可以及时发现和诊断可能存在的结构问题。
3.2 故障诊断振动分析可以用于故障诊断，以检测和诊断机械设备的故障和异常情况。
通过分析机械设备的振动信号，可以判断是否存在轴承故障、不平衡、松动等问题，从而进行及时维修和更换。
振动理论09(1)-多自由度系统
正定系统中的各阶固有频率恒取正值 半正定系统的每个零值固有频率对应着系统的一种刚
体运动形式：即系统没有弹性变形、离开中性平衡位 置的整体的刚体转动或平动
例：三圆盘转动惯量均为I，中间两段轴的扭转刚度均 为 ，求系统的固有频率及主振型
解：系统的动能为和势能分别为Leabharlann 代入拉格朗日方程，得到振动方程
下式中的 是一个对角矩阵，称为主刚度矩阵
正则振型
主振型列阵表示系统作主振动时各坐标间的幅值的相 对大小
由这样的主振型列阵构成振型矩阵，然后求得主质量 矩阵，其对角元素 各不相等
为方便起见，将各主振型正则化：对于每一阶主振动 ，定义一组特定的主振型－正则振型(Orthonormal mode)，满足
k21 m21 2
k22 m22 2
k2n2 m2n2 2
k2n1 m2n1 2
k2n m2n 2
kn21 m n21 2 kn22 m n22 2
k
n11
m
n11
2
kn12 m n12 2
k n 2 n 2 mn2n2 2 kn1n2 mn1n2 2
1
1
2
2
代入拉格朗日方程
外力虚功之和
P1 x1 m1
P2
P3
x2
x3
m2
m3
集中质量梁振动方程－柔度影响系数法
利用 ’
原理，把惯性力和外力共同作用在质量
上，由柔度影响系数求得变形，从而建立振动微分方程
P1
P2
P3
x1
x2
x3
m1
m2
m3
刚性支座上的无重量杆，杆上三个质量 1、 2、 上的位移分别为 1、 2、 3. 是柔度影响系数
体运动形式：即系统没有弹性变形、离开中性平衡位 置的整体的刚体转动或平动
例：三圆盘转动惯量均为I，中间两段轴的扭转刚度均 为 ，求系统的固有频率及主振型
解：系统的动能为和势能分别为Leabharlann 代入拉格朗日方程，得到振动方程
下式中的 是一个对角矩阵，称为主刚度矩阵
正则振型
主振型列阵表示系统作主振动时各坐标间的幅值的相 对大小
由这样的主振型列阵构成振型矩阵，然后求得主质量 矩阵，其对角元素 各不相等
为方便起见，将各主振型正则化：对于每一阶主振动 ，定义一组特定的主振型－正则振型(Orthonormal mode)，满足
k21 m21 2
k22 m22 2
k2n2 m2n2 2
k2n1 m2n1 2
k2n m2n 2
kn21 m n21 2 kn22 m n22 2
k
n11
m
n11
2
kn12 m n12 2
k n 2 n 2 mn2n2 2 kn1n2 mn1n2 2
1
1
2
2
代入拉格朗日方程
外力虚功之和
P1 x1 m1
P2
P3
x2
x3
m2
m3
集中质量梁振动方程－柔度影响系数法
利用 ’
原理，把惯性力和外力共同作用在质量
上，由柔度影响系数求得变形，从而建立振动微分方程
P1
P2
P3
x1
x2
x3
m1
m2
m3
刚性支座上的无重量杆，杆上三个质量 1、 2、 上的位移分别为 1、 2、 3. 是柔度影响系数
振动力学与结构动力学-(第一章).
摩擦力： Fd cdx2sgxn
c d ：阻力系数
在运动方向不变的半个周期内计算耗散能量，再乘2：
Ecdx2sgxndx2
T/4
c T/4 d
x3dt
8 3
cd02
A2
等效粘性阻尼系数：
ce
8
3
cd0
A
24
四、结构阻尼
由于材料为非完全弹性，在变形过程中材料的内摩擦所引起 的阻尼称为结构阻尼
特征：应力－应变曲线存在滞回曲线
6
第一章 概 论
§1-1 动荷载及其分类 - 从广义上讲，如果表征一种运动的物理量作时而增大时而减
小的反复变化，就可以称这种运动为振动。 - 如果变化的物理量是一些机械量或力学量，例如物体的位移
、速度、加速度、应力及应变等，这种振动便称为机械振动 。 - 各种物理现象，诸如声、光、热等都包含振动
7
– 知识要点：结构被动控制、主动控制的基本概念。常用主动 控制方法的原理。结构主动控制在机械、土木结构工程中应 用简介。
– 重点难点：理解各种控制方法的原理及其具体实现。 – 教学方法：课堂讲授与引导讨论相结合。
主要参考书： • 刘延柱.振动力学.北京：高等教育出版社,1998 • 倪振华. 振动力学. 西安：西安交通大学出版社，1989 • 张准、汪凤泉. 振动分析.南京：东南大学出版社，1991 • 陈予恕.非线性振动. 天津：天津科技出版社，1983 • 龙驭球等编著.《结构力学》下册. 北京：高等教育出版 社，1994
– 教学方法：课堂讲授与引导讨论相结合
• 第六章 结构反应谱与地震荷载计算（8学 时）
– 知识要点：结构反应谱、单自由度和多自由度地震 荷载计算公式、规范中地震荷载计算公式。
结构动力学之多自由度体系的振动问题
3 13.027
2.760 3.342 1
0.163
0.924
2.76
柔度法
利用刚度法的方程间接导出柔度法方程：
由刚度法振幅方程：
令λ=1/ω2 得频率方程：
( [K]－ω2 [M] ){Y}={0}
前乘[K]－1=[δ]后得： ( [I ]－ω2 [δ] [M] ){Y}={0} ( [δ] [M] － λ [I ] ){Y}={0} ┃ [δ] [M] － λ [I ] ┃=0
刚度法
2）如果初始条件是任意的，则任其自然 后， 系统所发生的振动就不是按主振型的简谐自由 振动，而是复杂的周期振动，这时可以用各阶 主振动的线性组合来描述它，也就是说其通解 表为各个特解之和，即
y j sin( j t v j )
j 1 n
所以系统的任意振动可以表示为各个主振动 的叠加。
Yij为正时表示质1 1.293 5Y11 6.70Y21 3 0 量mi的运动方向与单 3Y 1.707 0
21
Y
(1)
0.163 0.569 1
0.569
5Y13 5.027Y23 3 0 (1) Y 3Y21 10.027 0 3.342 1.227
1 1 4 0 , m m 2 9
展开得: 解之:
3 15 2 42 30 0
ξ1=11.601，ξ2=2.246，ξ3=1.151
1 m
三个频率为：
1 0.2936
1 1 3 0.9319 m m 3）求主振型： （令Y3i=1）将λ1代入振型方程： （[δ] [M ]－λ1[I]）{Y}＝0的前两式：
2.760 3.342 1
0.163
0.924
2.76
柔度法
利用刚度法的方程间接导出柔度法方程：
由刚度法振幅方程：
令λ=1/ω2 得频率方程：
( [K]－ω2 [M] ){Y}={0}
前乘[K]－1=[δ]后得： ( [I ]－ω2 [δ] [M] ){Y}={0} ( [δ] [M] － λ [I ] ){Y}={0} ┃ [δ] [M] － λ [I ] ┃=0
刚度法
2）如果初始条件是任意的，则任其自然 后， 系统所发生的振动就不是按主振型的简谐自由 振动，而是复杂的周期振动，这时可以用各阶 主振动的线性组合来描述它，也就是说其通解 表为各个特解之和，即
y j sin( j t v j )
j 1 n
所以系统的任意振动可以表示为各个主振动 的叠加。
Yij为正时表示质1 1.293 5Y11 6.70Y21 3 0 量mi的运动方向与单 3Y 1.707 0
21
Y
(1)
0.163 0.569 1
0.569
5Y13 5.027Y23 3 0 (1) Y 3Y21 10.027 0 3.342 1.227
1 1 4 0 , m m 2 9
展开得: 解之:
3 15 2 42 30 0
ξ1=11.601，ξ2=2.246，ξ3=1.151
1 m
三个频率为：
1 0.2936
1 1 3 0.9319 m m 3）求主振型： （令Y3i=1）将λ1代入振型方程： （[δ] [M ]－λ1[I]）{Y}＝0的前两式：
随机振动--第1章-1.1
影响乘坐的舒适性；降低机器及仪表的精度
危害人体健康；引起机械设备及土木结构的破坏；
琴弦振动；振动沉桩、振动拔桩以及振动捣固等；振动检测；
?
√
√．系统设计和系统辨识
系统尚不存在，需要设计合理的系统参数，使系统在已知激励下达到给定的响应水平。
系统已经存在，需要根据测量获得的激励和响应识别系统参数，
以便更好地研究系统特性。
?√√已知系统的激励和响应
求系统参数
?√√确定系统的激励
实际系统力学原理微分
方程
解析
解
数学工具
理论分析
解决振动问题的方法。
动力学(第1章)
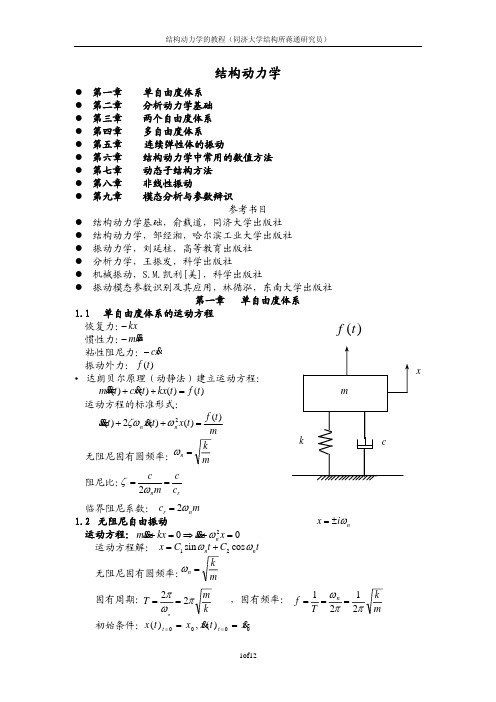
f
(t)
=
2P0
ωt π
∫ ∫ bi
=
2 T
T 0
f (t) sin(iωt)dt = 4ω π
π 2ω 0
f
(t) sin(iωt)dt
=
8P0 i2π 2
i −1
(−1) 2 (i
= 1,3,5,⋅⋅⋅)
6of12
结构动力学的教程（同济大学结构所蒋通研究员）
∑ 取
i=1~3
β1 算得：
=
1
−
1 ω2
= 1−ω
2ζω 3 2 + (2ζω )2
1+ 4ζ 2ω 2 (1− ω 2 )2 + (2ζω )2
5of12
结构动力学的教程（同济大学结构所蒋通研究员）
隔振要求： 频率比： ω
=
ω
>
2⇒
ωn
阻尼比小：ζ ↓⇒ A ↓
B
A <1 B
但过小通过共振区不利
主动隔振：将振源隔开，使振动传播不出去（隔振器）
+ϕ)
振幅与相位角： A=
x02
+
⎜⎜⎝⎛
x&0 ωn
⎟⎟⎠⎞2
,ϕ
=
arctg
ωn x0 x&0
x
A
x&0
x0
t ϕ /ωn
t t +T
例题 1-1 求图示体系的固有频率
悬臂梁刚度：k1
=
3EI l3
与 K2 并联后等效刚度：k = k1 + k2 固有频率:ωn = k / m （串联弹簧）
l m
• •
能量守衡：We +Wd + Wf = 0 → ω = ωn →
多自由度体系
最后求第三主振型。将将3和3代入式（a),得
-6.054
K
32M
=
k 15
5
0
5 -5.027
3
0
3
-10.027
代入式（4-3-4），后两个方程为
-5Y13 5.027Y23 +3Y33 0 3Y23 +10.027Y33 0
令Y33 1，故式（f）的解为
Y (3) = Y13，Y23，Y33 T 2.760, 3.342,1T
M
M
kn1
kn2
L
k1n
k2n
0
M
knn -2mn
（4-3-3b）
n个根12，22， n2
Y (i)表示与频率i相应的主振型：
Y (i)T =（Y1i Y2i Yni )
将i和Y (i)代入式（4-3-2）得
（K i2M）Y (i) 0
（4-3-4）
令，i 1, 2,, n，可得n个向量方程，由此可求的n个主振型向量 Y (1)，Y (2)，，Y (n)
（1）验算正交关系式（4-3-8）
2 0 0 0.924
Y (1)T MY (2) =(0.163, 0.569,1) 0 1 0 1.227 m
0 0 1 1
m0.163 2 (0.924) 0.5691 (1.227) 111
0.0006m 0
同理，
Y (1)T MY (3) 0.002m 0，Y (2)T MY (3) 0.002m 0
3
0
3
1.707
代入式（4-3-4）中并展开，保留后两个方程，得
-5Y11 6.707Y21 3Y31 3Y21 1.707Y31 0
-6.054
K
32M
=
k 15
5
0
5 -5.027
3
0
3
-10.027
代入式（4-3-4），后两个方程为
-5Y13 5.027Y23 +3Y33 0 3Y23 +10.027Y33 0
令Y33 1，故式（f）的解为
Y (3) = Y13，Y23，Y33 T 2.760, 3.342,1T
M
M
kn1
kn2
L
k1n
k2n
0
M
knn -2mn
（4-3-3b）
n个根12，22， n2
Y (i)表示与频率i相应的主振型：
Y (i)T =（Y1i Y2i Yni )
将i和Y (i)代入式（4-3-2）得
（K i2M）Y (i) 0
（4-3-4）
令，i 1, 2,, n，可得n个向量方程，由此可求的n个主振型向量 Y (1)，Y (2)，，Y (n)
（1）验算正交关系式（4-3-8）
2 0 0 0.924
Y (1)T MY (2) =(0.163, 0.569,1) 0 1 0 1.227 m
0 0 1 1
m0.163 2 (0.924) 0.5691 (1.227) 111
0.0006m 0
同理，
Y (1)T MY (3) 0.002m 0，Y (2)T MY (3) 0.002m 0
3
0
3
1.707
代入式（4-3-4）中并展开，保留后两个方程，得
-5Y11 6.707Y21 3Y31 3Y21 1.707Y31 0
多自由度系统振动理论及应用
多自由度系统的作用力方程
对一些较简单的问题,用牛顿定律来建立振动微分方程是简便的.
图４-１所示为无阻尼三自由度弹簧质量系统,可参照二自由度系统的方
法,写出其微分方程:
下一页
返回
４.１
多自由度系统的振动微分方程
或更一般地写成
该式可简单地写成
式(４-２)称为用矩阵符号表示的作用力方程,它可以代表许多种运动方程
种心灵的孤独。
2. 与 个 别 人 难 以 相 处
一些学生能够与多数人保持良好的关系,但与个别人交往
不 良 。 因 此 ,常 会 影 响 情 绪 ,如 鲠 在 喉 。
上一页 下一页
返回
任 务 一了解自己与人交往的现状
3. 与 他 人 交 往 平 淡
一些学生虽然能与他人交往,但多属点头之交,没有关系
人际关系新起点
1
任 务 一 了解自己与人交往的现状
2
任 务 二 调整不良交际心态
任 务 一了解自己与人交往的现状
任 务 提 出 :了 解 自 己 与 人 交 往 的 现 状 。
任 务 目 标 :了 解 自 己 与 人 交 往 的 现 状 ,激 发 学 习 热 情 ,明 确 努
力方向。
喜欢独来独往。
(3) 嫉 妒 心 理 。 部 分 大 学 生 不 能 正 确 对 待 别 人 的 长 处 和 优
点,看到别人冒尖心里嫉妒,对比自己水平高的同学采取
讽 刺 、 挖 苦 、 打 击 、 嘲 笑 等 不 当 方 式 ,给 别 人 造 成 伤 害 ,严
重影响了同学之间的沟通。
上一页
对一些较简单的问题,用牛顿定律来建立振动微分方程是简便的.
图４-１所示为无阻尼三自由度弹簧质量系统,可参照二自由度系统的方
法,写出其微分方程:
下一页
返回
４.１
多自由度系统的振动微分方程
或更一般地写成
该式可简单地写成
式(４-２)称为用矩阵符号表示的作用力方程,它可以代表许多种运动方程
种心灵的孤独。
2. 与 个 别 人 难 以 相 处
一些学生能够与多数人保持良好的关系,但与个别人交往
不 良 。 因 此 ,常 会 影 响 情 绪 ,如 鲠 在 喉 。
上一页 下一页
返回
任 务 一了解自己与人交往的现状
3. 与 他 人 交 往 平 淡
一些学生虽然能与他人交往,但多属点头之交,没有关系
人际关系新起点
1
任 务 一 了解自己与人交往的现状
2
任 务 二 调整不良交际心态
任 务 一了解自己与人交往的现状
任 务 提 出 :了 解 自 己 与 人 交 往 的 现 状 。
任 务 目 标 :了 解 自 己 与 人 交 往 的 现 状 ,激 发 学 习 热 情 ,明 确 努
力方向。
喜欢独来独往。
(3) 嫉 妒 心 理 。 部 分 大 学 生 不 能 正 确 对 待 别 人 的 长 处 和 优
点,看到别人冒尖心里嫉妒,对比自己水平高的同学采取
讽 刺 、 挖 苦 、 打 击 、 嘲 笑 等 不 当 方 式 ,给 别 人 造 成 伤 害 ,严
重影响了同学之间的沟通。
上一页
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
y1a
y2a
y3a
荷载b:
p1b
p2b
p3b
y1b
y2b
y3b
情况1（先加载荷载a，然后加载荷载b）：
加荷载a：
1 Waa 2
pia
yia
1 2
pTa
ya
加荷载b：
Wbb
Wab
1 2
pTb
yb
pTb ya
总功为：
W1 Waa Wbb Wab
1 2
k m a 0 频2量个率、多由kkk余振回频21n.111方.代.率型.程.入方..，iii.特222程.mmm..通.征式.12n1常11方（可程1kkk0以.n（21.－222，.由.14.k称20.于）.－.为校.求iii.2223..mmm关）.核得.12n.于2，2解2系. 固以的统....有k获2正....n....个频得确固k率kk对性.2n1.有nnn.应。..频a的..的率.振.iii.222.振.mmm1幅..型12n.n向nn.a向2量量aaa{1an2。后1}.：.式aa，..11（可an1以0a-将16000、.aT任）一是、(1个一0固-n52有) k
pTa
ya
1 2
pTb
yb
pTb
ya
情况2（先加载荷载b，然后加载荷载a）：
加荷载b：
Wbb
1 2
pib
yib
1 2
pTb
yb
加荷载a：
Waa
Wba
1 2
pTa
ya
pTa yb
总功为：
W2 Wbb Waa Wba
1 2
第1章多自由度体系自由振动分 析
结构动力特性分析－特征值问题的性质 由于将式（（101－0－5）6b式）振对幅应向方量程除组以是a确1后定，的可，以可按以以从下中红解线得将n-系1个数未矩知阵量[k]：
a2/和a1振、幅a3/向a1、量…划、分a为n/a子1，矩因阵此表可示以：得到对应方程（10－5）的一组振幅向
振型矩阵：
所有n个标准振型向量构成了一个方阵[Φ]:
2 ... n
1
2
...
n
2
...
22
...
...
n
2
... ...
n
n1ቤተ መጻሕፍቲ ባይዱ
...
nn
称为振型矩阵。
多自由度体系动力特性分析（举例）
如图所示结构，E=2.6x107kN/m2，
k12 k21 312 EI / 43 9EI /16
则质量阵和刚度阵为
m
60
0
0 40
k
35/ 48 EI 9 /16
9 /16
9 /16
k11
k22
Δ1＝1
k12
频率方程为： km 0 35EI / 48 60
荷载，振型即为惯性力荷载作用引起的
位移（如右图所示）。对此体系应用
Betti定理：
fI Tmn
f
I
T n
m
(I)
由于惯性力向量可表达为：
fI m m2 mm
f
I
n
n2 m n
将此代入式(I)，并注意[m]对称性，得：
振型“n”: fI1n
fI 2n
fI 3n
振型 “m”:
振型2（令 2 a2 1T ）：
35EI / 48 602 a2 9EI /16 0
a2 0.751 1 a2 1T 0.751 1T
振型正交性（1）Betti定理
荷载a:
p1a
p2a
p3a
Betti定理：若一结构分别受两种荷载体系作 用并引起了相应的位移，则荷载体系1在荷 载体系2对应位移上所作的功等于荷载体系2 在荷载体系1对应位移上所作的功。
e3n
........
en2
en3
...
enn
标准振型：
通常固有频率 对应k2的振幅向量（振型）用其无量纲形式给出，将{a}中 各分量均除以它的最大分量，即得到第k 标准振型：
k k
2k
...
T nk
式中：φik表示第k振型曲线中第 i 自由度对应的无量纲化位移。
pTb
yb
1 2
pTa
ya
pTa
yb
由于结构变形与加载次序无关，因 此在两种情况下荷载作功应相等：
W1 W2
pTa yb pTb ya
振型正交性（2）利用Betti定理证明振型正交性
如将自由振动看作由惯性力引起的变
形，将两个振型对应的惯性力作为施加
各柱尺寸0.6x0.6m.
4m
求自振频率和振型。
解：用刚度法得
6m
k11 312 EI 1/ 63 1/ 43 35EI / 48
k22 312 EI / 43 9EI /16
EI=∞ m2=40t EI=∞ m1=60t
1.0 0.887
k21
1.0 0.751
Δ2＝1
9EI /16 0
9EI /16 9EI /16 40
由频率方程解得： 445 .35 6915 .93
振型1（令 1 a1 1T ）：
35EI / 48 60 a1 9EI /16 0
a1 0.887 1 a1 1T 0.887 1T
k 00 e11 k 01 e12 e22 ... e1n k 10 e21 e31 ... en1 T
(10-6a)
(10-6b)
e22 e23 ... e2n
k 11
e32
.......
e33 ... ....... ...
上式中，由于系数矩阵
量除以a1，并记 拆分为两个独立的系列：
eij kij k2mij
k 的行i2 列m以a式及为 零a2，/ a因1 此a是3 /不a1定，方.式..程(1a。0n－对/ a5振1)可T幅以向
式中：
k00 k01a 0 k10 k11a 0