材料力学答案第六章
材料力学习题第六章应力状态答案详解.
(1)电阻片沿图示 方向粘贴于轴的表面,设
(2)取单元体如图,
16、如图所示,薄壁圆筒受扭矩和轴向力作用。已知圆筒外径D=52mm,壁厚t=2mm,外力偶矩m=600 ,拉力F=20kN。试用单元体表示出D点的应力状态;求出与母线AB成 角的斜截面上的应力;求出该点的主应力与主平面位置(并在单元体上画出)。
7、广义胡克定律适用范围,有下列四种答案,正确答案是(C)。
(A)脆性材料;(B)塑性材料;
(C)材料为各向同性,且处于线弹性范围内;(D)任何材料;
8、三个弹性常数之间的关系: 适用于(C)。
(A)任何材料在任何变形阶级;(B)各向同性材料在任何变形阶级;
(C)各向同性材料应力在比例极限范围内;(D)任何材料在弹性变形范围内。
解析:在推导公式过程中用到了虎克定律,且G、E、v为材料在比例极限内的材料常数,故适应于各向同性材料,应力在比例极限范围内
9、点在三向应力状态中,若 ,则关于 的表达式有以下四种答案,正确答案是(C)。
(A) ;(B) ;(C)0;(D) 。
解析:
10、图示单元体处于纯剪切应力状态,关于 方向上和线应变,现有四种答案,正确答案是(C)。
5、对于图示三种应力状态(a)、(b)、(c)之间的关系,有下列四种答案,正确答案是(D)。
(A)三种应力状态均相同;(B)三种应力状态均不同;
(C)(b)和(c)相同;(D)(a)和(c)相同;
6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是(B)。
解答: 发生在 成 的斜截面上
(A)等于零;(B)大于零;(C)小于零;(D)不能确定。
解析:
11、图示应力状态,现有四种答案,正确答案是(B)。
第二版《材料力学》第六章至第九章习题解答-(华中科大版-倪樵主编)

2 z
W
M
2 x
W2
[ ]
7-17 图示直角曲拐,C端受铅垂集中力F作用。已知a=160mm,AB杆直径D=40mm,
l=200mm ,E=200GPa, μ=0.3,实验测得D点沿45º方向的线应变 ε45º=0.265 × 10-3。试求:
(1)力F的大小;(2)若AB杆的[σ]=140MPa,试按最大切应力理论校核其强度。
T Wp
16 M 0
D3
16 125 .6
0.023
79.96MPa
单元体可画成平面单元体如图(从上往下观察)
A
6-5 试用求下列各单元体中ab面上的应力(单位MPa) 。
解:(a)
x 70
y 70
xy 0
30
x
y
2
x
y
2
cos(2 30 )
70 1 2
35
(MPa)
x y sin(2 30 ) 70
2
3 60.62 (MPa) 2
(b)
x 70
y 70
xy 0
30
x
y
2
x
y
2
cos(2 30 )
70
(MPa)
x
y
2
sin(2 30 )
0
6-6 各单元体的受力如图所示,试求:(1)主应力大小及方向并在原单元体图上绘出主 单元体;(2)最大切应力(单位MPa) 。
解: (3) My 、Mz、Mx 和F 同时作用,拉弯扭组合,任一截 面D1点是危险点
应力状态:
D1
FN M F
M
2 y
M
2 z
y
AW A
材料力学习题册答案_第6章_弯曲变形

得 x=0.519l
所以
W
m
ax
=0.00652
ql 4 EI
3 用叠加法求如图 7 所示各梁截面 A 的挠度和转角。EI 为已知常数。
解 A 截面的挠度为 P 单独作用与 M 0 单独作用所产生的挠度之和。 查表得:
y AP
Pl 3 24 EI
y = M 0l 2 Pl 3
AM 0
8EI
度 y = Fl 3 。 C 32 EI
4. 如图 4 所示两梁的横截面大小形状均相同,跨度为 l , 则两梁的力 图 相同 ,两梁的变形 不同 。(填“相同”或“不同”)
5. 提高梁的刚度措施有 提高Wz 、 降低 M MAX 等。 四、计算题 1 用积分法求图 5 所示梁 A 截面的挠度和 B 截面的转角。
8EI
y y 则 y A
AP
= Pl 3
AM0 12 EI
同理,A 截面的转角为 P 单独作用与 M 0 单独作用所产生的转角之和。
查表得
AP
Pl 2 8EI
对于 AM0 可求得该转角满足方程 EI =-Plx+C 边界条件 x=0 0 可得 C=0
现 4 个积分常数,这些积分常数需要用梁的 边界 条件和 光滑连
续 条件来确定。
2. 用积分法求图 2 所示梁变形法时,边界条件为:YA 0,A 0,YD 0 ;
连续条件为:
YA
1
YA
2
,
B
1
B
2
,
YC3.
如图
3
所示的外伸梁,已知
B
截面转角
B
=
Fl 2 16 EI
,则 C 截面的挠
于零的截面处。
工程力学--材料力学(北京科大、东北大学版)第4版第六章习题答案

第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
材料力学课后标准答案

解:取轴向长为 的管分析:微元 上,作用力为
向分量 ,积分得
则: ,而
则:
题6-12图题6-13图
6-13长输水管受内压 ,管的内径为 , , ,用第四强度理论计算壁厚。(提示:可设管的轴向应变为零。)
解: ,数据代入,得:
,
所以
现已知
,
得
题6-5图
题6-6图题6-7图
6-6图示简支梁为 工字梁, , 。 点所在截面在集中力 的左侧,且无限接近 力作用的截面。试求: 点在指定斜截面上的应力; 点的主应力及主平面位置(用单元体表示)。
解: 所处截面上弯矩、剪力:
,
查型钢表后, 点以下表面对中性轴静矩:
,
同理,积分得
所以, 处转角为 ,为顺时针方向; 处挠度为 ,为竖直向下。
8-6试求图示各刚架 点的竖直位移,已知刚架各杆的 相等。
解: 段: ; 段上
由卡氏定理, 处的竖直位移
分段带入后面积分:
为正值,则与 同向,竖直向下
分析可知, 处已经作用有竖直方向的力,为了能利用卡氏定理解题, 处和竖杆中间处的 分别为
(压), (拉)
进而求得 (拉),由
求得:
8-3计算图示各杆件结构的变形能。
题8-3图
解: 首先求解 处的约束反力为
弯矩方程为:
则
分段积分:
解: 以逆时针方向为正,
,积分得
8-4试求图示各梁的 点的挠度的转角。
题8-4图
解: 以 点为 轴起点,结构的弯矩方程为:
则:
得
撤去 和 ,在 处作用逆时针向
《材料力学》第6章 简单超静定问题 习题解
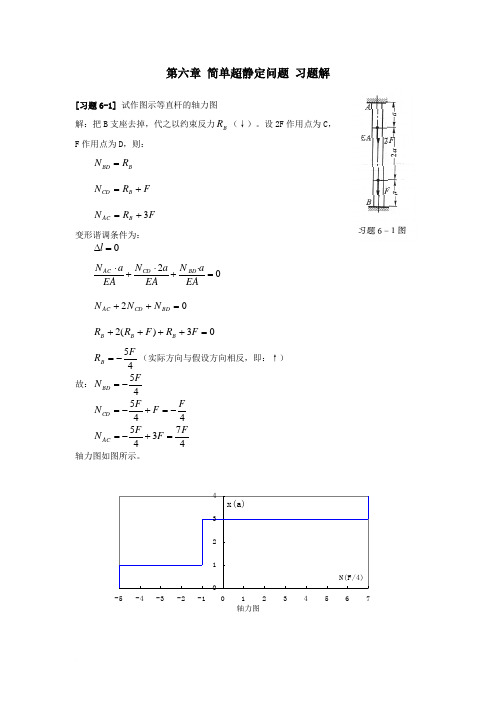
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第6章 圆轴扭转

习题 6-6 图
τ 套 max =
Mx Wp 2
T2 ≤ 60 × 10 6 ×
∴
Tmax ≤ T2 = 2883 N·m = 2.88 ×10 3 N·m
4
6-7 由同一材料制成的实心和空心圆轴,二者长度和质量均相等。设实心轴半径为 R0,空心圆轴的内、外半径分别为 R1 和 R2,且 R1/R2 =n;二者所承受的外加扭转力偶矩分 别为 Mes 和 Meh。若二者横截面上的最大剪应力相等,试证明:
该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6-5 图
解:1. τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2. M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3. τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
eBook
工程力学
(静力学与材料力学)
习题详细解答
(教师用书) (第 6 章) 范钦珊 唐静静
2006-12-18
1
第 6 章 圆轴扭转
工程力学--材料力学(北京科大、东北大学版)第4版第六章习题答案

第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六弯曲应力第六章答案6.1钢丝直径d=0.4mm, 弹性模量E=200GPa, 若将钢丝弯成直径D=400mm 的圆弧时,试求钢丝横截面上的最大弯曲正应力。
(200MPa ) 解:钢丝的弯矩和中性层曲率半径之间的关系为:EIM =ρ1则: ρEIM =,由弯曲正应力公式得ρσmaxmax My ==ρmaxEy ,钢丝弯成圆弧后,产生的弯曲变形,其中性层的曲率半径22Dd D ≈+=ρ 2)2(maxD dE =σ==D Ed MPa 2004004.0102003=⨯⨯6.2 矩形截面梁如图所示。
b = 8cm, h =12cm, 试求危险截面上a 、c 、d 三点的弯曲正应力。
(20.8MPa, 10.4MPa, 0) 解:由平衡方程0)(=∑F M A得到: KN F F B A 44221=⨯⨯== 危险截面在梁的中点处:KNm ql M 442818122max =⨯⨯==I z =1212h b ⨯⨯=44310115212080121mm ⨯=⨯⨯MP a I My MPa I MyI My z d d z c c za a 83.201011526010442.101011523010404646=⨯⨯⨯===⨯⨯⨯====σσσA F BF s F MM机械土木6.3 从直径为d 的圆木中截取一矩形截面梁,试根据强度观点求出所截取的矩形截面的最合理的高h 和宽b 。
(h=d 36, b=d 33) 解:最大弯曲正应力:zz W My I M m a x m a x m a x m a x ==σ h/b 的最佳值应应使梁的抗弯截面系数为最大。
抗弯截面系数: )(61)(616132222b b d b d b bh W -=-==为b 为自变量的函数。
由 06322=-=b d dt dW 36 333222db d h d d b =-===6.4 图示两根简支梁,其跨度、荷载及截面面积都相同。
一个是整体截面梁,另一个是由两根方木叠置而成(二方木之间不加任何联系),试画出沿截面高度的弯曲正应力分布图,并分别计算梁中的最大弯曲正应力。
(32a16ql 3,32a8ql 3)解:做出梁的弯矩图如右所示:(1)对于整体截面梁: 32232)2(3161a a a bh W z =⋅==故:3232maxmax 1633281a ql a qlW M z===σ (2)对于两根方木叠置由于这是两个相同的方木叠合而成, 且其之间不加任何的联系,故有32163a ql 32163a ql M1机械土木M 8323211max3max 218361)81(21,61,21a ql a ql W M a W M M M z z =⋅=====σ 6.5 某梁的矩形截面如图,弯曲剪力Q y =40kN ,求截面上a 、b 、c 三点的弯曲剪应力。
(MPa 2a =τ,MPa 5.1b =τ,0c =τ)解:从图形上可以看出截面形心在其对称中心上, 且有483310200150121121mm bh I z =⨯⨯==3510625.57515050mm S z ⨯=⨯⨯=再有矩形截面梁的弯曲正应力bI S F z z S *=τ ,故 ,0=c τ 0.2200150104023233=⨯⨯⨯=⨯=A F S a τ MPa 5.11501010625.51040853=⨯⨯⨯⨯==*b I S F z z S b τ MPa 6.6 图示简支梁由三块木板胶合而成,l=1m, 胶缝的许用剪应力为[]MPa 5.0=τ,木材的许用弯曲正应力为[]MP a 10=σ,许用剪应力为[]MPa 1=τ,试求许可荷载P 。
(P=8.1kN )解:依题给条件,对梁进行受力分析, 由平衡条件,列平衡方程,做出剪力图和弯矩图如右所示 (1)按木材弯曲正应力强度要求确定许可荷载[]101209061141412max max=≤⨯⨯⨯===σσP WPl W MN P 8640≤⇒ (2)按木材剪应力强度要求确定许可荷载 []112090212323max =≤⨯⨯=⨯=ττPA F SN P 14400≤⇒s F P Pl 1M2P Pl 4机械土木(3)按胶合面剪应力强度要求确定许可荷载[]5.09012090121)409040(21'3'=≤⨯⨯⨯⨯⨯⨯==*ττP bI SF z z SN P 8100≤⇒综上所述可知 P=8100N=8.1KN6.7 在图a 中,若以虚线所示的纵向面和横向面从梁中截出一部分,如图b 所示,试求在纵向面abcd 上由dA τ组成的内力系的合力,并说明它与什么力平衡。
(Q=x )x l (h4q3-) 解:有剪应力互等定律可知,纵向截面 上剪应力与横向截面上剪应力大小相等, 中性层上剪应力变化规律为:()()()Bh x l q Bh qx ql A x F x S 423 221323-=⎪⎭⎫ ⎝⎛-==τ纵截面abcd 上剪应力合力为:()()()hx l qx dx B Bhx l q dx B x F xx 423 4230-=⋅-=⋅=⎰⎰τ6.8 图示梁由两根36a 工字钢铆接而成。
铆钉的间距为s=150mm, 直径d = 20mm, 许用剪应力[]MP a 90=τ。
梁横截面上的剪力F s = 40kN 。
试校核铆钉的剪切强度。
(MPa 2.16=τ) 解:查表可得,36a 工字钢的惯性矩 415800cm Ιz =,截面面积248.76cm =A 截面高度cm h 36=。
组合惯性矩为()()422812004876181580022cm .A d ΙΙz zc =⨯+=+=一根工字钢的截面对中性轴的静面矩为:3138048.7618cm S zc =⨯=*铆钉连接处的纵截面上的剪力流: m KN I S F f zzc /6810812001013801040863=⨯⨯⨯⨯==--*有铆钉间距 fQ S 铆2=,得每个铆钉承受的剪力为:a 'a 'b 'cd2h)()x τN sf Q 51002106815.023=⨯⨯==铆 铆钉的剪应力: 2.1614.3412=⨯⨯=d Q 铆τMPa < []τ=90 Mpa故,校核安全。
6.9 半径为r 的圆形截面梁,切掉画阴影线的部分后,反而有可能使抗弯截面模量增大(何故?)。
试求使W 为极值的α,并问这对梁的抗弯刚度有何影响?(O 78=α)解:切掉阴影部分后剩余的面积,是由4个相同的直角三角形和4个相同的扇形面积组成,一个直角三角形面积对水平直径的惯性矩为:()()a a r a r a r bh I x 33331sin cos 41cos sin 4141⋅===一个扇型面积对水平直径的惯性矩为:()()⎪⎭⎫⎝⎛-=⋅=⋅⋅=⋅=⎰⎰⎰⎰⋅a a r d d d d dAy I rarAx sin 4124sin sin 4023222θθρρρθρθρ因为圆截面在中性轴附近聚集了较多的材料而离中性轴远处的材料却较少,当切掉适当的小弓形面积后,使之离中性轴远处的材料密集度增大,因而抗弯截面系数笔增大。
剩余面积对水平直径的惯性矩为:()a a r a a r a a r I I I xx x 4sin 48sin cos 2sin 41244434421-=⋅+⎪⎭⎫ ⎝⎛-=+=抗弯截面系数: ()()aa a r a a a y I W xx s i n 84s i n 4s i n 44s i n 4813m a x -=-== ()()()()7800cos 4sin 4sin 4cos 440sin cos sin 4sin cos 4482443==⇒=---⇒=⎥⎦⎤⎢⎣⎡---=a a a a a a a a a a a a a r da dW x 或者3max 791.0r W x =, 4774.0r I x =未切前 4433785.014.341785.014.341r r I r r W x x =⨯⨯==⨯⨯=比较后可知,切后抗弯截面系数增大,而抗弯刚度降低,因而使梁的抗断能力提高,抗弯曲变形能力降低6.10 试求图示梁的最大弯曲正应力和最大弯曲剪应力。
(提示:max τ发生在中性轴上。
)(MPa 00.9max =σ,MPa 05.1max =τ)解:KN ql F s 1523102max ,=⨯==KNm ql M 25.118310822max =⨯==2*48448750002550100502001001025.1)100200(121mm S mm I z z =⨯⨯-⨯⨯=⨯=-=MPa y I M z 00.91001025.11025.1186max max max=⨯⨯⨯==σMPa bI S F z zs 05.11001025.1875000101583*max ,max =⨯⨯⨯⨯==τ6.11 图示铸铁梁,材料的许用拉应力[]MPa 40t =σ,许用压应力[]MPa 100c =σ,4z cm 5965I =,mm 5.157y C =。
试校核梁的强度。
(MPa 8.52max c =σ,MPa 4.26max t =σ)KN F A 30452104120=⨯⨯+⨯=KN F B 10412104320=⨯⨯-⨯=KNm M KNm M 10,2021== mmy 5.725.1572301=-=sF M1AF BF 1y sF MM 机械土木A F BFMPa y I M MPa y I M MPa y I M MPa y I M c z cz t c z cz t16.125.72105965101040.265.157105965101081.525.157105965102031.245.721059651020461max,24611max ,2461max,14611max ,1=⨯⨯⨯===⨯⨯⨯===⨯⨯⨯===⨯⨯⨯==σσσσ][40.26][81.52max ,max ,t t c c MPa MPa σσσσ≤=≤=6.12 图示一铸铁梁,材料的许用拉应力与许用压应力之比为[][]3/1/c t =σσ,试求水平翼缘板的合理宽度b 。
(b=316mm )170230170303034060)602340(3034030601+⨯+=⨯+⨯+⨯⨯+⨯⨯=b b b b y 1701701703701702301703040040012+⨯+=+⨯+-=-=b b b b y y][][2max ,1max ,c zc t zt y I My I Mσσσσ====][][21c t y y σσ=m mb b b b b 72.31590370170170690170690170901701703703117017037023017030=-⨯-⨯=⨯+=⨯+=⨯+⨯+6.13 图所示矩形截面悬臂梁,承受载荷 F y 和 F z 作用,且F y = F z = F = 1.0 kN,截面高度h = 80 mm ,宽度b = 40 mm ,许用应力[]MPa 160=σ,a = 800 mm 。
