计量经济学:时间序列模型习题与解析
计量经济学:时间序列模型习题与解析

计量经济学:时间序列模型习题与解析第九章时间序列计量经济学模型的理论与⽅法练习题1、请描述平稳时间序列的条件。
2、单整变量的单位根检验为什么从DF检验发展到ADF检验?23、设X t cost si n t,0 t 1,其中,是相互独⽴的正态分布N(0, )随机变量,是实数。
试证:{x t,0 t 1}为平稳过程。
LB5、利⽤4中数据,⽤ADF法对居民消费总额时间序列进⾏平稳性检验。
6、利⽤4中数据,对居民消费总额时间序列进⾏单整性分析。
7、根据6中的结论,对居民消费总额的差分平稳时间序列进⾏模型识别。
8、⽤Yule Walker法和最⼩⼆乘法对7中的居民消费总额的差分平稳时间序列进⾏时间序列模型估计,并⽐较估计结果。
9、有如下AR(2)随机过程:X t 0.1X t1 0.06X t 2 t该过程是否是平稳过程?10、求MA(3)模型y t 1 u t 0.8u t 1 0.5u t 2 0.3u t 3的⾃协⽅差和⾃相关函数。
11、设动态数据x10.8,x20.7, x3 0.9, x4 0.74, x5 0.82,x6 0.92, x7 0.78,X8 0.86, X9 0.72, X10 0.84,求样本均值x,样本⽅差?。
,样本⾃协⽅差?、?2和样本⾃相关函数?1、?2。
12、判断如下ARMA过程是否是平稳过程:x t 0.7x t 1 0.1x t 2 t 0.14 t 113、以Q t表⽰粮⾷产量,A t表⽰播种⾯积,C t表⽰化肥施⽤量,经检验,他们取对数后都是I (1)变量且相互之间存在CI( 1,1)关系。
同时经过检验并剔除了不显著的变量(包括滞后变量),得到如下粮⾷⽣产模型:In Q o In Q [ 21n A t 31n C t 4In C t 1 t推导误差修正模型的表达式,并指出误差修正模型中每个待估参数的经济意义。
14、固定资产存量模型K t 0 1K t 1 2I t 3I t 1 t中,经检验,K t ~ I (2), 11 ~ I (1),试写出由该ADL模型导出的误差修正模型的表达式。
第十章时间序列计量经济学课后题
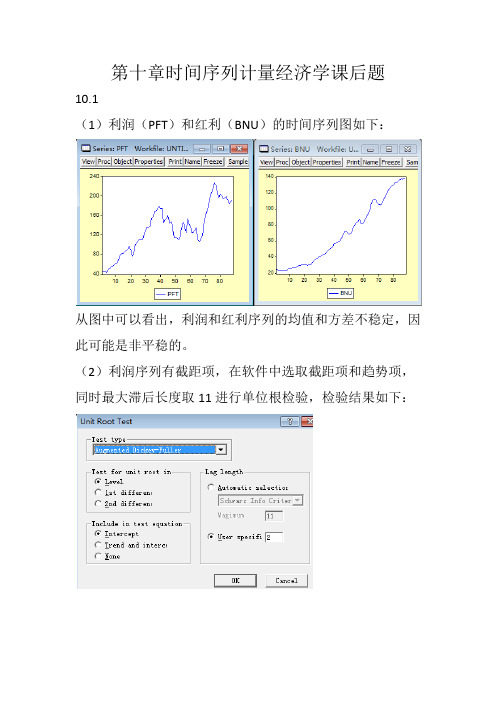
第十章时间序列计量经济学课后题10.1(1)利润(PFT)和红利(BNU)的时间序列图如下:从图中可以看出,利润和红利序列的均值和方差不稳定,因此可能是非平稳的。
(2)利润序列有截距项,在软件中选取截距项和趋势项,同时最大滞后长度取11进行单位根检验,检验结果如下:如图可知,t检验统计量值-1.602658大于相应临界值-3.509281,-2.895924,-2.585172,从而不能拒绝H0,表明利润(PFT)序列存在单位根,是非平稳序列。
红利序列有截距项,在软件中选取截距项,同时最大滞后长度取11进行单位根检验,检验结果如下:如图可知,t统计量值0.671989大于相应临界人,从而表明红利序列存在单位根,是非平稳序列。
10.3(连着10.1继续做)(1)回归的结果是虚假的。
回归结果如下:如图所示,根据Granger和Newbold提出的一个经验型规则,档R^2大于DW时,所估计的回归式就存在虚假回归。
本题中R^2=0.6214远远大于DW=0.0833,说明所估计的回归式存在伪回归。
(2)一阶差分时间序列结果如下:T统计量值小于所有显著水平以下的对应临界值,从而拒绝H0,表明利润的差分序列不存在单位根,是平稳序列。
如图所示,T统计量值小于所有显著水平以下的对应临界值,从而拒绝H0,表明红利的差分序列不存在单位根,是平稳序列。
10.2X序列有截距项,在软件中选取截距项和趋势项,同时最大滞后长度取11进行单位根检验,检验结果如下:如图可知,t统计量值-1.097564大于相应临界值,从而表明销售量序列存在单位根,是非平稳序列。
固定厂房设备投资(Y)序列有截距项,在软件中选取截距项和趋势项,同时最大滞后长度取11进行单位根检验,检验结果如下:如图可知,t统计量值-0.21627大于相应临界值,从而表明固定厂房投资设备序列存在单位根,是非平稳序列。
10.5(1)税收和财政收入时间序列图如下:lnY序列有截距项,在软件中选取截距项和趋势项,同时最大滞后长度取11进行单位根检验,检验结果如下:如图可知,t统计量值1.0945大于相应临界值,从而表明财政收入序列存在单位根,是非平稳序列。
第九章时间序列计量经济学模型案例

第九章时间序列计量经济学模型案例1、1949—2001年中国人口时间序列数据见表8,由该数据(1)画时间序列图和差分图;(2)求中国人口序列的相关图和偏相关图,识别模型形式;(3)估计时间序列模型;(4)样本外预测。
表9.1 中国人口时间序列数据(单位:亿人)年份人口y t 年份人口y t年份人口y t年份人口y t年份人口y t 1949 5.4167 1960 6.6207 1971 8.5229 1982 10.159 1993 11.8517 1950 5.5196 1961 6.5859 1972 8.7177 1983 10.2764 1994 11.985 1951 5.63 1962 6.7295 1973 8.9211 1984 10.3876 1995 12.1121 1952 5.7482 1963 6.9172 1974 9.0859 1985 10.5851 1996 12.2389 1953 5.8796 1964 7.0499 1975 9.242 1986 10.7507 1997 12.3626 1954 6.0266 1965 7.2538 1976 9.3717 1987 10.93 1998 12.4761 1955 6.1465 1966 7.4542 1977 9.4974 1988 11.1026 1999 12.5786 1956 6.2828 1967 7.6368 1978 9.6259 1989 11.2704 2000 12.6743 1957 6.4653 1968 7.8534 1979 9.7542 1990 11.4333 2001 12.7627 1958 6.5994 1969 8.0671 1980 9.8705 1991 11.58231959 6.7207 1970 8.2992 1981 10.0072 1992 11.7171(1)画时间序列图y的数据窗口打开t得到中国人口序列图求中国人口差分图:中国人口差分图如下:从人口序列图和人口差分序列图可以看出我国人口总水平除在1960年和1961年两年出现回落外,其余年份基本上保持线性增长趋势。
计量经济学试题时间序列分析与ARIMA模型

计量经济学试题时间序列分析与ARIMA模型计量经济学试题:时间序列分析与ARIMA模型1. 引言时间序列分析是计量经济学中重要的分析方法之一,能够揭示变量随时间变化的规律,并为未来趋势的预测提供依据。
ARIMA模型(差分自回归滑动平均模型)是时间序列分析中常用的模型之一,具有较强的建模和预测能力。
本文将介绍时间序列分析方法以及ARIMA模型的理论基础,并通过试题案例讲解其具体应用。
2. 时间序列分析方法概述时间序列是按时间顺序排列的一系列数据点,其特点是数据之间存在一定的时间关联性和趋势性。
时间序列分析方法可用于研究时间序列的规律,并对未来的变化进行预测。
常用的时间序列分析方法包括:平稳性检验、自相关函数(ACF)和偏自相关函数(PACF)的分析、白噪声检验、差分运算等。
3. ARIMA模型的基本原理ARIMA模型是一种广义的线性时间序列模型,它结合了自回归(AR)模型、差分(I)运算和滑动平均(MA)模型。
ARIMA模型的建立一般包括以下几个步骤:确定时间序列的平稳性、确定模型的阶数、拟合模型参数、模型检验与预测。
4. 时间序列分析与ARIMA模型的应用案例以某工业品生产量的时间序列数据为例,我们来演示时间序列分析与ARIMA模型的具体应用过程。
4.1 数据准备与描述性分析首先,我们收集了过去36个月的某工业品生产量数据,用于进行时间序列分析和ARIMA建模。
通过对数据的描述性统计分析,我们可以了解数据的分布特征、趋势以及季节性等信息。
4.2 平稳性检验为了应用ARIMA模型,首先需要检验时间序列的平稳性。
我们可以使用单位根检验(ADF检验)等方法判断时间序列是否平稳。
若时间序列不平稳,需要进行差分操作,直至得到平稳序列。
4.3 确定模型的阶数在ARIMA模型中,AR阶数表示自回归模型中的滞后阶数,MA阶数表示滑动平均模型中的滞后阶数。
通过观察自相关函数ACF和偏自相关函数PACF的图像,可以确定ARIMA模型的阶数。
时间序列第2-3章习题解答

样本自相关系数图
1.2 1
0.8 0.6 0.4 0.2
0 -0.2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 -0.4 -0.6 -0.8
-1
自相关系数如下:
延迟
1
2
3
4
.4570 0.0812 -0.3201 -0.6188 -0.7210 -0.6293 -0.3396
从差分序列时序图看,该系列是平稳的。从样本自相关图可见,自相关系数具有短期的 自相关性,然后快速衰减,故该差分系列是平稳的。
纯随机检验如下: 延迟 6 12 18 24
LB 统计量值 29.46 35.94 38.61 57.43
P值 <0.001 <0.001 <0.01 <0.001
P 值都非常小,表明该序列不是纯随机序列。
解 由于 =
解得 = , = 。
,
,即
=
,且
,
,
,
3. 已知某 AR(2)模型为: , ,其中 , , 。
解 模型改写为:
于是
;
又由
解得
, =
,
,求 ,
,
,
,
;
,即
,
,
,
4. 已知 AR(2)序列为:
,其中 为白噪声序列。确定 的取值范围,
以保证 为平稳序列,并给出该序列 的表达式。
解 由 AR(2)的平稳域知, 满足:
故该可逆的中心化 MA(1)模型为: +
,求该模型的表达式。 或
8. 确定常数 的值,以保证如下表达式为 MA(2)模型:
计量经济学 时间序列
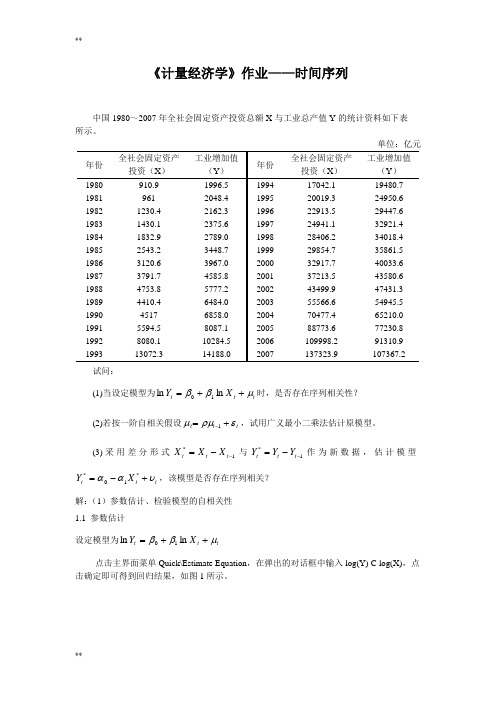
《计量经济学》作业——时间序列中国1980~2007年全社会固定资产投资总额X 与工业总产值Y 的统计资料如下表所示。
单位:亿元 年份 全社会固定资产投资(X )工业增加值(Y ) 年份 全社会固定资产投资(X )工业增加值(Y ) 1980 910.9 1996.5 1994 17042.1 19480.7 1981 961 2048.4 1995 20019.3 24950.6 1982 1230.4 2162.3 1996 22913.5 29447.6 1983 1430.1 2375.6 1997 24941.1 32921.4 1984 1832.9 2789.0 1998 28406.2 34018.4 1985 2543.2 3448.7 1999 29854.7 35861.5 1986 3120.6 3967.0 2000 32917.7 40033.6 1987 3791.7 4585.8 2001 37213.5 43580.6 1988 4753.8 5777.2 2002 43499.9 47431.3 1989 4410.4 6484.0 2003 55566.6 54945.5 1990 4517 6858.0 2004 70477.4 65210.0 1991 5594.5 8087.1 2005 88773.6 77230.8 1992 8080.1 10284.5 2006 109998.2 91310.9 1993 13072.314188.02007137323.9107367.2试问:(1)当设定模型为t t t X Y μββ++=ln ln 10时,是否存在序列相关性? (2)若按一阶自相关假设t t t ερμμ+=-1,试用广义最小二乘法估计原模型。
(3)采用差分形式1*--=t t t X X X 与1*--=t t t Y Y Y 作为新数据,估计模型t t t X Y υαα+-=*10*,该模型是否存在序列相关?解:(1)参数估计、检验模型的自相关性 1.1 参数估计设定模型为t t t X Y μββ++=ln ln 10点击主界面菜单Quick\Estimate Equation ,在弹出的对话框中输入log(Y) C log(X),点击确定即可得到回归结果,如图1所示。
计量经济学题库第12章时间序列模型

第12章 时间序列模型习 题一、问答题1.ARMA 模型的建模思想、特点。
2.噪声过程 3. 平稳过程4.对于如下AR(2)随机过程:,该过程是否是平稳过程?5.对于MA(3)过程,求的自协方差和自相关函数。
6.判断ARMA 过程的平稳性。
7.判断ARMA 过程的可逆性。
二、计算题1.以下为我国手机拥有量(万户)的月度数据(1999年4月-2008年2月)。
表1 我国手机拥有量(万户)的月度数据(万户)时间 数量 时间 数量时间 数量 时间 数量 时间 数量 时间1999-04 2824.5 2000-12 7086 2002-08 18485.5 2004-04 29575 2005-12 39342.8 2007-1999-05 2978.6 2001-0189762002-09 19039.1 2004-05 30055.9 2006-01 39879.9 2007-1999-06 3109.4 2001-02 9490.7 2002-10 19583.3 2004-06 30528.3 2006-02 40407.2 2007-1999-07 3489.4 2001-03 10031.4 2002-11 20031.3 2004-07 31021.8 2006-03 40969.3 2007-1999-08 3619.4 2001-04 10519.8 2002-12 20661.6 2004-08 31510 2006-04 41664.4 2007-1999-09 3759.5 2001-05 11108 2003-01 21243.9 2004-09 32007.1 2006-05 42082.3 2008-1999-10 3992 2001-06 11676.1 2003-02 21639.8 2004-10 32503.4 2006-06 42637.1 2008-1999-11 4198.4 2001-07 12060.5 2003-03 22149.1 2004-11 32992.4 2006-07 43179.9 1999-12 4323.8 2001-08 12577.4 2003-04 22571.7 2004-12 33482.4 2006-08 43747.5 2000-01 4502 2001-09 13091 2003-05 23005.6 2005-01 33979.6 2006-09 44315.4 2000-02 4772 2001-10 13601.9 2003-06 23447.2 2005-02 34407.3 2006-10 44902.1 2000-03 5015 2001-11 13992.2 2003-07 23945.9 2005-03 34905 2006-11 45503 2000-04 5295 2001-12 14481.2 2003-08 24411.8 2005-04 35371.1 2006-12 46108.2 2000-05 5605.9 2002-01 14990.9 2003-09 24997.4 2005-05 35854.8 2007-01 46741 2000-06 5929 2002-02 15585.2 2003-10 25693.8 2005-06 36316.8 2007-02 47392.9tt t t X X X ε++=--2106.01.03213.05.08.01---+-++=t t t t t u u u u y ty 12114.01.07.0----+-=t t t t t x x x εε12114.01.07.0----+-=t t t t t x x x εε2000-07 6117 2002-03 16150 2003-11 26347.8 2005-07 36801.5 2007-03 48065.2 2000-08 6319 2002-04 16664.8 2003-12 26869.3 2005-08 37277.6 2007-04 48743.4 2000-09 6506 2002-05 17138 2004-01 27680.2 2005-09 37792.4 2007-05 49459.6 2000-10 6723 2002-06 17616.9 2004-02 28232.7 2005-10 38304.2 2007-06 50164.8 2000-11 6939 2002-07 18031.8 2004-03 29030.5 2005-11 38816.1 2007-07 50856.4数据来源:中经网数据库。
计量经济学:时间序列模型习题与解析(1)复习课程
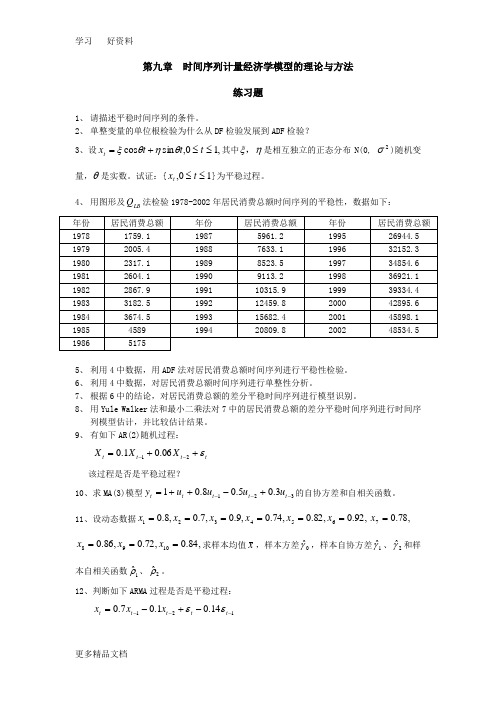
第九章 时间序列计量经济学模型的理论与方法练习题1、 请描述平稳时间序列的条件。
2、 单整变量的单位根检验为什么从DF 检验发展到ADF 检验?3、设,10,sin cos ≤≤+=t t t x t θηθξ其中ηξ,是相互独立的正态分布N(0, 2σ)随机变量,θ是实数。
试证:{10,≤≤t x t }为平稳过程。
4、 用图形及LB Q 法检验1978-2002年居民消费总额时间序列的平稳性,数据如下:5、 利用4中数据,用ADF 法对居民消费总额时间序列进行平稳性检验。
6、 利用4中数据,对居民消费总额时间序列进行单整性分析。
7、 根据6中的结论,对居民消费总额的差分平稳时间序列进行模型识别。
8、 用Yule Walker 法和最小二乘法对7中的居民消费总额的差分平稳时间序列进行时间序列模型估计,并比较估计结果。
9、 有如下AR(2)随机过程: t t t t X X X ε++=--2106.01.0 该过程是否是平稳过程?10、求MA(3)模型3213.05.08.01---+-++=t t t t t u u u u y 的自协方差和自相关函数。
11、设动态数据,92.0,82.0,74.0,9.0,7.0,8.0654321======x x x x x x ,78.07=x,84.0,72.0,86.01098===x x x 求样本均值x ,样本方差0ˆγ,样本自协方差1ˆγ、2ˆγ和样本自相关函数1ˆρ、2ˆρ。
12、判断如下ARMA 过程是否是平稳过程:12114.01.07.0----+-=t t t t t x x x εε13、以t Q 表示粮食产量,t A 表示播种面积,t C 表示化肥施用量,经检验,他们取对数后都是I (1)变量且相互之间存在CI (1,1)关系。
同时经过检验并剔除了不显著的变量(包括滞后变量),得到如下粮食生产模型:t t t t t t C C A Q Q μααααα+++++=--1432110ln ln ln ln ln推导误差修正模型的表达式,并指出误差修正模型中每个待估参数的经济意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章时间序列计量经济学模型的理论与方法练习题1、请描述平稳时间序列的条件。
2、单整变量的单位根检验为什么从DF检验发展到ADF检验?23、设X t cost si n t,0 t 1,其中,是相互独立的正态分布N(0, )随机变量,是实数。
试证:{x t,0 t 1}为平稳过程。
LB5、利用4中数据,用ADF法对居民消费总额时间序列进行平稳性检验。
6、利用4中数据,对居民消费总额时间序列进行单整性分析。
7、根据6中的结论,对居民消费总额的差分平稳时间序列进行模型识别。
8、用Yule Walker法和最小二乘法对7中的居民消费总额的差分平稳时间序列进行时间序列模型估计,并比较估计结果。
9、有如下AR(2)随机过程:X t 0.1X t1 0.06X t 2 t该过程是否是平稳过程?10、求MA(3)模型y t 1 u t 0.8u t 1 0.5u t 2 0.3u t 3的自协方差和自相关函数。
11、设动态数据x10.8,x20.7, x3 0.9, x4 0.74, x5 0.82,x6 0.92, x7 0.78,X8 0.86, X9 0.72, X10 0.84,求样本均值x,样本方差?。
,样本自协方差?、?2和样本自相关函数?1、?2。
12、判断如下ARMA过程是否是平稳过程:x t 0.7x t 1 0.1x t 2 t 0.14 t 113、以Q t表示粮食产量,A t表示播种面积,C t表示化肥施用量,经检验,他们取对数后都是I (1)变量且相互之间存在CI( 1,1)关系。
同时经过检验并剔除了不显著的变量(包括滞后变量),得到如下粮食生产模型:In Q o In Q [ 21n A t 31n C t 4In C t 1 t推导误差修正模型的表达式,并指出误差修正模型中每个待估参数的经济意义。
14、固定资产存量模型K t 0 1K t 1 2I t 3I t 1 t中,经检验,K t ~ I (2), 11 ~ I (1),试写出由该ADL模型导出的误差修正模型的表达式。
15参考答案1如果时间序列{X t}满足下列条件:1) 均值E(X t)与时间t无关的常数;2) 方差var(XJ o2与时间t无关的常数;3) 协方差cov(X t X t k) k只与时期间隔k有关,与时间t无关的常数。
则称该随机时间序列是平稳的。
2、在使用DF检验时,实际上假定了时间序列是由具有白噪声随机误差项的一阶自回归过程(AR(1))生成的。
但在实际检验中,时间序列可能是由更高阶的自回归过程生成的,或者随机误差项并非是白噪声,这样用OLS法进行估计均会表现出随机误差项出现自相关,导致DF检验无效。
另外,如果时间序列包含有明显的随时间变化的某种趋势(如上升或下降) ,则也容易导致上述检验中的自相关随机误差项问题。
为了保证DF检验中随机误差项的白噪声特性,Dicky和Fuller对DF检验进行了扩充,形成了ADF检验。
3、E ( X t)=cc )s tE( ) sin tE( )0r k E(X t 卜<X t) E{[ cos (t k) sin (t k)][ cos t sin t]}cos (t 2k)cos tE( ) sin (t 2k)sin tE( ) cos (t k)sin tE( ) sin (t 2[cos (t k)cos t sin (t k)sin t]2coskvar(X t) r0 2所以{ x t,0 t 1}为平稳过程k) cos tE()序列图表现出了一个持续上升的过程, 即在不同的时间段上, 其均值是不同的,因此可初步判断是非平稳的。
居民消费总额时间序列相关图及相关系数、Q LB 统计量:Autocorrelation Partial Correlation1 0.3G3 0.888 22.202 2 0.7B7 -0.105 99.4703 0.642 -0.007 52 1134 0,51 B -0.068 60.7295 0.391 -0.096 65.3355 0.260 4J.11D 63.269 7 0.130 -0.100 68 922 a 0.016 -0.034 G3.932 9 -0.075 -0.003 E9.170 10 -0.145 -0.006 70.117 11 -0.200 -0 025 72 042 12 -0.246 -0.052 75 180从图中可以看出,样本自相关系数是缓慢下降的,表明了该序列的非平稳性。
滞后12期的Q LB 统计量计算值为75.18,超过了显著性水平 5%时的临界值21.03,因此进一步否定了该 时间序列的自相关系数在滞后一期之后的值全部为 0的假设。
这样,结论是1978~2002年间居民消费总额时间序列是非平稳序列。
5、经过偿试,模型 3取了 3阶滞后:X t 894.85 195.14T 0.06X t 1 1.24 X t 10.78 X t 2 0.23 X t 3(-1.37)(2.17) (-1.68)(5.17 ) (-2.33)(0.94)DW 值为2.03,可见残差序列不存在自相关性,因此该模型的设定是正确的。
从X t 1的参数值看,其t 统计量的绝对值小于临界值绝对值,不能拒绝存在单位根的 零假设。
同时,由于时间AC PAC Q-Stat4、居民消费总额时间序列图:50000T的t统计量也小于ADF分布表中的临界值,因此不能拒绝不存在趋势项的零假设。
需进一步检验模型2 。
经试验,模型2中滞后项取 3 阶:X t 401.61 0.01X t 1 1.43 X t1 0.95 X t 2 0.30 X t 3(1.38 ) (0.33) (5.84) (-2.62) (1.14 )DW值为2.01,模型残差不存在自相关性,因此该模型的设定是正确的。
从X t1的参数值看,其t 统计量为正值,大于临界值,不能拒绝存在单位根的零假设。
同时,常数项的t 统计量也小于ADF分布表中的临界值,因此不能拒绝不存常数项的零假设。
需进一步检验模型1。
经试验,模型 1 中滞后项取 3 阶:X t 0.01X t 1 1.53 X t 1 1.02 X t 2 0.35 X t 3(0.63) (6.35) (-2.77) (1.29)DW值为1.99,残差不存在自相关性,因此模型的设定是正确的。
从X t 1的参数值看,其t统计量为正值,大于临界值,不能拒绝存在单位根的零假设。
至此,可断定居民消费总额时间序列是非平稳的。
6、利用ADF检验,经过试算,发现居民消费总额是2阶单整的,适当的检验模型为:3 2 33X t 0.854 2X t1 0.471 3X t 1( -3.87 ) (2.30 )Correlogram-Q-Statistics 检验证明随机误差项已不存在自相关。
从2X t 1的参数值看,其t 统计量绝对值 3.87 大于临界值的绝对值,所以拒绝零假设,认为居民消费总额的二阶差分是平稳的时间序列,即居民消费总额是2阶单整的。
7、居民消费总额经二阶差分后的新序列X2的样本自相关函数图与偏自相关函数图及数据如图所示:Adocorelation Partial CorrelationAC PAC而自相关函数是拖尾的,可认定该序列是一个 2阶自回归过程。
8、有如下 Yule Walker方程:? ■i1 10.41 0.41 ?■20.4110.23解为:?1 0.606, ?20.479用OLS 法回归的结果为:X2t0.617X2t 10.471X2t 2t(3.04)(-2.30)R 20.348 .—2R =0.313 DW.=2.082、、n > ■> I i i ] iI0.417 (二阶差分后样本数匚i > I i i■ ii|i1 0 410 0.4102 0.230 -0.473 3 ^0 412 -0.1204 -0.221 -0.0625 「0 093 ^0.2326 0 050 0.0540 110 -0.073 8 0 061 -0.075 g -0 101 -0/ 47 10 0 085 0.024 11 -0.014-0.094 12 0 033 ■0.Q47 13 -0.048 -0.150 14 「0 043 -0.042 15 0.059 0.037 1C 0 029 0192 17 0.0050.057代七007-0.10619 -0.002 -0.05620 0 0060,015 n 为23),偏自相关函数值的绝对值在k>2后均小于此值,加入常数项,回归如下式X2t 111.022 0.607X2t1 0.488X2t 2(0.62 ) (2.94 ) (-2.32 )2 2R =0.361 . R =0.291 DW.=2.119、1 0.1z 0.06z20特征方程为:(1 0.2z)(1 0.3z) 0z15, z210/3特征方程的根都在单位圆外,所以该过程是平稳的。
10、12、 X t 0.7x t 1 0.1x t 2 t 0.14 t 1ARMA 模型的平稳性取决于 AR 部分的平稳性。
对于 AR 部分,特征方程为:1 0.7z 0.1z 2乙 2,Z 25特征方程的根都在单位圆外,所以该 AR 过程是平稳的,可知 ARMA 过程也是平稳的。
13、In Q t In Q t ln Q t 10 ( 1 1) ln Q t 1 2 (ln A t In A t 1) 2ln A 1 3(ln C t In C t1)(34 ) ln C t 1 t2 lnA t3 lnC t (1 1)(lnQ t1 0J ln A t 13——ln C t 1) t1111 1 1短期播种面积变化1%将引起粮食产量变化 2%短期化肥施用量变化1%将引起粮食产量变化3% -( 1-1 )的大小反映了对偏离长期均衡的调整力度。
0 (1 2 122)23丿2[1 ( 0.8)21 ( 1 12 2 3)2[0.8 0.52(21 3) u2 [0.5 ( 0.3)(323 u0.3 u 2r k0,k :30 11 1 /r ° 0.1262 2 /r °0.13133/r 。
0.1520.8, 20.5, 30.30.52 ( 0.3)2] U 1.98 U 2 (0.8) 0.5 ( 0.3)] U 0.25 2 20.8)] u0.26 u11、1010 t 1 Xt0.8081 10 2(X t x) 0.00497610 t 1帚(X t10 t 1x)(X t X)0.0026784810t1(Xtx)(X tX) 0.0009712?1/ ?00.538 2?2 / ?0 0.19515、(1)、初步分析首先,将人均食品支出和人均年生活费收入消除物价变动的影响, 得到实际人均年食品支出 C 和实际人均年生活费收入Y ;然后对C 和Y 分别取对数,记c=lnC,y=lnY(2)、单整的单位跟检验容易验证lnC 与InGDP 是一阶单整的,它们适合的检验模型如下:2 2c t 0.736 c t 1( -4.723 )DW=2.032y t 0.425 y t 1 0.173 2y t 1 0.070 2 y t 2( -2.332 )DW=1.89在5%的显著性水平下,上述两方程的 ADF 检验临界值分别为-1.95与-1.95 。
