大学物理麦克斯韦速率分布律
合集下载
麦克斯韦速率分布
M1W1 M 2W2 M nWn
真实值
N足够大：平均值
----统计平均值 涨落：统计规律总伴随有涨落 N越大，涨落越小；N越小，涨落越大。 热学系统，N足够大，涨落很小。
二、麦克斯韦速率分布律
1、速率分布函数
按统计假设，各种速率下的分子都存在， 用某一速率区间内分子数占总分子数的百分比， 表示分子按速率的分布规律。 N: 总分子数 dN: 速率区间 v v dv 内的分子数
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 8.31 300 v 508m / s 3 29 10
2
3kT v m
§6. 麦克斯韦速率分布律/三.麦克斯韦速率分布律应用
【讨论题】： 1.如图所示，SA= SB，v0代表什么？
S A f (v ) dv
0
v0
f (v )
S B f ( v ) dv
总分子数的百分比; 也表示在速率 v 附近单位 速率间隔内分子出现的概率，即概率密度。
2) 速率分布曲线： 即 f(v)~v 曲线
dN f (v ) Ndv dN f (vdv
v
dN N
§6. 麦克斯韦速率分布律/ 二、麦克斯韦速率分布规律
3) 在 f(v)~v 曲线下的面积为该速率区间 内分子出现的概率。
dN 表示速率区间 v v dv 内的分子 ： N 数占总分子数的百分比，也表示在速率 区间 v dv 内分子出现的概率。 v
大学物理04第四章
第四章 气体动理论一、基本要求1．理解平衡态的概念。
2．了解气体分子热运动图像和理想气体分子的微观模型，能从宏观和统计意义上理解压强、温度、内能等概念。
3．初步掌握气体动理论的研究方法，了解系统的宏观性质是微观运动的统计表现。
4．理解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义，理解气体分子运动的最概然速率、平均速率、方均根速率的意义，了解玻尔兹曼能量分布律。
5．理解能量按自由度均分定理及内能的概念，会用能量均分定理计算理想气体的内能。
6．了解气体分子平均碰撞频率及平均自由程的意义及其简单的计算。
二、基本内容1. 平衡态在不受外界影响的条件下，一个系统的宏观性质不随时间改变的状态。
2. 理想气体状态方程在平衡态下，理想气体各参量之间满足关系式pV vRT =或 nkT p =式中v 为气体摩尔数，R 为摩尔气体常量 118.31R J mol K --=⋅⋅，k 为玻尔兹曼常量 2311.3810k J K --=⨯⋅3. 理想气体压强的微观公式21233t p nm n ε==v4. 温度及其微观统计意义温度是决定一个系统能否与其它系统处于热平衡的宏观性质，在微观统计上32t kT ε=5. 能量均分定理在平衡态下，分子热运动的每个自由度的平均动能都相等，且等于2kT 。
以i 表示分子热运动的总自由度，则一个分子的总平均动能为2t i kT ε=6. 速率分布函数()dNf Nd =v v麦克斯韦速率分布函数232/22()4()2m kT m f e kTππ-=v v v7. 三种速率最概然速率p ==≈v 平均速率==≈v 方均根速率==≈8. 玻尔兹曼分布律平衡态下某状态区间（粒子能量为ε）的粒子数正比于kT e /ε-。
重力场中粒子数密度按高度的分布（温度均匀）：kT mgh e n n /0-=9. 范德瓦尔斯方程采用相互作用的刚性球分子模型，对于1mol 气体RT b V V ap m m=-+))((2 10. 气体分子的平均自由程λ==11. 输运过程 内摩擦dS dz du df z 0)(η-=， 1133mn ηλρλ==v v 热传导dSdt dz dT dQ z 0)(κ-= 13v c κρλ=v 扩散dSdt dz d D dM z 0)(ρ-= 13D λ=v三、习题选解4-1 一根铜棒的两端分别与冰水混合物和沸水接触，经过足够长的时间后，系统也可以达到一个宏观性质不随时间变化的状态。
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律
解
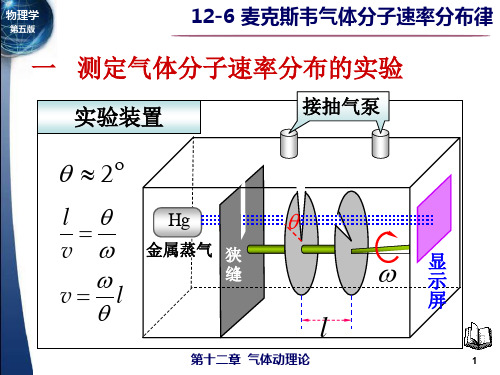
m(H 2 ) m(O2 ) v p ( H 2 ) v p (O 2 )
vp (H2 ) 2 000m.s-1
2kT vp m
o
2 000
v/ ms
1
vp ( H 2 )
m( O 2 ) 32 4 v p (O 2 ) m( H 2 ) 2
vp (O2 ) 500m.s
f ( v)
dS
dN f ( v)dv dS N
v
第十二章 气体动理论
o
v v dv
概率密度
3
物理学
第五版
12-6 麦克斯韦气体分子速率分布律
f (v)dv物理意义
表示在温度为 T 的平衡状态下，速 率在 v 附近单位速率区间 的分子数占总 数的百分比 .
f (v)dv 的物理意义：
表示速率在 v v dv 区间的分 子数占总分子数的百分比.
第十二章 气体动理论
4
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
dN Nf ( v)dv 速率在 v v dv 内分子数： 速率位于 v1 v2区间的分子数： v2 N v N f (v)dv 1 速率位于 v1 v2 区间的分 f ( v)
-1
第十二章 气体动理论
17
f (v )
vp v v
2
第十二章 气体动理论
vp v 2 v
v
15
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
讨论 1 已知分子数 N ，分子质量 m ，分布函 数 f ( v) . 求 （1） 速率在 vp ~ v 间的分子 数；（2）速率在 vp ~ 间所有分子动能 之和 . 解 （ 1）
大学物理麦克斯韦分子速率分布定律资料
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
11
例: 设有N个气体分子，其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A；(2)最概然速率，平均速率和方均根；
(3)速率介于0~0/3之间的分子数；(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解： (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意：速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子，其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: （1）归一化常数A的值；（2）最概然速率
（3）N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子，速度大小和方向都是偶然的， 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
11
例: 设有N个气体分子，其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A；(2)最概然速率，平均速率和方均根；
(3)速率介于0~0/3之间的分子数；(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解： (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意：速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子，其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: （1）归一化常数A的值；（2）最概然速率
（3）N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子，速度大小和方向都是偶然的， 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
大学物理05_5麦克斯韦速率分布律
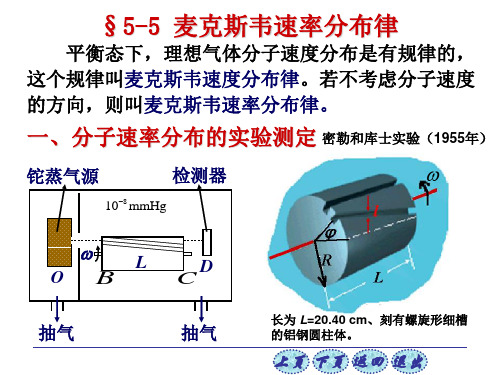
气体分子速率可以取从0到∞之间
的一切数值。速率很大和速率很
小的分子数所占的比率都很小，
f(0)=f(∞)=0 ， 而 具 有 中 等 速 率 的
分子数所占的比率却很大。
上页 下页 返回 退出
例题5-5 从速率分布函数推算分子的三个统计速率
(1)算术平均速率
v
vf (v)dv
v4π(
m
)
3
2
O
v exp
mv2 2kT
共同作用的结果。
上页 下页 返回 退出
麦克斯韦（James Clerk Maxwell 1831—1879）
•他提出了有旋电场和位移电流概念，建 立了经典电磁理论（麦克斯韦方程组）， 预言了以光速传播的电磁波的存在。
•1873年，他的《电磁学通论》问世，这 是一本划时代巨著，它与牛顿的《自然哲 学的数学原理》并驾齐驱，它是人类探索 19世纪伟大的英国 电磁规律的一个里程碑。 物理学家、数学家。 经典电磁理论的奠 •在气体动理论方面，他还提出气体分子 基人，气体动理论 按速率（速度）分布的统计规律。 的创始人之一。
当 v 0时，v dv ；N dN； 2. 速率分布函数 f(v) 的定义 f(v)
f (v) lim N dN v0 vN Ndv
注意：
在平衡态下，f(v)仅是v的函数。 O
v v+Δv
v
上页 下页 返回 退出
3. 速率分布函数 f(v) 的意义：概率密度函数
※分布在速率 v 附近单位速率间隔内的分子数占总 分子数的百分比(比率)；
m不变，T vp
2kT m
曲线的峰值右移，由于曲线下 面积为1不变，所以峰值降低。O
T2 T1
大学物理,气体动理论14-06 麦克斯韦气体分子速率分布律
i ~ i 1
N i
N i N
5
14.6 麦克斯韦速率分布律
第14章 气体动理论
气体分子按速率分布的统计规律最早是由麦克 斯韦于1859年在概率论的基础上导出的，1877年玻 耳兹曼由经典统计力学导出。 由于技术条件的限制，测定气体分子速率分布 的实验，直到20世纪二十年代才实现。 1920年斯特 恩首先测出银蒸汽分子的速率分布；1934年我国物 理学家葛正权测出铋蒸汽分子的速率分布；1955年 密勒和库士测出钍蒸汽分子的速率分布。 斯特恩实验是历史上最早验证麦克斯韦速率分 布律的实验。实验证实了麦克斯韦的分子按速率分 布的统计规律。
14.6 麦克斯韦速率分布律
一 测定气体分子速率分布的实验
第14章 气体动理论
实验装置
接抽气泵
2
l v
Hg
金属蒸汽 狭 缝
v l
显 示 屏
8
l
14.6 麦克斯韦速率分布律
第14章 气体动理论
9
14.6 麦克斯韦速率分布律
测量原理
第14章 气体动理论
(1) 能通过细槽到达检测 器的分子所满足的条件 L v L v (2) 通过改变角速度ω的 大小，选择速率 v
28
14.6 麦克斯韦速率分布律
第14章 气体动理论
求：速率在 v1 ~ v2 之间的分子的平均速率。
(3) 通过细槽的宽度，选择不同的速率区间 L v v 2
(4) 沉积在检测器上相应的金属层厚度必定正比 相应速率下的分子数。
10
14.6 麦克斯韦速率分布律
速率区间 (m/s) 实验数据 氧分子在 273K时的 速率分布
大学物理 专题五气体分子运动论
如： （V、P、T）、热容量C 等
质量M 体积V 内能E
压强p 温度T 分子数密度n
2、微观量（Microscopic quantity）
分子的大小d
表征单个分子特征的物理量 位置 r
微观量与宏观量有一定的内在联系
速度 v 质量 m
宏观量是微观量的统计平均值
能量 E
5、试指出：对于理想气体，下列各式所表示的物理意义
v
v dv
比较：
2kT 最概然速率 v p m
平均速率
v 8kT
m
f (v)
方均根速率 v 2 3kT m
o
vp v v2
v
v
0 f (v)dv
4、什么是宏观量？什么是微观量？什么是微观量的统计平均值？ 指出下列各物理量中哪些是宏观量？哪些是微观量？哪些是微 观量的统计平均值？
(3), v2 f (v)dv 0
f (v)dv 平衡态下，气体分子速率在v —v+dv区间内的分子数
占总分子数的百分比。
v2 f (v)dv 平衡态下，气体分子速率在v1 —v2区间内的分子数
v1
占总分子数的百分比。
(1), Nf (v)dv:平衡态下，气体分子速率在v —v+dv区间内的分子数。
5、气体分子热运动的基本特征
1). 麦克斯韦速率分布律
分布函数： f (v) 4 v2
m
32
e mv 2 2kT
2 kT
概率:
dN f (v)dv N
掌握速率分布函数及其各种形式（解析式、图形）的物理意义
2).三种统计速率：
最概然速率：v p
2kT m
2RT M
大学物理第8章第5节-麦克斯韦-玻尔兹曼分布律
v0 0
f (v)dv
f (v)dv
a
2v 0
v0 v0
f (v)dv
f (v)dv 1
2v 0
0
v0
2v0
v
0
(a v0 )vdv
2v0
v0
[2a (a v0 )v]dv 0dv 1
2v0
a 1 v0
(3) 由图可知, 分布曲线在 v 0 处取极大
0
a v v dv 2 0
7 v0 0.778v0 9
说明: (4)、(5)、(6)中有误.
麦克斯韦速度分布律
2 2 2 m(vx v y vz ) dN m dvx dv y dvz exp N 2 k T 2 k T B B 在 vx ~ vx dvx , vy ~ vy dvy , vz ~ vz dvz 区 32
值
2a
f (v)
a
0
v0
2v0
v
v p v0
(4) N 个粒子的平均速率
v vf (v)dv
0
v0
(a v0 )v 2 dv v[2a (a v0 )v]dv v 0dv v0
0 v0 2v 0
2v 0
(5) 0~ v0 2 内的粒子数
v0 2
N
0
v0 2
dN
0
v0 2
Nf (v)dv
0
N a N vdv v0 8
(6) v0 2 ~ v0 内分子的平均速率
f (v)dv
f (v)dv
a
2v 0
v0 v0
f (v)dv
f (v)dv 1
2v 0
0
v0
2v0
v
0
(a v0 )vdv
2v0
v0
[2a (a v0 )v]dv 0dv 1
2v0
a 1 v0
(3) 由图可知, 分布曲线在 v 0 处取极大
0
a v v dv 2 0
7 v0 0.778v0 9
说明: (4)、(5)、(6)中有误.
麦克斯韦速度分布律
2 2 2 m(vx v y vz ) dN m dvx dv y dvz exp N 2 k T 2 k T B B 在 vx ~ vx dvx , vy ~ vy dvy , vz ~ vz dvz 区 32
值
2a
f (v)
a
0
v0
2v0
v
v p v0
(4) N 个粒子的平均速率
v vf (v)dv
0
v0
(a v0 )v 2 dv v[2a (a v0 )v]dv v 0dv v0
0 v0 2v 0
2v 0
(5) 0~ v0 2 内的粒子数
v0 2
N
0
v0 2
dN
0
v0 2
Nf (v)dv
0
N a N vdv v0 8
(6) v0 2 ~ v0 内分子的平均速率
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
m
M mol
M mol
（3）方均根速率: v2
v2 3kT 3RT 1.73 RT
m
M mol
M mol
上页
下页
(4) 三种统计速率讨论
v p v v2
都与 T 成正比， 与 m（或 M ）成反比
一定温度时， f(v)
vp v v2
三个速率在不 同情况下使用
vp v v2
v
上页
下页
温度越高，速率大的分子数越多.
S P
GP
分子源 狭缝 圆筒
G 弯曲玻璃板,可沉积 射到上面的各种速率分子
圆筒不转，分子束的 分子都射在P处
圆筒转动，分子束的速率不同的分子将射在不同位置
上页
下页
四. 三种统计速率
（1）最概然速率v p
！ 速—率—为v vp 附p 的近分单子位数速最率多区？间的分
子数最多
f v
可用求极值的方法求得。
令 d f v 0 解出 v
dv
得
vp
22kkTTN0 mmN0
2RT
RT
vp 1.41
v
vp
m: 一个分子的质量
k=1.3810-23 [SI]
N0=6.0221023
R=8.31 [SI]
: 一摩尔分子的质量
上页
下页
（2）平均速率： v
v
Nivi
vf
v
dv
N
0
v 8kT 8RT 1.60 RT
RT 394 ms 1
2
v2 447 ms 1
v22 483 ms 1
上页
下页
1. 平衡态——麦克斯韦速率分布函数
f v 4
m
2 3
e
mv2 2kT
.v 2
2kT
2. 三种统计速率
RT
vp 1.41
v
8RT
M mol
v2
上页
3RT M mol
下页
f v 4
m
2 3
e
mv2 2kT
v
2
2kT
f v
T1< T2
T1
T2
对于给定气体f（v）只是T 的函数。 T，速率分布曲线如何变化？
温度升高，速率大的分子 数增 多，曲线峰右移，曲线下面积 v保持不变，所以峰值下降。
上页
下页
测定分子速率分布的实验装置
真空室 B
•••
A••• •••
s f v v N
f(v)
当△v→0时
N f (v) lim N dN v0 Nv Ndv
速率分布函数
f(vp)
2、不同速率区间的分子数占总数
的百分比不同, 概率不同
v p v v+dv
3、曲线下的总面积是一,
v
归一化条件
f
v
v
1
0
上页
下页
三. 麦克斯韦速率分布律
平衡态——麦克斯韦速率分布函数
f(v)
f(vp1)
T1
温度升高，分布曲线中的最可几 速率vp增大，但归一化条件要求曲 线下总面积不变，因此分布曲线 变平坦，高度降低。
f(vp2) f(vp3)
T2
T3 T1 T2 T3
vp
v
上页
下页
例1. 求：27oC 时氢分子、氧分子的最概然速率、平
均速率和方均根速率。
解 系统的热力学温度 T 273.15 27 300.15 K
例如气体分子按速率的分布
速率
v1 ～ v2 v2 ～ v3 … vi ～ vi +Δv
…
分子数按速率
的分布
ΔN1
ΔN2
…
ΔNi
…
分子数比率 按速率的分布
ΔN1/N
ΔN2/N
…
ΔNi/N
…
△N
f v dN
Ndv
当△v→0
△Ni
△vi
v
dv
上页
V(m/s) 下页
二. 速率分布函数
1、曲线下的小面积表示速率在v v v 区间的分子数占总数的百分比
氢分子的摩尔质量 1 2.02103 kg mol 1
v p1 1.41
RT 1.41
1
8.31 300.15 2.02 103
1567
ms 1
v1 1.6
RT 1778 ms 1
1
v12 1.73
ቤተ መጻሕፍቲ ባይዱ
RT 1922 ms 1
1
氧分子的摩尔质量 2 32103 kg mol 1
v p2 1.41