周期信号的功率证明 (2)
合集下载
樊昌信《通信原理》(第7版)课后习题(确知信号)【圣才出品】
第2章确知信号思考题2-1 何谓确知信号？答：确知信号是指其取值在任何时间都是确定和可预知的信号，通常可以用数学公式表示它在任何时间的取值。
例如，振幅、频率和相位都是确定的一段正弦波，它就是一个确知信号。
2-2 试分别说明能量信号和功率信号的特性。
答：（1）能量信号的能量为一个有限正值，但其平均功率等于零。
（2）功率信号的能量为无穷大，其平均功率为一个有限正值。
2-3 试用语言（文字）描述单位冲激函数的定义。
答：单位冲击函数是指宽度无穷小，高度为无穷大，积分面积为1的脉冲。
其仅有理论上的意义，是不可能物理实现的一种信号。
2-4 试画出单位阶跃函数的曲线。
答：如图2-1所示。
图2-12-5 试述信号的四种频率特性分别适用于何种信号。
答：（1）功率信号的频谱适用于周期性的功率信号。
（2）能量信号的频谱密度适用于能量信号。
（3）能量信号的能量谱密度适用于能量信号。
（4）功率信号的功率谱密度适用于功率信号。
2-6 频谱密度S（f）和频谱C（jnω0）的量纲分别是什么？答：频谱密度的量纲是伏特/赫兹（V/Hz）；频谱的量纲是伏特（V）。
2-7 自相关函数有哪些性质？答：自相关函数的性质：（1）自相关函数是偶函数；（2）与信号的能谱密度函数或功率谱密度函数是傅立叶变换对的关系；（3）当τ＝0时，能量信号的自相关函数R（0）等于信号的能量，功率信号的自相关函数R（0）等于信号的平均功率。
2-8 冲激响应的定义是什么？冲激响应的傅里叶变换等于什么？答：（1）冲激响应的定义：输入为单位冲激函数时系统的零状态响应，一般记作h（t）。
（2）冲激响应的傅里叶变换等于系统的频率响应，即H（f）。
习题2-1 试判断下列信号是周期信号还是非周期信号，能量信号还是功率信号：（1）s1（t）＝e－t u（t）（2）s2（t）＝sin（6πt）＋2cos（10πt）（3）s3（t）＝e－2t解：若0＜E＜∞，而功率P→0，则为能量信号；若能量E→0，而0＜P＜∞，则为功率信号。
3.2 周期信号的傅里叶级数分析
f (t )
n
F e
n
jn1t
E T1
n1 jn1t Sa( 2 )e n
20
E f (t ) T1
n1 jn1t Sa( 2 )e n
E n1 Fn Sa( ) T1 2
2 E n1 cn Sa( ) T1 2 E c0 T1 n0
E cos(n t )dt
2 1 2
2E 2E n1 2 sin(n1t ) sin( ) T1n1 n 2 2
E1
n1 2 E n1 Sa( ) Sa( ) 2 T1 2
E 2 E f (t ) T1 T1
n1 Sa( 2 ) cos(n1t ) n 1
f1 t
f1 (t ) 1 f (t )
1
f (t)
练习P 3 7 171
2
－T
T T 0
2
T 2
T
2T
t
T 2
0 －1
T 2
T
2T
t
注意：不可左右移动，否则改变了 原信号的对称性。
11
四、傅里叶有限级数与最小方均误差
f (t ) a0 (an cos n1t bn sin n1t )
32
1 1 2 2 2 2 2 P a0 (an bn ) c0 cn 2 n 1 2 n 1 1 2 2 2 c0 (2 Fn 2 F n ) 2 n 1 c0 Fn F n
2 2 2 n 1 n 1 n
2 b2 T1
T1 2 T 1 2
1周期信号(2)
复杂周期信号
第一章 信号及其描述 b) 非周期信号： 非周期信号：再不会重复出现的信号。 再不会重复出现的信号。
准周期信号
准周期信号: 准周期信号:由多个周期信号合成， 由多个周期信号合成，但各周期信号的频率不成公 倍数， 倍数，其合成信号不是周期信号。 其合成信号不是周期信号。如：x(t) = sin(t)+sin( t) 瞬态信号
瞬态信号
第一章 信号及其描述 b) 功率信号 在所分析的区间（ 在所分析的区间（-∞，∞ ），能量不是有限值 ），能量不是有限值． 能量不是有限值．此 时，研究信号的平均功率更为合适。 研究信号的平均功率更为合适。
lim
T → ∞
1 2T
∫
T
−T
x 2 (t )dt < ∞
一般持续时间无限的信号都属于功率信号。 一般持续时间无限的信号都属于功率信号。
x( t ) = a
2 n
0
+
2 n
∑
n+ 1
A
n
sin(
an bn
nω
0
t + φ
n
)
An = a + b
tg φ n =
φn = arctg
bn an
ห้องสมุดไป่ตู้
第一章 信号及其描述
分析： 分析： a） x(t) 展成为富氏级数是一个无穷级数，即 n→∞ 。表明
信号中可能包含无穷多个频率成分。 b） c） 由于 n 是整数，所以相邻频率间隔△ω=ω0=2π/T0 。 若以 ω 为横坐标并绘出各频率下的谱线，就得A—ω与φ—ω
噪声信号(平稳)
噪声信号(非平稳)
统计特性变异
第一章 信号及其描述
第四章(2)周期信号的频谱
周期性矩形脉冲信号的频谱还有自己的特点 周期性矩形脉冲信号的频谱还有自己的特点 : 1、各谱线的幅度按包络线 T 、
ωτ
= m π ( m = ±1, ± 2,...)
τ
Sa (
ωτ
2
) 的规律变化。 的规律变化。
各处， 的各处， 在 2 各处，即 的各处， τ 包络为零，其相应的谱线， 包络为零，其相应的谱线，亦即相应的频谱分量也等 于零。 于零。 2、周期矩形脉冲信号包含无限多条谱线，也就是说， 、周期矩形脉冲信号包含无限多条谱线，也就是说， 它可分解为无限多个频率分量。 它可分解为无限多个频率分量。 通常把频率范围 0 ≤ f ≤ τ (0 ≤ ω ≤ τ ) 称为周期矩形脉冲 带宽， 表示， 信号的带宽 信号的带宽，用符号 ∆F 表示，即周期矩形脉冲信 1 号的频带宽度为 ∆F = 。 τ
Fn F ( jω ) = lim = lim FnT T →∞ 1 / T T →∞
为频谱密度函数。 称 F ( jω )为频谱密度函数。
Fn lim = lim FnT 如何求频谱密度函数？ 如何求频谱密度函数？ F ( jω ) = T →∞ 1 / T T →∞
由式 f ( t ) =
n = −∞
T 2T f (t) T=8τ
0
3T
4T t
0 1/ 8
T f (t) T=16τ
0
2T
t
0 1/16
0
T
t
0
f (t) T→∞ τ/T
0 t 0
图4.3-5 周期与频谱的关系
思考： 思考：
1 1 1 f (t ) = [sin(Ωt ) + sin(3Ωt ) + sin(5Ωt ) + .... + sin(nΩt ) + ...] 3 5 n π 4
周期信号的频谱
当 n1 0
2
即 n1 0
基波分量的幅度：A Sa1
T 2
Fn
A
T
San1
2
Fn
为最大值 ：A T
二次谐波分量的幅度：
A Sa 21
T 2
编辑版
15
3.3.2 双边频谱与信号的带宽
3.相位的确定
Fn
A
T
San1
2
是 n1 的实函数
Fn Fnejn Fn(consjsinn) Fn cosn
• 周期信号频谱的特点：
❖离散性：
由不连续的谱线组成，每一条谱线代表一个正弦分量，所以
此频谱称为不连续谱或离散谱；每条谱线间的距离为 ❖谐波性：
1
2
T
每一条谱线只能出现在基波频率 1 的整数倍频率上，即含 有 1 的各次谐波分量，而决不含有非 1 的谐波分量。
❖收敛性：
各次谐波分量的振幅虽然随 n1 的变化有起伏变化，但总的 趋势是随着 n1的增大而逐渐减小。
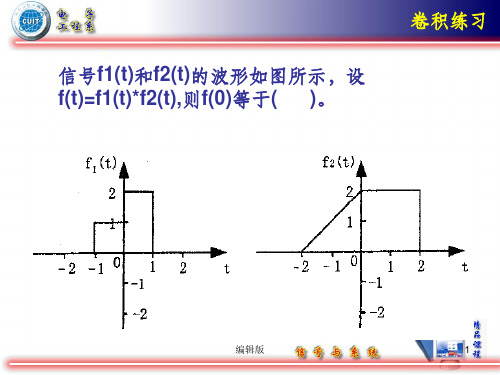
信号f1(t)和f2(t)的波形如图所示，设 f(t)=f1(t)*f2(t),则f(0)等于( )。
卷积练习
编辑版
1
3.3 周期信号的频谱
编辑版
2
3.3 周期信号的频谱
• 3.3.1 周期信号频谱的特点 • 3.3.2 双边频谱与信号的带宽 • 3.3.3 周期信号的功率
编辑版
3
3.3.1 周期信号频谱的特点
1
e jn1t
T n
1
2 T
编辑版
33
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
以相位为纵坐标所得到的谱线图
§3.2 周期信号的频谱和功率谱
不变，T增大，谱线间隔
1
2 T
减小，谱线逐渐密集，幅度
A T
பைடு நூலகம்
减
小
当 T
1 0
A 0 T
非周期信号连续频谱
非周期信号 n1 连续频率
2.当T不变， 减小时
T不变
1
2 间隔不变
T
A 振幅为0的谐波频率
T
2
,
4
,......
信号与系统
练习：周期信号的频谱描绘
不改变 不改变 不改变
Fn
2 T
2
f (t)dt
T
2 A
2
Adt
2
T
信号与系统
练习：周期信号的频谱描绘
a 2 nT
T
2 T
2
f (t) cos n1tdt
2A sin n n T
2 A
T
sin n
T
n
2A Sa(n )
T
T
T
f (t)
A
T
2 A
T
n 1
Sa( n
T
)
cos(n1t )
A 2A
TT
S a(
立叶展开式并画出其频谱图。
1
解: f(t) 在一个周期内可写为如下形式
Tt
f (t) 2 t T t T
T
22
f(t) 是奇函数，故 an 0
信号与系统
4
bn T
T 2 0
f (t) sin n1tdt
4 T
T 2 0
2t T
sin
n1tdt
(1
2
T
)
An &n 2
信号分析3功率谱和能量谱
7 页
X
2 T
Lim
T 2
FT ( jw) T 则
2
dw
定义 : 功率谱 ( w) Lim 1 P 2
FT ( jw) T
( w)dw
功率谱表示单位频带内信号功率随频率的变化情况,功 率谱曲线所覆盖的面积在数值上等于信号的总功率 X
第
作业: 3-30 3-32 3-42
X
第
三功率信号的功率谱
ET
6 页
对功率有限信号 f (t ), 如截取一个周期 f T (t ), 其能量为:
f T2 (t )dt
T 2 T 2
f 2 (t ) d t
信号f (t )的平均功率表示为 : 1 P Lim T T
T 2 T 2
1 f (t ) d t 2
5 页
E G ( )d
1 G ( ) F 2 ( j ) 2
说明：
表示单位频率下的信号能量。 1)能量是整个频域范围内能量谱曲线下的面积 2)能量谱只取决于信号的幅频特性,而与相位无关. 通过能量谱曲线可以了解信号能量在频域 中的分布情况，以便正确选择电路和系统的通 频带，充分利用信号的能量。
E 况下的具体体现; 能量既可在时域中计算，也可在频域中计算，且只与 幅频谱有关，而与相频谱无关.时域和频域能量守恒. X
1
F ( j )d
2
0
F ( j )d
2
频域法
第
能量谱:
不同频率下信号的实际振幅为无穷小,能 量实际也为无穷小,为描述不同频率下能量的 分布情况,引入能量密度频谱函数G(w),
§4.2 傅里叶级数
bn =0，展开为余弦级数。
2.f(t)为奇函数——对称于原点
f (t ) f (t )
an =0，展开为正弦级数。
▲ ■ 第 10 页
3.f(t)为奇谐函数——f(t) = –f(t±T/2) 其傅里叶级数中只含 奇次谐波分量，不含 偶次谐波分量；即 a0=a2=…=b2=b4=…=0
2 an T
T 2 T 2
2 f (t ) cos( nt ) d t bn T
T 2 T 2
f (t ) sin( nt ) d t
an是n的偶函数，bn是n的奇函数。
▲ ■ 第 3页
将上式同频率项合并
A0 f (t ) An cos( nt n ) 2 n 1 bn 2 2 n arctan 式中，A0 = a0 An a n bn an An是n的偶函数， n是n的奇函数。
T , cosnt cosmt dt 2 0, T T , 2 T2 sin nt sin mt dt 2 0,
▲
T 2 T 2 T 2 T 2
cosnt sin mt dt 0
mn mn
f (t )
n
Fn e j nt
T 2 T 2
系数Fn 称复傅里叶系数
1 Fn T
f (t )e j nt d t
用cosx =(ejx + e–jx)/2从三角形式推出： 推导
▲ ■ 第 12 页
指数形式付氏级数推导
A0 f (t ) An cos( nt n ) 2 n 1
§4.2
傅里叶级数
• 傅里叶级数的三角形式 • 波形的对称性与谐波特性 • 傅里叶级数的指数形式 • 周期信号的功率——Parseval等式
2.f(t)为奇函数——对称于原点
f (t ) f (t )
an =0，展开为正弦级数。
▲ ■ 第 10 页
3.f(t)为奇谐函数——f(t) = –f(t±T/2) 其傅里叶级数中只含 奇次谐波分量，不含 偶次谐波分量；即 a0=a2=…=b2=b4=…=0
2 an T
T 2 T 2
2 f (t ) cos( nt ) d t bn T
T 2 T 2
f (t ) sin( nt ) d t
an是n的偶函数，bn是n的奇函数。
▲ ■ 第 3页
将上式同频率项合并
A0 f (t ) An cos( nt n ) 2 n 1 bn 2 2 n arctan 式中，A0 = a0 An a n bn an An是n的偶函数， n是n的奇函数。
T , cosnt cosmt dt 2 0, T T , 2 T2 sin nt sin mt dt 2 0,
▲
T 2 T 2 T 2 T 2
cosnt sin mt dt 0
mn mn
f (t )
n
Fn e j nt
T 2 T 2
系数Fn 称复傅里叶系数
1 Fn T
f (t )e j nt d t
用cosx =(ejx + e–jx)/2从三角形式推出： 推导
▲ ■ 第 12 页
指数形式付氏级数推导
A0 f (t ) An cos( nt n ) 2 n 1
§4.2
傅里叶级数
• 傅里叶级数的三角形式 • 波形的对称性与谐波特性 • 傅里叶级数的指数形式 • 周期信号的功率——Parseval等式
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
T /2
T / 2
f ( t )dt F0
2
2
2 Fn
n 1
n
F
2
n
jh jh
X
jh 2 jh
An ,因此，上式可化为：
2
X
第 3 页
P
1 T
T /2
T / 2
f ( t )dt (
2
A0 2
)
2 n 1
1 2
An
2
总平均功率=各次谐波的平均功率之和 上式表明：
由于 | Fn | 是n的偶函数，且| Fn | 1 2
2
An , 上式可改写为：
P
T
1
第
证明1:
P
1 T
T /2
T / 2
f ( t )dt
2
1 页
将f(t)的指数形式的傅里叶级数展开式代入上式， 得：
P 1 T
T /2
T / 2
[ f ( t ) Fn e
n
jnt
]dt
n
Fn
1 T
T /2
T / 2
f ( t )e
P 1 T
2 T 2
[
A0 2
An cos(nt n )] dt
2 n 1
将上式被积函数展开，在展开式中具有 cos(nt n )形式 的余弦项，其在一个周期内的积分等于零；具有 An cos(nt n ) Am cos(mt m ),当m n时，其积分值为 零，对于m nFn F n
2
n
Fn
2
P
1 T
T /2
T / 2
f ( t )dt
n
F
2
n
jh 上式称为帕斯瓦尔恒等式。 jh
X
第
设f(t)为实函数 证明2：
归一化的平均功率：
P 1 T
T /2
2 页
T / 2
f ( t )dt
2
将f(t)的三角形式的傅里叶级数展开式代入上式， 得： T