Butterworth滤波在CUDA上的实现
mathematica进行巴特沃斯滤波

mathematica进行巴特沃斯滤波摘要:1.巴特沃斯滤波的定义与应用2.Mathematica 软件介绍3.在Mathematica 中实现巴特沃斯滤波的步骤4.实例演示5.总结正文:1.巴特沃斯滤波的定义与应用巴特沃斯滤波(Butterworth Filter)是一种常用的数字滤波方法,主要用于去除信号中的高频噪声。
它具有频率响应平滑、无纹波等优点,广泛应用于信号处理、图像处理等领域。
2.Mathematica 软件介绍Mathematica 是一款功能强大的数学软件,可以进行各种数学计算、数据分析和可视化等操作。
它具有丰富的函数库和用户友好的界面,广泛应用于科学研究、工程设计等领域。
3.在Mathematica 中实现巴特沃斯滤波的步骤在Mathematica 中实现巴特沃斯滤波主要可以分为以下几个步骤:(1)导入所需的库:如SignalProcessing`(2)定义信号:如一个包含噪声的音频信号(3)应用巴特沃斯滤波函数:如ButterworthFilter(4)绘制滤波前后的信号:如使用Plot 函数4.实例演示下面是一个简单的Mathematica 代码示例,演示如何对一个包含噪声的音频信号进行巴特沃斯滤波:```mathematica<<SignalProcessing`(* 定义音频信号*)audioSignal = Sound[Sin[2 Pi 1000 t] + RandomReal[{-1, 1}, 1000]];(* 巴特沃斯滤波*)butterworthFilter = ButterworthFilter[audioSignal, 10, 5];(* 绘制滤波前后的信号*)Plot[audioSignal, {t, 0, 10}, PlotLegends -> {"audioSignal", "butterworthFilter"},AxesLabel -> {"Time", "Amplitude"}];```5.总结通过Mathematica 软件,我们可以方便地实现巴特沃斯滤波,有效去除信号中的高频噪声。
低通巴特沃斯滤波C语言实现

低通巴特沃斯滤波C语言实现巴特沃斯滤波是一种常见的信号处理滤波器,能够将高频信号从输入信号中滤除,只保留低频信号。
它在信号处理、音频信号处理、图像处理等领域有广泛的应用。
下面是一个使用C语言实现的低通巴特沃斯滤波器的例子。
首先,我们需要定义一些常量和变量来表示滤波器的参数和状态。
我们将使用一个全局变量来保存滤波器的历史输入和输出数据:```c#define FILTER_ORDER 4 // 滤波器阶数#define FILTER_CUTOFF 200 // 截止频率,单位为Hzdouble input[FILTER_ORDER + 1]; // 输入历史数据double output[FILTER_ORDER + 1]; // 输出历史数据```接下来,我们需要初始化滤波器的历史数据。
这里使用一个函数来完成初始化操作:```cvoid initFiltefor (int i = 0; i <= FILTER_ORDER; i++)input[i] = 0.0;output[i] = 0.0;}```接下来,我们需要定义一个滤波函数来实现滤波的操作。
这里使用递归计算方式来实现滤波:```cdouble filter(double x)//更新历史输入数据for (int i = FILTER_ORDER; i > 0; i--)input[i] = input[i-1];}input[0] = x;//更新历史输出数据for (int i = FILTER_ORDER; i > 0; i--)output[i] = output[i-1];}//计算输出output[0] = (input[0] + 2 * input[1] + input[2] -(0.7408 * output[1]) - (0.2042 * output[2])) /1.3403;return output[0];```在上面的代码中,我们使用了巴特沃斯低通滤波器的差分方程来实现滤波。
二维巴特沃斯滤波器c语言

二维巴特沃斯滤波器1. 简介二维巴特沃斯滤波器是一种常用的图像处理方法,用于对图像进行频域滤波。
它基于巴特沃斯滤波器的原理,在频域中对图像进行平滑或增强。
本文将详细介绍二维巴特沃斯滤波器的原理、实现步骤以及应用案例。
2. 巴特沃斯滤波器原理巴特沃斯滤波器是一种频率域滤波器,通过调整截止频率和阶数来控制信号的频率响应。
其传输函数可以表示为:H (u,v )=11+(D (u,v )D 0)2n其中,D (u,v ) 是图像中每个点到中心点的距离,D 0 是截止频率,n 是阶数。
当 n 取不同值时,巴特沃斯滤波器可以实现不同程度的平滑或增强效果。
当 n >1 时,增加了阶数可以使得低频信号更加平坦;当 n <1 时,减小了阶数可以使得低频信号更加突出。
3. 实现步骤二维巴特沃斯滤波器的实现步骤如下:步骤 1:读取图像首先,需要从文件中读取待处理的图像。
可以使用 C 语言中的图像处理库,如 OpenCV ,来实现图像读取功能。
#include <opencv2/opencv.hpp>int main() {// 读取图像cv::Mat image = cv::imread("input.jpg", cv::IMREAD_GRAYSCALE);// 其他处理步骤...return 0;}步骤 2:进行傅里叶变换将读取的图像进行傅里叶变换,得到频域表示。
可以使用 OpenCV 提供的函数dft 来实现傅里叶变换。
#include <opencv2/opencv.hpp>int main() {// 读取图像cv::Mat image = cv::imread("input.jpg", cv::IMREAD_GRAYSCALE);// 进行傅里叶变换cv::Mat frequencyDomain;cv::dft(image, frequencyDomain, cv::DFT_COMPLEX_OUTPUT);// 其他处理步骤...return 0;}步骤 3:生成巴特沃斯滤波器根据巴特沃斯滤波器的传输函数公式,可以生成巴特沃斯滤波器的频域表示。
Butterworth 滤波器实验

double dTemp; for(int i = 0; i < h; i++) for(int j = 0; j < w; j++) { dTemp=TD[i * w + j].real(); //move back if((i+j)%2) dTemp=-dTemp; // 判断是否超过 if (dTemp > 255) dTemp = 255; else if (dTemp<0) dTemp=0; lpSrc = (unsigned char*)pDoc->m_pDib->m_lpImage + lLineBytes * (lHeight - 1 - i) + j; // 更新源图像 * (lpSrc) = (BYTE)(dTemp); }
ห้องสมุดไป่ตู้
int CImgProcView::DoIFFT(complex<double>* TD, complex<double>* FD, int w, int h) { CImgProcDoc* pDoc = GetDocument(); unsigned char* lpSrc; int wp=int(log((double) w)/log(2.0)); int hp=int(log((double) h)/log(2.0)); for(int i = 0; i < w; i++) // 对x方向进行快速付立叶变换 IFFT( &FD[i * h],&TD[i * h], hp); // 保存变换结果 for(int i = 0; i < h; i++) for(int j = 0; j < w; j++) FD[j + w * i] = TD[i + h * j];//w*h for(int i = 0; i < h; i++) // 对y方向进行快速付立叶变换 IFFT(&FD[w * i],&TD[w * i],wp);
c++ 3阶巴特沃斯低通滤波算法

C++ 3阶巴特沃斯低通滤波算法在信号处理领域,巴特沃斯低通滤波算法是一种常用的数字滤波算法,它能够有效地去除信号中高频成分,保留低频成分,常用于音频处理、图像处理等领域。
C++作为一种高效的编程语言,能够很好地支持这一算法的实现。
本文将结合C++语言,深入探讨3阶巴特沃斯低通滤波算法的原理、实现和应用。
1. 巴特沃斯低通滤波算法概述巴特沃斯低通滤波器是一种能够通过滤波器将信号中高频成分抑制、低频成分保留的数字滤波器。
其传输函数具有一定的特点,采用巴特沃斯低通滤波器可以实现对信号的平滑处理,去除高频噪声,保留低频信号。
3阶巴特沃斯低通滤波器具有更加优化的特性,能够更好地滤除高频噪声,保留低频信号,因此在实际应用中具有广泛的价值。
2. 3阶巴特沃斯低通滤波算法原理3阶巴特沃斯低通滤波算法是建立在巴特沃斯低通滤波器基础上的改进版本,其核心原理是通过多级滤波器级联的方式,增强滤波效果,同时减少不必要的波纹和相位失真。
其数学模型和传输函数较为复杂,需要通过C++编程语言实现。
3. C++实现3阶巴特沃斯低通滤波算法在C++中实现3阶巴特沃斯低通滤波算法,需要充分利用C++语言的面向对象特性、模板编程等特点。
可以采用模块化的设计思路,将滤波器的设计、参数设置、滤波处理等功能进行封装,从而提高代码的可复用性和可维护性。
C++的性能优势也能够保证算法的高效性。
4. 应用案例分析3阶巴特沃斯低通滤波算法在信号处理领域具有广泛的应用,比如在音频去噪、图像平滑处理、信号恢复等方面均有重要作用。
通过具体的应用案例分析,可以更好地展现算法的效果和实用性,也有助于读者深入理解算法的具体应用场景。
5. 个人观点和总结作为一种经典的数字滤波算法,3阶巴特沃斯低通滤波算法在实际应用中能够发挥重要作用。
在C++语言中实现该算法,既能够充分发挥C++语言的优势,也能够更好地与实际应用结合,为信号处理领域的工程实践提供技术支持。
在未来的发展中,可以进一步优化算法的性能、扩展算法的适用范围,从而更好地满足不同领域的需求。
cuda均值滤波

CUDA是一种并行计算平台和编程模型,用于在NVIDIA GPU上加速计算任务。
均值滤波是一种图像处理技术,用于平滑图像并减少噪声。
结合CUDA和均值滤波,可以通过并行计算在GPU上高效地实现图像的均值滤波。
下面是使用CUDA进行均值滤波的大致步骤:
1. 将图像数据从主机(CPU)内存复制到GPU设备内存。
2. 在GPU上创建一个与原始图像相同大小的输出缓冲区。
3. 使用CUDA核函数(也称为GPU内核)来对每个像素进行均值计算。
- 在均值计算期间,将像素周围的邻域像素值相加,并求得平均值。
4. 将结果从GPU设备内存复制回主机内存。
5. 可选地,对输出图像进行进一步处理或显示。
需要注意的是,实现具体的CUDA均值滤波算法可能涉及到以下方面:
- 图像的分割和划分:将图像划分为小块,每个块由一个线程块(thread block)处理。
- 内存访问模式:利用共享内存(shared memory)来提高访问效率。
- 线程协作:在一个线程块中的线程之间进行数据通信和同步。
- 边界处理:对于图像边缘的像素,需要进行特殊处理,以防止越界访问。
以上是大致的步骤和注意事项。
具体实现细节可以根据具体情况和需求进行调整和优化。
1。
butterworth模拟低通滤波器阶数公式推导

概述1. 滤波器是信号处理中常用的一种工具,可以用来去除信号中的噪声或对信号进行降噪处理。
而Butterworth滤波器是一种常见的模拟低通滤波器,被广泛应用于电子工程领域。
Butterworth滤波器的基本原理2. Butterworth滤波器是一种模拟滤波器,以其频率响应的平坦特性而闻名。
它的特点是在通带内具有最大的平坦度,这意味着在通带内信号的幅频特性变化很小。
Butterworth滤波器对于对信号幅度变化敏感的应用非常适用。
Butterworth滤波器的频率响应函数3. Butterworth滤波器的频率响应函数是一个标准的低通滤波器形式:H(jω) = 1 / [1 + (jω / ωc)^n]其中,H(jω)表示滤波器的复频率响应,ω表示频率,ωc表示截止频率,n表示滤波器的阶数。
Butterworth滤波器的阶数公式推导4. Butterworth滤波器的阶数与其频率响应函数的形式有着密切的关系。
下面将从频率响应函数的角度推导Butterworth滤波器的阶数公式。
在频域中,频率响应函数H(jω)的幅度响应由以下公式给出:|H(jω)| = 1 / √[1 + (ω / ωc)^2n]其中,|H(jω)|表示频率响应函数的幅度响应。
为了使Butterworth滤波器在截止频率处的幅度响应下降为1/√2倍,即√2/2,我们需要满足下面的条件:|H(jωc)| = 1 / √2代入频率响应函数的表达式,可以得到:1 / √[1 + (ωc / ωc)^2n] = 1 / √2整理可得:2 = 1 + (ωc / ωc)^2n经过整理可以得到Butterworth滤波器的阶数公式:n = log(2) / [2 * log(ω /ωc)]结论5. 经过推导得到了Butterworth滤波器的阶数公式,这个公式可以用来确定Butterworth滤波器的阶数,从而在实际应用中提供了理论依据。
巴特沃斯(Butterworth)滤波器(1)
巴特沃斯(Butterworth)滤波器(1)
下面深入浅出讲一下Butterworth原理及其代码编写。
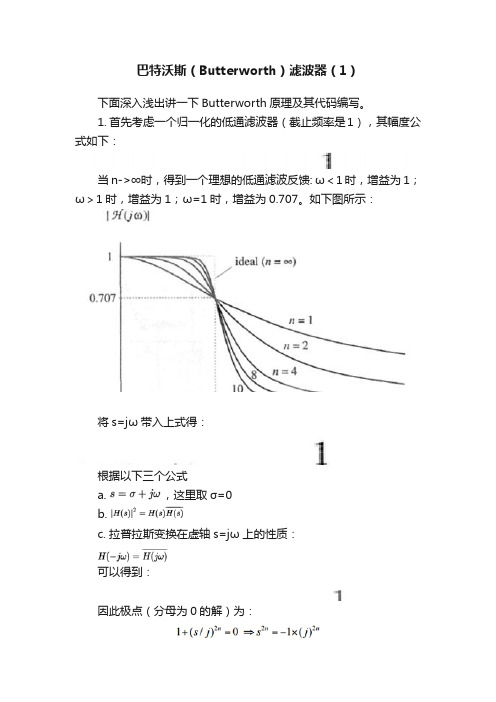
1. 首先考虑一个归一化的低通滤波器(截止频率是1),其幅度公式如下:
当n->∞时,得到一个理想的低通滤波反馈: ω<1时,增益为1;ω>1时,增益为1;ω=1时,增益为0.707。
如下图所示:
将s=jω带入上式得:
根据以下三个公式
a. ,这里取σ=0
b.
c. 拉普拉斯变换在虚轴s=jω上的性质:
可以得到:
因此极点(分母为0的解)为:
根据和得到:
因此可以求得极点在单位圆上:
如果k从0开始的话,上式括号里可以写作2k+n+1:
由于我们只对H(s)感兴趣,而不考虑H(-s)。
因此低通滤波器的极点全部在负实半平面单位圆上:
该滤波器的传递函数为
下面是n=1到4阶的极点位置:
例如四阶Butterworth低通滤波器的极点所在角度为:
5π/8, 7π/8, 9π/8, 11π/8
极点位置在:
因此传递函数为:
1到10阶的Butterworth多项式因子表格如下:
以上我们考虑的是幅度-3分贝时的截止频率为1时的情况:
其它截止频率可将传递函数中的s替换为:
例如二阶截止频率为100的传递函数为:。
