材料力学习题详解(范钦珊)第12章
浙江工业大学材料力学第12章答案
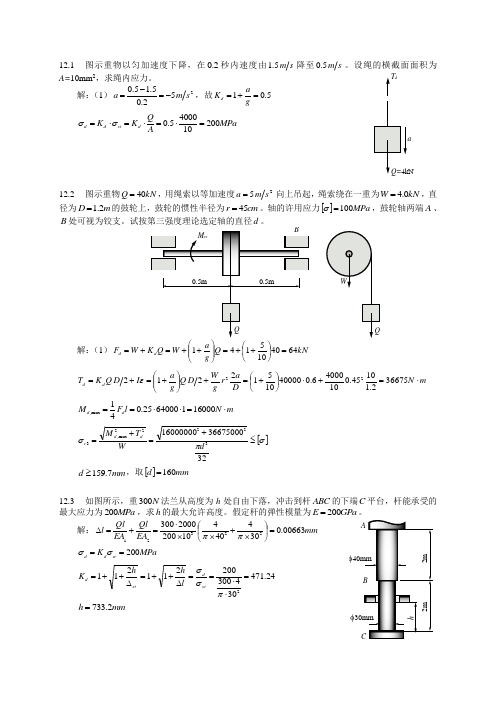
12.1 图示重物以匀加速度下降,在2.0秒内速度由s m 5.1降至s m 5.0。
设绳的横截面面积为A=10mm 2,求绳内应力。
解:(1)252.05.15.0s m a -=-=,故5.01=+=g a K dMPa A Q K K d st d d 2001040005.0=⋅=⋅=⋅=σσ12.2 图示重物kN Q 40=,用绳索以等加速度25s m a =向上吊起,绳索绕在一重为kN W 0.4=,直径为m D 2.1=的鼓轮上,鼓轮的惯性半径为cm r 45=。
轴的许用应力[]MPa 100=σ,鼓轮轴两端A 、B解:(1)kN Q g a W Q K W F d d 6440105141=⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=+= m N D a r g W D Q g a I D Q K T d d ⋅=+⋅⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+=+=366752.11045.01040006.0400001051221222ε m N l F M d d ⋅=⋅⋅==1600016400025.041max , []σπσ≤+=+=32366750001600000032222max ,3d WT M d d rmm d 7.159≥,取[]mm d 160=12.3 如图所示,重N 300法兰从高度为h 处自由下落,冲击到杆ABC 的下端C 平台,杆能承受的最大应力为MPa 200,求h 的最大允许高度。
假定杆的弹性模量为E 200=解:mm EA Ql EA Ql l 00663.030440410200200030022321=⎪⎭⎫ ⎝⎛⨯+⨯⨯⋅=+=∆ππ MPa K st d d 200==σσ24.4713043002002112112=⋅⋅==∆++=∆++=πσσst d st d l h h K mm h 2.733=12.4 如图所示,重N 100物体从mm h 500=位置自由下落到铝制梁AB 上的C 点,求截面C 的位移和梁上的最大应力。
范钦珊版材料力学习题全解 第12章 简单的静不定系统

(a)
(b) 习题 12-4 图
(A) FQA = FQB = 0 , FNA = FNB = 0 , M A = M B = 3( M / 3) ; (B)需解超静定才能确定; (C) FQA = FQB = 0 , FNA
= FNB = 0 ,MA 、MB 需解超静定才能确定;
M 。 2
(D) FQA = FQB = FNA = FNB ,但需解超静定才能确定具体数值, M A = M B =
X 1δ11 + X 2δ12 + ∆1FP = 0 ⎫ ⎪ ⎬ X 1δ 21 + X 2δ 22 + ∆2 FP = 0 ⎪ ⎭
(a)
10
(a)
(b) 习题 12-7 (b) 解的图-1
利用图乘法求其中的位移,作用在静定基本系统上的载荷(图 c)以及沿多余约束力 X1 和 X2 方向施加的单位力(图 e 和 g)所产生的弯矩图分别如图 f 和 h 所示。据此,可以求得:
由此解得:
1 5 FP = FP (→) 6 3 10 考虑静定基本系统平衡,得到全部约束力 11 F Ax = FP + FRD = FP (←) 10 FRD =
M A = FP ⋅ l = FP l (逆)
12-7 平面刚架各杆的刚度都相同,所受载荷如图所示。若忽略轴力和剪力影响,试用 图乘法确定其约束力,并画出弯矩图,确定绝对值最大的弯矩值及其所在横截面。
应用卡氏定理,建立变形协调条件 ∆Dx = 0 。
∂M 3 = x3 ∂FRD
∆Dx =
l l ⎤ ∂M 3 ∂M 1 ∂M 2 1 ⎡ l dx1 + ∫ M 2 ( x2 ) dx2 + ∫ M 3 ( x3 ) dx3 ⎥ ⎢ ∫ 0 M 1 ( x1 ) 0 0 ∂FRD ∂FRD ∂FRD EI ⎣ ⎦
材料力学_范钦珊_习题参考解答
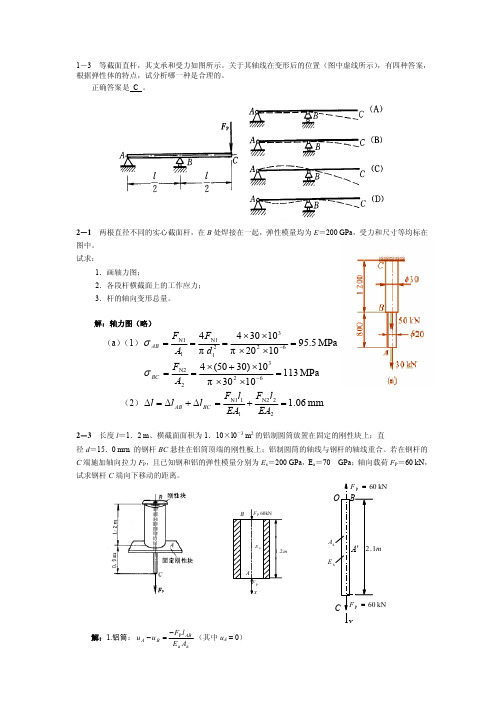
2-11 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 的正方形,钢和铸铁各占横截面的一 半(b×2b)。载荷 FP,通过刚性板沿铅垂方向加在组合柱上。已知钢和铸铁的弹性模量分别为 Es=196 GPa, Ei=98.0 GPa。今欲使刚性板保持水平位置,试求加力点的位置 x=?
解: ∑ M 0
( ) ( ) τmax
AB
= M xAB WPAB
= M xAB πd13
= π×
2936 70 ×10-3
3
= 43.6 MPa
16
16
BC 段:
M xBC = M e1 = 1171 N ⋅ m
( ) ( ) τmax
BC
=
M xBC WP 2
= M xBC
πd
3 2
= π×
1171 50 ×10−3
解:1. τ1max
=
Mx WP
=T WP
=T πd 3
= 3 ×103 ×16 = 70.7 MPa π× 0.063
16
∫ ∫ 2.
Mr =
ρ ⋅τdA =
A1
r
ρ
⋅
M
x
ρ ⋅ 2πρdρ
=
2πM x
⋅
r4
0 Ip
Ip
4
M r = 2πr 4 = 2πr 4 = 16r 4 = 16 × (15 )4 = 1 = 6.25%
Mx
4Ip
4 ⋅ πd 4
d4
60 16
32
3.
τ 2 max
=
Mx Wp
=
T
=75.4MPa
πd 3 ⎜⎛1 − ( 1 )4 ⎟⎞
材料力学第2版 课后习题答案 第12章 变形能法
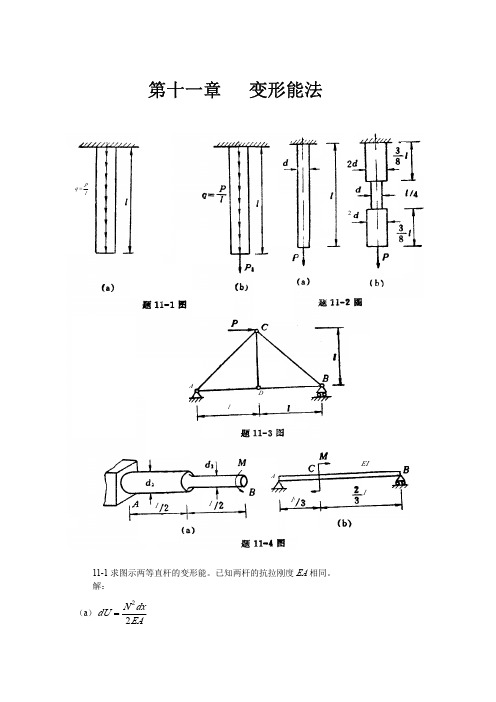
3 d1 ; 2
(b) 梁的抗弯刚度EI,略去剪切变形的影响。 解: (a) M n1 = m
M n2 = m U2 = J P2 =
9.6m 2 l Gπd14
U1 = J P1 =
m 2l 4GJ P1 π 4 d1 32
m 2l 4GJ P2 π 4 5.06π 4 d2 = d1 32 32
故
U a 16 = Ub 7
11-3 图示桁架各杆材料相同,截面面积相等,试求在 P 力作用下,桁架的变形能。 解:
支反力
R Ax = P R Ay = R B =
各杆的轴力和变形能如表所示 杆号 1 内力 Ni 杆长 各杆的变形能 Ui
P 2
2P 2
2l
2 P 2 l (4 EA)
2
− 2P 2
求 θA
M 0 ( x1 ) = −1 M 0 ( x 2 ) = −1
θA =
1 EJ
⎡ ⎛L ⎤ 1 ⎞ − P⎜ + x2 ⎟(− 1)⎥ dx 2 ∫0 (− Px1 )(− 1)dx1 + 2EJ ∫0 2 ⎢ ⎠ ⎣ ⎝2 ⎦
2
L
L
1 L2 1 = ⋅P⋅ + EJ 8 2 EJ =
求 δB
0
2l
l l l
2 P 2 l (4 EA)
0
3 4 5ຫໍສະໝຸດ P 2 P 2P 2 l (8EA) P 2l (8 EA)
故珩架的变形能为
5
U = ∑ Ui =
i =1
2 2 + 1 P 2l P 2l = 0.957 4 EA EA
11-4 试计算图示各杆的变形能。 (a) 轴材料的剪切弹性模量为G, d 2 =
范钦珊《工程力学》习题解答
rAB
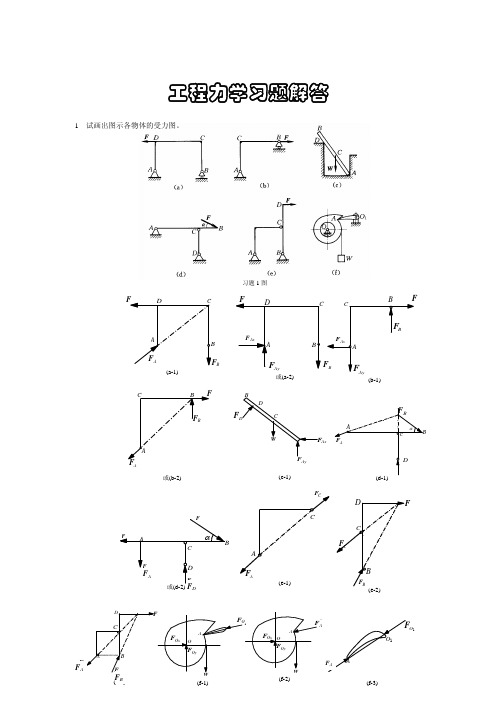
9 齿轮箱有三个轴,其中 A 轴水平,B 和 C 轴位于 yz 铅垂平面内,轴上作用的力偶如图所示。试求合力 偶。 解:MA =(1, 0, 0)MA =3.6(1, 0, 0)kN·m MB =(0, sin40°,cos40°)MB =6(0, sin40°,cos40°)kN·m MC =(0, sin40°,-cos40°)MC =6(0, sin40°,-cos40°)kN·m ∴ M = ΣMi = MA+ MB + MC =(3.6, 12sin40°, 0)kN·m
即 ∴
2 FR·MO = − FO (l3 + l1 + l2)= 0 l1 + l2 + l3 = 0
12 齿轮箱两个外伸轴上作用的力偶如图所示。为保持齿轮箱平衡,试求螺栓 A、B 处所提供的约束 力的铅垂分力。
FBy
FAy
解:ΣMi = 0, −500 + 125 + FAy × 0.5 = 0 FAy = 750N(↓) FBy = 750N(↑) (本题中 FAx ,FBx 等值反向,对力偶系合成结果无贡献。 ) 13 试求图示结构中杆 1、2、3 所受的力。 解:3 杆为二力杆 图(a) :ΣM = 0, F3 ⋅ d − M = 0
10 图示电动机固定在支架上,它受到自重 160N、轴上的力 120N 以及力偶矩为 25N·m 的力偶的作 用。试求此力系向点 A 简化的结果。
z
75
z
F1
A
r
75 25 200 75
y
x
F2
习题 10 图
M
(a)
解:由已知 F1 =160N,F2 =120N,F3 =25N·m F1 =(0, 0, -160)N F2 =(-120, 0, 0)N M =(25, 0, 0)N·m r =(0.075, 0.2, 0.025)m 向 A 点简化,得 FR = F1 + F2 =(-120, 0, -160)N M A = M + r × F1 + r × F2
材料力学范钦珊答案

材料力学范钦珊答案1. 弹性力学1.1 弹性模量弹性模量是描述材料抵抗力学变形的能力的一个重要参数。
弹性模量E可以表示为材料的应力和应变之间的比例关系,计算公式如下:E = (σ / ε)其中,E是弹性模量,σ是应力,ε是应变。
在弹性力学中,当材料受到力的作用时,会发生弹性变形,即材料在去除力后能够回复原状。
弹性模量越大,材料的刚性越高,抵抗变形的能力越强。
1.2 剪切模量剪切模量描述了材料在受到剪切应力时抵抗剪切变形的能力。
剪切模量G可以表示为剪切应力和剪切应变之间的比例关系,计算公式如下:G = (τ / γ)其中,G是剪切模量,τ是剪切应力,γ是剪切应变。
剪切模量越大,材料的抗剪切能力越强。
1.3 泊松比泊松比描述了材料在受到应力时,沿着应力方向的变形与垂直于应力方向的变形之间的比例关系。
泊松比ν可以表示为侧向应变和纵向应变之间的比例关系,计算公式如下:ν = (-ε横/ ε纵)其中,ν是泊松比,ε横是侧向应变,ε纵是纵向应变。
泊松比的取值范围在0和0.5之间,材料越接近0.5,其纵向应变和侧向应变之间的耦合效应越强。
2. 拉伸性能材料的拉伸性能指的是材料在受到拉伸应力时的响应能力。
常见的拉伸性能参数包括杨氏模量、屈服强度、抗拉强度和伸长率。
2.1 杨氏模量杨氏模量描述了材料在拉伸应力作用下的线弹性变形能力。
杨氏模量可以表示为应力和应变之间的比例关系,计算公式如下:E = (σ / ε)其中,E是杨氏模量,σ是应力,ε是应变。
杨氏模量越大,材料的刚性越高,抵抗变形的能力越强。
2.2 屈服强度材料的屈服强度是指材料在拉伸过程中开始出现塑性变形的应力值。
在应力达到屈服强度之后,材料会发生塑性变形,即无法完全恢复原状。
屈服强度通常用σy表示。
2.3 抗拉强度材料的抗拉强度是指材料在拉伸过程中能够承受的最大应力值。
抗拉强度通常用σmax表示。
2.4 伸长率伸长率描述了材料在拉伸过程中发生塑性变形后的延展性能。
清华出版社工程力学答案-第12章 简单的静不定问题
①
②
③ l
(a)
A a FP A
B a
C
FN1
FN2 B a
FN3 C
(b) a
FP A1 (c) A Δl1 A′
习题 12-4 图
B1 B B′
Δl2
C′ Δl3 C
即
Δl1 − Δl3 = 2Δl2
3. 物理方程
(b)
Δl1 =
FN1l , EA 5FP , 6
Δl2 =
FN 2l , EA
Δl3 =
FP 铜,Ec=105GPa 铝,Ea=70GPa
300
25 60
FP
习题 12-2 图
ε=
0.24 = 8 × 10 − 4 300
轴向载荷等于二者受力之和:
FP = σ cu Acu + σ al Aal = Ecu εAcu + Eal εAal
π π = 105 × 109 × 8 × 10−4 × × 252 × 10 −6 +70 × 109 × 8 × 10−4 × ( 602 − 252 ) × 10−6 4 4 = 172.1 kN
4. 联立求解 将(a) 、 (b) 、 (c)三式联立,求得:
F1 =
(16 + 2 ) l
2 Eδ
2 EAδ
, F2 =
1
(16 + 2 ) l
4 EAδ
1
据此求得二杆横截面上的正应力分别为:
F1杆 = F2杆 =
(16 + 2 ) l
4 Eδ
=
2 × 200 ×109 × 1. 5 × 10−3
7
FA =
7F 4
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
工程力学(静力学和材料力学)范钦珊主编答案全集 (1)
(a) (b) 习题1-1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影,比较两种情形下所得的分力与投影。
解:图(a ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b ): 分力:22)tan sin cos (i F ϕααF F x −= , 22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ−=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图,并加以比较。
比较:解a 图与解b 图,两种情形下受力不同,二者的F R D 值大小也不同。
DR习题1-2b 解图DR习题1-2a 解2图C习题1-2a 解1图(a) (b)习题1-2图1一3 试画出图示各构件的受力图。
习题1-3图B F 习题1-3a 解2图 B习题1-3a 解1图习题1-3b 解1图F Ay Ax 习题1-3c 解图 A习题1-3b 解2图习题1-3d 解1图习题1-3e 解1图习题1-3e 解2图1-4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重,BD 杆自重为W ,作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1习题1-3f 解1图F习题1-3e 解3图'A习题1-3f 解2图1O 习题1-3f 解3图F F'F 1习题1-4d 解2图F y B 21习题1-4c 解1图 AA B 1B FDx y2B 习题1-4b 解2图 1习题1-4b 解3图 F y B 2习题1-4c 解2图 F A B1B FAxF'习题1-5b 解3图E D(a-3)E B F习题1-5b 解2图习题1-5b 解1图'AxFF B习题1-5c 解图1一5 试画出图示结构中各杆的受力图。
材料力学全部习题解答
弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解:1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解:1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得: FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程(2);得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解:杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I( za) I( zR ) =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;,y轴不变; 图示截面对z,轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
δ12 =
δ 21 = δ 12
1 ⎛ 1 l3 ⎞ l l l − × × = − ⎟ EI ⎜ 2 EI ⎝ 2 ⎠
1 ⎛1 2 ⎞ l3 δ13 = ⎜ l × l × l ⎟ = 3 ⎠ 3EI EI ⎝ 2
Δ1F =
P
⎞ ql 4 1 ⎛ 1 ql 2 × × × l l ⎜ ⎟= EI ⎝ 3 2 ⎠ 6 EI
F , MA = MB =0。 2
(D) FNA = FQA = FNB = FQB =
解:从铰链处拆开,根据铰链的约束性质,应该有两个约束力-水平方向与铅垂方向, 但是根据对称性,只能有对称的约束力,这表明铅垂方向约束力必须等于零。 再应用水平方向的平衡条件,A、C 二处水平方向的约束力与外力平衡,同时应用对称 性,这二处的约束力大小相等、方向相同。于是,拆开后的半圆环的受力如图 b 所示。
正确答案是 A 。 解:这是平面结构承受平面外载荷作用的情形,在结构平面内没有外载荷作用,所以
结构平面内的所有内力分量均为零。 AE、BD,AE 为对称面,从 A、B 二处将结构截出三分之一,如图所示。 应用力偶矩矢量判断力偶的对称性:两力偶矩矢量若为反对称,其对应的的力偶则相 互对称;反之,如果两力偶矩矢量是对称的,其所对应的力偶则是反对称的。 据此,作用在截开部分上的外力偶 M,可以分为两大小相等方向相同的两个力偶(M /2)这两个力偶矩矢量是反对称的,所以两个力偶(M/2)是对称的。 应用对称性, 在对称面 A、 B 上只有对称的内力分量即弯矩, 二者大小相等,M A = M B , 矢量方向如图所示(力偶矩矢反对称) ,应用力矩矢量平衡条件,有
F ,FQA、FNB、MB 需求解超静定才能确定; 2
F F F F F F ,MA = , FNB = , FQB = , M B = ( − )R ; π π 2 2 π π
(C) FNA =
F FR F , FQA = 0 , M A = 0 , FNB = 0 , FQB = , M B = ; 2 2 2
2M A sin 60° = M ,
MA = MB = 3 M。 3
12-5 三根长度为 l、横截面面积为 A、材料均为线弹性的直杆,在 A、B、C、D 四处 铰结成图示的结构,F、l、E、A 等已知。试用卡氏定理确定各杆的拉力。
(a)
(b) 习题 12-5 图
解:解除 B 处的约束,使结构变成静定的,即静定基本系统;然后,在解除约束处加 上多余约束力 FRB ,应用对称性,由
第 12 章 简单的静不定系统
12-1 关于求解图 a 所示的超静定结构,解除多余约束有图 b、c、d、e 所示四种选择, 试判断下列结论中哪一种是正确的。 (A)b、c、d 都正确; (B)b、d 正确; (C)b、c、e 正确; (D)仅 e 是正确的。
习题 12-1 图
解:正确答案是
D
。
12-2 两个弯由刚度 EI 相同、半径为 R 的半圆环,在 A、C 两处铰链连接,加力方式 如图所示。关于 A、B 两处截面上的内力分量的绝对值,有如下四种结论,试分析哪一种是 正确的。
= 0 , FNB =
FR F ,MB = 。 2 2
解:从铰链处拆开,根据铰链的约束性质,应该有两个约束力-水平方向与铅垂方向, 但是根据对称性,只能有对称的约束力,这表明水平约束力必须等于零。 再应用铅垂方向的平衡条件,因为铅垂方向没有外力作用,所以,铅垂方向的约束力也 变形等于零。 于是,拆开后的半圆环的受力如图 b 所示。A、B 截面的内力分量分别为: F M A = 0 , FQA = 2 ∑ Fx = 0 , F FNB = FQA = 2 ∑MB = 0,
(a) 习题 12-6 图
(b)
解:此为一次静不定结构,解除 D 处的约束,使之变成静定的,即静定基本系统,如 图 b 所示。分段写弯矩方程并对多余约束力求偏导数
M 1 ( x1 ) = FRD x1 ,
∂M 1 = x1 ∂FRD
∂M 2 =l ∂FRD
M 2 ( x 2 ) = FRD l ,
M 3 ( x 3 ) = FRD x3 − FP (l − x3 ) ,
ΔBx = 0 X 1δ11 + Δ1FP = 0
2 1 2 2l 3 l ⋅l ⋅ l = EI 2 3 3EI
(a)
利用图乘法求其中的位移,作用在静定基本系统上的载荷(图 c)以及沿这多余约束力 方向施加的单位力(图 e)所产生的弯矩图分别如图 d 和 f 所示。据此,可以求得:
δ 11 =
Δ 1F
ql 2 1 3 3 11 2 M =− + × ql × l = ql 28 2 7 7 196
最大弯矩发生在固定端处横截面上
M max = −
ql 2 1 3 3 3 2 + × ql × l = ql 28 2 7 7 28
题(c)解:此为 1 次静不定问题,将 B 处的水平约束作为多余约束,解除多余约束,
∑F
x
=0,
FNA + FNC − F = 0 , FNA = FNC =
于是,A、B 截面的内力分量分别为:
F 2
FNA =
F , FQ A = 0 , M A = 0 2
F F ,MB = R 。 2 2
FN B = 0 , FQB =
所以,正确答案是 C 。
12-4 闭口圆环在三个等分点 C、D、E 处,承受环绕杆轴线转动的外力偶如图所示。关 于 A、B 两截面上内力分量数值,有以下四种结论,试分析哪一种是正确的。
∑ Fy = 0 ,
FN1 = FN 3 = ( F − FRB ) 2 , FN 2 2
= FRB
∂FN 2 ∂FN1 ∂FN 3 2 =− =1 = , 2 ∂FRB ∂FRB ∂FRB
应用卡氏定理(内力分量形式)建立变形协调条件
∂Vε =0 ∂FRB
l F l F l F ∂Vε ∂F ∂F ∂F = ∫ N1 N1 dx + ∫ N3 N3 dx + ∫ N2 N2 dx 0 EA ∂F 0 EA ∂F 0 EA ∂F ∂FRB RB RB RB
=
l l 1 ⎡ l 2 2 F x x F l x d d + + 2 ∫ 0 ( FRD x3 − FP ( l − x3 ) ) x3dx3 ⎤ ⎥ ⎣ ∫ 0 RD 1 1 ∫ 0 RD ⎦ EI ⎢ 1 ⎛5 1 ⎞ FRD l 3 − FP l 3 ⎟ = 0 = ⎜ EI ⎝ 3 6 ⎠
到静定基本系统。在静定基本系统上加上载荷以及多余约束力,得到相当系统如图 b 所示。 为了使两个系统完全相当,必须使相当系统在 A 处的水平位移以及 B 处的铅垂位移都 等于零。于是,变形协调条件为
(a)
(b) 习题 13 图(b)-1
X 1δ11 + X 2δ12 + Δ1FP = 0 ⎪ ⎫ ⎬ X 1δ 21 + X 2δ 22 + Δ2 FP = 0 ⎪ ⎭
3 1 ⎛1 2 ⎞ 4l δ11 = ⎜ l × l × l + l × l × l ⎟ = EI ⎝ 2 3 ⎠ 3EI
(a)
利用图乘法求其中的位移,作用在静定基本系统上的载荷(图 c)以及沿多余约束力 X1 和 X2 方向施加的单位力(图 e 和 g)所产生的弯矩图分别如图 f 和 h 所示。据此,可以求得:
(a)
(b)
(c)
(d)
(e) 习题 12-7(a)图
(f)
题(a) 解:此为 1 次静不定问题,将 B 处的水平约束作为多余约束,解除多余约束, 得到静定基本系统。 在静定基本系统上加上载荷以及多余约束力, 得到相当系统如图 b 所示。 为了使两个系统完全相当,必须使相当系统在 B 处的水平位移等于零。于是,变形协 调条件为
Δ2 F
P
1 ⎛ 1 ql 2 3 ⎞ ql 4 = ×l × l ⎟ = − ⎜− × EI ⎝ 3 2 4 ⎠ 8 EI
将上述位移代入变形协调方程,解得 A、B 二处的多余约束力:
X1 =
X2 =
ql (←) 28
3 ql (↑) 7
(c)
(d)
(e)
(f)
(g) 习题 13 图(b)-2
(h)
(a)
(b) 习题 12-4 图
(A) FQA = FQB = 0 , FNA = FNB = 0 , M A = M B = 3( M / 3) ; (B)需解超静定才能确定; (C) FQA = FQB = 0 , FNA
= FNB = 0 ,MA 、MB 需解超静定才能确定;
M 。 2
(D) FQA = FQB = FNA = FNB ,但需解超静定才能确定具体数值, M A = M B =
MB = F ⋅R 2
所以,正确答案是
D
。
12-3 两个弯曲刚度 EI 相同,半径为 R 的半圆环,在 A、C 两处铰接。关于在图示受 力情形下 A、B 两处截面上的内力分量数值有以下四种结论,试分析哪一种是正确的。
(a) 习题 12-3 图
(b)
(A) FNA = F / 2 , M A = 0 , FNB = (B) FNA = F / 2 , FQA =
再以相当系统作为平衡对象,即可求得全部约束力:
FCx =
FCy =
ql (→) 28
4 ql (↑) 7 ql 2 3 MC = − − l × X 1 + l × X 2 = − ql 2 (顺时针方向) 2 28
(i) 习题 13 图(b)-3
(j)
据此,可以画出剪力图和弯矩图,分别如图 i 和 j 所示。极值点弯矩
(b)
FBy =
7 ql (↑) 16
