高等数学定积分的概念
合集下载
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界， 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
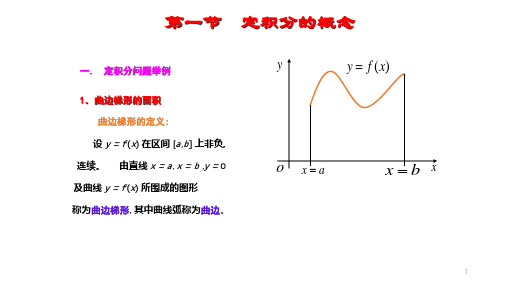
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动：
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
（2）近似代替
y Ai f (i )xi
(i 1,2,, n)
（3）求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
高等数学定积分概念
前页 后页 返回
代，虽然为此会产生误差，但当分割越来越细的 时候，矩形面积之和就越来越接近于曲边梯形面
积.
一分为二 y
y
b
x
前页 后页 返回
一分为四
y
y f x
S ( A)
O
a
x1
x2
x3
b
x
前页 后页 返回
一分为八
y
y f x
S ( A)
i 1
前页 后页 返回
给定的 0, 能够找到 0, 使得当
T max Δxi 时, 对任意 i [ xi 1 , xi ] ,
都有
f ( )Δx －S
i 1 i i
n
.
对于另外两个实际问题,也可类似地归结为黎曼和 的极限.
总结以上分析，下面给出定积分定义.
与 S 的差距 就会越来越小.
问题是：
i 1
(1) 如何刻画分割越来 越细？
(2) 如何刻画 f ( i )Δxi 越来越逼近于 S ?
i 1 n
下面依次讨论这两个问题.
前页 后页 返回
(1) 对于一般的 T : a0 x0 x1
xn b, 不能
用 n 来表示分割 T 越来越细,因为可能某些
f ( )x
i 1 i
b
n
i
J ,
n
则称 f 在 [a , b] 上可积， 并称 J 为 f 在 [a,b]上的
定积分,记作 J a f ( x )dx lim
T 0
f ( i )Δxi .
i 1
前页 后页 返回
其中称 f 为被积函数, [a , b] 为积分区间, x 为积
代，虽然为此会产生误差，但当分割越来越细的 时候，矩形面积之和就越来越接近于曲边梯形面
积.
一分为二 y
y
b
x
前页 后页 返回
一分为四
y
y f x
S ( A)
O
a
x1
x2
x3
b
x
前页 后页 返回
一分为八
y
y f x
S ( A)
i 1
前页 后页 返回
给定的 0, 能够找到 0, 使得当
T max Δxi 时, 对任意 i [ xi 1 , xi ] ,
都有
f ( )Δx －S
i 1 i i
n
.
对于另外两个实际问题,也可类似地归结为黎曼和 的极限.
总结以上分析，下面给出定积分定义.
与 S 的差距 就会越来越小.
问题是：
i 1
(1) 如何刻画分割越来 越细？
(2) 如何刻画 f ( i )Δxi 越来越逼近于 S ?
i 1 n
下面依次讨论这两个问题.
前页 后页 返回
(1) 对于一般的 T : a0 x0 x1
xn b, 不能
用 n 来表示分割 T 越来越细,因为可能某些
f ( )x
i 1 i
b
n
i
J ,
n
则称 f 在 [a , b] 上可积， 并称 J 为 f 在 [a,b]上的
定积分,记作 J a f ( x )dx lim
T 0
f ( i )Δxi .
i 1
前页 后页 返回
其中称 f 为被积函数, [a , b] 为积分区间, x 为积
高等数学-定积分的概念与性质
= σ=1 ( ) .
→0
其中()称为被积函数，()称为被积表达式，称为积分变量,
[, ]称为积分区间，称为积分下限，称为积分上限．
15
02 定积分的定义
注（1）定积分)( 是一个数值，它只与被积函数()
和积分区间[, ]有关，而与积分变量的符号无关，即
(2)近似（“以直代曲”）
在区间 [−1 , ] 上任取一点 ，以 ( ) 为高，
y
y=()
以 为底，作小矩形．小矩形的面积为
( ) ，用该结果近似代替[−1 , ]上的小
O
a
x i -1 ξ i x i
b
x
曲边梯形的面积 ，即
≈ ( ) （ = 1, 2, ⋯ , ）．
)(
=
)(
=
)( ．
（2）定积分存在，与区间的分法和每个小区间内 的取法无关.
Hale Waihona Puke （3）按照定积分的定义，记号)( 中的, 应满足关系
< ，为了研究的方便，我们补充规定：
① 当 =
② 当 >
时， = )( = )( 0；
在区间 [1,2] 内， 0 ≤ < 2 < 1 ，
则( )3 < .由性质5.5的推论1，得
2
1
>
2
1 ( )3 ．
28
极限，得 σ=1 ( ) .
→0
如果对于[, ]的任意分法及小区间[−1 , ]上点 的任意
取法，上述极限都存在，则称函数()在区间[, ]上可积，
高等数学 第五章 定积分的概念及其性质
() a,( ) b, a (t) b,t [, ]
则有定积分换元公式：
b a f (x)dx
例1：计算定积分
(1)
4
cos(2
x
)dx
0
4
1
(2)
1 x2 dx
0
定积分的计算
解：(1)
4
cos(2
x
)dx
0
4
1
4
cos(2
x
)d
(2
x
)
20
4
4
令 t 2x ，则当 x 时，t
解：(2)、 y 1 x2
y2 x2 1( y 0)
如图
y
1S
o
1x
（2）
定积分的概念及性质 4、定积分的计算法则
法则1 常数因子可以提到积分号外.即
法则2 两个函数代数和的定积分等于它们定积分的代数和，即
法则3 (积分区间的可加性) 对任意的点c,若函数在区间
上均可积，则有
定积分的概念及性质
4
4
4
则当 x 0时，t ，有：
原式 1 2
4
4
cos
tdt
4
1 sin t 4 2 4
2 2
(2) 1 1 x2 dx 0
令 x sin t ，则当 x 1 时，t
2
则当 x 0时，t 0 ，有：
原式 2 1 sin2 td sin t 0
2
cos2
tdt
例2
求
1
0 (
x3
x
1)dx
．
解
1
(
x
3
x
1)dx
高等数学5.1 定积分概念
1
1 0
x 2 dx lim
0
i 1
n
1 f(x i )x i lim 1 (1+1 )(2+1 ) ． n n n 3 6
利用几何意义求定积分：
求积分
0 (1 - x)dx
1
．
解 以y=1-x为曲边，以区间[0, 1]为底的曲边梯形为一直角 三角形， 所以
O
a x 1 x1 x 2 x2n i 1xi-1 Nhomakorabeaxi xi
xn-1 b x
•曲边梯形的面积近似为：A f (x i )xi ．
•记 max{x1, x2， · ·x n }．则 ·,
•曲边梯形的面积的精确值为：A= lim f (x i )xi ． 0
i 1 n
(2)和 f (x i )xi 通常称为f (x)的积分和．
i 1 n
b
b
b
定积分的可积性问题：
如果f(x)在[a, b]上的定积分存在，我们就说f(x)在[a, b]上可 积． 定理1 设f (x)在区间[a，b]上连续，则f (x) 在[a，b]上可积． 定理2 设f (x)在区间[a，b]上有界，且只有有限个间断点，则 f (x) 在[a，b]上可积．
把区间[a，b]分成n个小区间
[x0，x1]，[x1，x2]，· ，[xn-1，xn] ， · · 各小段区间的长依次为
x1x1-x0，x2x2-x1，· ，xn xn -xn-1． · ·
任取xi [xi-1，xi] ，作函数值 f (xi)与小区间长度xi的乘积 f (xi) xi (i1，2，· ，n) ， · · 并作出和 S=
高等数学 第五章定积分习题课
∫
b
a
f ( x )dx ≤ ∫ g ( x )dx
a
b
⑧估值定理：设M 和 m 分别是函数 f ( x )在区间[a, b ]上的 估值定理： 最大值和最小值， 最大值和最小值，则
m (b − a ) ≤ ∫ f ( x )dx ≤ M (b − a )
a b
上连续, ⑨定积分中值定理：如果函数 f ( x ) 在闭区间[a, b ] 上连续 定积分中值定理： 则至少存在一点ξ ∈(a , b) ,使下式成立： 使下式成立： 使下式成立
b b b
b
a
b
b
∫
b
a
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a c
c
b
⑤区间长： ∫ 1dx = b − a 区间长：
a
b
保号性： ⑥保号性：如果在区间[a, b ]上, f ( x ) ≥ 0 ，则∫ a f ( x )dx ≥ 0
b
⑦单调性：如果在区间 [a, b ] 上, f ( x ) ≤ g ( x ) 则 单调性：
b
∫
b
a
f ( x )dx = lim ∫ f ( x )dx −
t →b a
t
设 c ( a < c < b ) 为 f ( x ) 的瑕点，则有 的瑕点，
∫
b a
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a c
c
b
= lim ∫ f ( x )dx + lim ∫ f ( x )dx − +
∫
b
a
f ′( x )dx = [ f ( x )] a = f (b) − f (a ) = a − b
高等数学定积分的概念及性质课件
2.可积的充分条件：
定理1.函数f (x)在[a,b]上连续，则f (x)在[a,b]可积。 定理2.函数f (x)在[a,b]上有界，且只有有限个间断点， 则f (x)在[a,b]可积。
(1) f (x) 0,
b
a f (x)dx A
定积分等于曲边梯形的面积
(2) f (x) 0,
n
A Ai i 1
2.取近似
y
f (i )
y f (x)
Ai
o
x0 x1 x2
x xi1 i
x
x x xn2 n1 n
2.取近似
任取i xi1, xi , Ai f (i )xi
n
A f (i )xi
i =1
3.取极限
y
分割越来越细（也就是插入的分点越来越多）
确定的常数I，则称f (x)在[a,b]上可积，称此极限I为函数
f (x)在区间[a,b]上的定积分, 记作 b f (x)dx，即 a
b
n
a
f (x)dx lim 0 i1
f (i )xi
积分上限 a,b称为积分区间
积分号
b
n
a
f (x)dx lim 0 i1
b
a f (x)dx A
定积分等于曲边梯形面积的相反数
(3) f (x)在区间a,b变号时,
b
a f (x)dx A1 A2 +A3 A4 A5
定积分等于各部分面积的代数和
例1 计算 b f (x)dx a
解：此曲边梯形是高为1,
底边长为b a的矩形
f (x) 0
b
a dx b a
定积分是高等数学中占有重要地位的
1
b a
g(x)dx
b
f (x)g(x)dx = f (ε)
a
但若
1
b a
g(x)dx
b
f (x)g(x)dx = Mf
a
则
b
(Mf − f (x))g(x)dx = 0
a
由 (Mf − f (x))g(x) 0 导出 (Mf − f (x))g(x) = 0
从而由
b a
g(x)dx
=
0，存在
ε
∈
(a,
−
h
x0 a
f (t)dt
−
f (x0)|
=|
x0 +h x0
f
(t)dt
−
h
x0 x0
+h
f
(x0
)dt
|
1 h
x0 +h
|f (t) − f (x0)|dt
x0
因为 f(x) 在 x0 连续，从而对 ε > 0，存在 δ > 0，当 |t − x0| δ 时， |f (t) − f (x0)| < ε，从而当 0 < h < δ 时，
1 h
x0 +h
|f (t) − f (x0)|dt < ε
x0
从而
lim
h→+0
x0 +h a
f
(t)dt
−
h
x0 a
f (t)dt
=
f (x0)
同样方法：
lim
h→−0
x0 −h a
f
(t)dt
−
h
x0 a
f (t)dt
=
高等数学第6章
• 另外，如果这个极限存在，也称广义积分 • 收敛，否则称广义积分
发散。
• 同样可定义广义积分 及其收敛
• 和发散。对广义积分 •
，
存在的充分必要条件是对任意 实数a,两个广义积分 和
都收敛。
• 6.5.2 无界函数的定积分
• 定义6.5.2 设函数 f (x)在[a,b)有定义，且当 x→b-时，f (x)→∞，设δ＞0，积分
• 如果极限
• 存在，这个极限就称为无界函数 f (x)在[a,b] 上的广义积分，记为
• 也称广义积分
极限 •
收敛。否则，如果
不存在，就称广义积分
是发散的。
• 类似地，如果当x→a+时，f(x)→∞，可以类
似地定义广义积分 为：
• 而对当a＜c＜b,当x→c时，f(x)→∞，规定广
义积分 • 和 存在当且仅当广义积分 都存在，且
• 6.3 微积分学基本定理 • 6.3.1 变限定积分 • 定理6.3.1 如果函数f (x)是区间[a,b]上的一个
连续函数，那么当a≤x≤b时，变上限积分
• 是一个可导函数，且
• 定理6.3.2 在区间[a,b]上连续的函数 f (x)的
• 原函数一定存在，且变上限积分
• 就是它的一个原函数。 • 例6.3.4 设 f (x)，g(x)和h(x)都是连续函数，
• 令各小区间的最大长度
，
• 如果不论小区间怎样划分，也不论在小区
间[xk-1,xk]上如何取ξk，当λ→0时，极限
•
• 为
总是存在，则这一极限就称
为函数 f (x)在区间[a,b]上的定积分。记 ，即：
• 关于定积分的定义，我们做如下说明：
定积分的参数化代换法
定积分的参数化代换法定积分是高等数学中的一个重要分支，它对于各个领域的数学科学都有着重要的贡献。
在计算一些较为复杂的定积分时，常常采用参数化代换法，该方法通过对被积函数进行参数化，将复杂的积分式转化为简单的形式，从而方便计算。
以下，我们将从定积分的概念入手，详细介绍参数化代换法的具体应用。
一、定积分的概念在高等数学中，定积分是指对于一个函数f(x)，确定其在区间[a,b]上的某一部分的面积。
这个面积可以看作是由一系列无限小的短条形成的。
在[ a, b ]之间分出n等份，每份长度为(xᵢ₊₁- xᵢ)，取一点xᵢ*，其中i=0,1,2,...,n-1。
这时将[ xᵢ, xᵢ₊₁ ]看做一个小区间，将函数在这个小区间内的取值f(xᵢ*)看做是小区间的高，则小区间面积为f(xᵢ*)·(xᵢ₊₁ - xᵢ)，将所有小区间面积相加，这个和即为定积分，记作∫(下限a,上限b)f(x)dx。
具体公式如下：∫(a,b)f(x)dx=lim(Δt→0)Σf(xᵢ*)Δx二、参数化代换法的含义在实际计算定积分时，有时我们会面对一些较为复杂的被积函数，此时如果采用传统的积分方法，往往会变得非常繁琐。
这时，我们可以通过参数化代换法，对被积函数进行参数化，将变量替换成一组新的参数，从而化繁为简，方便计算。
具体来说，参数化代换法即是将原来的自变量x用一个或多个新的参数t表示出来，即x=x(t)，然后将原来的被积函数f(x)写成f(x(t))，此时，对于变量t，可以进行简单的积分计算，从而方便求出整个定积分。
这个过程可以看作是将原来的积分区域用一定的方式变形，从而使得被积函数变得更加简单。
三、参数化代换法的基本思路在采用参数化代换法计算定积分时，我们需要遵循以下基本思路：（1）选取合适的替代变量：一般情况下，我们会选择对称、周期或者特殊的函数作为替代变量。
（2）确定替换公式：确定替代变量后，需要根据替代变量和原函数的关系确定替换公式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
xi xi xi1,(i1,2,,n)， 在各小区间上任取一点
i(i[xi1， xi]), 作乘积 f(i)xi (i1,2,,n)， n 并作和 S f(i )xi i1
记 m x a 1 , x x 2 , , x n ， 如果不论对区间[a , b]
n
a
f (x)
dx
lim 0 i1
f (i )xi
积分和
积分下限
被
积
函
数
被 积 表 达 式
积 分
变 [a , b ] ：积分区间
量
9
注意：
b
(1) f ( x )dx是一个确定的常数. a
(2)积分值与被积函数及积分区间有关，而与积分变量
使用的字母无关. b f ( x) dx
3
曲边梯形如图所示，
(1)分割： 在区间[a,b]内插入若干个分点， a x 0 x 1 x 2 x n 1 x n b ,
把区间[a,b]分成n个小区间[xi1, xi ]，长度为
xi xi xi1;i1,2, ,n.
(2)近似：
y
在每个小区间[xi1, xi ]
ti ti ti1
(2)近似 部分路程近似值 si v( i ) t i
n
(3)求和 s v(i )ti
ti1 ti t i
(4)取极限
i1
m t 1 ,a t2 , x , tn } {
i
t
n
路程的精确值 slim 0i1v(i)ti
上任取一点 i ，以
[xi1, xi ]为底，f(i)为 o a x 1
b xi1 i x i xn1
x
高的小矩形面积为 f(i)xi 则 Ai f(i)xi
4
n
(3)作和式：曲边梯形面积的近似值为 Af(i)xi
i1
(4)取极限：当分割的无限细密，即最大的小区间的长度
n
而曲边梯形面积
Alim
0i1
f(i)xi
7
二.定积分的定义
定义 设函数 f (x)在[a , b]上有界，在[a , b]中任意插入若
干个分点 a x x x x x b 把区间
012
n 1 n
[a , b] 分成 n个小区间，各小区间的长度依次为
b
f (t)dt
b
f (u)du
a割方法无关，与 i 的取法无关.
(4)当函数 f(x)在区间[a,b]上的定积分存在时，称 f(x)
在区间[a, b]上可积.
n
b
(5)
曲边梯形面积
Alim 0i1
f(i)xi
n
a
f (x)
变速直线运动的路程 slim 0i1v(i)ti
面积的代数和.
即
b
af(x)dxA 1 A 2A 3 A 4 12
b
f ( x )dx的几何意义：它是介于x轴、函数 f (x)的图形
a
及两条直线x=a，x=b之间的各部分面积的代数和. 且
x轴上方的面积取正号；在x轴下方的面积取负号.
即 a bf(x)dxA 1 A 2A 3 A 4
图形的面积都可以转化为曲边梯形面积的代数和.
y
y
y
oa
b x oa
bx o a
bx
(3)求由连续函数 yf(x)(f(x)0)和三条直线x=a,
x=b,y=0所围成的封闭图形的面积.
2
用矩形面积近似代替曲边梯形面积
y
y
oa
b xo a
bx
（四个小矩形）
（九个小矩形）
显然: 小矩形越多，矩形总面积越接近曲边梯形面积．
[T1,T2]上t 的一个连续函数，且 v(t) 0，求物体在这
段时间内所经过的路程. 思路：把整段时间分割成若干小段，每小段上速度 看作不变，求出各小段的路程再相加，便得到路程 的近似值，最后通过对时间的无限细分过程，求得 路程的精确值
6
(1)分割 T 1 t 0 t 1 t 2 t n 1 t n T 2
11
四.定积分的几何意义
b
1. 当 f(x)0时， f (x)dx A 曲边梯形的面积 a
2. 当 f(x)0时， b f (x)dxA曲边梯形面积的负值 a
y yf(x) y
a
b
o
A
oa
bx
x
A
yf(x)
A3
A1
A2 o
A4
b
3. 当 f (x) 在[a,b]上有正有负时， f ( x)dx表示各部分 a
5-1定积分的概念
一、问题的提出 实例1：求曲边梯形的面积.
(1)曲边梯形定义：由一条连续曲线 yf(x)(f(x)0) 和三
条直线 x=a, x=b, y=0 所围成的封闭图形.
y yf(x)
y yf(x)
y yf(x)
oa
bx o a
bx o a
bx
1
(2)求曲边梯形面积的意义：由平面曲线所围成的平面
怎样的分法，也不论在小区间[xi1, xi ]上点 i 怎样
的取法，只要当 0时，和 S总趋于确定的极限I 8
n
我们称这个极限
I lim 0 i1
f(i )xi
为函数 f (x) 在区间
[a , b]上的定积分，记为
b
f ( x ) dx.
简称：积分
a
积分上限
b
a
A1
A3y=f(x)
A2
b
A4
13
五.定积分的性质
一.基本内容
对定积分的补充规定:
(1)当a=b时, b f (x)dx0；即 a f (x)dx 0；
a
a
dx. vT2
T1
(
t
)dt
10
三.存在定理 定理1 如果函数f(x)在区间[a,b]可积，则f(x)
在区间[a , b] 上有界. 定理2 如果函数f(x)在区间[a,b]上连续或仅有有限个
第一类间断点，则函数f(x)在区间[a,b]上可积.
即 b f ( x) dx存在. a
以上定理的证明省略,只要求记住结论.
m a x 1 , x x 2, {, x n }趋于零时，
曲边梯形面积为:
y
n
Alim 0i1
f(i)xi
以上做法的步骤:
oa x1
分割,近似,取和,求极限.
b xi1 i x i xn1
x
5
实例2 ：求变速直线运动的路程.
设某物体作直线运动，已知速度 v v(t)是时间间隔