t梁预应力张拉伸长量计算
T梁张拉计算公式
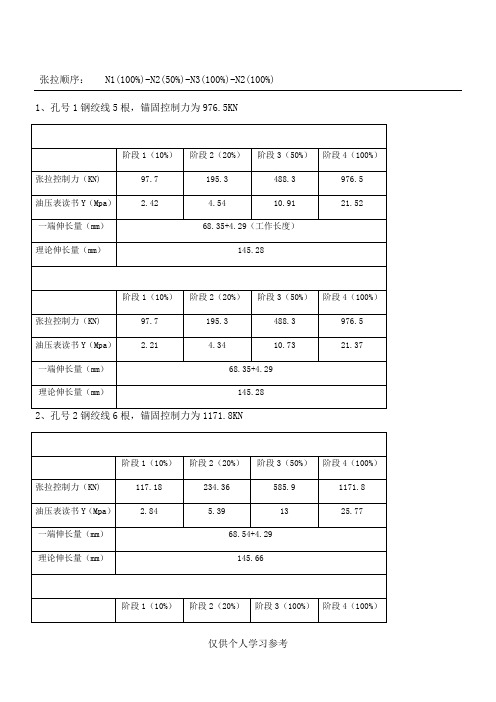
张拉顺序:N1(100%)-N2(50%)-N3(100%)-N2(100%) 1、孔号1钢绞线5根,锚固控制力为976.5KN3、孔号3钢绞线6根,锚固控制力为1171.8KN实测伸长值等于从初应力(10%)到锚固应力(100%)的实测伸长值+初应力以下的推算伸长值(采用相邻级的伸长值,即10%到20%应力的伸长值)。
一、张拉力的计算:根据设计图纸提供φ15.2钢铰线:公称直径d=15.2mm,抗拉强度标准值fpk=1860Mpa,张拉控制应力:σcon=0.75fpk=0.75×1860=1395Mpa;单根钢铰线截面积(查钢绞线质量证明书)为:Ap=140mm2单根钢铰线的张拉力为:P=σcon×Ap=1395×140=195.3KN=195.3×5=976.5KN单束(5根)钢铰线张拉力为:P7单束(6根)钢铰线张拉力为:P=195.3×6=1171.8KN81(1(2其中:LApEpx:从张拉端至计算截面孔道长度(m)θ:从张拉端至计算截面曲线孔道部分切线的夹角之和(rad)k:孔道每米局部偏差对摩擦的影响系数μ:预应力钢绞线孔道壁的磨擦系数2、根据设计图纸及材料试验检验提供数据:钢铰线弹性模量Ep=1.95×105Mpa;锚具变形、钢筋回缩按6mm(一端)计算;塑料波纹管摩阻系数μ=0.25,偏差系数K=0.0015;钢绞线一端工作长度为:0.600m,一端伸长量4.29mm。
三、各钢束理论伸长值计算终点力P1=P×e-(kx+μθ)=967.8KN平均张拉力Pp=P[1-e-(kx+μθ)]/(kx+μθ)=972.1KNΔL1′=ΔL=PpL1/ApEp=42.62mm②L2=2.118mθ=0.1059KL+μθ=0.0015×2.118+0.25×0.1059=0.0296522e-(kx+μθ)=0.97078=967.8KN张拉端力P=P1终点力P=P×e-(kx+μθ)=939.5KN2Pp=P[1-e-(kx+μθ)]/(kx+μθ)=953.6KNΔL2③+KL3e-ΔL3所以计算理论伸长值ΔL=2*ΔL=136.7mmN12、以T梁中板N2管道为例,其余管道及负弯矩处钢绞线伸长值计算见附表。
T梁张拉计算

张拉计算、计算公式及参数依据1、计算依据:根据《公路桥涵施工技术规范》(JTJ041-2000)及 《上社大桥、罗溪中桥、西江溪大桥图纸》。
2、计算公式:①预应力筋的理论伸长值计算公式:PLA L = -P ——A p E p式中:AL —理论伸长值P p ——预应力筋的平均张拉力(N),直线筋取张拉端的拉力, 两端张拉的曲线筋。
预应力筋的长度(mm)-预应力筋的截面面积(mm 2); -预应力筋的弹性模量(N / mm 2)。
②预应力筋平均张拉力计算公式:式中:Pp —预应力筋平均张拉力(N)P —预应力筋张拉端的张拉力(N)x —从张拉端至计算截面的孔道长度(m)。
一从张拉端至计算截面的曲线孔道部分切线的夹角之和(rad) k —孔道每米局部偏差对摩擦的影响系数:u 一预应力筋与孔道壁的摩擦系数。
AP E在此计算时,切记不能将平均张拉力按照起终点力平均求解,因 为每段钢绞线力的衰减非正比例。
同时,进行分段计算时,靠近张拉 端第一段的终点力即为第二段的起点力,每段的终点力与起点力的关 系如下式:P = P* e -(-kx+u0)P —分段终点力(N) zP —分段的起点力(N)8、X 、k 、u —意义同上其他各段的起终点力可以从张拉端开始进行逐步的计算。
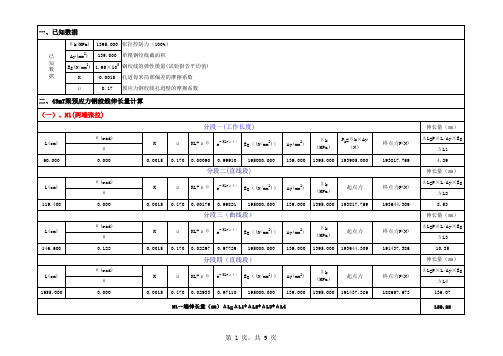
3、计算参数:设计采用标准强度f pk =1860MPa 的低松弛高强度钢绞线,公称直 径15.2mm ,公称面积A P =139mm 2,弹性模量E P =1.95x105Mpa ,孔道 摩擦系数 ^=0.25, k=0.0015;单根钢绞线张拉锚下控制应力为: 8 k =0.75 f pk =1860x0.75 = 1395Mpa单根预应力筋张拉力为:1395x139 = 193905N,取193.9KN二、张拉理论伸长值计算本标段40、35、30mT 梁采用两端对称张拉,钢绞线为曲线计算, 先按图纸计算1/2片梁的张拉理论伸长值,分三段计算,A 、B 、C 段, 其中A 和C 段为直线段,B 段为曲线段。
40m、45m预应力T梁张拉伸长量计算表
分段四(直线段)
θ(rad) L(cm) θ 1705.200 0.000 0.0015 0.170 0.02558 K μ KL+μθ e-(KL+μθ) 0.97475 Eg((N/mm2)) 195000.000
N1一端伸长量( ㎜)ΔL=ΔL1+ΔL2+ΔL3+ΔL4
第 5 页,共 9 页
(二)、N2(两端张拉) 分段一(工作长度)
分段四(直线段)
θ(rad) L(cm) θ 191.000 0.000 0.0015 0.170 0.00287 K μ KL+μθ e-(KL+μθ) 0.99714 Eg((N/mm2)) 195000.000
N4一端伸长量( ㎜)ΔL=ΔL1+ΔL2+ΔL3+ΔL4
第 4 页,共 9 页
二、40mT梁预应力钢绞线伸长量计算 (一)、N1(两端张拉) 分段一(工作长度)
分段四(直线段)
θ(rad) L(cm) θ 1955.000 0.000 0.0015 0.170 0.02933 K μ KL+μθ e-(KL+μθ) 0.97110 Eg((N/mm2)) 195000.000
N1一端伸长量( ㎜)ΔL=ΔL1+ΔL2+ΔL3+ΔL4
第 1 页,共 9 页
(二)、N2(两端张拉) 分段一(工作长度)
θ(rad) L(cm) θ 60.000 0.000 0.0015 0.170 0.00090 K μ KL+μθ e-(KL+μθ) 0.99910 Eg((N/mm2)) 195000.000 Ay(mm2) δk(MPa) 139.000 1395.000 起点力 193905.000 终点力P(N) 193817.769 伸长量(㎜) ΔL=P×L/Ay×Eg ΔL1 4.29 伸长量(㎜) Ay(mm2) δk(MPa) 139.000 1395.000 起点力 193817.769 终点力P(N) 193506.879 ΔL=P×L/Ay×Eg ΔL2 15.28 伸长量(㎜) Ay(mm2) δk(MPa) 139.000 1395.000 起点力 193506.879 终点力P(N) 190631.191 ΔL=P×L/Ay×Eg ΔL3 29.46 伸长量(㎜) ΔL=P×L/Ay×Eg ΔL4 0.0015 0.170 0.02011 0.98009 195000.000 139.000 1395.000 190631.191 188727.555 93.33 142.37
预应力张拉计算书

预应力张拉计算书预应力张拉为T梁质量控制的关键工序,为了规范梁场内预制梁张拉施工工序,特制定张拉计算书进行指导现场规范施工。
一、锚外控制力计算:P=Ay*σk/(1-η)*nP—锚外控制力,Nσ k—张拉控制应力,MPaAy —钢绞线面积,mm2η—锚口喇叭损失,暂取设计图提供6%计算,根据铁科院实际摩阻计算。
n—计算预应力孔道的钢绞线根数二、理论伸长量计算:由于梁的预应力筋是有直线与曲线组成的多线段预应力筋,故采用要分段计算然后叠加。
1、直线段预应力伸长量计算预应力筋的理论伸长值⊿L(mm)可按下式计算:⊿L=PpL/(ApEp)式中:Pp---预应力筋的平均张拉力(N),直线筋取张拉端的拉力,两端张拉的曲线筋,取张拉端的拉力与跨中扣除孔道摩阻损失后拉力的平均值(计算方法见曲线段计算);L--- 预应力筋的长度;Ap---预应力筋的截面面积(mm2);Ep---预应力筋的弹性模量,根据材料试验确定(N/ mm2)。
2.曲线段预应力伸长量计算⑴ 计算截面张拉力计算后张法结构由于预应力筋与管道之间存在摩擦阻力,预应力筋沿长度方向各个截面的张拉力并非均匀,而是从张拉端开始逐渐减小,因此,计算伸长量时,应取计算段内的钢筋拉力的平均值。
同时考虑管道局部偏差摩阻影响,计算段终点截面内的预应力筋的拉力为:① ()()N e p k s p μθι+−⋅=S P ——从计算起点经过l 长度之后至终点截面的预应力筋的张拉力,单位为N;μ——预应力筋与孔道壁之间的摩擦系数,根据铁科院摩阻试验确定; θ——预应力筋计算起点至计算截面曲线孔道部分的夹角(rad),θ=0,即为直线。
K——每米长度局部偏差的摩擦系数,根据铁科院试验确定;ι——从计算点至计算截面的孔道长度。
② L 段内预应力之平均值为:Pp = P(1-e-(kl+µθ))/(kl+µθ)Pp——从计算点至计算截面的预应力筋的张拉力,单位为N;其余同上。
30米t梁公路预制梁钢绞线张拉伸长量计算

预制梁钢绞线张拉伸长量计算一、计算公式及有关参数(依据)1、本计算依照《公路桥涵施工技术规范》JTJ041—2000;2、预应力钢绞线的伸长值△L(mm)计算公式及说明:△L=P p L/A p E p (12.8.3-1)式中:P p—预应力筋的平均张拉力(N),直线筋取张拉端的拉力,两端张拉的曲线筋计算方法见附录6—8式.P p=P[1-e-(kx+µθ)]/(kx+µθ) P=σ控×A p所以△L= P[1-e-(kx+µθ)]×L/(kx+µθ)A p E p=[1-e-(kx+µθ)]σ控L/ (kx+µθ)E p =ησ控L/E p 式中: L—预应力筋的长度(计算长度);A p—预应力筋的截面面积;E p—预应力筋的弹性模量(N/mm2),钢绞线E=195±10Gpa;P—预应力筋的张拉端至张拉力p=σ控A p;X—从张拉端至计算截面的孔道长度;θ—从张拉端至计算截面曲线孔道部分切线的夹角之和(rad);k—孔道每米局部偏差对摩擦的影响系数;对于预埋合金螺旋管道:k=0.0015;µ—预应力筋于孔道壁的摩擦系数µ=(0.2+0.25)/2=0.225二、论伸长量(梁长30米)的计算:N1束 L=3113.37cm k=0.0015 x=L/2=1556.686cm µ=0.225 θ=0.122171rad (1度=0.017453 rad)η=[1-e-(kx+µθ)]÷(kx+µθ)=[1-e-(0.0015×15.56686+0.225×0.087265)]÷(0.0015×15.56686+0.225x0.087265) =(1-e-0.050838765)/0.050838765=0.9750△L=ησ控L/E p=0.9750×1395×106Pa×31133.7mm/(195x109Pa)=217.16mm N2束 L=3117.98cm k=0.0015 x=L/2=1558.99cm µ=0.225 θ=0.122171radη=[1-e-(kx+µθ)]/(kx+µθ)=0.97499△L=ησ控L/E p=0.97499×1395×106Pa×31179.8mm/(195×109Pa)=217.48mm N3、N4束 L=3114.14cm k=0.0015 x=L/2=1557.07cm µ=0.225θ=0.034906radη=[1-e-(kx+µθ)]/(kx+µθ)=0.98456△L=ησ控L/E p=0.98456×1395×106Pa×31141.4mm/(195×109Pa)=219.34mm三、预应力钢绞线张拉伸长量值的修正计算:取前述N1~N4钢绞线平均伸长率作为:每延米伸长量作为值修正参数.N1伸长率:217.16/31133.7=6.98‰N2伸长率:217.48/31179.8=6.98‰N3、N4伸长率:219.34/31141.4=7.04‰平均伸长率:( 6.98‰+6.98‰+7.04‰+7.04‰)/4=7.01‰四、实测伸长量值计算与修正:1.实测伸长量值计算(计算长度=孔道长+千斤顶内预应力筋长度,按每端0.5米计)△L实测=(σ控下张拉伸长值之和-σ初始张拉伸长值之和-A)/0.9式中:A—锚具回缩(在σ控与σ初始之间的锚具回缩,含夹片回缩)2.千斤顶内钢绞线伸长量BB=2×500×7.01‰=7mm3.张拉伸长量修正值(计算长度=孔道长)C=△L实测-B五、张拉精度评价|(C/△L)×100%—100%| ≤ 6%六、各束伸长量(单位mm):N1 :210.16 N2:210.48 N3 :210.34N4 :210.34。
16m连续T梁张拉伸长量计算
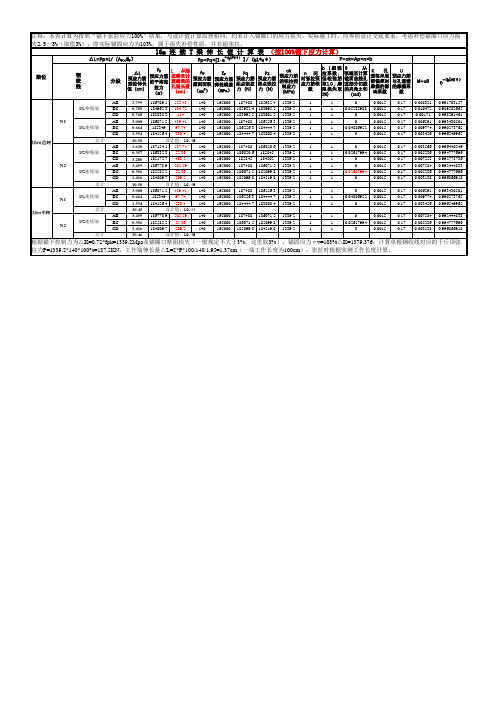
16m 连 续 T 梁 伸 长 值 计 算 表 (按100%锚下应力计算)
N2
设计值:10.46
根据锚下控制力为△K=0.72*fpk=1339.2Mpa及锚圈口摩阻损失(一般规定不大于3%,这里取3%),锚固应力σ v=103%△K=1379.376;计算单根钢绞线对应的千斤 顶张拉力P=1339.2*140*100%=187.5KN,工作端伸长量△L=2*P*100/140/1.95=1.37cm(一端工作长度为100cm),张拉时根据实测工作长度计算。
△L=Pp×L/(AP×EP) Pp=Pq×[1-e-(kl+Uθ
)
]/ (kl+uθ )
P=σk×Ap×n×b
K U 孔道每米 预应力筋 局部偏差 与孔道壁 kl+uθ 对摩擦的 的摩擦系 影响系数 数 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.0015 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.008331 0.010472 0.00171 0.006591 0.009774 0.003456 0.003566 0.005236 0.007253 0.007584 0.005236 0.003138 0.006591 0.009774 0.003456 0.007584 0.005236 0.003138
40米T梁张拉力及伸长量计算

杨柳河大桥40米预应力T梁张拉计算书编制:复核:审核:2011年3月15日杨柳河大桥40米预应力T梁张拉计算书一、张拉施工方案我合同段施工的阁丫沟大桥40米T梁预应力钢绞线采用高强度低松弛钢铰线,f pk=1860Mpa,公称直径d=15.2mm,公称面积Ay=139mm2,弹性模量Ey=1.95×105Mpa。
40米T梁正弯矩钢束采用8股、9股,钢束控制张拉力σcon=0.75 f pk=1395Mpa。
锚具采用15-8型、15-9型系列整套锚具,管道成孔采用钢波纹管。
所有锚具及钢绞线按材料检验批量抽检,严禁使用无部级以上级别技术鉴定和产品鉴定的材料。
材料要有厂方提供的质量说明书和出厂时间。
钢铰线要防止生锈和影响水泥粘结的油污。
钢铰线下料采用砂轮切割机按加工长度下料,并以22#铁丝编束。
钢筋绑扎结束,装模前由专人对波纹管进行检查,若有孔眼须用胶布缠好,严禁进浆。
预应力张拉前先试压同条件养护砼试件,主梁达到设计强度85%以上且养护龄期不小于7天方可张拉,钢束张拉时应两端对称、均匀张拉,不得集中张拉,并观察主梁的侧弯情况,张拉前先对张拉千斤顶进行校核。
张拉顺序为:50%N2、N3→100%N1→100%N2、N3→100%N4,张拉程序:0-初始应力(10%σk)-σk(持荷2分钟锚固)。
张拉时实行双控,理论伸长量与实际伸长量相差应控制在-6%~+6%之间,否则应分析原因或重新张拉。
张拉严格控制滑丝和断丝,每束不超过1根,累计全片梁小于1%。
张拉完割除钢铰线头,及时压浆。
张拉时做好施工记录。
二、理论伸长值计算1、理论伸长量计算钢铰线采用15.2mm 单根截面面积139mm2标准强度f pk =1860MPa 弹性模量Ey=1.95×105MPa 管道摩擦系数μ=0.25 管道偏差系数K=0.0015锚下控制应力σcon=0.75×f pk=1860×0.75=1395MPa每股控制张拉力1395×139=193905N4股钢绞线控制张拉力N=193905×4=775620N=775.62KN8股钢绞线控制张拉力N=193905×8=1551240N=1551.24KN9股钢绞线控制张拉力N=193905×9=1745145N=1745.15KN计算公式:P P=P(1-e(kx+μθ))/(kx+μθ)△L=P P×L/AP×EP式中:P P--预应力筋平均张拉力(N)P--预应力筋张拉端的张拉力(N)e—常数(e =2.7183)k—孔道摩擦系数(取0.0015)x—从张拉端至计算截面积的孔道长度(米)μ—孔道偏差系数(取0.2)θ—从张拉端至计算截面积曲线孔道部分切线的夹角之和(rad)L--预应力筋的长度(mm)A P --预应力筋的截面面积(mm2)(取139mm2)E P --预应力筋的弹性模量(取1.95*105N/mm2)计算说明:T梁两端对称张拉,所以采用单端计算的方法进行计算。
T 梁预应力张拉计算书

T 梁预应力张拉计算书一.控制应力1.控制张拉应力:σcon=0.75R y b=0.75×1860Mpa=1395Mpa2.钢绞线张拉控制力:P K=σcon·A g·n·1/1000(KN)式中A g为钢绞线的公称面积,n为钢绞线的根数一根钢绞线的张拉控制力为P K=1395Mpa×140mm2=195.3KN 中梁: N1=195.3KN×6=1171.8KNN2=195.3KN×6=1171.8KNN3=N4=195.3KN×7=1367.1KN边梁: N1=195.3KN×7=1367.1KNN2=195.3KN×7=1367.1KNN3=N4=195.3KN×7=1367.1KN二.伸长量1.理论伸长量(△L)计算△L=P p·L/(A p·E g)P p=P·[1-e-(kx+μθ)]/(kx+μθ)其中P P是钢绞线的平均张拉力(N),L是钢绞线的长度(m),A P是钢绞线截面积(mm2),E g是钢绞线的弹性模量(N/mm2),P 是钢绞线张拉端的张拉力(N),x是从张位端至计算截面的钢绞线长度(m),θ是从张位端至计算截面曲线部分切线的夹角之和(rad),k为孔道偏差系数,取k=0.0015,μ为摩阻系数,取μ=0.20中梁各束钢绞线伸长量⑴N1束θ=0.15708(rad) x=16.015mP p=1171.8×[1-e-(0.0015×16.015+0.20×0.15708)]/ (0.0015×16.015+0.20×0.15708)=1139.9KN△L=1139.9×32.03/(6×140×195)=222.9mm每端的伸长量△L=111.45mm⑵N2束θ=0.15708(rad) x=16.03mP p=1171.8×[1-e-(0.0015×16.03+0.20×0.15708)]/ (0.0015×16.03+0.20×0.15708)=1139.9KN△L=1139.9×32.06/(6×140×195)=223.1mm每端的伸长量△L=111.55mm⑶N3,N4束θ=0.07505(rad) x=15.94mP p=1367.1×[1-e-(0.0015×15.94+0.20×0.07505)]/ (0.0015×15.94+0.20×0.07505)=1340.8 KN△L=1340.8×31.88/(7×140×195)=223.7mm每端的伸长量△L=111.84mm边梁各束钢绞线伸长量⑴N1束θ=0.15708(rad) x=14.945mP p=1367.1×[1-e-(0.0015×14.945+0.20×0.15708)]/ (0.0015×14.945+0.20×0.15708)=1331KN△L=1331×29.89/(7×140×195)=208.2mm每端的伸长量△L=104.1mm⑵N2束θ=0.15708(rad) x=14.96mP p=1367.1×[1-e-(0.0015×14.96+0.20×0.15708)]/ (0.0015×14.96+0.20×0.15708)=1330.9 KN△L=1330.9×29.92/(7×140×195)=208.4mm每端的伸长量△L=104.2mm⑶N3,N4束θ=0.07505(rad) x=14.87mP p=1367.1×[1-e-(0.0015×14.87+0.20×0.07505)]/ (0.0015×14.87+0.20×0.07505)=1341.9 KN△L=1341.9×29.74/(7×140×195)=208.8mm每端的伸长量△L=104.4mm16米空心板预应力张拉计算书一、控制应力1、控制张拉应力:σcon=0.75R y b=0.75×1860Mpa=1395Mpa2、钢绞线张拉控制力:P K=σcon·A g·n·1/1000(KN)式中A g为钢绞线的公称面积,n为钢绞线的根数一根钢绞线的张拉控制力为P K=1395Mpa×140mm2=195.3KN 梁: N1=195.3KN×5=976.5KNN2=195.3KN×5=976.5KN二、伸长量1、理论伸长量(△L)计算△L=P p·L/(A p·E g)P p=P·[1-e-(kx+μθ)]/(kx+μθ)其中P P是钢绞线的平均张拉力(N),L是钢绞线的长度(m),A P是钢绞线截面积(mm2),E g是钢绞线的弹性模量(N/mm2),P 是钢绞线张拉端的张拉力(N),x是从张位端至计算截面的钢绞线长度(m),θ是从张位端至计算截面曲线部分切线的夹角之和(rad),k为孔道偏差系数,取k=0.0015,μ为摩阻系数,取μ=0.20梁各束钢绞线伸长量⑴N1束θ=0.0436(rad) x=15.6mP p=976.5×[1-e-(0.0015×15.6+0.20×0.0436)]/ (0.0015×15.6+0.20×0.0436)=961.3KN单根张拉力:961.3/9.8=98.1T/5=19.6T1#油表:32.043Mpa 2#油表:32.9MPa△L=961.3×15.6/(5×140×195)=10.98mm每端的伸长量△L=5.49mm⑵N2束θ=0.209(rad) x=15.668mP p=976.5×[1-e-(0.0015×15.668+0.20×0.209]/ (0.0015×15.668+0.20×0.209)=945.1KN=96.4T/5=19.28T=31.5Mpa=32.366Mpa单根张拉力:945.1/9.8=96.4T/5=19.28T1#油表:31.5Mpa 2#油表:32.366MPa△L=945.1×15.668/(5×140×195)=10.84mm每端的伸长量△L=5.42mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t梁预应力张拉伸长量计算
梁是建筑和土木工程中常见的结构元素,其承载着重要的荷载和力学性能要求。
为了增强梁的承载能力和抗震性能,预应力技术被广泛应用于梁的设计和施工中。
预应力张拉伸长量计算是预应力梁设计中的重要一环,本文将详细介绍该计算方法。
预应力张拉伸长量是指在预应力张拉过程中,钢束或钢丝的伸长量。
在预应力梁的设计中,通常需要根据预定的预应力水平和设计要求计算出钢束或钢丝的张拉伸长量,以确保梁在使用过程中的性能和安全。
预应力张拉伸长量的计算需要考虑多个因素,包括预应力钢束的特性、混凝土的材料特性以及梁的几何参数等。
其中,预应力钢束的特性包括钢束的弹性模量、钢束的截面面积以及钢束的预应力水平等。
混凝土的材料特性包括混凝土的弹性模量、混凝土的收缩和蠕变特性等。
梁的几何参数包括梁的截面尺寸、梁的跨度以及梁的受荷情况等。
在进行预应力张拉伸长量计算时,首先需要确定预应力钢束的预应力水平。
预应力水平的确定通常需要考虑梁的设计要求和结构安全要求。
根据预应力水平和钢束的特性,可以计算出钢束在张拉过程中的应变量。
应变量与钢束的伸长量之间存在一定的线性关系,通过线性关系可以计算出钢束的伸长量。
在计算钢束的伸长量时,还需要考虑混凝土的收缩和蠕变效应。
混凝土的收缩和蠕变是混凝土在负荷作用下发生的一种变形现象,会导致混凝土的体积缩小和变形。
在预应力梁中,混凝土的收缩和蠕变会对钢束的伸长量产生影响,需要进行相应的修正计算。
在进行预应力张拉伸长量计算时,还需要考虑梁的几何参数。
梁的几何参数不仅会影响梁的刚度和变形特性,也会对钢束的伸长量产生影响。
通过考虑梁的几何参数,可以计算出钢束的有效伸长量。
预应力张拉伸长量计算是预应力梁设计中的重要一环。
通过考虑预应力钢束的特性、混凝土的材料特性以及梁的几何参数,可以计算出钢束的伸长量。
预应力张拉伸长量计算的准确性对于梁的设计和施工具有重要意义,能够确保梁在使用过程中的性能和安全。
因此,在预应力梁设计中,需要严格按照相关规范和标准进行预应力张拉伸长量的计算,以确保梁的质量和使用效果。
