第三章配合物的化学键理论
配合物的化学键理论

配合物的化学键理论配合物的化学键理论摘要:化学键理论在配位化学中有着重要的运用,它现在主要有三大流派。
本文就回顾化学键的发展历程,并对三大化学键理论做出仔细的阐述。
关键字:化学键价键理论分子轨道理论晶体场理论配位场理论化学键的发展历程最早化学家假设原子和原子之间是用一个神秘的钩钩住的,这种设想至今仍留下痕迹,化学键的键字就有钩的意思。
1916年,德国科学家柯塞尔考察大量的事实后得出结论:任何元素的原子都要使最外层满足8 电子稳定结构。
柯塞尔的理论能解释许多离子化合物的形成,但无法解释非离子型化合物。
1923 年,美国化学家路易斯发展了柯塞尔的理论,提出共价键的电子理论:两种元素的原子可以相互共用一对或多对电子,以便达到稀有气体原子的电子结构,这样形成的化学健叫做共价健。
柯塞尔和路易斯的理论常叫原子价电子理论。
它只能定性地描述分子的形成,化学家更需要对化学键做定量阐述。
1927 年,海特勒和伦敦用量子力学处理氢分子,用近似方法计算出氢分子体系的波函数和能量获得成功,这是用量子力学解决共价键问题的首例。
1930 年,鲍林更提出原子成键的杂化理论(杂化轨道理论),洪德把单键、多键分成δ和∏键两类。
δ健是指在沿着连接两个原子核的直线(对称轴)上电子云有最大重叠的共价键,这种键比较稳定。
∏键是指沿电子云垂直于这条直线方向上结合而成的键,这种键比较活泼。
这就使价键理论进一步系统化,使经典的化合价和化学键有机地结合在一起了。
由于上述的价键理论对共扼分子、氧气分子的顺磁性等事实不能有效解释,因此本世纪30 年代后又产生一种新的理论——分子轨道理论。
分子轨道理论在1932 年首先由美国化学家马利肯提出。
他用的方法跟经典化学相距很远,一时不被化学界接受,后经密立根、洪德、休克尔、伦纳德等人努力,使分子轨道理论得到充实和完善。
它把分子看作一个整体,原子化合成分子时,由原子轨道组合成分子轨道,原子的电子属于分子整体。
分子轨道就是电子云占据间,它们可相互重叠成键。
配位化学-配合物的化学键理论
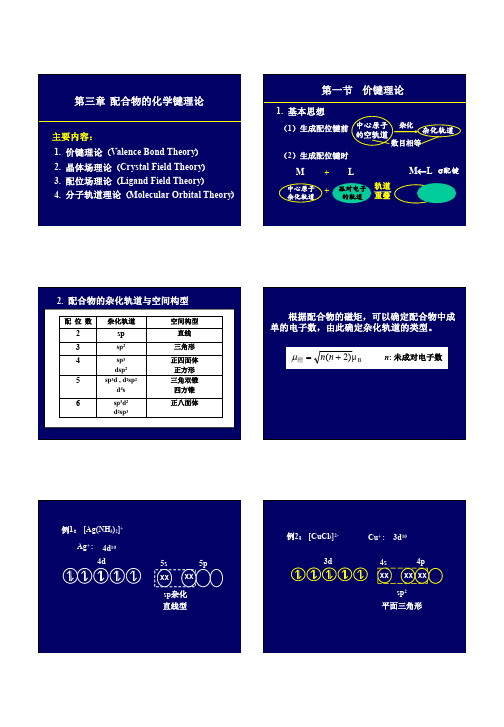
3d
4s
4p
xx xx xx
sp2 平面三角形
1
2017-9-12
例3: [Co(NCS)4]23d
Co2+ 3d7
4s
4p
xx xx xx xx
sp3 四面体
例4:[Ni(CN)4]2- Ni2+: 3d8
3d
4s
4p
电子归并, 杂化
xx xx xx xx dsp2
平面正方形
问题:什么情况下,内层d电子归并?
d. 价键理论不能解释配合物的颜色及吸收光谱。
e. 对非经典配合物无法解释。
3
2017-9-12
第二节 晶体场理论 1929年由Bethe提出
基本思想:
50年代以后得到发展
中心原子 静电作用
配体
①
具有电子结构
无电子结构 静电场
的离子
② 在配体静电场作用下,中心原子原来简并的5个d轨道能
级发生分裂,分裂能量的大小与空间构型及配体、中心原子 的性质有关。
2017-9-12
第三章 配合物的化学键理论
主要内容: 1. 价键理论(Valence Bond Theory) 2. 晶体场理论(Crystal Field Theory) 3. 配位场理论(Ligand Field Theory) 4. 分子轨道理论(Molecular Orbital Theory)
的排斥作用相对较小,能量降低。 dxz
eg (dx2—y2、dz2)
o
d
自由金属离子 球形场
t2g (dxy、dyz、dxz)
八面体场
d轨道在八面体场中的分裂
o:(1)由电子光谱得到;(2)由量子力学微扰理
高中化学—— 配合物的价键理论
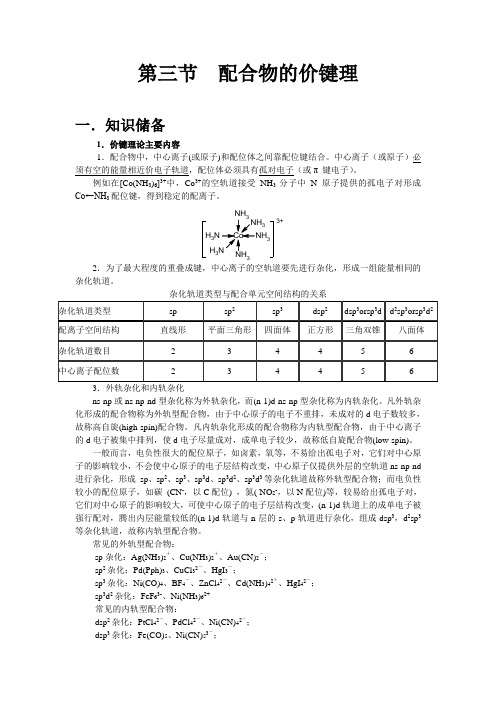
Fe3+ Fe2+ Co3+ Co2+ Mn2+ Fe3+ Co3+ Mn2+ Ni2+
sp3d2 sp3d2 sp3d2 sp3d2 sp3 d2sp3 d2sp3 d2sp3 dsp2
5
5.92
5.88 正八面体
4
4.90
4.为了增加配合物的稳定性,在某些配合物中除了形成 σ 配键外,还能形成反馈 π 配键。
(1)电中性原理:在形成一个稳定的分子或配离子时,其电子结构是竭力设法使每个 原子的静电荷基本上等于零。
(2)反馈 π 键:当配位体给出电子对与中心元素形成 σ 键时,如果中心元素的某些 d 轨道有孤电子对,而配位体有空的 π 分子轨道或空的 p 或 d 轨道,而两者的对称性又合适时, 则中心元素的孤对 d 电子也可以反过来给予配位体形成所谓的“反馈 π 键”。
1.A 的化学式 Cr(NH3)3O4 或 CrN3H9O4 A 的可能结构式如下图:
NH3
O
O
O
O Cr
O and/or O Cr
NH3
O
NH3
O
NH3
NH3
NH3
2.A 中铬的氧化数为+4 3.氧化还原性(或易分解或不稳定等) 4.化学方程式:CrO42-+3NH3+3H2O2=Cr(NH3)3(O2)2+O2+2H2O+2OH-
2.设配合物中碳原子数为 nC,则:nC︰nN=17.74/12︰31.04/14=0.667 已知 nN=2×2+2=6, 所以,nC=0.677×6=4 求出摩尔质量,由于剩余量过小,只能设 A 是氮氢化合物,由此得氢数,可
推得配体 A 为 H2NCH2CH2NH2,
H2C
配合物的结构示意图为:
Fe(CN)63-
配合物的化学键理论

杂化
轨道 sp3d2 d2sp3
sp3
dsp2
配键 类型 外轨型 内轨型
外轨型
内轨型
Kf 1014
稳定性
<
1042
107. 96
1031. 3
<
磁性
Ni2+的d电子构型 杂化轨道 配键类型
未成对电子数 磁性
[Ni(NH3)4]2+ [Ni(CN)4]2 d8
sp3 外轨型
dsp2 内轨型
2 顺磁性
弱场配体
强场配体
——以上称为光谱化学序列
4. 电子成对能和配合物高、低自旋
电子在分裂后轨道上的分布遵循: 能量最低原理和洪特规则
如 Cr3+ d3
eg
E t2g
八面体场
d4d7构型的离子, d电子分布有高、低自旋两种方式。
如 Cr2+ d4
[Cr(H2O)6]2+
eg
△o t2g
[Cr(CN)6]4-
中心离子和配体之间以静电引力相互作用而形 成化学键。
中心离子的5个能量相同的d轨道受配体负电场 的排斥作用,发生能级分裂(有的轨道能量升 高,有的能量降低)。
2. 正八面体场中d轨道的能级分裂
无外电场作用下的d轨道 Edxy= Edxz= Edyz= Edx2-y2= Edz2
在带负电荷均匀球形场的作用下,d轨道能量 均升高相同值,能级不发生分裂。
请问: [Zn(NH3)4]2+、 [Ag(NH3)2]+呈现什么颜色?
中心离子d 轨道全空(d0)或全满(d10), 不能发生 d-d跃迁,其水合离子为无色。
解释配合物的稳定性
Eeg=+0.
配合物化学键理论

强场:o > P 弱场:o < P
d5 型
强场o > P
弱场o < P
(4) 影响CFSE的因素 ① d电子数目; ② 配位体的强弱; ③ 晶体场的类型
表1 过渡金属络离子的稳定化能(CFSE)
弱场CFSE/Dq
dn d0 离子 Ca2+,Sc3+ 正方型 0 正八面体 0 正四面 体 0 正方型 0
中心离子用外层(n-1)d,ns,np杂化轨道与电负性 较小的配位原子,如CN-、NO2-等形成内轨型配合 物。例如[Fe(CN)6]3-配离子,Fe采用d2sp3内轨型 杂化轨道,配合物的键能大,稳定,在水中不易 离解。
(3)内、外轨型配合物的测定---磁矩
由磁矩可判断内轨或外轨型配合物
s n—分子中未成对电子数
z
y
x
x
dz2
y z
dx2-y2
z
x
x
y
dxy
dxz
dyz
1.分裂能 (1)分裂能与配合物几何构型的关系
八面体型的配合物
在八面体型的配合物中,6个配位体分别占据八 面体的6个顶点,由此产生的静电场叫做八面体场。
(1)八面体场
八面体场中d轨道能级分裂
dz2 dx2-y2 eg 3 5 Δo =6Dq Δ o =10Dq 2 5 Δ o = 4Dq t2g dxy dxz dyz
[CrCl6]313600
[MoCl6]319200
分裂能与配位体的关系:光谱化学序列
[CoF6]3- [Co(H2O)6]3+ [Co(NH3)6]3+ o/cm-1 13000 18600 22900 [Co(CN)6]334000
配合物中的化学键理论.
例:(见例4、例6、)
8
②、内轨型配合物: A、定义: 指形成配合物时,中心离子提供外层 ( ns,np ) 和 次 外 层 空 轨 道 (n - 1)d 进 行 杂 化而与配体结合所形成的配合物。 B、特点: a、提供外层(ns, np)和次外层空轨道 (n-1)d进行杂化成键。 b、杂化类型为:dsp2和d2sp3杂化。 c、配合物有较少(或没有)未成对电子数。
10
例 : [Co(NH3)6]2+ 为 外 轨 型 , 则 [Co(NH3)6]3+为内轨型。 D、内轨型配离子的稳定性大于外轨型配离 子。
原因:由于次外层轨道能级比最外层的 低。
11
内容小结:
①:杂化——构型——类型
n M用以杂 杂化 空间构型 类型 化的轨道 轨道
示例
2 ns、np sp 直线型
外层轨道
成键类型: 外轨配键
内轨配键
配合物的类型: 外轨型
内轨型
成单电子状态: 高自旋
低自旋
空间构型
正四面体
平面正方形
5
规律:中心离子dsp2 杂化,配离子的空间构 型为平面正方形。
类似有:[Cu(NH3)4]2+、[Pt(NH3)4]2+等。
③、配位数为6的配离子 也有两种成键方式
A、以 SP3d2 杂化轨道成键: 例:
Ag(NH3)2+
4 ns、np sp3 正四面体 外轨型 Ni(NH3)42+
(n-1)d、 dsp2 平面四方 内轨型 Ni(CN)42ns、np
6 ns、np、 sp3d 正八面体 外轨型
nd
2
第三章配合物的化学键理论

8
8
4
4
0
0
0 1 2 3 4d电5子6数 7 8 9 1 0
低自旋配合物的晶体场稳定化能
•配合物的热力学性质 离子的水合热(-H):
Mn+(g) + xH2O = [M(H2O)6]n+ (aq) + (-H)
水 合 能
Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn
离子半径
由于随核电荷增 加,d电子也增加, 但d电子不能将增加 的核电荷完全屏蔽, 单从这个因素考虑应 单调下降。
—光谱化学序列 (Spectrochemical Series)
• 计算分裂能的经验公式 Jørgensen公式: = f·g f:配体因子 g:中心金属离子因子
2-4 电子成对能(P)与配合物自旋状态
问题:正八面体场Fe3+ (d5)中的电子如何排布呢?
Paulli原理 需要满足三个条件: 能量最低原理
M(H2O)6的值
金属离子
(M)
V
Cr
Fe
二价 12600 13900 10400
Co 9300
三价 17700 17400 13700 13600
• 配体的影响 (金属离子相同时)
:I- < Br- < Cl- < N3- < OH- < C2O42- < H2O < NH3 < NH2OH < phen < CO~CN-
Fe2+ (d6):
[Fe(CN)6]4-:
•• ••
•• •• •• ••
3d
4s 4p
d2sp3杂化,内轨型配合物 (低自旋)
第三章配合物的化学键理论

2
思考题2
利用光谱化学序列和磁矩数据确定下列配合 物的配体哪些是强场配体,哪些是弱场配体? 并确定d电子的排布及未成对电子数。
[Co(NO2)6]3- = 0 B.M. [Fe(NH3)6]2+ = 5.2 B.M.
[Fe(CN)6]3[FeF6]3-
2019/11/1
3
思考题3
已知Co3+的p=17800cm-1,Co3+与下列配体
L
t*2g
eg* 10Dq
t2g
t2g
t2g 由p轨道构成
F-
Mn+
M t2*g
eg*由*轨t2道g 构成
t2g CO
2019/11/1
40
形成p-d键,使得分裂能减小 形成d - *反馈键,使得分裂能增大
2019/11/1
41
三种理论比较
价键理论:中心原子采取杂化轨道与配体形成配位 键。对于说明比较简单的分子的结构和反应性是有 用的,但是往往不适用于说明非经典配合物
9
思考题1
已知: [Co(H2O)6]2+ = 4.3 B.M. [Co(EDTA)]- = 0 B.M.
指出分子构型、中心离子的价层电子排布和杂化方式
2019/11/1
10
价键理论的优缺点
很好地解释了配合物的空间构型、磁性,直 观明了
无法解释配合物的颜色(吸收光谱) 无法解释配合物的稳定性随Mn+的d电子数目
( 1
4)
1 2
( 2
5)
1 2
( 3
6)
eg,e*g t1u,t*1u
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 计算分裂能的经验公式
Jø rgensen公式: = f· g
f:配体因子 g:中心金属离子因子
2-4 电子成对能(P)与配合物自旋状态
问题:正八面体场Fe3+ (d5)中的电子如何排布呢?
Paulli原理 需要满足三个条件: 能量最低原理
Hund规则
eg
o
eg
o
t2g
低自旋 高自旋
低自旋配合物的晶体场稳定化能
•配合物的热力学性质 离子的水合热(-H):
Mn+(g) + xH2O = [M(H2O)6]n+ (aq) + (-H)
水 合 能
Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn
100
离子半径
由于随核电荷增 加,d电子也增加, 但d电子不能将增加 的核电荷完全屏蔽, 单从这个因素考虑应 单调下降。
dyz , dxz dxy, dyz , dxz
dxy
2
dxy dyz , dxz
Z轴缩短的 正八面体场 Oh 八面体(D4h)
Z轴拉长的 八面体(D4h)
dx2-y2 dz2, dx2-y2
d
dz2 dxy dxy , dyz , dxz
dyz , dxz 拉长八面体场中Cu2+ (d9)的电子排布
如[Fe(H2O)6]2+/3+,[FeX6]3-等
③ P: 自旋交叉
㈡ 晶体场理论对配合物高低自旋状态的预测
•[Fe(CN)6]4-: = 33000 cm-1, P = 17600 cm-1
>P,t2g6,低自旋 ( = 0)
•[Fe(H2O)6]2+: = 10400 cm-1, P = 17600 cm-1 <P,t2g4eg2,高自旋 ( = 4.9 B.M.)
配合物的化学键理论主要有: 静电理论(I.B.T.) kossel 1916年 Magnus 1922年 价键理论(V.B.T.) Pauling 1931年 晶体场理论(C.F.T.) Bethe 1929年 分子轨道理论(M.O.T) Van Vleck 1935年 角度重叠模型(A.O.T )山畸 1958年
M(H2O)6的值 金属离子 (M)
二价 三价 V 12600 17700 Cr 13900 17400 Fe 10400 13700 Co 9300 13600
• 配体的影响 (金属离子相同时)
:I- < Br- < Cl- < N3- < OH- < C2O42- < H2O < NH3 < NH2OH < phen < CO~CN—光谱化学序列 (Spectrochemical Series)
根据△G=△H -T△S=-RTlnK, 配合物的稳定性将 由△G决定, 由于各种配合物的△S相差不大, 所以主要决 定于△H, 显然, △H值越负, 则MLm愈稳定。
设m=6、4……时, 上述配合反应的△H值为 △H正八面体=6△bH(M-L)-CFSE正八面体 △H正四面体=4△bH(M-L)-CFSE正四面体 △H正方形 =4△bH(M-L)-CFSE正方形 ……
CFSE = 1/2
dx2-y2 dz2, dx2-y2 dz2 dxy dxy , dyz , dxz
d
八面体场中Ni2+ (d8)的电子排布 不发生畸变(t2g6eg2) CFSE = 0
dyz , dxz
无论采用哪一种几何畸变 , 都会 引起能级的进一步分裂, 消除简并, 其 中一个能级降低 , 从而获得额外的稳 定化能(左图为第一种情况的能级图)。 姜-泰勒效应不能指出究竟应该 发生哪种几何畸变, 但实验证明, Cu的 六配位配合物 , 几乎都是拉长的八面 体, 这是因为, 在无其他能量因素影响 时 , 形成两条长键四条短键比形成两 条短键四条长键的总键能要大之故。
(a) 低自旋
(b) 高自旋
Fe2+在卟啉环中的位置
(图中黑球代表Fe,白球代表N,P代表蛋白质中多肽链)
2-6 姜-泰勒效应 (Jahn-Teller Effect)
•Mn-O8 1.69
•Mn-N2 1.72 •Mn-O7 2.06 •Mn-N1 2.14 •Mn-O6 2.33
•Mn-O5 2.37
eg
6 Dq
t2g
-4 Dq
C F S E /D q
0 1 2 3 4 5 6 7 8 91 0 1 2 1 2 8 4 0 8 4 0 0 1 2 3 4 5 6 7 8 91 0 d电子数
高自旋配合物的晶体场稳定化能
C F S E /D q
0 1 2 3 4 5 6 7 8 91 0 2 4 2 4 2 0 1 6 1 2 8 4 0 2 0 1 6 1 2 8 4 0 0 1 2 3 4d电子数 5 6 7 8 91 0
思考:除了Cu2+以外,还有那些组态的离子 的八面体构型会发生畸变?
t2g1
t2g3eg1 t2g5 t2g5eg2, t2g6eg1 t2g6eg2
t2g2
Cr(II), Mn(III) t2g3eg2
t2g3
t2g4 t2g4eg2 Co(II), Ni(III)
t2g6eg4
思考:从稳定性角度考虑,[Ti(H2O)6]3+的优 势畸变构型是拉长八面体还是压扁八面体?
第一节 价键理论
1-1 理论要点 •中心原子的杂化空轨道接受配体提供的 电子对形成配位键 •内轨型 •内层和外层的d轨道均可参与杂化 •外轨型
1-2 内轨型和外轨型配合物
Fe2+ (d6): [Fe(H2O)6]2+:
•• •• •• •• •• ••
3d
4s
4p
4d
sp3d2杂化, 外轨型配合物 (高自旋)
t2g
[Fe(H2O)6]3+
[Fe(CN)6]3-
正八面体d5体系的两种电子排布情况
㈠ 电子成对能(P): 电子成对所需能量 P
静电排斥能
交换能损失
三种可能的电排布:
① >P: 低自旋(强场配体)
如[M(CN)6]3- (M=Fe,Co),[Fe(phen)3]2+等 ② <P:高自旋(弱场配体)
Fe2+ (d6): [Fe(CN)6]4-:
•• •• •• •• •• ••
3d
4s
4p
d2sp3杂化,内轨型配合物 (低自旋)
1-3 价键理论的优点 很好地解释了配合物的空间构型和配位数
配位数 2 3 4 5 6 杂化轨道 空间构型 sp sp2 sp3 d2sp2 d2sp3 直线型 三角形 正四面体 四方锥 举例 [Ag(CN)2][CuCl3]2[MnCl4]2NiBr3(PR3)
(dx2-y2)2(dz2)1 压扁八面体
例:Cu2+ (d9, t2g6eg3)
(dz2)2(dx2-y2)1 拉长八面体
z
z
x
y
x
y
dz2
y x z
dx2-y2
z y y z x
拉长八面体场中的5个d轨道
dxy
dyz
dxz
dz2 dx2-y2
dz2, dx2-y2
dx2-y2
1
dz2
能 量
i. 不能预测配合物的高、低自旋状态
ii. 不能解释配合物的可见-紫外吸收光谱性质
例如, 为了说明Cu2+配合物的平面四方形构型问题, 认为3d电 子被激发到4p能级从而发生dsp2杂化。 Cu2+ 4X- CuX42- dsp2 这里, X是一价阴离子的配体。在此过程中, 自由离子 Cu2+要由 3d激发一个电子到 4p需要的激发能为1422.6 kJ·mol-1, 看不出 这么大的能量从何而来。要补赏这个能量, 必须使CuX键键能 至少要达到-356 kJ·mol-1, 已知Cl-Cl键键能为-243 kJ·mol -1, 这表明, 形成Cu-Cl键放出的能量比形成Cl-Cl键放出的能量 还要大, 这可能是不真实的。 根据这个结构, 可以推测Cu2+的配合物应当很容易地失去未配对 的4p电子而迅速氧化为Cu3+, 但事实并非如此。 因此, 价键理论被配位场理论或分子轨道理论取代是十分必然的。
80
(b)
离子半径/pm
70
60
50
Sc+3
0
Ti+3
1
V+3
2
Cr+3
3
Mn+3
4
Fe+3
5
Co+3 Ni+3
6 7 8 9
Ga+3
10
n
第一系列过渡金属离子 (M2 + ) 和 (M3 + ) 的离子半径
由于自旋状态不同引起离子半径的差异,在生物化学中 有重要意义。
例如:在血红蛋白中,血红素辅基的Fe2+能可逆载氧,载氧时Fe2+的状态 为低自旋,半径较小,能嵌入卟啉环的平面中,呈六配位体。而 脱氧后Fe2+呈高自旋态,半径较大。不能嵌入卟啉环的平面中,高 出平面70—80 pm,为五配位。
离子半径/pm
90 80 70 60 50
(a)
Ca+2 Zn+2 0 1
2
V+2 Ti+2
3 4
Mn+2 Cr+2
5 6
Co+2 Fe+2
7 8
Cu+2
9
Ni+2
10
n
实际上,由于 LFSE 的影响,HS 型 出现向下双峰,LS 型出现向下单峰,这 是 LFSE 的能量效应 对微观结构的影响。 八面体 配 位时 , HS 态的半径比LS态的 半径大。
