圆补充定理(圆幂,割线,公共弦)及习题
切割线定理割线定理相交弦定理等及几何题解
切割线定理割线定理相交弦定理等及几何题解南江石 2018年4月7日星期六圆的切线,与圆(圆弧)只有一个公共交点的直线叫做圆的切线。
圆的割线,与圆(圆弧)有两个公共点的直线叫做圆的割线。
圆的弦,圆(圆弧)上两点的连接线段叫做圆(圆弧)的弦。
弦是割线的部分线段。
公共弦线:两圆相交,两交点的连线为公共弦线——共弦线,共割线。
公共切线:两圆相切,过两圆切点的公切线为公共切线——共切线。
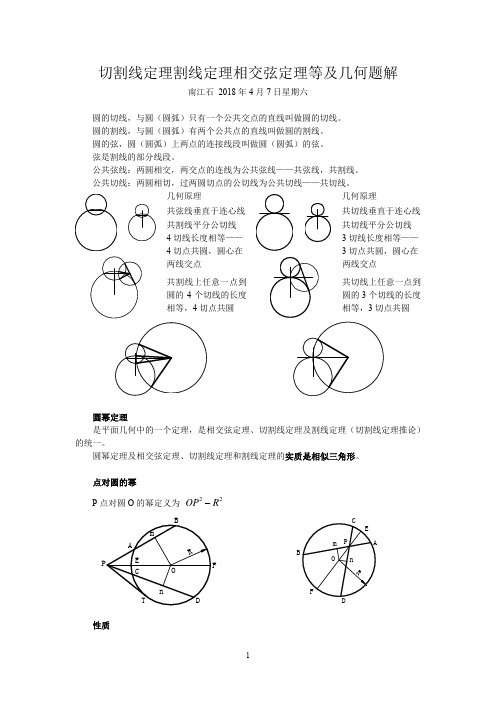
几何原理 几何原理共弦线垂直于连心线共切线垂直于连心线共割线平分公切线 共切线平分公切线4切线长度相等—— 4切点共圆,圆心在两线交点3切线长度相等——3切点共圆,圆心在两线交点共割线上任意一点到圆的4个切线的长度相等,4切点共圆共切线上任意一点到圆的3个切线的长度相等,3切点共圆圆幂定理是平面几何中的一个定理,是相交弦定理、切割线定理及割线定理(切割线定理推论)的统一。
圆幂定理及相交弦定理、切割线定理和割线定理的实质是相似三角形。
点对圆的幂P 点对圆O 的幂定义为22R OP FB性质点P 对圆O 的幂的值,和点P 与圆O 的位置关系有下述关系: 点P 在圆O 内→P 对圆O 的幂为负数; 点P 在圆O 外→P 对圆O 的幂为正数; 点P 在圆O 上→P 对圆O 的幂为0。
切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
PBPTPT PA =PB PA PT ∙=2 222Am Pm PT -=割线定理(切割线定理的推论)从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
PD PC PB PA ∙=∙2222Cn Pn Am Pm -=-相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等,或经过圆内一点引两条弦,各弦被这点所分成的两线段的积相等。
PD PC PB PA ∙=∙2222A Pn Cn Pm m -=-垂径定理(相交弦定理推论)如果弦与直径垂直相交,那么弦的一半是它所分直径所成的两条线段的比例中项。
3.15圆幂定理与托勒密定理

圆幂定理【知识点学习】圆幂定理:(1)相交弦定理:圆的两条相交弦中,每条弦被交点所分的两条线段的乘积相等。
(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的两条线段的积相等。
(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段的比例中项。
三个定理统称为圆幂定理。
PPDPCPBPA⋅=⋅PDPCPBPA⋅=⋅PCPBPA⋅=2【例题与练习】1.已知:如图,⊙O的弦AD、BC互相垂直,垂足为E,53sin=∠BAD,31cos=∠CAD,2=AC,求EC和AD。
ADOCBE2. 如图,已知⊙O 的割线PAB 交⊙O 于A 、B 两点,PO 与⊙O 交于点C ,cm AB PA 6==,cm PO 12=,求⊙O 的半径。
P3. 如图,已知⊙O 与⊙'O 相交于A 、B 两点,点P 在BA 的延长线上,⊙O 的割线PCD 交⊙O于点D C 、,PE 与⊙'O 相切于点E ,4=PC ,8=CD ,求线段PE 的长。
BAC P DO O'E4. 如图,已知⊙1O 与⊙2O 相交于D C 、两点,AB 为外公切线,B A 、为切点,CD 的延长线与AB 相交于点M ,12=AB ,9=CD ,求线段MD 的长。
5. 如图,P 为⊙O 外的一点,过点P 作⊙O 的两条割线,分别交⊙O 于A 、B 和C 、D ,且AB是⊙O 的直径,已知4==OA PA ,CD AC =. (1)求CD 的长; (2)求B ∠cos 的值.CAO B PD6. 已知:如图,在ABC ∆中,︒=∠90C ,BE 是角平分线,BE DE ⊥交AB 于D ,⊙O 是BDE ∆的外接圆,若6=AD ,26=AE ,求DE 的长.EOAD BC7. 已知,△ABC 外接于⊙O ,且BC AB =,BC AO ⊥,垂足为点D , (1) 求证:△ABC 为等边三角形;(2) 点E 为BC 上的一动点(不于C B 、重合),连结AE 并延长交⊙O 于点P ,已知1=AB ,x AE =,y PE =,求y 关于x 的解析式并求其定义域;(3) 在(2)的条件下,设α=∠PAC ,β=∠EPC ,当y 取何值时,1sin sin 22=+βα.【练习】:1、 如图,BC 是半圆⊙O 的直径,BC EF ⊥于点F ,5=FCBF.已知点A 在CE 的延长线上,AB 与半圆交于D ,且8=AB ,2=AE ,求AD 的长。
初三数学圆相关复习重点及试题(二)

初三数学圆相关知识点及试题七.切线长定理考点速览: 考点1切线长概念:经过圆外一点做圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 切线长和切线的区别切线是直线,不可度量;而切线长是切线上一条线段的长,而圆外一已知点到切点之间的距离,可以度量. 考点2 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.要注意:此定理包含两个结论,如图,PA 、PB 切⊙O 于A 、B 两点,①PA=PB ②PO 平分APB ∠. 考点3 两个结论:圆的外切四边形对边和相等;圆的外切等腰梯形的中位线等于腰长. 经典例题:例1 已知PA 、PB 、DE 分别切⊙O 于A 、B 、C 三点,若PO=13㎝,PED ∆的周长为24㎝, 求:①⊙O 的半径;②若40APB ∠=︒,EOD ∠的度数.例2 如图,⊙O 分别切ABC ∆的三边AB 、BC 、CA 于点D 、E 、F ,若,,BC a AC b AB c ===. (1)求AD 、BE 、CF 的长;(2)当90C ∠=︒,求内切圆半径r .例3.如图,一圆内切四边形ABCD ,且AB=16,CD=10,则四边形的周长为?例4 如图甲,直线343+-=x y 与x 轴相交于点A ,与y 轴相交于点B ,点C ()n m ,是第二象限内任意一点,以点C 为圆心与圆与x 轴相切于点E ,与直线AB 相切于点F.(1)当四边形OBCE 是矩形时,求点C 的坐标;(2)如图乙,若⊙C 与y 轴相切于点D ,求⊙C 的半径r ; (3)求m 与n 之间的函数关系式;(4)在⊙C 的移动过程中,能否使OEF ∆是等边三角形(只回答“能”或“不能”)?· FDOAB· EFDCOAB考点速练1:1.如图,⊙O 是ABC ∆的内切圆,D 、E 、F 为切点,::4:3:2A B C ∠∠∠=,则DEF ∠= . FEC ∠= .2.直角三角形的两条直角边为5㎝、12㎝,则此直角三角形的外接圆半径为 ㎝,内切圆半径为 ㎝.3.如图,直线AB 、BC 、CD 分别与⊙O 相切于点E 、F 、G ,且AB ∥CD ,若OB=6㎝,OC=8㎝,则BOC ∠= ,⊙O 的半径= ㎝,BE+CG= ㎝.4.如图,PA 、PB 是⊙O 的切线,AB 交OP 于点M ,若2,OM cm AB PB ==,则⊙O 的半径是 ㎝.·A O CDBEF· AO C D B E FG· AOPBM考点速练(2)1.如图,在Rt ABC ∆中,90,3,4C AC BC ∠=︒==,以BC 边上一点O 为圆心作⊙O 与AB 相切于E ,与AC 相切于C ,又⊙O 与BC 的另一个交点D ,则线段BD 的长 . 2.如图,ABC ∆内接于⊙O ,AB 为⊙O 直径,过C 点的切线交直径AB 的延长线于P ,25BAC ∠=︒,则P ∠= .4、(广西)PA 、PB 是⊙O 切线,A 、B 切点,∠APB =780,点C 是⊙O 上异于A 、B 任一点,那么∠ACB =_____。
初三圆复习带例题讲解详细解答

(2)点C与⊙B的位置关系;
(3)AB、AC的中点D、E与⊙B的位置关系.
分析:(1)由勾股定理易求AB===4(cm),而4cm>3cm,所以点A在⊙B外;(2)点C在圆上;(3)由(1)知AB=4cm,则AB的中点D到B点的距离为2cm,而2cm<3cm,所以点D在圆内,根据“直角三角形斜边上的中线等于斜边的一半”易得BE=2.5cm,而2.5cm<3cm,所以点E也在圆内.
三、切线长定理
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
四、圆幂定理
1、相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:
推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:
2、切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
分析:要求△ABC的外接圆的面积,只需求出外接圆半径即可,连接AO并延长,交BC于D,由垂径定理可知AD⊥BC于D,连接BO,构造Rt△OBD,最后利用勾股定理求出外接圆半径.
解:连接AO并Байду номын сангаас长,交BC于D,连接BO,
∵AB=AC,∴=.
又∵AD过点O,∴AD⊥BC.
在等腰三角形ABC中,BD=BC=×6=3(cm),
知识
一、直线与圆的位置关系
1、直线与圆相离 无交点;
2、直线与圆相切 有一个交点;
3、直线与圆相交 有两个交点;
二、切线的性质与判定定理
1、判定定理:过半径外端且垂直于半径的直线是切线
(两个条件,缺一不可)
2、性质定理:切线垂直于过切点的半径
相交弦定理、切割线定理、割线定理综合训练(最新整理)

7.如图,PA切 ⊙ O于A,PBC是 ⊙ O的割线,如果PB = 2,PC = 4,则PA的长为________.
试卷第 1 页,总 3 页
8.如图,PAB、PCD是 ⊙ O的割线,PA = 3,PB = 6,PC = 2,则PD = ________. 9.如图,PT是 ⊙ O的切线,T为切点,PAB是 ⊙ O的割线,PA = 5cm,AB = 4cm,则 PT = ________cm.
三、解答题 10.如图,在半径为5cm的 ⊙ O中,直径AB与弦CD相交于点P,∠CAB = 50 ∘ ,∠APD = 80 ∘ . (1)求∠ABD的大小; (2)求弦BD的长.
11.如图,⊙O 直径 AB 和弦 CD 相交于点 E,AE=4,EB=8,∠DEB=30°,求弦 CD 长.
12.如图,弦 AB 和弦 CD 相交于⊙O 内一点 E,AD=CB,求证:AB=CD.
相交弦定理、切割线定理、割线定理
一、单选题 1.如图,PA与 ⊙ O切于点A,PBC是 ⊙ O的割线,如果PB = BC = 2,那么PA 的长为( )
A.2 B.2 2 C.4 D.8
2.P是 ⊙ O外一点,PA切 ⊙ O于A,割线PBC交 ⊙ O于点B、C,若PB = BC = 3,则PA的长
是(
)
A.9 B.3 C.3 2 D.18
二、填空题
3.如图,半圆
O
的直径
AB=7,两弦
AC、BD
相交于点
E,弦
CD=7,且
2
BD=5,
则 DE=_____.
九年级数学圆弧、弦、圆心角间的关系圆周角定理及其推论精选例题和练习

九年级数学圆弧、弦、圆心角间的关系圆周角定理及其推论精选例题和练习2011-2012学年九年级数学第5课时圆2 弧、弦、圆心角间的关系圆周角定理及其推论一、知识点总结1.圆心角:顶点在圆心的角.注意:圆心角的底数等于它所对弧的度数.2.在同圆或等圆中,圆心角、弧、弦、弦心距中,只要有一组量相等,那么另外三组量也分别相等.3.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对圆心角的一半.4.圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.注:有直径时,常添加辅助线,构造直径所对的圆周角,由此转化为直角三角形的问题.思维导图如下:二、弧、弦、圆心角、弦心距间的关系举例例1 如图,AB为⊙O的弦,点C、D为弦AB上两点,且OC=OD,延长OC、OD分别交⊙O于点E、F,试证明弧AE=弧BF.分析:“弧AE=弧BF”←“∠______=∠______”Array把证弧相等转化为证________________.证明:例2 如图,点O 是∠EPF 的平分线上的一点,以O 为圆心的圆和角的两边分别交于点A 、B 和C 、D .求证:AB=CD .分析:把证明弦相等转化为证明________相等.证明:例3(2008广东湛江)如图所示,已知AB 为⊙O 的直径,CD 是弦,且AB ⊥CD 于点E ,连接AC 、OC 、BC .(1)求证:∠ACO=∠BCD .(2)若EB=8cm ,CD=24cm ,求⊙O 的直径.分析:(1)∠ACO=∠______,而∠______=∠______.(2)在Rt ⊿______中,利用勾股定理列方程求解.解:P例4 已知,如图,在⊿ABC中,AD,BD分别平分∠BAC和∠ABC,延长AD交⊿ABC的外接圆于E,连接BE.求证:BE=DE.分析:把证BE=DE转化为证∠____=∠____.证明:二、圆周角定理及推论举例例1 如图所示,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=______°.A例2 (2009江苏泰安)如图,⊙O的半径为1,AB是⊙O的一条弦,且AB 所对的圆周角为______.注意:如下图所示,同一条弦所对的弧有两种情况,两弧所对的圆周角之和为______.例3 已知:如图,AB 为⊙O 的直径,C ,D 为⊙O 上的两点,且C 为弧AD 的中点,若∠BAD=20°,求∠ACO 的度数.分析:∠BAD 是圆周角,它所对应的圆心角是∠______.例4 已知,如图,在⊿ABC 中,AB=AC ,以AB 为直径的圆交BC 于D .求证:D 为BC 的中点.分析:注意AB 是直径,添加辅助线,构造直径所对的圆周角.证明:CA。
圆幂定理试题及答案

圆幂定理试题及答案一、选择题1. 圆幂定理指的是()A. 圆上任意两点的距离等于它们到圆心的距离之和B. 圆上任意两点的距离等于它们到圆心的距离之差C. 圆上任意一点到圆心的距离等于该点到圆上其他点的距离之和D. 圆上任意一点到圆心的距离等于该点到圆上其他点的距离之差2. 在圆幂定理中,如果圆上一点P到圆心O的距离为OP,点P到圆上另一点A的距离为PA,则以下哪个表达式是正确的?()A. OP = PAB. OP + PA = 2RC. OP - PA = RD. OP × PA = R^2二、填空题3. 若圆的半径为5cm,圆上一点到圆心的距离为3cm,则该点到圆上任意一点的距离之和为_________。
4. 已知圆幂定理中的OP = 8cm,PA = 6cm,且点A在圆上,则圆的半径R为_________。
三、解答题5. 如图所示,圆O的半径为10cm,点P在圆上,OP(点P到圆心O的距离)为12cm。
求点P到圆上另一点B的距离PB。
6. 在一个半径为7cm的圆中,有两点A和B,已知OA(点A到圆心O 的距离)为5cm,求AB的长度。
四、证明题7. 证明圆幂定理:在一个给定的圆中,圆上任意一点到圆心的距离与该点到圆上其他点的距离之和等于圆的直径。
答案一、选择题1. 正确答案:D2. 正确答案:B二、填空题3. 该点到圆上任意一点的距离之和为10cm + 10cm = 20cm。
4. 圆的半径R可以通过勾股定理计算得出:R^2 = OP^2 - OA^2,所以R^2 = 8^2 - 6^2 = 64 - 36 = 28,因此R = √28 ≈ 5.29cm。
三、解答题5. 由于OP > OA,根据圆幂定理,PB = 2R - OP = 2 * 10 - 12 = 20 - 12 = 8cm。
6. 同样使用圆幂定理,AB = 2R - OA - OB,但是OB = OA = 5cm,所以AB = 2 * 7 - 5 - 5 = 14 - 10 = 4cm。
圆与相似综合题的有关定理

圆和相似综合题有关定理1、圆幂定理(在证明比例式、求线段长度时将发挥重要作用。
)2、托勒密定理:圆内接四边形两组对边乘积之和,等于两条对角线的乘积。
已知:四边形ABCD 内接于圆,如图,求证:AB·CD + BC·AD = AC·BD证明:在∠BAD 内作∠BAE=∠CAD ,交BD 于E 。
因∠ABE=∠ACD ,所以△ABE ∽△ACD ,从而AB BE ACCD =得 AB·CD = AC·BE ①; … 易证△ADE ∽△ACB ,从而BC AC DE AD = 得BC·AD = AC·DE ②; ①+② 得AB·CD + BC·AD = AC (BE+DE )= AC·BD定理 图形已知 结论 证法 相交*弦定理⊙O 中,AB 、CD 为弦,交于点P 。
PA·PB =PC·PD 连结AC 、BD , 证:△APC ∽△DPB 切 、割线定理 ⊙O 中,PT 切⊙O 于点T ,割线PB 交⊙O 于点A 。
PT 2=PA·PB连结TA 、TB , 证:△PTB ∽△PAT }割线定理PB 、PD 为⊙O 的两条割线,交⊙O 于A 、C 两点。
PA·PB =PC·PD ~ 过P 作PT 切⊙O 于T ,用两次切割线定理 C E3、弦切角定理:顶点在圆上,一边和圆相交,另一边和圆相切的角称为弦切角。
弦切角等于弦与切线所夹弧所对的圆周角。
}弦切角定理的证明:已知:AP切⊙O于P,PQ是弦,则∠APQ是弦切角,∠APQ夹的弧是弧PQ,弧PQ所对的圆周角记为∠PCQ证明:∠APQ=∠PCQ (弦切角的位置分以下三种情况)】1°圆心O在∠APQ外部过P作直径BP,联结BC则BP⊥AP,∠APB=90°,且∠BCP是直径BP所对的圆周角,∠BCP=90°#则有∠APB=∠BCP,即∠APQ+∠BPQ=∠BCQ+∠PCQ由于∠BPQ,∠BCQ都是弧BQ所对的圆周角,所以∠BPQ=∠BCQ所以∠APQ=∠PCQ2°圆心O在∠APQ的一边,PQ上此时PQ是直径,则PQ⊥AP,∠APQ=90°而且∠PCQ是直径PQ所对的圆周角,∠PCQ=90°所以∠APQ=∠PCQ3°圆心O在∠APQ内部过P作直径BP,联结BC则BP⊥AP,∠APB=90°,且∠BCP是直径BP所对的圆周角,∠BCP=90°则有∠APB=∠BCP由于∠BPQ,∠BCQ都是弧BQ所对的圆周角,所以∠BPQ=∠BCQ所以∠APB+∠BPQ=∠BCP+∠BCQ即∠APQ=∠PCQ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AB=8.由点O1向⊙O2作切线O1C,切点为C,则O1C的长为
图1
图2
练习2:如图2,⊙O1与⊙O2相交于A、B.已知两圆的半径
r1=10,r2=17,圆心距O1O2=21,公共弦AB等于( )
A.2
B.16
C.6
D.17
练习3:已知相交两圆的半径分别为5cm和4cm,公共弦长为6cm,则这两
圆补充定理及习题(20151218)
板块一:圆幂定理 (1)相交弦定理:圆内两弦相交,交点分得的两条线 Image
段的乘积相等。
即:在⊙中,∵弦、相交于点,
∴
(2)相交弦定理推论:如果弦与直径垂直相交,那么弦的一半是它分
直径所成的两条线段的比例中项。
即:在⊙中,∵直径,
Image
∴
(3)切割线定理:从圆外一点 Image 引圆的切线和割线,切线长是这 点到割线与圆交点的两条线段长 的比例中项。 即:在⊙中,∵是切线,是割线
∴
(4)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆 的交点的两条线段长的积相等(如图)。 即:在⊙中,∵、是割线
∴
1:如图,圆中两条弦AB,CD相交于圆内一点P,已知PA=PB=4,PC=PD,求 CD的长
2:E是圆内两弦AB和CD的交点,直线EF//CB,交AD的延长线于F,切圆于
板块三:圆的公切线 两圆公切线长的计算公式:
(1)公切线长:中,; (2)外公切线长:是半径之差; 半径之和 。
Image 内公切线长:是
G。
求证(1)
(2)EF=FG
3:两圆相交于A,B两点,P为两圆公共弦AB上任一点,从P引两圆的切线 PC,PD,求证PC=PD
4.如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延 长线交⊙O于点E,且EM>MC.连接DE,DE= ,求EM的长.
板块二:两圆公共弦定理 圆公共弦定理:两圆圆心的连线垂直并且平分这两 Image 个圆的的公共弦。 如图:垂直平分。 即:∵⊙、⊙相交于、两点,∴垂直平分
个圆的圆心距是cm. Nhomakorabea分析:此题综合运用了相交两圆的性质以及勾股定理.注意此题应
考虑两种情况.
图4 图4 图3 图3 图5 图5
.
C
A B
. .
注意此题应考虑两种情况(图3和图4). 练习4:如图5,⊙O1和⊙O2相交于点A,B,它们的半径分别为2和 , 公共弦AB长为2,若圆心O1、O2在AB的同侧,则∠O1AO2= 度.
