mathematica样本方差
方差的计算方法

方差的计算方法方差是描述数据分散程度的统计量,它衡量了数据点与其均值之间的偏离程度。
在实际问题中,我们经常需要计算方差来分析数据的离散程度,从而更好地理解数据的特征和规律。
下面将介绍两种常见的方差计算方法,样本方差和总体方差。
首先,我们来看样本方差的计算方法。
对于给定的包含n个数据点的样本,其样本方差的计算公式如下:\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i \bar{x})^2 \]其中,\( x_i \) 代表第i个数据点,\( \bar{x} \) 代表样本的均值,n代表样本的大小。
样本方差的计算步骤如下:1. 首先计算样本的均值 \( \bar{x} \);2. 然后计算每个数据点与均值的差值,并进行平方;3. 最后将所有平方差值相加,并除以n-1,即可得到样本方差。
样本方差的计算方法能够更好地估计总体方差,因为它使用了样本的均值而不是总体的均值,从而减小了估计误差。
接下来,我们来看总体方差的计算方法。
对于包含N个数据点的总体,其总体方差的计算公式如下:\[ \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i \mu)^2 \]其中,\( x_i \) 代表第i个数据点,\( \mu \) 代表总体的均值,N代表总体的大小。
总体方差的计算步骤与样本方差类似,只是均值的计算和样本方差稍有不同。
总体方差的计算方法可以帮助我们更好地理解总体数据的分散程度,从而进行更准确的分析和预测。
在实际问题中,我们需要根据具体的数据类型和分析目的选择合适的方差计算方法。
无论是样本方差还是总体方差,都能够帮助我们更好地理解数据的特征和规律,从而做出更准确的决策。
总之,方差是描述数据分散程度的重要统计量,通过合理选择计算方法和准确计算方差值,我们可以更好地理解数据的特征和规律,为实际问题的分析和决策提供有力支持。
方差的计算公式有几种

方差的计算公式有几种方差是描述数据分散程度的统计指标,表示数据各个观测值与均值之间差异的平均程度。
方差的计算公式有以下三种:样本方差、总体方差和平均方差。
下面将详细介绍这三种方差的计算公式。
1. 样本方差(Sample Variance):样本方差是根据样本数据计算得到的方差。
用s²表示样本方差,计算公式为:s² = ∑(xi - x̄)² / (n - 1)其中,xi表示样本的第i个观测值,x̄表示样本的均值,n表示样本的观测值个数。
样本方差的计算步骤如下:a.计算样本数据的均值x̄;b. 对每一个样本数据 xi,计算与均值的差值 (xi - x̄);c. 对每一个差值 (xi - x̄),进行平方运算得到 (xi - x̄)²;d. 对所有的 (xi - x̄)² 进行求和,得到∑(xi - x̄)²;e. 将∑(xi - x̄)² 除以样本数据个数减1,得到样本方差 s²。
2. 总体方差(Population Variance):总体方差是根据总体数据计算得到的方差。
用σ²表示总体方差,计算公式为:σ² = ∑(xi - μ)² / N其中,xi表示总体的第i个观测值,μ表示总体的均值,N表示总体的观测值个数。
总体方差的计算公式与样本方差的计算公式类似,只是在除以差值个数时除以总体数据个数N而不是样本数据个数n。
3. 平均方差(Mean Variance):平均方差是一种将多个方差估算值加权平均得到的方差估计方法,用于多个总体方差的比较。
平均方差的计算公式为:V = [(n1-1)s1² + (n2-1)s2² + … + (nk-1)sk²] / (n1 + n2 + … + nk - k)其中,n1、n2、..、nk表示各个总体的观测值个数,s1²、s2²、..、sk²表示各个总体的样本方差,k表示总体的个数。
mathematica

Mathematica简介Mathematica是一款强大的数学软件,由Stephen Wolfram和Wolfram Research公司开发。
它可以进行符号计算、数值计算、数据分析和可视化等各种数学任务。
Mathematica提供了一个交互式的界面,使用户能够轻松地输入数学表达式和命令,并得到相应的结果。
Mathematica的功能非常广泛,涵盖了数学、物理、工程、统计学等多个领域,被广泛用于教学、研究和工程应用。
特点强大的符号计算能力Mathematica可以进行符号计算,能够处理各种数学表达式、方程、不等式等。
它能够对表达式进行简化、展开、合并等操作,并能够在数学中进行推导和证明。
Mathematica还提供了大量的预定义函数和符号,可以直接使用,或者通过定义新的函数和符号来进一步扩展功能。
多种数值计算方法除了符号计算,Mathematica还提供了各种数值计算方法。
它可以进行数值积分、数值求解方程、数值逼近等操作。
Mathematica使用高精度算法进行数值计算,可以得到非常精确的结果。
同时,Mathematica还支持并行计算和分布式计算,可以利用多台计算机进行计算,加快计算速度。
数据分析和可视化功能Mathematica拥有强大的数据分析和可视化功能。
它可以导入各种数据格式,包括Excel、CSV、数据库等,进行数据清洗、分析和建模。
Mathematica提供了丰富的数据处理函数和图形函数,可以对数据进行统计分析、机器学习、图像处理等操作。
同时,Mathematica还可以生成各种图表、图形和动画,直观地展示数据和结果。
丰富的拓展包和资源Mathematica拥有丰富的拓展包和资源。
它提供了大量的内置函数和算法,涵盖了数学、物理、工程、统计学等多个领域。
此外,Mathematica还支持第三方拓展包,用户可以下载和安装各种拓展包,扩展Mathematica的功能。
对于数学教育和研究领域的用户,Mathematica还提供了丰富的教程、文档和示例代码,用户可以参考和学习。
Mathematica数学实验——简单数理统计

教师指导实验6实验名称:简单数理统计一、问题:求样本数据的特征数字值;绘制样本的频率分布条形图和直方图。
二、实验目的:学会使用Mathematica求求样本数据的极差、中位数、均值、方差及标准差;绘制样本的频率分布直方图并作简单的修饰。
三、预备知识:本实验所用的Mathematica命令提示1、SampleRange[data] 求样本数据data的极差(最大数减最小数);Median[data] 求样本数据data的中位数;Mean[data] 求样本数据data的均值;2、VarianceMLE[data] 求样本数据data的方差;StandardVarianceMLE[data] 求样本数据data的标准差;3、BarChart[data1, data2,…] 分别绘制样本数据data1,data2,…的条形图图形修饰选项:BarSpacing 设置两条形的总宽度,设置值是实际宽度相对于区间宽度的比值;BarGroupSpacing 设置相邻条形的宽度,设置值是条形的实际宽度相对于条形的总宽度的比值;BarStyle 条形风格设置;BarEdgeStyle 条形边界风格设置;BarLabels 条形标签设置,PlotLabel 图形名称设置,4、Histogram[data] 绘制样本数据data的频率分布直方图图形修饰选项:Ticks设置标记相对于条形的位置;HistogramScale 设置条形高度为频率密度,使条形的面积和为所设置的值。
四、实验的内容和要求:1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差;2、对以上数据绘制样本频率分布直方图;3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。
五、操作提示1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差;In[1]:=<<Statistics`DescriptiveStatistics`In[2]:=data=Table[Random[Integer,{1,20}],{60}];In[3]:=SampleRange[data]Out[3]= 19In[4]:= Median[data] Out[4]= 11In[5]:=Mean[data]Out[5]=221 20In[6]:=VarianceMLE[data]Out[6]=44017 1200In[7]:=StandarDevarianceMLE[data]Out[7]=2、对以上数据绘制样本频率分布直方图;In[8]:=<<Graphics`Graphics`In[9]:=Histogram[data]Out[9]= -Graphics-In[10]:=Histogram[data,Ticks->IntervalCenters, HistogramScale->1]Out[10]= -Graphics-In[11]:=Histogram[data,Ticks->IntervalBoundaries,HistogramScale->2]Out[11]= -Graphics-3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。
Mathematica常用命令

Mathem atica常用命令软件学习2010-10-1921:02:15 阅读127评论0 字号:大中小订阅 .M athem atica的内部常数Pi ,或π(从基本输入工具栏输入,或“Es c”+“p”+“Es c”)圆周率πE(从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入,或“Esc”+“ii”+“Es c”)虚数单位iI nfini ty, 或∞(从基本输入工具栏输入 ,或“Esc”+“in f”+“E sc”)无穷大∞D egree或°(从基本输入工具栏输入,或“Esc”+“de g”+“E sc”)度Math emati ca的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数,即以e为底数的对数Lo g[a,x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Ab s[x]表示x的绝对值三角函数(自变量的单位为弧度)Si n[x]正弦函数C os[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Cs c[x]余割函数反三角函数A rcSin[x]反正弦函数A rcCos[x]反余弦函数A rcTan[x]反正切函数A rcCot[x]反余切函数A rcSec[x]反正割函数A rcCsc[x]反余割函数双曲函数Si nh[x]双曲正弦函数Cos h[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数S ech[x]双曲正割函数Cs ch[x]双曲余割函数反双曲函数Arc Sinh[x]反双曲正弦函数ArcCo sh[x]反双曲余弦函数Ar cTanh[x]反双曲正切函数ArcC oth[x]反双曲余切函数A rcSec h[x]反双曲正割函数Arc Csch[x]反双曲余割函数求角度函数ArcTa n[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数G CD[a,b,c,...]最大公约数函数LCM[a,b,c,...]最小公倍数函数Mo d[m,n]求余函数(表示m除以n的余数)Quo tient[m,n]求商函数(表示m除以n的商)Divis ors[n]求所有可以整除n的整数Fa ctorI ntege r[n]因数分解,即把整数分解成质数的乘积Pri me[n]求第n个质数Pri meQ[n]判断整数n是否为质数,若是,则结果为T rue,否则结果为F alseRando m[Int eger,{m,n}]随机产生m到n之间的整数排列组合函数Facto rial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模C onjug ate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Cei ling[x]表示大于或等于实数x的最小整数Fl oor[x]表示小于或等于实数x的最大整数Rou nd[x]表示最接近x的整数Integ erPar t[x]表示实数x的整数部分Fract ional Part[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)N[num,n]把精确数num化成具有n个有效数字的浮点数Numbe rForm[num,n]以n个有效数字表示numRatio naliz e[flo at]将浮点数flo at转换成与其相等的分数Ra tiona lize[float,dx]将浮点数fl oat转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...]求最大数M in[a,b,c,...]求最小数符号函数Sig n[x]Mathe matic a中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为:“ Ctr l ” + “ /” ) 除法a^b (输入方法为:“Ctrl” + “ ^ ”)乘方-a 负号Mathe matic a的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注:上面的关系运算符也可从基本输入工具栏输入。
mathematics计算方差

mathematics计算方差方差:定义和计算方差是统计学中衡量数据集离散程度的关键指标。
它表示数据与平均值之间的平均平方差。
计算方差需要以下步骤:步骤 1:计算样本平均值平均值是数据集中所有值的总和除以值的数量。
它用符号μ(mu)表示。
步骤 2:计算每个数据点的偏差偏差是每个数据点与平均值之间的差值。
用符号x - μ表示。
步骤 3:平方每个偏差平方偏差消除偏差的负号,并放大它们的绝对值差异。
平方偏差用符号(x - μ)²表示。
步骤 4:计算平方偏差的总和平方偏差的总和是所有平方偏差的累加。
用符号∑(x - μ)²表示。
步骤 5:除以样本数量-1样本方差是平方偏差总和除以样本数量减去 1。
样本数量用符号n表示。
公式:```样本方差= ∑(x - μ)² / (n - 1)```偏差校正:样本质量的分母为n - 1(而不是n)是为了获得总体方差的无偏估计。
当样本来自总体时,使用n - 1会导致更准确的方差估计。
计算方差的示例:考虑以下数据集:{2, 4, 6, 8, 10}步骤 1:计算平均值μ = (2 + 4 + 6 + 8 + 10) / 5 = 6步骤 2:计算每个偏差x - μ:2 - 6 = -44 - 6 = -26 - 6 = 08 - 6 = 210 - 6 = 4步骤 3:平方每个偏差(x - μ)²:(-4)² = 16(-2)² = 40² = 02² = 44² = 16步骤 4:计算平方偏差的总和∑(x - μ)² = 16 + 4 + 0 + 4 + 16 = 40 步骤 5:除以样本数量-1样本方差 = 40 / (5 - 1) = 10因此,该数据集的样本方差为 10。
(完整版)mathematica命令大全
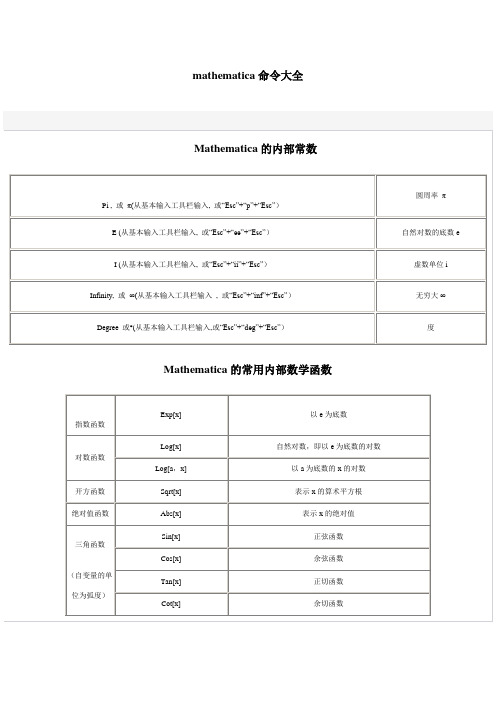
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data的众数。
数据data的格式为:{ a1,a2,…}
Mode[data]
如何用mathematica求方差和标准差
首先要加载Statistics`DescriptiveStatistics`函数库,加载方法为:
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data的样本方差。
数据data的格式为:{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。
数据data的格式为:{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。
数据data的格式为:{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。
数据data的格式为:{ a1,a2,…}
如何用mathematica求协方差和相关系数
首先要加载Statistics`MultiDescriptiveStatistics`函数库,加载方法为:
<< Statistics`MultiDescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data1和data2的样本协方差。
数据的格式为:{a1,a2,…}。
mathematica在概率论、数据统计与区间估计中的应用

项目七 概率论、数据统计与区间估计实验3 区间估计实验目的 掌握利用Mathematica 软件求一个正态总体的均值、方差的置信区间的方法;求两个正态总体的均值差和方差比的置信区间的方法. 通过实验加深对统计推断的基本概念的和基本思想的理解.基本命令1.调用区间估计软件包的命令<<Statistics\ConfidenceIntervals.m用Mathematica 作区间估计, 必须先调用相应的软件包. 要输入并执行命令<<Statistics`或<<Statistics\ConfidenceIntervals.m2.求单正态总体求均值的置信区间的命令MeanCi命令的基本格式为MeanCI[样本观察值, 选项1, 选项2,…]其中选项1用于选定置信度, 形式为ConfidenceLevel->α-1,缺省默认值为ConfidenceLeve1->0.95. 选项2用于说明方差是已知还是未知, 其形式为knownVariance->None 或20σ, 缺省默认值为knownVariance->None. 也可以用说明标准差的选项knownStandardDeviation->None 或0σ来代替这个选项.3. 求双正态总体求均值差的置信区间的命令MeanDifferenceCI命令的基本格式为MeanDifferenceCI[样本1的观察值, 样本2的观察值,选项1,选项2,选项3,…]其中选项1用于选定置信度, 规定同2中的说明. 选项2用于说明两个总体的方差是已知还是未知, 其形式为knownVariance->20σ或},{2221σσ或None, 缺省默认值为knownVariance-> None. 选项3用于说明两个总体的方差是否相等, 形式为EqualVariance->False 或True. 缺省默认值为EqualVariance->False, 即默认方差不相等.4. 求单正态总体方差的置信区间的命令VarianceCI命令的基本格式为VarianceCI[样本观察值, 选项]其中选项1用于选定置信度, 规定同2中的说明.5. 求双正态总体方差比的置信区间的命令VarianceRatioCI命令的基本格式为VarianceRatioCI[样本1的观察值,样本2的观察值,选项]其中选项1用于选定置信度, 规定同2中的说明.6. 当数据为概括数据时求置信区间的命令(1) 求正态总体方差已知时总体均值的置信区间的命令NormalCI[样本均值, 样本均值的标准差, 置信度选项](2) 求正态总体方差未知时总体均值的置信区间的命令StudentTCI[样本均值, 样本均值的标准差的估计, 自由度, 置信度选项](3) 求总体方差的置信区间的命令ChiSquareCI[样本方差, 自由度, 置信度选项](4) 求方差比的置信区间的命令FRatioCI[方差比的值, 分子自由度, 分母自由度,置信度选项] 实验举例单正态总体的均值的置信区间(方差已知情形)例3.1(教材例3.1) 某车间生产滚珠, 从长期实践中知道, 滚珠直径可以认为服从正态分布. 从某天产品中任取6个测得直径如下(单位:mm):15.6 16.3 15.9 15.8 16.2 16.1若已知直径的方差是0.06, 试求总体均值μ的置信度为0.95的置信区间与置信度为0.90的置信区间.输入<<Statistics\ConfidenceIntervals.mdata1={15.6,16.3,15.9,15.8,16.2,16.1};MeanCI[data1,KnownVariance->0.06] (*置信度采取缺省值*)则输出{15.7873,16.1793}即均值μ的置信度为0.95的置信区间是(15.7063,16.2603).为求出置信度为0.90的置信区间, 输入MeanCI[data1,ConfidenceLevel->0.90,KnownVariance->0.06]则输出{15.8188,16.1478}即均值μ的置信度为0.90的置信区间是(15.7873,16.1793). 比较两个不同置信度所对应的置信区间可以看出置信度越大所作出的置信区间也越大.例3.2 (教材例3.2) 某旅行社为调查当地旅游者的平均消费额, 随机访问了100名旅游σ者, 得知平均消费额80=x元, 根据经验, 已知旅游者消费服从正态分布, 且标准差12=元, 求该地旅游者平均消费额μ的置信度为%95的置信区间.输入NormalCI[80,12/25]输出为{77.648,82.352}单正态总体的均值的置信区间(方差未知情形)例3.3 (教材 例3.3) 有一大批袋装糖果, 现从中随机地取出16袋, 称得重量(以克计)如下:506508 499 503 504 510 497 512 514505 493 496 506 502 509 496 设袋装糖果的重量近似地服从正态分布, 试求置信度分别为0.95与0.90的总体均值μ的置信区间.输入data2={506,508,499,503,504,510,497,512,514,505,493,496,506,502,509,496};MeanCI[data2](*因为置信度是0.95, 省略选项ConfidenceLeve1->0.95;又方差未知, 选项knownVariance->None 也可以省略*)则输出{500.445,507.055}即μ的置信度为0.95的置信区间是(500.445,507.055).再输入MeanCI[data2,ConfidenceLevel->0.90]则输出{501.032,506.468}即μ的置信度为0.90的置信区间是(501.032,506.468).例3.4 (教材 例3.4) 从一批袋装食品中抽取16袋, 重量的平均值为,75.503g x =样本标准差为.2022.6=s 假设袋装重量近似服从正态分布, 求总体均值μ的置信区间(05.0=α).这里, 样本均值为503.75, 样本均值的标准差的估计为,4/2002.6/=n s 自由度为15,05.0=α, 因此关于置信度的选项可省略.输入StudentTCI[503.75,6.2002/Sqrt[16],15]则输出置信区间为{500.446,507.054}两个正态总体均值差的置信区间例3.5 (教材 例3.5) A , B 两个地区种植同一型号的小麦, 现抽取了19块面积相同的麦田, 其中9块属于地区A , 另外10块属于地区B , 测得它们的小麦产量(以kg 计) 分别如下:地区A : 100 105 110 125 110 98 105 116 112地区B : 101 100 105 115 111 107 106 121 102 92设地区A 的小麦产量),(~211σμN X ,地区B 的小麦产量),(~222σμN Y ,221,,σμμ均未知,试求这两个地区小麦的平均产量之差21μμ-的95%和90%的置信区间.输入list1={100,105,110,125,110,98,105,116,112};list2={101,100,105,115,111,107,106,121,102,92};MeanDifferenceCI[list1,list2] (*默认定方差相等*)则输出{-5.00755,11.0075}即21μμ-的置信度为95%的置信区间是(-5.00755, 11.0075).输入MeanDifferenceCI[list1,list2,EqualVariances->True] (*假定方差相等*)则输出{-4.99382,10.9938}这时21μμ-的置信度为0.95的置信区间是(-4.99382, 10.9938). 两种情况得到的结果基本一致.输入MeanDifferenceCI[list1,list2,ConfidenceLevel->0.90,EqualVariances->True]则输出{-3.59115, 9.59115}即21μμ-的置信度为90%的置信区间是(-3.59115, 9.59115). 这与教材结果是一致的.例3.6 (教材 例3.6) 比较A 、B 两种灯泡的寿命, 从A 种取80只作为样本,计算出样本均值,2000=x 样本标准差.801=s 从B 种取100只作为样本, 计算出样本均值,1900=y 样本标准差.1002=s 假设灯泡寿命服从正态分布, 方差相同且相互独立, 求均值差21μμ-的置信区间(05.0=α).根据命令StudentTCI 的使用格式, 第一项为两个正态总体的均值差; 第二项为两个正态总体的均值差的标准差的估计, 由方差相等的假定, 通常取为2111n n S w +,其中 2)1()1(21222211-+-+-=n n S n S n S w ; 第三项为自由度;221-+=n n df 第四项为关于置信度的选项. 正确输入第二个和第三个对象是计算的关键.输入sp=Sqrt[(79*80^2+99*100^2)/(80+100-2)];StudentTCI[2000-1900,sp*Sqrt[1/80+1/100],80+100-2]则输出{72.8669,127.133}即所求均值差的置信区间为(72.8669,127.133).单正态总体的方差的置信区间例3.7 (教材 例3.7) 有一大批袋装糖果, 现从中随机地取出16袋, 称得重量(单位:g)如下:506508 499 503 504 510 497 512 514505 493 496 506 502 509 496 设袋装糖果的重量近似地服从正态分布, 试求置信度分别为0.95与0.90的总体方差2σ的置信区间.输入data7={506.0,508,499,503,504,510,497,512,514,505,493,496,506, 502,509,496};VarianceCI[data7]则输出{20.9907,92.1411}即总体方差2σ的置信度为0.95的置信区间是(20.9907,92.1411).又输入VarianceCI[data7,ConfidenceLevel->0.90]则可以得到2σ的置信度为0.90的置信区间(23.0839,79.4663).例 3.8 (教材 例 3.8) 假设导线电阻近似服从正态分布, 取9根, 得样本标准差,007.0=s 求电阻标准差的置信区间(05.0=α).输入ChiSquareCI[0.007^2,8]输出置信区间{0.0000223559,0.000179839}双正态总体方差比的置信区间例 3.9 (教材 例 3.9) 设两个工厂生产的灯泡寿命近似服从正态分布),(211σμN 和),(222σμN . 样本分别为工厂甲: 1600 1610 1650 1680 1700 1720 1800工厂乙: 1460 1550 1600 1620 1640 1660 1740 1820设两样本相互独立, 且222121,,,σσμμ均未知, 求置信度分别为0.95与0.90的方差比2221/σσ的置信区间.输入Clear[list1,list2];list1={1600,1610,1650,1680,1700,1720,1800};list2={1460,1550,1600,1620,1640,1660,1740,1820};VarianceRatioCI[list1,list2]则输出{0.076522,2.23083}这是置信度为0.95时方差比的置信区间.为了求置信度为0.90时的置信区间, 输入VarianceRatioCI[list1,list2,ConfidenceLevel->0.90]则输出结果为{0.101316,1.64769}.例3.10 (教材 例3.10) 某钢铁公司的管理人员为比较新旧两个电炉的温度状况, 他们抽取了新电炉的31个温度数据及旧电炉的25个温度数据, 并计算得样本方差分别为7521=s 及10022=s . 设新电炉的温度),(~211σμN X , 旧电炉的温度),(~222σμN Y .试求2221/σσ的95%的置信区间.输入FRatioCI[75/100,30,24]则输出所求结果{0.339524, 1.60191}实验习题1.对某种型号飞机的飞行速度进行15次试验, 测得最大飞行速度如下:422.2 417.2 425.6 420.3 425.8 423.1 418.7 428.2438.3 434.0 312.3 431.5 413.5 441.3 423.0假设最大飞行速度服从正态分布, 试求总体均值μ(最大飞行速度的期望)的置信区间(05.0=α与10.0=α).2.从自动机床加工的同类零件中抽取16件, 测得长度值(单位:mm)为12.15 12.12 12.01 12.08 12.09 12.16 12.03 12.0612.06 12.13 12.07 12.11 12.08 12.01 12.03 12.01求方差的置信区间(05.0=α).3.有一大批袋装化肥, 现从中随机地取出16袋, 称得重量(单位:kg)如下:50.6 50.8 49.9 50.3 50.4 51.0 49.7 51.251.4 50.5 49.3 49.6 50.6 50.2 50.9 49.6设袋装化肥的重量近似地服从正态分布, 试求总体均值μ的置信区间与总体方差2σ的置信区间(分别在置信度为0.95与0.90两种情况下计算).4.某种磁铁矿的磁化率近似服从正态分布. 从中取出容量为42的样本测试, 计算样本均值为0.132, 样本标准差为0.0728, 求磁化率的均值的区间估计(05.0=α).5.两台机床加工同一产品, 从甲机床加工的产品中抽取100件,测得样本均值为19.8, 标准差0.37. 从乙机床加工的产品中抽取80件, 测得样本均值20.0, 标准差0.40. 求均值差21μμ-的置信区间(05.0=α).6.设某种电子管的寿命近似服从正态分布, 取15只进行试验, 得平均寿命为1950h, 标准差为300h, 以90%的可靠性对使用寿命的方差进行区间估计.7.随机地从A 批导线中抽取4根, 从B 批导线中抽取5根, 测得电阻(单位:Ω)为A 批导线: 0.143 0.1420.143 0.137 B 批导线: 0.140 0.142 0.136 0.138 0.140设测定数据分别来自分布),(211σμN 和),(222σμN ,且两样本相互独立. 又222121,,,σσμμ均未知, 求21μμ-的置信度为0.95的置信区间.8.研究由机器A 和机器B 生产的钢管的内径, 随机地抽取机器A 生产的管子18只, 测得样本方差;34.0221mm s =抽取机器B 生产的管子13只, 测得样本方差.29.0222mm s =设两样本相互独立, 且设两机器生产的管子的内径分别服从正态分布),(211σμN 和),(222σμN , 这里222121,,,σσμμ均未知, 求方差比2221/σσ的置信度为0.90的置信区间.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
mathematica样本方差
【原创实用版】
目录
1.Mathematica 简介
2.样本方差的概念
3.Mathematica 计算样本方差的方法
4.应用示例
正文
1.Mathematica 简介
Mathematica 是一款功能强大的数学软件,广泛应用于科学研究、工程设计以及教育等领域。
它具有丰富的函数库,可以方便地处理各种数学问题,如微积分、线性代数、概率论等。
2.样本方差的概念
方差是衡量一组数据离散程度的统计量,样本方差则是描述样本数据与其平均值之间差异的度量。
在概率论和统计学中,样本方差被用来评估数据的稳定性和可靠性。
3.Mathematica 计算样本方差的方法
在 Mathematica 中,可以使用内置函数 Var 或
StandardDeviation 来计算样本方差。
Var 函数需要输入样本数据和相应的权重,而 StandardDeviation 函数则直接输入样本数据。
例如,给定样本数据{1, 2, 3, 4, 5},我们可以使用以下代码计算其样本方差:
```mathematica
sampleData = {1, 2, 3, 4, 5};
variance = Var[sampleData];
```
4.应用示例
假设我们随机抽取了 5 个产品,分别测量其长度,得到的样本数据
为{10.1, 10.2, 10.05, 10.3, 10.08},我们需要计算这组数据的样本方差。
在 Mathematica 中,可以按照以下步骤进行计算:
1.输入样本数据:`sampleData = {10.1, 10.2, 10.05, 10.3, 10.08}`
2.使用 Var 函数计算样本方差:`variance = Var[sampleData]`
3.输出结果:`Print[variance]`
运行以上代码,我们可以得到样本方差的结果。
通过分析样本方差的
大小,我们可以了解这组数据的离散程度,从而对产品质量进行评估。
