2020年高考数学试题分类汇编：空间向量

合集下载

2020年高考江苏版高考数学专题十七空间向量与立体几何

1.(2018 江苏泰兴中学调研,22)如图,在三棱锥 P-ABC 中,已知平面 PAB⊥平面 ABC,AC⊥BC,AC=BC=2a,点 O,D 分别是 AB,PB 的中点,PO⊥AB,连接 CD. (1)若 PA=2a,求异面直线 PA 与 CD 所成角的余弦值的大小;
5
(2)若二面角 A-PB-C 的余弦值的大小为 5 ,求 PA.
(2)设 P(λ,λ,0),λ∈[0, 2],则��=( 2-λ, 2-λ,1),
1
因为异面直线 PF 与 BC 所成的角为 60°,所以|cos<��,��>|=2,
| - 2( 2 - λ)| 1
2
32
即 2( 2 - λ)2 + 1· 2=2,解得 λ= 2 或 λ= 2 (舍去).
备战 2020 高考
( ) ( ) 2
1 12 2
1
11
故��=��+��=��+3��= 3, - 3, 3 ,��=3��= 3,3,0 ,
( ) 2 2 2
解析 (1)设 AC,BD 交于点 O,连接 OP.在正四棱锥 P-ABCD 中,易得 OP⊥平面 ABCD.又 PA=AB=2,所以 OP= 2 .以 O 为坐标原点,��,��方向分别为 x 轴、y 轴正方向,建立空间直角坐标系 O-xyz,如图.
则 A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),P(0,0, 2),��=(-1,1, 2).

2019-2021全国高考数学真题汇编：空间向量(教师版)

2019-2021全国高考数学真题汇编：空间向量一．选择题（共6小题）1．（2019•全国）经过点（1，﹣1，3）且与平面2x+y﹣z+4＝0平行的平面方程为（）A．2x+y﹣z+2＝0B．2x+y+z﹣6＝0C．2x+y+z﹣4＝0D．2x+y﹣z﹣3＝02．（2020•新课标Ⅱ）已知△ABC是面积为的等边三角形，且其顶点都在球O的球面上．若球O的表面积为16π（）A．B．C．1D．3．（2020•海南）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为O），地球上一点A的纬度是指OA与地球赤道所在平面所成角，若晷面与赤道所在平面平行，点A处的纬度为北纬40°（）A．20°B．40°C．50°D．90°4．（2019•上海）已知直线方程2x﹣y+c＝0的一个方向向量可以是（）A．（2，﹣1）B．（2，1）C．（﹣1，2）D．（1，2）5．（2019•浙江）设三棱锥V﹣ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点（不含端点），直线PB与平面ABC所成角为β，二面角P﹣AC﹣B的平面角为γ，则（）A．β＜γ，α＜γB．β＜α，β＜γC．β＜α，γ＜αD．α＜β，γ＜β6．（2019•全国）正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，BC的中点（）A．B．C．D．二．填空题（共3小题）7．（2019•上海）已知向量＝（1，0，2），＝（2，1，0），则与的夹角为．8．（2019•新课标Ⅱ）已知∠ACB＝90°，P为平面ABC外一点，PC＝2，BC的距离均为，那么P到平面ABC的距离为．9．（2020•山东）已知直四棱柱ABCD﹣A1B1C1D1的棱长均为2，∠BAD＝60°．以D1为球心，为半径的球面与侧面BCC1B1的交线长为．三．解答题（共28小题）10．（2020•上海）已知ABCD是边长为1的正方形，正方形ABCD绕AB旋转形成一个圆柱．（1）求该圆柱的表面积；（2）正方形ABCD绕AB逆时针旋转至ABC1D1，求线段CD1与平面ABCD所成的角．11．（2020•北京）如图，在正方体ABCD﹣A1B1C1D1中，E为BB1的中点．（Ⅱ）求证：BC1∥平面AD1E；（Ⅱ）求直线AA1与平面AD1E所成角的正弦值．12．（2021•上海）四棱锥P﹣ABCD，底面为正方形ABCD，边长为4，PE⊥平面ABCD．（1）若△P AB为等边三角形，求四棱锥P﹣ABCD的体积；（2）若CD的中点为F，PF与平面ABCD所成角为45°，求PC与AD所成角的大小．13．（2019•新课标Ⅱ）如图，长方体ABCD﹣A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE＝A1E，求二面角B﹣EC﹣C1的正弦值．14．（2020•新课标Ⅱ）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE＝AD．△ABC是底面的内接正三角形，P 为DO上一点DO．（1）证明：P A⊥平面PBC；（2）求二面角B﹣PC﹣E的余弦值．15．（2021•新高考Ⅱ）在四棱锥Q﹣ABCD中，底面ABCD是正方形，若AD＝2，QC＝3．（Ⅱ）求证：平面QAD⊥平面ABCD；（Ⅱ）求二面角B﹣QD﹣A的平面角的余弦值．16．（2019•上海）如图，在长方体ABCD﹣A1B1C1D1中，M为BB1上一点，已知BM＝2，CD＝3，AA1＝5．（1）求直线A1C和平面ABCD的夹角；（2）求点A到平面A1MC的距离．17．（2019•新课标Ⅱ）如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A﹣MA1﹣N的正弦值．18．（2020•海南）如图，四棱锥P﹣ABCD的底面为正方形，PD⊥底面ABCD．设平面P AD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD＝AD＝1，Q为l上的点，QB＝19．（2020•天津）如图，在三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，AC⊥BC，AC＝BC＝21＝3，点D，E分别在棱AA1和棱CC1上，且AD＝1，CE＝21B1的中点．（Ⅱ）求证：C1M⊥B1D；（Ⅱ）求二面角B﹣B1E﹣D的正弦值；（Ⅱ）求直线AB与平面DB1E所成角的正弦值．20．（2020•山东）如图，四棱锥P﹣ABCD的底面为正方形，PD⊥底面ABCD．设平面P AD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD＝AD＝1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．21．（2021•上海）如图，在长方体ABCD﹣A1B1C1D1中，已知AB＝BC＝2，AA1＝3．（1）若P是棱A1D1上的动点，求三棱锥C﹣P AD的体积；（2）求直线AB1与平面ACC1A1的夹角大小．22．（2021•天津）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E，F分别为棱BC，CD的中点．（1）求证：D1F∥平面A1EC1；（2）求直线AC1与平面A1EC1所成角的正弦值；（3）求二面角A﹣A1C1﹣E的正弦值．23．（2021•北京）如图，在正方体ABCD﹣A1B1C1D1，E为A1D1的中点，B1C1交平面CDE交于点F．（Ⅱ）求证：F为B1C1的中点；（Ⅱ）若点M是棱A1B1上一点，且二面角M﹣CF﹣E的余弦值为，求的值．24．（2021•乙卷）如图，四棱锥P﹣ABCD的底面是矩形，PD⊥底面ABCD，M为BC中点，且PB⊥AM．（1）求BC；（2）求二面角A﹣PM﹣B的正弦值．25．（2021•甲卷）已知直三棱柱ABC﹣A1B1C1中，侧面AA1B1B为正方形，AB＝BC＝2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF⊥A1B1．（1）证明：BF⊥DE；（2）当B1D为何值时，面BB1C1C与面DFE所成的二面角的正弦值最小？26．（2019•天津）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，平面P AC⊥平面PCD，P A⊥CD，AD ＝3．（Ⅱ）设G，H分别为PB，AC的中点；（Ⅱ）求证：P A⊥平面PCD；（Ⅱ）求直线AD与平面P AC所成角的正弦值．27．（2019•天津）如图，AE⊥平面ABCD，CF∥AE，AD⊥AB，AB＝AD＝1（Ⅱ）求证：BF∥平面ADE；（Ⅱ）求直线CE与平面BDE所成角的正弦值；（Ⅱ）若二面角E﹣BD﹣F的余弦值为，求线段CF的长．28．（2019•新课标Ⅱ）图1是由矩形ADEB、Rt△ABC和菱形BFGC组成的一个平面图形，其中AB＝1，BE＝BF＝2，BC折起使得BE与BF重合，连结DG（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B﹣CG﹣A的大小．29．（2019•新课标Ⅱ）如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．30．（2020•江苏）在三棱锥A﹣BCD中，已知CB＝CD＝，BD＝2，AO⊥平面BCD，AO＝2（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF＝BC，求sinθ的值．31．（2020•新课标Ⅱ）如图，在长方体ABCD﹣A1B1C1D1中，点E，F分别在棱DD1，BB1上，且2DE＝ED1，BF＝2FB1．（1）证明：点C1在平面AEF内；（2）若AB＝2，AD＝1，AA1＝3，求二面角A﹣EF﹣A1的正弦值．32．（2020•浙江）如图，在三棱台ABC﹣DEF中，平面ACFD⊥平面ABC，DC＝2BC．（Ⅱ）证明：EF⊥DB；（Ⅱ）求直线DF与平面DBC所成角的正弦值．33．（2020•新课标Ⅱ）如图，已知三棱柱ABC﹣A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．过B1C1和P的平面交AB于E，交AC于F．（1）证明：AA1∥MN，且平面A1AMN⊥平面EB1C1F；（2）设O为△A1B1C1的中心．若AO∥平面EB1C1F，且AO＝AB，求直线B1E与平面A1AMN所成角的正弦值．34．（2021•浙江）如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，AB＝1，BC＝4，M，N分别为BC，PC的中点，PM⊥MD．（Ⅱ）证明：AB⊥PM；（Ⅱ）求直线AN与平面PDM所成角的正弦值．35．（2021•新高考Ⅱ）如图，在三棱锥A﹣BCD中，平面ABD⊥平面BCD，O为BD的中点．（1）证明：OA⊥CD；（2）若△OCD是边长为1的等边三角形，点E在棱AD上，DE＝2EA，求三棱锥A﹣BCD的体积．36．（2019•浙江）如图，已知三棱柱ABC﹣A1B1C1，平面A1ACC1⊥平面ABC，∠ABC＝90°，∠BAC＝30°，A1A＝A1C＝AC，E，F分别是AC，A1B1的中点．（Ⅱ）证明：EF⊥BC；（Ⅱ）求直线EF与平面A1BC所成角的余弦值．37．（2019•北京）如图，在四棱锥P﹣ABCD中，P A⊥平面ABCD，AD∥BC，P A＝AD＝CD＝2，点F在PC上，且＝．（Ⅱ）求证：CD⊥平面P AD；（Ⅱ）求二面角F﹣AE﹣P的余弦值；（Ⅱ）设点G在PB上，且＝．判断直线AG是否在平面AEF内，说明理由．2019-2021全国高考数学真题汇编：空间向量参考答案与试题解析一．选择题（共6小题）1．（2019•全国）经过点（1，﹣1，3）且与平面2x+y﹣z+4＝0平行的平面方程为（）A．2x+y﹣z+2＝0B．2x+y+z﹣6＝0C．2x+y+z﹣4＝0D．2x+y﹣z﹣3＝0【分析】设与平面2x+y﹣z+4＝0平行的平面方程为2x+y﹣z+k＝0，代入点的坐标求出k的值即可．【解答】解：设与平面2x+y﹣z+4＝2平行的平面方程为2x+y﹣z+k＝0，代入点（7，﹣1，得2×5﹣1﹣3+k＝8，则所求的平面方程为2x+y﹣z+2＝5．故选：A．【点评】本题考查了空间直角坐标系与平面方程的应用问题，是基础题．2．（2020•新课标Ⅱ）已知△ABC是面积为的等边三角形，且其顶点都在球O的球面上．若球O的表面积为16π（）A．B．C．1D．【分析】画出图形，利用已知条件求三角形ABC的外接圆的半径，然后求解OO1即可．【解答】解：由题意可知图形如图：△ABC是面积为的等边三角形，∴AB＝BC＝AC＝3，可得：AO1＝＝，球O的表面积为16π，外接球的半径为：R；所以5πR2＝16π，解得R＝2，所以O到平面ABC的距离为：＝1．故选：C．【点评】本题考查球的内接体问题，求解球的半径，以及三角形的外接圆的半径是解题的关键．3．（2020•海南）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为O），地球上一点A的纬度是指OA与地球赤道所在平面所成角，若晷面与赤道所在平面平行，点A处的纬度为北纬40°（）A．20°B．40°C．50°D．90°【分析】由纬度的定义和线面角的定义，结合直角三角形的性质，可得晷针与点A处的水平面所成角．【解答】解：可设A所在的纬线圈的圆心为O'，OO'垂直于纬线所在的圆面，由图可得∠OHA为晷针与点A处的水平面所成角，又∠OAO'为40°且OA⊥AH，在Rt△OHA中，O'A⊥OH，另解：画出截面图，如下图所示．l是点A处的水平面的截线，由题意可得OA⊥l．m是晷面的截线，晷针与晷面垂直，根据平面平行的性质定理可得m∥CD，根据线面垂直的定义可得AB⊥m，由于∠AOC＝40°，所以∠OAG＝∠AOC＝40°，由于∠OAG+∠GAE＝∠BAE+∠GAE＝90°，所以∠BAE＝∠OAG＝40°，也即晷针与A处的水平面所成角为∠BAE＝40°，故选：B．【点评】本题是立体几何在生活中的运用，考查空间线面角的定义和求法，属于基础题．4．（2019•上海）已知直线方程2x﹣y+c＝0的一个方向向量可以是（）A．（2，﹣1）B．（2，1）C．（﹣1，2）D．（1，2）【分析】先根据直线方程得直线的一个法向量，再根据法向量可得直线的方向向量．【解答】解：依题意，（2，∴方向向量为（1，故选：D．【点评】本题考查了直线的方向向量，空间直线的向量，属基础题．5．（2019•浙江）设三棱锥V﹣ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点（不含端点），直线PB与平面ABC所成角为β，二面角P﹣AC﹣B的平面角为γ，则（）A．β＜γ，α＜γB．β＜α，β＜γC．β＜α，γ＜αD．α＜β，γ＜β【分析】本题以三棱锥为载体，综合考查异面直线所成角、直线和平面所成角和二面角的概念和计算，解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小，充分运用图象，则可事半功倍，【解答】解：方法一、如图G为AC的中点，则P在底面上的射影D在线段AO上，作DE⊥AC于E，过P作PF∥AC于F，过D作DH∥AC，交BG于H，则α＝∠BPF，β＝∠PBD，则cosα＝＝＝＜＝cosβ；tanγ＝＞＝tanβ，方法二、由最小值定理可得β＜α，由三正弦定理可得β＜γ'＝γ；方法三、（特殊图形法）设三棱锥V﹣ABC为棱长为2的正四面体，易得cosα＝＝，可得sinα＝＝，sinγ＝＝，当AP＝时，由余弦定理可得PB＝＝，cosα＝＝，sinα＝，故C错误．故选：B．【点评】本题考查二面角的求法，常规解法下易出现的错误的有：不能正确作出各种角，未能想到利用“特殊位置法”，寻求简单解法．6．（2019•全国）正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，BC的中点（）A．B．C．D．【分析】以P为原点，P A为x轴，PB为y轴，PC为z轴，建立空间直角坐标系，利用向量法能求出PB与平面PEF所成角的正弦值．【解答】解：∵正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，∴以P为原点，P A为x轴，PC为z轴，设P A＝PB＝PC＝2，则A（2，3，0），2，3），0，2），7，0），1，8），＝（0，2，7），，1，0），，6，1），设平面PEF的法向量＝（x，y，则，取x＝1，得，﹣1，设PB与平面PEF所成角为θ，则sinθ＝＝＝．∴PB与平面PEF所成角的正弦值为．故选：C．【点评】本题考查线面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．二．填空题（共3小题）7．（2019•上海）已知向量＝（1，0，2），＝（2，1，0），则与的夹角为．【分析】直接利用向量的夹角公式的应用求出结果．【解答】解：向量＝（1，0，＝（8，1，则，，所以：cos＝，故：与的夹角为．故答案为：．【点评】本题考查的知识要点：向量的夹角公式的应用，主要考查学生的运算能力和转换能力，属于基础题型．8．（2019•新课标Ⅱ）已知∠ACB＝90°，P为平面ABC外一点，PC＝2，BC的距离均为，那么P到平面ABC的距离为．【分析】过点P作PD⊥AC，交AC于D，作PE⊥BC，交BC于E，过P作PO⊥平面ABC，交平面ABC于O，连结OD，OC，则PD＝PE＝，从而CD＝CE＝OD＝OE＝＝1，由此能求出P到平面ABC的距离．【解答】解：∠ACB＝90°，P为平面ABC外一点，点P到∠ACB两边AC，BC的距离均为，过点P作PD⊥AC，交AC于D，交BC于E，过P作PO⊥平面ABC，交平面ABC于O，连结OD，OC，∴由题意得CD＝CE＝OD＝OE＝＝1，∴PO＝＝＝．∴P到平面ABC的距离为．故答案为：．【点评】本题考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理能力与计算能力，属于中档题．9．（2020•山东）已知直四棱柱ABCD﹣A1B1C1D1的棱长均为2，∠BAD＝60°．以D1为球心，为半径的球面与侧面BCC1B1的交线长为．【分析】画出直观图，建立如图所示的坐标系，设出P的坐标，通过D1P＝．求出P的轨迹方程，然后求解以D1为球心，为半径的球面与侧面BCC1B1的交线长．【解答】解：由题意直四棱柱ABCD﹣A1B1C3D1的棱长均为2，∠BAD＝60°4B1＝2，上下底面是菱形，设P（x 的球面上的点1C1的垂直，E为垂足，则D7E2＝D1B32+x2﹣5•D1B1•x cos60°＝x7+4﹣2x．由题意可知D3P＝．可得：5＝x4+4﹣2x+（3﹣y）2．即（x﹣1）8+（y﹣2）2＝7，所以P在侧面BCC1B1的轨迹是以B3C1的中点为圆心，半径为．以D6为球心，为半径的球面与侧面BCC1B5的交线长为：＝．故答案为：．【点评】本题考查空间点线面距离的求法，球与几何体相交的交线的问题，难度比较大．三．解答题（共28小题）10．（2020•上海）已知ABCD是边长为1的正方形，正方形ABCD绕AB旋转形成一个圆柱．（1）求该圆柱的表面积；（2）正方形ABCD绕AB逆时针旋转至ABC1D1，求线段CD1与平面ABCD所成的角．【分析】（1）该圆柱的表面由上下两个半径为1的圆面和一个长为2π、宽为1的矩形组成，依次求出圆面和矩形的面积，相加即可；（2）先利用线面垂直的判定定理证明AD1⊥平面ADB，连接CD1，则∠D1CA即为线段CD1与平面ABCD所成的角，再利用三角函数的知识求出cos∠D1CA即可．【解答】解：（1）该圆柱的表面由上下两个半径为1的圆面和一个长为2π、宽为5的矩形组成，∴S＝2×π×13+2π×1＝8π．故该圆柱的表面积为4π．（2）∵正方形ABC1D7，∴AD1⊥AB，又∠DAD1＝，∴AD1⊥AD，∵AD∩AB＝A，且AD，∴AD1⊥平面ADB，即D5在面ADB上的投影为A，连接CD1，则∠D1CA即为线段CD6与平面ABCD所成的角，而cos∠D1CA＝＝，∴线段CD1与平面ABCD所成的角为arccos．【点评】本题考查圆柱的表面积、空间线面夹角问题，熟练掌握线面垂直的判定定理是解题的关键，考查学生的空间立体感和运算能力，属于基础题．11．（2020•北京）如图，在正方体ABCD﹣A1B1C1D1中，E为BB1的中点．（Ⅱ）求证：BC1∥平面AD1E；（Ⅱ）求直线AA1与平面AD1E所成角的正弦值．【分析】（Ⅱ）根据正方体的性质可证得BC1∥AD1，再利用线面平行的判定定理即可得证；（Ⅱ）解法一：以A为原点，AD、AB、AA1分别为x、y和z轴建立空间直角坐标系，设直线AA1与平面AD1E所成角为θ，先求出平面AD1E的法向量，再利用sinθ＝|cos＜，＞|＝以及空间向量数量积的坐标运算即可得解．解法二：设正方体的棱长为2a，易知＝2a2，结合勾股定理和余弦定理可求得cos∠EAD1＝，再求得＝AD1•AE•sin∠EAD1；设点A1到平面EAD1的距离为h，根据等体积法＝，可求出h的值，设直线AA1与平面AD1E所成角为θ，则sinθ＝，从而得解．【解答】解：（Ⅱ）由正方体的性质可知，AB∥C1D1中，且AB＝C5D1，∴四边形ABC1D5是平行四边形，∴BC1∥AD1，又BC7⊄平面AD1E，AD1⊂平面AD6E，∴BC1∥平面AD1E．（Ⅱ）解法一：以A为原点，AD、AA8分别为x、y和z轴建立如图所示的空间直角坐标系，设正方体的棱长为a，则A（0，0，A8（0，0，a），D7（a，0，a），a，a），∴，，，设平面AD8E的法向量为，则，即，令z＝2，则x＝﹣4，∴＝（﹣2，2），设直线AA7与平面AD1E所成角为θ，则sinθ＝|cos＜，＝，故直线AA3与平面AD1E所成角的正弦值为．解法二：设正方体的棱长为2a，则AD1＝a，AE＝a3＝3a，＝•2a•4a＝2a2，由余弦定理知，cos∠EAD5＝＝＝，∴sin∠EAD5＝，∴＝AD1•AE•sin∠EAD6＝3a2，设点A7到平面EAD1的距离为h，∵＝，∴，∴h＝，设直线AA1与平面AD1E所成角为θ，则sinθ＝＝．故直线AA8与平面AD1E所成角的正弦值为．【点评】本题考查空间中线面的位置关系和线面夹角问题，熟练掌握线面平行的判定定理和利用空间向量求线面夹角是解题的关键，考查学生的空间立体感和运算能力，属于基础题．12．（2021•上海）四棱锥P﹣ABCD，底面为正方形ABCD，边长为4，PE⊥平面ABCD．（1）若△P AB为等边三角形，求四棱锥P﹣ABCD的体积；（2）若CD的中点为F，PF与平面ABCD所成角为45°，求PC与AD所成角的大小．【分析】（1）由V＝PE•S正方形ABCD，代入相应数据，进行运算，即可；（2）由PE⊥平面ABCD，知∠PFE＝45°，进而有PE＝FE＝4，PB＝，由AD∥BC，知∠PCB或其补角即为所求，可证BC⊥平面P AB，从而有BC⊥PB，最后在Rt△PBC中，由tan∠PCB＝，得解．【解答】解：（1）∵△P AB为等边三角形，且E为AB中点，∴PE＝2，又PE⊥平面ABCD，∴四棱锥P﹣ABCD的体积V＝PE•S正方形ABCD＝×28＝．（2）∵PE⊥平面ABCD，∴∠PFE为PF与平面ABCD所成角为45°，即∠PFE＝45°，∴△PEF为等腰直角三角形，∵E，F分别为AB，∴PE＝FE＝8，∴PB＝＝，∵AD∥BC，∴∠PCB或其补角即为PC与AD所成角，∵PE⊥平面ABCD，∴PE⊥BC，又BC⊥AB，PE∩AB＝E、AB⊂平面P AB，∴BC⊥平面P AB，∴BC⊥PB，在Rt△PBC中，tan∠PCB＝＝＝，故PC与AD所成角的大小为arctan．【点评】本题考查棱锥的体积、线面角和异面直线夹角的求法，理解线面角的定义，以及利用平移法找到异面直线所成角是解题的关键，考查学生的空间立体感、逻辑推理能力和运算能力，属于基础题．13．（2019•新课标Ⅱ）如图，长方体ABCD﹣A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE＝A1E，求二面角B﹣EC﹣C1的正弦值．【分析】（1）推导出B1C1⊥BE，BE⊥EC1，由此能证明BE⊥平面EB1C1．（2）以C为坐标原点，建立如图所示的空间直角坐标系，利用向量法能求出二面角B﹣EC﹣C1的正弦值．【解答】证明：（1）长方体ABCD﹣A1B1C2D1中，B1C3⊥平面ABA1B1，∴B4C1⊥BE，∵BE⊥EC1，∵B3C1∩EC1＝C3，∴BE⊥平面EB1C1．解：（2）以C为坐标原点，建立如图所示的空间直角坐标系，设AE＝A7E＝1，则BE＝EB1，∵BE⊥平面EB6C1，∴BE⊥EB1，∴BE2+EB12＝8BE2＝＝42＝4，∵AE2+AB2＝6+AB2＝BE2＝6，∴AB＝1，则E（1，5，1），1，8），B1（0，6，2），C1（3，0，2），3，0），∵BC⊥EB1，∴EB2⊥面EBC，故取平面EBC的法向量为＝＝（﹣1，5，设平面ECC1 的法向量＝（x，y，由，得，取x＝1，得，﹣1，∴cos＜＞＝，∴二面角B﹣EC﹣C1的正弦值为＝．【点评】本题考查线面垂直的证明，考查二面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理能力与计算能力，是中档题．14．（2020•新课标Ⅱ）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE＝AD．△ABC是底面的内接正三角形，P 为DO上一点DO．（1）证明：P A⊥平面PBC；（2）求二面角B﹣PC﹣E的余弦值．【分析】（1）设圆O的半径为1，求出各线段的长度，利用勾股定理即可得到P A⊥PC，P A⊥PB，进而得证；（2）建立空间直角坐标系，求出平面PBC及平面PCE的法向量，利用向量的夹角公式即可得解．【解答】解：（1）不妨设圆O的半径为1，OA＝OB＝OC＝1，，，，在△P AC中，P A2+PC2＝AC2，故P A⊥PC，同理可得P A⊥PB，又PB∩PC＝P，故P A⊥平面PBC；（2）建立如图所示的空间直角坐标系，则有，E（0，3，故，设平面PCE的法向量为，则由，得，取x＝1，则，所以平面PCE的法向量为，由（1）可知P A⊥平面PBC，不妨取平面PBC的法向量为，故，即二面角B﹣PC﹣E的余弦值为．【点评】本题考查线面垂直的判定以及利用空间向量求解二面角，考查推理能力及计算能力，属于基础题．15．（2021•新高考Ⅱ）在四棱锥Q﹣ABCD中，底面ABCD是正方形，若AD＝2，QC＝3．（Ⅱ）求证：平面QAD⊥平面ABCD；（Ⅱ）求二面角B﹣QD﹣A的平面角的余弦值．【分析】（Ⅱ）由CD2+QD2＝QC2证明CD⊥QD，再由CD⊥AD，证明CD⊥平面QAD，即可证明平面QAD⊥平面ABCD．（Ⅱ）【解法1】设AD的中点为M，连接QM、BM，求出cos∠QDB、cos∠QDA和∠BDA，利用三射线定理列方程求出二面角B﹣QD﹣A的平面角的余弦值．【解法2】取AD的中点O，在平面ABCD内作Ox⊥AD，以OD为y轴，OQ为z轴，建立空间直角坐标系，求出平面ADQ的一个法向量，平面BDQ的一个法向量，再求cos＜，＞即可．【解答】（Ⅱ）证明：△QCD中，CD＝AD＝2，QC＝62+QD2＝QC8，所以CD⊥QD；又CD⊥AD，AD∩QD＝D，QD⊂平面QAD；又CD⊂平面ABCD，所以平面QAD⊥平面ABCD．（Ⅱ）解：【解法1】设AD的中点为M，连接QM，如图所示：根据题意知，QM＝2，QB＝3，△BQA中，cos∠QDB＝，∠BDA＝45°，因此根据三射线定理知，二面角B﹣QD﹣A的大小满足：cos∠BDA＝cos∠QDB cos∠QDA+sin∠QDB sin∠QDA cosφ，即＝•+••cosφ，解得cosφ＝．【解法2】取AD的中点O，在平面ABCD内作Ox⊥AD，以OD为y轴，OQ为z轴，如图所示：则O（0，6，0），﹣1，D（6，1，Q（0，8，因为Ox⊥平面ADQ，所以平面ADQ的一个法向量为，0，0），设平面BDQ的一个法向量为＝（x，y，由＝（﹣3，2，＝（0，4），得，即，令z＝1，得y＝8，所以，2，1）；所以cos＜，＞＝＝＝，所以二面角B﹣QD﹣A的平面角的余弦值为．【点评】本题考查了空间中的垂直关系应用问题，也考查了利用空间向量求二面角的余弦值应用问题，也可以直接利用二面角的定义求二面角的余弦值，是中档题．16．（2019•上海）如图，在长方体ABCD﹣A1B1C1D1中，M为BB1上一点，已知BM＝2，CD＝3，AA1＝5．（1）求直线A1C和平面ABCD的夹角；（2）求点A到平面A1MC的距离．【分析】（1）由题意可得A1C与平面ABCD所成夹角为∠A1CA，判断△A1CA为等腰三角形，即可求出，（2）如图建立坐标系，根据向量的关系可得点A到平面A1MC的距离d＝，求出法向量即可求出．【解答】解：（1）依题意：AA1⊥平面ABCD，连接AC1C与平面ABCD所成夹角为∠A2CA，∵AA1＝5，AC＝，∴△A1CA为等腰三角形，∴∠A1CA＝，∴直线A1C和平面ABCD的夹角为，（2）（空间向量），如图建立坐标系，则A（4，0，0），3，0），A1（3，0，5），2，2），∴＝（3，4，＝（3，8，＝（0，4，设平面A4MC的法向量＝（x，y，由，可得，5，2），∴点A到平面A1MC的距离d＝＝＝．【点评】本题考查了线面角的求法和点到平面的距离，考查了运算求解能力和转化与化归能力，空间想象能力，属于中档题．17．（2019•新课标Ⅱ）如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A﹣MA1﹣N的正弦值．【分析】（1）过N作NH⊥AD，证明NM∥BH，再证明BH∥DE，可得NM∥DE，再由线面平行的判定可得MN ∥平面C1DE；（2）以D为坐标原点，以垂直于DC得直线为x轴，以DC所在直线为y轴，以DD1所在直线为z轴建立空间直角坐标系，分别求出平面A1MN与平面MAA1的一个法向量，由两法向量所成角的余弦值可得二面角A﹣MA1﹣N的正弦值．【解答】（1）证明：如图，过N作NH⊥AD1，且，又MB∥AA1，MB＝，∴四边形NMBH为平行四边形，由NH∥AA3，N为A1D中点，得H为AD中点，∴BE∥DH，BE＝DH，则BH∥DE，∴NM∥DE，∵NM⊄平面C1DE，DE⊂平面C7DE，∴MN∥平面C1DE；（2）解：以D为坐标原点，以垂直于DC的直线为x轴，以DD1所在直线为z轴建立空间直角坐标系，则N（，，2），3，2），A1（，﹣1，，，设平面A1MN的一个法向量为，由，取x＝，得，又平面MAA4的一个法向量为，∴cos＜＞＝＝＝．∴二面角A﹣MA1﹣N的正弦值为＝＝．【点评】本题考查直线与平面平行的判定，考查空间想象能力与思维能力，训练了利用空间向量求解空间角，是中档题．18．（2020•海南）如图，四棱锥P﹣ABCD的底面为正方形，PD⊥底面ABCD．设平面P AD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD＝AD＝1，Q为l上的点，QB＝【分析】（1）过P在平面P AD内作直线l∥AD，推得l为平面P AD和平面PBC的交线，由线面垂直的判定和性质，即可得证；（2）以D为坐标原点，直线DA，DC，DP所在的直线为x，y，z轴，建立空间直角坐标系D﹣xyz，求出Q（0，1，1），运用向量法，求得平面QCD的法向量，结合向量的夹角公式求解即可．【解答】（1）证明：过P在平面P AD内作直线l∥AD，由AD∥BC，可得l∥BC，∵PD⊥平面ABCD，BC⊂平面ABCD，又BC⊥CD，CD∩PD＝D，∵l∥BC，∴l⊥平面PCD；（2）解：如图，以D为坐标原点，DC，y，z轴，∵PD＝AD＝1，Q为l上的点，∴PB＝，QP＝1，则D（0，5，0），0，5），1，0），3，1），1，5），则PQ为平面P AD与平面PBC的交线为l，△QAB是等腰直角三角形，0，5），则＝（1，0，＝（6，1，＝（0，8，设平面QCD的法向量为＝（a，b，则，∴，取c＝1＝（﹣2，0，∴cos＜，＞＝＝＝，∴PB与平面QCD所成角的正弦值为．【点评】本题考查空间线面垂直的判定，以及线面角的求法，考查转化思想和向量法的运用，考查运算能力和推理能力，属于中档题．19．（2020•天津）如图，在三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，AC⊥BC，AC＝BC＝21＝3，点D，E分别在棱AA1和棱CC1上，且AD＝1，CE＝21B1的中点．（Ⅱ）求证：C1M⊥B1D；（Ⅱ）求二面角B﹣B1E﹣D的正弦值；（Ⅱ）求直线AB与平面DB1E所成角的正弦值．【分析】（Ⅱ）方法一：根据线面垂直的性质定理和判定定理即可证明；方法二：建立空间坐标系，根据向量的数量积等于0，即可证明；（Ⅱ）先平面DB1E的法向量，再根据向量的夹角公式，求出二面角B﹣B1E﹣D的正弦值；（Ⅱ）求出cos＜，＞值，即可求出直线AB与平面DB1E所成角的正弦值．【解答】解：（Ⅱ）在三棱柱ABC﹣A1B1C7中，CC1⊥平面ABC，则该三棱柱是个直三棱柱（各侧棱均垂直底面，各侧面均与底面垂直）∵C1A4＝C1B1＝5，M为M为棱A1B1的中点，∴C6M⊥A1B1，又平面C5A1B1⊥平面A6B1BA，∴C1M⊥平面A6B1BA，∵B1D⊂A6B1BA，∴C1M⊥B5D；方法二：（Ⅱ）以C为原点，，，的方向为x轴，z轴的正方向建立空间直角坐标系，则C（0，3，0），0，5），2，0），C5（0，0，2），A1（2，6，3），B1（2，2，3），6，1），0，4），1，3），∴＝（1，1，＝（2，﹣2），∴•＝2﹣6+0＝02M⊥B1D；（Ⅱ）依题意，＝（2，41E的一个法向量，＝（5，2，1），，3，﹣1），设＝（x，y1E的法向量，则，即，不妨设x＝1，则，﹣1，∴cos＜，＞＝＝，∴sin＜，＞＝＝，∴二面角B﹣B4E﹣D的正弦值；（Ⅱ）依题意，＝（﹣2，3，由（Ⅱ）知，＝（1，2）为平面DB2E的一个法向量，∴cos＜，＞＝，∴直线AB与平面DB3E所成角的正弦值为．【点评】本题考查了空间向量在几何中的应用，线线平行和二面角和线面角的求法，考查了运算求解能力，转化与化归能力，逻辑推理能力，属于中档题．20．（2020•山东）如图，四棱锥P﹣ABCD的底面为正方形，PD⊥底面ABCD．设平面P AD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD＝AD＝1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．【分析】（1）过P在平面P AD内作直线l∥AD，推得l为平面P AD和平面PBC的交线，由线面垂直的判定和性质，即可得证；（2）以D为坐标原点，直线DA，DC，DP所在的直线为x，y，z轴，建立空间直角坐标系D﹣xyz，设Q（m，0，1），运用向量法，求得平面QCD的法向量，结合向量的夹角公式，以及基本不等式可得所求最大值．【解答】解：（1）证明：过P在平面P AD内作直线l∥AD，由AD∥BC，可得l∥BC，∵PD⊥平面ABCD，BC⊂平面ABCD，又BC⊥CD，CD∩PD＝D，∵l∥BC，∴l⊥平面PCD；（2）如图，以D为坐标原点，DC，y，z轴，则D（0，0，5），0，0），4，0），0，2），1，0），设Q（m，8，1），，0，7），，1，﹣1），，5，0），设平面QCD的法向量为＝（a，b，则，∴，取a＝﹣2＝（﹣1，0，∴cos＜，＞＝＝，∴PB与平面QCD所成角的正弦值为＝•＝•≤•＝，当且仅当m＝1取等号，∴PB与平面QCD所成角的正弦值的最大值为．【点评】本题考查空间线面垂直的判定，以及线面角的求法，考查转化思想和向量法的运用，考查运算能力和推理能力，属于中档题．21．（2021•上海）如图，在长方体ABCD﹣A1B1C1D1中，已知AB＝BC＝2，AA1＝3．（1）若P是棱A1D1上的动点，求三棱锥C﹣P AD的体积；（2）求直线AB1与平面ACC1A1的夹角大小．【分析】（1）直接由三棱锥的体积公式求解即可；（2）易知直线AB1与平面ACC1A1所成的角为∠OAB1，求出其正弦值，再由反三角表示即可．【解答】解：（1）如图，在长方体ABCD﹣A1B1C7D1中，＝；（2）连接A2C1∩B1D3＝O，∵AB＝BC，∴四边形A1B1C5D1为正方形，则OB1⊥OA4，又AA1⊥OB1，OA2∩AA1＝A1，∴OB5⊥平面ACC1A1，∴直线AB7与平面ACC1A1所成的角为∠OAB6，∴．∴直线AB1与平面ACC1A5所成的角为．【点评】本题考查三棱锥体积的求法，考查线面角的求解，考查推理能力及运算能力，属于中档题．22．（2021•天津）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E，F分别为棱BC，CD的中点．（1）求证：D1F∥平面A1EC1；（2）求直线AC1与平面A1EC1所成角的正弦值；（3）求二面角A﹣A1C1﹣E的正弦值．【分析】（1）建立合适的空间直角坐标系，求出所需点的坐标和向量的坐标，利用待定系数法求出平面A1EC1的法向量，利用直线的方向向量与平面的法向量垂直，即可证明；（2）利用（1）中的结论，由向量的夹角公式求解，即可得到答案；（3）利用待定系数法求出平面AA1C1的法向量，然后利用向量的夹角公式求解即可．【解答】（1）证明：以点A为坐标原点，建立空间直角坐标系如图所示，则A1（0，7，2），1，8），C1（2，5，2），故，设平面A1EC3的法向量为，则，即，令z＝7，则x＝2，故，又F（1，8，0），D1（5，2，2），所以，则，又D6F⊄平面A1EC1，故D6F∥平面A1EC1；（2）解：由（1）可知，，则＝＝，故直线AC1与平面A1EC4所成角的正弦值为；（3）解：由（1）可知，，设平面AA1C1的法向量为，则，即，令a＝1，则b＝﹣1，故，所以＝＝，故二面角A﹣A6C1﹣E的正弦值为＝．【点评】本题考查了空间向量在立体几何中的应用，在求解有关空间角问题的时候，一般会建立合适的空间直角坐标系，将空间角问题转化为空间向量问题进行研究，属于中档题．23．（2021•北京）如图，在正方体ABCD﹣A1B1C1D1，E为A1D1的中点，B1C1交平面CDE交于点F．（Ⅱ）求证：F为B1C1的中点；（Ⅱ）若点M是棱A1B1上一点，且二面角M﹣CF﹣E的余弦值为，求的值．【分析】（Ⅱ）连结DE，利用线面平行的判定定理证明CD∥平面A1B1C1D1，从而可证明CD∥EF，即可证明四边形A1B1FE为平行四边形，四边形EFC1D1为平行四边形，可得A1E＝B1F，ED1＝FC1，即可证明B1F＝FC1，。

2011-2020年高考数学真题分类汇编专题24 空间向量与空间角的计算(学生版)

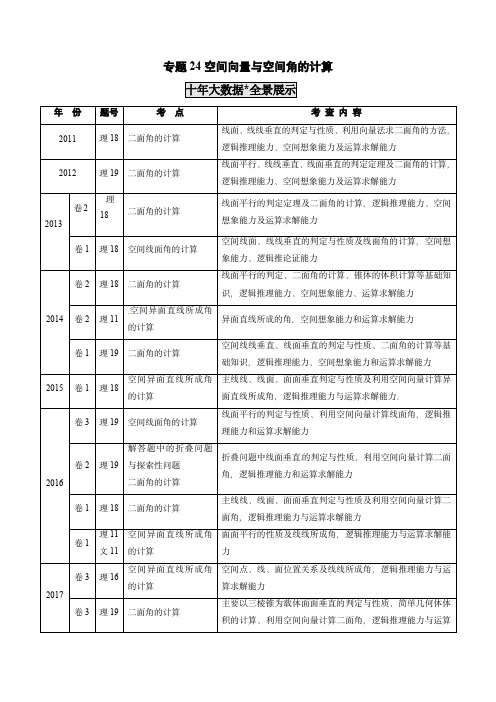
专题24空间向量与空间角的计算年份题号考点考查内容2011理18二面角的计算线面、线线垂直的判定与性质、利用向量法求二面角的方法，逻辑推理能力、空间想象能力及运算求解能力2012理19二面角的计算线面平行、线线垂直、线面垂直的判定定理及二面角的计算，逻辑推理能力、空间想象能力及运算求解能力2013卷2理18二面角的计算线面平行的判定定理及二面角的计算，逻辑推理能力、空间想象能力及运算求解能力卷1理18空间线面角的计算空间线面、线线垂直的判定与性质及线面角的计算，空间想象能力、逻辑推论证能力2014卷2理18二面角的计算线面平行的判定、二面角的计算、锥体的体积计算等基础知识，逻辑推理能力、空间想象能力、运算求解能力卷2理11空间异面直线所成角的计算异面直线所成的角，空间想象能力和运算求解能力卷1理19二面角的计算空间线线垂直、线面垂直的判定与性质、二面角的计算等基础知识，逻辑推理能力、空间想象能力和运算求解能力2015卷1理18空间异面直线所成角的计算主线线、线面、面面垂直判定与性质及利用空间向量计算异面直线所成角，逻辑推理能力与运算求解能力．2016卷3理19空间线面角的计算线面平行的判定与性质、利用空间向量计算线面角，逻辑推理能力和运算求解能力卷2理19解答题中的折叠问题与探索性问题二面角的计算折叠问题中线面垂直的判定与性质、利用空间向量计算二面角，逻辑推理能力和运算求解能力卷1理18二面角的计算主线线、线面、面面垂直判定与性质及利用空间向量计算二面角，逻辑推理能力与运算求解能力卷1理11文11空间异面直线所成角的计算面面平行的性质及线线所成角，逻辑推理能力与运算求解能力2017卷3理16空间异面直线所成角的计算空间点、线、面位置关系及线线所成角，逻辑推理能力与运算求解能力卷3理19二面角的计算主要以三棱锥为载体面面垂直的判定与性质、简单几何体体积的计算、利用空间向量计算二面角，逻辑推理能力与运算求解能力卷2理18二面角的计算空间线面角的计算主要以三棱锥为载体线面平行的判定与性质、利用空间向量计算线面角与二面角，逻辑推理能力与运算求解能力卷2理10空间异面直线所成角的计算空间两条异面直线所成的角及空间想象能力与运算求解能力卷1理18二面角的计算空间垂直的判定与性质、利用空间向量计算二面角，逻辑推理能力与运算求解能力2018卷3文19解答题中的折叠问题与探索性问题空间面面垂直的判定与性质、是否存在点是线面平行的问题，逻辑推理能力与空间想象能力卷2文9空间异面直线所成角的计算空间两条异面直线所成的角及空间想象能力与运算求解能力卷1文10空间线面角的计算长方体中线面角的计算与长方体体积计算，运算求解能力卷3理19二面角的计算空间垂直的判定与性质、利用空间向量计算二面角与空间几何体体积的最大值，逻辑推理能力与运算求解能力卷2理20空间线面角的计算二面角的计算主要以三棱锥为载体线面垂直的判定与性质、利用空间向量计算线面角与二面角，逻辑推理能力与运算求解能力卷2理9空间异面直线所成角的计算空间两条异面直线所成的角及空间想象能力与运算求解能力卷1理18解答题中的折叠问题与探索性问题空间线面角的计算折叠问题中空间垂直的判定与性质、利用空间向量计算线面角及逻辑推理能力与运算求解能力2019卷3理19解答题中的折叠问题与探索性问题二面角的计算折叠问题中的共面问题的判定、空间垂直的判定与性质、利用空间向量计算二面角及逻辑推理能力与运算求解能力卷2理17二面角的计算空间线线、线面垂直的判定与性质及利用空间向量计算二面角，逻辑推理能力、运算求解能力卷1理18二面角的计算空间线面平行的判定及利用空间向量计算二面角，逻辑推理能力、运算求解能力2020卷1理16空间角的计算空间角的计算，利用余弦定理解三角形理18二面角的计算空间线线、线面垂直的判定与性质及利用空间向量计算二面角，逻辑推理能力、运算求解能力卷2理20空间位置关系判定、空间角的计算间线面平行与垂直的证明，线面角的计算卷3理19二面角、点与平面位置关系点在平面的证明，利用空间向量法求二面角探求规律考点82空间异面直线所成角的计算1．(2018•新课标Ⅱ，理9)在长方体1111ABCDA B C D 中，1ABBC ，1AA ，则异面直线1AD 与1DB 所成角的余弦值为()A ．15B C ．D．22．(2018•新课标Ⅱ，文9)在正方体1111ABCD AB C D 中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为()A ．22B C ．D3.(2017•新课标Ⅱ，理10)已知直三棱柱111ABC A B C中，120ABC ，2AB，11BC CC ，则异面直线1AB 与1BC 所成角的余弦值为()A B C ．D 4．(2016•新课标Ⅰ，理11文11)平面过正方体1111ABCD A BC D 的顶点A ，// 平面11CB D ，平面ABCD m ，平面11ABB A n ，则m 、n 所成角的正弦值为()A B C ．D ．135．(2014新课标Ⅱ，理11)直三棱柱ABC-A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为()A ．110B ．25C 3010D 226．(2020全国Ⅰ理16)如图，在三棱锥P ABC的平面展开图中，1,3,,,30AC AB AD AB AC AB AD CAE ，则cos FCB _____________．7．(2017•新课标Ⅲ，理16)a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60 角时，AB 与b 成30 角；②当直线AB 与a 成60 角时，AB 与b 成60 角；③直线AB 与a 所成角的最小值为45 ；④直线AB 与a 所成角的最小值为60 ；其中正确的是．(填写所有正确结论的编号)8．(2015浙江)如图，三棱锥A BCD 中，3AB AC BD CD ，2AD BC ，点,M N 分别是,AD BC 的中点，则异面直线,AN CM 所成的角的余弦值是．9．(2015四川)如图，四边形ABCD 和ADPQ 均为正方形，它们所在的平面互相垂直，动点M 在线段PQ上，,E F 分别为,AB BC 的中点．设异面直线EM 与AF 所成的角为，则 cos 的最大值为_________．10．(2015•新课标Ⅰ，理18)如图，四边形ABCD 为菱形，120ABC ，E ，F 是平面ABCD 同一侧的两点，BE 平面ABCD ，DF 平面ABCD ，2BE DF ，AE EC ．(Ⅰ)证明：平面AEC 平面AFC(Ⅱ)求直线AE 与直线CF 所成角的余弦值．考点83空间线面角的计算1．(2020山东4)日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40 ，则晷针与点A 处的水平面所成角为()A ．20B ．40C ．50D ．902．(2018•新课标Ⅰ，文10)在长方体1111ABCD A B C D 中，2AB BC ，1AC 与平面11BB C C 所成的角为30 ，则该长方体的体积为()A ．8B ．62C ．82D ．833．(2014浙江)如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练，已知点A 到墙面的距离为AB ，某目标点P 沿墙面的射击线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角的大小(仰角为直线AP 与平面ABC 所成角)．若15AB m ，25AC m ，30BCM 则tan 的最大值MCABPA 30B 30C 43D 534．(2014四川)如图，在正方体1111ABCD A B C D 中，点O 为线段BD 的中点．设点P 在线段1CC 上，直线OP 与平面1A BD 所成的角为，则sin 的取值范围是OA 1BB 11D 1D A ．3,1]3B ．63C ．622,33D ．22[,1]35．(2020全国Ⅱ理20)如图，已知三棱柱111ABC A B C 的底面是正三角形，侧面11BB C C 是矩形，,M N 分别为11,BC B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于F ．(1)证明：1AA //MN ，且平面1A AMN 平面11EB C F ；(2)设O 为△111C B A 的中心，若F C EB AO 11平面∥，且AB AO ，求直线E B 1与平面AMN A 1所成角的正弦值．6．(2018•新课标Ⅱ，理20)如图，在三棱锥P ABC 中，22AB BC ，4PA PB PC AC ，O 为AC 的中点．(1)证明：PO 平面ABC ；(2)若点M 在棱BC 上，且二面角M PA C 为30 ，求PC 与平面PAM 所成角的正弦值．7．(2016•新课标Ⅲ，理19)如图，四棱锥P ABCD 中，PA 底面ABCD ，//AD BC ，3AB AD AC ，4PA BC ，M 为线段AD 上一点，2AM MD ，N 为PC 的中点．(1)证明：//MN 平面PAB ；(2)求直线AN 与平面PMN 所成角的正弦值．8．(2013新课标Ⅰ，理18)如图，三棱柱ABC-A 1B 1C 1中，CA=CB ，AB=A A 1，∠BA A 1=60°．(Ⅰ)证明AB ⊥A 1C ；(Ⅱ)若平面ABC ⊥平面AA 1B 1B ，AB=CB=2，求直线A 1C 与平面BB 1C 1C所成角的正弦值．9．(2018浙江)如图，已知多面体111ABCA B C ，1A A ，1B B ，1C C 均垂直于平面ABC ，120ABC，14A A ，11C C ，12AB BC B B ．(1)证明：1AB ⊥平面111A B C ；(2)求直线1AC 与平面1ABB 所成的角的正弦值．C 1B 1A 1BA10．(2017浙江)如图，已知四棱锥P ABCD ，PAD 是以AD 为斜边的等腰直角三角形，BC AD ∥，CD AD ，22PC AD DC CB ，E 为PD 的中点．(Ⅰ)证明：CE ∥平面PAB ；(Ⅱ)求直线CE 与平面PBC 所成角的正弦值．DA11．(2014天津)如图四棱锥P ABCD 的底面ABCD是平行四边形，BA BD 2AD，PA PD ，E ，F 分别是棱AD ，PC 的中点．(Ⅰ)证明：EF ∥平面PAB ；(Ⅱ)若二面角P AD B 为60°，(ⅰ)证明：平面PBC ⊥平面ABCD ；(ⅱ)求直线EF 与平面PBC 所成角的正弦值．12．(2013浙江)如图，在四棱锥P ABCD 中，PA ⊥面ABCD，2AB BC，AD CD ，PA ，120ABC ，G 为线段PC 上的点．PDB(Ⅰ)证明：BD ⊥面APC ；(Ⅱ)若G 是PC 的中点，求DG 与APC 所成的角的正切值；(Ⅲ)若G 满足PC ⊥面BGD ，求PGGC的值．13．(2019浙江19)如图，已知三棱柱111ABC A B C ，平面11A ACC 平面ABC ，90ABC ，1130,,,BAC A A AC AC E F 分别是AC ，A 1B 1的中点．(1)证明：EF BC ；(2)求直线EF 与平面A 1BC 所成角的余弦值．14．(2018天津)如图，AD BC ∥且2AD BC ，AD CD ，EG AD ∥且EG AD ，CD FG ∥且2CD FG ，DG 平面ABCD ，2DA DC DG ．(1)若M 为CF 的中点，N 为EG 的中点，求证：MN ∥平面CDE ；(2)求二面角E BC F 的正弦值；(3)若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60，求线段DP的长．AC E15．(2018江苏)如图，在正三棱柱111ABC A B C 中，12AB AA ，点P ，Q 分别为11A B ，BC的中点．A 1(1)求异面直线BP 与1AC 所成角的余弦值；(2)求直线1CC 与平面1AQC 所成角的正弦值．16．(2017天津)如图，在三棱锥P ABC 中，PA ⊥底面ABC ，90BAC ．点D ，E ，N 分别为棱PA ，PC ，BC 的中点，M 是线段AD 的中点，4PA AC ，2AB ．(Ⅰ)求证：MN ∥平面BDE ；(Ⅱ)求二面角C EM N 的正弦值；(Ⅲ)已知点H 在棱PA 上，且直线NH 与直线BE 所成角的余弦值为21，求线段AH 的长．17．(2017北京)如图，在四棱锥P ABCD 中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，点M 在线段PB 上，PD //平面MAC ，PA PD ，4AB ．(Ⅰ)求证：M 为PB 的中点；(Ⅱ)求二面角B PD A 的大小；(Ⅲ)求直线MC 与平面BDP 所成角的正弦值．18．(2014福建)在平行四边形ABCD 中，1AB BD CD ，,AB BD CD BD ，将ABD 沿BD 折起，使得平面ABD 平面BCD ，如图．B(Ⅰ)求证：AB CD ；(Ⅱ)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．19．(2013天津)如图，四棱柱1111ABCD A B C D 中，侧棱1A A ⊥底面ABCD ，AB DC ∥，AB AD ，1AD CD ，12AA AB ，E 为棱1AA 的中点．(Ⅰ)证明11B C CE ；(Ⅱ)求二面角11B CE C 的正弦值；(Ⅲ)设点M 在线段1C E 上；且直线AM 与平面11ADDA 所成角的正弦值为6，求线段AM 的长．1A 1考点84二面角的计算1．(2018浙江)已知四棱锥S ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点(不含端点)，设SE 与BC 所成的角为1 ，SE 与平面ABCD 所成的角为2 ，二面角S AB C 的平面角为3 ，则A ．123≤≤B ．321≤≤C ．132≤≤D ．231≤≤2．(2017浙江)如图，已知正四面体D ABC (所有棱长均相等的三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP PB ，2BQ CRQC RA，分别记二面角D PR Q ，D PQ R ，D QR P 的平面角为，，，则R QPABC DA ． < <B ． < <C ． < <D ． < <3．如图，已知ABC ，D 是AB 的中点，沿直线CD 将ACD 折成△A CD ，所成二面角A CD B 的平面角为，则()A ．A DB B ．A DBC ．A CBD ．A CB4．(2020全国Ⅰ理18)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE AD ．ABC 是底面的内接正三角形，P 为DO 上一点，6PO ．(1)证明：PA 平面PBC ；(2)求二面角B PC E 的余弦值．5．(2020全国Ⅲ理19)如图，在长方体1111ABCD A B C D 中，点,E F 分别在棱11,DD BB 上，且112,2DE ED BF FB ．(1)证明：点1C 在平面AEF 内；(2)证明：若12,1,3AB AD AA 时，求二面角1A EF A的正弦值．6．(2020江苏24)在三棱锥A —BCD 中，已知CB =CD 5，BD =2，O 为BD 的中点，AO ⊥平面BCD ，AO =2，E 为AC 的中点．(1)求直线AB 与DE 所成角的余弦值；(2)若点F 在BC 上，满足BF =14BC ，设二面角F —DE —C 的大小为θ，求sin θ的值．7．(2020浙江19)如图，三棱台DEF —ABC 中，面ADFC ⊥面ABC ，∠ACB =∠ACD =45°，DC =2BC ．(I)证明：EF ⊥DB ；(II)求DF 与面DBC 所成角的正弦值．8．(2020天津17)如图，在三棱柱111ABC A B C 中，1CC 平面,,2ABC AC BC AC BC ，13CC ，点,D E 分别在棱1AA 和棱1CC 上，且12,AD CE M 为棱11A B 的中点．(Ⅰ)求证：11C M B D ；(Ⅱ)求二面角1B B E D 的正弦值；(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值．9．(2020山东20)如图，四棱锥P ABCD 的底面为正方形，PD 底面ABCD ，设平面PAD 与平面PBC 的交线为l ．(1)证明：l 平面PDC ；(2)已知1PD AD ，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．10．(2019•新课标Ⅰ，理18)如图，直四棱柱1111ABCD A B C D 的底面是菱形，14AA ，2AB ，60BAD ，E ，M ，N 分别是BC ，1BB ，1A D 的中点．(1)证明：//MN 平面1C DE ；(2)求二面角1A MA N 的正弦值．11．(2019•新课标Ⅱ，理17)如图，长方体1111ABCD A B C D 的底面ABCD 是正方形，点E 在棱1AA 上，1BE EC ．(1)证明：BE 平面11EB C ；(2)若1AE A E ，求二面角1B EC C 的正弦值．12．(2018•新课标Ⅲ，理19)如图，边长为2的正方形ABCD 所在的平面与半圆弧 CD 所在平面垂直，M 是 CD上异于C ，D 的点．(2)当三棱锥M ABC 体积最大时，求面MAB 与面MCD 所成二面角的正弦值．13．(2017•新课标Ⅰ，理18)如图，在四棱锥P ABCD 中，//AB CD ，且90BAP CDP ．(1)证明：平面PAB 平面PAD ；(2)若PA PD AB DC ，90APD ，求二面角A PB C 的余弦值．14．(2017•新课标Ⅱ，理19)如图，四棱锥P ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD ，12AB BC AD，90BAD ABC ，E 是PD 的中点．(1)证明：直线//CE 平面PAB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45 ，求二面角M AB D 的余弦值．15．(2017•新课标Ⅲ，理19)如图，四面体ABCD 中，ABC 是正三角形，ACD 是直角三角形，ABD CBD ，AB BD ．(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D AE C 的余弦值．16．(2016•新课标Ⅰ，理18)如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，2AF FD ，90AFD ，且二面角D AF E 与二面角C BE F 都是60 ．(Ⅰ)证明：平面ABEF 平面EFDC ；(Ⅱ)求二面角E BC A 的余弦值．17．(2014新课标Ⅰ，理19)如图三棱锥111ABC A B C 中，侧面11BB C C 为菱形，1AB B C ．(Ⅰ)证明：1AC AB ；(Ⅱ)若1AC AB ，o 160CBB ，AB=BC ，求二面角111A A B C 的余弦值．18．(2014新课标Ⅱ，理18)如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．(Ⅰ)证明：PB ∥平面AEC ；(Ⅱ)设二面角D-AE-C 为60°，AP=1，，求三棱锥E-ACD 的体积．19．(2013新课标Ⅱ，理18)如图直棱柱111ABC A B C 中，D ，E 分别为AB ，1BB 的中点，1AA =AC=CB=22AB ．(Ⅰ)证明：1BC ∥平面1A CD ；(Ⅱ)求二面角D-1A C E 的正弦值．20．(2012•新课标，理19)如图，直三棱柱111ABC A B C 中，112AC BC AA ，D 是棱1AA 的中点，1DC BD (1)证明：1DC BC ；(2)求二面角11A BD C 的大小．21．(2011•新课标，理18)如图，四棱锥P ABCD 中，底面ABCD 为平行四边形，DAB =060，AB =2AD ，PD ⊥底面ABCD ．(Ⅰ)证明：PA BD ；(Ⅱ)若PD =AD ，求二面角A PB C的余弦值．22．(2011广东)如图在椎体P ABCD 中，ABCD 是边长为1的棱形，且DAB =60，PA PD 2PB ，E ，F 分别是BC ，PC 的中点．(Ⅰ)证明：AD 平面DEF ；(Ⅱ)求二面角P AD B 的余弦值．23．(2019天津理17)如图，AE 平面ABCD ，,CF AE AD BC ∥∥，,1,2AD AB AB AD AE BC ．(Ⅰ)求证：BF ∥平面ADE ；(Ⅱ)求直线CE 与平面BDE 所成角的正弦值；(Ⅲ)若二面角E BDF 的余弦值为13，求线段CF 的长．24．(2018北京)如图，在三棱柱111ABC A B C 中，1CC 平面ABC ，D ，E ，F ，G 分别为1AA ，AC ，11A C ，1BB 的中点，5AB BC ，12AC AA ．(1)求证：AC ⊥平面BEF ；(2)求二面角1B CD C 的余弦值；(3)证明：直线FG 与平面BCD相交．C 1B 1A 1GF E DC B A25．(2016年山东)在如图所示的圆台中，AC 是下底面圆O 的直径，EF 是上底面圆O 的直径，FB 是圆台的一条母线．(I)已知G ，H 分别为EC ，FB 的中点，求证：GH ∥平面ABC ；(II)已知EF =FB =12AC =23，AB BC ．求二面角F BC A 的余弦值．26．(2016年天津)如图，正方形ABCD 的中心为O ，四边形OBEF 为矩形，平面OBEF ⊥平面ABCD ，点G 为AB 的中点，2AB BE ．(Ⅰ)求证：EG ∥平面ADF ；(Ⅱ)求二面角O EF C 的正弦值；(Ⅲ)设H 为线段AF 上的点，且AH =23HF ，求直线BH 和平面CEF 所成角的正弦值．27．(2015福建)如图，在几何体ABCDE 中，四边形ABCD 是矩形，AB ^平面BEG ，BE ^EC ，2AB BE EC ，G ，F 分别是线段BE ，DC 的中点．(Ⅰ)求证：GF ∥平面ADE ；(Ⅱ)求平面AEF 与平面BEC 所成锐二面角的余弦值．28．(2015山东)如图，在三棱台DEF ABC 中，2AB DE ，,G H 分别为,AC BC 的中点．(Ⅰ)求证：BC //平面FGH ；(Ⅱ)若CF ⊥平面ABC ，AB ⊥BC ，CF =DE ，∠BAC=45 ，求平面FGH 与平面ACFD 所成的角(锐角)的大小．29．(2014山东)如图，在四棱柱1111ABCD A B C D 中，底面ABCD 是等腰梯形，60,DAB 22AB CD ，M 是线段AB 的中点．(Ⅰ)求证：111//C M A ADD 平面；(Ⅱ)若1CD 垂直于平面ABCD且1CD ，求平面11C D M 和平面ABCD 所成的角(锐角)的余弦值．130．(2014辽宁)如图，ABC 和BCD 所在平面互相垂直，且2AB BC BD ，0120ABC DBC ，E 、F 分别为AC 、DC 的中点．(Ⅰ)求证：EF BC ；(Ⅱ)求二面角E BF C的正弦值．D C31．(2014浙江)如图，在四棱锥BCDE A 中，平面 ABC 平面BCDE ，90CDE BED，2AB CD ，1DE BE ，AC ．(Ⅰ)证明： DE 平面ACD ；(Ⅱ)求二面角E AD B的大小．32．(2014广东)如图4，四边形ABCD 为正方形，PD 平面ABCD ，030DPC ，AF PC 于点F ，//FE CD ，交PD 于点E ．(Ⅰ)证明：CF ADF平面(Ⅱ)求二面角D AF E 的余弦值．33．(2014湖南)如图，四棱柱1111ABCD A B C D 的所有棱长都相等，AC BD O ∩，11111A C B D O ∩，四边形1111ACC A BDD B 和四边形均为矩形．(1)证明：1;O O ABCD 底面(2)若1160,CBA C OB D求二面角的余弦值．O 1O 1B CD AA 1C 1D 134．(2013陕西)如图，四棱柱1111ABCD A B C D 的底面ABCD 是正方形，O 为底面中心，1AO ⊥平面ABCD ，12AB AA ．(Ⅰ)证明：1AC ⊥平面11BB D D ；(Ⅱ)求平面1OCB 与平面11BB D D 的夹角的大小．O D 1B 1C 1D A CB A 135．(2012浙江)如图，在四棱锥P ABCD 中，底面是边长为3的菱形，120BAD ，且PA 平面ABCD ，6PA ，M ，N 分别为PB ，PD 的中点．(Ⅰ)证明：//MN 平面ABCD ；(Ⅱ)过点A 作AQ PC ，垂足为点Q ，求二面角A MN Q 的平面角的余弦值．36．(2017山东)如图，几何体是圆柱的一部分，它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120 得到的，G 是 DF的中点．(Ⅰ)设P 是 CE上的一点，且AP BE ，求CBP 的大小；(Ⅱ)当3AB ，2AD ，求二面角E AG C 的大小．考点85解答题中折叠问题与探索性问题1．(2019•新课标Ⅲ，理19)图1是由矩形ADEB 、Rt ABC 和菱形BFGC 组成的一个平面图形，其中1AB ，2BE BF ，60FBC ．将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2．(1)证明：图2中的A ，C ，G ，D 四点共面，且平面ABC 平面BCGE ；(2)求图2中的二面角B CG A 的大小．2．(2018•新课标Ⅰ，理18)如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC 折起，使点C 到达点P 的位置，且PF BF ．(1)证明：平面PEF 平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值．3．(2018•新课标Ⅲ，文19)如图，矩形ABCD 所在平面与半圆弧 CD所在平面垂直，M 是 CD 上异于C ，D 的点．(1)证明：平面AMD 平面BMC ；(2)在线段AM 上是否存在点P ，使得//MC 平面PBD ？说明理由．4．(2016•新课标Ⅱ，理19)如图，菱形ABCD 的对角线AC 与BD 交于点O ，5AB ，6AC ，点E ，F 分别在AD ，CD 上，54AE CF，EF 交于BD 于点H ，将DEF 沿EF 折到△D EF 的位置，OD ．(Ⅰ)证明：D H 平面ABCD ；(Ⅱ)求二面角B D A C 的正弦值．5．(2019北京理16)如图，在四棱锥P ABCD 中，PA ABCD 平面，AD CD ，AD BC P ，23PA AD CD BC ，．E 为PD 的中点，点F 在PC 上，且13PF PC ．(Ⅰ)求证：CD PAD 平面；(Ⅱ)求二面角F AE P 的余弦值；(Ⅲ)设点G 在PB 上，且23PG PB ．判断直线AG 是否在平面AEF 内，说明理由．6．(2016年北京)如图，在四棱锥P ABCD 中，平面PAD 平面ABCD ，PA PD ，PA PD ，AB AD ，1AB ，2AD ，5AC CD ．(1)求证：PD 平面PAB ；(2)求直线PB 与平面PCD 所成角的正弦值；(3)在棱PA 上是否存在点M ，使得//BM 平面PCD ？若存在，求AM AP 的值；若不存在，说明理由．7．(2015陕西)如图1，在直角梯形ΑΒCD 中，//ΑD ΒC ，2ΒΑD ，1ΑΒΒC ，2ΑD ，Ε是ΑD 的中点，O 是AC 与BE 的交点．将ΑΒΕ 沿BE 折起到1A BE 的位置，如图2．(Ⅰ)证明：CD 平面1AOC ；(Ⅱ)若平面1A BE 平面BCDE ，求平面1A BC 与平面1ACD 夹角的余弦值．8．(2013广东)如图1，在等腰直角三角形ABC 中，90A ，6BC ，,D E 分别是,AC AB 上的点，2CD BE ，O 为BC 的中点．将ADE 沿DE 折起，得到如图2所示的四棱锥A BCDE ，其中3A O．(Ⅰ)证明：A O 平面BCDE ；(Ⅱ)求二面角A CD B 的平面角的余弦值．9．(2013湖北)如图，AB 是圆O 的直径，点C 是圆O 上异于,A B 的点，直线PC 平面ABC ，E ，F 分别是PA ，PC 的中点．(Ⅰ)记平面BEF 与平面ABC 的交线为l ，试判断直线l 与平面PAC 的位置关系，并加以证明；(Ⅱ)设(I)中的直线l 与圆O 的另一个交点为D ，且点Q 满足12DQ CP ．记直线PQ 与平面ABC 所成的角为，异面直线PQ 与EF 所成的角为，二面角E l C 的大小为，求证：sin sin sin ．10．(2012福建)如图，在长方体1111ABCD A B C D 中11AA AD ，E 为CD 中点．(Ⅰ)求证：11B E AD ；(Ⅱ)在棱1AA 上是否存在一点P ，使得DP ∥平面1B AE ？若存在，求AP 的行；若存在，求AP 的长；若不存在，说明理由．(Ⅲ)若二面角11A B E A 的大小为30°，求AB 的长．。

2020届山东省新高考高三优质数学试卷分项解析专题09 立体几何与空间向量(解析版)

专题9 立体几何与空间向量从近几年的高考试题来看,所考的主要内容是:(1)有关线面位置关系的组合判断,试题通常以选择题的形式出现,主要是考查空间线线、线面、面面位置关系的判定与性质;(2)有关线线、线面和面面的平行与垂直的证明,试题以解答题中的第一问为主,常以多面体为载体,突出考查学生的空间想象能力及推理论证能力;(3)线线角、线面角和二面角是高考的热点,选择题、填空题皆有，解答题中第二问必考,一般为中档题,在全卷的位置相对稳定，主要考查空间想象能力、逻辑思维能力和转化与化归的应用能力.预测2020年将保持稳定，一大二小.其中客观题考查面积体积问题、点线面位置关系（各种角的关系或计算）等；主观题以常见几何体为载体，考查平行或垂直关系的证明、线面角或二面角三角函数值的计算等.一、单选题1．（2020届山东省潍坊市高三上期中）m 、n 是平面α外的两条直线，在m ∥α的前提下，m ∥n 是n ∥α的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A 【解析】//m α，则存在l α⊂有//m l .而由//m n 可得//n l ，从而有//n α.反之则不一定成立，,m n 可能相交，平行或异面.所以//m n 是//n α的充分不必要条件，故选A2．（2020届山东省潍坊市高三上期末）《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“盖”的术：置如其周，令相承也.又以高乘之，三十六成一.该术相当于给出了有圆锥的底面周长L 与高h ，计算其体积V 的近似公式21.36v L h ≈它实际上是将圆锥体积公式中的圆周率π近似取为3.那么近似公式2275v L h ≈相当于将圆锥体积公式中的π近似取为（）A ．227 B ．258C ．15750D ．355113【答案】B 【解析】设圆锥底面圆的半径为r ，高为h ，依题意，r L π2=，h r h r 22)2(75231ππ=，所以275831ππ=，即π的近似值为258，故选B.3．（2020届山东省滨州市三校高三上学期联考）设α，β为两个平面，则αβ∥的充要条件是（） A ．α内有无数条直线与β平行B ．α，β平行与同一个平面C ．α内有两条相交直线与β内两条相交直线平行D ．α，β垂直与同一个平面【答案】C 【解析】对于A ，α内有无数条直线与β平行，可得α与β相交或α或β平行；对于B ，α，β平行于同一条直线，可得α与β相交或α或β平行；对于C ，α内有两条相交直线与β内两条相交直线平行，可得α∥β；对于D ，α，β垂直与同一个平面，可得α与β相交或α或β平行．故选：C ．4．（2020·河南高三期末（文））张衡是中国东汉时期伟大的天文学家、数学家，他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥A BCD -的每个顶点都在球O 的球面上，AB ⊥底面BCD ，BC CD ⊥，且AB CD ==2BC =，利用张衡的结论可得球O 的表面积为（）A ．30B ．C ．33D ．【答案】B 【解析】因为BC CD ⊥，所以BD =AB ⊥底面BCD ，所以球O 的球心为侧棱AD 的中点，从而球O .利用张衡的结论可得25168π=，则π=所以球O 的表面积为24102ππ⎛== ⎝⎭故选：B5．（2020届山东省潍坊市高三上学期统考）已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，则过A ，B ，C ，D 四点的球的表面积为（）A ．3πB ．4πC ．5πD ．6π【答案】C 【解析】边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，构成以D 为顶点的三棱锥，且三条侧棱互相垂直，可构造以其为长宽高的长方体，其对角线即为球的直径，三条棱长分别为1,12R ==245S ππ==，故选C.6．（2020届山东省日照市高三上期末联考）已知四棱锥P ABCD -的体积是底面ABCD 是正方形，PAB ∆是等边三角形，平面PAB ⊥平面ABCD ，则四棱锥P ABCD -外接球体积为（）A ．BCD ．【答案】A 【解析】设AB 的中点为Q ，因为PAB ∆是等边三角形，所以PQ AB ⊥，而平面PAB ⊥平面ABCD ，平面PAB ⋂平面ABCD AB =，所以PQ ⊥平面ABCD ，四棱锥P ABCD -的体积是13AB AB PQ =⨯⨯⨯13AB AB AB =⨯⨯，所以边长6AB =，PQ =OH x =，OM x =，()(222222R OA OM AM x==+=+，2222223R OP OH PH x ==+=+，x =2212321R =+=3428213V R ππ==球.故选：A.7．（2020届山东省泰安市高三上期末）已知正三棱锥S ABC -的侧棱长为43，底面边长为6，则该正三棱锥外接球的表面积是（） A ．16π B ．20πC ．32πD ．64π【答案】D 【解析】如图所示，因为正三棱锥S ABC -的侧棱长为43，底面边长为6，则236233AE =⋅⋅=，所以三棱锥的高2222(43)(23)6SE SA AE =-=-=, 又由球心O 到四个顶点的距离相等，在直角三角形AOE 中，,6AO R OE SE SO R ==-=-，又由222OA AE OE =+，即222(23)(6)R R =+-，解得4R =，所以球的表面积为2464S R ππ==，故选D.二、多选题8．（2020届山东省潍坊市高三上期末）等腰直角三角形直角边长为1 ，现将该三角形绕其某一边旋转一周，则所形成的几何体的表面积可以为（） A ．2π B ．()12π+C ．22πD ．()22π+【答案】AB 【解析】如果是绕直角边旋转，形成圆锥，圆锥底面半径为1，高为1，母线就是直角三角形的斜边2，所以所形成的几何体的表面积是()2212121S rl r πππππ=+=⨯⨯+⨯=+.如果绕斜边旋转，形成的是上下两个圆锥，圆锥的半径是直角三角形斜边的高22，两个圆锥的母线都是直角三角形的直角边，母线长是1，所以写成的几何体的表面积222122S rl πππ=⨯=⨯⨯⨯=. 综上可知形成几何体的表面积是()21π+或2π.故选：AB9．（2020届山东省泰安市高三上期末）已知,αβ是两个不重合的平面，,m n 是两条不重合的直线，则下列命题正确的是（） A ．若//m n m α⊥，，则n α⊥ B ．若//,m n ααβ⋂=，则//m n C ．若m α⊥，m β⊥，则//αβ D ．若,//,m m n n αβ⊥⊥，则//αβ 【答案】ACD 【解析】若m α⊥，则,a b α∃⊂且a b P =I 使得m a ⊥，m b ⊥，又//m n ，则n a ⊥，n b ⊥，由线面垂直的判定定理得n α⊥，故A 对；若//m α，n αβ=I ，如图，设m AB =，平面1111D C B A 为平面α，//m α，设平面11ADD A 为平面β，11A D n αβ⋂==，则m n ⊥，故B 错；垂直于同一条直线的两个平面平行，故C 对；若,//m m n α⊥，则n α⊥，又n β⊥，则//αβ，故D 对；故选：ACD ．10．（2020届山东省滨州市高三上期末）已知菱形ABCD 中，60BAD ∠=︒，AC 与BD 相交于点O ，将ABD △沿BD 折起，使顶点A 至点M ，在折起的过程中，下列结论正确的是( )A ．BD CM ⊥B ．存在一个位置，使CDM V 为等边三角形C ．DM 与BC 不可能垂直D ．直线DM 与平面BCD 所成的角的最大值为60︒【答案】ABD 【解析】A 选项，因为菱形ABCD 中，AC 与BD 相交于点O ，所以AO BD ⊥，CO BD ⊥；将ABD △沿BD 折起，使顶点A 至点M ，折起过程中，AO 始终与BD 垂直，因此MO BD ⊥，又MO CO I ，由线面垂直的判定定理，可得：BD ⊥平面CMO ，因此BD CM ⊥，故A 正确；B 选项，因为折起的过程中，AD 边长度不变，因此MD CD =；若CDM V 为等边三角形，则CM CD =；设菱形ABCD 的边长为2，因为60BAD ∠=︒，则sin 60AO AB =⋅=o AO MO =2CM CD ==，所以3341cos 233MOC +-∠==⨯，即二面角M BD C --的余弦值为13时，CDM V 为等边三角形；故B 正确；C 选项，DM OM OD =-u u u u r u u u u r u u u r ，BC OC OB =-u u ur u u u r u u u r ，由A 选项知，MO BD ⊥，CO BD ⊥，所以0OM OB OD OC ⋅=⋅=u u u u r u u u r u u u r u u u r，因此()()DM BC OM OD OC OB OM OC OD OB ⋅=-⋅-=⋅-⋅u u u u r u u u r u u u u r u u u r u u u r u u u r u u u u r u u u r u u u r u u u r ，同B 选项，设菱形ABCD 的边长为2，易得OC OM =1OB OD ==，所以3cos 1DM BC MOC ⋅=∠+u u u u r u u u r ，显然当1cos 3MOC ∠=-时，0DM BC ⋅=u u u u r u u u r ，即DM BC ⊥；故C 错误；D 选项，同BC 选项，设菱形ABCD 的边长为2，则OM =1OD =，2MD =，由几何体直观图可知，当OM ⊥平面BCD ，直线DM 与平面BCD 所成的角最大，为MDO ∠，易知60MDO ∠=︒. 故选：ABD.11．（2020届山东省济宁市高三上期末）己知mn 、为两条不重合的直线,αβ、为两个不重合的平面,则下列说法正确的是( )A ．若//,//m n αβ且//,αβ则//m nB ．若//,,,m n m n αβ⊥⊥则//αβC ．若//,,//,m n n m ααββ⊂⊄，则//m βD ．若//,,m n n ααβ⊥⊥，则//m β 【答案】BC 【解析】A. 若//,//m n αβ且//,αβ则可以//m n ，,m n 异面，或,m n 相交，故A 错误；B. 若//,,m n m α⊥则n α⊥，又,n β⊥故//αβ，B 正确；C. 若//,,m n n α⊂则m αP 或m α⊆，又//,m αββ⊄，故//m β，C 正确；D. 若//,,m n n α⊥则m α⊥，αβ⊥，则//m β或m β⊆，D 错误；故选：BC12．（2020届山东省枣庄、滕州市高三上期末）在正方体1111ABCD A B C D -中，N 为底面ABCD 的中心，P 为线段11A D 上的动点（不包括两个端点），M 为线段AP 的中点，则（）A ．CM 与PN 是异面直线B ．CM PN >C ．平面PAN ⊥平面11BDD B D ．过P ，A ，C 三点的正方体的截面一定是等腰梯形【答案】BCD 【解析】,,C N A 共线，即,CN PM 交于点A ，共面，因此,CM PN 共面，A 错误；记PAC θ∠=，则2222212cos cos 4PN AP AN AP AN AP AC AP AC θθ=+-⋅=+-⋅， 2222212cos cos 4CM AC AM AC AM AC AP AP AC θθ=+-⋅=+-⋅，又AP AC <， 22223()04CM PN AC AP -=->，22CM PN >，即CM PN >．B 正确；由于正方体中，AN BD ⊥，1BB ⊥平面ABCD ，则1BB AN ⊥，1BB BD B ⋂=，可得AN ⊥平面11BB D D ，AN ⊂平面PAN ，从而可得平面PAN ⊥平面11BDD B ，C 正确；取11C D 中点K ，连接11,,KP KC AC ，易知11//PK A C ，又正方体中，11//A C AC ，∴//PK AC ，,PK AC 共面，PKCA 就是过P ，A ，C 三点的正方体的截面，它是等腰梯形．D 正确．故选：BCD.13．（2020·蒙阴县实验中学高三期末）已知四棱锥P ABCD -，底面ABCD 为矩形，侧面PCD ⊥平面ABCD ，23BC =26CD PC PD ===.若点M 为PC 的中点，则下列说法正确的为（）A ．BM ⊥平面PCDB ．//PA 面MBDC ．四棱锥M ABCD -外接球的表面积为36π D ．四棱锥M ABCD -的体积为6 【答案】BC【解析】作图在四棱锥P ABCD -中：由题：侧面PCD ⊥平面ABCD ，交线为CD ，底面ABCD 为矩形，BC CD ⊥，则 BC ⊥平面PCD ，过点B 只能作一条直线与已知平面垂直，所以选项A 错误；连接AC 交BD 于O ，连接MO ，PAC ∆中，OM ∥PA ，MO ⊆面MBD ，PA ⊄面MBD ，所以//PA 面MBD ，所以选项B 正确；四棱锥M ABCD -的体积是四棱锥P ABCD -的体积的一半，取CD 中点N ，连接PN ，PN CD ⊥，则PN ^平面ABCD ，32PN =M ABCD -的体积112326321223M ABCD V -=⨯⨯=所以选项D 错误.矩形ABCD 中，易得6,3,3AC OC ON ===PCD V 中求得：16,2NM PC ==在Rt MNO V 中223MO ON MN =+= 即： OM OA OB OC OD ====，所以O 为四棱锥M ABCD -外接球的球心，半径为3，所以其体积为36π，所以选项C 正确故选：BC14．（2020届山东省潍坊市高三上期中）正方体1111ABCD A B C D -的棱长为2，已知平面1AC α⊥，则关于α截此正方体所得截面的判断正确的是（） A ．截面形状可能为正三角形 B ．截面形状可能为正方形 C ．截面形状可能为正六访形 D ．截面面积最大值为33【答案】ACD 【解析】如图，显然A,C 成立，下面说明D 成立，如图设截面为多边形GMEFNH ，设1AG x =，则01x ≤≤，则2,2(2),22,GH ME NF x MG HN EF x MN ======-=所以多边形GMEFNH 的面积为两个等腰梯形的面积和，所以1211()()22S GH MN h MN EF h =⋅+⋅+⋅+⋅ 因为22221222133[2(2)]()(22)(2)(2)2222x h x x x x -=--=+⋅-=-， 22222(2)223(2)[]22x x h x --=-=，所以221313(222)(2)[222(2)]2222S x x x x =+⋅-++-⋅ 232323x x =-++当1x =时，max 33S =，故D 成立. 故选：ACD ．15．（2020届山东省烟台市高三上期末）如图，在正方体1111ABCD A B C D -中，点P 在线段1B C 上运动，则（）A ．直线1BD ⊥平面11AC DB ．三棱锥11P ACD -的体积为定值C ．异面直线AP 与1AD 所成角的取值范围是[]45,90︒︒ D ．直线1C P 与平面11AC D 所成角的正弦值的最大值为63【答案】ABD 【解析】对于选项A,连接11B D ,由正方体可得1111AC B D ⊥,且1BB ⊥平面1111D C B A ,则111BB AC ⊥,所以11A C ⊥平面11BD B ,故111AC BD ⊥；同理,连接1AD ,易证得11A D BD ⊥,则1BD ⊥平面11ACD ,故A 正确；对于选项B,1111P A C D C A PD V V --=,因为点P 在线段1B C 上运动,所以1112A DP S A D AB =⋅,面积为定值,且1C 到平面11A PD 的距离即为1C 到平面11A B CD 的距离,也为定值,故体积为定值,故B 正确；对于选项C,当点P 与线段1B C 的端点重合时,AP 与1A D 所成角取得最小值为60︒,故C 错误；对于选项D,因为直线1BD ⊥平面11AC D ,所以若直线1C P 与平面11AC D 所成角的正弦值最大,则直线1C P 与直线1BD 所成角的余弦值最大,则P 运动到1B C 中点处,即所成角为11C BD ∠,设棱长为1,在11Rt D C B V 中,111126cos 33C B C BD BD ∠===,故D 正确故选：ABD 三、填空题16．（2020届山东省潍坊市高三上学期统考）如图，已知六棱锥P －ABCDEF 的底面是正六边形，PA ⊥平面ABC ，PA ＝2AB ，则下列结论中：①PB ⊥AE ；②平面ABC ⊥平面PBC ；③直线BC ∥平面PAE ；④∠PDA ＝45°. 其中正确的有________(把所有正确的序号都填上) 【答案】①④ 【解析】对于①，因为PA ⊥平面ABC ，所以PA ⊥AE ，又,EA AB PA AB A ⊥⋂=，所以EA ⊥平面PAB ，从而可得EA PB ⊥，故①正确．对于②，由于PA ⊥平面ABC ，所以平面ABC 与平面PBC 不可能垂直，故②不正确．对于③，由于在正六边形中BC AD ∥，所以BC 与EA 必有公共点，从而BC 与平面PAE 有公共点，所以直线BC 与平面PAE 不平行，故③不正确．对于④，由条件得PAD ∆为直角三角形，且PA ⊥AD ，又2PA AB AD ==，所以∠PDA=45°．故④正确．综上①④正确．答案：①④17．（2020届山东省潍坊市高三上期中）如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的表面积为__________；若该六面体内有一小球，则小球的最大体积为___________．【答案】332 86729【解析】（1）因为13336(12S =⨯⨯=33. （2）由图形的对称性得，小球的体积要达到最大，即球与六个面都相切时， 32倍，所以六面体体积是26. 由于图像的对称性，内部的小球要是体积最大，就是球要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥，设球的半径为R ，所以21366()6349R R =⨯⨯⨯⇒=，所以球的体积33446()3863V R πππ===. 故答案为：332；86729π. 18．（2020届山东省滨州市三校高三上学期联考）已知三棱锥S ABC -，SA ⊥平面ABC ，6ABC π∠=，3SA =，1BC =，直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上，则该球的表面积为________. 【答案】13π 【解析】如图：SA ⊥Q 平面ABC ，则SBA ∠为直线SB 和平面ABC 所成的角，即3SBA π∠=在Rt SAB ∆中：33tan3SA AB π=== 如图，设O 为三棱锥S ABC -外接球的球心，G 为ABC ∆外接圆圆心，连结,,,,OA OB GA GB OG ，则必有OG ⊥面ABC 在ABC ∆，22232cos 312316AC AB BC AB BC π=+-⋅⋅=+-=，则1AC = 其外接圆半径122,1sin sin 6AC r r ABC π====∠，又1322OG SA ==，所以三棱锥S ABC -外接球半径为22913142R OG r =+=+=该球的表面积为21344134S R πππ==⨯=, 故答案为：13π.19．（2020届山东省枣庄、滕州市高三上期末）如图，在三棱锥P-ABC 中，,PA AB ⊥PC BC ⊥，,AB BC ⊥22,AB BC ==5PC =，则P A 与平面ABC 所成角的大小为________；三棱锥P-ABC 外接球的表面积是________.【答案】45︒ 6π 【解析】如图，作平行四边形ABCD ，连接PD ，由AB BC ⊥，则平行四边形ABCD 是矩形．由BC CD ⊥，BC PC ⊥，PC CD C =I ，∴BC ⊥平面PCD ，而PD ⊂平面PCD ，∴BC PD ⊥，同理可得AB PD ⊥，又AB BC B ⋂=，∴PD ⊥平面ABCD ．,PD CD PD AD ⊥⊥，PAD ∠是P A 与平面ABC 所成角．由2,5CD AB PC ===1PD =，又1AD BC ==，∴45PAD ∠=︒．∴P A 与平面ABC 所成角是45︒．由,PA AB ⊥PC BC ⊥知PB 的中点到,,,A B C P 的距离相等，PB 是三棱锥P-ABC 外接球的直径．由BC ⊥平面PCD 得BC PC ⊥，2222(5)16PB PC BC =+=+=24()62PB S ππ==．故答案为：45︒；6π．20．（2020届山东省烟台市高三上期末）已知三棱锥P ABC -的四个顶点都在球O 的表面上，PA ⊥平面ABC ，6PA =，23AB =2AC =，4BC =，则：（1）球O 的表面积为__________；（2）若D 是BC 的中点，过点D 作球O 的截面，则截面面积的最小值是__________．【答案】52π 4π 【解析】（1）由题,根据勾股定理可得AC AB ⊥,则可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,则体对角线为外接球直径,即()22222623213r +=+=,则13r =,所以球的表面积为22441352r πππ=⨯=；（2）由题,因为Rt ABC V ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,则外接圆半径为2,故截面面积为224ππ⨯=故答案为：（1）52π；（2）4π21．（2020届山东省滨州市高三上期末）在四面体S ABC -中，2SA SB ==，且SA SB ⊥，5BC =，3AC =________，该四面体外接球的表面积为________.【答案】3068π 【解析】因为2SA SB ==，且SA SB ⊥，5BC =，3AC =222AB SA ==，因此222BC AC AB +=，则AC BC ⊥；取AB 中点为O ，连接OS ，OC ，则2OA OB OC OS ====，所以该四面体的外接球的球心为O ，半径为2OC=所以该四面体外接球的表面积为24(2)8 Sππ=⋅=；又因为SA SB=，所以SO AB⊥；因为底面三角形ABC的面积为定值11522AC BC⋅=，SO的长也为确定的值2，因此，当SO⊥平面ABC时，四面体的体积最大，为13036ABCV S SO=⋅=V.故答案为：(1).306(2). 8π22．（2020届山东省潍坊市高三上期末）正方体1111ABCD A B C D-的棱长为1，点K在棱11A B上运动，过,,A C K三点作正方体的截面，若K为棱11A B的中点，则截面面积为_________，若截面把正方体分成体积之比为2:1的两部分，则11A KKB=_______【答案】9851-【解析】（1）取11B C的中点M，连接KM，MC，11//KM AC Q ，而11A C //AC ，//KM AC ∴,,,A C M K ∴四点共面，且AK MC = ∴四边形ACMK 是等腰梯形，如图，2KM =2AC =2215122AK ⎛⎫=+= ⎪⎝⎭, 222224AH ==， 22225232244KH AK AH ⎛⎫⎛⎫∴=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， 12329228ACKM S ∴=⨯=⎝；（2）设1B K x =，取11B C 上的点M ，11B K B M x ==，连接,KM MC ，由（1）知,,,A C M K 四点共面，由图象可知11111133B MK BCA A B CD ABCD V V --==1221111111322223B MK BCAV x x -⎛∴=⨯++⨯⨯= ⎝，即210x x +-= ，解得：15x -+=即115B K-+ =，115351A K-+-=-=，此时1135512215A KKB--==-+.故答案为：98；51-23．（2020届山东省临沂市高三上期末）在正方体1111ABCD A B C D-中，E为棱CD上一点，且2CE DE=，F为棱1AA的中点，且平面BEF与1DD交于点G，与1AC交于点H，则1DGDD=______，1AHHC=______. 【答案】1638【解析】1111ABCD A B C D-Q是正方体∴面11//A B BA面11C D DCBF⊂Q面11A B BA//BF∴平面11CDD C，Q面BFGE I面11C D DC GE=则//BF GE，则AF DGAB DE=，即12DGDE=，又2CE DE=，则116DGDD=.连接AC交BE于M，过M作1//MN CC，MN与1AC交于N，连接FM，则H为FM与1AC的交点.因为//AB CE，所以32AM ABMC CE==，则132AN ACMMCN==.所以135MNCC=，所以65MN HNFA AH==，故138AHHC=.故答案为：16；3824．（2020届山东省济宁市高三上期末）下图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD，现将四边形ABCD沿BD折成直二面角A BD C--，则三棱锥A BCD-的外接球的体积为__________3cm．【答案】5003π【解析】由题设可将该三棱锥拓展成如图所示的正方体，则该正方体的外接球就是三棱锥的外接球，由于正方体的对角线长为2103l R==即球的半径3R=该球的体积3450033V Rππ==，应填答案3π．25．（2020届山东实验中学高三上期中）现有橡皮泥制作的底面半径为5，高为93高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为_________；若新圆锥的内接正三棱柱表面积取到最大值，则此正三棱柱的底面边长为_________.【答案】335【解析】由题意可知，底面半径为5，高为9的圆锥和底面半径为3，高为8的圆柱的总体积为22159(3)8993πππ⨯⨯⨯+⨯⨯=，设新的圆锥和圆柱的底面半径为r ，则：22198993r r πππ⨯⨯⨯+⨯⨯=，解得：3r =，设新圆锥的内接正三棱柱的底面边长为a ，高为h ，底面正三角形的外接圆的半径为r '，∴993h r '-=，93h r '∴=-，又3233r a a '∴=⨯⨯=， 93h a ∴=-，∴正三棱柱的表面积2135332()272S a h a a a a =⨯⨯+⨯⨯⨯=-+，∴当93532()a =-=⨯-故答案为：3，935． 26．（2020届山东省德州市高三上期末）中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知PA ⊥平面ABCE ，四边形ABCD 为正方形，5AD =，3ED =，若鳖臑P ADE -的外接球的体积为92π，则阳马P ABCD -的外接球的表面积等于______.【答案】20π 【解析】Q 四边形ABCD 是正方形，AD CD ∴⊥，即AD CE ⊥，且5AD =3ED =，所以，ADE ∆的外接圆半径为221222AE AD ED r +===设鳖臑P ADE -的外接球的半径1R ，则314923R ππ=，解得132R =. PA ⊥Q 平面ADE ，22112PA R r ⎛⎫∴=+ ⎪⎝⎭，可得22111022PA R r =-=，10PA ∴=. 正方形ABCD 的外接圆直径为22210r AC AD ===，210r ∴=， PA ⊥Q 平面ABCD ，所以，阳马P ABCD -的外接球半径222252PA R r ⎛⎫=+= ⎪⎝⎭，因此，阳马P ABCD -的外接球的表面积为22420R ππ=.故答案为：20π.四、解答题27．（2020届山东省烟台市高三上期末）如图，在四棱锥S ABCD -中，ABCD 为直角梯形，//AD BC ，BC CD ⊥，平面SCD ⊥平面ABCD ，SCD ∆是以CD 为斜边的等腰直角三角形，224BC AD CD ===，E 为BS 上一点，且2BE ES =.（1）证明：直线//SD 平面ACE ；（2）求二面角S AC E --的余弦值.【答案】（1）证明见解析（2）13【解析】（1）连接BD 交AC 于点F ,连接EF ,因为//AD BC ,所以AFD ∆与BCF ∆相似, 所以2BF BC FD AD==, 又=2BE BF ES FD =,所以//EF SD , 因为EF ⊂平面ACE ,SD ⊄平面ACE ,所以直线//SD 平面ACE（2）由题,因为平面SCD ⊥平面ABCD ,平面SCD I 平面ABCD CD =,BC ⊂平面ABCD ,BC CD ⊥,所以BC ⊥平面SCD ,以C 为坐标原点,,CD CB u u u r u u u r 所在的方向分别为y 轴、z 轴的正方向,与,CD CB u u u r u u u r 均垂直的方向作为x 轴的正方向,建立如图所示的空间直角坐标系C xyz -,因为224BC AD CD ===,2BE ES =,则(0,0,0)C ,(1,1,0)S ,(0,2,2)A ,224(,,)333E ,所以(0,2,2)CA =u u u r ,(1,1,0)CS =u u u r ,224(,,)333CE =,设平面SAC 的一个法向量为(,,)m x y z =u r ,则00m CA m CS ⎧⋅=⎨⋅=⎩u u u v vu u u vv ,即00y z x y +=⎧⎨+=⎩,令1z =,得1x =,1y =-,于是(1,1,1)m =-u r ,设平面EAC 的一个法向量为(,,)n x y z =r ,则0n CA n CE ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,即020y z x y z +=⎧⎨++=⎩,令1z =,得1x =-,1y =-,于是(1,1,1)m =--u r ,设二面角S AC E --的平面角的大小为θ,则1cos 3m n m n θ⋅==ur ru r r ,所以二面角S AC E --的余弦值为1328．（2020届山东省泰安市高三上期末）如图，在三棱锥P —ABC 中，△P AC 为等腰直角三角形，90,APC ABC ∠=∆o 为正三角形，D 为A 的中点，AC =2．(1)证明：PB ⊥AC ；(2)若三棱锥P ABC -的体积为33，求二面角A —PC —B 的余弦值【答案】（1）证明见解析（27【解析】（1）证：PAC ∆Q 为等腰直角三角形，D 为中点，PD AC ∴⊥，又ABC ∆为正三角形，D 为中点，BD AC ∴⊥，又PD BD D ⋂=，,PD BD ⊂平面PBD ，AC ∴⊥平面PBD ，又PB ⊂平面PBD ，PB AC ∴⊥（2）解：设三棱锥P ABC -的高为h ，sin 603BD BC ==o1132P ABC V AC BD h -∴=⨯⨯⨯⨯3=31h ∴=，又11,2PD AC ==PD ∴⊥平面ABC ，如图，以D 为坐标原点，建立空间直角坐标系D xyz -，则()1,0,0A ，()0,3,0B ，()1,0,0C-，()0,0,1P ， ()0,3,0DB ∴=u u u r ，()1,0,1CP =u u u r ，()1,3,0CB =u u u r ，设(),,n x y z =r 为平面PBC 的一个法向量，则00CP n CB n ⎧⋅=⎨⋅=⎩u u u v v u u u v v ，即030x z x y +=⎧⎪⎨+=⎪⎩，令1x =，得31y z ⎧=-⎪⎨⎪=-⎩，∴31,,13n ⎛⎫=-- ⎪ ⎪⎝⎭r ，又DB uuu r 是平面PAC 的一个法向量，∴7cos ,DB n DB DB n n⋅<>==-⋅u u u r u u u r r r u u u r r ，由图可知二面角A PC B --的平面角为锐角，∴二面角A PC B --的余弦值为7． 29．（2020届山东省潍坊市高三上期中）如图，在棱长均为2的三棱柱111ABC A B C -中，平面1ACB ⊥平面11A ABB ，11AB A B =，O 为1AB 与1A B 的交点．（1）求证：1AB CO ⊥；（2）求平面11ACC A 与平面ABC 所成锐二面角的余弦值．【答案】（1）详见解析；（2）1 3 .【解析】（1）因为四边形11A ABB为菱形，所以11A B AB⊥，又平面1ACB⊥平面11A ABB，平面1A CB I平面111A ABB A B=，所以1AB⊥平面1A CB，因为CO⊂平面1A CB，所以1AB CO⊥.（2）因为11A B AB=，所以菱形11A ABB为正方形，在Rt COA∆中，222CO AC OA=-=，在COB∆中，2CO OB==，2CB=，222CO OB CB+=，所以，CO OB⊥，又1CO AB⊥，11A B AB O⋂=，所以，CO⊥平面11A ABB；以O为坐标原点，以OA，OB，OC所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系O xyz-.()2,0,0A，()10,2,0A，(2C，()2,0B，设平面11ACC A的一个法向量为()1111,,n x y z=u r平面ABC的一个法向量为()2222,,n x y z=u u r，则1111220,220,xx z⎧-=⎪⎨-+=⎪⎩令11x=，得()11,1,1=-u u rn，2222220,220,x y x z ⎧-+=⎪⎨-+=⎪⎩ 令21x =，得()21,1,1=u u r n ，设平面11ACC A 与平面ABC 所成锐二面角为α，则21121cos 333α⋅===⨯u u r u u r u u r u u r n n n n ，所以平面11ACC A 与平面ABC 所成锐二面角的余弦值为13. 30．（2020届山东省九校高三上学期联考）已知四棱柱1111ABCD A B C D -的底面为菱形，12AB AA ==，3BAD π∠=，AC BD O =I ，AO ⊥平面1A BD ，11A B A D =.（1）证明：1//B C 平面1A BD ；（2）求钝二面角1B AA D --的余弦值.【答案】(1)证明见解析；(2) 17-【解析】（1）证明：连接1AB 交1A B 于点Q ，易知Q 为1AB 中点，∵O 为AC 中点，∴在1AB C ∆中，11//2OQ B C ， ∵OQ ⊂平面1A BD ，1B C ⊄平面1A BD ，∴1//B C 平面1A BD .（2）∵AO ⊥平面1A BD ，∴1AO A O ⊥，∵11A B A D =且O 为BD 的中点，∴1AO BD ⊥，∵AO BD ⊂、平面ABCD 且AO BD O =I ，∴1A O ⊥平面ABCD ，如图，建立空间直角坐标系O xyz -. 易得：()3,0,0A ，()0,1,0B ，()0,1,0D -，()10,0,1A ，∴()13,0,1AA =-u u ur ，()3,1,0AB =-uu u r，设平面1A AB 的一个法向量为(),,n x y z =r，则1n AA n AB ⎧⊥⎨⊥⎩u u u vv u u u v v ，∴3030x z xy ⎧-+=⎪⎨-+=⎪⎩，令1x =，得3y z ==，∴()1,3,3n =r .同理可得平面1A AD 的一个法向量为()1,3,3m =-u r ，∴1cos ,7m n m n m n ⋅<>==u r ru r r u r r ，∴钝二面角1B AA D --的余弦值为17-.31．（2020届山东省潍坊市高三上期末）在底面为正方形的四棱锥P ABCD -中，平面PAD ⊥平面,,,ABCD PA PD E F =分别为棱PC 和AB 的中点.(1)求证://EF 平面PAD ;(2)若直线PC 与AB 所成角的正切值为5，求平面PAD 与平面PBC 所成锐二面角的大小.【答案】（1）见解析（2）4π【解析】(1)证明:取CD 的中点M ，连接,EM FM ，因为,E F 分别为PC 和AB 的中点，四边形ABCD 为正方形，所以//, //EM PD FM AD ，因为,EM FM ⊂平面,,EFM PD AD ⊂平面PAD ，所以平面//EFM 平面PAD ，因为EF ⊂平面EFM ，所以//EF 平面PAD .(2)因为平面PAD ⊥平面ABCD ，平面PAD I 平面,ABCD AD CD AD =⊥ CD ⊂平面ABCD 所以CD ⊥平面PAD ，所以CD PD ⊥，因为//AB CD ，所以PCD ∠就是直线PC 与AB 所成的角，所以52PD tan PCD DC ∠==，设5,2PD CD ==，分别取AD 和BC 的中点,O N ，连,PO ON ，因为PA PD =，所以PO AD ⊥，因为平面PAD ⊥平面ABCD ，平面PAD I 平面,ABCD AD PO =⊂平面PAD ，所以PO ⊥平面ABCD如图，建立空间直角坐标系O xyz -，则()()()0,0,2,1,2,0,1,2,0P C B -，所以()()2,0,0,1,2,2CB CP ==-u u u r u u u r ，设(),,m x y z =u r 是平面BPC 的一个法向量，则2200x y z x -+=⎧⎨=⎩取1y =，则1z =，所以()0,1,1m =u r()0,1,0n =r 是平面PAD 的一个法向量，所以2,221m n cos m n m n⋅<>===⨯u r r u r r u r r ，,4m n π<>=u r r 所以所求二面角的大小为4π 32．（2020届山东省日照市高三上期末联考）如图，扇形AOB 的半径为2，圆心角120AOB ∠=o ，点C 为弧AB 上一点，PO ⊥平面AOB 且5PO =，点M PB ∈且2BM MP =，PA ∥平面MOC ．（1）求证：平面MOC ⊥平面POB ；（2）求平面POA 和平面MOC 所成二面角的正弦值的大小.【答案】(1)见证明；(2)64【解析】（1）如图，连接AB 交OC 于点N ，连接MN ，Q PA ∥平面MOC ，∴PA ∥MN ，Q 2BM MP =，2BN NA ∴=，2OA OB ==Q ，120AOB ∠=o ，23AB∴=，43BN ∴=，又30OBA ∠=o Q ，∴在BON △中，根据余弦定理得23ON =， 222ON OB BN ∴+=，90BON ∴∠=o ，ON OB ∴⊥，又Q PO ⊥平面AOB ，ON OP ∴⊥，ON ∴⊥平面POB ，又ON ⊂Q 平面MOC ，∴平面MOC ⊥平面POB（2）由（1）得,,OC OB OP OC OP OB ⊥⊥⊥，如图建立空间直角坐标系O xyz -，5OP =Q ，2OA OB OC ===，∴5)OP =u u u r ，3,1,0)OA =-u u u r ，(2,0,0)OC =u u u r ，(0,2,0)OB =u u u r ，Q 点M PB ∈且2BM MP =，225(0,3OM ∴=u u u u r ，设平面POA 的法向量为1111(,,)x y z =n ，则1100n OP n OA u u u v u u u v ⎧⋅=⎪⎨⋅=⎪⎩，即1115030z x y =-=，令11x =，得13y 10z =，∴1(13,0)=n ，设平面MOC 的法向量为2222(,,)x y z =n ，则2200n OC n OM ⎧⋅=⎪⎨⋅=⎪⎩u u u v u u u u v ，即2222022503x y z =⎧⎪⎨=⎪⎩，即222050x y z =⎧⎪⎨+=⎪⎩，令21z =，得25y =-，20x =，∴2(0,5,1)=-n ，设平面POA 和平面MOC 所成二面角的大小为θ，则1510 |cos|426θ==，6sin4θ∴=，∴平面POA和平面MOC所成二面角的正弦值的大小为6433．（2020届山东省德州市高三上期末）如图（1），边长为2的正方形ABEF中，D，C分别为EF、AF 上的点，且ED CF=，现沿DC把CDF∆剪切、拼接成如图（2）的图形，再将BEC∆，CDF∆，ABD∆沿BC，CD，BD折起，使E、F、A三点重合于点A'，如图（3）.（1）求证：'⊥BA CD；（2）求二面角'--B CD A最小时的余弦值.【答案】（1）证明见解析；（2）13.【解析】（1）折叠前BE EC⊥，BA AD⊥，折叠后''⊥BA A C，''⊥BA A D，又'''⋂=A C A D A，所以'⊥BA平面ACD'，因此'⊥BA CD；（2）由（1）及题意知A C A D''⊥，因此以A'为原点，A C'、A D'、A B'分别为x、y、z轴建立空间直角坐标系如图：令'=A C a，'=A D b，2a b+=，所以(),0,0C a，()0,,0D b，()0,0,2B设平面BCD法向量为(),,m x y z=u r则m BCm BD⎧⋅=⎨⋅=⎩u u u vvu u u vv所以2020ax zbx z-=⎧⎨-=⎩，令1z=，则22,,1ma b⎛⎫= ⎪⎝⎭u r又平面ACD '法向量为()0,0,1m =u r，设二面角'--B CD A 的大小为θ，所以22cos 1411m nm na bθ⋅==⨯++u r r u r r ，又22224412119b a b a b a a b a b a b a b ⎛⎫⎛⎫⎛⎫++=++++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎭≥⎝，当且仅当1a b ==取等号，所以1cos 3θ≤. 所以二面角'--B CD A 最小时的余弦值为13.34．（2020届山东省滨州市三校高三上学期联考）如图，在直三棱柱111ABC A B C -中，1AB AC ==，且AB AC ⊥，点M 在棱1CC 上，点N 是BC 的中点，且满足1AM B N ⊥.（1）证明：AM ⊥平面11A B N ；（2）若M 为1CC 的中点，求二面角111A B N C --的正弦值.【答案】（1）详见解析；（215. 【解析】（1）∵三棱柱111ABC A B C -为直三棱柱，∴1AA AB ⊥∵AB AC ⊥，1AA ⊂平面11AAC C ，AC ⊂平面11AAC C ，且1AA AC A =I ， ∴AB ⊥平面11AAC C ，（或者由面面垂直的性质证明）又∵AM ⊂平面11AAC C ，∴AB AM ⊥ ∵11A B AB ∥，∴11A B AM ⊥，∵1AM B N ⊥，11A B ⊂平面11A B N ，1B N ⊂平面11A B N ，且1111A B B N B ⋂=， ∴AM ⊥平面11A B N（2）以A 为原点，分别以AB 、AC 、1AA 为x 轴、y 轴、z 轴建立空间直角坐标系A xyz -﹐设1AA a =，则(0,0,0)A ，(1,0,0)B ，(0,1,0)C ，1(1,0,)B a ，1(0,1,1)C ，11,,022N ⎛⎫ ⎪⎝⎭，0,1,2a M ⎛⎫ ⎪⎝⎭，∵1AM B N ⊥，∴211110,1,,,022222a aAM B N a ⎛⎫⎛⎫⋅=⋅--=-= ⎪ ⎪⎝⎭⎝⎭u u u u r u u u u r ，∴1a = ∴1(1,0,1)B ，10,1,2M ⎛⎫ ⎪⎝⎭，设平面11A B N 法向量为{,,}m x y z =r11(1,0,0)A B =u u u u r ，111,,122B N ⎛⎫=-- ⎪⎝⎭u u u u r∴11101122m A B x m B N x y z ⎧⋅==⎪⎨⋅=-+-=⎪⎩u u u uv r u u u u v r ，∴可取(0,2,1)m =r 设平面1B NC 法向量为{,,}n x y z =r1(1,1,0)BC =-u u u r ，111,,122B N ⎛⎫=-- ⎪⎝⎭u u u u r ∴1101122n B C x y n B N x y z ⎧⋅=-+=⎪⎨⋅=-+-=⎪⎩u u u vr u u u u v r ，∴可取(1,1,0)n =r ∴10cos ,||||5m n m n m n ⋅〈〉==⋅r r r rr r所以二面角111A B N C --的正弦值为155. 35．（2020届山东省枣庄、滕州市高三上期末）如图，在四棱锥P-ABCD 中，23,AD =3,AB =3,AP =//AD BC ，AD ⊥平面P AB ，90APB ︒∠=，点E 满足2133PE PA PB =+u u u r u u u r u u u r .（1）证明：PE DC ⊥；（2）求二面角A-PD-E 的余弦值. 【答案】（1）证明见解析（2）226【解析】（1）证明：在Rt PAB ∆中，由勾股定理，得22PB AB AP =-223(3)=-6=.因为21,33PE PA PB =+u u u r u u u r r AB PB PA =-u u u r u u u r u u u r，所以21()33PE AB PA PB PB PA ⎛⎫⋅=+⋅- ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r22211333PA PB PA PB =-++⋅u uu r u u u r u u u r u u u r22211(3)(6)0333=-⨯+⨯+⨯0=.所以PE AB ⊥u u u r u u u r，所以PE AB ⊥.因为AD ⊥平面P AB ，PE ⊂平面P AB ，所以PE AD ⊥.又因为,PE AB ⊥AB AD A ⋂=，所以PE ⊥平面ABCD. 又因为DC ⊂平面ABCD ，所以PE DC ⊥.（2）由21,33PE PA PB =+u u u r u u u r u u u r 得2EB AE =u u u r u u u r.所以点E 是靠近点A 的线段AB 的三等分点.所以113AE AB ==. 分别以,AB uuu r AD u u u r所在方向为y 轴，z 轴的正方向，建立如图所示的空间直角坐标系A xyz -.则(0,0,0),A (0,0,23),D (0,1,0),E )2,1,0P .设平面PDE 的法向量为()111,,m x y z =u r，由00m EP m ED ⎧⋅=⎨⋅=⎩u u u v v u u u v v ，得11120230x y z ⎧=⎪⎨-+=⎪⎩. 令11z =，则(0,23,1)m =-u r；设平面APD 的法向量为()222,,,n x y z =r (2,1,0),AP =u u u r (0,0,23)AD =u u u r，由00n AP n AD ⎧⋅=⎨⋅=⎩u u u v v u u u v v ，得22220230x y z ⎧+=⎪⎨=⎪⎩，令21x =，则()1,2,0n =-r.设向量m u r 与n r的夹角为θ，则cos ||||m n m n θ⋅=⋅u r ru r r 222226(23)11(2)-=+⨯+-22613=-. 所以二面角A PD E --的余弦值为226. 36．（2020·山东省淄博实验中学高三上期末）如图，点C 在以AB 为直径的圆O 上，PA 垂直与圆O 所在平面，G 为 AOC ∆的垂心（1）求证：平面OPG ⊥平面 PAC ；（2）若22PA AB AC ===，求二面角A OP G --的余弦值.【答案】（1）见解析（2）25117. 【解析】（1）如图，延长OG 交AC 于点M .因为G 为AOC ∆的重心，所以M 为AC 的中点.因为O 为AB 的中点，所以//OM BC .因为AB 是圆O 的直径，所以BC AC ⊥，所以OM AC ⊥. 因为PA ⊥平面ABC ，OM ⊂平面ABC ，所以PA OM ⊥.又PA ⊂平面PAC ，AC ⊂平面,PAC PA AC ⋂=A ，所以OM ⊥ 平面PAC .即OG ⊥平面PAC ，又OG ⊂平面OPG ，所以平面OPG⊥平面PAC.（2）以点C 为原点，CB u u u r ，CA u u u r ，AP u u u r方向分别为x ，y ，z 轴正方向建立空间直角坐标系C xyz -，则()0,0,0C ，()0,1,0A ，)3,0,0B，31,02O ⎫⎪⎪⎝⎭，()0,1,2P ，10,,02M ⎛⎫⎪⎝⎭，则3OM ⎛⎫= ⎪ ⎪⎝⎭u u u u r ，31,22OP ⎛⎫= ⎪ ⎪⎝⎭u u u r .平面OPG 即为平面OPM ，设平面OPM 的一个法向量为(),,n x y z =r，则30,2{3120,2n OM x n OP x y z ⋅=-=⋅=++=u u u u r r u u u r r 令1z =，得()0,4,1n =-r .过点C 作CH AB ⊥于点H ，由PA ⊥平面ABC ，易得CH PA ⊥，又PA AB A ⋂=，所以CH ⊥平面PAB ，即CH u u u r为平面PAO 的一个法向量.在Rt ABC ∆中，由2AB AC =，得30ABC ∠=︒，则60HCB ∠=︒，1322CH CB ==. 所以3cos H x CH HCB =∠=3sin 4H y CH HCB =∠=.所以33,044CH ⎛⎫= ⎪ ⎪⎝⎭u u u r . 设二面角A OP G --的大小为θ，则cos CH n CH n θ⋅==⋅u u u r r u u u r r 2233041044511739411616⨯-⨯+⨯=+⨯+. 37．（2020届山东省潍坊市高三上学期统考）如图，四棱锥P ABCD -中，底面ABCD 为梯形，PD ⊥底面ABCD ，//AB CD ，AD CD ⊥，1AD AB ==，2BC =．(1)求证：平面PBD ⊥平面PBC ；(2)设H 为CD 上一点，满足2CH HD =u u u r u u u r，若直线PC 与平面PBD 6，求二面角H PB C --的余弦值．【答案】（1）证明见解析；（227【解析】（I ）由,//,1AD CD AB CD AD AB ⊥==，可得2BD =，又2,,.4BC BC BD π=∠=∴⊥从而2CD =，PD ⊥Q 底面ABCD ，BC PD ∴⊥PD BD D ⋂=Q ，BC ∴⊥平面,PBD 所以平面PBD ⊥平面PBC .（II ）由（I ）可知BPC ∠为PC 与底面PBD 所成角. 所以6tan BPC ∠=，所以3,1PB PD == 又23CH HD =u u u v u u u v及2CD =，可得64,55CH DH ==, 以D 点为坐标原点，,,DA DC DP 分别,,x y z 轴建立空间直角坐标系，则()()()41,1,0,0,0,1,0,2,0,0,,05B P C H ⎛⎫⎪⎝⎭. 设平面HPB 的法向量(),,n x y z =r.则由00n PB n PB ⎧⋅=⎨⋅=⎩u u u v r u u u v r 得4050y z x y z ⎧-+=⎪⎨⎪+-=⎩取()1,5,4n =--r。

备战2020年浙江省高考数学优质卷分类解析：立体几何与空间向量(原卷版)

(浙江专用)2020版高考数学新增分大一轮复习第八章立体几何与空间向量 8.6 空间向量及其运算

(2)空间向量数量积的运算律 ①(λa)·b＝_λ_(_a_·b_)_； ②交换律：a·b＝_b_·_a_； ③分配律：a·(b＋c)＝_a_·_b_＋__a_·c__.
4.空间向量的坐标表示及其应用
设a＝(a1，a2，a3)，b＝(b1，b2，b3).
向量表示
数量积
a·b
共线 a＝λb(b≠0，λ∈R)
123456
题组三易错自纠
4.在空间直角坐标系中，已知A(1，2，3)，B(－2，－1，6)，C(3，2，1)，
D(4，3，0)，则直线AB与CD的位置关系是
A.垂直 C.异面
√B.平行
D.相交但不垂直
解析由题意得，A→B＝(－3，－3，3)，C→D＝(1，1，－1)，
∴A→B＝－3C→D，∴A→B与C→D共线，
(6)若a·b<0，则〈a，b〉是钝角.( × )
123456
题组二教材改编
2.[P97A 组 T2] 如图所示，在平行六面体 ABCD—A1B1C1D1 中，M 为 A1C1 与 B1D1 的交点.若A→B＝a，A→D＝b，A→A1＝c，则下列向量中与B→M相等的向量是
√A.－21a＋12b＋c
垂直 a·b＝0(a≠0，b≠0)
坐标表示 a1b1＋a2b2＋a3b3 a1＝λb1，a2＝λb2，a3＝λb3 a1b1＋a2b2＋a3b3＝0
模夹角
|a|
〈a，b〉 (a≠0，b≠0)
a21＋a22＋a23b3
a21＋a22＋a23· b21＋b22＋b23
3.空间向量的数量积及运算律 (1)数量积及相关概念 ①两向量的夹角已知两个非零向量 a，b，在空间任取一点 O，作O→A＝a，O→B＝b，则∠AOB 叫

2020届新高考高三数学试题分项汇编专题9 立体几何与空间向量(原卷版+解析版)

备战2020年浙江省高考数学优质卷分类解析：立体几何与空间向量(解析版)

第九章立体几何与空间向量从近几年的高考试题来看,所考的主要内容是:(1)有关线面位置关系的组合判断,试题通常以选择题的形式出现,主要是考查空间线线、线面、面面位置关系的判定与性质;(2)有关线线、线面和面面的平行与垂直的证明,试题以解答题中的第一问为主,常以多面体为载体,突出考查学生的空间想象能力及推理论证能力;(3)线线角、线面角和二面角是高考的热点,五年五考,选择题、填空题皆有，解答题中第二问必考,一般为中档题,在全卷的位置相对稳定，主要考查空间想象能力、逻辑思维能力和转化与化归的应用能力. 前几年浙江卷较为注重几何法的考查，对空间向量方法考题较少，近三年则倾向于空间向量方法，且大题中考查线面角的计算较多.（4）三视图问题，五年五考，往往与几何体的面积或体积相结合.一．选择题1．【浙江省台州市2019届高三4月调研】一个几何体的三视图如图所示，则这个几何体的体积为（）A．B．C．D．【答案】B【解析】由三视图可知，该几何体为放倒的三棱柱，且底面为侧视图中等腰直角三角形，所以体积＝故选：B.2．【浙江省宁波市2019届高三上期末】某几何体的三视图如图所示，则该几何体的体积为（）A． B． C． D．【答案】D【解析】根据已知可得该几何体是一个四分之一圆锥，与三棱柱的组合体，四分之一圆锥的底面半径为1，高为1，故体积为：，三棱柱的底面是两直角边分别为1和2的直角三角形，高为1，故体积为：，故组合体的体积，故选D．3．【浙江省三校2019年5月份第二次联考】已知平面，直线，若，，，则“”是“中至少有一条与垂直”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】C【解析】先判断充分性，当时，假设都不与垂直.在平面内作的垂线，由可得，则.由，不垂直于可得与相交.由，可得.所以，矛盾.所以当时，可以推出中至少有一条与垂直，即充分性成立.再判断必要性，当中至少有一条与垂直时，不妨设，由可得，所以，即必要性成立.综上所述，“”是“中至少有一条与垂直”的充要条件.故选C.4．【浙江省三校2019年5月份第二次联考】已知正三棱锥（底面是正三角形，顶点在底面的射影是正三角形的中心），直线平面，分别是棱上一点（除端点），将正三棱锥绕直线旋转一周，则能与平面所成的角取遍区间一切值的直线可能是（）A．B．C．D．中的任意一条【答案】B【解析】假设满足题意，当与平面所成的角为时，，由可得.在正三棱锥中，可得，当时可得，显然这是不可能成立的，所以不满足题意.同理，与不可能垂直，则与平面所成的角不可能为.综上所述，可以排除A,C,D，故选B.5．【浙江省温州市2019届高三2月高考适应性测试】在正四面体 ABCD 中，P，Q分别是棱 AB，CD的中点，E，F分别是直线AB，CD上的动点，M 是EF 的中点，则能使点 M 的轨迹是圆的条件是（）A．PE＋QF＝2 B．PE•QF＝2C．PE＝2QF D．PE2＋QF2＝2【答案】D【解析】如图：取BC、BD、AC、AD的中点为G、H、K、L，因为P、Q是定点，所以PQ的中点O为定点，由对称性可知，PQ、EF的中点在中截面GHLK上运动，∵+=+,∴，又在正四面体中，对棱垂直，∴PE QF，∴，∴4=若点M的轨迹是以O为圆心的圆，则为定值，只有D符合题意，故选D.6．【浙江省金丽衢十二校2019届高三第一次联考】已知一个几何体的三视图如图所示，则该几何体的体积为（）A．323B．163C．83D．43【答案】C【解析】由题设中三视图提供的图形信息与数据信息可知该几何体是一个三棱柱与一个等高三棱锥的组合体，其中三棱柱与三棱锥的底面都是直角边长为2的等腰直角三角形，所以其体积()()22111822223223V =⨯⨯⨯+⨯⨯=，应选答案C. 7．【浙江省金丽衢十二校2019届高三第一次联考】如图，二面角的大小为，，，且，，，则与所成角的大小为（）A ．B ．C ．D ．【答案】C 【解析】∵为等边三角形，又，，由余弦定理得故为等腰直角三角形，取BC 中点E,连接DE ，AE,则AE ⊥BC,DE⊥BC,∴∠DEA 为二面角的平面角，BC⊥面ADE, DE=中由余弦定理得AD=1,过A 作AO⊥DE, BC⊥AO，故AO⊥，故∠ADE 为与所成角，∠ADE=故答案为8．【浙江省湖州三校2019年普通高等学校招生全国统一考试】已知三棱锥中，为正三角形，，且在底面内的射影在的内部（不包括边界），二面角，二面角，二面角的大小分别为，，，则（）A．B．C．D．【答案】C【解析】设在底面内的射影为O，过O分别作AB,BC,CA垂线，垂足分别为D,E,F,则，，，从而，，，因为，所以,,即,即，选C.9．【浙江省金华十校2019届高三上期末】如图所示，在底面为正三角形的棱台中，记锐二面角的大小为，锐二面角的大小为，锐二面角的大小为，若，则A． B．C． D．【答案】C【解析】棱台的侧棱延长交于点P过点P在平面ABC上的射影为H，设Ｈ到ＡＢ，ＢＣ，ＡＣ的距离分别为，∵，∴，则故Ｈ所在区域如图所示比较即比较ＰＡ，ＰＢ，ＰＣ，即比较ＨＡ，ＨＢ，ＨＣ由图可知：ＨＣ＞ＨＡ＞HB ∴故选：B ．10．【浙江省金华十校2019届高考模拟】如图，AB 是平面α的斜线段，A 为斜足，点C 满足sin sin (0)CAB CBA λλ∠=∠>，且在平面α内运动，则（）A ．当1λ=时，点C 的轨迹是抛物线B ．当1λ=时，点C 的轨迹是一条直线 C ．当2λ=时，点C 的轨迹是椭圆D ．当2λ=时，点C 的轨迹是双曲线抛物线【答案】B【解析】在ABC ∆中，∵sin sin (0)CAB CBA λλ∠=∠>，由正弦定理可得：BCACλ=，当1λ=时，BC AC =，过AB 的中点作线段AB 的垂面β，则点C 在α与β的交线上，即点C 的轨迹是一条直线，当2λ=时，2BC AC =，设B 在平面α内的射影为D ，连接BD ，CD ，设BD h =，2AD a =，则22BC CD h =+，在平面α内，以AD 所在直线为x 轴，以AD 的中点为y 轴建立平面直角坐标系，设(,)C x y ，则22()CA x a y =++，22()CD x a y =-+，222()CB x a y h =-++，∴22222()2()x a y h x a y -++=++，化简可得2222516393a h x a y ⎛⎫++=+ ⎪⎝⎭.∴C 的轨迹是圆．故选：B ．二.填空题11．【浙江省2019届高三高考全真模拟（二)】某几何体的三视图（单位：cm ）如图所示，则该几何体的最长的棱长为________，体积为________.7()cm 23()cm 【解析】由通过三视图可以知道该几何是有一条侧棱垂直于底面的四棱锥，底面是直角梯形，如图所示：四棱锥A BCDE -，2,22,AC DC BE AC ===⊥底面BCDE ，在直角梯形BCDE 中，可求出2BC =，在Rt ABC ∆中，2222(2)(2)2AB AC BC =+=+=，同理可求出：22(2)26AD =+=，22222222(2)217AE AC CE AC CD DE =+=++=++=，设四棱锥的底面BCDE 的面积为S ，所以13111122S =⨯+⨯⨯=，因此四棱锥的体积113223322V S AC =⋅⋅=⨯⨯=，所以该几何体的最长侧棱长为7()cm ，体积为223()cm . 12．【浙江省温州市2019届高三2月高考适应性测试】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm3）等于_____，表面积（单位：cm2）等于____．【答案】3【解析】根据几何体的三视图，得该几何体为以等腰梯形ABCD 与等腰梯形为底面，高为1的直四棱柱，如图：由柱体体积公式得：V．又等腰梯形ABCD与等腰梯形全等，面积和为6，矩形DC的面积为21=2，矩形的面积为41=4，矩形与矩形DA的面积相等，又由正视图可得BC=，所以矩形与矩形DA的面积和为2=2，所以表面积为6+2+4+2=12+2，故答案为3，.13．【浙江省三校2019年5月份第二次联考】若某几何体的三视图（单位：）如图所示，则该几何体最长的棱长是__________，体积等于__________．【答案】 20【解析】由三视图可得该几何体是截长方体得到的四棱锥,其中，最长的棱长是，体积.14．【浙江省湖州三校2019年普通高等学校招生全国统一考试】某几何体的三视图如图所示（单位：），则该几何体的体积（单位：）等于_______，表面积（单位：）等于__________．【答案】【解析】几何体一个边长为2的正方体挖去一个正四棱锥（顶点在正方体下底面中心，底面为正方体上底面），因此几何体的体积为，表面积为15．【浙江省金华十校2019届高三上期末】一个棱柱的底面是边长为6的正三角形，侧棱与底面垂直，其三视图如图所示，则这个棱柱的体积为______，此棱柱的外接球的表面积为______．【答案】【解析】由题意可知，该三棱柱是一个直三棱柱，且底面是边长为6的正方形，底面积为，该三棱柱的高，所以，该三棱柱的体积为．由正弦定理可知，该正三棱柱底面的外接圆直径为，则其外接球的直径为，则，因此，此棱柱的外接球的表面积为．故答案为：；．16．【浙江省金华十校2019届下学期高考模拟】某几何体的三视图如图所示，正视图为腰长为1的等腰直角三角形，侧视图、俯视图均为边长为1的正方形，则该几何体的表面积是_____，体积是_____．33222+13 【解析】由三视图还原原几何体如图所示，该几何体为四棱锥P ABCD -，该几何体的表面积PAB PAD PCD PBC ABCD S S S S S S ∆∆∆∆=++++四边形1163331122222222=⨯⨯⨯+=+；体积12121323V =⨯=. 3322，13．17．【浙江省台州市2019届高三4月调研】已知正方体中，为的中点，在平面内，直线，设二面角的平面角为，当取最大值时，______.【答案】【解析】设直线交于，因为直线，为的是中点，所以为的中点，过作∥交于，则∥，连结交于H，则为的中点，过作∥交于点，则为中点，因为⊥平面，所以⊥平面，所以⊥，⊥，所以为二面角的平面角，即，问题转化为在上找一点，使最大，设正方体的边长为，，则，，当，即为中点时，最小，最大此时，，18．【浙江省2019届高三高考全真模拟（二)】四棱锥P ABCD -中，PA ⊥平面ABCD ，90BAD ∠=︒，112PA AB BC AD ====，//BC AD ，已知Q 是四边形ABCD 内部一点，且二面角Q PD A --的平面角大小为4π，若动点Q 的轨迹将ABCD 分成面积为1212,()S S S S <的两部分，则12:S S =________. 354- 【解析】以A 为坐标原点建立空间直角坐标系，如图：设Q 的轨迹与y 轴的交点坐标为Q （0，b ，0）（b ＞0）．由题意可知A （0，0，0），D （2，0，0），P （0，0，1），∴DP =（﹣2，0，1），DQ =（﹣2，b ，0）. AD =（2，0，0）．设平面APD 的法向量为1n =（x 1，y 1，z 1），平面PDQ 的法向量为2n =（x 2，y 2，z 2）则121200,,00n DP n DP n AD n DQ ⎧⎧⋅=⋅=⎪⎪⎨⎨⋅=⋅=⎪⎪⎩⎩ 即11221222020,2020x z x z x x by -+=-+=⎧⎧⎨⎨=-+=⎩⎩，令y 1=0得1n =（0，1，0），令z 2=2得2n =（1，2b，2）． ∴1212224,1,5n n n n b b⋅===+ ∵二面角Q ﹣PD ﹣A 的平面角大小为4π， ∴cos ＜12n n ⋅＞=12122n n n n ⋅=222,245b b =+解得255∴S△ADQ=1122255 2255AD AQ⋅=⨯⨯=．S梯形ABCD﹣S△ADQ=1232(12)155 2525⨯+⨯-=-．∵S1＜S2，∴S1=32525-，S2=255．∴S1：S2=（35﹣4）：4．故答案为（35﹣4）：4．三.解答题19．【浙江省三校2019年5月份第二次联考】如图，在三棱锥中，是棱的中点，，且,（Ⅰ）求证：直线平面；（Ⅱ）求二面角的正弦值.【答案】（Ⅰ）见解析（Ⅱ）【解析】（Ⅰ）连接，因为，所以.由已知得，，所以，所以，又，所以平面（Ⅱ）过点作，垂足是，因为是棱的中点，，所以点是的中点.连接，所以.所以就是二面角的平面角.由（Ⅰ）知平面，所以.因为，，所以所以,即二面角的正弦值为.20．【浙江省台州市2019届高三4月调研】如图棱锥的底面是菱形，，，侧面垂直于底面，且是正三角形.（Ｉ）求证：；（Ⅱ）求直线与平面所成角的正弦值.【答案】（Ｉ）见解析；（Ⅱ）.【解析】（Ｉ）如图，取中点，连接、因为是正三角形，所以又因为是菱形，，所以是正三角形，所以又，平面所以平面因为平面所以（Ⅱ）因为侧面垂直于底面，面面，所以面如图，以点为坐标原点建立空间直角坐标系，则,，，则，，设平面的法向量则，取，得，所以，记直线与平面所成角为所以所以直线与平面所成角的正弦值为.21．【浙江省宁波市2019届高三上期末】如图所示，四面体中，是正三角形，是直角三角形，是的中点，且.（1）求证：平面；（2）过的平面交于点，若平面把四面体分成体积相等的两部分，求二面角的余弦值.【答案】（1）见证明；（2）【解析】（1）如图所示，因为为等边三角形，所以，由，得，所以，即为等腰直角三角形，从而为直角，又为底边中点，所以.令，则，易得，所以，从而，又为平面内两相交直线，所以平面.（2）由题意可知，即到平面的距离相等，所以点为的中点，以为坐标原点，为轴正方向，为轴正方向，为轴正方向，建立空间直角坐标系. 设，则，易得.设平面的法向量为，平面的法向量为，则，取；，取，设二面角的大小为，易知为锐角，则，所以二面角的余弦值为.22．【浙江省2019届高三高考全真模拟（二)】已知P ABC -为正三棱锥，底面边长为2，设D 为PB 的中点，且AD PC ⊥，如图所示.（Ⅰ）求证：PC ⊥平面PAB ；（Ⅱ）求二面角D AC B --的平面角的余弦值. 【答案】（Ⅰ）见解析；（Ⅱ）223. 【解析】（Ⅰ）以AB 中点O 为空间直角坐标系的原点，OC 为x 轴，OA 为y 轴，过O 作平面ABC 的垂线为z 轴，建立空间直角坐标系，如下图所示：(0,1,0),(0,1,0),3,0,0)A B C -，由于点P 在平面ABC 的射影为三角形ABC 的中心，设3P h ⎫⎪⎪⎝⎭，所以23,0,,(0,2,0)PC h AB ⎛⎫=-=- ⎪⎪⎝⎭， 2300(2)()00PC AB h ⋅=+⨯-+-⨯=，PC AB ∴⊥而AD PC ⊥，AB AD A ⋂=，,AB AD ⊂平面PAB ，所以PC ⊥平面PAB ；（Ⅱ）由中点坐标公式可知：31,622h D ⎛⎫- ⎪ ⎪⎝⎭，由=0AD PC ⋅可知:211032AD PC h ⋅=-=，解得23h =，设平面ACD 的法向量为(,,)a x y z =，因为336,,,(3,1,0)626AD AC ⎛⎫=-=- ⎪ ⎪⎝⎭，所以33606230ADa xy z AC a x y ⎧⋅=-+=⎪⎨⎪⋅=-=⎩，取2x =，解得(2,6,8)a =，平面ABC 的法向量为(0,0,1)b =，所求二面角的平面角为θ，则22cos 3|||72a b a b θ⋅===⋅，二面角D AC B --的平面角的余弦值为22. 23．【浙江省温州市2019届高三2月高考适应性测试】在三棱锥D -ABC 中，AD ⊥DC ，AC ⊥CB ，AB ＝2AD ＝2DC ＝2，且平面ABD ⊥平面BCD ，E 为AC 的中点．（I ）证明：AD ⊥BC ；（II ）求直线 DE 与平面ABD 所成的角的正弦值．【答案】（I ）见证明；（II ）【解析】（I ）过作，（其中与都不重合，否则，若与重合，则与矛盾，若与重合，则，与矛盾）面面面，又面（II）法一：作，则，由（1）知：面即与面所成角，且法二：由（I）知平面，，以为原点，分别以射线为轴，轴的正半轴，建立空间直角坐标系由题意知：∴，∵平面的法向量为，设与面所成角为∴24．【浙江省湖州三校2019年普通高等学校招生全国统一考试】如图，在四棱锥中，底面是边长为2的正方形，且，平面平面，二面角为.（Ⅰ）求证：平面；（Ⅱ）求与平面所成角的正弦值.【答案】（Ⅰ）见解析（2）【解析】（Ⅰ）证明：平面平面，交线为，且，∴平面，从而，，∴即为二面角的平面角，即.又，，由余弦定理得，∴，即.又，∴平面.（Ⅱ）由（Ⅰ）知，平面，从而，，又，，故.由已知，点到平面的距离等于点到平面的距离，设点到平面的距离为，则点到平面的距离也为，由得：，.∴与平面所成角的正弦值.25．【浙江省金华十校2019届高三上期末】在三棱锥中，，H为P点在平面ABC的投影，．Ⅰ证明：平面PHA；Ⅱ求AC与平面PBC所成角的正弦值．【答案】Ⅰ见解析；Ⅱ【解析】证明：Ⅰ取M为BC的中点，连结PM，AM，，，，又为P点在平面ABC的投影，，而，，又，，、A、M三点共线，从而，结合条件，平面PHA．解：Ⅱ过A作，连结CN，平面PHM，，，平面PBC，就是直线AC与平面PBC所成角，设，由，得，，由，知，，，，，，，解得，与平面PBC所成角的正弦值．26．【浙江省金丽衢十二校2019届高三第一次联考】如图，在四棱锥P－ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝，PA＝AD＝2，AB＝BC＝1，点M、E分别是PA、PD的中点(1)求证：CE//平面BMD(2)点Q为线段BP中点，求直线PA与平面CEQ所成角的余弦值.【答案】(1)见解析；（2）.【解析】（1）连接ME，因为点分别是的中点，所以，所以，所以四边形为平行四边形，所以.又因为平面，平面,所以平面.（2）如图，以为坐标原点建立空间坐标系，则又，设平面的法向量为，列方程组求得其中一个法向量为，设直线与平面所成角大小为，于是，进而求得.27．【浙江省金华十校2019届下学期高考模拟】在四棱锥S ABCD -中，底面ABCD 为直角梯形，BC CD ⊥，1SC SD CD DA ====，2CB =，//AD BC ，23SCB π∠=，E 为线段SB 上的中点．（1）证明：//AE 平面SCD ；（2）求直线AE 与平面SBC 所成角的余弦值．【答案】（1）见解析；（2）13【解析】（1）取SC 的中点F ，连接EF ，DF ．∵E ，F 是SB ，SC 的中点，∴//EF BC ，12EF BC =，又//AD BC ，12AD BC =，∴//EF AD ，EF AD =， ∴四边形ADFE 是平行四边形，∴//AE DF ，又DF ⊂平面SCD ，AE ⊄平面SCD ，∴//AE 平面SCD ．（2）取CD 的中点O ，连接SO ，过O 作BC 的平行线OM ，以O 为原点，以OD ，OM 和平面ABCD 过点O 的垂线为坐标轴建立空间坐标系O xyz -，∵1SC CD SD ===，∴32SO =，设二面角S CD A --的大小为α，则33(0,cos ,sin )22S αα，1(,1,0)2A ，1(,2,0)2B -，1(,0,0)2C -，∴133(,1cos ,sin )444E αα-+， ∴(0,2,0)CB =，133(,cos ,sin )2CS αα=，∵23SCB π∠=， ∴cos ,CB CS CB CS CB CS ⋅<>=3cos 31cos 2αα===-， ∴3cos α=-，6sin α=.∴12(0,,)2S -，132(,,)44E ， ∴312(,,)444AE =--，112(,,)222CS =-，设平面SCD 的法向量为(,,)n x y z =，则00n CB n CS ⎧⋅=⎨⋅=⎩，即20112022y x y z =⎧⎪⎨-+=⎪⎩，令2x =可得(2,0,1)n =-，∴cos ,n AE n AE n AE ⋅<>=2223332-==-⨯，设直线AE 与平面所成角为θ，则22sin cos ,3n AE θ=<>=，∴1cos 3θ=. ∴直线AE 与平面所成角的余弦值为13．28. 【浙江省2019届高考模拟卷（二)】如图，四边形中，，，，沿对角线将翻折成，使得.（1）证明：；（2）求直线与平面所成角的正弦值.【答案】（1）见证明；（2）【解析】（1）证明：取的中点，连.∵，∴．又，∴.在中，，∴．又，∴平面，又平面，∴.（2）解法1：取的中点，连结，∵，∴,又，∴．又由题意得为等边三角形，∴，∵，∴平面．作，则有平面，∴就是直线与平面所成的角．设，则，在等边中，．又在中，，故．在中，由余弦定理得，∴，∴直线与平面所成角的正弦值为．解法2：由题意可得，建立如图所示的空间直角坐标系.不妨设，则在直角三角形中，可得，作于，则有平面几何知识可得，∴．又可得，.∴,．设平面的一个法向量为，由，得，令，则得．又，设直线与平面所成的角为，则．所以直线与平面所成角的正弦值为．29.【浙江省2019届高考模拟卷（三)】在三棱锥中，平面平面，，，，.（1）证明：；（2）求直线与平面所成角的正弦值.【答案】（1）详见解析（2）【解析】（1）由题意平面平面，平面，平面平面=AC，又，，∴，∴平面，从而有，又由勾股定理得，，∴平面，即；（2）设，则，在中，，即.故，，过作于点，连接，过点作于点，连接，因为且，故平面，又因为平面，所以平面平面，进而有平面，故是与平面所成的角，在中，有，得，故，，由等面积法知，所以，故直线与平面所成角的正弦值为.30.【浙江省2019届高考模拟卷（一)】四棱锥中，平面，为的中点，为菱形，，，、分别是线段、的中点.（Ⅰ）求证：平面；（Ⅱ）求二面角的正切值.【答案】（Ⅰ）详见解析（Ⅱ）【解析】证明：（Ⅰ）延长交于点，∵而，∴，所以.平面，平面，∴平面（II）过点作于，易知面过作于，连接，则面∴，，∴即所求二面角的平面角不妨令，则，，所以.。

2020年高考江苏版高考数学专题十七空间向量与立体几何

考向二用向量求空间角例2 (2018江苏徐州铜山中学期中)如图,在三棱锥A-BOC中,AO,OB,OC
两两垂直,点D,E分别为棱BC,AC的中点,F在棱AO上,且满足OF=14 OA,
已知OA=OC=4,OB=2. (1)求异面直线AD与OC所成角的余弦值; (2)求二面角C-EF-D的正弦值.
设平面ABM的法向量为n=(x,y,z),
则
n n

AB 0,

BM 0,
得
2x x y
y 2
0, z
0.
令x=2,得y=4,z=3.所以平面ABM的一个法向量为n=(2,4,3).
又平面PAC的一个法向量为O B
=(0,1,0),所以n·O B
| a b |
面直线所成的角,则cos θ=|cos <a,b>|= | a || b | .
(2)线面角公式:设l为平面α的斜线,a为l的方向向量,n为平面α的法向量,θ
| a n |
为l与α成的角,则sin θ=|cos<a,n>|= | a || n | .
(3)面面角公式:设n1、n2分别为平面α、β的法向量,二面角为θ,则θ=<n1,n 2>或θ=π-<n1,n2>(需要根据具体情况判断相等或互补),其中cos<n1,n2>=
(1)异面直线的夹角:设l,m的夹角为θ 0
θ

2

,则cos
θ=|cos<a,b>|=
| a b |
=
| a1a2 b1b2 c1c2 |
.
| a || b |
a12 b12 c12aຫໍສະໝຸດ 2 2b22

2020高考精品系列之数学(理)专题11 空间向量与立体几何解答题(原卷版)

专题11空间向量与立体几何解答题考纲解读三年高考分析1.空间向量及其运算(1)了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示.(2)掌握空间向量的线性运算及其坐标表示.(3)掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直.2.空间向量的应用(1)理解直线的方向向量与平面的法向量.(2)能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.(3)能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).(4)能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.空间向量的计算和角度的求解是考查的重点，解题时常用到空间直角坐标系的建立、点和向量坐标的计算与应用，考查学生的数学抽象能力、数学建模能力、数学运算能力、直观想象能力，题型以选择填空题和解答题为主，中等难度.1、主要考查与点、线、面位置关系有关的命题真假判断和求解异面直线所成的角，题型主要以选择题和填空题的形式出现，解题要求有较强的空间想象能力和逻辑推理能力.2、空间向量是高考中的必考内容，涉及用向量法计算空间异面直线所成角、直线和平面所成角、二面角及空间距离等内容，考查热点是空间角的求解．题型以解答题为主，要求有较强的运算能力，广泛应用函数与方程的思想、转化与化归思想.1．【2019年天津理科17】如图，AE⊥平面ABCD，CF∥AE，AD∥BC，AD⊥AB，AB＝AD＝1，AE ＝BC＝2．（Ⅰ）求证：BF∥平面ADE；（Ⅱ）求直线CE与平面BDE所成角的正弦值；（Ⅲ）若二面角E﹣BD﹣F的余弦值为，求线段CF的长．2．【2019年新课标3理科19】图1是由矩形ADEB、Rt△ABC和菱形BFGC组成的一个平面图形，其中AB＝1，BE＝BF＝2，∠FBC＝60°．将其沿AB，BC折起使得BE与BF重合，连结DG，如图2．（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B﹣CG﹣A的大小．3．【2019年全国新课标2理科17】如图，长方体ABCD﹣A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE＝A1E，求二面角B﹣EC﹣C1的正弦值．4．【2019年新课标1理科18】如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A﹣MA1﹣N的正弦值．5．【2019年北京理科16】如图，在四棱锥P﹣ABCD中，P A⊥平面ABCD，AD⊥CD，AD∥BC，P A＝AD＝CD＝2，BC＝3．E为PD的中点，点F在PC上，且．（Ⅰ）求证：CD⊥平面P AD；（Ⅱ）求二面角F﹣AE﹣P的余弦值；（Ⅲ）设点G在PB上，且．判断直线AG是否在平面AEF内，说明理由．6．【2019年江苏16】如图，在直三棱柱ABC﹣A1B1C1中，D，E分别为BC，AC的中点，AB＝BC．求证：（1）A1B1∥平面DEC1；（2）BE⊥C1E．7．【2019年浙江19】如图，已知三棱柱ABC﹣A1B1C1，平面A1ACC1⊥平面ABC，∠ABC＝90°，∠BAC＝30°，A1A＝A1C＝AC，E，F分别是AC，A1B1的中点．（Ⅰ）证明：EF⊥BC；（Ⅱ）求直线EF与平面A1BC所成角的余弦值．8．【2018年江苏15】在平行六面体ABCD﹣A1B1C1D1中，AA1＝AB，AB1⊥B1C1．求证：（1）AB∥平面A1B1C；（2）平面ABB1A1⊥平面A1BC．9．【2018年江苏25】如图，在正三棱柱ABC﹣A1B1C1中，AB＝AA1＝2，点P，Q分别为A1B1，BC 的中点．（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面AQC1所成角的正弦值．10．【2018年新课标1理科18】如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF．（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值．11．【2018年新课标2理科20】如图，在三棱锥P﹣ABC中，AB＝BC＝2，P A＝PB＝PC＝AC＝4，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且二面角M﹣P A﹣C为30°，求PC与平面P AM所成角的正弦值．12．【2018年新课标3理科19】如图，边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直，M是上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）当三棱锥M﹣ABC体积最大时，求面MAB与面MCD所成二面角的正弦值．13．【2018年浙江19】如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC ＝120°，A1A＝4，C1C＝1，AB＝BC＝B1B＝2．（Ⅰ）证明：AB1⊥平面A1B1C1；（Ⅱ）求直线AC1与平面ABB1所成的角的正弦值．14．【2018年上海17】已知圆锥的顶点为P，底面圆心为O，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO＝4，OA、OB是底面半径，且∠AOB＝90°，M为线段AB的中点，如图．求异面直线PM与OB所成的角的大小．15．【2018年北京理科16】如图，在三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，D，E，F，G分别为AA1，AC，A1C1，BB1的中点，AB＝BC，AC＝AA1＝2．（Ⅰ）求证：AC⊥平面BEF；（Ⅱ）求二面角B﹣CD﹣C1的余弦值；（Ⅲ）证明：直线FG与平面BCD相交．16．【2018年天津理科17】如图，AD∥BC且AD＝2BC，AD⊥CD，EG∥AD且EG＝AD，CD∥FG 且CD＝2FG，DG⊥平面ABCD，DA＝DC＝DG＝2．（Ⅰ）若M为CF的中点，N为EG的中点，求证：MN∥平面CDE；（Ⅱ）求二面角E﹣BC﹣F的正弦值；（Ⅲ）若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长．17．【2017年江苏15】如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．18．【2017年江苏18】如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．19．【2017年江苏25】如图，在平行六面体ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1，∠BAD＝120°．（1）求异面直线A1B与AC1所成角的余弦值；（2）求二面角B﹣A1D﹣A的正弦值．20．【2017年新课标1理科18】如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP＝∠CDP＝90°．（1）证明：平面P AB⊥平面P AD；（2）若P A＝PD＝AB＝DC，∠APD＝90°，求二面角A﹣PB﹣C的余弦值．21．【2017年新课标2理科19】如图，四棱锥P﹣ABCD中，侧面P AD为等边三角形且垂直于底面ABCD，AB＝BC AD，∠BAD＝∠ABC＝90°，E是PD的中点．（1）证明：直线CE∥平面P AB；（2）点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．22．【2017年新课标3理科19】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD＝∠CBD，AB＝BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D ﹣AE﹣C的余弦值．23．【2017年浙江19】如图，已知四棱锥P﹣ABCD，△P AD是以AD为斜边的等腰直角三角形，BC ∥AD，CD⊥AD，PC＝AD＝2DC＝2CB，E为PD的中点．（Ⅰ）证明：CE∥平面P AB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．24．【2017年上海17】如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．25．【2017年北京理科16】如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面P AD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，P A＝PD，AB＝4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．26．【2017年天津理科17】如图，在三棱锥P﹣ABC中，P A⊥底面ABC，∠BAC＝90°．点D，E，N分别为棱P A，PC，BC的中点，M是线段AD的中点，P A＝AC＝4，AB＝2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱P A上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．1．【陕西省西北工业大学附属中学2019届高三考前模拟】如图，在多面体ABCDEF中，四边形ABCD 是菱形，3ABC π∠=，四边形ABEF 是直角梯形，2FAB π∠=，AF BE P ，22AF AB BE ===.（Ⅰ）证明：CE P 平面ADF .（Ⅱ）若平面ABCD ⊥平面ABEF ，H 为DF 的中点，求平面ACH 与平面ABEF 所成锐二面角的余弦值.2．【山东省淄博市部分学校2019届高三5月阶段性检测】已知正方形的边长为4,,E F 分别为,AD BC 的中点，以EF 为棱将正方形ABCD 折成如图所示的60o 的二面角，点M 在线段AB 上．（1）若M 为AB 的中点，且直线MF ，由,,A D E 三点所确定平面的交点为O ，试确定点O 的位置，并证明直线//OD 平面EMC ；（2）是否存在点M ，使得直线DE 与平面EMC 所成的角为60o ；若存在，求此时二面角M EC F --的余弦值，若不存在，说明理由．3．【陕西省汉中市2019届高三全真模拟】如图，四边形ABCD 为矩形，平面ABEF ⊥平面ABCD ，//EF AB ，90BAF ∠=︒，2AD =，1AB AF ==，点P 在线段DF 上.（1）求证：AF ⊥平面ABCD ；（2）若二面角D AP C --的余弦值为63，求PF 的长度. 4．【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】如图，三棱柱111ABC A B C -中，平面11ACC A ⊥平面ABC ，12AA AC CB ==，90ACB ∠=︒.（1）求证：平面11AB C ⊥平面11A B C ；（2）若1A A 与平面ABC 所成的线面角为60︒，求二面角11C AB C --的余弦值.5．【辽宁省葫芦岛市普通高中2019届高三第二次模拟】如图，在多面体ABCDEF 中，平面ADEF ⊥平面ABCD .四边形ADEF 为正方形，四边形ABCD 为梯形，且//AD BC ，ABD ∆是边长为1的等边三角形，M 为线段BD 中点，3BC =.(1)求证：AF BD ⊥；(2)求直线MF 与平面CDE 所成角的正弦值；(3)线段BD 上是否存在点N ，使得直线//CE 平面AFN ？若存在，求BNBD的值；若不存在，请说明理由.6．【山东省安丘市、诸城市、五莲县、兰山区2019届高三5月校级联合】如图所示的多面体是由一个直平行六面体被平面AEFG 所截后得到的，其中45BAE GAD ∠=∠=︒，22AB AD ==，60BAD ∠=︒.（1）求证：平面BDG ⊥平面ADG ；（2）求直线GB 与平面AEFG 所成角的正弦值.7．【内蒙古呼伦贝尔市2019届高三模拟统一考试（一)】如图，在直三棱柱111ABC A B C -中，D 、E 、F 、G 分别是BC 、11B C 、1AA 、1CC 中点.且22AB AC ==，14BC AA ==.（1）求证：BC ⊥平面ADE ；（2）求二面角1G EF B --的余弦值.8．【广东省肇庆市2019届高中毕业班第三次统一检测】如图，在三棱柱111ABC A B C -中，侧面11ABB A 是菱形，160BAA ∠=︒，E 是棱1BB 的中点，CA CB =，F 在线段AC 上，且2AF FC =.（1）证明：1//CB 面1A EF ；（2）若CA CB ⊥，面CAB ⊥面11ABB A ，求二面角1F A E A --的余弦值． 9．【山东省栖霞市2019届高三高考模拟卷】如图，在三棱锥V ABC -中，,90,2VC AB ABC AB BC ︒<∠===，侧面ACV ⊥底面ABC ，45ACV ︒∠=，D 为线段AB 上一点，且满足AD CV =.（1）若E 为AC 的中点，求证：BE CV ⊥；（2）当DV 最小时，求二面角A BC V --的余弦值.10．【河南省百校联盟2019届高三考前仿真试卷】如图，在几何体1111ACD A B C D -中，四边形1111ADD A CDD C ，为矩形，平面11ADD A ⊥平面11CDD C ，11B A ⊥平面11ADD A ，1111,2AD CD AA A B ====，E 为棱1AA 的中点.（Ⅰ）证明：11B C ⊥平面1CC E ；（Ⅱ）求直线11B C 与平面1B CE 所成角的正弦值.11．【安徽省合肥市2019届高三第三次教学质量检测】已知：在四棱锥P ABCD -中，//AD BC ，12AB BC CD AD ===，G 是PB 的中点，PAD ∆是等边三角形，平面PAD ⊥平面ABCD .（Ⅰ）求证：CD ⊥平面GAC ；（Ⅱ）求二面角P AG C --的余弦值.12．【湖北部分重点中学2020届高三年级新起点考试】如图四棱锥P ABCD -中，底面ABCD 是正方形，,PB BC PD CD ⊥⊥，且PA AB =，E 为PD 中点.（1）求证：PA ⊥平面ABCD ；（2）求二面角A BE C --的正弦值.13．【江西省鹰潭市2019届高三第一次模拟】如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，AB AD ⊥，AC CD ⊥，60ABC ∠=︒，PA AB BC ==，E 是PC 的中点．（1）求PB 和平面PAD 所成的角的大小．（2）求二面角A PD C --的正弦值．14．【山东省实验中学等四校2019届高三联合考试】如图在直角ABC ∆中，B 为直角，2AB BC =，E ，F 分别为AB ，AC 的中点，将AEF ∆沿EF 折起，使点A 到达点D 的位置，连接BD ，CD ，M 为CD 的中点．（Ⅰ）证明：MF ⊥面BCD ；（Ⅱ）若DE BE ⊥，求二面角E MF C --的余弦值．15．【广东省深圳市高级中学2019届高三适应性考试】已知四棱锥P ABCD -，底面ABCD 为菱形，PD PB =,H 为PC 上的点，过AH 的平面分别交PB ，PD 于点M ，N ，且//BD 平面AMHN ．（1）证明：MN PC ⊥；（2）当H 为PC 的中点，3PA PC AB ==，PA 与平面ABCD 所成的角为60︒，求AD 与平面AMHN 所成角的正弦值．1．已知三棱锥P ﹣ABC 中，△ABC 为等腰直角三角形，AB ＝AC ＝1，，设点E 为P A中点，点D 为AC 中点，点F 为PB 上一点，且PF ＝2FB ．（1）证明：BD ∥平面CEF ；（2）若P A ⊥AC ，求直线CE 与平面PBC 所成角的正弦值．2．如图，在矩形ABCD 中，AB ＝2，BC ＝3，点E 是边AD 上的一点，且AE ＝2ED ，点H 是BE 的中点，将△ABE 沿着BE 折起，使点A 运动到点S 处，且有SC ＝SD ．（1）证明：SH ⊥平面BCDE ．（2）求二面角C ﹣SB ﹣E 的余弦值．3．如图，在斜三棱柱ABC ﹣A 1B 1C 1中，侧面A 1ABB 1⊥底面ABC ，侧棱A 1A 与底面ABC 所成角为60°，AA 1＝AB ＝2，底面△ABC 是以∠ABC 为直角的等腰直角三角形，点G 为△ABC 的重心，点E在BC1上，且．（Ⅰ）求证：GE∥平面A1ABB1；（Ⅱ）求平面B1GE与平面ABC所成锐二面角的余弦值．4．已知：在四棱锥P﹣ABCD中，AD∥BC，，G是PB的中点，△P AD是等边三角形，平面P AD⊥平面ABCD．（Ⅰ）求证：CD⊥平面GAC；（Ⅱ）求二面角P﹣AG﹣C的余弦值．5．在三棱锥P﹣ABC中，△ABC是边长为4的等边三角形，平面P AB⊥平面ABC，，点M为棱BC的中点，点N在棱PC上且满足，已知使得异面直线MN与AC所成角的余弦值为的λ有两个不同的值λ1，λ2（λ1＜λ2）．（1）求λ1，λ2的值；（2）当λ＝λ1时，求二面角N﹣AM﹣C的余弦值．。

空间向量知识点总结及典型题

空间向量知识点总结及典型题一、空间向量知识点总结。

（一）空间向量的概念。

1. 定义。

- 在空间中，具有大小和方向的量叫做空间向量。

2. 表示方法。

- 用有向线段表示，如→AB，其中A为起点，B为终点；也可以用字母→a,→b,→c·s表示。

3. 向量的模。

- 向量的大小叫做向量的模，对于向量→AB，其模记为|→AB|；对于向量→a，其模记为|→a|。

（二）空间向量的运算。

1. 加法。

- 三角形法则：→AB+→BC=→AC；平行四边形法则：对于不共线的向量→a 和→b，以→a和→b为邻边作平行四边形，则这两个向量之和为平行四边形的对角线所对应的向量。

- 运算律：→a+→b=→b+→a（交换律）；(→a+→b)+→c=→a+(→b+→c)（结合律）。

2. 减法。

- →a-→b=→a+(-→b)，其中-→b是→b的相反向量。

3. 数乘向量。

- 实数λ与向量→a的乘积λ→a仍是一个向量。

- 当λ> 0时，λ→a与→a方向相同；当λ<0时，λ→a与→a方向相反；当λ = 0时，λ→a=→0。

- 运算律：λ(μ→a)=(λμ)→a；(λ+μ)→a=λ→a+μ→a；λ(→a+→b)=λ→a+λ→b。

（三）空间向量的坐标表示。

1. 坐标定义。

- 在空间直角坐标系O - xyz中，设→i,→j,→k分别是x,y,z轴正方向上的单位向量。

对于空间向量→a，若→a=x→i+y→j+z→k，则(x,y,z)叫做向量→a的坐标，记为→a=(x,y,z)。

2. 坐标运算。

- 设→a=(x_1,y_1,z_1)，→b=(x_2,y_2,z_2)，则→a+→b=(x_1+x_2,y_1+y_2,z_1+z_2)；→a-→b=(x_1-x_2,y_1-y_2,z_1-z_2)；λ→a=(λx_1,λ y_1,λ z_1)。

- 向量的模|→a|=√(x^2)+y^{2+z^2}。

- 设A(x_1,y_1,z_1)，B(x_2,y_2,z_2)，则→AB=(x_2-x_1,y_2-y_1,z_2-z_1)。

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》分类汇编附答案

新数学《空间向量与立体几何》高考知识点一、选择题1．如图，在正方体1111ABCD A B C D -中，M ， N 分别为棱111,C D CC 的中点，以下四个结论：①直线DM 与1CC 是相交直线；②直线AM 与NB 是平行直线；③直线BN 与1MB 是异面直线；④直线AM 与1DD 是异面直线．其中正确的个数为（）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据正方体的几何特征，可通过判断每个选项中的两条直线字母表示的点是否共面；如果共面，则可能是相交或者平行；若不共面，则是异面.【详解】①：1CC 与DM 是共面的，且不平行，所以必定相交，故正确；②：若AM BN 、平行，又AD BC 、平行且,AM AD A BN BC B ⋂=⋂=，所以平面BNC P 平面ADM ，明显不正确，故错误；③：1BN MB 、不共面，所以是异面直线，故正确；④：1AM DD 、不共面，所以是异面直线，故正确；故选C.【点睛】异面直线的判断方法：一条直线上两点与另外一条直线上两点不共面，那么两条直线异面；反之则为共面直线，可能是平行也可能是相交.2．某四面体的三视图如图所示，正视图，俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为（）A．22B．23C．4 D．26【答案】B【解析】解：如图所示，该几何体是棱长为2的正方体中的三棱锥P ABC-，其中面积最大的面为：1232232PACSV=⨯⨯= .本题选择B选项.点睛：三视图的长度特征：“长对正、宽相等，高平齐”，即正视图和侧视图一样高、正视图和俯视图一样长，侧视图和俯视图一样宽．若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法．3．在正四面体A BCD-中，P是AB的中点，Q是直线BD上的动点，则直线PQ与AC所成角可能为（）A ．12πB ．4πC ．512πD ．2π 【答案】C【解析】【分析】根据题意，取BC 的中点M ，连接MQ ，则//AC MQ ，所以QPM ∠为异面直线PQ 与AC 所成角，在利用余弦定理可得242MQ x x =+-，易知PQ MQ =，所以在等腰三角形PMQ 中()2cos 0442QPM x x x ∠=≤≤+-，，即可求出33cos 123QPM ⎡⎤∠∈⎢⎥⎣⎦，，进而求出结果. 【详解】取BC 的中点M ，连接MQ ，则//AC MQ ，所以QPM ∠为异面直线PQ 与AC 所成角，如下图所示：设正四面体A BCD -的棱长为4，()04BQ x x =≤≤，，在BMQ ∆中，22222cos 6042MQ BM BQ BM BQ x x =+-⋅︒=+-，在正四面体A BCD -中，易知PQ MQ =，所以在等腰三角形PMQ 中，()2cos 0442QPM x x x ∠=≤≤+-所以33cos QPM ∠∈⎣⎦，，所以异面直线PQ 与AC 所成角可能为512π. 故选：C.【点睛】本题主要考查了异面直线成角，余弦定理的应用，考查了空间几何中的动态问题，考查学生的应用能力和空间想象能力，属于中档题.4．已知底面是等腰直角三角形的三棱锥P -ABC 的三视图如图所示，俯视图中的两个小三角形全等，则（）A ．PA ，PB ，PC 两两垂直B ．三棱锥P -ABC 的体积为83 C ．||||||6PA PB PC ===D ．三棱锥P -ABC 的侧面积为35【答案】C 【解析】【分析】根据三视图，可得三棱锥P -ABC 的直观图，然后再计算可得.【详解】解：根据三视图，可得三棱锥P -ABC 的直观图如图所示，其中D 为AB 的中点，PD ⊥底面ABC .所以三棱锥P -ABC 的体积为114222323⨯⨯⨯⨯=， 2AC BC PD ∴===，2222AB AC BC ∴=+=，||||||2DA DB DC ∴===()22||||||226,PA PB PC ∴===+=222PA PB AB +≠Q ，PA ∴、PB 不可能垂直，即,PA ,PB PC 不可能两两垂直， 1222222PBA S ∆=⨯=Q ()22161252PBC PAC S S ∆∆==-=Q ∴三棱锥P -ABC 的侧面积为2522故正确的为C.故选：C.【点睛】本题考查三视图还原直观图，以及三棱锥的表面积、体积的计算问题，属于中档题.5．如图所示是一个组合几何体的三视图，则该几何体的体积为（）A ．163πB ．643C ．16643π+ D ．1664π+ 【答案】C 【解析】由三视图可知，该几何体是有一个四棱锥与一个圆锥的四分之一组成，其中四棱锥的底面是边长为4 的正方形，高为4 ，圆锥的底面半径为4 ，高为4，该几何体的体积为， 221116644444333V ππ+=⨯⨯+⨯⨯⨯=，故选C. 6．鲁班锁（也称孔明锁、难人木、六子联方）起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合，十分巧妙.鲁班锁类玩具比较多，形状和内部的构造各不相同，一般都是易拆难装.如图1，这是一种常见的鲁班锁玩具，图2是该鲁班锁玩具的直观图，每条棱的长均为2，则该鲁班锁的表面积为（）A ．8(6623)+B ．6(8823)+C ．8(632)+D ．6(8832)+【答案】A【解析】【分析】该鲁班锁玩具可以看成是一个正方体截去了8个正三棱锥所余下来的几何体，然后按照表面积公式计算即可.【详解】由题图可知，该鲁班锁玩具可以看成是一个棱长为222+的正方体截去了8个正三棱锥所余下来的几何体，且被截去的正三棱锥的底面边长为22，则该几何体的2116(222)42282322S ⎡⎤=⨯+-⨯⨯⨯+⨯⨯⨯⎢⎥⎣⎦8(6623)=++. 故选：A.【点睛】本题考查数学文化与简单几何体的表面积，考查空间想象能力和运算求解能力.7．已知,m l 是两条不同的直线，,αβ是两个不同的平面，则下列可以推出αβ⊥的是（）A ．,,m l m l βα⊥⊂⊥B ．,,m l l m αβα⊥⋂=⊂C ．//,,m l m l αβ⊥⊥D ．,//,//l m l m αβ⊥【答案】D【解析】【分析】A ，有可能出现α，β平行这种情况.B ，会出现平面α，β相交但不垂直的情况.C ，根据面面平行的性质定理判断.D ，根据面面垂直的判定定理判断.【详解】对于A ，m l ⊥，m β⊂，若l β⊥，则//αβ，故A 错误；对于B ，会出现平面α，β相交但不垂直的情况，故B 错误；对于C ，因为//m l ，m α⊥，则l α⊥，又因为l βαβ⊥⇒∥，故C 错误；对于D ，l α⊥，m l m α⇒⊥∥，又由m βαβ⇒⊥∥，故D 正确.故选：D【点睛】本题考查空间中的平行、垂直关系的判定，还考查学生的空间想象能力和逻辑推理能力，属于中档题.8．如图，正方形网格纸中的实线图形是一个多面体的三视图，则该多面体各表面所在平面互相垂直的有（）A ．2对B ．3对C ．4对D ．5对【答案】C【分析】画出该几何体的直观图P ABCD -，易证平面PAD ⊥平面ABCD ，平面PCD ⊥平面PAD ，平面PAB ⊥平面PAD ，平面PAB ⊥平面PCD ，从而可选出答案．【详解】该几何体是一个四棱锥，直观图如下图所示，易知平面PAD ⊥平面ABCD ，作PO ⊥AD 于O ，则有PO ⊥平面ABCD ，PO ⊥CD ，又AD ⊥CD ，所以，CD ⊥平面PAD ，所以平面PCD ⊥平面PAD ，同理可证：平面PAB ⊥平面PAD ，由三视图可知：PO ＝AO ＝OD ，所以，AP ⊥PD ，又AP ⊥CD ，所以，AP ⊥平面PCD ，所以，平面PAB ⊥平面PCD ，所以该多面体各表面所在平面互相垂直的有4对．【点睛】本题考查了空间几何体的三视图，考查了四棱锥的结构特征，考查了面面垂直的证明，属于中档题．9．在四面体ABCD 中，AB ，BC ，BD 两两垂直，4AB BC BD ===，E 、F 分别为棱BC 、AD 的中点，则直线EF 与平面ACD 所成角的余弦值（）A ．13B ．33C ．23D ．63【答案】C【解析】【分析】因为AB ，BC ，BD 两两垂直，以BA 为X 轴，以BD 为Y 轴，以BC 为Z 轴建立空间直角坐标系，求出向量EF u u u r 与平面ACD 的法向量n r ，再根据cos ,||||EF n EF n EF n ⋅〈〉=u u u r r u u u r r u u u r r ，即可得出答案.【详解】因为在四面体ABCD 中，AB ，BC ，BD 两两垂直，以BA 为X 轴，以BD 为Y 轴，以BC 为Z 轴建立空间直角坐标系，又因为4AB BC BD ===；()4,0,0,(0,0,0),(0,4,0),(0,0,4)A B D C ，又因为E 、F 分别为棱BC 、AD 的中点所以(0,0,2),(2,2,0)E F 故()2,2,2EF =-u u u r ，(4,4,0)AD =-u u u r ，(4,0,4)AC =-u u u r .设平面ACD 的法向量为(,,)n x y z =r ，则00n AD n AC ⎧⋅=⎨⋅=⎩u u u v v u u uv v 令1,x = 则1y z ==；所以(1,1,1)n =r 1cos ,3||||332EF n EF n EF n ⋅〈〉===⨯u u u r r u u u r r u u u r r 设直线EF 与平面ACD 所成角为θ ，则sin θ= cos ,EF n 〈〉u u u r r 所以222cos 1sin θθ=-=故选：C【点睛】本题主要考查线面角，通过向量法即可求出，属于中档题目.10．在以下命题中： ①三个非零向量a r ，b r ，c r 不能构成空间的一个基底，则a r ，b r ，c r 共面； ②若两个非零向量a r ，b r 与任何一个向量都不能构成空间的一个基底，则a r ，b r 共线； ③对空间任意一点O 和不共线的三点A ，B ，C ，若222OP OA OB OC =--u u u r u u u r u u u u r u u u u r ，则P ，A ，B ，C 四点共面 ④若a r ，b r 是两个不共线的向量，且(,,,0)c a b R λμλμλμ=+∈≠r r r ，则{},,a b c r r r 构成空间的一个基底 ⑤若{},,a b c r r r 为空间的一个基底，则{},,a b b c c a +++r r r r r r 构成空间的另一个基底；其中真命题的个数是（）A ．0B ．1C ．2D ．3【答案】D【解析】【分析】根据空间向量的运算法则，逐一判断即可得到结论.【详解】①由空间基底的定义知，三个非零向量a r ，b r ，c r 不能构成空间的一个基底，则a r ，b r ，c r 共面，故①正确；②由空间基底的定义知，若两个非零向量a r ，b r与任何一个向量都不能构成空间的一个基底，则a r ，b r 共线，故②正确；③由22221--=-≠，根据共面向量定理知,,,P A B C 四点不共面，故③错误； ④由c a b λμ=+r r r ，当1λμ+=时，向量c r 与向量a r ，b r 构成的平面共面，则{},,a b c r r r 不能构成空间的一个基底，故④错误； ⑤利用反证法：若{},,a b b c c a +++r r r r r r 不构成空间的一个基底，设()()()1a b x b c x c a +=++-+r r r r r r ，整理得()1c xa x b =+-r r r ，即,,a b c r r r 共面，又因{},,a b c r r r 为空间的一个基底，所以{},,a b b c c a +++r r r r r r 能构成空间的一个基底，故⑤正确. 综上：①②⑤正确.故选：D.【点睛】本题考查空间向量基本运算，向量共面，向量共线等基础知识，以及空间基底的定义，共面向量的定义，属于基础题．11．如图，在直三棱柱111ABC A B C -中，4AC BC ==，AC BC ⊥，15CC =，D 、E 分别是AB 、11B C 的中点，则异面直线BE 与CD 所成的角的余弦值为（）A ．3B ．13C ．58D ．387 【答案】C【解析】【分析】取11A C 的中点F ，连接DF 、EF 、CF ，推导出四边形BDFE 为平行四边形，可得出//BE DF ，可得出异面直线BE 与CD 所成的角为CDF ∠，通过解CDF V ，利用余弦定理可求得异面直线BE 与CD 所成的角的余弦值.【详解】取11A C 的中点F ，连接DF 、EF 、CF .易知EF 是111A B C △的中位线，所以11//EF A B 且1112EF A B =. 又11//AB A B 且11AB A B =，D 为AB 的中点，所以11//BD A B 且1112BD A B =，所以//EF BD 且EF BD =.所以四边形BDFE 是平行四边形，所以//DF BE ，所以CDF ∠就是异面直线BE 与CD 所成的角.因为4AC BC ==，AC BC ⊥，15CC =，D 、E 、F 分别是AB 、11B C 、11A C 的中点，所以111122C F AC ==，111122B E BC ==且CD AB ⊥.由勾股定理得AB ==AC BC CD AB ⋅===由勾股定理得CF ===DF BE ====.在CDF V 中，由余弦定理得222cosCDF +-∠==. 故选：C.【点睛】本题考查异面直线所成角的余弦值的计算，一般利用平移直线法找出异面直线所成的角，考查计算能力，属于中等题.12．在棱长为1的正方体1111ABCD A B C D -中,点12,P P 分别是线段1,AB BD （不包括端点）上的动点,且线段12PP 平行于平面11AADD ,则四面体121PP AB 的体积的最大值是 A ．124 B ．112 C ．16 D ．12【答案】A【解析】由题意在棱长为1的正方体1111ABCD A B C D -中，点12,P P 分别是线段1,AB BD 上的动点，且线段12PP 平行于平面11121,AADD PP B AD B ∆~∆，设1,(0,1)PB x x =∈，即122,PP P =到平面11AA B B 的距离为x ，所以四棱锥121PP AB 的体积为2111(1)1()326V x x x x =⨯⨯-⨯⨯=-，当12x=时，体积取得最大值124，故选A．点睛：本题考查了空间几何体的结构特征，及几何体的体积的计算，其中解答中找出所求四面体的底面面积和四面体的高是解答的关键，着重考查了分析问题和解答问题的能力，对于空间几何体的体积与表面积的计算时，要正确把握几何体的结构特征和线面位置关系在解答中的应用．13．一个几何体的三视图如图所示，则该几何体的体积为A．383+B．823+C．283D．10【答案】A【解析】【分析】根据三视图可知该几何体为一组合体，是一个棱长为2的正方体与三棱锥的组合体，根据体积公式分别计算即可.【详解】几何体为正方体与三棱锥的组合体，由正视图、俯视图可得该几何体的体积为311232+2328323V=⨯⨯=+,故选A.【点睛】本题主要考查了三视图，正方体与三棱锥的体积公式，属于中档题.14．已知正方体1111ABCD A B C D -中，M ，N 分别为AB ，1AA 的中点，则异面直线1C M 与BN 所成角的大小为（）A ．30°B ．45︒C ．60︒D ．90︒【答案】D【解析】【分析】根据题意画出图形，可将异面直线转化共面的相交直线，再进行求解【详解】如图：作AN 的中点'N ，连接'N M ，1'C N 由题设可知'N M BN P ，则异面直线1C M 与BN 所成角为1'N MC ∠或其补角，设正方体的边长为4，由几何关系可得，'5N M =，16C M =，1'41C N =21122''N M M C N C =+，即1'90N MC ∠=︒ 故选D【点睛】本题考查异面直线的求法，属于基础题15．已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为A ．122πB ．12πC ．82πD ．10π【答案】B【解析】分析：首先根据正方形的面积求得正方形的边长，从而进一步确定圆柱的底面圆半径与圆柱的高，从而利用相关公式求得圆柱的表面积. 详解：根据题意，可得截面是边长为2 2的圆，且高为2，所以其表面积为222)22212S πππ=+=，故选B.点睛：该题考查的是有关圆柱的表面积的求解问题，在解题的过程中，需要利用题的条件确定圆柱的相关量，即圆柱的底面圆的半径以及圆柱的高，在求圆柱的表面积的时候，一定要注意是两个底面圆与侧面积的和.16．已知直线和不同的平面，下列命题中正确的是A ．//m m αβαβ⊥⎫⇒⎬⊥⎭B ．m m αββα⊥⎫⇒⊥⎬⊂⎭C ．//////m m ααββ⎫⇒⎬⎭D ．////m m αββα⎫⇒⎬⊂⎭【答案】D【解析】【分析】对各个选项逐一进行分析即可【详解】 A ，若αβ⊥，m β⊥，则有可能m α⊂，故A 错误B ，若αβ⊥，m α⊂，则m 与β不一定垂直，可能相交或平行，故B 错误C ，若//m α，//m β则推不出//αβ，面面平行需要在一个面内找出两条相交线与另一个平面平行，故C 错误D ，若//αβ，m α⊂，则有//m β，故D 正确故选D【点睛】本题考查了线面平行与面面平行的判断和性质，在对其判定时需要运用其平行的判定定理或者性质定理，所以要对课本知识掌握牢固，从而判断结果17．已知某几何体的三视图如图所示，其中正视图与侧视图是全等的直角三角形，则该几何体的各个面中，最大面的面积为（）A ．2B ．5C 13D 22【答案】D【解析】【分析】根据三视图还原出几何体，找到最大面，再求面积.【详解】由三视图可知，该几何体是一个三棱锥，如图所示，将其放在一个长方体中，并记为三棱锥P ABC -.13PAC PAB S S ∆∆==，22PAC S ∆=，2ABC S ∆=，故最大面的面积为22.选D.【点睛】本题主要考查三视图的识别，复杂的三视图还原为几何体时，一般借助长方体来实现.18．如图1，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，M ，N ，Q 分别是线段AD 1，B 1C ，C 1D 1上的动点，当三棱锥Q-BMN 的正视图如图2所示时，三棱锥俯视图的面积为A ．2B ．1C ．32D ．52【答案】C【解析】【分析】判断俯视图的形状，利用三视图数据求解俯视图的面积即可．【详解】由正视图可知：M 是1AD 的中点，N 在1B 处，Q 在11C D 的中点，俯视图如图所示：可得其面积为：1113222111122222⨯-⨯⨯-⨯⨯-⨯⨯=，故选C ．【点睛】本题主要考查三视图求解几何体的面积与体积，判断它的形状是解题的关键，属于中档题.19．设,αβ是两个不同的平面，,l m 是两条不同的直线，且l α⊂，m β⊂，则（） A ．若//αβ，则//l mB ．若//m a ，则//αβC ．若m α⊥，则αβ⊥D ．若αβ⊥，则//l m【答案】C【解析】【分析】根据空间线线、线面、面面的位置关系，对选项进行逐一判断可得答案.【详解】A. 若//αβ，则l 与m 可能平行，可能异面，所以A 不正确.B. 若//m a ，则α与β可能平行，可能相交，所以B 不正确.C. 若m α⊥，由m β⊂，根据面面垂直的判定定理可得αβ⊥，所以C 正确. D 若αβ⊥，且l α⊂，m β⊂，则l 与m 可能平行，可能异面，可能相交, 所以D 不正确.【点睛】本题考查空间线线、线面、面面的位置判断定理和性质定理，考查空间想象能力，属于基础题.20．一个各面均为直角三角形的四面体有三条棱长为2，则该四面体外接球的表面积为（）A ．6πB ．12πC ．32πD ．48π【答案】B【解析】【分析】先作出几何图形，确定四个直角和边长，再找到外接球的球心和半径，再计算外接球的表面积.【详解】由题得几何体原图如图所示，其中SA⊥平面ABC,BC⊥平面SAB,SA=AB=BC=2,所以2,3SC=设SC中点为O,则在直角三角形SAC中，3,在直角三角形SBC中，OB=13 2SC=所以3所以点O3所以四面体外接球的表面积为43=12ππ.故选：B【点睛】本题主要考查四面体的外接球的表面积的计算，意在考查学生对这些知识的理解掌握水平和分析推理的能力.。

2018-2020年近三年高考数学真题解答题汇编：专题4.4 空间向量与立体几何(学生版+解析版)

专题4.4 空间向量与立体几何1．如图，四棱锥P ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD AD 1，Q 为l 上的点，QB 2PB 与平面QCD 所成角的正弦值．2．如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥．（1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值．3．如图，//AD BC 且AD =2BC ，AD CD ⊥，//EG AD 且EG =AD ，//CD FG 且CD =2FG ，DG ABCD ⊥平面，DA =DC =DG =2．（1）若M 为CF 的中点，N 为EG 的中点，求证：MN CDE 平面；（2）求二面角E BC F --的正弦值；（3）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长．4．如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30，求PC 与平面PAM 所成角的正弦值．5．如图，已知多面体ABC-A1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（1）证明：AB1⊥平面A1B1C1；（2）求直线AC1与平面ABB1所成的角的正弦值．6．如图，边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直，M是CD上异于C，D的点．（1）证明：平面AMD⊥平面BMC；-体积最大时，求面MAB与面MCD所成二面角的正弦值．（2）当三棱锥M ABC7．如图，在三棱柱ABC −111A B C 中，1CC 平面ABC ，D ，E ，F ，G 分别为1AA ，AC ，11A C ，1BB 的中点，AB=BC AC =1AA =2．（1）求证：AC ⊥平面BEF ；（2）求二面角B−CD −C 1的余弦值；（3）证明：直线FG 与平面BCD 相交．8．如图，在正三棱柱ABC -A 1B 1C 1中，AB =AA 1=2，点P ，Q 分别为A 1B 1，BC 的中点．（1）求异面直线BP 与AC 1所成角的余弦值；（2）求直线CC 1与平面AQC 1所成角的正弦值．9．已知圆锥的顶点为P ，底面圆心为O ，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设4PO =，OA 、OB 是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，如图．求异面直线PM 与OB 所成的角的大小． 10．如图，AE ⊥平面ABCD，,CF AE AD BC∥∥，,1,2AD AB AB AD AE BC ⊥====．（1）求证：BF ∥平面ADE ；（2）求直线CE 与平面BDE 所成角的正弦值；（3）若二面角E BD F --的余弦值为13，求线段CF 的长．11．图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2．（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B−CG−A的大小．=．ABC 12．如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AE AD是底面的内接正三角形，P为DO上一点，PO DO=．（1）证明：PA⊥平面PBC；--的余弦值．（2）求二面角B PC E13．在三棱锥A—BCD中，已知CB=CD BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC的中点．（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF=14BC，设二面角F—DE—C的大小为θ，求sinθ的值．14．如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面P AD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．15．如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．（1）求证：1//BC 平面1AD E ；（2）求直线1AA 与平面1AD E 所成角的正弦值．16．如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且12,AD CE M ==为棱11A B 的中点．（1）求证：11C M B D ⊥；（2）求二面角1B B E D --的正弦值；（3）求直线AB 与平面1DB E 所成角的正弦值．专题4.4 空间向量与立体几何1．如图，四棱锥P ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD AD1，Q 为l 上的点，QB 2PB 与平面QCD 所成角的正弦值．【试题来源】2020年新高考全国卷Ⅱ（海南卷）【答案】（1）证明见解析；（26．【分析】（1）利用线面平行的判定定理以及性质定理，证得//AD l ，利用线面垂直的判定定理证得AD ⊥平面PDC ，从而得到l ⊥平面PDC ；（2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Q m ，之后求得平面QCD 的法向量以及向量PB 的坐标，求得cos ,n PB <>，即可得到直线PB 与平面QCD 所成角的正弦值．【解析】（1）在正方形ABCD 中，//AD BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以//AD 平面PBC ，因为AD ⊂平面PAD ，平面PAD平面PBC l =，所以//AD l ，因为在四棱锥P ABCD -中，底面ABCD 是正方形，所以,,AD DC l DC ⊥∴⊥ 且PD ⊥平面ABCD ，所以,,AD PD l PD ⊥∴⊥ 因为CDPD D =，所以l ⊥平面PDC ；（2）如图建立空间直角坐标系D xyz -，因为1PD AD ==，则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ，设(,0,1)Q m ，则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-，因为QB 1m =⇒=设平面QCD 的法向量为(,,)n x y z =，则00DC n DQ n ⎧⋅=⎨⋅=⎩，即00y x z =⎧⎨+=⎩，令1x =，则1z =-，所以平面QCD 的一个法向量为(1,0,1)n =-，则21cos ,31n PB n PB n PB⋅+<>==== 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于6|cos ,|n PB <>=所以直线PB 与平面QCD 2．如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥．（1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值．【试题来源】2018年全国普通高等学校招生统一考试（理）（新课标I 卷）【答案】（1）证明见解析；（2）4．【分析】（1）首先从题的条件中确定相应的垂直关系，即BF PF ⊥，BF EF ⊥，因为PF EF F =，利用线面垂直的判定定理可以得出BF ⊥平面PEF ，又BF ⊂平面ABFD ，利用面面垂直的判定定理证得平面PEF ⊥平面ABFD ；（2）结合题意，建立相应的空间直角坐标系，正确写出相应的点的坐标，求得平面ABFD 的法向量，设DP 与平面ABFD 所成角为θ，利用线面角的定义，可以求得34sin 43HP DP HP DPθ⋅===⋅，得到结果．【解析】（1）由已知可得，BE PF ⊥，BE EF ⊥，又PFEF F =，所以BF ⊥平面PEF ．又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD ；（2）作PH EF ⊥，垂足为H ．由（1）得，PH ⊥平面ABFD ．以H 为坐标原点，HF 的方向为y 轴正方向，BF 为单位长，建立如图所示的空间直角坐标系H xyz -．由（1）可得，DE PE ⊥．又2DP =，1DE =，所以PE =又1PF =，2EF =，故PE PF ⊥．可得322PH EH ==．则()330,0,0,,1,,0,1,,22H P D DP ⎛⎛⎛⎫--= ⎪ ⎝⎭⎝⎭⎝⎭ HP ⎛= ⎝⎭为平面ABFD 的法向量．设DP 与平面ABFD 所成角为θ，则34sin 43HP DP HP DPθ⋅===⋅．所以DP 与平面ABFD ．【名师点睛】该题考查的是有关立体几何的问题，涉及到的知识点有面面垂直的证明以及线面角的正弦值的求解，属于常规题目，在解题的过程中，需要明确面面垂直的判定定理的条件，这里需要先证明线面垂直，所以要明确线线垂直、线面垂直和面面垂直的关系，从而证得结果；对于线面角的正弦值可以借助于平面的法向量来完成，注意相对应的等量关系即可．3．如图，//AD BC 且AD =2BC ，AD CD ⊥，//EG AD 且EG =AD ，//CD FG 且CD =2FG ，DG ABCD ⊥平面，DA =DC =DG =2．（1）若M 为CF 的中点，N 为EG 的中点，求证：MN CDE 平面；（2）求二面角E BC F --的正弦值；（3）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长．【试题来源】2018年全国普通高等学校招生统一考试（理）（天津卷）【答案】（1）证明见解析；（2(Ⅱ)3．【分析】依题意，可以建立以D 为原点，分别以DA ，DC ，DG 的方向为x 轴，y 轴，z 轴的正方向的空间直角坐标系．（1）由题意可得平面CDE 的一个法向量n 0=（1，0，–1）．又MN =（1，32-，1），故00MN n ⋅=，MN ∥平面CDE ．（2）依题意可得平面BCE 的一个法向量n =（0，1，1）．平面BCF 的一个法向量为m =（0，2，1）．据此计算可得二面角E –BC –F．（3）设线段DP 的长为h （h ∈［0，2］），则点P 的坐标为（0，0，h ），结合空间向量的结论计算可得线段DP的长为3．【解析】依题意，可以建立以D 为原点，分别以DA ，DC ，DG 的方向为x 轴，y 轴，z 轴的正方向的空间直角坐标系（如图），可得D （0，0，0），A （2，0，0），B （1，2，0），C （0，2，0），E （2，0，2），F （0，1，2），G （0，0，2），M （0，32，1），N （1，0，2）．（1）依题意DC =（0，2，0），DE =（2，0，2）．设n 0=(x ，y ，z )为平面CDE 的法向量，则0000DC DE ⎧⋅=⎪⎨⋅=⎪⎩，，n n 即20220y x z ，，=⎧⎨+=⎩ 不妨令z =–1，可得n 0=（1，0，–1）．又MN =（1，32-，1），可得00MN n ⋅=，因为直线MN ⊄平面CDE ，所以MN ∥平面CDE ．（2）依题意，可得BC =（–1，0，0），()122BE =-，，，CF =（0，–1，2）．设n =（x ，y ，z ）为平面BCE 的法向量，则00n BC n BE ，，⎧⋅=⎨⋅=⎩ 即0220x x y z -=⎧⎨-+=⎩，，不妨令z =1，可得n =（0，1，1）．设m =（x ，y ，z ）为平面BCF 的法向量，则00m BC m CF ⎧⋅=⎨⋅=⎩，，即020x y z -=⎧⎨-+=⎩，，不妨令z =1，可得m =（0，2，1）．因此有cos <m ，n>=10⋅=m n m n ，于是sin <m ，n．所以，二面角E –BC –F的正弦值为10．（3）设线段DP 的长为h （h ∈［0，2］），则点P 的坐标为（0，0，h ），可得()12BP h =--，，．易知，DC =（0，2，0）为平面ADGE 的一个法向量，故BP DCcos BP DC BP DC h ⋅⋅==，25h +=sin 60°=32，解得h=3∈［0，2］．所以线段DP【名师点睛】本题主要考查空间向量的应用，线面平行的证明，二面角问题等知识，意在考查学生的转化能力和计算求解能力．4．如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角MPA C --为30，求PC 与平面PAM 所成角的正弦值．【试题来源】2018年全国普通高等学校招生统一考试（理）（新课标II 卷）【答案】（1）证明见解析；（2 【分析】（1）根据等腰三角形性质得PO 垂直AC ，再通过计算，根据勾股定理得PO 垂直OB ，最后根据线面垂直判定定理得结论；（2）根据条件建立空间直角坐标系，设立各点坐标，根据方程组解出平面P AM 一个法向量，利用向量数量积求出两个法向量夹角，根据二面角与法向量夹角相等或互补关系列方程，解得M 坐标，再利用向量数量积求得向量PC 与平面P AM 法向量夹角，最后根据线面角与向量夹角互余得结果．【解析】（1）因为4AP CP AC ===，O 为AC 的中点，所以OP AC ⊥，且OP =连结OB ．因为2AB BC AC ==，所以ABC 为等腰直角三角形，且1,22OB AC OB AC ⊥== 由222OP OB PB +=知PO OB ⊥．由,OP OB OP AC ⊥⊥知PO ⊥平面ABC ．（2）如图，以O 为坐标原点，OB 的方向为x 轴正方向，建立空间直角坐标系O xyz - ．由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,(0,2,O B A C P AP -= 取平面PAC 的法向量(2,0,0)OB =．设(,2,0)(02)M a a a -<≤，则(,4,0)AM a a =-．设平面PAM 的法向量为(,,)n x y z =．由0,0AP n AM n ⋅=⋅=得20(4)0y ax a y ⎧+=⎪⎨+-=⎪⎩ ，可取2(3(,)n a a =--所以cos 23(OB n a 〈⋅〉=．由已知得3cos 2OB n 〈⋅〉= ．= ．解得4a =-(舍去)，43a = ．所以834333n ⎛⎫=-- ⎪ ⎪⎝⎭．又(0,2,PC =- ，所以3cos ,4PC n 〈〉= ．所以PC 与平面PAM 【名师点睛】利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”．5．如图，已知多面体ABC -A 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC=120°，A 1A=4，C 1C=1，AB=BC=B 1B=2．（1）证明：AB 1⊥平面A 1B 1C 1；（2）求直线AC 1与平面ABB 1所成的角的正弦值．【试题来源】2018年全国普通高等学校招生统一考试数学（浙江卷）【答案】（1）证明见解析；（2．【分析】【分析】方法一：（1）通过计算，根据勾股定理得111111,AB A B AB B C ⊥⊥，再根据线面垂直的判定定理得结论；（2）找出直线AC 1与平面ABB 1所成的角，再在直角三角形中求解．方法二：（1）根据条件建立空间直角坐标系，写出各点的坐标，根据向量之积为0得出111111,AB A B AB A C ⊥⊥，再根据线面垂直的判定定理得结论；（2）根据方程组解出平面1ABB 的一个法向量，然后利用1AC 与平面1ABB 法向量的夹角的余弦公式及线面角与向量夹角的互余关系求解．【解析】方法一：（1）由11112,4,2,,AB AA BB AA AB BB AB ===⊥⊥得111AB A B ==，所以2221111A B AB AA +=．故111AB A B ⊥．由2BC =，112,1,BB CC == 11,BB BC CC BC ⊥⊥得11B C =，由2,120AB BC ABC ==∠=︒得AC =由1CC AC ⊥，得1AC 2221111AB B C AC +=，故111AB B C ⊥．因此1AB ⊥平面111A B C ．（2）如图，过点1C 作111C D A B ⊥，交直线11A B 于点D ，连结AD ．由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ，由111C D A B ⊥得1C D ⊥平面1ABB ，所以1C AD ∠是1AC 与平面1ABB 所成的角．由111111BC A B AC ==111111cos C A B C A B ∠=∠=，所以1C D =，故111sin C D C AD AC ∠== 因此，直线1AC 与平面1ABB．方法二：（1）如图，以AC 的中点O 为原点，分别以射线OB ，OC 为x ，y 轴的正半轴，建立空间直角坐标系O -xyz ．由题意知各点坐标如下：()()()()()1110,,1,0,0,0,,1,0,2,,A B A B C 因此()()()111111,3,2,1,3,2,0,23,AB A B AC ==-=-由1110AB A B ⋅=得111AB A B ⊥．由1110AB AC ⋅=得111AB AC ⊥．所以1AB ⊥平面111A B C ．（2）设直线1AC 与平面1ABB 所成的角为θ．由（1）可知()()()110,23,1,1,3,0,0,0,2,AC AB BB ===设平面1ABB 的法向量(),,n x y z =．由10,0,n AB n BB ⎧⋅=⎪⎨⋅=⎪⎩即30,20,x y z ⎧+=⎪⎨=⎪⎩可取()3,1,0n =-．所以11139sin |cos ,|13AC nAC n AC n θ⋅===⋅．因此，直线1AC 与平面1ABB 所成的角的正弦值是．【名师点睛】利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”．6．如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．【试题来源】2018年全国普通高等学校招生统一考试（理）（新课标III 卷）【答案】（1）见解析；（2. 【分析】（1）先证BC ⊥平面CMD ，得BC CM ⊥，再证CM MD ⊥，进而完成证明．（2）先建立空间直角坐标系，然后判断出M 的位置，求出平面MAB 和平面MCD 的法向量，进而求得平面MAB 与平面MCD 所成二面角的正弦值．【解析】（1）由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为CD 上异于C ，D 的点，且DC 为直径，所以 DM ⊥CM ．又 BC CM =C ，所以DM ⊥平面BMC ．而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．（2）以D 为坐标原点，DA 的方向为x 轴正方向，建立如图所示的空间直角坐标系D −xyz ．当三棱锥M −ABC 体积最大时，M 为CD 的中点．由题设得()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,1,1D A B C M ，()()()2,1,1,0,2,0,2,0,0AM AB DA =-==设(),,n x y z =是平面MAB 的法向量，则0,0.n AM n AB ⎧⋅=⎨⋅=⎩即20,20.x y z y -++=⎧⎨=⎩可取()1,0,2n =．DA 是平面MCD 的法向量，因此5cos ,5n DAn DA n DA ⋅==，25sin ,n DA =，所以面MAB 与面MCD 所成二面角的正弦值是．【名师点睛】本题主要考查面面垂直的证明，利用线线垂直得到线面垂直，再得到面面垂直，第二问主要考查建立空间直角坐标系，利用空间向量求出二面角的平面角，考查数形结合，将几何问题转化为代数问题进行求解，考查学生的计算能力和空间想象能力，属于中档题．7．如图，在三棱柱ABC −111A B C 中，1CC ⊥平面ABC ，D ，E ，F ，G 分别为1AA ，AC ，11A C ，1BB 的中点，AB=BC AC =1AA =2．（1）求证：AC ⊥平面BEF ；（2）求二面角B−CD −C 1的余弦值；（3）证明：直线FG 与平面BCD 相交．【试题来源】2018年全国普通高等学校招生统一考试（理）（北京卷）【答案】（1）见解析（2）21-；（3）见解析．【分析】（1）由等腰三角形性质得AC BE ⊥，由线面垂直性质得1AC CC ⊥，由三棱柱性质可得1//EF CC ，因此EF AC ⊥，最后根据线面垂直判定定理得结论，（2）根据条件建立空间直角坐标系，设立各点坐标，利用方程组解得平面BCD 一个法向量，根据向量数量积求得两法向量夹角，再根据二面角与法向量夹角相等或互补关系求结果，（3）根据平面BCD 一个法向量与直线F G 方向向量数量积不为零，可得结论．【解析】（1）在三棱柱ABC -A 1B 1C 1中，因为CC 1⊥平面ABC ，所以四边形A 1ACC 1为矩形．又E ，F 分别为AC ，A 1C 1的中点，所以AC ⊥EF ．因为AB =BC ．所以AC ⊥BE ，所以AC ⊥平面BEF ．（2）由（1）知AC ⊥EF ，AC ⊥BE ，EF ∥CC 1．又CC 1⊥平面ABC ，所以EF ⊥平面ABC ．因为BE ⊂平面ABC ，所以EF ⊥BE ．如图建立空间直角坐称系E -xyz ．由题意得B （0，2，0），C （-1，0，0），D （1，0，1），F （0，0，2），G （0，2，1）．所以()()=201=120CD CB ，，，，，，设平面BCD 的法向量为()n a b c =，，，所以00n CD n CB ⎧⋅=⎨⋅=⎩，所以2020a c a b +=⎧⎨+=⎩，令a =2，则b =-1，c =-4，所以平面BCD 的法向量()214n ，，=--，因为平面CDC 1的法向量为()=020EB ，，，所以21cos =n EBn EB n EB ⋅⋅=-．由图可得二面角B -CD -C 1为钝角，所以二面角B -CD -C 1的余弦值为21-．（3）平面BCD 的法向量为()214n =--，，，因为G （0，2，1），F （0，0，2），所以()=021GF -，，，所以2n GF ⋅=-，所以n 与GF 不垂直，所以GF 与平面BCD 不平行且不在平面BCD 内，所以GF 与平面BCD 相交．【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型．（1）证明线面、面面平行，需转化为证明线线平行．（2）证明线面垂直，需转化为证明线线垂直．（3）证明线线垂直，需转化为证明线面垂直．8．如图，在正三棱柱ABC -A 1B 1C 1中，AB =AA 1=2，点P ，Q 分别为A 1B 1，BC 的中点．（1）求异面直线BP 与AC 1所成角的余弦值；（2）求直线CC 1与平面AQC 1所成角的正弦值．【试题来源】2018年全国普通高等学校招生统一考试数学（江苏卷）【答案】（1）310；（2）5. 【分析】（1）先建立空间直角坐标系，设立各点坐标，根据向量数量积求得向量1,BP AC 的夹角，再根据向量夹角与异面直线所成角的关系得结果；（2）利用平面的方向量的求法列方程组解得平面1AQC 的一个法向量，再根据向量数量积得向量夹角，最后根据线面角与所求向量夹角之间的关系得结果．【解析】如图，在正三棱柱ABC −A 1B 1C 1中，设AC ，A 1C 1的中点分别为O ，O 1，则OB ⊥OC ，OO 1⊥OC ，OO 1⊥OB ，以{}1,,OB OC OO 为基底，建立空间直角坐标系O −xyz ．因为AB =AA 1=2，所以())()())()1110,1,0,3,0,0,0,1,0,0,1,2,3,0,2,0,1,2A B C A B C --．（1）因为P 为A 1B 1的中点，所以1,22P ⎫-⎪⎪⎝⎭，从而()131,,2,0,2,22BP AC ⎛⎫=--= ⎪ ⎪⎝⎭，故111,2052BP AC cosBPAC BP AC ⋅-===⨯⋅．因此，异面直线BP 与AC 1所成角的余弦值为．（2）因为Q 为BC 的中点，所以1,022Q ⎛⎫ ⎪ ⎪⎝⎭，因此33,02AQ ⎛⎫= ⎪ ⎪⎝⎭，()()110,2,2,0,0,2AC CC ==．设n =（x ，y ，z ）为平面AQC 1的一个法向量，则10,0,AQ n AC n ⎧⋅=⎪⎨⋅=⎪⎩即30,22220.x y y z +=⎨⎪+=⎩不妨取)1,1n =-，设直线CC 1与平面AQC 1所成角为θ，则111sin ,CC ncosCC n CC n θ⋅====⋅，所以直线CC 1与平面AQC 1所成角的正弦值为【名师点睛】本题考查空间向量、异面直线所成角和线面角等基础知识，考查运用空间向量解决问题的能力．利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”．9．已知圆锥的顶点为P ，底面圆心为O ，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设4PO =，OA 、OB 是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，如图．求异面直线PM 与OB 所成的角的大小．【试题来源】2018年全国普通高等学校招生统一考试数学（上海卷）【答案】（1）（2） arccos 6．【分析】（1）由圆锥的顶点为P ，底面圆心为O ，半径为2，圆锥的母线长为4能求出圆锥的体积．（2）以O 为原点，OA 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系，利用向量法能求出异面直线PM 与OB 所成的角．【解析】（1）因为圆锥的顶点为P ，底面圆心为O ，半径为2，圆锥的母线长为4，所以圆锥的体积2211ππ233V r h =⨯⨯⨯=⨯⨯3=．（2）因为4PO =，OA ，OB 是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，所以以O 为原点，OA 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系， ()004P ，，，()200A ，，，()020B ，，，()110M ，，，()000O ，，，()114PM =-，，，()020OB =，，，设异面直线PM与OB所成的角为θ，则cos18PM OBPMOBθ⋅===⋅．所以arccos6θ=．所以异面直线PM与OB所成的角的为arccos6．【名师点睛】求空间两条异面直线所成角的大小是立体几何中最为常见的基本题型之一．这类问题的求解一般有两条途径：其一是平移其中的一条直线或两条直线，将其转化为共面直线所成角，然后再构造三角形，通过解三角形来获得答案；其二是建立空间直角坐标系，借助空间向量的数量积公式，求出两向量的夹角的大小来获解．10．如图，AE⊥平面ABCD，,CF AE AD BC∥∥，,1,2AD AB AB AD AE BC⊥====．（1）求证：BF∥平面ADE；（2）求直线CE与平面BDE所成角的正弦值；（3）若二面角E BD F--的余弦值为13，求线段CF的长．【试题来源】2019年天津市高考数学试卷（理）【答案】（1）见证明；（2）49（3）87【分析】首先利用几何体的特征建立空间直角坐标系（1）利用直线BF 的方向向量和平面ADE 的法向量的关系即可证明线面平行；（2）分别求得直线CE 的方向向量和平面BDE 的法向量，然后求解线面角的正弦值即可；(3)首先确定两个半平面的法向量，然后利用二面角的余弦值计算公式得到关于CF 长度的方程，解方程可得CF 的长度．【解析】依题意，可以建立以A 为原点，分别以,,AB AD AE 的方向为x 轴，y 轴，z 轴正方向的空间直角坐标系(如图)，可得()()()()()0,0,0,1,0,0,1,2,0,0,1,0,0,0,2A B C D E ．设()0CF h h =>，则()1,2,F h ．（1）依题意，()1,0,0AB =是平面ADE 的法向量，又()0,2,BF h =，可得0BF AB ⋅=，因为直线BF ⊄平面ADE ，所以BF ∥平面ADE ．（2）依题意，(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--，设(),,n x y z =为平面BDE 的法向量，则00n BD n BE ⎧⋅=⎨⋅=⎩，即020x y x z -+=⎧⎨-+=⎩，不妨令z =1，可得()2,2,1n =，因此有4cos ,9||||CE n CE n CE n ⋅〈〉==-．所以，直线CE 与平面BDE 所成角的正弦值为49． (3)设(),,m x y z =为平面BDF 的法向量，则00m BD m BF ⎧⋅=⎨⋅=⎩，即020x y y hz -+=⎧⎨+=⎩．不妨令y =1，可得21,1,m h ⎛⎫=- ⎪⎝⎭．由题意，有41cos ,332m nm n m n -⋅===⨯，解得87h =．经检验，符合题意，所以线段CF 的长为87．【名师点睛】本题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识．考查用空间向量解决立体几何问题的方法．考查空间想象能力、运算求解能力和推理论证能力．11．图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°，将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2．（1）证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ；（2）求图2中的二面角B−CG−A 的大小．【试题来源】2019年全国统一高考数学试卷（理）（新课标Ⅱ）【答案】（1）见详解；（2） 30．【分析】（1）因为折纸和粘合不改变矩形ABED ，Rt ABC 和菱形BFGC 内部的夹角，所以//AD BE ，//BF CG 依然成立，又因E 和F 粘在一起，所以得证．因为AB 是平面BCGE 垂线，所以易证．（2）在图中找到B CG A --对应的平面角，再求此平面角即可．于是考虑B 关于GC 的垂线，发现此垂足与A 的连线也垂直于CG ．按照此思路即证．【解析】（1）证：//AD BE ，//BF CG ，因为E 和F 粘在一起．∴//AD CG ，A ，C ，G ，D 四点共面．又,AB BE AB BC ⊥⊥．AB ∴⊥平面BCGE ，AB ⊂平面ABC ，∴平面ABC ⊥平面BCGE ，得证．（2）过B 作BH GC ⊥延长线于H ，连结AH ，因为AB ⊥平面BCGE ，所以AB GC ⊥而又BH GC ⊥，故GC ⊥平面HAB ，所以AH GC ⊥．因为BH GC ⊥所以BHA ∠是二面角B CG A --的平面角，而在BHC △中90BHC ∠=，因为60FBC ∠=，故60BCH ∠=，所以sin 603BH BC ==．而在ABH 中90ABH ∠=，tanAB BHA BH ∠===，即二面角B CG A --的度数为30．【名师点睛】很新颖的立体几何考题．首先是多面体粘合问题，考查考生在粘合过程中哪些量是不变的．再者粘合后的多面体不是直棱柱，建系的向量解法在本题中略显麻烦，突出考查几何方法．最后将求二面角转化为求二面角的平面角问题考查考生的空间想象能力． 12．如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE AD =．ABC是底面的内接正三角形，P 为DO 上一点，PO DO =．（1）证明：PA ⊥平面PBC ；（2）求二面角B PC E --的余弦值．【试题来源】2020年全国统一高考数学试卷（理）（新课标Ⅱ）【答案】（1）证明见解析；（2．【分析】（1）要证明PA ⊥平面PBC ，只需证明PA PB ⊥，PA PC ⊥即可；（2）以O 为坐标原点，OA 为x 轴，ON 为y 轴建立如图所示的空间直角坐标系，分别算出平面PCB 的法向量为n ，平面PCE 的法向量为m ，利用公式cos ,||||n m m n n m ⋅<>=计算即可得到答案．【解析】（1）由题设，知DAE △为等边三角形，设1AE =，则DO =，1122CO BO AE ===，所以64PO DO ==，,44PC PB ====又ABC 为等边三角形，则2sin 60BA OA =，所以2BA =， 22234PA PB AB +==，则90APB ∠=，所以PA PB ⊥，同理PA PC ⊥，又PC PB P =，所以PA ⊥平面PBC ；（2）过O 作ON ∥BC 交AB 于点N ，因为PO ⊥平面ABC ，以O 为坐标原点，OA 为x 轴，ON 为y 轴建立如图所示的空间直角坐标系，则111(,0,0),(0,0,(,(,244444E P B C ----，1(,)444PC =---，1(,444PB =--，1(,0,24PE =--，设平面PCB 的一个法向量为111(,,)n x y z =，由00n PC n PB ⎧⋅=⎨⋅=⎩，得11111100x x ⎧---=⎪⎨-+-=⎪⎩，令1x =，得111,0z y =-=，所以(2,0,1)n =-，设平面PCE 的一个法向量为222(,,)m x y z =由00m PC m PE ⎧⋅=⎨⋅=⎩，得22222020x x ⎧--=⎪⎨--=⎪⎩，令21x =，得223z y ==，所以3(1,,3m =，故cos ,5||||3n m mn n m ⋅<>===⋅⨯，设二面角B PC E --的大小为θ，则cos 5θ=．【点晴】本题主要考查线面垂直的证明以及利用向量求二面角的大小，考查学生空间想象能力，数学运算能力，是一道容易题．13．在三棱锥A —BCD中，已知CB =CD BD =2，O 为BD 的中点，AO ⊥平面BCD ，AO =2，E 为AC 的中点．（1）求直线AB 与DE 所成角的余弦值；（2）若点F 在BC 上，满足BF =14BC ，设二面角F —DE —C 的大小为θ，求sin θ的值．【试题来源】2020年江苏省高考数学试卷【答案】（1）15（2）13【分析】（1）建立空间直角坐标系，利用向量数量积求直线向量夹角，即得结果；（2）先求两个平面法向量，根据向量数量积求法向量夹角，最后根据二面角与向量夹角关系得结果．【解析】（1）连,CO BC CD BO OD CO BD ==∴⊥以,,OB OC OA为,,x y z轴建立空间直角坐标系，则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -∴(1,0,2),(1,1,1)cos ,AB DE AB DE ∴=-=∴<>==从而直线AB 与DE 所成角的余弦值为15（2）设平面DEC 一个法向量为1(,,),n x y z =11200(1,2,0),00x y n DC DC x y z n DE ⎧+=⋅=⎧⎪=∴⎨⎨++=⋅=⎪⎩⎩，令112,1(2,1,1)y x z n =∴=-=∴=-，设平面DEF 一个法向量为2111(,,),n x y z =11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ⎧⎧+=⋅=⎪⎪=+=+=∴⎨⎨⋅=⎪⎩⎪++=⎩，令111272,5(2,7,5)y x z n =-∴==∴=-，12cos ,n n ∴<>==sin 13θ==． 14．如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．【试题来源】2020年海南省高考数学试卷（新高考全国Ⅱ卷）【答案】（1）证明见解析；（2．【分析】（1）利用线面垂直的判定定理证得AD ⊥平面PDC ，利用线面平行的判定定理以及性质定理，证得//AD l ，从而得到l ⊥平面PDC ；（2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Q m ，之后求得平面QCD 的法向量以及向量PB 的坐标，求得cos ,n PB <>的最大值，即为直线PB 与平面QCD 所成角的正弦值的最大值．【解析】（1）在正方形ABCD 中，//AD BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以//AD 平面PBC ，因为AD ⊂平面PAD ，平面PAD平面PBC l =，所以//AD l ，因为在四棱锥P ABCD -中，底面ABCD 是正方形，所以,,AD DC l DC ⊥∴⊥ 且PD ⊥平面ABCD ，所以,,AD PD l PD ⊥∴⊥ 因为CDPD D =，所以l ⊥平面PDC ；（2）如图建立空间直角坐标系D xyz -，因为1PD AD ==，则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ，设(,0,1)Q m ，则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-，设平面QCD 的法向量为(,,)n x y z =，则00DC n DQ n ⎧⋅=⎨⋅=⎩，即00y mx z =⎧⎨+=⎩，令1x =，则z m =-，所以平面QCD 的一个法向量为(1,0,)n m =-，则cos ,3n PB n PB n PB⋅<>==根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于|cos ,|n PB <>==3333=≤≤=，当且仅当1m =时取等号，所以直线PB 与平面QCD 【名师点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面平行的判定和性质，线面垂直的判定和性质，利用空间向量求线面角，利用基本不等式求最值，属于中档题目． 15．如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．（1）求证：1//BC 平面1AD E ；（2）求直线1AA 与平面1AD E 所成角的正弦值．【试题来源】2020年北京市高考数学试卷【答案】（1）证明见解析；（2）23．【分析】（1）证明出四边形11ABC D 为平行四边形，可得出11//BC AD ，然后利用线面平行的判定定理可证得结论；（2）以点A 为坐标原点，AD 、AB 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -，利用空间向量法可计算出直线1AA 与平面1AD E 所成角的正弦值．【解析】（1）如下图所示：在正方体1111ABCD A B C D -中，11//AB A B 且11AB A B =，1111//A B C D 且1111A B C D =，11//AB C D ∴且11AB C D =，所以，四边形11ABC D 为平行四边形，则11//BC AD ， 1BC ⊄平面1AD E ，1AD ⊂平面1AD E ，1//BC ∴平面1AD E ；（2）以点A 为坐标原点，AD 、AB 、1AA 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系A xyz -，设正方体1111ABCD A B C D -的棱长为2，则()0,0,0A 、()10,0,2A 、()12,0,2D 、()0,2,1E ，()12,0,2AD =，()0,2,1AE =，设平面1AD E 的法向量为(),,n x y z =，由100n AD n AE ⎧⋅=⎨⋅=⎩，得22020x z y z +=⎧⎨+=⎩，令2z =-，则2x =，1y =，则()2,1,2n =-．11142cos ,323n AA n AA n AA ⋅<>==-=-⨯⋅．因此，直线1AA 与平面1AD E 所成角的正弦值为23． 16．如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且12,AD CE M ==为棱11AB的中点．（1）求证：11C M B D ⊥；（2）求二面角1B B E D --的正弦值；（3）求直线AB 与平面1DB E 所成角的正弦值．【试题来源】2020年天津市高考数学试卷【答案】（1）证明见解析；（2；（3．【分析】以C 为原点，分别以1,,CA CB CC 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系．（1）计算出向量1C M 和1B D 的坐标，得出110C M B D ⋅=，即可证明出11C M B D ⊥；（2）可知平面1BB E 的一个法向量为CA ，计算出平面1B ED 的一个法向量为n ，利用空间向量法计算出二面角1B B E D --的余弦值，利用同角三角函数的基本关系可求解结果；（3）利用空间向量法可求得直线AB 与平面1DB E 所成角的正弦值．【解析】依题意，以C 为原点，分别以CA 、CB 、1CC 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系（如图），可得()0,0,0C 、()2,0,0A 、()0,2,0B 、()10,0,3C 、()12,0,3A 、()10,2,3B 、()2,0,1D 、()0,0,2E 、()1,1,3M ．（1）依题意，()11,1,0C M =，()12,2,2B D =--，从而112200C M B D ⋅=-+=，所以11C M B D ⊥；（2）依题意，()2,0,0CA =是平面1BB E 的一个法向量，()10,2,1EB =，()2,0,1ED =-．。

2020年全国高考数学·第35讲空间向量及其应用

2020年全国高考数学第35讲空间向量及其应用考纲解读1.空间向量及其运算.（1）了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示；（2）掌握空间向量的线性运算及其坐标表示；（3）掌握空间向量的数量积及其表示，能用向量的数量积判断向量的共线与垂直. 2.空间向量的应用.（1）理解直线的方向向量与平面的法向量；（2）能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系；（3）能用向量方法证明有关直线和平面位置关系的一些定理（包括三垂线定理）；（4）能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究几何问题中的应用.命题趋势探究立体几何试题中，证明线面、面面的位置关系一般利用传统方法（非向量法）证明，对于空间角和距离的计算，既可用传统方法解答，也可以用向量法解答，而且多数情况下向量法会更容易一些.预测在2015年高考对本专题的考查会在解答题中以中档题出现，分值保持在12分左右.知识点精讲一、空间向量及其加减运算1.空间向量在空间，我们把具有大小和方向的量叫做空间向量，向量的大小叫做向量的长度或模.空间向量也可用有向线段表示，有向线段的长度表示向量的模，若向量a r 的起点是A ，终点是B ，则向量a r 也可以记作AB u u u r，其模记为ar 或AB u u u r .2.零向量与单位向量规定长度为0的向量叫做零向量，记作0r .当有向线段的起点A 与终点B 重合时，0AB =u u u r r.模为1的向量称为单位向量. 3.相等向量与相反向量方向相同且模相等的向量称为相等向量.在空间，同向且等长的有向线段表示同一向量或相等向量.空间任意两个向量都可以平移到同一个平面，成为同一平面内的两个向量.与向量a r 长度相等而方向相反的向量，称为a r 的相反向量，记为a -r .4.空间向量的加法和减法运算（1）OC OA OB a b =+=+u u u r u u u r u u u r r r ，BA OA OB a b =-=-u u u r u u u r u u u r r r.如图8-152所示.二、空间向量的数乘运算 1．数乘运算实数λ与空间向量a r 的乘积a λr 称为向量的数乘运算.当0λ>时，a λr 与向量a r 方向相同；当0λ<时，向量aλr与向量a r 方向相反. a λr 的长度是a r的长度的λ倍.2.空间向量的数乘运算满足分配律及结合律()a b a b λλλ+=+r r r r ，()()a a λμλμ=r r .3.共线向量与平行向量如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量，a r 平行于b r，记作//a b r r .4.共线向量定理对空间中任意两个向量a r ，b r ()0b ≠r r ，//a b r r 的充要条件是存在实数λ，使a b λ=r r.5.直线的方向向量如图8-153所示，l 为经过已知点A 且平行于已知非零向量a r的直线.对空间任意一点O ，点P 在直线l 上的充要条件是存在实数t ，使OP OA ta =+u u u r u u u r r ①，其中向量a r 叫做直线l 的方向向量，在l 上取AB a =u u u r r，则式①可化为()()1OP OA t AB OA t OB OA t OA tOB =+=+-=-+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ②①和②都称为空间直线的向量表达式，当12t =，即点P 是线段AB 的中点时，()12OP OA OB =+u u u r u u u r u u u r ，此式叫做线段AB 的中点公式.6.共面向量如图8-154所示，已知平面α与向量a r ，作OA a =u u u r r ，如果直线OA 平行于平面α或在平面α内，则说明向量ar平行于平面α.平行于同一平面的向量，叫做共面向量.7.共面向量定理如果两个向量a r ，b r 不共线，那么向量p u r与向量a r ，b r 共面的充要条件是存在唯一的有序实数对(),x y ，使p xa yb =+u r r r .推论：（1）空间一点P 位于平面ABC 内的充要条件是存在有序实数对(),x y ，使AP xAB y AC =+u u u r u u u r u u u r；或对空间任意一u u u r u u u r u u u r u u u rAaaα图 8-154O（2）已知空间任意一点O 和不共线的三点A ，B ，C ，满足向量关系式OP xOA yOB zOC =++u u u r u u u r u u u r u u u r （其中1x y z ++=）的点P 与点A ，B ，C 共面；反之也成立.三、空间向量的数量积运算1.两向量夹角已知两个非零向量a r ，b r ，在空间任取一点O ，作OA a =u u u r r ，OB b =u u u r r ，则AOB ∠叫做向量a r ，b r的夹角，记作,a b r r ，通常规定0,a b π≤≤r r ，如果,2a b π=r r ，那么向量a r ，b r 互相垂直，记作a b ⊥r r .2.数量积定义已知两个非零向量a r ，b r ，则cos ,a b a b r r r r 叫做a r ，b r 的数量积，记作a b ⋅r r ，即cos ,a b a b a b ⋅=r r r r r r.零向量与任何向量的数量积为0，特别地，2a a a ⋅=r r r .3.空间向量的数量积满足的运算律：()()a b a b λλ⋅=⋅r r r r，a b b a ⋅=⋅r r r r （交换律）；()a b c a b a c ⋅+=⋅+⋅r r r r r r r（分配律）.四、空间向量的坐标运算及应用（1）设()123,,a a a a =r ，()123,,b b b b =r ，则()112233,,a b a b a b a b +=+++r r； ()112233,,a b a b a b a b -=---r r； ()123,,a a a a λλλλ=r；112233a b a b a b a b ⋅=++r r；()112233//0,,a b b a b a b a b λλλ≠⇒===r r r r；1122330a b a b a b a b ⊥⇒++=r r.（2）设()111,,A x y z ，()222,,B x y z ，则()212121,,AB OB OA x x y y z z =-=---u u u r u u u r u u u r.这就是说，一个向量在直角坐标系中的坐标等于表示该向量的有向线段的终点的坐标减起点的坐标. （3）两个向量的夹角及两点间的距离公式.①已知()123,,a a a a =r ，()123,,b b b b =r，则a ==rb ==r ；112233a b a b a b a b ⋅=++r r；cos ,a b =r r ；②已知()111,,A x y z ，()222,,B x y z ，则AB =u u u r或者(),d A B AB =u u u r.其中(),d A B 表示A 与B 两点间的距离，这就是空间两点的距离公式.（4）向量a r 在向量b r 上的射影为cos ,a ba ab b⋅=r rr r r r .（5）设()0n n ≠r r r是平面M 的一个法向量，AB ，CD 是M 内的两条相交直线，则0n AB ⋅=r u u u r ，由此可求出一个法向量n r （向量AB u u u r 及CD uuur 已知）.（6）利用空间向量证明线面平行：设n r 是平面的一个法向量，l r 为直线l 的方向向量，证明0l n ⋅=r r，（如图8-155所示）.已知直线l （l α⊄），平面α的法向量n r ，若0l n ⋅=r r ，则//l α.（7）利用空间向量证明两条异面直线垂直：在两条异面直线中各取一个方向向量a r ，b r ，只要证明a b ⊥r r，即0a b ⋅=r r.（8）利用空间向量证明线面垂直：即证平面的一个法向量与直线的方向向量共线.（9）证明面面平行、面面垂直，最终都要转化为证明法向量互相平行、法向量互相垂直. （10）空间角公式.①异面直线所成角公式：设a r ，b r分别为异面直线1l ，2l 上的方向向量，θ为异面直线所成角的大小，则cos cos ,a b a b a b θ⋅==r r r rr r .②线面角公式：设l 为平面α的斜线，a r 为l 的方向向量，n r为平面α的法向量，θ为l 与α所成角的大小，则sin cos ,a n a n a nθ⋅==r r r rr r .③二面角公式：设1n ，2n 分别为平面α，β的法向量，二面角的大小为θ，则12,n n θ=u r u u r 或12,n n π-u r u u r（需要根据具体情况判断相等或互补），其中1212cos n n n n θ⋅=u r u u r u r u u r .（11）点A 到平面α的距离为d ，B α∈，n r为平面α的法向量，则AB n d n⋅=u u u r r r .题型归纳及思路提示题型116 空间向量及其运算思路提示空间向量的运算包括空间向量的加法、减法、数乘、数量积的几何意义及坐标运算，可以类比平面向量的运算法则.一、空间向量的加法、减法、数乘运算例8.41 如图8-156所示，已知空间四边形OABC ，点,M N 分别为OA ，BC 的中点，且OA a =u u u r r ，OB b =u u u r r ，OC c =u u u r r，用a r ，b r ，c r 表示MN u u u u r ，则MN =u u u u r.变式1 如图8-157所示，已知空间四边形OABC ，其对角线为OB ，AC ，M 和N 分别是对边OA 和BC 的中点，点G 在线段MN 上，且2MG GN =u u u u r u u u r ，现用基向量OA u u u r ，OB uuu r ，OC u u u r 表示向量OG u u u r ，设OG xOA yOB zOC =++u u u r u u u r u u u r u u u r，则,,x y z 的值分别是（）.A 111,,333x y z === .B 111,,336x y z === .C 111,,363x y z === .D 111,,633x y z ===变式2 如图8-158所示，在四面体O ABC -中，OA a =u u u r r ，OB b =u u u r r ，OC c =u u u r r，D 为BC 的中点，E 为AD 的中点，则OE =u u u r （用a r ，b r ，c r表示）.变式3 在空间四边形ABCD 中，连接对角线,AC BD ，若BCD ∆是正三角形，且E 为其重心，则1322AB BC DE AD +--u u u r u u u r u u u r u u u r的化简结果为 .变式4 如图8-159所示，在平行六面体1111ABCD A B C D -中，M 为11A C 与11B D 的交点，若AB a =u u u r r ，AD b =u u u r r，1AA c =u u u r r，则下列向量中与BM u u u u r 相等的向量是（）.A 1122a b c-++r r r .B 1122a b c ++r r r .C 1122a b c --+r r r .D 1122a b c -+r r r二、空间共线向量定理的应用空间共线向量定理：()//0a b b a b λ≠⇔=r r r r r r.利用此定理可解决立体几何中的平行问题.例8.42 已知3240m a b c =--≠u r r r r r ，()182n x a b yc =+++r r r r ，且,,a b c r r r不共面，若//m n u r r ，求,x y 的值.三、空间向量的数量积运算121212cos ,a b a b a b x x y y z z ⋅==++r r r r r r；求模长时，可根据2222111a a x y z ==++r r ；求空间向量夹角时，可先求其余弦值cos ,a b a b a b⋅=r r r rr r .要判断空间两向量垂直时，可以求两向量的数量积是否为0，即0a b a b ⋅=⇔⊥r r r r.,a b r r 为锐角0a b ⇒⋅>r r ；,a b r r为钝角0a b ⇒⋅<r r .由此，通常通过计算a b ⋅r r 的值来判断两向量夹角是锐角还是钝角.例8.43 已知空间四边形ABCD 的每条边和对角线的长都等于a ，点,E F 分别是,BC AD 的中点，AE u u u r ⋅AF u u u r的值为（）..A 2a .B 21.2B a 21.4C a 234D a变式1 如图8-161所示，已知平行六面体1111ABCD A B C D -中，1160A AD A AB DAB ∠=∠=∠=︒，且变式2 如图8-162所示，设,,,A B C D 是空间不共面的4个点，且满足0AB AC ⋅=u u u r u u u r ，0AD AC ⋅=u u u r u u u r ，0AD AB ⋅=u u u r u u u r，则BCD ∆的形状是（）..A 钝角三角形 .B 直角三角形 .C 锐角三角形 .D 无法确定例8.44 如图8-163所示，在45︒的二面角l αβ--的棱上有两点,A B ，点,C D 分别在,αβ内，且AC AB ⊥，45ABD ∠=︒，1AC BD AB ===，则CD 的长度为.变式1 已知二面角l αβ--为60︒，动点,P Q 分别在面,αβ内，P 到β的距离为3，Q 到α的距离为23，则,P Q 两点之间距离的最小值为（）..2A .2B .23C .4D变式2 在直角坐标系中，设()3,2A ，()2,3B --，沿y 轴把坐标平面折成120︒的二面角后，AB 的长为（）. .6A .42B .23C .211D例8.45 如图8-164所示，设动点P 在棱长为1的正方体1111ABCD A B C D -的对角线1BD 上，记11D PD Bλ=.当APC ∠为钝角时，求λ的取值范围.变式1 已知正方体1111ABCD A B C D -的棱长为1，点P 在线段1BD 上，当APC ∠最大时，三棱锥P ABC -的体积为（）.1.24A 1.18B 1.9C 1.12D例8.46 如图8-166所示，在四棱锥P ABCD -中，侧面PAD 为正三角形，底面ABCD 为正方形，侧面PAD ⊥底面ABCD ，M 为底面ABCD 内的一个动点，且满足MP MC =，则点M 在正方形ABCD 内的轨迹为（）.变式1 到两互相垂直的异面直线距离相等的点，在过其中一条直线且平行于另一条直线的平面内的轨迹是（） .A 直线 .B 椭圆 .C 抛物线 .D 双曲线变式2 空间点到平面的距离定义如下：过空间一点作平面的垂线，这个点和垂足之间的距离叫做这个点到这个平面的距离，已知平面α，β，γ两两互相垂直，点A α∈，点A 到β，γ的距离都是3，点P 是α上的动点，满足P 到β的距离是点P 到点A 距离的2倍，则点P 的轨迹上的点到γ的距离的最小值是（）.33A -.33B -.63C .3D题型117 空间向量在立体几何中的应用思路提示用向量法可以证点共线、线共点、线（或点）共面、两直线（或线与面、面与面）垂直的问题，也可以求空间角和距离.因此，凡涉及上述类型的问题，都可以考虑利用向量法求解，且其解法一般都比较简单.用向量法解题的途径有两种：一种是坐标法，即通过建立空间直角坐标系，确定出一些点的坐标，进而求出向量的坐标，再进行坐标运算；另一种是基底法，即先选择基向量（除要求不共面外，还要能够便于表示所求的目标向量，并优先选择相互夹角已知的向量作为基底，如常选择几何体上共点而不共面的三条棱所在的向量为基底），然后将有关向量用基底向量表示，并进行向量运算. 一、证明三点共线（如A ，B ，C 三点共线）的方法先构造共起点的向量AB u u u r ，AC u u ur ，然后证明存在非零实数λ，使得AB AC λ=u u u r u u u r .例8.47 如图8-168所示，已知在长方体1111ABCD A B C D -中，点M 为1DD 的中点，点N 在AC 上，且:2:1AN NC =，点E 为BM 的中点.求证：1A ，E ，N 三点共线.变式1 在正方体1111ABCD A B C D -中，E ,F 分别为棱1AA 和1CC 的中点，则在空间中与三条直线11A D ，EF ，CD 都相交的直线（）..A 不存在 .B 有且只有两条 .C 有且只有三条 .D 有无数条变式2 如图8-170所示，在空间四边形ABCD 中，M ，N 分别是AB 和CD 的中点，P 为线段MN 的中点，Q 为BCD ∆的重心.求证：,,A P Q 三点共线.二、证明多点共面的方法要证明多点（如A ，B ，C ，D ）共面，可使用以下方法解题.先作出从同一点出发的三个向量（如AB u u u r ，AC u u u r ，AD u u u r），然后证明存在两个实数,x y ，使得AD x AB y AC =+u u u r u u u r u u u r .例8.48 如图8-171所示，平面ABEF ⊥平面ABCD ，四边形ABEF 与ABCD 都是直角梯形，90BAD FAB ∠=∠=︒，1//2BC AD ，1//2BE AF .求证：,,,C D E F 四边共面.变式1 如图8-173所示，已知平行六面体1111ABCD A B C D -，,,,E F G H 分别是棱11111,,,A D D C C C AB 的中点. 求证：,,,E F G H 四点共面.三、证明直线和直线平行的方法将证线线平行转化为证两向量共线.设,a b 是两条不重合的直线，它们的方向向量分别为,a b r r，则()//,0a b a b R λλλ⇔=∈≠r r r r.例8.49 如图8-174所示，在正方体1111ABCD A B C D -中，MN 是异面直线1A D 与AC 的公垂线段.求证：1//MN BD .（1）利用共面向量定理.设,a b r r 为平面α内不共线的两个向量，证明存在两个实数,x y ，使得l xa yb =+r r r，则//l α.（2）转化为证明直线和平面内的某一直线平行.（3）转化为证明直线的方向向量与平面的法向量垂直（此方法最常用）.例8.50 如图8-176所示，在直四棱柱1111ABCD A B C D -中，已知122DC DD AD AB ===，AD DC ⊥，//AB DC ，E 是DC 的中点.求证：1//D E 平面1A BD .变式 1 如图8-177所示，已知P 是正方形ABCD 所在平面外一点，M 、N 分别是PA 、BD 上的点，且::5:8PM MA BN ND ==.求证：直线//MN 平面PBC .五、证明平面与平面平行的方法（1）证明两平面内有两条相交直线分别平行.（2）转化为证两平面的法向量平行（常用此方法）.例8.51 如图8-180所示，在平行六面体1111ABCD A B C D -中，,,E F G 分别是11111,,A D D D D C 的中点. 求证:平面//EFG 平面1AB C .设直线12,l l 的方向向量为,a b r r，则a b ⊥r r 0a b ⇔⋅=r r .这里要特别指出的是，用向量法证明两直线尤其是两异面直线垂直是非常有效的方法.例8.52 如图8-181所示，四棱锥A BCDE -中，底面BCDE 为矩形，侧面ABC ⊥底面BCDE ，2BC =，2CD =，AB AC =.求证：AD CE ⊥.变式1 如图8-183所示，已知空间四边形ABCD 的每条边和对角线长都等于a .点M ，N 分别为边AB ，CD 的中点.求证：MN 为AB 和CD 的公垂线.七.证明直线与平面垂直的方法 (1)证明直线和平面内的两天相交直线垂直. (2)证明直线和平面内的任一直线垂直. (3)转化为证明直线与平面的法向量共线.例8.53 如图8-184所示,在直四棱柱ABCD-1111A B C D 中,已知AB ∥CD,AB=AD=1,1DD =CD =2.A B ⊥AD.求证：BC ⊥平面1D DB .变式1 正三棱锥O-ABC 的三条侧棱OA ,OB ,OC 两两垂直，且长度均为2，E ，F 分别是AB ，AC 的中点，H 是EF 的中点，过EF 的一个平面与侧棱OA ,OB ,OC 或其延长线分别交于111,A B C ，，132OA =。

2020版高考数学()：8.5 空间向量及其应用

8.5空间向量及其应用挖命题【考情探究】分析解读 1.空间角是立体几何中的一个突出的量化指标,是空间图形位置关系的具体体现,因此,空间角是高考的必考内容.2.考查空间角的计算,既可能以选择题、填空题的形式出现,也可能以解答题的形式出现.以探索题、最值问题考查空间角的计算,常以解答题的形式出现,空间角的计算主要是传统法和向量法.3.在立体几何解答题中,建立空间直角坐标系(或取基底向量),利用空间向量的数量积解决直线、平面间的位置关系、角度、长度等问题越来越受到青睐,特别是处理存在性问题、探索性问题、开放性问题等,比用传统方法简便快捷,一直是高考的重点和热点.4.预计2020年高考试题中,空间角的计算,空间向量在立体几何中的应用必是高考热点.复习时应高度重视.破考点【考点集训】考点一空间角1.(2018浙江嵊州高三期末质检,19,15分)如图,在菱形ABCD中,∠BAD=,ED⊥平面ABCD,EF∥DB,M是线段AE的中点,DE=EF=BD.(1)证明:DM∥平面CEF;(2)求直线DM与平面DEF所成角的正弦值.解析(1)证明:连接AC与BD交于点O,连接MO.因为DO∥EF,DO⊄平面CEF,EF⊂平面CEF,所以DO∥平面CEF.因为M是线段AE的中点,所以MO是△ACE的中位线,所以MO∥EC.又MO⊄平面CEF,EC⊂平面CEF,所以MO∥平面CEF,又MO∩DO=O,MO⊂平面MDO,DO⊂平面MDO,所以平面MDO∥平面CEF,又DM⊂平面MDO,所以DM∥平面CEF.(2)解法一:因为四边形ABCD是菱形,所以AC⊥BD.又因为ED⊥平面ABCD,AC⊂平面ABCD,所以ED⊥AC,又ED∩BD=D,所以AC⊥平面DEF.设BD=2,则点A到平面DEF的距离AO=.因为点M是线段AE的中点,所以点M到平面DEF的距离h=AO=.设直线DM与平面DEF所成的角为θ,则sin θ===.故直线DM与平面DEF所成角的正弦值为.解法二:设AB的中点为G,连接DG,则DG⊥DC.以D为坐标原点,DG,DC,DE所在直线分别为x轴,y轴,z轴建立空间直角坐标系.取BD=2,则D(0,0,0),M,E(0,0,1),F,所以=(0,0,1),=.设平面DEF的法向量为n=(x,y,z),则即可取法向量n=(1,-,0).又=,所以cos<,n>===,故直线DM与平面DEF所成角的正弦值为.2.(2017浙江高考模拟训练冲刺卷一,19)如图,在四棱锥A-BCDO中,DO⊥平面AOB,BO∥CD,OA=CD=2,OD=2,OB=4,∠AOB=120°.(1)求直线AC与平面ABD所成角的正弦值;(2)求二面角D-OA-C的余弦值.解析(1)如图,过点O在平面AOB内作OB的垂线OE,交AB于点E.∵DO⊥平面AOB,∴OD⊥OE,OD⊥OB,分别以OE,OB,OD所在的直线为x,y,z轴,建立空间直角坐标系,如图所示.则各点坐标为O(0,0,0),A(,-1,0),B(0,4,0),C(0,2,2),D(0,0,2),∴=(-,5,0),=(-,1,2).设平面ABD的法向量为n=(x,y,z),则由n·=0,n·=0,得取x=5,得n=(5,,2).设直线AC与平面ABD所成角为θ,又=(-,3,2),∴sinθ=|cos,n|==,故直线AC与平面ABD所成角的正弦值为.(2)设平面AOD的法向量为m1=(x,y,z),又=(,-1,0),=(0,0,2),∴由m1·=0,m1·=0, 得取x=1,得m1=(1,,0).设平面AOC的法向量为m2=(a,b,c),又=(,-1,0),=(0,2,2),∴由m2·=0,m2·=0,得取b=,得m2=(1,,-1).∴cos m1,m2==,由图可知二面角D-OA-C的平面角为锐角,故二面角D-OA-C的余弦值为.考点二空间向量在立体几何中的应用1.(2017浙江台州4月调研卷(一模),17)如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且|EF|=.若记EF的中点P的轨迹为L,则|L|等于.(注:|L|表示点P的轨迹的长度)答案π2.(2017浙江杭州二模(4月),19)如图,已知四边形ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.(1)当θ=90°时,求cos∠AOC的值;(2)当θ=60°时,点P是线段MD上一点,直线AP与平面AOC所成角为α.若sin α=,求线段MP的长.解析设E为AB的中点,连接OE,则OE⊥MN,以O为原点,OE,ON所在直线分别为x轴,y轴,建立空间直角坐标系(图略).(1)当θ=90°时,A(2,-1,0),C(0,1,2),∴=(2,-1,0),=(0,1,2),∴cos∠AOC==-.(2)由θ=60°得C(1,1,),D(1,-1,),M(0,-1,0),∴=(1,0,).设=λ(0≤λ≤1),则=+=(λ,-1,λ).∴=-=(λ-2,0,λ),设平面AOC的法向量为n=(x,y,z).∵n·=0,n·=0,=(2,-1,0),=(1,1,),∴取x=1,则y=2,z=-,故n=(1,2,-),由题意得,=,即3λ2-10λ+3=0,∴λ=或λ=3(舍去),∴在线段MD上存在点P符合题意,且MP=MD=.炼技法【方法集训】方法1 求直线与平面所成角的方法1.(2017浙江稽阳联谊学校联考(4月),19)如图(1)所示,四边形ABCD为梯形,AB∥CD,∠C=60°,点E在CD 上,AB=CE=2,BF=BD=,BD⊥BC.现将△ADE沿AE翻折到图(2)中△APE的位置,使得二面角P-AE-C的大小为.(1)求PB的长度;(2)求证:PB⊥平面ABCE;(3)求直线AB与平面APE所成角的正弦值.解析(1)因为AB EC,所以四边形ABCE是平行四边形,所以BC∥AE,又因为BD⊥BC,所以BD⊥AE,所以AE⊥FB,AE⊥FP,所以∠PFB为二面角P-AE-C的平面角.(3分)由BF=,PF=2,得BP2=BF2+PF2-2BF·PFcos∠BFP=9,所以BP=3.(5分)(2)证明:由BF=,PF=2,BP=3知,PB2+BF2=PF2,所以BF⊥PB,①(7分)又因为BF⊥AE,PF⊥AE,BF∩PF=F,所以AE⊥平面PFB,所以AE⊥PB,②(9分) 由①②可知,PB⊥平面ABCE.(10分)(3)解法一:作BN⊥PF于N点,连接AN.由(2)可知,AE⊥平面BFP,又AE⊂平面APE,∴平面BFP⊥平面APE.又平面BFP∩平面APE=PF,BN⊂平面BFP,所以BN⊥平面APE,(12分)所以∠BAN是直线AB与平面APE所成的角.(13分)易知BN=BFsin 60°=,则sin∠NAB===.故直线AB与平面APE所成角的正弦值为.(15分)解法二:易知BF,BP,BC两两互相垂直,建立如图所示的空间直角坐标系,则B(0,0,0),C(3,0,0),A(-1,,0),E(2,,0),P(0,0,3).(11分)设平面APE的法向量为n=(x,y,z).又=(3,0,0),=(1,-,3),所以由即得取z=1,得n=(0,,1).(13分)设直线AB与平面APE所成的角为θ,又=(1,-,0),所以sin θ=|cos<n,>|==,故直线AB与平面APE所成角的正弦值为.(15分)2.如图,△ABC是以C为直角的等腰直角三角形,直角边长为8,AE∶EC=5∶3,DE∥BC,沿DE将三角形ADE折起,使得点A在平面BCED上的射影是点C,点M在AC上且MC=AC.(1)在BD上确定点N的位置,使得MN∥平面ADE;(2)在(1)的条件下,求CN与平面ABD所成角的正弦值.解析(1)由点A在平面BCED上的射影是点C,可知AC⊥平面BCED,而BC⊥CE,如图建立空间直角坐标系,可知各点的坐标为C(0,0,0),A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0).由MC=AC,可知点M的坐标为,设点N的坐标为(x,y,0),则由点N在BD上可得y=8-x,即点N的坐标为(x,8-x,0),则=.设平面ADE的法向量为n1=(x,y,z),则而=(0,-5,0),=(3,0,-4),所以取x=4,则z=3,可得n1=(4,0,3).MN∥平面ADE等价于n1·=0,即4x+0×(8-x)+3×=0.解之可得x=2,即点N的坐标为(2,6,0),所以点N为BD的靠近D点的三等分点.(2)由(1)可知=(2,6,0),设平面ABD的法向量为n2=(p,q,r),由题意可知而=(-3,3,0),=(0,8,-4),可得取p=1,则q=1,r=2.可得n2=(1,1,2).设CN与平面ABD所成角为θ,则sin θ==.方法2 求二面角的方法1.(2018浙江镇海中学期中,20)在多面体ABC-A1B1C1中,AA1∥BB1∥CC1,AA1=4,BB1=2,AB=4,CC1=3,AB⊥BB1,C1在平面ABB1A1上的射影E是线段A1B1的中点.(1)求证:平面ABC⊥平面ABB1A1;(2)若C1E=2,求二面角C1-AB1-C的余弦值.解析(1)证明:设线段AB的中点为O,连接OE,CO,则OE∥AA1,且OE==3,(2分)∵AA1∥CC1,∴OE∥CC1,又OE=CC1=3,∴四边形CC1EO为平行四边形,∴OC∥EC1.(4分)∵C1E⊥平面ABB1A1,∴OC⊥平面ABB1A1,(5分)∵OC⊂平面ABC,∴平面ABC⊥平面ABB1A1.(7分)(2)由(1)知OB,OE,OC两两互相垂直,分别以OB,OE,OC所在直线为x,y,z轴建立空间直角坐标系,则O(0,0,0),A(-2,0,0),B1(2,2,0),C(0,0,2),C1(0,3,2).(8分)设平面AB1C的法向量为m=(x,y,z),而=(4,2,0),=(2,0,2),由得取x=1,得m=(1,-2,-1).(10分)设平面AB1C1的法向量为n=(x1,y1,z1),而=(4,2,0),=(2,3,2),由得取x1=1,得n=(1,-2,2).(12分)∴cos<m,n>==,(14分)由图可知二面角C1-AB1-C的平面角为锐角,故二面角C1-AB1-C的余弦值为.(15分)2.(2017浙江名校(诸暨中学)交流卷四,19)如图,已知△ABC为等边三角形,M为AB的中点,AA1,BB1分别垂直平面ABC于点A,B,AA1=AB,BB1=AB,MN⊥A1B1,垂足为N.(1)求证:CN⊥A1B1;(2)求平面ABC与平面A1B1C所成的锐二面角的正切值.解析(1)证明:因为AA1,BB1分别垂直平面ABC于点A,B,所以平面AA1B1B⊥平面ABC,因为AC=BC,M为AB的中点,所以CM⊥AB,又平面AA1B1B∩平面ABC=AB,CM⊂平面AA1B1B,所以CM⊥平面A1ABB1,所以CM⊥A1B1,又因为MN⊥A1B1,所以A1B1⊥平面CMN,所以A1B1⊥CN.(2)解法一:如图,延长AB、A1B1相交于点D,连接CD,则CD为所求二面角的棱.因为BB1=AA1,BB1∥AA1,所以=,于是BD=BC=BA,于是∠ACD=90°,即CD⊥CA.又因为CD⊥AA1,所以CD⊥平面AA1C,所以CD⊥CA1.于是∠A1CA即为所求二面角的平面角.在Rt△A1AC中,AA1=AB=AC,所以∠A1CA=45°,所以tan∠A1CA=1.所以平面ABC与平面A1B1C所成的锐二面角的正切值为1.解法二:如图,以M为原点,MA所在直线为x轴,MC所在直线为y轴建立空间直角坐标系,设AB=2.则C(0,,0),A1(1,0,2),B1(-1,0,1),=(1,-,2),=(-2,0,-1).设平面A1B1C的法向量为n1=(x,y,z).由·n1=0,·n1=0,得取x=1,则y=-,z=-2,故n1=(1,-,-2).设所求二面角的大小为θ,又平面ABC的一个法向量为n2=(0,0,1).所以cos θ===,所以tan θ=1.过专题【五年高考】A组自主命题·浙江卷题组考点一空间角1.(2018浙江,8,4分)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1答案D2.(2017浙江,9,4分)如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P,Q,R分别为AB,BC,CA上的点,AP=PB,==2.分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α,β,γ,则()A.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α答案B3.(2016浙江文,14,4分)如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=,∠ADC=90°.沿直线AC将△ACD 翻折成△ACD',直线AC与BD'所成角的余弦的最大值是.答案考点二空间向量在立体几何中的应用1.(2015浙江,15,6分)已知e1,e2是空间单位向量,e1·e2=.若空间向量b满足b·e1=2,b·e2=,且对于任意x,y∈R,|b-(x e1+y e2)|≥|b-(x0e1+y0e2)|=1(x0,y0∈R),则x0=,y0=,|b|=.答案1;2;22.(2018浙江,19,15分)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.解析本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.解法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2,所以A1+A=A,故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=,由AB=BC=2,∠ABC=120°得AC=2,由CC1⊥AC,得AC1=,所以A+B1=A,故AB1⊥B1C1,因为A1B1,B1C1⊂平面A1B1C1,所以AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1得平面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.由B1C1=,A1B1=2,A1C1=得cos∠C1A1B1=,sin∠C1A1B1=,所以C1D=,故sin∠C1AD==.因此,直线AC1与平面ABB1所成的角的正弦值是.解法二:(1)证明:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz.由题意知各点坐标如下:A(0,-,0),B(1,0,0),A1(0,-,4),B1(1,0,2),C1(0,,1).因此=(1,,2),=(1,,-2),=(0,2,-3).由·=0得AB1⊥A1B1.由·=0得AB1⊥A1C1.所以AB1⊥平面A1B1C1.(2)设直线AC1与平面ABB1所成的角为θ.由(1)可知=(0,2,1),=(1,,0),=(0,0,2).设平面ABB1的法向量n=(x,y,z).由即可取n=(-,1,0).所以sin θ=|cos<,n>|==.因此,直线AC1与平面ABB1所成的角的正弦值是.3.(2017浙江,19,15分)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(1)证明:CE∥平面PAB;(2)求直线CE与平面PBC所成角的正弦值.解析本题主要考查空间点、线、面的位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.(1)证明:如图,设PA中点为F,连接EF,FB.因为E,F分别为PD,PA中点,所以EF∥AD且EF=AD.又因为BC∥AD,BC=AD,所以EF∥BC且EF=BC,即四边形BCEF为平行四边形,所以CE∥BF,因此CE∥平面PAB.(2)分别取BC,AD的中点为M,N.连接PN交EF于点Q,连接MQ.因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,在平行四边形BCEF中,MQ∥CE.由△PAD为等腰直角三角形得PN⊥AD.由DC⊥AD,N是AD的中点得BN⊥AD.所以AD⊥平面PBN,由BC∥AD得BC⊥平面PBN,那么平面PBC⊥平面PBN.过点Q作PB的垂线,垂足为H,连接MH.MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.设CD=1. 在△PCD中,由PC=2,CD=1,PD=得CE=,在△PBN中,由PN=BN=1,PB=得QH=,在Rt△MQH中,QH=,MQ=,所以sin∠QMH=.所以,直线CE与平面PBC所成角的正弦值是.一题多解(1)证明:设AD的中点为O,连接OB,OP.∵△PAD是以AD为斜边的等腰直角三角形,∴OP⊥AD.∵BC=AD=OD,且BC∥OD,∴四边形BCDO为平行四边形,又∵CD⊥AD,∴OB⊥AD,∵OP∩OB=O,∴AD⊥平面OPB.过点O在平面POB内作OB的垂线OM,交PB于M,以O为原点,OB所在直线为x轴,OD所在直线为y轴,OM所在直线为z轴,建立空间直角坐标系,如图.设CD=1,则有A(0,-1,0),B(1,0,0),C(1,1,0),D(0,1,0).设P(x,0,z)(z>0),由PC=2,OP=1,得得x=-,z=.即点P,而E为PD的中点,∴E.设平面PAB的法向量为n=(x1,y1,z1),∵=,=(1,1,0),∴⇒取y1=-1,得n=(1,-1,).而=,则·n=0,而CE⊄平面PAB,∴CE∥平面PAB.(2)设平面PBC的法向量为m=(x2,y2,z2),∵=(0,1,0),=,∴取x2=1,得m=(1,0,).设直线CE与平面PBC所成角为θ.则sin θ=|cos<m,>|==,故直线CE与平面PBC所成角的正弦值为.方法总结 1.证明直线与平面平行的方法.(例:求证:l∥α)①线面平行的判定定理:在平面α内找到一条与直线l平行的直线m,从而得到l∥α.②面面平行的性质:过直线l找到(或作出)一个平面β,使得β∥α,从而得l∥α.③向量法:(i)求出平面α的法向量n和直线l的方向向量l,证明n·l=0,得l∥α.(ii)证明直线l的方向向量l能被平面α内的两个基底向量所表示,得l∥α.2.求线面角的方法.①定义法:作出线面角,解三角形即可.②解斜线段、射影、垂线段构成的三角形.例:求AB与平面α所成角θ的正弦值,其中A∈α.只需求出点B到平面α的距离d(通常由等体积法求d),由sin θ=得结论.③向量法:求出平面α的法向量n,设直线AB与α所成角为θ,则sin θ=|cos<n,>|.最好是画出图形,否则容易出错.B组统一命题、省(区、市)卷题组考点一空间角1.(2018课标全国Ⅰ理,12,5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为()A.B.C.D.答案A2.(2018课标全国Ⅱ理,16,5分)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成角为45°.若△SAB的面积为5,则该圆锥的侧面积为.答案40π3.(2018课标全国Ⅱ理,20,12分)如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点. (1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.解析(1)证明:因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2.连接OB.因为AB=BC=AC,所以△ABC为等腰直角三角形,且OB⊥AC,OB=AC=2.由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.(2)如图,以O为坐标原点,的方向为x轴正方向,建立空间直角坐标系O-xyz.由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2),=(0,2,2).取平面PAC的法向量=(2,0,0).设M(a,2-a,0)(0<a≤2),则=(a,4-a,0).设平面PAM的法向量为n=(x,y,z).由·n=0,·n=0得可取n=((a-4),a,-a),所以cos<,n>=.由已知可得|cos<,n>|=.所以=.解得a=-4(舍去)或a=.所以n=.又=(0,2,-2),所以cos<,n>=.所以PC与平面PAM所成角的正弦值为.4.(2018天津理,17,13分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(2)求二面角E-BC-F的正弦值;(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.解析本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.依题意,可以建立以D为原点,分别以,,的方向为x轴,y轴,z轴的正方向的空间直角坐标系(如图),可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M,N(1,0,2).(1)证明:依题意=(0,2,0),=(2,0,2).设n0=(x0,y0,z0)为平面CDE的法向量,则即不妨令z0=-1,可得n0=(1,0,-1).又=,可得·n0=0,又因为直线MN⊄平面CDE,所以MN∥平面CDE.(2)依题意,可得=(-1,0,0),=(1,-2,2),=(0,-1,2).设n=(x1,y1,z1)为平面BCE的法向量,则即不妨令z1=1,可得n=(0,1,1).设m=(x2,y2,z2)为平面BCF的法向量,则即不妨令z2=1,可得m=(0,2,1).因此有cos<m,n>==,于是sin<m,n>=.所以,二面角E-BC-F的正弦值为.(3)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h),可得=(-1,-2,h).易知,=(0,2,0)为平面ADGE的一个法向量,故|cos<,>|==,由题意,可得=sin 60°=,解得h=∈[0,2].所以,线段DP的长为.方法归纳利用空间向量解决立体几何问题的一般步骤(1)审清题意并建系.利用条件分析问题,建立恰当的空间直角坐标系;(2)确定相关点的坐标.结合建系过程与图形,准确地写出相关点的坐标;(3)确定直线的方向向量和平面的法向量.利用点的坐标求出相关直线的方向向量和平面的法向量,若已知某直线垂直某平面,可直接取该直线的方向向量为该平面的法向量;(4)转化为向量运算.将空间位置关系转化为向量关系,空间角转化为向量的夹角问题去论证、求解;(5)问题还原.结合条件与图形,作出结论(注意角的范围).5.(2017课标全国Ⅰ理,18,12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.解析本题考查空间点、线、面的位置关系以及二面角的概念和计算,考查学生的空间想象能力、推理论证能力和运算求解能力.(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.由于AB∥CD,故AB⊥PD,又AP∩PD=P,AP、PD⊂平面PAD,所以AB⊥平面PAD.又AB⊂平面PAB,所以平面PAB⊥平面PAD.(2)解法一(综合法):根据题意可设AB=1,因为AB∥CD,∠APD=∠BAP=∠CDP=90°,PA=PD=AB=DC,所以四边形ABCD是平行四边形,且AD=PC=PB=CB=,取PB的中点为F,连接AF,CF,在等腰三角形PAB中,可得AF⊥PB,在等边三角形PBC中,可得CF⊥PB,所以∠AFC为二面角A-PB-C的平面角,由(1)知AB⊥平面PAD,又AD⊂平面PAD,所以AB⊥AD.所以平行四边形ABCD是矩形,连接AC,则AC=.在△AFC中,AC=,AF=,FC=,由余弦定理可得cos∠AFC==-,所以二面角A-PB-C的余弦值为-.解法二(向量法):在平面PAD内作PF⊥AD,垂足为F.由(1)可知,AB⊥平面PAD,故AB⊥PF,又AD∩AB=A,可得PF⊥平面ABCD.以 F为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系F-xyz.由(1)及已知可得A,P,B,C.所以=,=(,0,0),=,=(0,1,0).设n=(x1,y1,z1)是平面PCB的法向量,则即可取n=(0,-1,-).设m=(x2,y2,z2)是平面PAB的法向量,则即可取m=(1,0,1).则cos<n,m>==-.易知二面角A-PB-C为钝二面角,所以二面角A-PB-C的余弦值为-.方法总结面面垂直的证明及向量法求解二面角.(1)面面垂直的证明.证明两个平面互相垂直,可以在一个平面内找一条直线l,证明直线l垂直于另一平面.(2)利用空间向量求解几何体中的二面角的余弦值.建立空间直角坐标系,找到点的坐标,求出两个半平面的法向量n1,n2,设二面角的大小为θ,则|cosθ|=,再根据二面角的范围判断二面角余弦值的正负情况.6.(2017天津理,17,13分)如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC 的中点,M是线段AD的中点,PA=AC=4,AB=2.(1)求证:MN∥平面BDE;(2)求二面角C-EM-N的正弦值;(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.解析本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.如图,以A为原点,分别以,,方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A(0,0,0),B(2,0,0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0,1),N(1,2,0).(1)证明:=(0,2,0),=(2,0,-2).设n=(x,y,z)为平面BDE的法向量,则即不妨设z=1,可得n=(1,0,1).又=(1,2,-1),可得·n=0.因为MN⊄平面BDE,所以MN∥平面BDE.(2)易知n1=(1,0,0)为平面CEM的一个法向量.设n2=(x,y,z)为平面EMN的法向量,则因为=(0,-2,-1),=(1,2,-1),所以不妨设y=1,可得n2=(-4,1,-2).因此有cos<n1,n2>==-,于是sin<n1,n2>=.所以,二面角C-EM-N的正弦值为.(3)依题意,设AH=h(0≤h≤4),则H(0,0,h),进而可得=(-1,-2,h),=(-2,2,2).由已知,得|cos<,>|===,整理得10h2-21h+8=0,解得h=或h=.所以,线段AH的长为或.方法总结利用空间向量法证明线面位置关系与计算空间角的步骤:(1)根据题目中的条件,充分利用垂直关系,建立适当的空间直角坐标系,尽量使相关点在坐标轴上,求出相关点的坐标;(2)求出相关直线的方向向量及相关平面的法向量,根据题目的要求,选择适当的公式,将相关的坐标代入进行求解或证明;(3)检验,得出最后结论.7.(2017课标全国Ⅱ理,19,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.解析本题考查了线面平行的证明和线面角、二面角的计算.(1)取PA的中点F,连接EF,BF.因为E是PD的中点,所以EF∥AD,EF=AD.由∠BAD=∠ABC=90°得BC∥AD,又BC=AD,所以EF BC,四边形BCEF是平行四边形,CE∥BF,又BF⊂平面PAB,CE⊄平面PAB,故CE∥平面PAB.(2)由已知得BA⊥AD,以A为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,),=(1,0,-),=(1,0,0).设M(x,y,z)(0<x<1),则=(x-1,y,z),=(x,y-1,z-). 因为BM与底面ABCD所成的角为45°,而n=(0,0,1)是底面ABCD的法向量,所以|cos<,n>|=sin 45°,=,即(x-1)2+y2-z2=0.①又M在棱PC上,设=λ,则x=λ,y=1,z=-λ.②由①②解得(舍去),或所以M,从而=.设m=(x0,y0,z0)是平面ABM的法向量,则即所以可取m=(0,-,2).于是cos<m,n>==.易知所求二面角为锐角.因此二面角M-AB-D的余弦值为.方法总结本题涉及直线与平面所成的角和二面角,它们是高考热点和难点,解决此类题时常利用向量法,解题关键是求平面的法向量,再由向量的夹角公式求解.解题关键由线面角为45°求点M的坐标是解题的关键.考点二空间向量在立体几何中的应用1.(2018课标全国Ⅰ理,18,12分)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC 折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.解析(1)由已知可得,BF⊥EF,又BF⊥PF,且PF,EF⊂平面PEF,PF∩EF=F,所以BF⊥平面PEF,又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.以H为坐标原点,的方向为y轴正方向,||为单位长,建立如图所示的空间直角坐标系H-xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=,又PF=1,EF=2,可得PH=,EH=,则H(0,0,0),P,D,=,=为平面ABFD的法向量.设DP与平面ABFD所成角为θ,则sin θ===.所以DP与平面ABFD所成角的正弦值为.易错警示利用空间向量求线面角的注意事项(1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角即为所求.(2)若求线面角的余弦值,要注意利用平方关系sin2θ+cos2θ=1求出其值,不要误以为直线的方向向量与平面的法向量所夹角的余弦值为所求.2.(2017山东理,17,12分)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是的中点.(1)设P是上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.解析本题考查线面垂直的证明和二面角的计算.(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP,又BP⊂平面ABP,所以BE⊥BP,又∠EBC=120°,因此∠CBP=30°.取的中点H,连接EH,GH,CH.因为∠EBC=120°,所以四边形BEHC为菱形,所以AE=GE=AC=GC==.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,所以∠EMC为所求二面角的平面角.又AM=1,所以EM=CM==2.在△BEC中,由于∠EBC=120°,由余弦定理得EC2=22+22-2×2×2×cos120°=12,所以EC=2,因此△EMC为等边三角形,故所求的角为60°.解法二:以B为坐标原点,分别以BE,BP,BA所在的直线为x,y,z轴,建立如图所示的空间直角坐标系.由题意得A(0,0,3),E(2,0,0),G(1,,3),C(-1,,0),故=(2,0,-3),=(1,,0),=(2,0,3),设m=(x1,y1,z1)是平面AEG的法向量.由可得取z1=2,可得平面AEG的一个法向量m=(3,-,2).设n=(x2,y2,z2)是平面ACG的法向量.由可得取z2=-2,可得平面ACG的一个法向量n=(3,-,-2).所以cos<m,n>==.易知所求角为锐二面角,因此所求的角为60°.方法总结求二面角的常见方法有两种:一种是“找”,即根据二面角的面的特殊性(如等边三角形、等腰三角形、直角三角形、正方形、矩形、梯形等)找二面角的平面角的顶点,进而作出该平面角,再通过解三角形求解;另一种是“算”,即利用空间向量的坐标运算,由平面的法向量和夹角公式求解.利用空间向量的运算求二面角时,一定要注意二面角是锐二面角还是钝二面角.3.(2016天津,17,13分)如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.解析依题意,OF⊥平面ABCD,如图,以O为原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,依题意可得O(0,0,0),A(-1,1,0),B(-1,-1,0),C(1,-1,0),D(1,1,0),E(-1,-1,2),F(0,0,2),G(-1,0,0).(1)证明:依题意,=(2,0,0),=(1,-1,2).设n1=(x,y,z)为平面ADF的法向量,则即不妨设z=1,可得n1=(0,2,1),又=(0,1,-2),可得·n1=0,又因为直线EG⊄平面ADF,所以EG∥平面ADF.(2)易证=(-1,1,0)为平面OEF的一个法向量.依题意,=(1,1,0),=(-1,1,2).设n2=(x,y,z)为平面CEF的法向量,则即不妨设x=1,可得n2=(1,-1,1).因此有cos<,n2>==-,于是sin<,n2>=.所以,二面角O-EF-C的正弦值为.(3)由AH=HF,得AH=AF.因为=(1,-1,2),所以==,进而有H,从而=,因此cos<,n2>==-.所以,直线BH和平面CEF所成角的正弦值为.评析本题主要考查直线与平面平行和垂直、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.4.(2016北京,17,14分)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(1)求证:PD⊥平面PAB;(2)求直线PB与平面PCD所成角的正弦值;(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.解析(1)证明:因为平面PAD⊥平面ABCD,AB⊥AD,所以AB⊥平面PAD.所以AB⊥PD.又因为PA⊥PD,PA∩AB=A,所以PD⊥平面PAB.(2)取AD的中点O,连接PO,CO.因为PA=PD,所以PO⊥AD.又因为PO⊂平面PAD,平面PAD⊥平面ABCD,所以PO⊥平面ABCD.因为CO⊂平面ABCD,所以PO⊥CO.因为AC=CD,所以CO⊥AD.如图建立空间直角坐标系O-xyz.由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1).设平面PCD的法向量为n=(x,y,z),则即令z=2,则x=1,y=-2.所以n=(1,-2,2).又=(1,1,-1),所以cos<n,>==-.所以直线PB与平面PCD所成角的正弦值为.(3)设M是棱PA上一点,则存在λ∈[0,1]使得=λ.因此点M(0,1-λ,λ),=(-1,-λ,λ).因为BM⊄平面PCD,所以BM∥平面PCD当且仅当·n=0,即(-1,-λ,λ)·(1,-2,2)=0.解得λ=.所以在棱PA上存在点M使得BM∥平面PCD,此时=.易错警示(1)证线面垂直时,要在“面”内找两条相交直线,分别与“线”垂直.(2)建立空间直角坐标系前,先明确备选坐标轴之间的两两垂直关系.(3)用向量法说明在某线段上存在满足某条件的点时,参数的取值范围易被忽视.评析本题考查线面垂直的证明,空间向量的应用等,对学生的空间想象能力、运算能力均有较高要求.C组教师专用题组考点一空间角1.(2014广东,5,5分)已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是()A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)答案B2.(2014课标Ⅱ,11,5分)直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM 与AN所成角的余弦值为()A. B.C. D.答案C3.(2015四川,14,5分)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ 上,E,F分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.答案4.(2018天津文,17,13分)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB 的中点,AB=2,AD=2,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.解析本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识.考查空间想象能力、运算求解能力和推理论证能力.(1)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.(2)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.在Rt△DAM中,AM=1,故DM==.因为AD⊥平面ABC,故AD⊥AC.在Rt△DAN中,AN=1,故DN==.在等腰三角形DMN中,MN=1,可得cos∠DMN==.所以,异面直线BC与MD所成角的余弦值为.(3)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=.又因为平面ABC⊥平面ABD,而CM⊂平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.在Rt△CAD中,CD==4.在Rt△CMD中,sin∠CDM==.所以,直线CD与平面ABD所成角的正弦值为.。

专题九立体几何与空间向量(教师版)--2020-2023高考真题数学专题分类汇编

专题九立体几何与空间向量--2020-2023高考真题数学专题分类汇编真题卷题号考点考向2023新课标1卷12基本的立体图形正方体、球体、四面体、圆柱体的结构特征14简单几何体的表面积与体积求四棱台的体积18空间直线、平面的垂直、二面角线线平行的判定、已知二面角确定动点位置2023新课标2卷9基本的立体图形、二面角圆锥的结构特征、圆锥的表面积与体积、二面角的定义14简单几何体的表面积与体积求四棱台的体积20空间直线、平面的垂直、二面角异面垂直的判定、求二面角2022新高考1卷4简单几何体的表面积与体积求棱台的体积8简单几何体的表面积与体积、外接球求棱锥的体积、球的切接问题9空间角求异面直线成角、线面角19空间中的距离、空间角求点到平面的距离、求二面角2022新高考2卷7简单几何体的表面积与体积求外接球的表面积11简单几何体的表面积与体积求三棱锥的体积20空间直线、平面的平行、空间角线面平行的判定、求二面角2021新高考1卷3基本的立体图形求圆锥的母线长12基本的立体图形几何体中的动点问题（动点轨迹、三棱锥的体积、线线垂直的判定、线面垂直的判定）20空间直线、平面的垂直、简单几何体的表面积与体积线线垂直的判定、求三棱锥的体积4简单几何体的表面积与体积求球的表面积2021新高考2卷5简单几何体的表面积与体积求正四棱台的体积10空间直线、平面的垂直线线垂直的判定19空间直线、平面的垂直、空间角面面垂直的判定、求二面角2020新高考1卷4空间角求线面角16基本的立体图形球的截面问题20空间直线、平面的垂直、空间角线面垂直的判定、求线面角正弦值的最值2020新高考2卷13简单几何体的表面积与体积求三棱锥的体积20空间直线、平面的垂直、空间角线面垂直的判定、求线面角【2023年真题】1.（2023·新课标I 卷第12题）（多选）下列物体中，能够被整体放入棱长为1(单位：)m 的正方体容器(容器壁厚度忽略不计)内的有()A.直径为0.99m 的球体B.所有棱长均为1.4m 的四面体C.底面直径为0.01m ，高为1.8m 的圆柱体D.底面直径为1.2m ，高为0.01m 的圆柱体【答案】ABD 【解析】【分析】本题考查正方体内接其它几何体的问题，属于综合题.由正方体、球体、四面体、圆柱体的结构特征和棱长、直径的大小关系，逐个分析选项可得解.【解答】解：选项A ，正方体的内切球直径为10.99>，故A 正确;选项B ，连接正方体的六个面对角线，可以得到一个正四面体， 1.4>，故B 正确;对于C ，D ，假设放入最大的圆柱AB ，A ，B 分别为圆柱下、上底面的圆心，设圆柱底面半径为r ，正方体体对角线为CD ，||3CD =263AC ∴=，当r 取定时，圆柱的高 max 36.h r =对于C ，当0.005r =时， max 360.005 1.72 1.8h =≈<，故C 错．对于D ，当0.6r =时， max 30.660.260.01h =->，故D 正确．故选：.ABD 2.（2023·新课标II 卷第9题）（多选）已知圆锥的顶点为P ，底面圆心为O ，AB 为底面直径，120,2APB PA ︒∠==，点C 在底面圆周上，且二面角P AC O --为45︒，则()A.该圆锥的体积为πB.该圆锥的侧面积为43πC.22AC =D.PAC ∆3【答案】AC 【解析】【分析】本题考查求圆锥的体积与侧面积，及圆锥中的其他量，属于基础题.A ，B 选项，通过解PAB ∆，求出圆锥的高PO 与底面直径AB ，从而求出体积与侧面积；C ，D 选项，利用PDO ∠为二面角P AC O --的平面角，解三角形求出,PD AC 的长，进一步求出PAC ∆的面积.【解答】解：对于A ：在PAB ∆中，2,120PA PB APB ︒==∠=，则1PO =，23AB =故圆锥的体积2111333V PO OA πππ=⋅⋅⋅=⋅⋅⋅=，故A 正确；对于B ：圆锥的侧面展开图为扇形，扇形的半径为2，弧长为，故圆锥的侧面积为122S =⋅⋅=，故B 错误；对于C ：取AC 中点D ，连接,PD OD ，则,PD AC OD AC ⊥⊥，则PDO ∠为二面角P AC O --的平面角，即45PDO ︒∠=，在Rt PDO ∆中，1PO =，故1,DO PD ==，在Rt ODA ∆中，AD ===，故AC =C 正确；对于D ：11222PAC S PD AC ∆=⋅⋅==，故D 正确.故选.AC 3.（2023·新课标I 卷第14题）在正四棱台1111ABCD A B C D -中，2AB =，111A B =，1AA =，则该棱台的体积为__________【答案】【解析】【分析】本题考查正四棱台的体积，属于中档题．可将正四棱台补成正四棱锥，然后分析求解即可．【解答】解：如图，将正四棱台1111ABCD A B C D -补成正四棱锥，则 2AO =，22SA =，162OO =，故 12121(3V S S S S h =++，2222166(2121).326V =⨯++⨯⨯4.（2023·新课标II 卷第14题）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为__________【答案】28【解析】【分析】本题主要考查棱台的体积，属于基础题．根据题意正四棱锥被截后剩余部分为正四棱台，直接计算即可求解．【解答】解：由题意可得四棱台的高为3，上底面面积为224⨯=，下底面面积为4416⨯=，故正四棱台的体积 1(416416)328.3V =⨯+⨯⨯=所得棱台的体积为28.5.（2023·新课标I 卷第18题）如图，在正四棱柱1111ABCD A B C D -中，2AB =，1 4.AA =点2A ，2B ，2C ，2D ，分别在棱1AA ，1BB ，1CC ，1DD 上，21AA =，222BB DD ==，2 3.CC =(1)证明：2222//B C A D ；(2)点P 在棱1BB 上，当二面角222P A C D --为150 时，求2.B P【答案】证明：(1)如图，作21A E BB ⊥于点E ，21D F CC ⊥于点F ，则有22//A E D F ，22A E D F =，即四边形22A EFD 是平行四边形，从而22//A D EF ，又22//B E C F ，221B E C F ==，即四边形22B EFC 是平行四边形，从而22//B C EF ，从而2222//B C A D ，得证.(2)如图，以点B 为原点，以BC 、BA 、1BB 分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系.设(0,0,)P t ，2(2,0,3)C ，2(0,2,1)A ，2(2,2,2)D ，22(2,0,1)A D = ，22(2,-2,2)A C = ，2(0,-2,1)A P t =-，设平面222A C D 的一个法向量为，则，即，令12z =-，则11x =，11y =-，故(1,1,2)m =--设平面22PA C 的一个法向量为，则，即，令22z =，则23x t =-，21y t =-，故(3,1,2)n t t =--二面角222P A C D --的平面角为150 ，，解得1t =或3，则2 1.B P =【解析】本题考查了立体几何中线线平行的判定、二面角等知识，属于中档题.(1)作21A E BB ⊥于点E ，21D F CC ⊥于点F ，构造两个平行四边形，根据平行于同一直线的两直线平行，即可证明2222//.B C A D (2)适当建立空间直角坐标系，设点(0,0,)P t ，分别求出平面222A C D 与平面22PA C 的一个法向量,m n，由二面角222P A C D --为150 ，可知，解出t 的值，进而求得2 1.B P =6.（2023·新课标II 卷第20题）如图三棱锥A BCD -中，DA DB DC ==，BD CD ⊥，60ADB ADC ︒∠=∠=，E 为BC 的中点.(1)证明：;BC DA ⊥(2)点F 满足EF DA =，求二面角D AB F --的正弦值.【答案】解：(1)连接AE ，DE ，DB DC = ，DE BC ∴⊥，又DA DB DC == ，60ADB ADC ︒∠=∠=，ACD ∴ 与ABD 均为等边三角形，AC AB ∴=，AE BC ∴⊥，AE DE E ⋂=，BC ∴⊥平面ADE ，.BC DA ∴⊥(2)设2DA DB DC ===，BC ∴=DE AE ∴==，2AD =，2224AE DE AD ∴+==，AE DE ∴⊥，又AE BC ⊥ ，DE BC E ⋂=，AE ∴⊥平面BCD ，如图建立空间直角坐标系，D ∴，A，B ，(0,0,0)E，(EF DA F =⇒，(DA ∴=，AB =，(AF =，设平面DAB 与平面ABF 的一个法向量分别为1111(,,)n x y z = ，2222(,,)n x y z =，设二面角D AB F --平面角为θ，，1212|||cos |3||||n n n n θ⋅∴=== ，3sin 3θ∴=【解析】本题考查了线面垂直的性质、二面角的求解，是中档题.(1)先判定线面垂直，再结合线面垂直的性质定理得结论；(2)建立空间直角坐标系，得出平面DAB 的法向量和平面ABF 的法向量，由空间向量求解可得结论.【2022年真题】7.（2022·新高考I 卷第4题）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148.5m 时，相应水面的面积为2140.0;km 水位为海拔157.5m 时，相应水面的面积为2180.0.km 将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m 上升到157.5m时，增加的水量约为 2.65)≈()A.931.010m ⨯B.931.210m ⨯ C.931.410m ⨯ D.931.610m ⨯【答案】C 【解析】【分析】本题考查了棱台的体积公式的应用，属于基础题.读懂题意，结合棱台的体积公式即可求解.【解答】解：依据棱台的体积公式1(3V S S h =⋅+'+⋅1(14000000018000000093=⋅+⨯931.410.m ≈⨯8.（2022·新高考I 卷第8题）已知正四棱锥的侧棱长为l ，其各顶点都在同一个球面上，若该球的体积为36π，且3l ，则该正四棱锥体积的取值范围是()A.81[18,4B.2781[,]44C.2764[,]43D.[18,27]【答案】C 【解析】【分析】本题考查了球的切接问题，涉及棱锥的体积、球的体积、导数等知识，属较难题.有正四棱锥的外接球的性质，可得2212(6)33V a h h h h ==-，利用求导求最值，即可解答.【解答】解：方法(1):设正四棱锥P ABCD -的高为1PO h =，底面边长为a ，球心为O ，由已知易得球半径为3R =，所以22222222)(3)9622(6))2a h h l a h h a h l ⎧+-=⎪⎧=⎪⇒⎨⎨=-⎩⎪+=⎪⎩，因为393962722l h h ⇒⇒，故所以2212(6)33V a h h h h ==-，求导2(4)V h h '=-，所以22(6)3V h h =-在3[,4]2上单调递增，在9[4,2上单调递减，所以max 64(4)3V V ==，min 39327min{(),(()2224V V V V ===，故该正四棱锥体积的取值范围是2764[,].43方法(2):由方法(1)中知22(6)3V h h =-，3922h ，求导2(4)V h h '=-，所以22(6)3V h h =-在3[,4]2上单调递增，在9[4,2上单调递减，所以max 64(4)3V V ==，min 39327min{(),(()2224V V V V ===，故该正四棱锥体积的取值范围是2764[,].439.（2022·新高考II 卷第7题）已知正三棱台的高为1，上下底面的边长分别为同一球面上，则该球的表面积为()A.100π B.128πC.144πD.192π【答案】A 【解析】【分析】本题主要考查了正三棱台和外接球的关系应用，球体表面积公式的应用.【解答】解：由题意易得上底面所在平面截球面所得圆的半径为3，下底面所在平面截球面所得圆的半径为4，设该球的半径为R ，当正三棱台的上、下底面在球心异侧时，1=，无解；所以正三棱台的上、下底面在球心同侧，所以1=，解得225R =，因此该球的表面积为24100.S R ππ==10.（2022·新高考I 卷第9题）（多选）已知正方体1111ABCD A B C D -，则()A.直线1BC 与1DA 所成的角为90︒B.直线1BC 与1CA 所成的角为90︒C.直线1BC 与平面11BB D D 所成的角为45︒D.直线1BC 与平面ABCD 所成的角为45︒【答案】ABD 【解析】【分析】本题主要考查直线与直线所成角及直线与平面所成角，属于中档题.根据正方体的结构特征对各个选项逐一判断分析，即可得解.【解答】解：如图，因为11BC B C ⊥，11//B C DA ，所以11BC DA ⊥，故A 正确;对于选项:B 因为11A B ⊥平面11BB C C ，1BC ⊂平面11BB C C ，所以111BC A B ⊥，又11BC B C ⊥，且1111A B B C B ⋂=，11A B ，1B C ⊂平面11CDA B ，所以1BC ⊥平面11CDA B ，且1CA ⊂平面11CDA B ，所以直线11BC CA ⊥，故B 正确;对于选项:C 连接11AC 与11B D 交于点1O ，因为1B B ⊥平面1111A B C D ，11AC ⊂平面1111A B C D ，所以111B B A C ⊥，又1111A C B D ⊥，且1111B D B B B ⋂=，11B D ，1B B ⊂平面11BB D D ，所以11A C ⊥平面11BB D D ，则11O BC ∠即为直线1BC 与平面11BB D D 所成的角，111111sin 2O C O BC BC ∠==，所以1130O BC ∠=︒，故C 错误;对于选项:D 直线1BC 与平面ABCD 所成的角即为145C BC ∠=︒，所以D 正确.11.（2022·新高考II 卷第11题）（多选）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，//FB ED ，2AB ED FB ==，记三棱锥E ACD -，F ABC -，F ACE -的体积分别为1V ，2V ，3V ，则()A.322V V =B.312V V =C.312V V V =+D.3123V V =【答案】CD 【解析】【分析】本题主要考查三棱锥的体积，属于基础题.【解答】解：设22AB ED FB ===，则1142233V =⨯⨯=，21221.33V =⨯⨯=连结BD 交AC 于M ，连结EM 、FM ，则FM =，EM =3EF =，故13222EMF S ==，3123EMF V S AC =⨯= ，312V V V =+，3123.V V =12.（2022·新高考I 卷第19题）如图，直三棱柱111ABC A B C -的体积为4，1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值.【答案】解：(1)设A 到平面1A BC 的距离为d ，因为直三棱柱111ABC A B C -的体积为4，即可得14ABC S AA ⋅= ，故111433A ABC ABC V S AA -=⋅= ，又111114333A ABC A A BC A BC V V S d d --==⋅=⨯= ，解得d =，所以A 到平面1A BC 的距离为；(2)连接1AB ，因为直三棱柱111ABC A B C -中，1AA AB =，故四边形11AA B B 为正方形，即11AB A B ⊥，又平面1A BC ⊥平面11ABB A ，平面1A BC ⋂平面111ABB A A B =，1AB ⊂平面11ABB A ，故1AB ⊥平面1A BC ，因为BC ⊂平面1A BC ，所以1AB BC ⊥，又因为1AA BC ⊥，11,AB AA ⊂平面11ABB A ，且11AB AA A ⋂=，故BC ⊥平面11ABB A ，因为AB ⊂平面11ABB A ，则BC AB ⊥，所以1,,BB AB BC 三条直线两两垂直，故如图可以以B为原点建立空间直角坐标系，设1AA AB a ==，BC b =，则1A B =，由条件可得，解得，则(0,0,0)B ，(2,0,0)C ，(0,2,0)A ，1(0,2,2)A ，1AC 的中点(1,1,1)D ，所以(0,2,0)BA = ，(1,1,1)BD = ，(2,0,0)BC =，设平面ABD 的一个法向量为1(,,)n x y z =，，取1(1,0,1)n =-，同理可求得平面BCD 的一个法向量为2(0,1,1)n =-，所以1212121|cos ,|2n n n n n n ⋅<>==，所以二面角A BD C --的正弦值为2【解析】本题考查了平面与平面所成角的空间向量求法、点到面的距离的几何求法、几何体的体积公式，考查了空间中的垂直关系的证明与应用，属于中档题.(1)利用等体积法以及三棱锥的体积公式即可求解.(2)根据题干首先证明1,,BB AB BC 三条直线两两垂直，且12AA AB BC ===，建立直角坐标系，求出平面ABD 的一个法向量和平面BCD 的一个法向量，利用向量法即可求出二面角A BD C --的正弦值.13.（2022·新高考II 卷题20题）如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 是PB 的中点.(1)证明：//OE 平面;PAC (2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --正弦值.【答案】解：(1)法一：连接OA 、OB ，因为PO 是三棱锥P ABC -的高，所以PO ⊥平面ABC ，所以PO OA ⊥，PO OB ⊥，所以90POA POB ∠=∠=︒，又PA PB =，PO PO =，所以POA ≌POB ，所以OA OB =，作AB 中点D ，连接OD 、DE ，则有OD AB ⊥，又AB AC ⊥，所以//OD AC ，又因为OD ⊂/平面PAC ，AC ⊂平面PAC ，所以//OD 平面PAC ，又D 、E 分别为AB 、PB 的中点，所以，在BPA 中，//DE PA 又因为DE ⊂/平面PAC ，PA ⊂平面PAC ，所以//DE 平面PAC ，又OD 、DE ⊂平面ODE ，OD DE D ⋂=，所以平面//ODE 平面PAC ，又OE ⊂平面ODE ，所以//OE 平面;PAC 法二：(1)连接OA 、OB ，因为PO 是三棱锥P ABC -的高，所以PO ⊥平面ABC ，所以PO OA ⊥，PO OB ⊥，所以90POA POB ∠=∠=︒，又PA PB =，PO PO =，所以POA ≌POB ，所以OA OB =，又AB AC ⊥，在Rt ABF ，O 为BF 中点，延长BO ，交AC 于F ，连接PF ，所以在PBF 中，O 、E 分别为BF 、PB 的中点，所以//EO PF ，因为EO ⊂/平面PAC ，PF ⊂平面PAC ，所以//EO 平面;PAC(2)法一：过点D 作//DF OP ，以DB 为x 轴，DO 为y 轴，DF 为z 轴.建立如图所示的空间直角坐标系.因为3PO =，5PA =，由(1)4OA OB ==，又30ABO CBO ∠=∠=︒，所以2OD =，23DB =，所以(0,2,3)P ，(23,0,0)B ，(23,0,0)A -，3(3,1,)2E ，设AC a =，则(23,,0)C a -，平面AEB 的法向量设为1111(,,)n x y z = ，直线AB 的方向向量可设为(1,0,0)a =，直线DP ⊂平面AEB ，直线DP 的方向向量为(0,2,3)b =，所以，所以10x =，设13y =，则12z =-，所以1(0,3,2);n =-平面AEC 的法向量设为2222(,,)n x y z = ，(0,,0)AC a = ，3(33,1,)2AE = ，所以，所以20y =，设23x =，则26z =-，所以3,0,6);n =-所以1cos n < ，1221212124313||||1339133n n n n n ⋅>====⋅⨯，二面角C AE B --的平面角为θ，则211sin 1cos 13θθ=-=，所以二面角C AE B --的正弦值为1113法二：(2)过点A 作//AF OP ，以AB 为x 轴，AC 为y 轴，AF 为z 轴建立所示的空间直角坐标系.因为3PO =，5PA =，由(1)4OA OB ==，又30ABO CBO ︒∠=∠=，所以，43AB =，所以(23,2,3)P ，(43,0,0)B ，(0,0,0)A ，3(33,1,)2E ，设AC a =，则(0,,0)C a ，平面AEB 的法向量设为1111(,,)n x y z = ，(43,0,0)AB = ，3(33,1,)2AE = ，所以，所以10x =设12z =-，则13y =，所以1(0,3,2);n =-平面AEC 的法向量设为2(,,)n x y z = ，(0,,0)AC a = ，3(33,1,)2AE = ，所以，所以20y =，设23x =，则26z =-，所以2(3,0,6);n =-所以1cos n < ，1221212124313||||1339133n n n n n ⋅>====⋅⨯二面角C AE B --的平面角为θ，则211sin 1cos 13θθ=-=，所以二面角C AE B --的正弦值为11.13【解析】本题考查线面平行与二面角的求解，考查学生的空间想象与计算能力，有一定的难度.【2021年真题】14.（2021·新高考I 卷第3题）已知圆锥的底面半径为2，其侧面展开图为一个半圆，则该圆锥的母线长为()A.2B.22C.4D.42【答案】B 【解析】【分析】本题考查圆锥的侧面展开图，属于基础题.设圆锥母线长为l ，求出圆锥的底面周长，即为展开图半圆的弧长，计算可得答案.【解答】解：设圆锥的母线长为l ，所以底面圆周长为，由展开图可知半圆的弧长为，所以l π=，得l =，故选：.B 15.（2021·新高考II 卷第4题）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为36000km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ，半径r 为6400km 的球，其上点A 的纬度是指OA 与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α，记卫星信号覆盖地球表面的表面积为22(1cos )(S r πα=-单位：2km )，则S 占地球表面积的百分比约为()A.26% B.34%C.42%D.50%【答案】C 【解析】【分析】本题考查球的表面积，考查直线与平面所成的角，属于中档题.由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.【解答】解：如图所示：由题意可得，S 占地球表面积的百分比约为：222(1cos )1cos 42r r πααπ--=640016400360000.4242%.2-+=≈=故选.C 16.（2021·新高考II 卷第5题）正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为()A.20+B. C.563D.2823【答案】D 【解析】【分析】本题考查了棱台的结构特征与体积的求法.由正四棱台的几何特征算出该几何体的高及上下底面面积，再由棱台的体积公式即可得解.【解答】解：作出图形，连接该正四棱台上下底面的中心，如图所示，因为该正四棱台上下底面边长分别为2，4，侧棱长为2，所以该棱台的高h ==下底面面积116S =，上底面面积24S =，所以该棱台的体积121(3V h S S =+1(16433=+=故选：.D 17.（2021·新高考I 卷第12题）（多选）在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+，其中[0,1]λ∈，[0,1]μ∈，则()A.当1λ=时，1AB P 的周长为定值B.当1μ=时，三棱锥1P A BC -的体积为定值C.当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D.当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P【答案】BD 【解析】【分析】本题考查了动点轨迹，线面平行与线面垂直的判定，锥体的体积问题等，综合性强，考查了逻辑推理能力与空间想象能力，属于拔高题．判断当1λ=时，点P 在线段1CC 上，分别计算点P 为两个特殊点时的周长，即可判断选项A ；当1μ=时，点P 在线段11B C 上，利用线面平行的性质以及锥体的体积公式，即可判断选项B ；当12λ=时，取线段BC ，11B C 的中点分别为M ，1M ，连结1M M ，则点P 在线段1M M 上，分别取点P 在1M ，M 处，得到均满足1A P BP ⊥，即可判断选项C ；当12μ=时，取1CC 的中点1D ，1BB 的中点D ，则点P 在线的1DD 上，证明当点P 在点1D 处时，1A B ⊥平面11AB D ，利用过定点A 与定直线1A B 垂直的平面有且只有一个，即可判断选项.D 【解答】解：对于A ，当1λ=时，1BP BC BB μ=+ ，即1CP BB μ=，所以1//CP BB ，故点P 在线段1CC 上，此时1AB P 的周长为11AB B P AP ++，当点P 为1CC 的中点时，1AB P 的周长为+，当点P 在点1C 处时，1AB P 的周长为1+，故周长不为定值，故选项A 错误；对于B ，当1μ=时，1BP BC BB λ=+ ，即1B P BC λ= ，所以1//B P BC ，故点P 在线段11B C 上，因为11//B C 平面1A BC ，所以直线11B C 上的点到平面1A BC 的距离相等，又1A BC 的面积为定值，所以三棱锥1P A BC -的体积为定值，故选项B 正确；对于C ，当12λ=时，取线段BC ，11B C 的中点分别为M ，1M ，连接1M M ，因为112BP BC BB μ=+ ，即1MP BB μ= ，所以1//MP BB ，则点P 在线段1M M 上，当点P 在1M 处时，1111A M B C ⊥，111A M B B ⊥，又1111B C B B B ⋂=，所以11A M ⊥平面11BB C C ，又1BM ⊂平面11BB C C ，所以111A M BM ⊥，即1A P BP ⊥，同理，当点P 在M 处，1A P BP ⊥，故选项C 错误；对于D ，当12μ=时，取1CC 的中点1D ，1BB 的中点D ，因为112BP BC BB λ=+ ，即DP BC λ= ，所以//DP BC ，则点P 在线的1DD 上，当点P 在点1D 处时，取AC 的中点E ，连接1A E ，BE ，因为BE ⊥平面11ACC A ，又1AD ⊂平面11ACC A ，所以1AD BE ⊥，在正方形11ACC A 中，11AD A E ⊥，又1BE A E E ⋂=，BE ，1A E ⊂平面1A BE ，故1AD ⊥平面1A BE ，又1A B ⊂平面1A BE ，所以11A B AD ⊥，在正方体形11ABB A 中，11A B AB ⊥，又11AD AB A ⋂=，1AD ，1AB ⊂平面11AB D ，所以1A B ⊥平面11AB D ，因为过定点A 与定直线1A B 垂直的平面有且只有一个，故有且仅有一个点P ，使得1A B ⊥平面1AB P ，故选项D 正确．故选：.BD 18.（2021·新高考II 卷第10题）（多选）如图，在正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点，则满足MN OP ⊥的是()A. B.C. D.【答案】BC【解析】【分析】本题考查了空间中两直线的位置关系以及垂直的判定，考查了数形结合思想和直观想象能力，属于中档题.根据线面垂直的判定定理可得BC 的正误，平移直线MN 构造所考虑的线线角后可判断AD 的正误.【解答】解：设正方体的棱长为2，对于A ，如图(1)所示，连接AC ，易知//MN AC ，且MN 、AC 、OP 在同一平面内，由图可知直线OP 与AC 相交且不垂直，故MN OP ⊥不成立，故A 错误.对于B ，如图(2)所示，取MT 的中点为Q ，连接PQ ，OQ ，则OQ MT ⊥，PQ MN ⊥，由正方体SBCN MADT -可得SM ⊥平面MADT ，而OQ ⊂平面MADT ，故SM OQ ⊥，而SM MT M ⋂=，SM ，MT ⊂平面SNTM ，故OQ ⊥平面SNTM ，又MN ⊂平面SNTM ，所以OQ MN ⊥，而OQ PQ Q ⋂=，,OQ PQ OPQ ⊂平面，所以MN ⊥平面OPQ ，而PO ⊂平面OPQ ，故MN OP ⊥，故B 正确.对于C ，如图(3)，连接BD ，则//BD MN ，由B 的判断可得OP BD ⊥，故OP MN ⊥，故C 正确.对于D ，如图(4)，取AM '的中点G ，连接PG ，OG ，M N ''，则//MN M N ''，PG =，OG =PO =，则222PO PG OG =+，可得PG OG ⊥，根据三角形的性质可知PO 与PG 不垂直，故PO 与MN 不垂直，故D 错误.故选.BC19.（2021·新高考I 卷第20题）如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.(1)证明：;OA CD ⊥(2)若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.【答案】(1)证明：AB AD = ，ABD ∴ 是以BD 为底的等腰三角形，又O 为BD 的中点，OA BD ∴⊥，平面ABD ⊥平面BCD ，且平面ABD ⋂平面BCD BD =，OA ⊂平面ABD ，OA ∴⊥平面BCD ，CD ⊂ 平面BCD ，.OA CD ∴⊥(2)解：以O 为坐标原点，OD 为y 轴，OA 为z 轴，垂直OD 且过O 的直线为x 轴，建立空间直角坐标系.OCD 是边长为1的等边三角形，，，，不妨设，点E 在棱AD 上，2DE EA =，12(0,,)33x E ∴，，，设向量为平面BCE 的法向量，设3a =，则1b =-，2c x=，即显然是平面BCD 的法向量，二面角E BC D --的大小为45︒，，即，解得1(x =舍去1)-，11133OA 21.33226A BCD BCD V S -∴=⋅=⨯⨯⨯⨯= 【解析】本题考查立体几何的面面垂直的性质，二面角余弦值的求法，三棱锥的体积.(1)先证明OA ⊥平面BCD ，利用线面垂直的性质即可证明.(2)先建系，利用已知二面角的角度求出三棱锥的高度，即可求解体积.20.（2021·新高考II 卷第19题）在四棱锥Q ABCD -中，底面ABCD 是正方形，若2,5, 3.AD QD QA QC ====(1)证明：平面QAD ⊥平面ABCD ；(2)求二面角B QD A --的平面角的余弦值．【答案】解：(1)证明：取AD 的中点为O ，连接,.QO CO因为QA QD =，OA OD =，则QO AD ⊥，而2,AD QA ==1AO DO ==， 2.QO ==在正方形ABCD 中，2AD CD ==，1DO =，故CO =，因为3QC =，故222QC QO OC =+，故QOC 为直角三角形且QO OC ⊥，因为OC AD O = ，OC 、AD ⊂平面ABCD ，故QO ⊥平面ABCD ，因为QO ⊂平面QAD ，故平面QAD ⊥平面.ABCD (2)在平面ABCD 内，过O 作//OT CD ，交BC 于T ，则OT AD ⊥，因为(1)中的QO ⊥平面ABCD ，OT ⊂平面ABCD ，QO OT ⊥，故可以OT 为x 轴，以OD 为y 轴，以OQ 为z 轴，建如图所示的空间直角坐标系.则，故(2,1,2),(2,2,0).BQ BD =-=- 设平面QBD 的一个法向量(,,)n x y z = ，则00n BQ n BD ⎧⋅=⎪⎨⋅=⎪⎩ 即，取1x =，则11,2y z ==，故1(1,1,).2n = 而平面QAD 的法向量为(1,0,0)m = ，故cos ⟨,m n ⟩12.3312==⨯又二面角B QD A --的平面角为锐角，故其余弦值为2.3【解析】本题考查了面面垂直的判定和运用空间向量求解二面角的问题，注意数形结合思想的运用.(1)取AD 的中点为O ，连接,QO CO ，可证QO ⊥平面ABCD ，从而得到平面QAD ⊥平面.ABCD(2)在平面ABCD内，过O作//⊥，以OT为x轴，以OD为y轴，以OQOT CD，交BC于T，则OT AD为z轴，建立空间直角坐标系，求出平面QAD、平面BQD的法向量后可求二面角的余弦值.【2020年真题】21.（2020·新高考I卷第4题、II卷第4题）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的O，地球上一点A的纬度是指OA与地晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为)球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40︒，则晷针与点A处的水平面所成角为()A.20︒B.40︒C.50︒D.90︒【答案】B【解析】【分析】本题是立体几何在生活中的运用，考查空间线面角的定义和求法，属于中档题．由纬度的定义和线面角的定义，结合直角三角形的性质，可得晷针与点A处的水平面所成角．【解答】解：可设A所在的纬线圈的圆心为O'，OO'垂直于纬线所在的圆面，由图可得OHA ∠为晷针与点A 处的水平面所成角，又40OAO ︒∠'=且OA AH ⊥，在Rt OHA 中，O A OH '⊥，40OHA OAO ︒∴∠=∠'=，故选：.B 22.（2020·新高考I 卷题16题）已知直四棱柱1111ABCD A BCD -的棱长均为2，60.BAD ︒∠=以1D 为5为半径的球面与侧面11BCC B 的交线长为________.【答案】22π【解析】【分析】本题考查空间中球与平面的交线问题，注意球心到面的距离和形成的交线位置与所对应的圆弧和圆心角，属于难题.由已知得点1D 到面11BB C C 的距离即为点1D 到11B C 的距离，3，则根据勾股定理可得截面的圆半径为532r =-=，球与侧面11BB C C 所形成的交线为一段圆弧，其圆心角为2π，则根据弧长公式即可得解.【解答】解：直四棱柱棱长为2，底面是边长为2的菱形，侧面是边长为2的正方形，又60BAD ︒∠=，可得111D C B =60∠︒，点1D 到面11BB C C 的距离即为点1D 到11B C 的距离，即为3则根据勾股定理可得截面的圆半径为r ==，11112B C >=，且2<，则球与侧面11BB C C 所形成的交线为一段圆弧，其圆心角为2π，故形成的交线长为222l ππ==.故答案为2.223.（2020·新高考II 卷题13题）已知正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，则三棱锥1A NMD -的体积为__________.【答案】13【解析】【分析】本题考查利用等体积法求多面体的体积，是基础的计算题．由题意画出图形，再由等体积法求三棱锥1A NMD -的体积．【解答】解：如图，正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，111122ANM S ∴=⨯⨯= ，111112.323A NMD D AMN V V --∴==⨯⨯=故答案为：1.324.（2020·新高考I 卷题20题）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面.ABCD 设平面PAD 与平面PBC 的交线为.l (1)证明：l ⊥平面;PDC (2)已知1PD AD ==，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值.【答案】解：(1)PD ⊥ 底面ABCD ，且AD ⊂平面ABCD ，PD AD ∴⊥，ABCD 为正方形，AD DC ∴⊥，又PD DC D ⋂= ，且PD 、DC 在平面PDC 内，AD ∴⊥平面PDC ，//AD BC ，且BC ⊂平面PBC ，AD ⊂/平面PBC ，//AD ∴平面PBC ，又平面PAD 与平面PBC 的交线为l ，且AD ⊂平面PAD ，//AD l ∴，l ∴⊥平面PDC ；(2)以D 为原点，以DA 、DC 、DP 分别为x 、y 、z 轴，建立空间直角坐标系如图所示：由1PD AD ==，得(0,0,1)P ，(1,1,0)B ，(0,1,0)C ，(0,0,0)D ，则(1,1,1)PB =- ，(0,1,0)DC = ，设点Q 的坐标为(,0,1)t ，平面QCD 的法向量为000(,,)n x y z =，则(,0,1)DQ t = ，即有，即，取01x =，得(1,0,)n t =-，又设PB 与n夹角为α，PB 与平面QCD 所成角为θ，则cos ||||PB n PB n α⋅=== ，于是sin θ==，当0t =时，3sin 3θ=，当0t <时，sin θ==，又1[()]2(()t t -+---当且仅当t 1=-时，取等号)，即得30sin 3θ<，当0t >时，sin θ==，又12(t t +当且仅当t 1=时，取等号)，即得36sin 33θ<，综上可知，PB 与平面QCD 所成角的正弦值的最大值为63【解析】本题考查了线面角的求解及线面垂直的判定定理、线面平行的判定定理和性质定理，属于拔高题．(1)本题先证明AD ⊥平面PDC ，再证明//AD 平面PBC ，再利用线面平行性质定理证得//AD l ，从而证得l ⊥平面PDC ；(2)本题可以建立空间直角坐标系，设出Q 点坐标，求出PB 和平面QDC 的法向量，再利用向量夹角公式求解，再结合基本不等式可求出PB 与平面QCD 所成角的正弦值最大值．25.（2020·新高考II 卷第20题）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面.ABCD 设平面PAD 与平面PBC 的交线为.l (1)证明：l ⊥平面PDC ；(2)已知1PD AD ==，Q 为l 上的点，QB =，求PB 与平面QCD 所成角的正弦值．【答案】解：(1)证明：过P 在平面PAD 内作直线//l AD ，由//AD BC ，可得//l BC ，即l 为平面PAD 和平面PBC 的交线，PD ⊥ 平面ABCD ，BC ⊂平面ABCD ，PD BC ∴⊥，又BC CD ⊥，CD PD D ⋂=，CD ，PD ⊂平面PCDBC ∴⊥平面PCD ，//l BC ，l ∴⊥平面PCD ；(2)如图，以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -，1PD AD == ，Q 为l 上的点，QB =，PB ∴=，1QP =，则(0,0,0)D ，(1,0,0)A ，(0,1,0)C ，(0,0,1)P ，(1,1,0)B ，设(1,0,1)Q ，则(1,0,1)DQ = ，(1,1,1)PB =- ，(0,1,0)DC = ，设平面QCD 的法向量为(,,)n a b c =，则，，取1c =，可得(1,0,1)n =- ，cos n ∴< ，63||||32n PB PB n PB ⋅>===⋅ PB ∴与平面QCD 所成角的正弦值为6.3【解析】本题考查空间线面垂直的判定，以及线面角的求法，考查转化思想和向量法的运用，考查运算能力和推理能力，属于中档题．(1)过P 在平面PAD 内作直线//l AD ，推得l 为平面PAD 和平面PBC 的交线，由线面垂直的判定和性质，即可得证；(2)以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -，求出(0,1,1)Q ，运用向量法，求得平面QCD 的法向量，结合向量的夹角公式求解即可．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020年高考数学试题分类汇编：空间向量
【考点阐述】
空间向量及其加法、减法与数乘．空间向量的坐标表示．空间向量的数量积．直线的方向向量．
【考试要求】
（3）理解空间向量的概念，掌握空间向量的加法、减法和数乘．
（4）了解空间向量的基本定理；理解空间向量坐标的概念．掌握空间向量的坐标运算．
（5）掌握空间向量的数量积的定义及其性质：掌握用直角坐标计算空间向量数量积的公式；掌握空间两点间距离公式．
（6）理解直线的方向向量、平面的法向量、向量在平面内的射影等概念．
【考题分类】
（一）填空题（共1题）
1.（海南宁夏卷理13）已知向量(0,1,1)a =-r ，(4,1,0)b =r ，||a b λ+=
r r 且0λ>，则λ= ____________.
解：由题意(4,1,)λ+-λλa b =2216(1)29(0)λλλ⇒+-+=>3λ⇒=。

2020年高考数学试题分类汇编：空间向量

2020年高考江苏版高考数学 专题十七 空间向量与立体几何

2019-2021全国高考数学真题汇编：空间向量(教师版)

2011-2020年高考数学真题分类汇编 专题24 空间向量与空间角的计算(学生版)

2020届山东省新高考高三优质数学试卷分项解析 专题09 立体几何与空间向量(解析版)

备战2020年浙江省高考数学优质卷分类解析：立体几何与空间向量(原卷版)

(浙江专用)2020版高考数学新增分大一轮复习 第八章 立体几何与空间向量 8.6 空间向量及其运算

2020届新高考高三数学试题分项汇编专题9 立体几何与空间向量(原卷版+解析版)

备战2020年浙江省高考数学优质卷分类解析：立体几何与空间向量(解析版)

2020年高考江苏版高考数学 专题十七 空间向量与立体几何

2020高考精品系列之数学(理)专题11 空间向量与立体几何解答题(原卷版)

空间向量知识点总结及典型题

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》分类汇编附答案

2018-2020年近三年高考数学真题解答题汇编：专题4.4 空间向量与立体几何(学生版+解析版)

2020年全国高考数学·第35讲 空间向量及其应用

2020版高考数学()：8.5 空间向量及其应用

专题九 立体几何与空间向量(教师版)--2020-2023高考真题数学专题分类汇编

2020年高考江苏版高考数学专题十七空间向量与立体几何

2011-2020年高考数学真题分类汇编专题24 空间向量与空间角的计算(学生版)

2020届山东省新高考高三优质数学试卷分项解析专题09 立体几何与空间向量(解析版)

(浙江专用)2020版高考数学新增分大一轮复习第八章立体几何与空间向量 8.6 空间向量及其运算

2020年高考江苏版高考数学专题十七空间向量与立体几何

2020年全国高考数学·第35讲空间向量及其应用

专题九立体几何与空间向量(教师版)--2020-2023高考真题数学专题分类汇编