投影与视图思维导图
《三视图》投影与视图PPT课件 (共24张PPT)
为了能完整确切地表达物体的形状和大小,必须 从多方面观察物体。
从正面看
从左边看
从 上 面 看
概 念
从上面看 从正面看到的图形叫做主视图; 从左面看到的图形叫做左视图; 从左面看 从正面看
三 视 图
从上面看到的图形叫做俯视图.
主视图 左视图 俯视图
(a)
(b)
(c)
你会了吗
2、由四个大小相同的小立方体搭成的几何体的
左视图如图所示,则这个几何体的搭
法不能是(
D
)
B''
A
B
C
D
挑战提高
六棱柱
1.一个直六棱柱的主视图和俯视图如图所示,请 补画它的左视图。
主视图 左视图
俯视图Βιβλιοθήκη ( 第1题 )挑战提高
2. 用4个完全相同的小立方块搭成一个主视图和 俯视图都是如图所示图形的几何体,则不同的 搭法有( B ) A. 1种 B. 2种 C. 3种 D. 4种
俯视图
主视图
任选两个视图 进行观察, 其中有没有 相等的线段
画三视图必须 遵循的法则:
a
h b h
左视图
a
b h
长对正 高平齐 宽相等
a b a h
俯视图
b
一个长方体的立体图如图3-18所示,请画 它的三视图.
主视方向 图3-18
已知一个直三棱柱的底面是等腰直角三角形,如图. 请画出它的三视图.
本节课给我们的启示:
从不同方向观察同一物体时,可能看 到不同的图形,从不同角度分析同一件事 或同一个人,结果可能也不一样。作为我 们同学,要学会全面地评价每一个同学, 我们今后看物、看人、看事都应从多角度、 多方向分析,这样,我们就会发现许多美 好的、闪光的东西,从而感受到我们生活 是多么的美好!
投影原理图解

投影原理图解
投影原理图解即为将三维物体在二维平面上展开的过程,通过此过程可以更清楚地了解物体的形状、结构和尺寸。
投影原理图解包括正投影和斜投影两种方法。
正投影是将物体垂直于投影平面的一侧透视图展开到投影平面上,得到的正投影图形是物体在投影平面上的投影形状。
在投影原理图解中,每个物体都有一个与之相对应的正投影图形,由于垂直于投影平面的透视视角的限制,正投影图形往往是物体的缩小版。
斜投影则是将物体沿着特定的斜线方向投射到投影平面上,得到的斜投影图形是物体在投影平面上的投影形状。
与正投影相比,斜投影图形在尺寸上更准确地反映了物体的实际大小和形态。
通过投影原理图解,我们可以更好地理解物体的几何构造和尺寸关系。
在实际应用中,投影原理图解被广泛应用于工程设计、建筑规划、产品制图等领域。
第二讲-投影体系和基本视图

Z
a'
b' Z
b'
a''(b'')
A
B
W a''(b'')
x
X
0
o
YW
a
a
b
Y
b
YH
• 与直线垂直旳投影面上旳投影积聚成一点。 • 在另外两个投影面上旳投影平行于相应旳投影轴反应真长。
例题2-6:鉴定直线AB、CD旳名称。
a’ X
c’ b’
OX
a
b
c
d’ O
d
2.3.2.4 两直线旳相对位置
(1)平行两直线 (2)相交两直线 (3)交叉两直线 (4)交叉两直线重影点旳可见性鉴别
S
平面P称为投影面,S称为投射中心,
需作出点ABC在平面P上旳图象。
将S与A连成直线,作出SA与平面 P旳交点a ,即为点A旳图象。直线SA 称为投射线,点a称为点A旳投影,这 种产生图象旳措施称为投影法。
A
C
B
a
c
b 投影面 P
投影法分为两类:中心投影法和平行投影法。
(1)中心投影法
前例即是中心投影法,即投射线都从投射中心出发旳,所 得旳投影称为中心投影。
C
Ac
B D
o
a
k
b
d
鉴别措施:
交点是两直线 旳共有点
d’ b’
k’
a’
x c’
o
c b
k a
d
若空间两直线相交,则其同名投影必相交,且交点旳
投影必符合空间一点旳投影规律。
例2-9:过C点作水平线CD与AB相交。
投影与视图三视图ppt

CAD软件具有精确的绘图功能,可以确保三视图的比例、尺寸和位置的准确性,避免手动 绘图时产生的误差。
可视化效果好
CAD软件可以生成三维模型,通过旋转、放大、缩小等操作,可以直观地观察三视图的位 置和形状,提高可视化和可理解性。
利用CAD技术辅助三视图的绘制
01
绘制主视图
在CAD软件中,使用平面绘图工具绘制主视图。由于主视图是物体在
投影与视图三视图ppt
xx年xx月xx日
目录
• 投影与视图的基本概念 • 正投影与三视图 • 三视图的画法与技巧 • 三视图的阅读与理解 • 三视图的应用与实例 • 三视图与CAD技术的结合应用
01
投影与视图的基本概念
投影的定义与分类
投影定义
投影是指将物体置于光源与屏幕之间,在 屏幕上呈现出该物体的影子。
技术要求
三视图可以标注尺寸和技术要求,为加工和制造提供准确的依据。
三视图在建筑制图中的应用
建筑平面图
建筑平面图是三视图的一种应用,可以展示建筑 物的平面布局和各房间的尺寸。
建筑立面图
建筑立面图可以展示建筑物的外观和立面效果, 为设计提供参考。
建筑剖面图
建筑剖面图可以展示建筑物内部的结构和空间关 系,为设计和施工提供帮助。
斜投影
光线投射到屏幕上的任意角度,形成物体 的斜投影。
投影分类
投影分为中心投影、平行投影和斜投影。
平行投影
光线平行投射到屏幕上,形成物体的平行 投影。
中心投影
光线汇聚到一个点,形成物体的中心投影 。
视图的基本概念
视图定义
视图是指从某一方向观察物体所得到的图形。
视图分类
视图分为主视图、俯视图、左视图和轴测图。
初中数学 相似与投影考点 知识点 思维导图 相似三角形 投影与视图

进行计算 利用比例尺,计算地图或
实际图形中的线段长或面积大小.
利用图形相似
根据相似比,确定相似形的周长和面积.
通过相似列出比例式,
运用方程思想,确定边长
通过相似求线段间的比值.
常作辅助线 是平行线 过三角形一边(或延长线)上的特殊点作另一边的平行线.
三角形的中线∶过中点作边的平行线;
或延长中线一倍,构造平行四边形.
把三视图还原成立体图形,
使数量关系更直观.
根据三视图进行计算.
同一时刻、同一地点各物体投影的方向相同.
学猪法导
投影
判断平行投影
定义
用光线照射物体,在某个平面上得到的影子.
中心投影
一般地,同一时刻,物体越高其影子越长.(影长与物高成正比)
使两物体成影的光线的交点即是. 太阳光线当成平行光线
确定光源的位置
出村节十十中宁
个Rt△与原Rt△相似
注意∶三角形相似具有传递性.
判断
结合三角形的性质,
三角形相似
确定三角形各角度数.
在正方形的网络中
结合勾股定理,
确定三角形相似
确定三角形各边长.
运用三角形相似的方法得出结论
已知三角形
逆向思维,依据仍是三角形判定条件.
探索得出的条件不唯一,
但只要相似的条件即可
相似,探索使
1.若有平行线,直接得出三角形相似.
2.若无平行线,按判定方法逐个判断.
在几何图形中
找三角形相似
判断多边形
的相似
相似三角形
判定
Rt△相似
结论
成的三角形与原三角形相似.
1.斜边和一直角边对应成比例
的两直角三角形相似.
中考数学一轮复习专题视图与投影
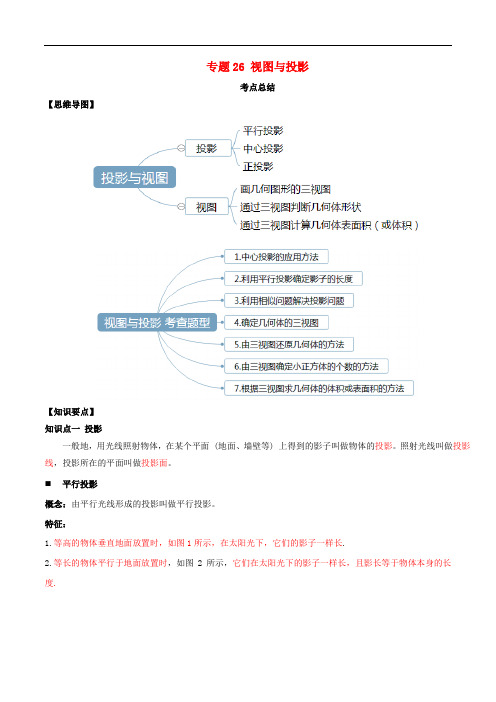
专题26 视图与投影考点总结【思维导图】【知识要点】知识点一投影一般地,用光线照射物体,在某个平面 (地面、墙壁等) 上得到的影子叫做物体的投影。
照射光线叫做投影线,投影所在的平面叫做投影面。
平行投影概念:由平行光线形成的投影叫做平行投影。
特征:1.等高的物体垂直地面放置时,如图1所示,在太阳光下,它们的影子一样长.2.等长的物体平行于地面放置时,如图2所示,它们在太阳光下的影子一样长,且影长等于物体本身的长度.平行投影变化规律:1.在不同时刻,同一物体的影子的方向和大小可能不同.不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚,物体影子的指向是:西→西北→北→东北→东,影长也是由长变短再变长.2.在同一时刻,不同物体的物高与影长成正比例. 即:.利用上面的关系式可以计算高大物体的高度,比如旗杆的高度等.注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.中心投影概念:由同一点 (点光源) 发出的光线形成的投影叫做中心投影。
特征:1.等高的物体垂直地面放置时,如图1所示,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.2等长的物体平行于地面放置时,如图2所示.一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.考查题型(求点光源的位置)点光源、物体边缘上的点以及它在影子上的对应点在同一条直线上,根据其中两个点,就可以求出第三个点的位置.中心投影与平行投影的区别与联系:正投影正投影的定义:如图所示,图(1)中的投影线集中于一点,形成中心投影;图(2)(3)中,投影线互相平行,形成平行投影;图(2)中,投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.1.线段的正投影分为三种情况.如图所示.①线段AB平行于投影面P时,它的正投影是线段A1B1,与线段AB的长相等;、②线段AB倾斜于投影面P时,它的正投影是线段A2B2,长小于线段AB的长;③线段AB垂直于投影面P时,它的正投影是一个点.2.平面图形正投影也分三种情况,如图所示.①当平面图形平行于投影面Q时,它的正投影与这个平面图形的形状、大小完全相同,即正投影与这个平面图形全等;②当平面图形倾斜于投影面Q时,平面图形的正投影与这个平面图形的形状、大小发生变化,即会缩小,是类似图形但不一定相似.③当平面图形垂直于投影面Q时,它的正投影是直线或直线的一部分.3.立体图形的正投影.物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最大截面全等.【典型例题】1.(2019·四川中考模拟)下列四幅图形中,表示两棵树在同一时刻阳光下的影子的图形可能是( ) A.B.C.D.【答案】A【解析】根据平行投影特点:在同一时刻,不同物体的影子同向,且不同物体的物高和影长成比例,依次分析各选项即得结果.A、影子平行,且较高的树的影子长度大于较低的树的影子,故本选项正确;B、影子的方向不相同,故本选项错误;C、影子的方向不相同,故本选项错误;D、相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,故本选项错误.故选A.2.(2019·广西中考模拟)如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子()A.逐渐变短B.先变短后变长C.先变长后变短D.逐渐变长【答案】B【详解】晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子先变短,再变长.故选B.3.(2019·北京清华附中中考模拟)如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下()A.小莉的影子比小玉的影子长B.小莉的影子比小玉的影子短C.小莉的影子与小玉的影子一样长D.无法判断谁的影子长【答案】D【解析】由一点所发出的光线形成的投影叫做中心投影,而中心投影的影子长短与距离光源的距离有关,由题意可得,小莉和小玉在同一路灯下由于位置不同,影长也不相同,故无法判断谁的影子长,故选D.4.(2019·河北中考模拟)一个长方形的正投影不可能是()A.正方形B.矩形C.线段D.点【答案】D【详解】解:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形.故长方形的正投影不可能是点,故选:D.5.(2019·湖北中考模拟)如图,左面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是()A.B.C.D.【答案】D【解析】试题分析:根据题意:水杯的杯口与投影面平行,即与光线垂直,则它的正投影图应是D.故选D.6.(2018·广东中考模拟)下面四幅图是在同一天同一地点不同时刻太阳照射同一根旗杆的影像图,其中表示太阳刚升起时的影像图是()A.B.C.D.【答案】C【解析】解:太阳东升西落,在不同的时刻,同一物体的影子的方向和大小不同,太阳从东方刚升起时,影子应在西方.故选C.考查题型一中心投影的应用方法1.(2018·河北中考模拟)如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( )A.越长B.越短C.一样长D.随时间变化而变化【答案】B【解析】由图易得AB<CD,那么离路灯越近,它的影子越短,故选B.2.(2020·银川外国语实验学校初三期末)如图,身高1.6米的小明站在距路灯底部O点10米的点A处,他的身高(线段AB)在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.(1)在OQ上画出表示路灯灯泡位置的点P;(2)小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;(3)若AM=2.5米,求路灯灯泡P 到地面的距离.【答案】(1)见解析;(2)见解析;(3)8米 【解析】()1如图:()2如图:()3//AB OP ,MAB ∴∽MOP ∆,AB AM OP OM ∴=,即1.6 2.510 2.5OP =+, 解得8OP =.即路灯灯泡P 到地面的距离是8米.3.(2019·泰兴市洋思中学初三期中)如图,王华晚上由路灯A 下的B 处走到C 处时,测得影子CD 的长为1米,继续往前走3米到达E 处时,测得影子EF 的长为2米,已知王华的身高是1.5米.(1)求路灯A的高度;(2)当王华再向前走2米,到达F处时,他的影长是多少?【答案】(1)路灯A有6米高(2)王华的影子长83米.【解析】试题分析:22. 解:(1)由题可知AB//MC//NE,∴,而MC=NE∴∵CD=1米,EF=2米,BF=BD+4,∴BD=4米,∴AB==6米所以路灯A有6米高(2)依题意,设影长为x,则解得米答:王华的影子长83米.考查题型二利用平行投影确定影子的长度1.(2019·吉林中考模拟)如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为_____米.【答案】6.4【详解】解:由题可知:1.628树高,解得:树高=6.4米.2.(2018·四川中考模拟)如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为_____.【答案】10cm【详解】解:如图,在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,∵△ABC∽△DEF,AB=5m,BC=3m,EF=6m∴ABBC=DEEF∴53=6DE∴DE=10(m)故答案为10m.3.(2015·甘肃中考真题)如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.(1)该小组的同学在这里利用的是投影的有关知识进行计算的;(2)试计算出电线杆的高度,并写出计算的过程.【答案】(1) 平行;(2)电线杆的高度为7米.【详解】(1)平行;(2)连接AM、CG,过点E作EN⊥AB于点N,过点G作GM⊥CD于点M,则BN=EF=2,GH=MD=3,EN=BF=10,DH=MG=5所以AN=10-2=8,由平行投影可知:即解得CD=7所以电线杆的高度为7m.考查题型三利用相似问题解决投影问题1.(2019·长沙市长郡双语实验中学中考模拟)如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为米.【答案】5。
初中数学思维导图完整版

初中数学思维导图完整版(包括中考考点)
2015-01-05 16:51脑记忆
一、全等三角形思维导图
编辑版word
二、相似三角形思维导图
编辑版word
编辑版word
三、几何初步和三角形思维导图
编辑版word
四、投影与视图思维导图
五、圆思维导图
编辑版word
编辑版word
六、实数思维导图
七、代数式思维导图
编辑版word
编辑版word
免费课:世界记忆大师汤世声老师,近日将通过网络免费分享快速记忆法、思维导图等知识,帮您孩子快速提升记忆力、学会高效学习方法,让学习事半功倍!
(此文档部分内容来源于网络,如有侵权请告知删除,文档可自行编辑修改内容,供参考,感谢您的配合和支持)
编辑版word。
《三视图》投影与视图PPT课件

小练习
例 :指出下列立体图形的对应的俯视图,在括号里填上对应的字母
( C ) ( A ) ( D) ( B)
解析:A是以圆锥,其俯视图是中 间带有一点的圆;B是一圆柱,其 俯视图是圆;C是一三棱锥,其俯 视图是三角形加中心到三个顶点 的连线;D是一长方体,其俯视图 是长方形。故答案为C,A,D,B。
知识梳理
知识点2:三视图的特征 主视图可以反映物体的长和高;俯视图可以反映物体的长和 宽;左视图可以反映物体的高和宽。
例 :如图,直三棱柱ABC-A1B1C1的侧棱长 和底面各边长均为2,其主视图是边长为2 的 正方形,则此直三棱柱左视图的面积为____
解析:
知识梳理
知识点3:三视图的画法 画三视图时要遵循主视图与俯视图的长对正,主视图与左视 图的高齐平,左视图与俯视图的宽相等的原则。 例 :画出如图所示几何体的三视图。
解析
练习
例 2 :画出下图所示的支架(一种小零件)的三视图,其中 支架的两个台阶的高度和宽度相等
解析:
知识梳理
知识点1:三视图的概念 一个物体在三个投影面内进行正投影,在正面内得到的由 前向后观察物体的视图,叫做主视图;在水平面内得到的 由上向下观察物体的视图叫做俯视图;在侧面内得到的由 左向右观察物体的视图,叫做左视图。
第29章 投影与视图
29.2 三视图
-.
教学新知 下图分别是从哪个方向看的呢?
教学新知
当我们从某一方向观察一个物体时,所看到的平面图叫做 物体的视图。
主视图的概念:在正面内得到的由前向后观察物体的视图, 叫做主视图。
在水平面内得到的由上向下观察物体的视图,叫做俯视图。 在侧面内得到由左向右观察物体的视图,叫做左视图。
教学新知
