机械原理--运动分析
合集下载
机械原理第三章 运动分析
例3-4 含三副构件的六杆机构运动分析
例3-5 已知图示机构各构件的尺寸及原动件1的角速度1，求 C点的速度vc及构件2和构件3的角速度2及 3；求E点的速度 vE 加速度aE 。 解： 1) 列矢量方程，分析 各矢量大小和方向。 2) 定比例尺，作矢量 图。 3) 量取图示尺寸，求 解未知量。 2 C
vB 3 vB 2 vB 3B 2
⊥BC ⊥AB ？ lAB1
v ？
m/s mm
1
A
1
B
2
方向： 大小： 定比例尺 作矢量图.
∥BC
？
3 C 4
vB3B 2 v b2b3
p b3 b2
vB 3 v pb3 3 lBC lBC
顺时针方向
2) 求构件3的角加速度3 列方程：
机械原理 第三章 平面机构的运动分析
§3-1 概述
§3-2 速度瞬心及其在平面机构速度分析中的应用 §3-3 平面机构运动分析的矢量方程图解法 §3-4 平面机构运动分析的复数矢量法 §3-5 平面机构运动分析的杆组法
§3-1 概述
1.机构运动分析的内容 机构尺寸和原动件运动规律已知时，求转动构件上某点 或移动构件的位移、速度、加速度及转动构件的角位移、 角速度、角加速度。 2.机构运动分析的目的
绝对速度相等的重合点。用Pij表示。
若该点绝对速度为零——绝对瞬心。 若该点绝对速度不为零——相对瞬心。 二、瞬心的数目 设N 为组成机构的构件数（含机架），K为瞬心数，则
2 K CN =N ( N 1) / 2
三、瞬心的位置 1.两构件组成转动副 P12
1 2
以转动副相联，瞬心在其中心处。
P12、P13 的位置（绝对瞬心），P23
机械原理-机构运动分析的解析法
l
1
φ θ
2
l
x
a2 x 2l cos al sin a2 y 2l sin al cos
已知：构件的长度L及运动参数角位置θ 、角速度ω 、 角加速度ε ，1点的运动参量。
求： 3点的运动参量。
解： P 3x P 1 x l cos( ) v3 x v1 x l sin( ) P v3 y v1 y l cos( ) 3y P 1 y l sin( )
运 动 副 点 号
要求赋值
构 件 号
构 件 长 度
角位置角速度角加速 度，位置 速度 加速 度 n1
r1
m>0——实线 M<=0——虚线
不赋值
已知： 外运动副N1的位置P、速度v、加速度a，导路上任意参考点 N2的位置P、 速度v、加速度a，构件1的长度及导路的角位置、角速度、角加速度。 求：内运动副N3的运动参量、构件①的运动参量、 r2、vr2、ar2
P 3x P 1x l1 cos 1 P 3y P 1 y l1 sin 1
P 3y P 2y 2 arctan P P 2x 3x
rrrk(m,n1,n2,n3,k1,k2,r1,r2,t,w,e,p,vp,ap)
装 配 模 式
n3 k1 k2 r2 n2 N3’
}
y
3
l
1
φ
l
2
θ
x
bark(n1,n2,n3,k,r1,r2,gam,t,w,e,p,vp,ap)
关 键 点 号 构 n n 件 1 1 号 n n ∠ n3 n1 2 3 间 间 n2 距 距 离 离 角位置角速度 角加速度，位 置 速度 加速度
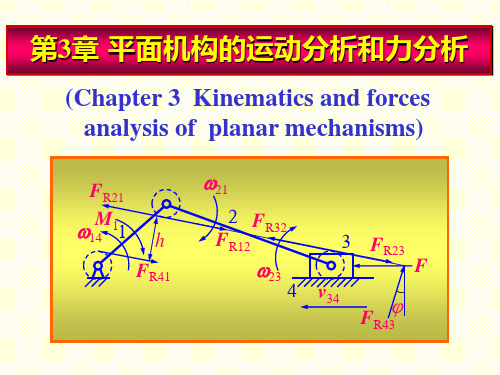
机械原理-第3章 平面机构的运动分析和力分析
a
大小:2w1×vB2B1=2w1vB2B1sin90°=2w1vB2B1; k B 2 B1 方向:将vB2B1的方向沿w1转过90°。
vB1B2 1
2 B
(B1B2)
vB1B2 1
2 B
(B1B2)
ω1
a
k B 2 B1
ω1
a
k B 2 B1
(3)注意事项
B (B1B2)
1
2
vB1 = vB2，aB1 = aB2，
目的： 了解现有机构的运动性能，为受力 分析奠定基础。 方法：1)瞬心法（求速度和角速度）; 2)矢量方程图解法; 3)解析法（上机计算）。
3.1
速度瞬心
(Instant center of velocity )
3.1.1 速度瞬心
两个互作平行平面运动的构件 定义：
上绝对速度相等、相对速度为
零的瞬时重合点称为这两个构 件的速度瞬心, 简称瞬心。瞬 心用符号Pij表示。
图(b) 2
(B1B2B3)
扩大刚体(扩大构件3)，看B点。
B 1 A
b2
C
vB3 = vB2 + vB3B2
方向：⊥BD ⊥AB 大小： ？ lAB w1 ∥CD ?
3
w1
D
4
p
选 v ，找 p 点 。
v
v B 3 pb3 μv ω3 （逆 ） l BD l BD
b3
(b)
例4:已知机构位臵、尺寸，w1为常数，求w2、a2。
C B
n t n t aC aC a B aCB aCB
2
1
E
方向:C→D ⊥CD B→A C→B ⊥CB 大小:lCD w32 ? lABw12 lCB w22 ?
机械原理第三章平面机构的运动分析
2 判定方法
通过违法副法、副移法或 推动法等方法进行判定。
3 应用举例
四连杆机构中的连杆2-连 杆3副是约束运动副。
运动副的数目
1
最大副数
运动副的最大数目取决于机构的自由度。
2
自由度
机构能够独立运动的最少块数。
3
计算方法
自由度 = 3 * （连杆总数 - 框架连杆数 - 3）
极迹法
极迹法是一种利用链接件的相对位置和运动方向进行运动分析的方法，通过 绘制链接件的轨迹，可以分析机构的运动特性。
机械原理第三章平面机构 的运动分析
平面机构是指运动发生在一个平面内的机械装置。本章将详细介绍平面机构 的分类、链接件运动、运动副的命名和判定以及优化设计等内容。
什么是平面机构
平面机构是运动发生在一个平面内的机械装置。它由链接件和运动副组成，可实现各种不同的运动效果。
平面机构的分类
四连杆机构
由四个连杆组成，可实现平面运动和转动。
由滑块和滑道组成的运动副。
键副
通过键配对组成的运动副。
独立运动副的判定
1 定义
独立运动副是能够单独实 现运动的副。
2 判定方法
通过遮挡法、违法副法或 推动法等方法进行判定。
3 应用举例
曲柄滑块机构中的曲柄-连 杆副是独立运动副。
约束运动副的判定
1 定义
约束运动副是通过其他副 的约束实现运动的副。
自由度的计算
自由度是机构能够独立运动的最少块数。通过计算机构的链接件数目和约束数目，可以确定机构的自由度。
平面机构的静力学分析
静力学分析是研究机构在静力平衡条件下的受力分布和力矩平衡的方法。通过分析机构的关节受力和连杆力矩， 可以确定机构的静力学特性。
机械原理-平面连杆机构的运动分析和设计
平面连杆机构的设计流程和方法
在这个部分中，我们将深入探讨平面连杆机构的设计，介绍流程和方法，提供实际案例分析，帮助您了解如何设 计成功的机械。
1.
需求分析
将客户的需求转化为机械设计
目标。
2.
构思和设计
基于机械原理构思和设计机械
装备支撑结构，并采用 CAD 软
件实施初始的草图或模型。
3.
材料选择
选择合适的材料和工艺，确保
结构和类型
平面连杆机构通常由零件精细制 造而成，以满足工业和商业目的 的要求。
工程应用
机械工程师们可以使用平面连杆 机构来完成各种复杂的任务，如 发动机和自动化流水线等。
日常应用
平面连杆机构可以进一步应用在 日常用品中，如钟表、洗衣机和 自动售货机等。
平面连杆机构的运动分析方法
在这个部分中，我们将探索平面连杆机构的运动学和动力学，介绍运动方程和速度方程，以及如何用数学 公式计算不同零件的运动和速度。
1 平衡条件
平衡是指物理系统中所有力和运动之间所需达到的状态，这是机械工程师需要考虑的重 要问题。
2 稳定性
稳定性是一个重要的物理学概念，涉及动量、速度和质量，能够帮助工程师在设计平面 连杆机构时考虑不同零件的状态和取向。
3 应用场景
平面连杆机构无处不在，具有开发良好设计的潜力，是自动化流水线的核心，也是钟表、 汽车和机器人的重要部分。
1
运动学
运动学研究物体运动的规律和运动参数，如位移、速度、加速度等。
2
动力学
动力学研究物体的运动状态和运动参数之间的关系，如动量、力和功等。
3
数值模拟
数字计算能够预测机械零件的运动，利用计算机模拟机械过程，提高设计效率。
机械原理_运动分析
大小： 大小： ？ ω1 1 A
2 C 3 4 D
υC1 = ω1lAC
υC2 =υC1 +υC2C1
√
? 方向： 方向： CD ⊥AC ∥AB ⊥
c2(c3)
(3)画速度图 画速度图 µυ =υC1 / pc1 ，(m/ s)/ mm
p c1
υC2 = pc2 iµv ω3 =υC3 / lCD (顺时针)
2 C 3 4 D
●依据原理 构件2的运动可以认为是随同构件1 构件2的运动可以认为是随同构件1的牵连运动 和构件2相对于构件1的相对运动的合成。 和构件2相对于构件1的相对运动的合成。
1.速度分析 【解】1.速度分析
B
C点为构件1、2、3的重合点 点为构件1 (1)求已知速度 求已知速度 (2)列方程 列方程
3.3 机构运动分析的矢量方程图解法
所依据的基本原理: ●所依据的基本原理: 运动合成原理
一构件上任一点（ 一构件上任一点（C）的运动υC ，可以看作是随同该构 件上另一点（ 的平动(牵连运动) 和绕该点的转动( 件上另一点（B）的平动(牵连运动)υB和绕该点的转动(相 对运动) 的合成。 对运动)υCB的合成。
ω1
A
υB ac
【解】 1.速度分析 速度分析 (1)求已知速度 求已知速度
E B 1 2 4 A 3 C
υB = ω1lAB
(2)列方程 列方程 方向 大小 (3)画速度图 画速度图
ω1
υB a c
υC =
？
υB + υCB
⊥ CB
？ p c √
水 平 ⊥ AB
p ─ 速度极点。 速度极点。 µυ =υB / pb ，(m/ s) / mm
2 C 3 4 D
υC1 = ω1lAC
υC2 =υC1 +υC2C1
√
? 方向： 方向： CD ⊥AC ∥AB ⊥
c2(c3)
(3)画速度图 画速度图 µυ =υC1 / pc1 ，(m/ s)/ mm
p c1
υC2 = pc2 iµv ω3 =υC3 / lCD (顺时针)
2 C 3 4 D
●依据原理 构件2的运动可以认为是随同构件1 构件2的运动可以认为是随同构件1的牵连运动 和构件2相对于构件1的相对运动的合成。 和构件2相对于构件1的相对运动的合成。
1.速度分析 【解】1.速度分析
B
C点为构件1、2、3的重合点 点为构件1 (1)求已知速度 求已知速度 (2)列方程 列方程
3.3 机构运动分析的矢量方程图解法
所依据的基本原理: ●所依据的基本原理: 运动合成原理
一构件上任一点（ 一构件上任一点（C）的运动υC ，可以看作是随同该构 件上另一点（ 的平动(牵连运动) 和绕该点的转动( 件上另一点（B）的平动(牵连运动)υB和绕该点的转动(相 对运动) 的合成。 对运动)υCB的合成。
ω1
A
υB ac
【解】 1.速度分析 速度分析 (1)求已知速度 求已知速度
E B 1 2 4 A 3 C
υB = ω1lAB
(2)列方程 列方程 方向 大小 (3)画速度图 画速度图
ω1
υB a c
υC =
？
υB + υCB
⊥ CB
？ p c √
水 平 ⊥ AB
p ─ 速度极点。 速度极点。 µυ =υB / pb ，(m/ s) / mm
机械原理-机构的运动分析
3、加速度分析
aC aB aCB
a C a C aB a CB a CB
n t n t
a B 12l AB
F
1
1 A B 2 E C
大小 lCD32
?
→A
lCB22 C→B
? ⊥CB
·
G
3
方向 C→D ⊥CD
取极点p’ ，按比例尺a作加速度图
1
4
D
' aC a p 'c ' aCB a b 'cc´
思考题：
P44 3-1
作业：
P44 3-3、3-6、3-8（b)
§3-3 用矢量方程图解法作机构的运动分析
一、矢量方程图解法的基本原理及作图法
1、基本原理 —— 相对运动原理 B（B1B2） 1
B
A
同一构件上两点间的运动关系
2
两构件重合点间的运动方程
vB v A vBA
aB a A aBA aA a
c´
aC a G e´
aCB
n2 ´ n2
p´
n3
aF
b´
加速度图分析小结： 1）p‘点代表所有构件上绝对加速度为零的影像点。 2）由p‘点指向图上任意点的矢量均代表机构图中对应点 的绝对加速度。 3）除 p′点之外，图中任意两个带“ ′”点间的连线 均代表机构图中对应两点间的相对加速度，其指向与加 速度的角标相反。 4）角加速度可用构件上任意两点之间的相对切向加速度 除于该两点之间的距离来求得，方向的判定采用矢量平 aCB b ' c ' 移法。 5）加速度影像原理：在加速度图上，同一构件上各点的 绝对加速度矢量终点构成的多边形与机构图中对应点构 成的多边形相似且角标字母绕行顺序相同。 6）加速度影像原理只能用于同一构件。
机械原理机械工程中的运动轨迹分析
机械原理机械工程中的运动轨迹分析在机械工程中，运动轨迹的分析是一个重要的研究领域。
机械工程师需要了解和预测不同机械部件的运动轨迹，以便设计和优化各种机械系统。
本文将探讨机械原理中的运动轨迹分析方法及其应用。
一、运动轨迹的概念和定义在机械工程中，运动轨迹是指物体在运动过程中所形成的路径。
它可以描述物体从起始位置到终止位置的运动方式和轨迹形状。
运动轨迹的分析是为了确定物体在不同时间点的位置和速度，以及预测物体在未来某一时间点的位置和速度。
二、运动轨迹的分析方法1. 几何分析法：几何分析法是运动轨迹分析中最基本的方法之一。
它基于几何学原理，通过绘制物体在不同时间点的位置坐标，在坐标平面上构成轨迹图形。
通过分析轨迹图形的形状和特征，可以了解物体的运动规律和性质。
2. 向量分析法：向量分析法是一种使用向量和矢量运算来描述和分析运动轨迹的方法。
通过将运动轨迹表示为向量的形式，可以方便地进行矢量运算，如加法、减法、叉乘和点乘等，从而得到更精确和具体的运动轨迹信息。
3. 动力学分析法：动力学分析法通过运用牛顿第二定律和其他动力学原理，结合运动方程和受力分析，来分析和求解物体在给定条件下的运动轨迹。
这种方法适用于复杂的运动系统，可以考虑更多因素对运动轨迹的影响。
三、运动轨迹分析的应用1. 机器人运动规划：机器人学是机械工程中重要的分支之一，机器人的运动轨迹分析在机器人的路径规划和控制中起着关键作用。
通过分析机器人的运动轨迹，可以确定其最佳的路径和轨迹规划策略，以提高机器人的运动效率和性能。
2. 车辆运动分析：在汽车工程和交通工程领域，运动轨迹分析可以用于分析和优化车辆的行驶轨迹，提高车辆运动的平稳性和安全性。
通过运动轨迹的分析，可以了解车辆在不同道路条件下的行驶特点和操纵性能，为车辆设计和驾驶控制提供依据。
3. 机械装置设计：在机械装置设计中，运动轨迹分析可以用来确定机械零件的设计参数和轨迹形状，以满足特定的要求和功能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 大小：3 lO B
2
?
2 12lO A 2 l AB
1
?
AB
n3
方向：B O2 O2 B A O1
B A
n2
t t b), aB aBA a (n2 b), aB a ( pb) a (n3
t a 2 BA
选 a , 作矢量封闭多边形，
2015-3-22
p
n3
), 3 aA3 a ( pa3
a tA3
2-1.图示为齿轮连杆机构。试求：
1
（1）该机构的瞬心数；
（2）图示位置时的全部瞬心； （3）ω3/ω5=？ 解：
N ( N 1) (1) k 2
(2)确定瞬心位置
5
4
2
3
P 12
P23
P24
P45
LAB= LBC=20mm,
LCD=40mm,
∠ α = ∠ β =900,ω 1=100 rad/s, 试用速
度瞬心法求C点速度大小和方向。
2015-3-22
22
2-5. 在 图 示 机 构 中 ， 已 知 长 度
LCD=40mm,
LAB= LBC=20mm,
∠ α = ∠ β =900,ω 1=100 rad/s, 试用速
2015-3-22
13
解：
vB3 vB2 vB3B2
1 l AB
BD
(b1 , b2 , b3 )
大小： ? 方向： BD
?
∥ BC
vB3 B2 0, vB3 vB2 1l AB , 3 2
作 BCD 的速度影像，得
1l AB
lBD
vC v pc 3lCD
2015-3-22
1l ABlCD
lBD
14
n t k r aB3 aB3 aB3 aB2 aB3B2 aB3B2
2 大小： 3 lBD ?
12l AB
B A
0
?
∥ BC
方向：
BD
BD
作 BCD 的加速度影像，得
n 2 aC a pc aB 3 l BD 3
2 12l AB
vB3B2 0,a k B3B2 23 vB3B2
2015-3-22
lBD 0
15
2-3 在图示六杆机构中，原动件2的角速度为 ω2 =10 rad/s. 机构 的比例尺为 μl =0.002m/mm。试： （1）分析该机构的自由度及机构的级别； （2）图解确定滑块6速度的大小及方向。（采用速度瞬心法或 相对运动图解法均可）
2
2015-3-22
4
vB
2
1
3
vA
连杆上另一点C的速度:
*1) abc ∽ ABC vC vA vCA vB vCB
?
AC
大小： √ 方向： √
√ √
?
BC
2) 图形 abc 称为
图形 ABC 的 速度影象.
vC v ( pc)
2015-3-22
16
2.确定滑块6速度大小和方向
v6 2 P 12 P 26
P34 P 12 P35 P 14
P23
P 16在
P56
2015-3-22
17
P36
P 13
P 16在
P34 P 12 P35
P 16在
v6 2 P 12 P 26
P 14
P26
P23 P56
v6
P 16在
2015-3-22
18
2-4 在图示机构中，已知各构件的尺寸及原动件 1 的角速度为
ω1 （常数）. 试求当φ 1=900 时，构件2的角速度ω2及构件3的
角速度ω3 。（比例尺任选）
P 12 P34 P 14 P 13
P23在
2015-3-22
19
2-5 在图示机构中，已知各构件的尺寸及原动件 1 的角速度为
度瞬心法求C点速度大小和方向。
P 12 P 13 P 14
P23
P34
2015-3-22 23
2015-3-22
24
1, 2
C1 , C2
2015-3-22
25
2015-3-22
26
基本原理： 相对运动原理
基本方法：
按向量方程、以一定的比例尺作向量多边形求解。
m 比例尺： 实际长度 （ ), l 图示长度 mm
实际速度 m s v （ ), 图示长度 mm
实际加速度 m s 2 v （ ). 图示长度 mm
2015-3-22 3
一)同一构件上各点速度之间、加速度之间的关系 实例: 已知各杆长度、杆1的转角 1 及匀角速度 1 ,
l AB
,
3 a l O B
2
tC的加速度可
利用加速度影象解决; 2)速度影象、加速度影象只能
n3
用于同一构件上点的运动求解。
n2
2015-3-22 8
二)组成移动副两构件重合点速度之间、加速度之间 的关系 1.选 , 作机构位置图;
第三章 平面机构的运动分析
一.速度瞬心法 二.运动分析的矢量图解法
三.解题实例
一.速度瞬心法
一)速度瞬心 ---两构件的同速点. 二)瞬心数目
k
2 CN
N ( N 1) 2
三)瞬心位置的确定
1)直接观察法 2)三心定理
四)应用瞬心法进行速度分析
2015-3-22 2
二.用相对运动图解法作机构的运动分析
1
3 2
?
∥O 2 A
方向： A O2 O 2 A A O1
O2A
O2
3
k
a1 (a2 )
vA3 A2 的方向沿 3 转过900。
选 a , 作矢量封闭多边形，
a3 ), a a (n3
t A3
a
r A3 A2
), a (k a3
lO2 A
10
a3
P 14
12
2-2. 在图示机构中,设已知各构件的尺寸, 原动件1的角速度 ω1 为常数 (顺时针方向 ),又其速度和加速度多边形分别如图 (b)及 (c)所示. 试求机构在图示位置时构件 3上 C点的速度及 加速度(要求列出必要的矢量方程式 ; 在图(b)及(c)上标注相 应的符号, 并写出vC及aC的表达式) ,并问机构中是否存在科 氏加速度?为什么?
2 3
2015-3-22
v A3
lO2 A
9
O1
1
1 2 A
2 , 3
p
a3
(a2 ) a1
n t k r aA3 aA3 aA3 aA2 aA3 A2 aA3 A2
2 大小： 3 lO2 A
科氏加速度
?
12lO A 23 vA A
2015-3-22
5
vB
2
1
3
vA
vBA
* pabc速度多边形，
1.
p 称为极点（代表 v 0 的点）；
2.从极点到任一点的矢量表示该点的绝对速度； 3.任两点间的矢量表示该两点间的相对速度.
2015-3-22 6
3.加速度分析;
aB aA aBA n t n t aB aB aA aBA aBA
P 13
1
2015-3-22
P 15
11
(2)确定瞬心位置
P 14
P 12
P23
P45
P 15
P 13
P24
P 12
P25 P45
P34 P25
P35
P34 P 13
P23
P24
1
P35
P 15
(3)3 / 5 P 15 P 35 / P 13P 35 EP 35 / AP 35.
2015-3-22
ω1 （常数）. 试求：
（1）标出机构中所有的瞬心位置； （2）用瞬心法确定M点的速度 VM 。
2015-3-22
20
P34在
P24 P23 P 13 P 12
P34在
P 14
P34在
vM 1 P 14 P 13 0
2015-3-22 21
2-6. 在 图 示 机 构 中 ， 已 知 长 度
l
O1
1
1 2 A
p
2.作速度分析;
a1 (a2 )
vA3 vA2 vA3 A2
1 lO A
1
O2
3
2 , 3
a3
大小： ? 方向： O2A
?
∥O 2 A
O1A
选 v , 作矢量封闭多边形，
vA3 v ( pa3 ), vA3 A2 v (a3a2 ),
求连杆上B点及C点的运动。
vB
1
2
1.选
l , 作机构位置图;
1
3
vA
vBA
2.作速度分析;
vB v A vBA
1 lO A
1
大小：?
?
AB
O 2 B O1A 方向：
vBA 选 v , 作矢量封闭多边形，
v (ab), vB v ( pb), v 2 v BA l , 3 B l AB O B
2
?
2 12lO A 2 l AB
1
?
AB
n3
方向：B O2 O2 B A O1
B A
n2
t t b), aB aBA a (n2 b), aB a ( pb) a (n3
t a 2 BA
选 a , 作矢量封闭多边形，
2015-3-22
p
n3
), 3 aA3 a ( pa3
a tA3
2-1.图示为齿轮连杆机构。试求：
1
（1）该机构的瞬心数；
（2）图示位置时的全部瞬心； （3）ω3/ω5=？ 解：
N ( N 1) (1) k 2
(2)确定瞬心位置
5
4
2
3
P 12
P23
P24
P45
LAB= LBC=20mm,
LCD=40mm,
∠ α = ∠ β =900,ω 1=100 rad/s, 试用速
度瞬心法求C点速度大小和方向。
2015-3-22
22
2-5. 在 图 示 机 构 中 ， 已 知 长 度
LCD=40mm,
LAB= LBC=20mm,
∠ α = ∠ β =900,ω 1=100 rad/s, 试用速
2015-3-22
13
解：
vB3 vB2 vB3B2
1 l AB
BD
(b1 , b2 , b3 )
大小： ? 方向： BD
?
∥ BC
vB3 B2 0, vB3 vB2 1l AB , 3 2
作 BCD 的速度影像，得
1l AB
lBD
vC v pc 3lCD
2015-3-22
1l ABlCD
lBD
14
n t k r aB3 aB3 aB3 aB2 aB3B2 aB3B2
2 大小： 3 lBD ?
12l AB
B A
0
?
∥ BC
方向：
BD
BD
作 BCD 的加速度影像，得
n 2 aC a pc aB 3 l BD 3
2 12l AB
vB3B2 0,a k B3B2 23 vB3B2
2015-3-22
lBD 0
15
2-3 在图示六杆机构中，原动件2的角速度为 ω2 =10 rad/s. 机构 的比例尺为 μl =0.002m/mm。试： （1）分析该机构的自由度及机构的级别； （2）图解确定滑块6速度的大小及方向。（采用速度瞬心法或 相对运动图解法均可）
2
2015-3-22
4
vB
2
1
3
vA
连杆上另一点C的速度:
*1) abc ∽ ABC vC vA vCA vB vCB
?
AC
大小： √ 方向： √
√ √
?
BC
2) 图形 abc 称为
图形 ABC 的 速度影象.
vC v ( pc)
2015-3-22
16
2.确定滑块6速度大小和方向
v6 2 P 12 P 26
P34 P 12 P35 P 14
P23
P 16在
P56
2015-3-22
17
P36
P 13
P 16在
P34 P 12 P35
P 16在
v6 2 P 12 P 26
P 14
P26
P23 P56
v6
P 16在
2015-3-22
18
2-4 在图示机构中，已知各构件的尺寸及原动件 1 的角速度为
ω1 （常数）. 试求当φ 1=900 时，构件2的角速度ω2及构件3的
角速度ω3 。（比例尺任选）
P 12 P34 P 14 P 13
P23在
2015-3-22
19
2-5 在图示机构中，已知各构件的尺寸及原动件 1 的角速度为
度瞬心法求C点速度大小和方向。
P 12 P 13 P 14
P23
P34
2015-3-22 23
2015-3-22
24
1, 2
C1 , C2
2015-3-22
25
2015-3-22
26
基本原理： 相对运动原理
基本方法：
按向量方程、以一定的比例尺作向量多边形求解。
m 比例尺： 实际长度 （ ), l 图示长度 mm
实际速度 m s v （ ), 图示长度 mm
实际加速度 m s 2 v （ ). 图示长度 mm
2015-3-22 3
一)同一构件上各点速度之间、加速度之间的关系 实例: 已知各杆长度、杆1的转角 1 及匀角速度 1 ,
l AB
,
3 a l O B
2
tC的加速度可
利用加速度影象解决; 2)速度影象、加速度影象只能
n3
用于同一构件上点的运动求解。
n2
2015-3-22 8
二)组成移动副两构件重合点速度之间、加速度之间 的关系 1.选 , 作机构位置图;
第三章 平面机构的运动分析
一.速度瞬心法 二.运动分析的矢量图解法
三.解题实例
一.速度瞬心法
一)速度瞬心 ---两构件的同速点. 二)瞬心数目
k
2 CN
N ( N 1) 2
三)瞬心位置的确定
1)直接观察法 2)三心定理
四)应用瞬心法进行速度分析
2015-3-22 2
二.用相对运动图解法作机构的运动分析
1
3 2
?
∥O 2 A
方向： A O2 O 2 A A O1
O2A
O2
3
k
a1 (a2 )
vA3 A2 的方向沿 3 转过900。
选 a , 作矢量封闭多边形，
a3 ), a a (n3
t A3
a
r A3 A2
), a (k a3
lO2 A
10
a3
P 14
12
2-2. 在图示机构中,设已知各构件的尺寸, 原动件1的角速度 ω1 为常数 (顺时针方向 ),又其速度和加速度多边形分别如图 (b)及 (c)所示. 试求机构在图示位置时构件 3上 C点的速度及 加速度(要求列出必要的矢量方程式 ; 在图(b)及(c)上标注相 应的符号, 并写出vC及aC的表达式) ,并问机构中是否存在科 氏加速度?为什么?
2 3
2015-3-22
v A3
lO2 A
9
O1
1
1 2 A
2 , 3
p
a3
(a2 ) a1
n t k r aA3 aA3 aA3 aA2 aA3 A2 aA3 A2
2 大小： 3 lO2 A
科氏加速度
?
12lO A 23 vA A
2015-3-22
5
vB
2
1
3
vA
vBA
* pabc速度多边形，
1.
p 称为极点（代表 v 0 的点）；
2.从极点到任一点的矢量表示该点的绝对速度； 3.任两点间的矢量表示该两点间的相对速度.
2015-3-22 6
3.加速度分析;
aB aA aBA n t n t aB aB aA aBA aBA
P 13
1
2015-3-22
P 15
11
(2)确定瞬心位置
P 14
P 12
P23
P45
P 15
P 13
P24
P 12
P25 P45
P34 P25
P35
P34 P 13
P23
P24
1
P35
P 15
(3)3 / 5 P 15 P 35 / P 13P 35 EP 35 / AP 35.
2015-3-22
ω1 （常数）. 试求：
（1）标出机构中所有的瞬心位置； （2）用瞬心法确定M点的速度 VM 。
2015-3-22
20
P34在
P24 P23 P 13 P 12
P34在
P 14
P34在
vM 1 P 14 P 13 0
2015-3-22 21
2-6. 在 图 示 机 构 中 ， 已 知 长 度
l
O1
1
1 2 A
p
2.作速度分析;
a1 (a2 )
vA3 vA2 vA3 A2
1 lO A
1
O2
3
2 , 3
a3
大小： ? 方向： O2A
?
∥O 2 A
O1A
选 v , 作矢量封闭多边形，
vA3 v ( pa3 ), vA3 A2 v (a3a2 ),
求连杆上B点及C点的运动。
vB
1
2
1.选
l , 作机构位置图;
1
3
vA
vBA
2.作速度分析;
vB v A vBA
1 lO A
1
大小：?
?
AB
O 2 B O1A 方向：
vBA 选 v , 作矢量封闭多边形，
v (ab), vB v ( pb), v 2 v BA l , 3 B l AB O B