高等数学教材习题全解

合集下载

【中大】高等数学习题及详细解答

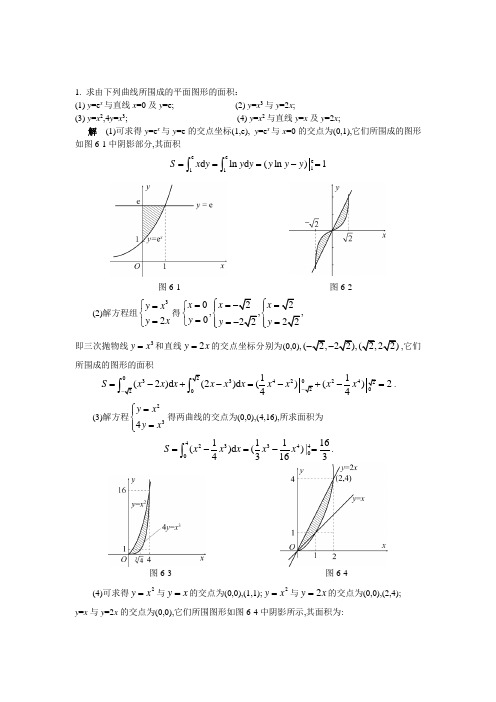
1. 求由下列曲线所围成的平面图形的面积：(1) y =e x 与直线x =0及y =e; (2) y =x 3与y =2x ;(3) y =x 2,4y =x 3; (4) y =x 2与直线y =x 及y =2x ;解 (1)可求得y =e x 与y =e 的交点坐标(1,e), y =e x 与x =0的交点为(0,1),它们所围成的图形如图6-1中阴影部分,其面积eee111d ln d (ln )1S x y y y y y y ===-=⎰⎰图6-1 图6-2(2)解方程组32y x y x ⎧=⎨=⎩得022,,,02222x x x y y y ⎧⎧==-=⎧⎪⎪⎨⎨⎨==-=⎩⎪⎪⎩⎩ 即三次抛物线3y x =和直线2y x =的交点坐标分别为(0,0),(2,22),(2,22)--,它们所围成的图形的面积20334224222011(2)d (2)d ()()244S x x x x x x x x x x --=-+-=-+-=⎰⎰.(3)解方程234y xy x⎧=⎪⎨=⎪⎩得两曲线的交点为(0,0),(4,16),所求面积为 4233440011116()d ()|43163S x x x x x =-=-=⎰.图6-3 图6-4(4)可求得2y x =与y x =的交点为(0,0),(1,1);2y x =与2y x =的交点为(0,0),(2,4); y =x 与y =2x 的交点为(0,0),它们所围图形如图6-4中阴影所示,其面积为:121122012231201(2)d (2)d d(2)d 117()236S x x x xx x x x x x xx x x =-+-=+-=+-=⎰⎰⎰⎰2. 求由下列曲线围成的平面图形绕指定轴旋转而成的旋转体的体积：(1) y =e x ,x =0,y =0,x =1,绕y 轴； (2) y =x 3,x =2,x 轴，分别绕x 轴与y 轴； (3) y =x 2,x =y 2，绕y 轴；解 (1)如图6-9所求旋转体的体积为矩形OABD ,与曲边梯形CBD 绕y 轴旋转所成的几何体体积之差,可求得y =e x 与x =1的交点为(1,e), y =e x 与y 轴的交点为(0,1),所以,所求旋转体的体积.222111(ln )(ln )2(ln )22(1)2(ln )eee11ee1πe πd πe πd πe πe ππe e π.d y V y y y y y y y y y ⎡⎤=⋅⋅-=--⎣⎦⎡⎤=-+=-+=-⎣⎦⎰⎰⎰72226200128(2)7ππd πd π7x x V y x x x ===⋅=⎰⎰ 2588228330036428323255πππd ππd ππy V x y y y y =⨯⨯-=-=-⋅⋅=⎰⎰.图6-5 图6-6(3)解方程组22y xx y⎧=⎪⎨=⎪⎩得交点(0,0),(1,1),所求旋转体的体积 25114100031025πd πd ππx x x V x x x x ⎛⎫=-=⋅=- ⎪⎝⎭⎰⎰.图6-8图6-73、.求二曲线θsin =r 与θcos 3=r 所围公共部分的面积解：当θ等于0和3π时，两曲线相交，所围公共部分的面积为4324π5d θθcos 321d θθsin 212π3π23π02-=+=⎰⎰A .4、设有一截锥体, 其高为h , 上、下底均为椭圆, 椭圆的轴长分别为2a 、2b 和2A 、2B , 求这截锥体的体积.解建立坐标系如图. 过y 轴上y 点作垂直于y 轴的平面, 则平面与截锥体的截面为椭圆, 易得其长短半轴分别为y h a A A --, y hb B B --.截面的面积为π)()(y hb B B y h a A A --⋅--.于是截锥体的体积为])(2[61)()(0bA aB AB ab h dy y h b B B y h a A A V h+++=--⋅--=⎰ππxyO3πθ=5、计算曲线x y ln =相对应于3=x 到8=x 的一段曲线弧长.解：由弧长的公式得:23ln 211d 1d 11d 1832832832+=+=+='+=⎰⎰⎰x x x x xx y s .6、求阿基米德螺线ρ=a θ (a >0)相应于θ 从0到2π 一段的弧长. 解: 弧长元素为θθθθd a d a a ds 22221+=+=.于是所求弧长为⎰+=πθθ2021d a s )]412ln(412[222ππππ++++=a .7、求星形线33cos sin x a ty a t ⎧=⎨=⎩的全长. 解：由弧长的参数方程公式得:446s t a θ===.1、电量为+q 的点电荷位于r 轴的坐标原点O 处它所产生的电场力使r 轴上的一个单位正电荷从r =a 处移动到r =b (a <b )处求电场力对单位正电荷所作的功.提示: 由物理学知道, 在电量为+q 的点电荷所产生的电场中, 距离点电荷r 处的单位正电荷所受到的电场力的大小为2r qkF = (k 是常数). 解: 在r 轴上, 当单位正电荷从r 移动到r +dr 时, 电场力对它所作的功近似为dr r qk2,即功元素为dr r qkdW 2=. 图6-9 于是所求的功为dr rkq W b a2⎰=b a r kq ]1[-=)11(b a kq -=.2、设把一金属杆的长度由a 拉长到x a +时，所需的力等于akx，其中k 为常数，试求将该金属杆由长度a 拉长到b 所作的功.解：由于金属杆拉长所需的力f 与拉长的长度成正比x ，且akxf =，其中k 为常数。

中国人民大学出版社(第四版)高等数学一第3章课后习题详解

第3章中值定理与导数的应用内容概要课后习题全解习题3-1★1.下列函数在给定区间上是否满足罗尔定理的所有条件？如满足，请求出满足定理的数值ξ。

（1）]511[32)(2.,,x x x f ---=；（2）]30[3)(,,x x x f -=。

知识点：罗尔中值定理。

思路：根据罗尔定理的条件和结论，求解方程0)(/=ξf ，得到的根ξ便为所求。

解：（1）∵32)(2--=x x x f 在]511[.,-上连续，在)5.1,1(-内可导，且0)51()1(==-.f f ，∴32)(2--=x x x f 在]511[.,-上满足罗尔定理的条件。

令()410f ξξ'=-=得)511(41.,ξ-∈=即为所求。

（2）∵x x x f -=3)(在]30[,上连续，在)30(,内可导，且0)3()0(==f f ， ∴x x x f -=3)(在]30[,上满足罗尔定理的条件。

令()0f ξ'==，得)30(2,ξ∈=即为所求。

★2.验证拉格朗日中值定理对函数25423-+-=x x x y 在区间]10[,上的正确性。

知识点：拉格朗日中值定理。

思路：根据拉格朗日中值定理的条件和结论，求解方程(1)(0)()10f f f ξ-'=-，若得到的根]10[,ξ∈则可验证定理的正确性。

解：∵32()452y f x x x x ==-+-在]10[,连续，在)10(,内可导，∴25423-+-=x x x y 在区间]10[,上满足拉格朗日中值定理的条件。

又2)0(2)1(-=-=,f f ，2()12101f x x x '=-+，∴要使(1)(0)()010f f f ξ-'==-，只要：5(01)12,ξ±=，∴5(01)12,ξ∃=∈，使(1)(0)()10f f f ξ-'=-，验证完毕。

★3.已知函数4)(x x f =在区间]21[,上满足拉格朗日中值定理的条件，试求满足定理的ξ。

高数课后题答案及详解高数课后习题答案解析

高数课后题答案及详解一、求下列极限1、sin ()lim x x x →−−22111；解一：()()12sin 1cos 1lim 02x x x x→−−==原式解二：()()11sin 1sin 1lim lim11x x x x x x →→−−==−+原式2、lim sin x x x →2203解一：00021311lim lim lim 6sin3cos39sin3cos39x x x x x x x x x →→→==⋅=原式解二：sin 3~30021limlim 6sin 3cos 39cos 39x xx x x x x xx x →→===原式3、20tan 2lim 3sin x x xx →解：()2tan 2~2,sin3~3222lim93x x x xx xx →=原式=4、0lim ln(1)x x x →+解一：()001lim lim 1111x x x x→→==+=+原式解二：()1011lim1ln ln 1x xex →===+原式5、2lim xx x x →∞−⎛⎞⎜⎟⎝⎠解一：()2222lim 1xx ex −⋅−−→∞⎛⎞=−=⎜⎟⎝⎠原式解二：()1211ln 2ln 22limlim ln2lim22lim x x x x xx x x x xx xx x x eeeee−−→∞→∞→∞−−−−−−→∞−−−=====原式6、()111lim 32x x x −→−解一：()()112220lim 12t x tt t e=−−−−→=−=令原式解二：1(2)221122221lim[1(22)]{lim[1(22)]}xx x x x x e−−→−−−→=+−=+−=i 原式7、30sin lim x x x x →−解：2001cos sin 1lim lim 366x x x x x x →→−===原式8、111lim ln 1x x x →⎛⎞−⎜⎟−⎝⎠解：111111ln 11lim lim lim 1(1)ln ln 1ln 11lim ln 112x x x x x x x x x x x x x x x xx →→→→−−+−===−−+−+−==−++原式9、12lim 22n n n n →∞+++⎛⎞−⎜⎟+⎝⎠⋯解：()()221122lim lim22221lim 422n n n n n n n n n n n n n n →∞→∞→∞⎛⎞+⎜⎟+−−=−=⎜⎟++⎜⎟⎝⎠−==−+原式10、329sin limx x t dtx →∫解：26686003sin 1sin 1lim lim 933x x x x x x x →→===原式11、arctan limx x tdt →+∞。

高等数学教材题目大全及解析

高等数学教材题目大全及解析第一部分：微积分1. 极限与连续题目：计算极限 $$\lim_{x\to 2}\frac{x^2-4}{x-2}$$ 并给出解析。

解析：首先观察分式的形式，可以看出分子是一个二次函数，分母是线性函数，而且在极限的点$x=2$处，分母为零。

这暗示我们可能要利用因式分解来化简分式。

$$\lim_{x\to 2}\frac{x^2-4}{x-2} = \lim_{x\to 2}\frac{(x+2)(x-2)}{x-2}$$当$x$接近2时，分子和分母都接近于0，因此我们可以将$(x+2)$和$(x-2)$都约去，最终得到：$$\lim_{x\to 2}\frac{x^2-4}{x-2} = \lim_{x\to 2}(x+2) = 4$$因此，该极限的解析为4。

2. 导数与微分题目：求函数$f(x) = x^3 + 2x^2 - 3x + 1$的导函数，并给出其解析。

解析：要求函数的导函数，我们需要对函数进行求导。

根据求导法则，我们可以逐项求导得到：$$\frac{d}{dx}(x^3 + 2x^2 - 3x + 1) = 3x^2 + 4x - 3$$因此，函数$f(x)$的导函数为$3x^2 + 4x - 3$。

3. 积分与定积分题目：计算定积分 $$\int_{0}^{2}\left(2xe^{x^2}+3\right)dx$$ 并给出解析。

解析：对于定积分，我们可以先求原函数，然后再代入上限和下限进行计算。

首先对被积函数的每一项进行积分得到：$$\int 2xe^{x^2}dx = e^{x^2} + C_1$$$$\int 3dx = 3x + C_2$$将两个结果相加得到原函数：$$F(x) = e^{x^2} + 3x + C$$根据上限和下限进行代入：$$\int_{0}^{2}\left(2xe^{x^2}+3\right)dx = F(2) - F(0) = (e^{4} + 6) - (e^{0} + 0) = e^{4} + 6$$因此，定积分的解析为$e^{4} + 6$。

高等数学教材习题答案详解

高等数学教材习题答案详解1. 一元函数与极限题目：计算极限 $\lim \limits_{x \to 0} \frac{e^x - 1 - x}{x^2}$。

解析：首先将分式分离为两个部分，得到：$\lim \limits_{x \to 0} \left( \frac{e^x - 1}{x} \cdot \frac{1}{x} -\frac{1}{x} \right)$。

根据极限的性质，我们将分别计算两个部分的极限。

先计算 $\lim \limits_{x \to 0} \frac{e^x - 1}{x}$。

将分子展开为泰勒级数：$e^x = 1 + x + \frac{x^2}{2!} +\frac{x^3}{3!} + \dots$。

代入式中，得到：$\lim \limits_{x \to 0} \left( \frac{1 + x + \frac{x^2}{2!} +\frac{x^3}{3!} + \dots - 1}{x} \right)$。

简化后得到：$\lim \limits_{x \to 0} \left( 1 + \frac{x}{2!} + \frac{x^2}{3!} + \dots \right) = 1$。

再计算 $\lim \limits_{x \to 0} \frac{1}{x}$。

由于分子为常数1，不随x变化，分母趋于0时，极限不存在。

将两个计算结果代入原式中，得到最终结果：$\lim \limits_{x \to 0} \frac{e^x - 1 - x}{x^2} = 1 - \lim \limits_{x \to 0} \frac{1}{x} = 1 - \infty = -\infty$。

2. 一元函数的导数与微分题目：求函数 $y = \sqrt{1 + x^2}$ 的导数。

解析：对于 $y = \sqrt{1 + x^2}$，可以通过链式法则求导。

令 $u = 1 + x^2$，则 $y = \sqrt{u}$。

高等数学课后习题及参考答案(第一章)

高等数学课后习题及参考答案（第一章）习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式.解 A ⋃B =(-∞, 3)⋃(5, +∞),A ⋂B =[-10, -5),A \B =(-∞, -10)⋃(5, +∞),A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C .证明因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f (A ⋃B )=f (A )⋃f (B );(2)f (A ⋂B )⊂f (A )⋂f (B ).证明因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B )⇔ y ∈f (A )⋃f (B ),所以 f (A ⋃B )=f (A )⋃f (B ).(2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )),所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A . 6. 求下列函数的自然定义域:(1)23+=x y ;解由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞).(3)211x xy --=; 解由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1].(4)241x y -=; 解由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2).(5)x y sin =;解由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解由|x -3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解由x +1>0得函数的定义域D =(-1, +∞).(10)x e y 1=.解由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同？为什么？(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y ,所以函数xx y -=1在区间(-∞, 1)内是单调增加的. (2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0ln )()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加. 11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数？(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211x x y +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数？对于周期函数, 指出其周期:(1)y =cos(x -2);解是周期函数, 周期为l =2π.(2)y =cos 4x ;解是周期函数, 周期为2π=l . (3)y =1+sin πx ;解是周期函数, 周期为l =2.(4)y =x cos x ;解不是周期函数.(5)y =sin 2x .解是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y ;解由31+=x y 得x =y 3-1, 所以31+=x y 的反函数为y =x 3-1.(2)xx y +-=11; 解由x x y +-=11得y y x +-=11, 所以x x y +-=11的反函数为xx y +-=11. (3)dcx b ax y ++=(ad -bc ≠0); 解由d cx b ax y ++=得a cy b dy x -+-=, 所以d cx b ax y ++=的反函数为acx b dx y -+-=. (4) y =2sin3x ;解由y =2sin 3x 得2arcsin 31y x =, 所以y =2sin3x 的反函数为2arcsin 31x y =. (5) y =1+ln(x +2);解由y =1+ln(x +2)得x =e y -1-2, 所以y =1+ln(x +2)的反函数为y =e x -1-2.(6)122+=x x y . 解由122+=x x y 得y y x -=1log 2, 所以122+=x x y 的反函数为x x y -=1log 2. 15. 设函数f (x )在数集X 上有定义, 试证: 函数f (x )在X 上有界的充分必要条件是它在X 上既有上界又有下界.证明先证必要性. 设函数f (x )在X 上有界, 则存在正数M , 使|f (x )|≤M , 即-M ≤f (x )≤M . 这就证明了f (x )在X 上有下界-M 和上界M .再证充分性. 设函数f (x )在X 上有下界K 1和上界K 2, 即K 1≤f (x )≤ K 2 . 取M =max{|K 1|, |K 2|}, 则 -M ≤ K 1≤f (x )≤ K 2≤M ,即 |f (x )|≤M .这就证明了f (x )在X 上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x 1和x 2的函数值:(1) y =u 2, u =sin x , 61π=x , 32π=x ; 解 y =sin 2x , 41)21(6sin 221===πy ,43)23(3sin 222===πy . (2) y =sin u , u =2x , 81π=x ,42π=x ; 解 y =sin2x , 224sin )82sin(1==⋅=ππy ,12sin )42sin(2==⋅=ππy .(3)u y =, u =1+x 2, x 1=1, x 2= 2;解 21x y +=, 21121=+=y , 52122=+=y .(4) y =e u , u =x 2, x 1 =0, x 2=1;解 2x e y =, 1201==e y , e e y ==212.(5) y =u 2 , u =e x , x 1=1, x 2=-1.解 y =e 2x , y 1=e 2⋅1=e 2, y 2=e 2⋅(-1)=e -2.17. 设f (x )的定义域D =[0, 1], 求下列各函数的定义域:(1) f (x 2);解由0≤x 2≤1得|x |≤1, 所以函数f (x 2)的定义域为[-1, 1].(2) f (sin x );解由0≤sin x ≤1得2n π≤x ≤(2n +1)π (n =0, ±1, ±2⋅ ⋅ ⋅), 所以函数f (sin x )的定义域为[2n π, (2n +1)π] (n =0, ±1, ±2⋅ ⋅ ⋅) .(3) f (x +a )(a >0);解由0≤x +a ≤1得-a ≤x ≤1-a , 所以函数f (x +a )的定义域为[-a , 1-a ].(4) f (x +a )+f (x -a )(a >0).解由0≤x +a ≤1且0≤x -a ≤1得: 当210≤<a 时, a ≤x ≤1-a ; 当21>a 时, 无解. 因此当210≤<a 时函数的定义域为[a , 1-a ], 当21>a 时函数无意义. 18. 设⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)(x x x x f , g (x )=e x , 求f [g (x )]和g [f (x )], 并作出这两个函数的图形.解 ⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)]([x x x e e e x g f , 即⎪⎩⎪⎨⎧>-=<=0 10 00 1)]([x x x x g f . ⎪⎩⎪⎨⎧>=<==-1|| 1||e 1|| )]([101)(x e x x e e xfg x f , 即⎪⎩⎪⎨⎧>=<=-1|| 1|| 11|| )]([1x e x x e x f g .19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40︒(图1-37). 当过水断面ABCD 的面积为定值S 0时, 求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式, 并指明其定义域.图1-37解 40sin h DC AB ==, 又从0)]40cot 2([21S h BC BC h =⋅++ 得h hS BC ⋅-= 40cot 0, 所以 h h S L40sin 40cos 20-+=. 自变量h 的取值范围应由不等式组h >0, 040cot 0>⋅-h hS 确定, 定义域为40cot 00S h <<.20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p 表示为订购量x 的函数;(2)将厂方所获的利润P 表示成订购量x 的函数;(3)某一商行订购了1000台, 厂方可获利润多少？解 (1)当0≤x ≤100时, p =90.令0.01(x 0-100)=90-75, 得x 0=1600. 因此当x ≥1600时, p =75.当100<x <1600时,p =90-(x -100)⨯0.01=91-0. 01x .综合上述结果得到⎪⎩⎪⎨⎧≥<<-≤≤=1600 75160010001.0911000 90x x x x p . (2)⎪⎩⎪⎨⎧≥<<-≤≤=-=1600 151600100 01.0311000 30)60(2x x x x x x x x p P .(3) P =31⨯1000-0.01⨯10002=21000(元).习题1-21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限:(1)nn x 21=; 解当n →∞时, nn x 21=→0, 021lim =∞→n n . (2)nx n n 1)1(-=; 解当n →∞时, n x n n 1)1(-=→0, 01)1(lim =-∞→nn n . (3)212nx n +=; 解当n →∞时, 212n x n +=→2, 2)12(lim 2=+∞→nn . (4)11+-=n n x n ; 解当n →∞时, 12111+-=+-=n n n x n →0, 111lim =+-∞→n n n . (5) x n =n (-1)n .解当n →∞时, x n =n (-1)n 没有极限.2. 设数列{x n }的一般项nn x n 2cos π=. 问n n x ∞→lim =? 求出N , 使当n >N 时, x n 与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N .解 0lim =∞→n n x . n n n x n 1|2cos ||0|≤=-π. ∀ε >0, 要使|x n -0|<ε , 只要ε<n 1, 也就是ε1>n . 取]1[ε=N , 则∀n >N , 有|x n -0|<ε .当ε =0.001时, ]1[ε=N =1000. 3. 根据数列极限的定义证明:(1)01lim 2=∞→n n ;分析要使ε<=-221|01|n n , 只须ε12>n , 即ε1>n . 证明因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<-|01|2n , 所以01lim 2=∞→n n . (2)231213lim =++∞→n n n ; 分析要使ε<<+=-++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n . 证明因为∀ε>0, ∃]41[ε=N , 当n >N 时, 有ε<-++|231213|n n , 所以231213lim =++∞→n n n . (3)1lim 22=+∞→na n n ; 分析要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<-+|1|22n a n , 所以1lim 22=+∞→na n n . (4)19 999.0lim =⋅⋅⋅∞→个n n . 分析要使|0.99 ⋅ ⋅ ⋅ 9-1|ε<=-1101n , 只须1101-n <ε , 即ε1lg 1+>n . 证明因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9-1|<ε , 所以19 999.0lim =⋅⋅⋅∞→个n n . 4. a u n n =∞→lim , 证明||||lim a u n n =∞→. 并举例说明: 如果数列{|x n |}有极限, 但数列{x n }未必有极限.证明因为a u n n =∞→lim , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有ε<-||a u n , 从而 ||u n |-|a ||≤|u n -a |<ε .这就证明了||||lim a u n n =∞→.数列{|x n |}有极限, 但数列{x n }未必有极限. 例如1|)1(|lim =-∞→n n , 但n n )1(lim -∞→不存在.5. 设数列{x n }有界, 又0lim =∞→n n y , 证明: 0lim =∞→n n n y x .证明因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M .又0lim =∞→n n y , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有M y n ε<||. 从而当n >N 时, 有εε=⋅<≤=-M M y M y x y x n n n n n |||||0|,所以0lim =∞→n n n y x .6. 对于数列{x n }, 若x 2k -1→a (k →∞), x 2k →a (k →∞), 证明: x n →a (n →∞).证明因为x 2k -1→a (k →∞), x 2k →a (k →∞), 所以∀ε>0, ∃K 1, 当2k -1>2K 1-1时, 有| x 2k -1-a |<ε ; ∃K 2, 当2k >2K 2时, 有|x 2k -a |<ε .取N =max{2K 1-1, 2K 2}, 只要n >N , 就有|x n -a |<ε . 因此x n →a (n →∞).习题1-31. 根据函数极限的定义证明: (1)8)13(lim 3=-→x x ;分析因为|(3x -1)-8|=|3x -9|=3|x -3|, 所以要使|(3x -1)-8|<ε , 只须ε31|3|<-x .证明因为∀ε>0, ∃εδ31=, 当0<|x -3|<δ时, 有|(3x -1)-8|<ε , 所以8)13(lim 3=-→x x .(2)12)25(lim 2=+→x x ;分析因为|(5x +2)-12|=|5x -10|=5|x -2|, 所以要使|(5x +2)-12|<ε , 只须ε51|2|<-x .证明因为∀ε >0, ∃εδ51=, 当0<|x -2|<δ时, 有 |(5x +2)-12|<ε , 所以12)25(lim 2=+→x x .(3)424lim 22-=+--→x x x ;分析因为|)2(||2|244)4(2422--=+=+++=--+-x x x x x x x , 所以要使ε<--+-)4(242x x , 只须ε<--|)2(|x . 证明因为∀ε >0, ∃εδ=, 当0<|x -(-2)|<δ时, 有ε<--+-)4(242x x , 所以424lim22-=+--→x x x .(4)21241lim 321=+--→x x x . 分析因为|)21(|2|221|212413--=--=-+-x x x x , 所以要使ε<-+-212413x x , 只须ε21|)21(|<--x .证明因为∀ε >0, ∃εδ21=, 当δ<--<|)21(|0x 时, 有ε<-+-212413x x , 所以21241lim 321=+--→x x x . 2. 根据函数极限的定义证明:(1)2121lim 33=+∞→x x x ; 分析因为333333||21212121x x x x x x =-+=-+, 所以要使ε<-+212133x x , 只须ε<3||21x , 即321||ε>x . 证明因为∀ε >0, ∃321ε=X , 当|x |>X 时, 有ε<-+212133x x , 所以2121lim 33=+∞→x x x . (2)0sin lim =+∞→xx x .分析因为xx x x x 1|sin |0sin ≤=-. 所以要使ε<-0sin x x , 只须ε<x1, 即21ε>x .证明因为∀ε>0, ∃21ε=X , 当x >X 时, 有ε<-0sin xx ,所以0sin lim =+∞→xx x .3. 当x →2时, y =x 2→4. 问δ等于多少, 使当|x -2|<δ时, |y -4|<0.001？解由于当x →2时, |x -2|→0, 故可设|x -2|<1, 即1<x <3. 要使|x 2-4|=|x +2||x -2|<5|x -2|<0.001, 只要0002.05001.0|2|=<-x .取δ=0.0002, 则当0<|x -2|<δ时, 就有|x 2-4|<0. 001.4. 当x →∞时, 13122→+-=x x y , 问X 等于多少, 使当|x |>X 时, |y -1|<0.01?解要使01.034131222<+=-+-x x x , 只要397301.04||=->x , 故397=X .5. 证明函数f (x )=|x |当x →0时极限为零.证明因为|f (x )-0|=||x |-0|=|x |=|x -0|, 所以要使|f (x )-0|<ε, 只须|x |<ε.因为对∀ε>0, ∃δ=ε, 使当0<|x -0|<δ, 时有 |f (x )-0|=||x |-0|<ε, 所以0||lim 0=→x x .6. 求,)(xx x f = x x x ||)(=ϕ当x →0时的左﹑右极限, 并说明它们在x →0时的极限是否存在. 证明因为11lim lim )(lim 000===---→→→x x x x x x f ,11lim lim )(lim 000===+++→→→x x x x x x f ,)(lim )(lim 0x f x f x x +→→=-,所以极限)(lim 0x f x →存在.因为1lim ||lim )(lim 000-=-==---→→→xx x x x x x x ϕ,1lim ||lim )(lim 000===+++→→→x x x x x x x x ϕ,)(lim )(lim 0x x x x ϕϕ+→→≠-,所以极限)(lim 0x x ϕ→不存在.7. 证明: 若x →+∞及x →-∞时, 函数f (x )的极限都存在且都等于A , 则A x f x =∞→)(lim .证明因为A x f x =-∞→)(lim , A x f x =+∞→)(lim , 所以∀ε>0, ∃X 1>0, 使当x <-X 1时, 有|f (x )-A |<ε ;∃X 2>0, 使当x >X 2时, 有|f (x )-A |<ε .取X =max{X 1, X 2}, 则当|x |>X 时, 有|f (x )-A |<ε , 即A x f x =∞→)(lim .8. 根据极限的定义证明: 函数f (x )当x →x 0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明先证明必要性. 设f (x )→A (x →x 0), 则∀ε>0, ∃δ>0, 使当0<|x -x 0|<δ 时, 有|f (x )-A |<ε .因此当x 0-δ<x <x 0和x 0<x <x 0+δ 时都有 |f (x )-A |<ε .这说明f (x )当x →x 0时左右极限都存在并且都等于A . 再证明充分性. 设f (x 0-0)=f (x 0+0)=A , 则∀ε>0, ∃δ1>0, 使当x 0-δ1<x <x 0时, 有| f (x )-A <ε ; ∃δ2>0, 使当x 0<x <x 0+δ2时, 有| f (x )-A |<ε .取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ 时, 有x 0-δ1<x <x 0及x 0<x <x 0+δ2 , 从而有 | f (x )-A |<ε ,即f (x )→A (x →x 0).9. 试给出x →∞时函数极限的局部有界性的定理, 并加以证明.解 x →∞时函数极限的局部有界性的定理: 如果f (x )当x →∞时的极限存在, 则存在X >0及M >0, 使当|x |>X 时, |f (x )|<M .证明设f (x )→A (x →∞), 则对于ε =1, ∃X >0, 当|x |>X 时, 有|f (x )-A |<ε =1. 所以 |f (x )|=|f (x )-A +A |≤|f (x )-A |+|A |<1+|A |.这就是说存在X >0及M >0, 使当|x |>X 时, |f (x )|<M , 其中M =1+|A |. 习题1-41. 两个无穷小的商是否一定是无穷小？举例说明之. 解不一定.例如, 当x →0时, α(x )=2x , β(x )=3x 都是无穷小, 但32)()(lim0=→x x x βα, )()(x x βα不是无穷小.2. 根据定义证明:(1)392+-=x x y 当x →3时为无穷小; (2)xx y 1sin =当x →0时为无穷小.证明 (1)当x ≠3时|3|39||2-=+-=x x x y . 因为∀ε>0, ∃δ=ε , 当0<|x -3|<δ时, 有εδ=<-=+-=|3|39||2x x x y ,所以当x →3时392+-=x x y 为无穷小. (2)当x ≠0时|0||1sin |||||-≤=x xx y . 因为∀ε>0, ∃δ=ε , 当0<|x -0|<δ时, 有εδ=<-≤=|0||1sin |||||x xx y ,所以当x →0时xx y 1sin =为无穷小.3. 根据定义证明: 函数xx y 21+=为当x →0时的无穷大. 问x 应满足什么条件,能使|y |>104？证明分析2||11221||-≥+=+=x x x x y , 要使|y |>M , 只须M x >-2||1, 即21||+<M x .证明因为∀M >0, ∃21+=M δ, 使当0<|x -0|<δ时, 有M x x >+21,所以当x →0时, 函数xx y 21+=是无穷大.取M =104, 则21014+=δ. 当2101|0|04+<-<x 时, |y |>104. 4. 求下列极限并说明理由: (1)xx x 12lim +∞→;(2)xx x --→11lim 20.解 (1)因为xx x 1212+=+, 而当x →∞ 时x 1是无穷小, 所以212lim =+∞→x x x .(2)因为x xx +=--1112(x ≠1), 而当x →0时x 为无穷小, 所以111lim 20=--→x x x .6. 函数y =x cos x 在(-∞, +∞)内是否有界？这个函数是否为当x →+∞ 时的无穷大？为什么？解函数y =x cos x 在(-∞, +∞)内无界.这是因为∀M >0, 在(-∞, +∞)内总能找到这样的x , 使得|y (x )|>M . 例如y (2k π)=2k π cos2k π=2k π (k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, 就有| y (2k π)|>M .当x →+∞ 时, 函数y =x cos x 不是无穷大.这是因为∀M >0, 找不到这样一个时刻N , 使对一切大于N 的x , 都有|y (x )|>M . 例如0)22cos()22()22(=++=+ππππππk k k y (k =0, 1, 2, ⋅ ⋅ ⋅),对任何大的N , 当k 充分大时, 总有N k x >+=22ππ, 但|y (x )|=0<M .7. 证明: 函数xx y 1sin 1=在区间(0, 1]上无界, 但这函数不是当x →0+时的无穷大.证明函数xx y 1sin 1=在区间(0, 1]上无界. 这是因为∀M >0, 在(0, 1]中总可以找到点x k , 使y (x k )>M . 例如当221ππ+=k x k (k =0, 1, 2, ⋅ ⋅ ⋅)时, 有22)(ππ+=k x y k ,当k 充分大时, y (x k )>M .当x →0+ 时, 函数xx y 1sin 1=不是无穷大. 这是因为∀M >0, 对所有的δ>0, 总可以找到这样的点x k , 使0<x k <δ, 但y (x k )<M . 例如可取πk x k 21=(k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, x k <δ, 但y (x k )=2k πsin2k π=0<M .习题1-51. 计算下列极限:(1)35lim 22-+→x x x ; 解 9325235lim 222-=-+=-+→x x x .(2)13lim 223+-→x x x ; 解 01)3(3)3(13lim 22223=+-=+-→x x x . (3)112lim 221-+-→x x x x ;解 02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x . (4)xx x x x x 2324lim2230++-→; 解 2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x . (5)hx h x h 220)(lim -+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→. (6))112(lim 2xx x +-∞→; 解 21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x . (7)121lim 22---∞→x x x x ; 解 2111211lim 121lim 2222=---=---∞→∞→xx x x x xx x . (8)13lim 242--+∞→x x x x x ; 解 013lim 242=--+∞→x x x x x (分子次数低于分母次数, 极限为零). 或 012111lim 13lim 4232242=--+=--+∞→∞→x x x x x x x x x x . (9)4586lim 224+-+-→x x x x x ; 解 32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x .(10))12)(11(lim 2x x x -+∞→;解 221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x . (11))21 41211(lim n n +⋅⋅⋅+++∞→;解 2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n . (12)2)1( 321limnn n -+⋅⋅⋅+++∞→; 解 211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n nn n n n n n . (13)35)3)(2)(1(limn n n n n +++∞→;解 515)3)(2)(1(lim 3=+++∞→nn n n n (分子与分母的次数相同, 极限为最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim 3=+++=+++∞→∞→n n n n n n n n n . (14))1311(lim 31x x x ---→;解 )1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 112lim21-=+++-=→x x x x . 2. 计算下列极限: (1)2232)2(2lim -+→x x x x ; 解因为01602)2(lim 2322==+-→x x x x , 所以∞=-+→2232)2(2lim x x x x . (2)12lim 2+∞→x x x ;解 ∞=+∞→12lim 2x x x (因为分子次数高于分母次数).(3))12(lim 3+-∞→x x x .解 ∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数).3. 计算下列极限: (1)xx x 1sin lim 20→;解 01sin lim 20=→xx x (当x →0时, x 2是无穷小, 而x 1sin 是有界变量).(2)xx x arctan lim ∞→.解 0arctan 1lim arctan lim =⋅=∞→∞→x x xx x x (当x →∞时, x 1是无穷小,而arctan x 是有界变量).4. 证明本节定理3中的(2).习题1-61. 计算下列极限: (1)xx x ωsin lim 0→;解 ωωωωω==→→x x xx x x sin lim sin lim 00.(2)xx x 3tan lim 0→;解 33cos 133sin lim 33tan lim 00=⋅=→→xx x x x x x .(3)xx x 5sin 2sin lim 0→;解 52525sin 522sin lim 5sin 2sin lim 00=⋅⋅=→→x x x x x x x x .(4)x x x cot lim 0→;解 1cos lim sin lim cos sin lim cot lim 0000=⋅=⋅=→→→→x x x x x x x x x x x x .(5)xx x x sin 2cos 1lim 0-→;解 2)sin (lim 2sin 2lim 2cos 1lim sin 2cos 1lim 20220200===-=-→→→→x x x x x x x x x x x x x . 或 2sin lim 2sin sin 2lim sin 2cos 1lim 0200===-→→→xx x x x x x x x x x . (6)n n n x 2sin 2lim ∞→(x 为不等于零的常数). 解 x x xx x nn n n nn =⋅=∞→∞→22sin lim2sin 2lim . 2. 计算下列极限:(1)x x x 1)1(lim -→; 解 11)(1)1()(101})](1[lim {)](1[lim )1(lim ---→--→→=-+=-+=-e x x x x x x x x x .(2)x x x 1)21(lim +→;解 2221221010])21(lim [)21(lim )21(lim e x x x x x x x x x =+=+=+→⋅→→.(3)x x xx 2)1(lim +∞→; 解 222])11(lim [)1(lim e xx x x x x x =+=+∞→∞→.(4)kx x x)11(lim -∞→(k 为正整数).解 k k x x kx x e xx ---∞→∞→=-+=-))(()11(lim )11(lim .3. 根据函数极限的定义, 证明极限存在的准则I '. 证明仅对x →x 0的情形加以证明.设ε为任一给定的正数, 由于A x g x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ1>0, 使得当0<|x -x 0|<δ1时, 恒有|g (x )-A |<ε, 即A -ε<g (x )<A +ε.由于A x h x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ2>0, 使得当0<|x -x 0|<δ2时, 恒有|h (x )-A |<ε, 即A -ε<h (x )<A +ε.取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ时, A -ε<g (x )<A +ε与A -ε<h (x )<A +ε 同时成立, 又因为g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε, 因此A x f x x =→)(lim 0.证明仅对x →x 0的情形加以证明. 因为A x g x x =→)(lim 0, A x h x x =→)(lim 0,所以对任一给定的ε>0, 存在δ>0, 使得当0<|x -x 0|<δ时, 恒有 |g (x )-A |<ε及|h (x )-A |<ε,即 A -ε<g (x )<A +ε及A -ε<h (x )<A +ε.又因为 g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε, 因此A x f x x =→)(lim 0.4. 利用极限存在准则证明: (1)111lim =+∞→nn ;证明因为n n 11111+<+<,而 11lim =∞→n 且1)11(lim =+∞→n n ,由极限存在准则I , 111lim =+∞→nn .(2)1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n ;证明因为πππππ+<++⋅⋅⋅++++<+2222222)1 211(n n n n n n n n n n , 而 1lim 22=+∞→πn n n n , 1lim 22=+∞→πn n n , 所以 1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n .(3)数列2,22+, 222++, ⋅ ⋅ ⋅ 的极限存在;证明 21=x , n n x x +=+21(n =1, 2, 3, ⋅ ⋅ ⋅). 先证明数列{x n }有界.当n =1时221<=x , 假定n =k 时x k <2, 则当n =k +1时, 22221=+<+=+k k x x , 所以x n <2(n =1, 2, 3, ⋅ ⋅ ⋅), 即数列{x n }有界.再证明数列单调增. 因为nn n n n n n n n n n n x x x x x x x x x x x x +++--=++-+=-+=-+2)1)(2(22221, 而x n -2<0, x n +1>0, 所以x n +1-x n >0, 即数列{x n }单调增.因为数列{x n }单调增加有上界, 所以此数列是有极限的. (4)11lim 0=+→n x x ;证明当|x |≤1时, 则有 1+x ≤1+|x |≤(1+|x |)n , 1+x ≥1-|x |≥(1-|x |)n , 从而有 ||11||1x x x n +≤+≤-. 因为 1|)|1(lim |)|1(lim 0=+=-→→x x x x ,根据夹逼准则, 有 11lim 0=+→n x x .(5)1]1[lim 0=+→xx x .证明因为x x x 1]1[11≤<-, 所以1]1[1≤<-xx x .又因为11lim )1(lim 00==-++→→x x x , 根据夹逼准则, 有1]1[lim 0=+→xx x .习题 1-71. 当x →0时, 2x -x 2 与x 2-x 3相比, 哪一个是高阶无穷小？解因为02lim 2lim 202320=--=--→→xx x x x x x x x ,所以当x →0时, x 2-x 3是高阶无穷小, 即x 2-x 3=o (2x -x 2).2. 当x →1时, 无穷小1-x 和(1)1-x 3, (2))1(212x -是否同阶？是否等价？解 (1)因为3)1(lim 1)1)(1(lim 11lim 212131=++=-++-=--→→→x x xx x x x x x x x , 所以当x →1时, 1-x 和1-x 3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim 211)1(21lim 121=+=--→→x x x x x , 所以当x →1时, 1-x 和)1(212x -是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x →0时, 有: (1) arctan x ~x ;(2)2~1sec 2x x -. 证明 (1)因为1tan limarctan lim 00==→→y yxx y x (提示: 令y =arctan x , 则当x →0时, y →0),所以当x →0时, arctan x ~x .(2)因为1)22sin 2(lim 22sin 2lim cos cos 1lim 2211sec lim 202202020===-=-→→→→x xx x x x x xx x x x x , 所以当x →0时, 2~1sec 2x x -. 4. 利用等价无穷小的性质, 求下列极限: (1)xx x 23tan lim 0→;(2)mn x x x )(sin )sin(lim 0→(n , m 为正整数);(3)x x x x 30sin sin tan lim -→; (4))1sin 1)(11(tan sin lim320-+-+-→x x x x x .解 (1)2323lim 23tan lim 00==→→x x x x x x .(2)⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim00. (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==-=-=-→→→→x x x x x x xx x x x x x x x x . (4)因为32221)2(2~2sin tan 2)1(cos tan tan sin x x x x x x x x x -=⋅--=-=-(x →0),23232223231~11)1(11x x x x x ++++=-+(x →0), x x x x x ~sin ~1sin 1sin 1sin 1++=-+(x →0), 所以 33121lim )1sin 1)(11(tan sin lim 230320-=⋅-=-+-+-→→x x x x x x x x x .5. 证明无穷小的等价关系具有下列性质: (1) α ~α (自反性);(2) 若α ~β, 则β~α(对称性); (3)若α ~β, β~γ, 则α~γ(传递性). 证明 (1)1lim =αα, 所以α ~α ;(2) 若α ~β, 则1lim =βα, 从而1lim=αβ. 因此β~α ;(3) 若α ~β, β~γ, 1lim limlim =⋅=βαγβγα. 因此α~γ. 习题1-81. 研究下列函数的连续性, 并画出函数的图形:(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f ;解已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的. 在x =1处, 因为f (1)=1, 并且1lim )(lim 211==--→→x x f x x , 1)2(lim )(lim 11=-=++→→x x f x x .所以1)(lim 1=→x f x , 从而函数f (x )在x =1处是连续的.综上所述，函数f (x )在[0, 2]上是连续函数.(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f .解只需考察函数在x =-1和x =1处的连续性. 在x =-1处, 因为f (-1)=-1, 并且)1(11lim )(lim 11-≠==---→-→f x f x x ,)1(1lim )(lim 11-=-==++-→-→f x x f x x ,所以函数在x =-1处间断, 但右连续. 在x =1处, 因为f (1)=1, 并且1lim )(lim 11==--→→x x f x x =f (1), 11lim )(lim 11==++→→x x x f =f (1),所以函数在x =1处连续.综合上述讨论, 函数在(-∞, -1)和(-1, +∞)内连续, 在x =-1处间断, 但右连续. 2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+--=x x x y , x =1, x =2;解 )1)(2()1)(1(23122---+=+--=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+--=→→231lim lim 2222x x x y x x , 所以x =2是函数的第二类间断点;因为2)2()1(limlim 11-=-+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处, 令y =-2, 则函数在x =1处成为连续的. (2)x x y tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅);解函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点.因∞=→x x k x tan lim π(k ≠0), 故x =k π(k ≠0)是第二类间断点;因为1tan lim0=→xx x , 0tan lim2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点.令y |x =0=1, 则函数在x =0处成为连续的;令2 ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的.(3)xy 1cos 2=, x =0;解因为函数x y 1cos 2=在x =0处无定义, 所以x =0是函数xy 1cos 2=的间断点.又因为xx 1cos lim 20→不存在, 所以x =0是函数的第二类间断点.(4)⎩⎨⎧>-≤-=1 311x x x x y , x =1.解因为0)1(lim )(lim 11=-=--→→x x f x x 2)3(lim )(lim 11=-=++→→x x f x x , 所以x =1是函数的第一类不可去间断点.3. 讨论函数x x x x f nnn 2211lim )(+-=∞→的连续性, 若有间断点, 判别其类型. 解 ⎪⎩⎪⎨⎧<=>-=+-=∞→1||1|| 01|| 11lim)(22x x x x x x x x x f nn n .在分段点x =-1处, 因为1)(lim )(lim 11=-=---→-→x x f x x , 1lim )(lim 11-==++-→-→x x f x x , 所以x =-1为函数的第一类不可去间断点.在分段点x =1处, 因为1lim )(lim 11==--→→x x f x x , 1)(lim )(lim 11-=-=++→→x x f x x , 所以x =1为函数的第一类不可去间断点.4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以0)()(lim 00>=→x f x f x x , 由极限的局部保号性定理, 存在x 0的某一去心邻域)(0x U , 使当x ∈)(0x U时f (x )>0, 从而当x ∈U (x 0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0. 5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点;解函数x x x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅处是间断的且这些点是函数的无穷间断点.(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;解函数⎩⎨⎧∉∈-=QQx x x f 1 1)(在R 上处处不连续, 但|f (x )|=1在R 上处处连续.(3)f (x )在R 上处处有定义, 但仅在一点连续.解函数⎩⎨⎧∉-∈=Q Qx x x x x f )(在R 上处处有定义, 它只在x =0处连续.习题1-91. 求函数633)(223-+--+=x x x x x x f 的连续区间, 并求极限)(lim 0x f x →, )(lim 3x f x -→及)(lim 2x f x →.解 )2)(3()1)(1)(3(633)(223-++-+=-+--+=x x x x x x x x x x x f , 函数在(-∞, +∞)内除点x =2和x =-3外是连续的, 所以函数f (x )的连续区间为(-∞, -3)、(-3, 2)、(2, +∞). 在函数的连续点x =0处, 21)0()(lim 0==→f x f x .在函数的间断点x =2和x =-3处, ∞=-++-+=→→)2)(3()1)(1)(3(lim)(lim 22x x x x x x f x x , 582)1)(1(lim )(lim 33-=-+-=-→-→x x x x f x x .2. 设函数f (x )与g (x )在点x 0连续, 证明函数ϕ(x )=max{f (x ), g (x )}, ψ(x )=min{f (x ), g (x )} 在点x 0也连续.证明已知)()(lim 00x f x f x x =→, )()(lim 00x g x g x x =→.可以验证] |)()(|)()([21)(x g x f x g x f x -++=ϕ,] |)()(|)()([21)(x g x f x g x f x --+=ψ.因此 ] |)()(|)()([21)(00000x g x f x g x f x -++=ϕ,] |)()(|)()([21)(00000x g x f x g x f x --+=ψ.因为] |)()(|)()([21lim )(lim 00x g x f x g x f x x x x x -++=→→ϕ] |)(lim )(lim |)(lim )(lim [210000x g x f x g x f x x x x x x x x →→→→-++=] |)()(|)()([210000x g x f x g x f -++==ϕ(x 0),所以ϕ(x )在点x 0也连续.同理可证明ψ(x )在点x 0也连续.3. 求下列极限: (1)52lim 20+-→x x x ;(2)34)2(sin lim x x π→;(3))2cos 2ln(lim 6x x π→;(4)xx x 11lim 0-+→;(5)145lim 1---→x x x x ;(6)a x a x a x --→sin sin lim ;(7))(lim 22x x x x x --++∞→.解 (1)因为函数52)(2+-=x x x f 是初等函数, f (x )在点x =0有定义, 所以 55020)0(52lim 220=+⋅-==+-→f x x x .(2)因为函数f (x )=(sin 2x )3是初等函数, f (x )在点4π=x 有定义, 所以1)42(sin )4()2(sin lim 334=⋅==→πππf x x .(3)因为函数f (x )=ln(2cos2x )是初等函数, f (x )在点6π=x 有定义, 所以0)62cos 2ln()6()2cos 2ln(lim 6=⋅==→πππf x x .(4))11(lim)11()11)(11(lim 11lim 000++=++++-+=-+→→→x x x x x x x x x x x x 211101111lim=++=++=→x x .(5))45)(1()45)(45(lim 145lim 11x x x x x x x x x x x x +--+---=---→→)45)(1(44lim 1x x x x x +---=→214154454lim 1=+-⋅=+-=→x x x .。

高等数学c教材课后答案详解

高等数学c教材课后答案详解1. 一元函数、多元函数与极限在高等数学C教材中的第一章中，我们学习了一元函数、多元函数与极限的概念和性质。

以下是课后习题的答案详解：1.1 一元函数1.1.1 定义域和值域对于一元函数f(x)，定域是指使函数f(x)有意义的x的取值范围。

而值域是指函数f(x)在定域上所能取到的所有值。

例如，对于函数f(x) = √(x-2)，我们需要满足x-2≥0，即x≥2。

因此，定域为[2, +∞)。

而在这个定域上，函数f(x)能够取到的值域为[0, +∞)。

1.1.2 奇偶性与周期性对于一元函数f(x)，奇偶性指的是函数图像关于y轴对称还是关于原点对称。

周期性指的是函数图像在一定区间内重复出现的性质。

例如，对于函数f(x) = sin(x)，它是奇函数，因为f(-x) = -f(x)；而它是周期函数，因为f(x+2π) = f(x)。

1.2 多元函数1.2.1 偏导数和全微分对于多元函数z = f(x, y)，它的偏导数指的是在变量x或y固定时，函数z对于x或y的变化率。

例如，对于函数z = x^2 + 2y^2，其关于x的偏导数为∂z/∂x = 2x，关于y的偏导数为∂z/∂y = 4y。

1.2.2 隐函数与显函数对于多元函数z = f(x, y)，如果可以通过一个显式的等式z = g(x, y)来表示，则称为显函数。

如果无法通过显式等式表示，而是通过一条方程F(x, y, z) = 0来定义，则称为隐函数。

例如，对于方程x^2 + y^2 - z^2 = 1，可以解出z = √(x^2 + y^2 - 1)，因此可以表示为显函数。

1.3 极限1.3.1 定义和性质在一元函数中，我们讨论了函数在某点的左极限、右极限以及极限存在的条件。

同时，我们也介绍了无穷大极限和无穷小极限的概念。

在多元函数中，我们引入了二重极限的概念，即函数在二元变量(x, y)逼近某一点时，同时有两个变量趋于该点的极限存在。

高数课后习题答案及其解析

第一章习题习题1.11.判断下列函数是否相同: ①定义域不同;②定义域对应法则相同同;2.解 25.125.01)5.0(,2)5.0(=+=-=f f5.解 ① 10,1,1222≤≤-±=-=y y x y x② +∞<<-∞+=+=-=-=y be b c x e c bx c bx e c bx e ay ay a y a y ,,,),ln(ln 6.解 ① x v v u u y sin ,3,ln 2=+== ② 52,arctan 3+==x u u y 习题1.24.解:① 无穷大 ② 无穷小 ③ 负无穷大 ④ 负无穷大 ⑤ 无穷小 ⑥ 无穷小5.求极限：⑴ 21lim 2lim 3)123(lim 13131=+-=+-→→→x x x x x x x⑵ 51)12(lim )3(lim 123lim 22222=+-=+-→→→x x x x x x x⑶ 0tan lim=∞→xxa x⑷-∞=∞--=------=----=+--→→→→32)1)(4(1lim )1)(4()1(2lim )1)(4(122lim 4532lim 11121x x x x x x x x x x x x x x x⑸ 4123lim )2)(2()2)(3(lim 465lim 22222-=+-=-+--=-+-→→→x x x x x x x x x x x x ⑹ )11)(11()11(lim 11lim22220220x x x x x x x x +++-++=+-→→2)11(lim )11(lim 202220-=++-=-++=→→x xx x x x ⑺ 311311lim 131lim 22=++=+++∞→+∞→xx x x x x⑻2132543232lim 25342332lim =⎪⎭⎫⎝⎛⋅+⎪⎭⎫ ⎝⎛⋅+=⋅+⋅⋅+⋅+∞→+∞→x xx x x x x x ⑼ 133)1)(1()2)(1(lim 12lim 1311lim 2132131-=-=+-+-+=+-+=⎪⎭⎫ ⎝⎛+-+-→-→-→x x x x x x x x x x x x x ⑽011lim )1()1)(1(lim)1(lim =++=++++-+=-+∞→∞→∞→nn n n n n n n n n n n n⑾ 1lim 1231lim 22222==⎪⎭⎫ ⎝⎛-+++∞→∞→n n n n n n x x ⑿221121211lim2121211lim 2=-⋅-=⎪⎭⎫ ⎝⎛+++∞→∞→n n n n 6.求极限 ⑴ 414tan lim0=→x x x⑵ 111sinlim1sin lim ==∞→∞→xx x x x x⑶ 2sin 2lim sin sin 2lim sin 2cos 1lim0200===-→→→xxx x x x x x x x x ⑷ x x n nn =⋅∞→2sin 2lim⑸ 21sin lim 212arcsin lim00==→→y y x x y x ⑹111sinlim1sin lim 1sinlim 22222-=-=-=-∞→-∞→-∞→x x x x x x x x x ⑺ k k xx k xx xkx e x x x x ----→---→-→=--=-=-])1()1[(lim )1(lim )1(lim2)(12)(120⑻ 22211lim 1lim e x x x x x xx =⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛+⋅∞→∞→⑼ 313tan 311cot 0])tan 31()tan 31[(lim )tan 31(lim e x x x xx x x =++=+→+→⑽ =⎪⎭⎫ ⎝⎛-+∞→32321lim x x x 343)34(23])321()321[(lim ---∞→=-⋅-e xx xx ⑾ []1)31(lim )31(lim )31(lim 03133311==+=+=+⋅-+∞→⋅⋅-+∞→-+∞→--e xx x x x x x x x x xxx⑿ 1333111lim 1111lim 1lim -+∞→+∞→+∞→==⎪⎭⎫ ⎝⎛+=⎪⎪⎪⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+e ex x x x x x x x x x习题1.31、⑴ 因为函数在x=1点处无定义，)2)(1()1)(1()(--+-=x x x x x f ，但是2)(lim 1-=→x f x ，x=1点是函数的第一类间断点（可去）。

中国人民大学出版社(第四版)高等数学一第5章课后习题详解

高等数学一第5章课后习题详解课后习题全解习题5-1★★1.利用定积分的定义计算由抛物线21y x =+，直线x a =，x b =()b a >及横轴所围成的图形的面积知识点：定积分的定义及几何意义思路：根据求定积分的三步骤做解:将[],a b 分成n 等分,取(1,2,)i i n ξ=为第i 个小区间1[(),()]i ia b a a b a n n-+-+-的右端点,则,i b a x n λ-=∆=,i b aa i nξ-=+ 显然, 0,n λ→⇔→∞于是根据定积分的几何意义,该图形面积lim ()nbi i ai A ydx y x λξ→===∆∑⎰ 21lim [()1]nn i b a b aa in n→∞=--=++∑ 22221()lim [12]n n i b a b a b a a ai i n n n→∞=---=+++∑222211()lim [(1)2]nnn i i b a b a b a n a a i in n n →∞==---=+++∑∑22232()(1)()1lim{()[1(1)(21)]}26n a b a n n b a b a a n n n n n →∞-+-=-+++++221()11()lim[1()(1)(1)(2)]6n b a b a a a b a n n n→∞-=-++-++++ 222()()[1]3b a b a a ab a -=-++-+33().3b a b a -=+- ★★2.利用定积分的定义计算下列积分：知识点：定积分的定义思路：根据求定积分的三步骤做(1)baxdx ⎰()a b <.解:易见函数[](),f x x C a b =∈，从而可积，将[],a b 分成n 等分，则,i b ax nλ-=∆=于是0,n λ→⇔→∞；取(1,2,)i i n ξ=为第i 个小区间的右端点，则,0,1,2,,1,ib aa ii n nξ-=+=-所以110lim ()lim ()n n bi i an i i b a b axdx f x a in nλξ--→→∞==--=∆=+∑∑⎰1()lim{[(0121)]}n b ab a na n n n→∞-=-+++++-2(1)()lim[]2n b a n n b a a n →∞--=-+1()lim[(1)]2n b a b a a n→∞-=-+-221()()().22b a b a a b a -=-+=-(2)1ln exdx ⎰解:用分点(0,1,,)i ni x e i n ==划分区间[]1,e ：11,1,2,,i i nni i i x x x e e i n --∆=-=-=，取i ξ是区间右端点，则 ,()ln()ln ,i i nnii i i i x e f e nξξξ=====作和，并取极限得：111ln lim ()lim ()i i nnenn i i n n i i i xdx f x e e nξ-→∞→∞===∆=-∑∑⎰111111lim{[()]}i i i nn n n nn i i i i e e e n n n --→∞==-=-+∑∑11111(1)lim lim (1)i nn n n i n e e e e n n e -→∞→∞=-=-=--∑111(1)lim ()1n n e e n e →∞=--- 记()1xx g x e =-，则当0x →时，()g x 是0型的，由洛必达法则，有 001lim lim 11x xx x x e e →→==---从而，当n →+∞时，有111lim 11n nne →+∞=--，故1ln (1) 1.exdx e e =+-=⎰★3．利用定积分的几何意义，说明下列等式：(1)121xdx =⎰.知识点：定积分的几何意义思路：定积分的几何意义为被积函数与边界所形成曲边梯形的面积解:等式左边为直线2y x =与x 轴和1x =三条直线所围成的面积，该面积等于11212==等式右边. (2)sin 0xdx ππ-=⎰解: 等式左边为正弦曲线sin y x =与x 轴在x π=及x π=-之间所围成的面积，其左右两边面积互为相反数. 则sin ()0xdx A A ππ-=-+==⎰等式右边★★4.用定积分的几何意义求a⎰(0)b >的值.知识点：定积分的几何意义思路：定积分的几何意义为被积函数与边界所形成曲边梯形的面积解:=是以2a b +为圆心，2b a-为半径的上半圆，其面积为：2221()()2228b a b a S r πππ--===由定积分的几何意义知：2().8ab a π-=⎰★★★5.试将和式的极限112lim p p pp n n n +→∞+++(0)p >表示成定积分.知识点：定积分的定义思路：根据定积分的定义推导过程可知,求和的极限公式可表示为定积分解: 112112limlim [()()()]p p p p pp p n n n n n n n nn +→∞→∞+++=+++11lim ()n pn i i n n→∞==∑设()p f x x =，则用定义求解1()f x dx ⎰为：①、等分[0,1]为n 个小区间：11[,], 1,2,, i i ii n x n nn-=∆=②、求和：取区间1[,]i i n n -上的右端点为i ξ，即i in ξ=，作和：111()n ni i i i i f x nn ξ==∆=⨯∑∑③、求极限：011111lim()lim ()lim ()nnn p pi i n n i i i i i f x nn n n λξ→→∞→∞===∆=⨯=∑∑∑∴1101121lim lim ()p p p n pp p n n i n i x dx n n n+→∞→∞=+++==∑⎰ ★★★6.有一河，宽为200米，从一岸到正对岸每隔20米测量一次水深，测得数据如下：试用梯形公式求此河横截面面积的近似值.知识点：定积分的几何意义思路：由定积分定义知：求定积分（曲边梯形面积）的第二步：用小矩形面积近似代替小曲边梯形面积，即1()()ii x i i x f x f x dx ξ-∆≈⎰，若用小梯形面积近似代替小曲边梯形面积则为：111[()()]()2i i x i i i x f x f x x f x dx --+∆≈⎰。

高等数学下(同济大学第五版)课后习题答案解析

word 完美格式第八章多元函数微分法及其应用第一节多元函数的基本概念本节主要概念，定理，公式和重要结论理解多元函数的概念，会表达函数，会求定义域；理解二重极限概念，注意A y x f y x y x =→),(lim ),(),(00是点),(y x 以任何方式趋于),(00y x ;注意理解本节中相关概念与一元函数中相应内容的区分与联系。

习题 8－11.求下列函数表达式:(1)xy y x y x f +=),(，求),(y x xy f +解：(,)()x yxy f xy x y xyx y ++=++(2)22),(y x y x y x f -=-+，求),(y x f解：(,)()()(,)f x y x y x y x y f x y xy +-=-+⇒= 2.求下列函数的定义域，并绘出定义域的图形: (1)221)1ln(yx x y x z --+-+=解：22221011010x y x y x y x y x +->⎧+>⎧⎪-->⇒⎨⎨+<⎩⎪≥⎩(2))12ln(2+-=y x z 解：2210x y -+>(3) |)|||1ln(),(y x y x f --= 解：1||||0||||1x y x y -->⇒+< 3.求下列极限:(1)22)1,0(),(1limy x xyx y x ++-→解：22(,)(0,1)1lim1x y x xyx y →-+=+ (2)xy xy y x 42lim)0,0(),(+-→解一：(,)(0,0)(,)(0,0)(,)(0,0)18lim2lim2lim 4x y x y x y xyxy →→→=-=-=-(3)yxy x y x )sin()2(lim )0,1(),(+→(4)2222011limy x y x y x +-+→→解一：(,)(1,0)(,)(1,0)sin()sin()lim (2)lim [(2)]3x y x y xy xy x x x y xy→→+=+=解二：(,)(1,0)(,)(1,0)(,)(1,0)sin()lim (2)lim (2)lim (2)3x y x y x y xy xyx x x x y y →→→+=+=+= (4)22220011limyx y x y x +-+→→解一：2222222200000011lim lim()022x x x y y y x y y x x y x y →→→→→→==⋅=++解二：222222000000x x x y y y y x y →→→→→→===+ 4.证明下列函数当)0,0(),(→y x 时极限不存在:(1)2222),(yx y x y x f +-=解：222222222222001lim lim 1x x y kxx y x k x k x y x k x k →→=---==+++ (2)22222)(),(y x y x y x y x f -+= 解：224222400lim lim 1()x x y x x y x x y x y x →→===+- 2222200lim 0()x y x y x y x y →==+- 5.下列函数在何处是间断的? (1) yx z -=1解：x y =(2)x y xy z 2222-+=解：22y x =第二节偏导数word 完美格式本节主要概念，定理，公式和重要结论1.偏导数：设),(y x f z =在),(00y x 的某一邻域有定义，则xy x f y x x f y x f x x ∆∆∆),(),(lim),(0000000-+=→， yy x f y y x f y x f y y ∆∆∆),(),(lim ),(0000000-+=→. ),(00y x f x 的几何意义为曲线⎩⎨⎧==0),(y y y x f z 在点)),(,,(0000y x f y x M 处的切线对x 轴的斜率.),(y x f 在任意点),(y x 处的偏导数),(y x f x 、),(y x f y 称为偏导函数，简称偏导数.求),(y x f x 时，只需把y 视为常数，对x 求导即可. 2.高阶偏导数),(y x f z =的偏导数),(),,(y x f y x f y x 的偏导数称为二阶偏导数，二阶偏导数的偏导数称为三阶偏导数，如此类推. 二阶偏导数依求导次序不同，有如下4个：xy zy x z y z x z ∂∂∂∂∂∂∂∂∂∂222222,,,，其中后两个称为混合偏导数. 若两个混合偏导数皆为连续函数，则它们相等，即可交换求偏导数的次序.高阶混合偏导数也有类似结果.习题 8－21.求下列函数的一阶偏导数:(1)xy y xz +=解：21,z z xy x x y y y∂∂=+=-+∂∂ (2)xyz arctan =解：2222222111,1()1()z y y z x y y x x x y y x x y x x∂--∂=⋅==⋅=∂+∂+++ (3))ln(22y x x z ++=解：(1z x ∂=+=∂z y ∂==∂ (4))ln(222z y x u ++=解：222222222222,,u x u y u z x x y z y x y z z x y z∂∂∂===∂++∂++∂++ (5)⎰=yzxzt dt e u 2解：22222222,,x z y z y z x z u u u ze ze ye xe x y z∂∂∂=-==-∂∂∂ (6)x y y x z cos sin = 解：2211cos cos sin sin ,cos cos sin sin z x y y x y u x x y x y x y y x x y x y y y x x y x ∂∂=+=--∂∂ (7)y x xy z ++=)1( (8))cos(ϕθϕθ-=+e u解：(1)[ln(1)],(1)[ln(1)]11x y x y z x y u x y xy xy y xy xy x x xy y xy ++∂+∂+=+++=+++∂+∂+ (8))cos(ϕθϕθ-=+e u解：[cos()sin()],[cos()sin()]u u e e θϕθϕθϕθϕθϕθϕθϕ++∂∂=---=-+-∂∂ 2.求下列函数在指定点处的一阶偏导数: （1）yxy x z arcsin)1(2-+=，求)1,0(x z 解：20(0,1)lim0x x x z x∆→∆==∆ （2）xyx e x z yarctan)1(2-+=，求)0,1(y z 解：01(1,0)lim1y y y e z y∆∆→-==-∆ 3.求下列函数的高阶偏导数:(1))ln(xy x z =，求22x z ∂∂，22yz ∂∂，y x z∂∂∂2解：ln()1,z z x xy x y y∂∂=+=∂∂ 22222211,,z z x z x x y y x y y∂∂∂==-=∂∂∂∂ (2))2(cos 2y x z +=，求22x z ∂∂，22yz ∂∂，y x z ∂∂∂2，x y z ∂∂∂2解：2cos(2)sin(2)sin 2(2)z x y x y x y x∂=-++=-+∂word 完美格式4cos(2)sin(2)2sin 2(2)zx y x y x y y∂=-++=-+∂ 222222cos 2(2),8cos 2(2),4cos 2(2)z z zx y x y x y x y x y∂∂∂=-+=-+=-+∂∂∂∂ (3)⎰+=22 y x xtdt e z ，求22x z ∂∂， yx z∂∂∂2解：22222222222,2(12),4x y x x y x x y z z z xe e x e e xye x x x y+++∂∂∂=-=+-=∂∂∂∂ 4.设⎪⎩⎪⎨⎧=+≠++-=0 00),(22222233y x y x y x xy y x y x f ，求)0,0(xy f 和)0,0(yx f .解：00(0)(0,0)00(0,0)lim lim 0x x x f x f f x x ∆→∆→∆--===∆∆，00(0,)(0,0)00(0,0)lim lim 0y y y f y f f y y ∆→∆→∆--===∆∆4224222224(,),0()x x x y y f x y y x y x y +-=+≠+ 4224222224(,),0()y x x y y f x y x x y x y --=+≠+ 54000(0,)(0,0)(0,0)lim lim 1x x xy y y y f y f y f y y∆→∆→-∆-∆-∆===-∆∆54000(,0)(0,0)(0,0)lim lim 1x x yx x x x f x f x f x x ∆→∆→∆-∆-∆===∆∆5.设)11(y x e z +-=，求证z y z y x z x222=∂∂+∂∂ 解: 1111()()2211,x y x y z z e ex x y y-+-+∂∂==∂∂ 111111()()()2222221122x yx y x y z z x y x e y e e z x y x y -+-+-+∂∂+=⋅+⋅==∂∂ 6.设222z y x r ++=，证明r zr y r x r 2222222=∂∂+∂∂+∂∂证明: 22222223,r x r x r r x r r x x r x r x r r r ∂--∂∂-∂=====∂∂由轮换对称性, 2222222323,r r y r r z y r z r∂-∂-==∂∂ 222222222223321r r r r x y z r x y z r r r∂∂∂---++===∂∂∂ 第三节全微分本节主要概念，定理，公式和重要结论1.全微分的定义若函数),(y x f z =在点),(00y x 处的全增量z ∆表示成22),(y x o y B x A z ∆+∆=+∆+∆=∆ρρ则称),(y x f z =在点),(00y x 可微，并称Bdy Adx y B x A +=+∆∆为),(y x f z =在点),(00y x 的全微分，记作dz .2.可微的必要条件：若),(y x f z =在),(00y x 可微，则（1）),(y x f 在),(00y x 处连续；（2）),(y x f 在),(00y x 处可偏导，且),(),,(0000y x f B y x f A y x ==，从而dy y x f dx y x f dz y x ),(),(0000+=.一般地，对于区域D 内可微函数， dy y x f dx y x f dz y x ),(),(+=.3.可微的充分条件：若),(y x f z =在),(00y x 的某邻域内可偏导，且偏导数在),(00y x 处连续，则),(y x f z =在),(00y x 可微。

高等数学第六版(同济大学)上册课后习题答案解析

高等数学第六版上册课后习题答案及解析第一章习题1-11. 设A=(-, -5)(5, +), B=[-10, 3), 写出A B, A B, A\B及A\(A\B)的表达式.解A B=(-, 3)(5, +),A B=[-10, -5),A\B=(-, -10)(5, +),A\(A\B)=[-10, -5).2. 设A、B是任意两个集合, 证明对偶律: (A B)C=A C B C.证明因为x(A B)C x A B x A或x B x A C或x B C x A C B C,所以(A B)C=A C B C.3. 设映射f : X Y, A X, B X . 证明(1)f(A B)=f(A)f(B);(2)f(A B)f(A)f(B).证明因为y f (A B )x A B , 使f (x )=y(因为x A 或x B ) y f (A )或y f (B )y f (A )f (B ), 所以 f (AB )=f (A )f (B ). (2)因为y f (A B )x A B , 使f (x )=y (因为x A 且x B ) y f (A )且y f (B ) y f (A )f (B ), 所以 f (A B )f (A )f (B ).4. 设映射f : X Y , 若存在一个映射g : Y X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个xX , 有I X x =x ; 对于每一个y Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明因为对于任意的yY , 有x =g (y )X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1x 2, 必有f (x 1)f (x 2), 否则若f (x 1)=f (x 2)g [ f (x 1)]=g [f (x 2)]x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y X , 因为对每个y Y , 有g (y )=x X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X Y , A X . 证明:(1)f -1(f (A ))A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x A f (x )=y f (A ) f -1(y )=x f -1(f (A )),所以 f -1(f (A ))A . (2)由(1)知f -1(f (A ))A .另一方面, 对于任意的xf -1(f (A ))存在y f (A ), 使f -1(y )=x f (x )=y . 因为y f (A )且f 是单射, 所以x A . 这就证明了f -1(f (A ))A . 因此f -1(f (A ))=A .6. 求下列函数的自然定义域:(1)23+=x y ; 解由3x +20得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解由1-x 20得x 1. 函数的定义域为(-, -1)(-1, 1)(1, +). (3)211x xy --=; 解由x0且1-x 20得函数的定义域D =[-1, 0)(0, 1].(4)241x y -=; 解由4-x 20得 |x | 2. 函数的定义域为(-2, 2).(5)x y sin =;解由x 0得函数的定义D =[0, +¥).(6) y =tan(x +1);解由21π≠+x (k =0, 1, 2, )得函数的定义域为 12-+≠ππk x (k =0, 1, 2, ). (7) y =arcsin(x -3);解由|x -3|1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解由3-x 0且x 0得函数的定义域D =(-¥, 0)È(0, 3).(9) y =ln(x +1);解由x +10得函数的定义域D =(-1, +¥). (10)x e y 1=.解由x0得函数的定义域D =(-¥, 0)È(0, +¥). 7. 下列各题中, 函数f (x )和g (x )是否相同？为什么？(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x 0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, j (-2), 并作出函数y =j (x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-, 1); (2)y =x +ln x , (0, +).证明 (1)对于任意的x 1, x 2(-, 1), 有1-x 10, 1-x 20. 因为当x 1x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数xx y -=1在区间(-, 1)内是单调增加的. (2)对于任意的x 1, x 2(0, +), 当x 1x 2时, 有0ln)()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明对于"x 1, x 2Î(-l , 0)且x 1<x 2, 有-x 1, -x 2Î(0, l )且-x 1-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以 f (-x 2)f (-x 1), -f (x 2)-f (x 1), f (x 2)f (x 1),这就证明了对于"x1, x2Î(-l, 0), 有f(x1)f(x2), 所以f(x)在(-l, 0)内也单调增加.11. 设下面所考虑的函数都是定义在对称区间(-l, l)上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明(1)设F(x)=f(x)+g(x). 如果f(x)和g(x)都是偶函数, 则F(-x)=f(-x)+g(-x)=f(x)+g(x)=F(x),所以F(x)为偶函数, 即两个偶函数的和是偶函数.如果f(x)和g(x)都是奇函数, 则F(-x)=f(-x)+g(-x)=-f(x)-g(x)=-F(x),所以F(x)为奇函数, 即两个奇函数的和是奇函数.(2)设F(x)=f(x)×g(x). 如果f(x)和g(x)都是偶函数, 则F(-x)=f(-x)×g(-x)=f(x)×g(x)=F(x),所以F(x)为偶函数, 即两个偶函数的积是偶函数.如果f(x)和g(x)都是奇函数, 则F(-x)=f(-x)×g(-x)=[-f(x)][-g(x)]=f(x)×g(x)=F(x),所以F(x)为偶函数, 即两个奇函数的积是偶函数.如果f(x)是偶函数, 而g(x)是奇函数, 则F(-x)=f(-x)×g(-x)=f(x)[-g(x)]=-f(x)×g(x)=-F(x),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数？(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211xxy +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数？对于周期函数, 指出其周期:(1)y =cos(x -2);解是周期函数, 周期为l =2p .(2)y =cos 4x ;解是周期函数, 周期为2π=l .(3)y =1+sin px ;解是周期函数, 周期为l =2.(4)y =x cos x ;解不是周期函数.(5)y =sin 2x .解是周期函数, 周期为l =p .14. 求下列函数的反函数:(1)31+=x y 错误!未指定书签。

高等数学教材习题及答案

高等数学教材习题及答案导言：高等数学是大学学习中的重要一门课程，对于培养学生的分析思维和问题解决能力具有重要作用。

习题是学生巩固知识、提高技能的重要方式之一。

本文将为大家提供一些常见高等数学习题及答案，以帮助各位同学更好地理解和掌握相关知识。

1. 一元函数与极限1.1 求函数$f(x)=\frac{1}{x}$的极限$\lim_{x\to+\infty}f(x)$。

解答：我们知道，当$x$趋向于正无穷时，分母$1/x$趋于0，所以函数$f(x)$的极限为0。

1.2 设函数$f(x)$满足$\lim_{x\to a} f(x) = A$，则下列哪个结论必定成立？A. $\lim_{x\to a} |f(x)| = |A|$B. $\lim_{x\to a} [f(x)]^2 = [A]^2$C. $\lim_{x\to a} [f(x)]^3 = [A]^3$D. $\lim_{x\to a} \sqrt{f(x)} = \sqrt{A}$答案：B. $\lim_{x\to a} [f(x)]^2 = [A]^2$2. 多元函数与偏导数2.1 函数$f(x, y) = x^2 + y^2$的偏导数$\frac{\partial f}{\partial x}$是多少？解答：对$x$求偏导数，保持$y$不变，即将$y^2$看作常数，所以$\frac{\partial f}{\partial x} = 2x$。

2.2 求函数$z = e^x \sin y$的偏导数$\frac{\partial^2 z}{\partial x\partial y}$。

解答：对$x$求偏导数得到$\frac{\partial z}{\partial x} = e^x \sin y$，再对$y$求偏导数得到$\frac{\partial^2 z}{\partial x \partial y} = e^x \cosy$。

3. 微分中值定理和泰勒公式3.1 利用微分中值定理证明：对于任意$x > 0$，恒有$\ln(1 + x) < x$。

高等数学(同济第七版)课后答案解析

解当0i时.s（t）二!F.
当I V，w2时，s（!）=I - y（2-/）2=一£f2+ 2/-1 ,
当/>2HhS（f） =1.
放
/>2.
Q 16.求联系华氏温度(用F表示)和扱氏温度(用C表示)的转换公式.并求
(1)90叩的等价摄氏温度和-5 °C的等价华氏温度：
(2)是否存在一个温度值.使华氏温度汁和摄氏温度汁的读数是样的？如果存在，那么该温度值是多少？
xi
所以/（存）>/（%）,即/（W在（0, + ao）内单调增加.
公5・设/U）为定义在（-/./）内的荷函数.若/（X）在（01）内单调増加，证明/（#）在（-L0）内也单凋増加.
证设-/<X, <X2<0,则0< “2 <-A,</,由/（、）是哉函数，從/g）V（X|）=-/（-知）+f（-旳）■因为/Xx）在（OJ）内单调増加.所以y（-X!）-/（-x2）>0.从而/（旳）>/（旳），即/（X〉在《・"0）内也単调增加.
解设尸.其中叽/，均为常数.
因为〃=32。相当于。=。。/ =212。相当于C= 100°.所以
7 "*=槌
故〃=1.80+32或C=扌（F-32）.
(1)F=90°. C =刑90-32)52.2。.
C=-5。，F= 1.Xx(-5)+32= 23°.
(2)设温度値，符合题意.则有
/ = 1.8/ +32,I =-40.
尸銘EC
> =
y=•<>«< w
y=cotZ；
y=arcfiin lx I C1；
G2.卜列各题中，函数/(x)和g(x)是否相同？为什么”⑴/U) =lg/,g⑴=21gx；

高等数学1教材答案解析完整版

高等数学1教材答案解析完整版一、函数与极限在高等数学1教材中，函数与极限是一个重要的章节。

本章主要介绍了函数的定义、性质和分类，以及极限的概念、性质和计算方法。

1. 函数的定义和性质函数是数学中的一个重要概念，用于描述两个数集之间的对应关系。

在高等数学1教材中，函数的定义为：设有两个非空数集A和B，如果对于每一个A中的元素x，都有且只有一个B中的元素y与之对应，那么就称这种对应为函数。

函数通常用f(x)表示。

函数还有一些重要的性质，包括定义域、值域和图像。

定义域是指函数的自变量可能取值的集合，值域是指函数的因变量可能取值的集合，图像是指函数在平面上的点的集合。

通过这些性质，我们可以更好地理解函数的特点。

2. 极限的概念和性质在高等数学1教材中，极限是函数与变量之间的重要关系。

极限的概念可以从两个方向进行讨论：自变量趋于某一点时的极限和自变量趋于无穷大时的极限。

对于函数f(x)，当自变量x无限接近某一点a时，如果函数值f(x)无限接近一个确定的值L，那么我们称L为函数f(x)当x趋于a时的极限。

极限还具有一些重要的性质，包括唯一性、局部有界性和保号性。

唯一性指的是函数的极限值是唯一确定的；局部有界性指的是在某一点的某一邻域内，函数的值有上界和下界；保号性指的是当函数的极限存在且不为零时，函数在某一点附近总是保持正号或负号。

二、导数与微分导数与微分是高等数学1教材中的另一个重要章节。

本章主要介绍了导数与微分的概念、性质和计算方法。

1. 导数的定义和性质导数是函数在某一点处的变化率，可以用来描述函数的局部性质。

在高等数学1教材中，导数的定义为：设函数f(x)在点x处有定义，在x处若极限\[f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} \]存在，则称此极限为函数f(x)在点x处的导数。

常用的导数符号为f'(x)或$\frac{df}{dx}$。

高等数学下册教材全解

高等数学下册教材全解在高等数学下册教材中，我们将学习一系列与微积分相关的概念和技巧。

本文将对教材中的主要内容进行全解，帮助读者深入理解这门学科。

第一章微分学微分学是高等数学的基础，它主要研究函数的变化率和极限。

在这一章中，我们将学习导数的概念以及一些常用的求导法则。

1.1 导数的定义导数描述了函数在某一点上的变化率。

定义如下：对于函数f(x)，在点x处的导数可表示为f'(x)，计算公式如下：f'(x) = lim┬(Δx→0)⁡〖( f(x+Δx) - f(x))/Δx 〗其中Δx表示极限中的自变量的增量。

1.2 求导法则为了更方便地求解导数，我们需要掌握一些常用的求导法则。

1) 常数法则：对于常数C，其导数为0，即(d/dx)c = 0。

2) 幂次法则：对于幂函数f(x) = x^n，其导数为f'(x) = nx^(n-1)。

3) 乘法法则：对于函数f(x) = u(x)v(x)，其导数为f'(x) = u'(x)v(x) + u(x)v'(x)。

4) 除法法则：对于函数f(x) = u(x)/v(x)，其导数为f'(x) = (u'(x)v(x) -u(x)v'(x))/[v(x)]^2。

5) 复合函数法则：对于复合函数f(g(x))，其导数为f'(g(x))g'(x)。

1.3 高阶导数除了一阶导数外，我们还可以计算更高阶的导数。

高阶导数可以通过多次求导得到。

例如，二阶导数就是一阶导数的导数。

第二章积分学积分学是微分学的补充，它主要研究函数的面积和累积效应。

在这一章中，我们将学习不定积分和定积分的概念，以及一些求积分的方法。

2.1 不定积分不定积分是求解函数的原函数的过程。

求解结果称为不定积分，记作∫f(x)dx。

2.2 定积分定积分是计算函数在一定区间上的累积效应，可以理解为求解曲线与坐标轴之间的面积。

高等数学教材同济答案详解

高等数学教材同济答案详解同济大学出版社出版的《高等数学》教材作为一本经典教材，深受广大高校学生喜爱。

然而，作为一门复杂的学科，高等数学常常令学生感到困惑。

为了帮助学生更好地理解和掌握教材，特撰写本篇文章《高等数学教材同济答案详解》，旨在解答同济《高等数学》教材中的习题，提供全面准确的答案解析。

第一章函数与极限1.1 函数及其性质题目：已知函数f(x) = x^2 - 2x + 1，求f(x)在区间[-1, 2]上的最大最小值和极值点。

解析：首先求导得f'(x) = 2x - 2，令其等于零，得到x = 1。

将x = -1、x = 1和x = 2代入f(x)求得f(-1) = 4，f(1) = 0，f(2) = 1。

可以得出f(x)在[-1, 2]上的最大值为4，最小值为0，且极值点为x = 1。

1.2 一元函数的连续性题目：证明函数f(x) = x^3 + 2x^2 + x + 1在区间[-∞, +∞]上处处连续。

解析：对于任意ε > 0，假设x1和x2是区间[-∞, +∞]上的两个任意实数，且|x1 - x2| < δ (δ > 0)。

因此，我们可以令δ = ε / (3C)，那么当|x1 - x2| < δ时，有：|f(x1) - f(x2)| ≤ δ(3C) = ε证明了对于任意ε > 0，总存在δ > 0，使得当|x1 - x2| < δ时，有|f(x1) - f(x2)| < ε，即函数f(x)在区间[-∞, +∞]上处处连续。

高等数学习题及解答电子稿

2.设()24x x f +=，求下列函数值（p.16，6.）()0f ，()1f ，()1-f ，⎪⎭⎫⎝⎛a f 1，(),0x f ()h x f +03．计算下列极限：（p.63，1.（9））(1) 4586lim 224+-+-→x x x x x （p.63，1.（9））(2) xxx ωsin lim0→ （p.71，1（1））(3) xx xx sin 2cos 1lim 0-→ （p.71，1（1））；(4) ()xx x 11lim 0-→ （p.71，2. (1)(3)）(5) xx x x 21lim ⎪⎭⎫ ⎝⎛+∞→（p.71，2. (3)）； 3. 解224468242(1)lim lim 254141x x x x x x x x →→-+--===-+-- 0000sin sin limlim 1cos 22sin lim lim 2sin x x x x x xx xx x x x x ωωωωω→→→→==-==(2)(3)()()()111lim 1lim 1lim 1xtt x x x x t t -→→→-++(4)令t=-x11 则＝== e22211(5)lim [lim 1]x xx x x e x x →∞→∞+⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭1．求下列函数的定义域：（1） 211x xy --=（p.16，4. (6)）（2） xx y 1arctan 3+-= （p.31，1. (4)）4.利用等价无穷小的性质，求下列极限：（p.74）x x x x 30sin sin tan lim -→32200001cos tan sin 1cos 111cos lim lim lim lim sin sin cos 2cos 2x x x x xx x x x x x x x x →→→→---====解：5.求下列函数的导数：（p.111）（1）x x y ln 2=（p.111,2.（7））（2）x e y x cos 3=（p.111,2.（8））（3）11+-=x x y （p.111,2.（14））（4）23x ey -=（p.118,1.(3)）；（5）x y 2sin =（p.118,1.(5)）（6）)arctan(x e y =（p.118,1.(9)）；（7）()[]x y ln ln ln =（p.119,3.(8)）；5.2221(1)'2ln 2ln (2)'3cos 3(sin )3(cos sin )(1)(1)2(3)'(1)(1)x x x y x x x x x x xy e x e x e x x x x y x x =+=+=+-=-+--==++223322(4)'(6)6(5)'2sin cos 1(6)'1()1x x x xx xy e x xe y x x e y e e e --=-=-===++1111(7)'[ln(ln )]'ln(ln )ln(ln )ln y x x x x x==6.用洛必达法则求下列极限：（1）xx x )1ln(lim 0+→（p.171，1.（1））；（2）xxx 2tan ln 7tan ln lim 0+→（p.171，1.（7））；（3）xxx 3tan tan lim2π→（p.171，1.（8）） 0001ln(1)11(1)lim lim lim 111x x x x x x x→→→++===+2200022220022007sec 7ln tan 7(ln tan 7)tan 7(2)lim lim lim 2sec 2ln tan 2(ln tan 2)tan 27sec 7tan 27cos 2tan 2lim lim2sec 2tan 72cos 7tan 77tan 27cos 72lim lim 12tan 72cos 27x x x x x x x xx x x xx x xx x x xx x x xx x x x →+→+→+→+→+→+→+'=='==⨯===⨯ 222222t a n c o s 36c o s 3s i n 33s i n 6(3)l i m l i m l i m l i m 3t a n 3c o s 2c o s s i n s i n 2x x x x xx x x x x x x x x ππππ→→→→-====- 7.求下列不定积分： (1)()⎰-dx xx 21（p.236,1.（13））；（2）⎰-x dx21（p.253,2.(3)）（3）⎰-222xa dx x （a ﹥0）（p.253,2.(34)）（4）⎰+xdx 21（p.253,2.(38)）(1)22(1)(12)x x x -=-+⎰⎰原式=22+C (2)⎰-xdx 21=()11112ln 122122d x x C x --=--+-⎰22222(3)11arcsin (arcsin arcsin 2222dxx a x a x a C Ca a a ==-++=-⎰(4)1(1(1ln(12d C ===+⎰22020000cos cos lim lim limcos 11x xx x x d t dt t dt dx x x →→→===⎰⎰解：9. 计算下列定积分：(1)⎰203cos sin πϕϕϕd （p.302,1(3)）(2)⎰+31221x xdx （p.302,1(10)）(3)⎰--1145xxdx（p.302,1(11)）(4)⎰-1dx xe x （p.306,1.）3342220011(1)sin cos cos cos cos |44d d πππϕϕϕϕϕϕ=-=-=⎰⎰23322(2)tan 1cos 1sec |tan sec sin sin 3x t t tdt dt t t t t ππππππ=⋅==-=⋅⎰⎰3444令则原式=123133(3)111(5)(5)|836uu du u u =-=--=⎰1原式=8 1111100002|(1)|1xxx x x xe dx xdee dx xe x e e-----=-=-=-+=-⎰⎰⎰(4) 8. 求下列极限：（p.295,9.(1)）xdt t xx ⎰→020cos lim1.设32a i j k =--，2b i j k =+- ，求（1）a b ⋅ 及a b ⨯ ；（2）(2)3a b -⋅ 及2a b ⨯ ；（3）,a b的夹角的余弦。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高等数学教材习题全解
一、选择题
1. 已知函数f(x) = 2x^3 - 3x^2 - 36x + 4，那么f(-2)的值为多少？
答：将x替换为-2，计算得到f(-2) = 2(-2)^3 - 3(-2)^2 - 36(-2) + 4 = 64 + 12 + 72 + 4 = 152。

2. 已知函数y = e^2x，那么y'(x)的值为多少？
答：对y = e^2x求导，得到y'(x) = 2e^2x。

3. 已知函数f(x) = ln(x^2 - 1)，那么f'(x)的值为多少？
答：对f(x) = ln(x^2 - 1)求导，得到f'(x) = 2x / (x^2 - 1)。

二、填空题
1. 若f(x) = x^2 + bx + c 是一个完全平方三项式，那么b和c的取值分别是多少？
答：对于完全平方三项式，b的取值为2ac，c的取值为a^2，其中
a、b、c为常数。

所以b = 2ac，c = a^2。

2. 若y = 3x^2 + k 在点(2, -5)处的切线与y轴垂直，那么k的值为多少？
答：求导得到y' = 6x，切线的斜率为6，因为与y轴垂直，所以斜率为0。

代入点(2, -5)得到6 * 2 + k = 0，解方程得到k = -12。

三、计算题
1. 计算∫(0 to π/2) sin^2 x dx。

答：∫sin^2 x dx = ∫(1/2 - 1/2cos2x) dx = 1/2x - 1/4sin2x + C。

将上限和下限代入得到1/2(π/2) - 1/4sin(2(π/2)) = π/4。

2. 计算∫√(1 + x^3) dx。

答：将√(1 + x^3)展开得到√(1 + x^3) = (1 + x^3)^(1/2) = (√(x^3 + 1))/(x + 1)。

所以∫√(1 + x^3) dx = ∫(√(x^3 + 1))/(x + 1) dx。

采用换元法，
令u = x^3 + 1，那么du = 3x^2 dx，将原式变换得到(1/3)∫(√u)/(x + 1) du。

再次换元，令v = √u，那么dv = (1/2√u) du，将原式变换得到(2/3)∫v/(x
+ 1) dv。

将v替换为√(x^3 + 1)，得到(2/3)∫(√(x^3 + 1))/(x + 1) dx =
(2/3)∫v/(x + 1) dv = (2/3)∫1/(x + 1) dv。

计算积分得到(2/3)ln|x + 1| + C。

四、证明题
证明：凸函数f(x)在[a, b]上的性质。

要证明凸函数f(x)在[a, b]上的性质，需要满足以下两个条件：
1. 对于任意的x1, x2 ∈ [a, b]，以及0 ≤ t ≤ 1，有f(tx1 + (1 - t)x2) ≤
tf(x1) + (1 - t)f(x2)。

2. 函数f(x)在[a, b]上连续，且在(a, b)内可导。

首先证明条件1：
假设函数f(x)满足条件1，那么对于任意的x1, x2 ∈ [a, b]，以及0
≤ t ≤ 1，有f(tx1 + (1 - t)x2) ≤ tf(x1) + (1 - t)f(x2)。

我们可以证明条件1等价于f''(x) ≥ 0，即二阶导数非负。

然后证明条件2：
根据条件2，可以得到函数f(x)在[a, b]上必须是连续的，并且在(a, b)内可导。

这是因为在(a, b)内可导可以保证有足够的导数信息来证明条件1，
并且连续性保证了函数f(x)在[a, b]上的无间断性。

综上所述，凸函数f(x)在[a, b]上的性质满足条件1和条件2。

五、应用题
某物体从100m的高度自由下落，设重力加速度为10m/s^2，求物
体落地时的速度。

设物体自由下落的时间为t，根据运动学公式s = vit + (1/2)at^2，其
中s为下落距离，vi为初始速度，a为重力加速度，t为时间。

根据题目设定，初始速度为0，下落距离为100m，重力加速度为
10m/s^2。

代入运动学公式得到100 = 0 + (1/2) * 10 * t^2，解方程得到t = √20。

落地时的速度可以通过求导的方式得到。

根据v = at，代入a = 10m/s^2和t = √20，计算得到v = 10 * √20 m/s。

这样，我们就完成了高等数学教材习题的全解。

以上展示了选择题、填空题、计算题、证明题和应用题的解答过程，希望对您的学习有所
帮助。