自然坐标系优秀课件
合集下载
自然坐标系圆周运动两类问题相对运动

已知: vA 1940km h1 vB 2192km h1
(2)在时间
t
t 3s
内矢径
r
AB 3.5km
所转过的角度
为
A
At
v A
1 2
t2 vA t 1 at t2
r 2r
飞机经过的路程为
r an
o
B
a
at
v B
s
r
v At
1 2
att
2
代入数据得
s 1722m
第11页/共26页
an (t) a 2 at2
[例 (旧考题)] 某质点的运动方程为 r (t) ti t2 j t3 k
23
(采用SI单位制) ,则t=1秒时该质点运动的切向加速
度大小为(单位:米/秒2)
(C )
(A) 0 (B) 2 (C) 3 (D) 5
第15页/共26页
第二类运动学问题技巧举例——
例 如图示,一实验者 A 在以 10 m/s 的速率沿水 平轨道前进的平板车上控制一台射弹器, 此射弹器以与 车前进方向呈120 度角斜向上射出一弹丸 . 此时站在地 面上的另一实验者 B 看到弹丸铅直向上运动, 求弹丸上 升的高度 . [分析:有相对运动,参考系间联系?]
v' v
解 设地面参考系为 S 系
[分析] 求什么?怎么求? (定义?原理?) 已知什么情形?
A
v A
r an
o
a
B
at
v B
解(1)因飞机作匀变速率
运动所以 at 和 为常量 .
at
dv dt
分离变量有
vB dv
vA
t
0 atdt
自然坐标系

r
t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a
an
v2 R
vB
B vA
R
O
A
大小,方向,作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er
ds dt
er
ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动, 法向加速度
v vB
vA
v vB
vA
Δv vB vA ,
AB R
lim lim ar
t 0
则:a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略:
(1)分析问题特点,建立恰当的坐标系 (2)由运动方程求解速度随时间变化的表达式 (3)分别计算出切向加速度与法向加速度,再 求解合加速度的大小和方向
解:根据加速度的定义:
ar
anern
a er
v2 R
ern
dv dt
er
a an2 a 2
v
ds dt
2
R
a
d
dt
1.2t
石大自然地理学课件01地球-4地理坐标

表示天体在天球上的位置 东度量,自0-24h。
黄道坐标系:黄纬和黄经
• 基圈是黄道
• 原点是春分点,始圈是 无名圈
• 纬度为黄纬,是天体相 对于黄道的方向和角距 离0-90度
表示日明行星在星 空间的位置和运动
• 经度称黄经,是天体所 在黄经圈相对于春分点 所在黄经圈的方向和角 距离,0-360度。以春 分点为起点向东度量。
天顶
天北极
天赤道
地平圈
天底
天南极
• 地平圈:两极为天顶、天底
• 天赤道:两极为天北极、天南 极
• 黄道:两极为黄北极、黄南极
天球视运动—周日运动
• 地外的天空,包括日月星辰均以与地球 自转相反的方向和相同的周期运动,即 天球周日运动。
• 在北半球,天球周日运动绕转中心是天 北极,紧邻天北极较明亮的恒星即为北 极星。
用于时间的度量
• 经度称时角,是天体所在 赤经圈相对于午圈的方向 和角距离,以上点为起点, 沿天赤道向西度量,为的 是使天体的时角与时俱增。
第二赤道坐标系:赤纬和赤经
• 基圈是天赤道,
• 原点是春分点,始圈是 春分圈。
• 纬度是赤纬,与第一赤 道坐标系相同
• 经度为赤经,天体所在 时圈相对于春分圈的方 向与角距离。赤经以春 分点为起点沿天赤道向
• 基圈是地平圈
• 原点通常是南点, 始圈是午圈
• 地平纬度称为高度, 是天体相对于地平 圈的方向和角距离,
• 地平经度为方位, 天体所在地平经圈 相对于午圈的方向 和角距离,以南点 为起点沿地平圈向 西度量。
第一赤道坐标系:赤纬和时角
• 基圈是天赤道
• 原点是上点,始圈是午圈
• 纬度称赤纬,是天体相对 于天赤道的南北方向与角 距离。
黄道坐标系:黄纬和黄经
• 基圈是黄道
• 原点是春分点,始圈是 无名圈
• 纬度为黄纬,是天体相 对于黄道的方向和角距 离0-90度
表示日明行星在星 空间的位置和运动
• 经度称黄经,是天体所 在黄经圈相对于春分点 所在黄经圈的方向和角 距离,0-360度。以春 分点为起点向东度量。
天顶
天北极
天赤道
地平圈
天底
天南极
• 地平圈:两极为天顶、天底
• 天赤道:两极为天北极、天南 极
• 黄道:两极为黄北极、黄南极
天球视运动—周日运动
• 地外的天空,包括日月星辰均以与地球 自转相反的方向和相同的周期运动,即 天球周日运动。
• 在北半球,天球周日运动绕转中心是天 北极,紧邻天北极较明亮的恒星即为北 极星。
用于时间的度量
• 经度称时角,是天体所在 赤经圈相对于午圈的方向 和角距离,以上点为起点, 沿天赤道向西度量,为的 是使天体的时角与时俱增。
第二赤道坐标系:赤纬和赤经
• 基圈是天赤道,
• 原点是春分点,始圈是 春分圈。
• 纬度是赤纬,与第一赤 道坐标系相同
• 经度为赤经,天体所在 时圈相对于春分圈的方 向与角距离。赤经以春 分点为起点沿天赤道向
• 基圈是地平圈
• 原点通常是南点, 始圈是午圈
• 地平纬度称为高度, 是天体相对于地平 圈的方向和角距离,
• 地平经度为方位, 天体所在地平经圈 相对于午圈的方向 和角距离,以南点 为起点沿地平圈向 西度量。
第一赤道坐标系:赤纬和时角
• 基圈是天赤道
• 原点是上点,始圈是午圈
• 纬度称赤纬,是天体相对 于天赤道的南北方向与角 距离。
自然坐标系 曲线运动

(- )/2 ,当 0, d
当 t 0 时
τ τ (t ) θ θ
τ // n τ θ n
θ θ s 1 dτ τ lim n lim n vn lim t 0 s t ρ dt t 0 t t 0 t
2
a an 2 aτ 2 230.5 m/s2
(2) 设t′时刻,质点的加速度与半径成45 角,则
o
aτ an
4
rω2 rβ
144t ' 24t ' t ' 0.55 s
2 4t ' 2.67 rad
3
2015-2-18 第1章 质点运动学 16
例4 一质点在水平面内以顺时针方向沿半径为2 m 的 圆形轨道运动。此质点的角速度与运动时间的平方成 正比,即ω=kt 2 ,k 为待定常数.已知质点在2 s 末的线 速度为 32 m/s 。求t =0.5 s 时质点的线速度和加速度。
1s t2 3s 之间的路程
。
解 质点运动速度为 速率为
dr d ˆ t2 ˆ ˆ 2t ˆ v (2ti j ) 2i j dt dt
2 2 2 2 2
v v x v y 2 4t 2 1 t
2
路程满足 ds v dt 2 1 t dt
ds dτ 1 v2 v v n n an dt dt ρ ρ
法向加速度: 大小为
2015-2-18
曲率半径
2 ρ 方向为
第1章 质点运动学
n
意义: 反映速度方向变化的快慢
它是与该点切 向垂直并指向 曲线凹侧的法 向单位矢量
4
法向加速度与切向加速度
2自然坐标系--切向加速度和法向加速度

证明以上两式22naaa???222vdtdv?????????????????????????????????对于平面曲线运动dtdav?dtdv?大小2切向加速度法向加速度二a??an例
第二节 自然坐标系 切向加速度 法向加速度
一、自然坐标系 •问题的提出: 在直角坐标系中,加速度公式无法看 出哪一部分是由速度大小变化产生的加速 度,哪一部分是由速度方向变化产生的加 速度,所以引入自然坐标系来描写。 1.自然坐标系 自然坐标系是建立在物体运动的轨 迹上的,有两个坐标轴,切向坐标和法 向坐标。
2. a C , an 0
3. a 0 , an C 4. a 0 , an 0
匀变速直线运动;
匀速率圆周运动; 变速曲线运动;
§2切向加速度、法向加速度/二、a、an
例
解:
vห้องสมุดไป่ตู้
a
g
an
v
想一想:何处 曲率半径最大? 何处最小?
dv a kR 解: 切向加速度 dt 2 2 ( kRt) v 2 2 法向加速度 a n k Rt R 2 2 加速度 a a an
kR k Rt
2 2
2 2
§2切向加速度、法向加速度/二、a、an
讨论下列几种运动情况:
1. a 0 , an 0 匀速直线运动;
v v 0 vnn0 (1)
v A n B v vB τ 其中 v 为速度增量在切线方向的分量;
vn
vn 为速度增量在法线方向的分量; 0 切线方向的单位矢量;
n0
vA
vA
法线方向的单位矢量。
§2切向加速度、法向加速度/二、a、an
第二节 自然坐标系 切向加速度 法向加速度
一、自然坐标系 •问题的提出: 在直角坐标系中,加速度公式无法看 出哪一部分是由速度大小变化产生的加速 度,哪一部分是由速度方向变化产生的加 速度,所以引入自然坐标系来描写。 1.自然坐标系 自然坐标系是建立在物体运动的轨 迹上的,有两个坐标轴,切向坐标和法 向坐标。
2. a C , an 0
3. a 0 , an C 4. a 0 , an 0
匀变速直线运动;
匀速率圆周运动; 变速曲线运动;
§2切向加速度、法向加速度/二、a、an
例
解:
vห้องสมุดไป่ตู้
a
g
an
v
想一想:何处 曲率半径最大? 何处最小?
dv a kR 解: 切向加速度 dt 2 2 ( kRt) v 2 2 法向加速度 a n k Rt R 2 2 加速度 a a an
kR k Rt
2 2
2 2
§2切向加速度、法向加速度/二、a、an
讨论下列几种运动情况:
1. a 0 , an 0 匀速直线运动;
v v 0 vnn0 (1)
v A n B v vB τ 其中 v 为速度增量在切线方向的分量;
vn
vn 为速度增量在法线方向的分量; 0 切线方向的单位矢量;
n0
vA
vA
法线方向的单位矢量。
§2切向加速度、法向加速度/二、a、an
自然坐标系

密切面——令点 无限趋近于点 M 时,由τ和 所确定的极限平面。
主法线——密切面与法平面的交线。其单位矢量用n表示。
副法线——法平面内垂直于密切面的法线。其单位矢量用b表示。
自然坐标系—由切线、主法线和副法线组成的正交坐标系。
自然坐标系随点的位置不同而改变。
5-5
M
b
n
密切面
法面
主法线
副法线
切线
M
s
M
τ
nτb
1.3 自然坐标系及运用
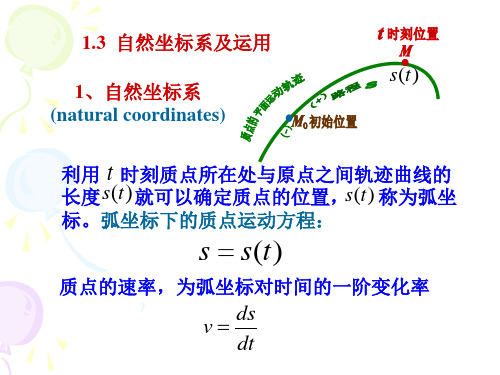
1.3 自然坐标系及运用 s (t )
1、自然坐标系 (natural coordinates)
利用 t 时刻质点所在处与原点之间轨迹曲线的
长度s(t) 就可以确定质点的位置,s(t) 称为弧坐
标。弧坐标下的质点运动方程:
s s(t)
质点的速率,为弧坐标对时间的一阶变化率
v ds dt
将两个相互垂直的切向和法向所组成的平面
24tR
a an
an R 2 144t 4R
a
a an
24t 144t 4
3 3
2 4t3 2
2
t3 1/2 3 3.15rad
3
0 t t 0 5s
例2:质点沿半径R=0.1m作圆周运动,其角坐标与
时间的关系为 2 4t 3 (SI),当切向加速度的
大小恰为总加速度的一半时,则
。
解:切向加速度大小为总加速度的一半,则
30 a / an tan 30
v R R d 12t 2R
dt
a
R
d 2
R dt 2
an
v
dˆ
dtv2nˆFra bibliotek aa
an
dv ˆ
dt
v2
nˆ
大小:a
a2 an2
( dv )2 (v2 )2
dt
当质点做直线运动时 ,因此法向加速度为零;
当质点做圆周运动时, 为圆周运动的半径 R ;
如果 v 为常数,则切向加速度为零,合加速度方
向指向圆心,称为向心加速度;
3 圆周运动的角量描述
0t
0
0t
1 2
t2
2
2 0
2
(
1、自然坐标系 (natural coordinates)
利用 t 时刻质点所在处与原点之间轨迹曲线的
长度s(t) 就可以确定质点的位置,s(t) 称为弧坐
标。弧坐标下的质点运动方程:
s s(t)
质点的速率,为弧坐标对时间的一阶变化率
v ds dt
将两个相互垂直的切向和法向所组成的平面
24tR
a an
an R 2 144t 4R
a
a an
24t 144t 4
3 3
2 4t3 2
2
t3 1/2 3 3.15rad
3
0 t t 0 5s
例2:质点沿半径R=0.1m作圆周运动,其角坐标与
时间的关系为 2 4t 3 (SI),当切向加速度的
大小恰为总加速度的一半时,则
。
解:切向加速度大小为总加速度的一半,则
30 a / an tan 30
v R R d 12t 2R
dt
a
R
d 2
R dt 2
an
v
dˆ
dtv2nˆFra bibliotek aa
an
dv ˆ
dt
v2
nˆ
大小:a
a2 an2
( dv )2 (v2 )2
dt
当质点做直线运动时 ,因此法向加速度为零;
当质点做圆周运动时, 为圆周运动的半径 R ;
如果 v 为常数,则切向加速度为零,合加速度方
向指向圆心,称为向心加速度;
3 圆周运动的角量描述
0t
0
0t
1 2
t2
2
2 0
2
(
坐标系的认识优秀课件

10
许多图形应用涉及到几何变换,主要包括平移、旋转、缩放。以矩 阵表达式来计算这些变换时,平移是矩阵相加,旋转和缩放则是矩 阵相乘,综合起来可以表示为p' = p *m1+ m2(m1旋转缩放矩阵, m2为平移矩阵, p为原向量 ,p'为变换后的向量)。引入齐次坐标 的目的主要是合并矩阵运算中的乘法和加法,表示为p' = p*M的形 式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点 集从一个坐标系变换到另一个坐标系的有效方法。
6
极坐标系
极坐标中会定一点为极点,再将一条通过极点的射线定 为极轴。若给定一角度θ,则可绘出通过极点,和极轴 夹角为θ的唯一射线(角度是以从极轴,依逆时针方向 旋转到射线),若再给定一实数r,可找出上述射线上, 距极点距离为有号整数r的一点[7]。
在极坐标系中,一坐标(r, θ)只会其对应唯一的一 点 , 但 每 一 点 均 可 对 应 许 多 个 坐 标 。 例 如 坐 标 ( r, θ)、 (r, θ+2π)及(−r, θ+π)都是对应同一 点的不同坐标。而极点的坐标为(0, θ),θ可为任 意值。
当汽车呼啸着从我们身边驶过,在我们的眼中,显然它 的运动就是在标系
所谓齐次坐标就是将一个原本是n维的向量用一个n+1维 向 量 来 表 示 。 例 如 , 二 维 点 (x,y) 的 齐 次 坐 标 表 示 为 (hx,hy,h)。由此可以看出,一个向量的齐次表示是不 唯一的,齐次坐标的h取不同的值都表示的是同一个点, 比 如 齐 次 坐 标 (8,4,2) 、 (4,2,1) 表 示 的 都 是 二 维 点 (4,2)。
4
笛卡儿坐标系
笛卡儿坐标系也称为直角坐标系,是最常用到的 一种坐标系。在平面上,选定二条互相垂直的线 为坐标轴,任一点距坐标轴的有号距离为另一轴 的坐标,这就是二维的笛卡儿坐标系,一般会选 一条指向右方水平线称为x轴,再选一条指向上方 的垂直线称为y轴
许多图形应用涉及到几何变换,主要包括平移、旋转、缩放。以矩 阵表达式来计算这些变换时,平移是矩阵相加,旋转和缩放则是矩 阵相乘,综合起来可以表示为p' = p *m1+ m2(m1旋转缩放矩阵, m2为平移矩阵, p为原向量 ,p'为变换后的向量)。引入齐次坐标 的目的主要是合并矩阵运算中的乘法和加法,表示为p' = p*M的形 式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点 集从一个坐标系变换到另一个坐标系的有效方法。
6
极坐标系
极坐标中会定一点为极点,再将一条通过极点的射线定 为极轴。若给定一角度θ,则可绘出通过极点,和极轴 夹角为θ的唯一射线(角度是以从极轴,依逆时针方向 旋转到射线),若再给定一实数r,可找出上述射线上, 距极点距离为有号整数r的一点[7]。
在极坐标系中,一坐标(r, θ)只会其对应唯一的一 点 , 但 每 一 点 均 可 对 应 许 多 个 坐 标 。 例 如 坐 标 ( r, θ)、 (r, θ+2π)及(−r, θ+π)都是对应同一 点的不同坐标。而极点的坐标为(0, θ),θ可为任 意值。
当汽车呼啸着从我们身边驶过,在我们的眼中,显然它 的运动就是在标系
所谓齐次坐标就是将一个原本是n维的向量用一个n+1维 向 量 来 表 示 。 例 如 , 二 维 点 (x,y) 的 齐 次 坐 标 表 示 为 (hx,hy,h)。由此可以看出,一个向量的齐次表示是不 唯一的,齐次坐标的h取不同的值都表示的是同一个点, 比 如 齐 次 坐 标 (8,4,2) 、 (4,2,1) 表 示 的 都 是 二 维 点 (4,2)。
4
笛卡儿坐标系
笛卡儿坐标系也称为直角坐标系,是最常用到的 一种坐标系。在平面上,选定二条互相垂直的线 为坐标轴,任一点距坐标轴的有号距离为另一轴 的坐标,这就是二维的笛卡儿坐标系,一般会选 一条指向右方水平线称为x轴,再选一条指向上方 的垂直线称为y轴
