基于奇异值分解计算MIMO信道容量
一种基于奇异值分解的mimo速度解模糊方法

一种基于奇异值分解的mimo速度解模糊方法
基于奇异值分解(SVD)的MIMO(多输入多输出)速度解模糊方法是一种通过分解MIMO系统传输矩阵来消除多径效应和多普勒效应的影响,从而提高通信系统性能的技术。
以下是该方法的具体步骤:
1. 采集数据:在MIMO通信系统中,天线阵列会接收到来自不同方向和速度的信号。
首先,需要对这些信号进行采集,并将其转换为数字信号。
2. 预处理:对采集到的信号进行预处理,如滤波、去噪等操作,以提高信号质量。
3. 奇异值分解:将预处理后的信号矩阵进行奇异值分解。
奇异值分解是将矩阵分解为三个矩阵的乘积,分别为酉矩阵U、对角矩阵Σ和酉矩阵V。
其中,对角矩阵Σ的对角线元素即为信号矩阵的奇异值。
4. 速度解模糊:根据奇异值分解的结果,可以将原始信号矩阵表示为酉矩阵UΣV^H(其中^H表示共轭转置)。
在此表示下,MIMO系统传输矩阵的各列表示不同速度的信号分量。
通过比较各列奇异值的大小,可以确定信号的传播速度。
5. 速度补偿:根据解模糊后的速度信息,对信号进行速度补偿,消除多径效应和多普勒效应的影响。
速度补偿后的信号可用于后续的信号处理和分析,如信道估计、信号解调等。
6. 性能优化:采用解模糊后的信号,可以提高通信系统的性能,如信噪比、误码率等指标。
此外,基于奇异值分解的速度解模糊方法还可以应用于多用户MIMO系统,实现用户间的干扰抑制。
总之,基于奇异值分解的MIMO速度解模糊方法通过将MIMO系统传输矩阵分解为奇异值,有效地消除多径效应和多普勒效应的影响,提高通信系统性能。
在实际应用中,该方法可应用于无线通信、雷达、声呐等领域。
2、MIMO信道容量推导

二、信道容量的推导主要研究基于VBLAST 的MIMO 系统:系统:串并变换调制调制调制VBLAST 检测器y1y2ym 比特分配功率分配b1bnb2信道估计丰富的散射信道2p 1p pn 数据图2.1 采用VBLAST 结构MIMO 系统框图系统框图MIMO 信道容量的推导:信道容量的推导:(信道容量定义为MIMO 系统在单位带宽上的数据传输速率)系统在单位带宽上的数据传输速率)根据奇异值分解(SVD)理论,在k 时刻,任何一个M ×N 矩阵H 可以写成可以写成HH =UDV 式中,D 是M ×N 非负对角矩阵;U 和V 分别是M ×M 和N ×N 的酉矩阵,且有H HM =UU I 和H N =VV I ,其中M I 和N I 是M ×M 和N ×N 单位阵。
D 的对角元素是矩阵H HH 的特征值的非负平方根。
H HH 的特征值(用l 表示)定义为定义为 H l =HH y y ,0¹y式中,y 是与l 对应的M ×1维矢量,称为特征矢量。
特征值的非负平方根也称为H 的奇异值,而且U 的列矢量是H HH 的特征矢量,V 的列矢量是HH H 的特征矢量。
矩阵H HH 的非零特征值的数量等于矩阵H 的秩,用m 示,其最大值为),min(N M m =。
则可以得到接收向量。
则可以得到接收向量 H =r UDV x +n引入几个变换H r'=U r ,H x'=V x ,H'n =U n ,这样等价的信道可以描述为:'''r =Dx +n 对于M ×N 矩阵H ,秩的最大值),min(N M m =,也就是说有m 个非零奇异值。
值。
将i l 代入上式,可以得到接收信号为:代入上式,可以得到接收信号为:'''i i i i r x n l =+(m i ,,2,1 =)''i i n r =(1,2,,i m m M =++ )可以看出等效的MIMO 信道是由m 去耦平行子信道组成的。
2、MIMO信道容量推导
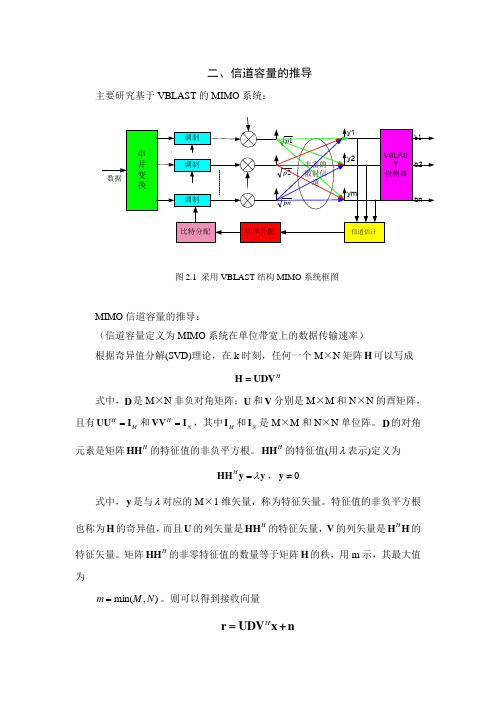
二、信道容量的推导主要研究基于VBLAST 的MIMO 系统:图2.1 采用VBLAST 结构MIMO 系统框图MIMO 信道容量的推导:(信道容量定义为MIMO 系统在单位带宽上的数据传输速率)根据奇异值分解(SVD)理论,在k 时刻,任何一个M ×N 矩阵H 可以写成H H =UDV式中,D 是M ×N 非负对角矩阵;U 和V 分别是M ×M 和N ×N 的酉矩阵,且有H M =UU I 和H N =VV I ,其中M I 和N I 是M ×M 和N ×N 单位阵。
D 的对角元素是矩阵H HH 的特征值的非负平方根。
H HH 的特征值(用λ表示)定义为H λ=HH y y ,0≠y式中,y 是与λ对应的M ×1维矢量,称为特征矢量。
特征值的非负平方根也称为H 的奇异值,而且U 的列矢量是H HH 的特征矢量,V 的列矢量是H H H 的特征矢量。
矩阵H HH 的非零特征值的数量等于矩阵H 的秩,用m 示,其最大值为),min(N M m =。
则可以得到接收向量H =r UDV x +n引入几个变换H r'=U r ,H x'=V x ,H 'n =U n ,这样等价的信道可以描述为:'''r =Dx +n对于M ×N 矩阵H ,秩的最大值),min(N M m =,也就是说有m 个非零奇异值。
将i λ代入上式,可以得到接收信号为:'''i i i r n =+(m i ,,2,1 =)''i i n r =(1,2,,i m m M =++ )可以看出等效的MIMO 信道是由m 去耦平行子信道组成的。
为每个子信道分配矩阵H 的奇异值,相当于信道的幅度增益。
因此,信道功率增益等于矩阵H HH 的特征值。
因为子信道是去耦的,所以信道容量可以直接看做由多个SISO 信道容量直接相加。
mimo信道容量推导

mimo信道容量推导MIMO是多输入多输出技术的缩写,它可以显著提高通信系统的传输速率和可靠性。
MIMO系统中,多个天线同时工作来传输数据,这种技术可以提高信号的容量。
下面我们将推导MIMO信道容量的公式。
对于一个MIMO系统,假设有Nt个发送天线和Nr个接收天线。
我们可以通过矩阵来描述MIMO信道。
假设H是Nt×Nr的复矩阵,表示发送天线的信号被接收天线接收到时,信道的响应。
假设s是发送天线的信号,n是接收天线的噪声,则接收信号可以表示为:y = Hs + n为了使信号传输更稳定,我们可以使用梅斯纳矩阵(Hermitian matrix)来表示发送信号s。
因此,我们可以将s表示为:s = Uf其中,U是梅斯纳矩阵,f是发送天线的数据。
因此,我们可以将接收信号表示为:y = HUf + n我们可以对函数进行线性变换,将其变换为:y = WF + n其中,W = HU是一个线性变换矩阵。
我们可以对矩阵进行奇异值分解,将其分解为:W = UΣV*其中,U和V*是梅斯纳矩阵,Σ是一个对角线上有奇异值的矩阵。
因此,我们可以将接收信号表示为:y = UΣV*f + n我们可以将接收信号y表示为一个向量,f表示为另一个向量。
接着,我们可以计算信道的容量,即最大可能的数据传输速率。
根据香农公式,信道容量可以表示为:C = log2(det(I + SNR/NT H HH))其中,NT是发送天线的数量,SNR是信噪比,det表示矩阵的行列式。
因此,我们可以得出MIMO信道容量的公式。
总之,通过对MIMO系统中的信道进行线性变换和奇异值分解,我们可以推导出MIMO信道容量的公式,这个公式可以用来计算最大可能的数据传输速率。
3D多输入多输出正交频分复用系统中基于奇异值分解的信道估计方法

3D多输入多输出正交频分复用系统中基于奇异值分解的信道估计方法摘要:随着通信技术的不断发展,3D多输入多输出正交频分复用系统正逐渐成为新一代移动通信系统的热门研究方向。
在这种系统中,对信道情况的准确估计对于系统性能具有至关重要的作用。
本文针对3D多输入多输出正交频分复用系统中的信道估计问题,提出了一种基于奇异值分解的信道估计方法,以提高系统的性能和稳定性。
通过仿真实验验证,该方法相较于传统的信道估计方法具有更好的性能和鲁棒性。
引言3D多输入多输出正交频分复用系统(3D MIMO-OFDM)是一种新兴的通信系统,它利用多个输入和输出天线以及正交频分复用技术,使系统能够实现更高的通信容量和更好的频谱利用率。
与传统的2D MIMO-OFDM系统相比,3D MIMO-OFDM系统在移动通信性能、数据传输速率和覆盖范围等方面都具有明显的优势。
在3D MIMO-OFDM系统中,信道估计是一项关键技术,它直接影响系统的性能和稳定性。
目前,针对3D MIMO-OFDM系统中的信道估计问题,已经提出了多种方法和算法。
传统的方法主要包括最小均方误差(MMSE)估计、线性最小二乘(LMMSE)估计和贝叶斯估计等。
虽然这些方法在一定程度上能够满足系统的信道估计需求,但是它们的性能和鲁棒性仍然存在一定的局限性。
如何设计一种更为有效的信道估计方法成为了当前的研究热点之一。
本文针对3D MIMO-OFDM系统中的信道估计问题,提出了一种基于奇异值分解的信道估计方法。
该方法能够有效地提高系统的性能和稳定性,从而使系统在复杂的通信环境下也能够获得良好的通信质量和覆盖范围。
接下来,本文将对该方法进行详细的介绍,并通过仿真实验来验证其有效性和可行性。
1. 3D MIMO-OFDM系统中的信道估计问题在3D MIMO-OFDM系统中,由于存在多个输入和输出天线,以及复杂的多径传播环境,信道估计变得非常复杂。
具体来说,3D MIMO-OFDM系统中的信道估计问题主要包括以下几个方面:(1)多径信道的估计:由于多径传播环境的存在,3D MIMO-OFDM系统中的信道不仅包括直射径信道,还包括多个反射径和散射径信道。
MIMO信道的信道容量

Pi 1/ 0 1/ i 0 P
其中 0 为某个门限值。由此得到信道容量为
i 0 i 0 (1-6)
C B log 2 (
i: i 0
i ) 0
对于有一个发送天线和多个接收天线的单入多出系统,或者有多个发送天线 一个接收天线的多入单出系统,也可以定义出收发都有理想信道信息时的容量。 这些信道可以通过多天线获得分集增益和阵列增益,但没有复用增益。当发送端 和接收端都已知信道信息时, 其容量等于信号在发送端或接收端进行最大比合并 后得到的 SISO 信道的容量为
1 引言
信道容量的计算是研究噪声信道的主要关注点之一。信道容量的定义是以任 意小的差错率传输信息的最大速率,它建立了可靠通信的基本极限。因此,信道 容量广泛应用于衡量通信系统的性能。本文的主要目标是研究与 MIMO 无线信 道有关的信道容量。 MIMO 信道的香农容量是能够以任意小的差错率传输的最大数据率。中断容 量则定义为能使中断率不超过某个数值的最大数据率。 信道容量的大小和收发两 端是否已知信道增益矩阵或其分布有关。 下文先给出不同信道信息假设下静态信 道的容量,它是其后讨论的衰落信道容量的基础。
MIMO 信道的信道容量
摘要
由于 MIMO 可以在不需要增加带宽或总发送功率耗损(transmit power expenditure)的情况下大幅地增加系统的资料吞吐量(throughput)及传送距离, 使得此技术于近几年受到许多瞩目。MIMO 的核心概念为利用多根发射天线与 多根接收天线所提供之空间自由度来有效提升无线通信系统之频谱效率, 以提升 传输速率并改善通信品质。研究 MIMO 信道的容量是对 MIMO 进行深入分析的 基础,本文分析了 MIMO 信道的容量计算方法,分别介绍了在静态信道中的注 水法、平均功率分配法信道容量,以及衰落信道中遍历容量和中断容量。 关键词:MIMO,信道容量,注水法,平均功率分配,遍历容量,中断容量
MIMO系统的原理及容量分析

MIMO系统的原理及容量分析MIMO (Multiple Input Multiple Output)系统是一种利用多个天线实现的无线通信系统。
相对于传统的单输入单输出(SISO)系统,MIMO系统可以显著提高信号传输的质量和容量。
本文将介绍MIMO系统的原理以及容量分析。
MIMO系统的原理是利用多个天线在发射端和接收端之间实现多路径信号的传输和接收。
与SISO系统相比,MIMO系统可以同时发送和接受多个独立的数据流。
通过多个天线同时工作,MIMO系统可以在相同的频谱带宽和发射功率下实现更高的数据传输速率和更好的抗干扰能力。
在MIMO系统中,发射端将输入的数据流通过独立的天线发送,接收端则通过多个天线接收到来自不同路径的信号。
每个接收天线可以接收到与发射天线相对应的信号,这些信号在传输过程中经历了不同的路径和衰减。
接收端通过对接收到的信号进行处理和合并,可以恢复出原始的信号流,从而提高系统的容量和性能。
MIMO系统的容量分析是评估系统的性能和限制的关键方法。
MIMO系统的容量主要由两个因素决定:空间多样性和信道状态信息。
空间多样性是指通过使用多个天线来利用信号在空间中的不同路径,从而提高系统的信号传输质量。
信道状态信息是指发送和接收端对信道状况的了解,包括信道增益、相位等信息。
MIMO系统的容量可以通过计算信道容量来评估。
信道容量表示在给定的信号传输条件下,所能达到的最大数据传输速率。
对于MIMO系统,信道容量可以通过计算信道的奇异值分解(SVD)来获得。
通过SVD分解,可以将原始信道分解为多个独立的子信道,每个子信道都具有不同的信道增益。
系统的总容量等于各个独立子信道容量的总和。
对于一个MIMO系统,其容量与天线的数量、信道状况和调制方式等因素密切相关。
通常情况下,增加天线的数量可以提高系统的容量。
在理想的条件下,如果天线数量等于信道的最小维度(最小值为发射端和接收端天线数量的较小值),则可以实现系统的最大容量。
MIMO-OFDMA系统中基于奇异值分解的信道估计

Abta t T i pp rpee t a ca n let t n agrh y s g l au eo p s i ( V src hs ae rsns h n e smai lo tm b i ua v le dc m oio S D)fr MI - F MA ss ms i o i n r tn o MO O D yt . e A crigt ed f e o nikt nmi inad smb l i t t cue tepooe h n e et ainmeh db sdo at q ae( S codn t e n dd w l a s s o n y o pl r tr. rp sdcan l s m t to ae nl s sur L ) oh i n r s o su h i o e
S D信 道 估 计 方 法 ,但 计 算 复 杂 度 要 低 ,并 且 对 导 频 的 要 求 比较 宽 松 ,具 有 广 泛 的 应 用 性 。 V
关 键词 M M O D L ; M S 奇 异 值 分解 I O; F M;S L M E;
中 图分 类 号 T 9 14 N 4 . 文 献标 识码 A 文章 编 号 10 0 3—3 0 2 0 )0—0 1 16(0 8 1 0 7一O 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于奇异值分解计算MIMO 信道容量
摘要 无线MIMO 技术是未来无线通信系统中实现高数据速率传输、改善传输质量、提高系统容量的重要途径,它被认为是现代通信技术中的重大突破之一,受到了广泛的研究与关注。
信道容量是信道的一个参数,反映了信道所能传输的最大信息量。
因此研究MIMO 的信道容量具有巨大的指导意义。
本文利用矩阵理论的相关知识,首先建立了MIMO 信道模型,利用信息论理论和奇异值分解的理论详细推导出MIMO 信道容量,并得出重要结论。
关键词: MIMO ;信道容量;奇异值分解
一、 引言
MIMO 系统是能够有效提高无线频谱利用率最重要的方案之一。
MIMO 系统使用多根发射天线、多根接收天线, 在系统容量、频谱效率、发射机和接收机的设计上都与传统的单发单收系统有很大差别。
然而,MIMO 无线系统大容量的实现和其它性能的提高极大地依赖于MIMO 无线信道的特性,MIMO 无线通信的难点也正在于信道的处理。
矩阵理论在通信,自动控制等工程领域里应用广泛,将矩阵理论与无线信道的研究是一个很好的切入点。
目前,MIMO 技术的信道容量和空时编码,空时复用等技术都离不开矩阵理论的应用。
二、 奇异值分解的概念
下面介绍一下矩阵奇异值分解的理论。
首先,给出奇异值的概念。
设,m n
H r
A C A A ⨯∈的特征值为
121n 0r r λλλλλ+≥≥≥>===……
(2.1)
则称1,2,...,)i i r σ=
=为矩阵A 的正奇异值。
进而,奇异值分解理论可以阐述为: 对任意矩阵m n
r
A C ⨯∈,12,,...,r σσσ是A 的r 个正奇异值,则存在m 阶酉矩阵U 及n 阶酉矩阵V ,
使得
D 0V 00A U ⎛⎫= ⎪⎝⎭
(2.2)
其中12D=diag ,,...,),r δδδ(而i δ满足||(1,2,...,)i i i r δσ==的复数。
三、 MIMO 信道模型的建立
为了描述MIMO 信道,考虑考虑基站(BS)天线数R n ,移动台(MS)天线数为T n 的两个均匀线性天线阵列,假定天线为全向辐射天线。
每个符号周期内,移动台天线阵列上的发射信号为
12()[(),(),...,()]T n s t s t s t s t =,其中()m s t 表示第m 个天线元上的发射信号。
同样地,基站天线阵列上的
接收信号可以表示为12()[(t),(t),...,(t)]R n y t y y y =。
当发送信号所占用的带宽足够小的时候,信道可以被认为是平坦的,这样,发射信号与接收信号的关系可以表示为
()()()y t Hs t n t =+ (3.1)
其中,H 是一个描述MIMO 系统信道的R T n n ⨯复数矩阵,H 的子元素,j i h 表示从第(1,2,...)R j j n =根发射天线到第(1,2,...)T i i n =根接收天线之间的空间信道衰落系数。
如下式(3.2)所示:
11
121212221
2
T T R T R R n n n n n n H h h h h h h h h h ⎡⎤
⎢⎥⎢⎥
=⎢
⎥⎢⎥⎢⎥⎣⎦
(3.2)
()n t 是信道加性噪声,服从循环对称复高斯分布,并且与发射信号()s t 不相关,假设n(t) 均值为0,功
率为2σ。
其协方差为
2
R H nn n R E nn I σ⎡⎤==⎣⎦
(3.3)
对于高斯信道,发射信号的最佳分布也是高斯分布。
因此,x 的元素是零均值独立同分布的高斯变量。
发送信号的协方差可以表示为:
{ss }H xx R E =
(3.4)
发送信号的功率可以表示为
()ss P tr R =
(3.5)
那么,接收信号的协方差可表示为
()()[]2[()(t)]()()()()()s ()n()n ()()()()s ()R
H yy H
H H H H H
H ss n R E y t y E Hs t n t Hs t n t HE s t t H E t t HE s t n t H E n t t HR H I σ=⎡⎤
=++⎣⎦⎡⎤⎡⎤⎡⎤=+++⎣⎦⎣⎦⎣⎦
=+ (3.6)
因为x 与噪声n 不相关,所以[]0H
E xn E nx ⎡⎤+=⎣⎦。
四、 奇异值分解计算MIMO 信道容量
由于MIMO 无线信道极其复杂,则直接对信道矩阵H 进行处理计算是很困难的。
若利用奇异值分
解将信道矩阵分解成简单的对角矩阵,则可使信道变得简单易分析,而且具体实现也变得简单。
下面就矩阵的奇异值分解来计算MIMO 的信道容量。
根据上文中所述的奇异值分解理论,信道矩阵H 可以写成:
H H UDV = (4.1)
式中,D 是R T n n ⨯的对角阵,其对角非零元素模值为H 的正奇异值,U 和V 分别为R R n n ⨯和T T
n n ⨯的酉矩阵。
把公式(4.1)代入公式(3.1),得:
(t)(()H y UDV s t n t =+)
(4.2)
对式(4.2)进行变换,两边同时左乘酉矩阵H U ,又因为H R
n U U I =,令'()y ()H U y t t =,
's ()()H t V s t =,'(t)()H n U n t =,得:
'''()()()y t Ds t n t =+ (4.3)
根据矩阵理论,矩阵H
HH 的特征值为非负数,()()min(,)H R T rank HH rank H r n n ===,
表示矩阵H 4.3)得:
'''()()()(1,2,...)i i i y t t n t i r =+= (4.4)
''()()(1,...)i i R y t n t i r n ==+
(4.5)
式(4.5)显示,接收元素'
(1,...)()R i i r n y t =+并不依赖于发射信号,即信道增益为零。
另一方面,
接收元素'(1,2...,)()i i r y t =仅仅取决于发射元素'
()i s t ,因此,可以认为通过式(4.4)和(3.5)得到的等
效MIMO 信道是由个去耦平行子信道组成的。
其信道增益为矩阵H 的奇异值。
可以进一步推导出'
()i y t ,'()i s t ,和'()i n t 的协方差和迹:
'''''n',,H H H y y yy s s ss n nn R U R U R V R V R U R U === (4.6)
''''''()(),()(),()()y y yy s s ss n n nn tr R tr R tr R tr R tr R tr R ===
(4.7)
若MIMO 系统的接收端信道参数已知,发射端未知,发射端功率平均分配,那么设发射机总功率为
T P ,则每个天线发射功率为/T T P n ,此时
{ss }H T
ss T
T n P R E I n ==
(4.8)
根据式(4.6)得:
''H T
s s ss T
T n P R V R V I n ==
(4.9)
信道容量的一般公式为
22log det /R H xx n HR H C B I bit s σ⎧⎫⎡
⎤⎪⎪
=+
⎨⎬⎢⎥⎪⎪⎣⎦⎩
⎭
(4.10)
把根据式(4.1)算出H
HH 和式(4.9)代入式(4.10)得:
22
1
log (1)/r
i T
i T
P C B bit s n λσ==+
∑ (4.11)
五、 结论
比较式(4.10)与式(4.11),我们可以看到,通过对MIMO 信道矩阵进行奇异值分解,原来的信道容量计算公式中信道矩阵的行列式运算简化成了一系列的加法运算,这减小运算复杂度。
同时从式(4.11)可以看出,MIMO 链路的信道容量很大程度上取决于新到矩阵H 的秩r 。
矩阵的秩越大,容量也越大。
所以,MIMO 正是利用无线信道的多径效应使相距超过半个波长的天线尽量不相关,从而使信道矩阵秩越大,进而在不增加带宽和发射功率的情况下增加系统容量。
六、 参考文献:
1.黄延祝,钟守铭,李正良.矩阵理论[M].北京:高等教育出版社,2003 2 孙丹,张晓光.MIMO 系统信道容量研究[J].现代电子技术,2006(19):4-6。
