第四章平面问题的极坐标解答
第四章平面问题的极坐标解答(讲)

第四章平面问题的极坐标解答§4-1 极坐标中的平衡微分方程对于由径向线和圆弧线围成的圆形、圆环形、楔形、扇形等的弹性体,宜用极坐标求解。
因为用极坐标表示其边界线非常方便,从而使边界条件的表示和方程的求解得到很大的简化。
在极坐标中,平面内任一点P的位置,用径向坐标ρ及环向坐标ϕ来表示,图4-1。
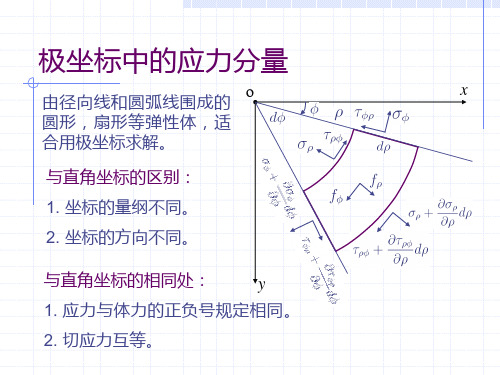
极坐标和直角坐标都是正交坐标系,但两者有如下区别:在直角坐标系中,x和y坐标线都是直线,有固定的方向,x和y坐标的量纲都是L。
在极坐标系中,ρ坐标线(ϕ=常数)和ϕ坐标线(ρ=常数)在不同的点有不同的方向;ρ坐标线是直线,而ϕ坐标线为圆ϕ坐标为量纲一的量。
这些区别将引弦曲线;ρ坐标的量纲是L,而起弹性力学基本方程的差异。
为了表明极坐标中的应力分量,从所考察的薄板或长柱形体中取出任一厚度等于1的微分体PACB,在xy平面上,这个微分体是由两条径向线(夹角为d ϕ)和两条环向线(距离为ρd )所围成,如图所示,沿ρ方向的正应力称为径向正应力,用ρσ代表;沿ϕ方向的正 应力称为环向正应力或切向正应力,用ϕσ代表;切应力用ϕρρϕττ及代表(根据切应力的互等关系,ϕρρϕττ=)。
各应力分量的正负号规定和直角坐标中一样,只是ρ方向代替了x 方向,ϕ方向代替了y 方向。
即正面上的应力以沿正坐标方向为正,负面上的应力以沿负坐标方向为正,反之为负。
图中所示的应力分量都是正的。
径向及环向的体力分量分别用ϕρf f 及代表,以沿正坐标方向为正,反之为负。
与直角坐标中相似,由于应力随坐标ρ的变化,设PB 面上的径向正应力为ρσ,则AC 面上的将为ρρσσρρd ∂∂+;同样,这两个面上的切应力分别为ρϕρϕττ及+ρρσϕd ∂∂。
PA 及BC 两个面上的环向正应力分别为ϕσ及ϕσ+ϕρσϕd ∂∂;这两个面上的切应力分别为ϕϕτττϕρϕρϕρd ∂∂+及。
对于极坐标中所取的微分体,应注意它的两个ρ面PB 及AC 的面积不相同,分别等于()ϕϕρϕρd d d +及;两个ϕ面PA 及BC 的面积都等于d ρ,但此两面不平行。
第四章 平面问题的极坐标解答-ppt01

(平面应力情形)
∂2 ∂2 ∂x 2 + ∂y 2 (σ x + σ y ) = 0 4 4 4 ∂ ϕ ∂ ϕ ∂ ϕ 4 ∇ ϕ = 4 +2 2 2 + 4 =0 ∂x ∂x ∂y ∂y
应力的应力函数表示:
∂ϕ σ x = 2 − Xx ∂y
2
∂ϕ σ y = 2 − Yy ∂x
τ rθ
—单元体上垂直r轴面上沿θ方向的应力
(3). 极坐标中的微元体
O
θ r dθ
rdθ
σr τ rθ
Pτ θr
σθ x
B
(r + dr )dθ dr A k r τ rθ + ∂τ rθ dr ∂r k
θ
∂ τ θr ∂σ θ dθ σθ + d θ τ θr + ∂θ ∂θ
y
C
∂σ r σr + dr ∂r
§4-1
1. 极坐标 (1) 极坐标系的建立
极坐标中的平衡微分方程
(2)极坐标系下基本变量
ur
uθ
εr
—沿r方向的位移,沿r伸长方向为正 —沿环向的位移,沿θ转正方向为正 —沿r方向相对伸长度
r —沿环向相对伸长度 r
εθ
γ rθ
σr
σθ
—由r与θ张开的直角改变量,角度减小为正
—单元体上垂直r轴面上的法向 应力,截面外法向上正应力为正 ; —单元体上平行r轴面上的法向应力,截面外法向上正应力为正
极坐标系的建立2极坐标系下基本变量沿r方向相对伸长度沿环向相对伸长度由r与张开的直角改变量角度减小为正单元体上平行r轴面上的法向应力截面外法向上正应力为正单元体上垂直r轴面上沿方向的应力rddr极坐标中的微元体应力正向规定
弹性力学第四章平面问题的极坐标解答
圆环或圆筒受均布压力(1)
q2 q1
边界条件:
圆环或圆筒受均布压力(2)
q2
q1
两个方程三个未知数,不能求解A,B,
C。因此,需引入位移单值条件:
该项必须为零,否则在环上同一点有两 个不同的位移,故B=0
圆环或圆筒受均布压力(3)
பைடு நூலகம்q2
q1 因此,得到圆筒受均匀压力的拉梅 ( me,1795—1870 ,法国)解答:
小孔口问题的特点:
1.集中性,孔附近的应力远大于较远处的应力。
2.局部性,孔口附近的应力扰动主要发生在距孔 边1.5倍孔口尺寸的范围内。在此区域外,由于开 孔引起的应力扰动一般小于5%,可以忽略不计。
注:圆孔的应力集中程度较低,有凹尖角的孔口 应力集中程度较高,因此,在设计结构时应尽量 避免有凹尖角的孔口。
o
x 在仅有径向位移的情况下,段
P P’ A
PA没有转动,因此:
A’
B
C
y
B’
极坐标中的几何方程(5)
— 纯环向位移下的线应变
o
x
很小,导致P’’A’’与PA
P P’’
的差别可以忽略,因此:
A
B B’’
D
D’
A’’
y
极坐标中的几何方程(6)
— 纯环向位移下的切应变
o
x
P
P’’
A
B B’’
D
D’
A’’
阶,因此假定:
半面体在边界上受集中力(2)
F
ao
c
ρ
代入极坐标中的相容方程:
b
得到:
半面体在边界上受集中力(3)
代入:
F
ao
弹性力学 第四章 平面问题的极坐标解答

s = sσ
(3) 多连体中的位移单值条件
§ 4-4 应力分量的坐标变换式
·问题的提出
工程中有些问题, 用极坐标计算方便, 但应力分量用直角坐 标表述更直观. 反之也存在.
由此需要对应力分量进行坐标变换.
§ 4-4 应力分量的坐标变换式
·坐标变换
已知 σx、σy、τxy , 求 σρ、συ、τρυ?
y
fρ τ + ∂τρυdρ ρυ ∂ρ ∂συ dυ συ+ ∂σρ ∂υ σρ+ dρ ∂τυρ C ∂ρ dυ τυρ+ ∂υ
B
fυ
§ 4-1 极坐标中的平衡微分方程
·平衡微分方程
x
υ dυ ρ
Σ Fρ = 0 :
συ
A
σρ τρυ P τυρ
∂σρ σρ+ dρ (ρ+dρ)dυ - σρ ρdυ ∂ρ ∂συ dυ - συ+ dυ dρ sin ∂υ 2 + τυρ+ - συ dρ sin
Σ Fυ = 0 :
συ = ?
§ 4-4 应力分量的坐标变换式
·坐标变换
συ = ?
将两坐标系下微元体组合
τyx σy σx συ
τυρ τxy
§ 4-4 应力分量的坐标变换式
·坐标变换
已知 σx、σy、τxy , 求 σρ、συ、τρυ?
O x
υ
τyx
σy σx
συ y
τυρ τxy
Σ Fυ = 0 :
O h/2 h/2 lqx源自(v)x=0, l = 0
应力边界条件: ( σy ) y=-h/2 = - q (τyx ) y=-h/2 = 0 ( σy ) y= h/2 = 0 (τyx ) y= h/2 = 0
弹性力学徐芝纶版第4章

第四章 平面问题的极坐标解答
比 较
1 f 0。 (a) x yx fx 0 x y
式(a)中第一、二、 四项与直角坐标的方 方程相似; 而第三项 分别由PB、AC面不 相等和PA、BC面不平 行引起。
为边界上已知的面力分量。
常数,或 常数,
故边界条件形式简单。
第四章 平面问题的极坐标解答
例:写出应力边界条件(集中力偶作用处为小边界) b a 0 d 0 0 a 0
a
b 0 b 0
0
q
2
2
0
0 0
l
q0
0
0
0
0
2
2
0
0
第四章 平面问题的极坐标解答
PB线应变 PB PB PC PB (ρ u ρ ) d υ ρ d υ u ρ ευ PB PB ρdυ ρ
第四章 平面问题的极坐标解答
PA转角 0, PB转角
O
d
x P
d
P
A
u
B C
u
A
u
d
y B ( u )d CB β tan u PC u d u ρ u ρ (u d υ) u ρ dυ υ υ ∴切应变为 ρ u d υ d
1.只有径向位移 u ,求形变。 P,A,B 变形后为 P', A', B', 在小变形假定 O x β 1 下, u P d d
弹性力学简明教程-第四章_平面问题的极坐标解答习题详解

第四章 平面问题的极坐标解答典型例题讲解例4-1 如图所示,矩形薄板在四边受纯剪切力作用,切应力大小为q 。
如果离板边较远处有一小圆孔, 试求孔边的最大和最小正应力。
例4-1图【解】(1)根据材料力学公式,求极值应力和量大正应力的方位角α0max min 2x y σσσσ+⎫=⎬⎭ 其中0,,x y x q σστ===得max min ,q q σσ==-。
最大正应力σmax 所在截面的方位角为α0max 0max 0tan 104yqq τασσπα=-=-=-→--=-qqx若在该纯剪切的矩形薄板中,沿与板边成π4方向截取矩形ABCD ,则在其边界上便承受集度为q 的拉力和压力,如图所示。
这样就把受纯剪切作用的板看作与一对边受拉,另一对边受压的板等效。
(2)取极坐标系如图。
由2222442222cos 2(1)(13),cos 2(13),(4-18)sin 2(1)(13).ρφρφr r σq φρρr σq φρr r τq φρρ⎫=--⎪⎪⎪⎪=-+⎬⎪⎪=--+⎪⎪⎭得矩形薄板ABCD 内的应力分量为()()()2222442222cos 2(1)(13)cos 2(13)sin 2(1)(13)ρφρφa a σq φa ρρa σq φb ρa a τq φc ρρ=--=-+=--+ 其中α为小孔的半径,而孔边最大与最小正应力由式(b ),在ρ=α处得到44cos 2(13)4cos 2,φa σq φaϕ=-+=-当φ=0,π时,孔边最小正应力为(σφ)min=−4q ,当φ=±π2时,孔边最大正应力为(σφ)max=4q 。
分析:矩形板ABCD 边界上各点的应力状态与板内无孔时的应力状态相同。
也可以应用叠加法,求解薄板的各种较复杂的平面应力(应变)问题。
习题全解4-1试比较极坐标和直角坐标中的平衡微分方程、几何方程和物理方程,指出哪些项是相似的,哪些项是极坐标中特有的?并说明产生这些项的原因。
第四章平面问题的极坐标解答

r 2 r r r 2 2
式中 (r, ) ,为应力函数。
应力函数与应力分量之间的关系,可按下述方法导出。
我们注意到,当 0时,x、y 轴分别与r、 轴重
合,此时应力分量
x、
y、
分别与应力分量
xy
r、 、 r 对应
r
( x ) 0
2
dr 2 r dr dr 2 r dr
展开上式得:
r 4 d 4 2r 3 d 3 r 2 d 2 r d 0
dr4
dr3
dr2 dr
这是一个变系数欧拉方程,其通解为
Aln r Br 2 ln r Cr 2 D
式中,A、B、C、D是待定系数。将代入式 (4-8),得应力分量:
1 E
(
r ),
r
2(1
E
)
r
或者
r
E
1 2
( r
),
E
1 2
(
r ),
r
E
2(1
)
r
4. 边界条件
力的边界条件:
r l r m Tr
r l m T
力均对称于它的中心轴(z),故其应力只与r有关,
与极角无关,由于对称性,只有正应力,而剪应 力为零,称此类问题为平面轴对称问题。对于象曲 杆纯弯曲这类问题,其应力也具有这种特点(与θ 无关),但结构不具有对称性,称为应力轴对称问题。
由应力分布的上述特点,可假设应力函数形式为:
(r)
相容方程: ( d 2 1 d )( d 2 1 d ) 0
弹性力学简明教程(第四版)_第四章_课后作业题答案

【4-8】 实心圆盘在 r 的周界上受有均布压力 q 的作用,试导出其解答。
【解答】实心圆盘是轴对称的,可引用轴对称应力解答,教材中的式(411),即
A 2
B(1 2 l n ) 2C
A 2
B( 3
2l
n
)
2C Fra bibliotek y 2
2
2 xy
q。
原来的问题变为矩形薄板在左右两边受均布拉力 q 而在上下两边受均布压力 q,如下 图所示。根据教材中的式(4-18)
3
σ
q cos 2(1
r 2)(1 2
3
r2 ) , 2
σ
q
cos
2( 1
3
r4 4
)
,
(a)
( R2 - r2)
2( R2 - r2 )
把 A,B,C 值代入轴对称应力状态下对应的位移分离,教材中式(4-12)。
u
qr 2 E( R2
r 2)
1
1
R2
I
cos
K
si n ,
(b)
u H I si n K cos 0。
【解答】(1)相容条件: 将应力函数 代入相容方程 4 0 , 显然满足。 (2)由 求应力分量表达式
1
=
2B si n 2 2B si n 2
2C 2C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ur
rd
1 ur
r
第2步:只有环向位移,而没有径向位移(图4-4(b))。
径向线元PA移到 PA ,环向线元PB 移到 PB 。
P点的位移:
u
A点的位移:
u
u r
dr
B点的位移:线元PA的正应变:
(2) r
PA PA
第四章 平面问题极坐标解法
§4-1 极坐标中的基本方程与边界条件 §4-2 极坐标中的应力函数 相容方程 §4-3 应力轴对称问题及其相应的位移 §4-4 圆环或圆筒问题 §4-5 曲梁的纯弯曲
§4-6 含小圆孔平板的拉伸 §4-7 楔形体在楔顶或楔面受力 §4-8 轴对称问题的位移解法
在求解弹性力学问题时,无论选取什么形式的 坐标系都不会影响问题本质的描述,但却涉及到解 决问题的难易程度。
r
dr)(r
dr)d
r rd
(
d )dr sin
d
2
dr sin
d
2
( r
r
d )dr cos d
2
r
dr
cos
d
2
Fr rddr
0
将微元体上的作用力向中心的切向方向投影,得切 向平衡方程:
(
AA PP PA
(u r
u r r
dr) ur
ur
dr
r
环向线元PB的正应变:
(1)
PB PB PB
(r ur )d rd
rd
ur r
直角的变化(剪应变):
(1)
r
BB PP (ur PB
ur
d )
1 E
(
r ),
r
2(1
E
)
r
或者
r
E
1 2
( r
),
E
1 2
(
r ),
在平面问题中,对于圆环、楔形、扇形之类的 物体,用极坐标比用直角坐标方便得多。这时,物 体的边界线与坐标线重合,边界条件的形式最为简 单。
在极坐标系中,平面内任一点的位置由径向坐
标r和环向坐标表示。在平面上r不变的曲线称为 坐标曲线,它是以原点为圆心的圆;平面上不变 的曲线称为r坐标曲线,它是过O点的直线。过这 一点沿r和增加的方向引两条坐标曲线的切线矢
(u
u r
dr) (r dr) u r
u
u
dr
r r
将(3)~(5)三式与(6)~(8)三式分别
叠加,得物体的任一点P的应变:
r
u r r
ur r
1 u
r
r
1 ur
r
u r
u
r
这就是极坐标平面问题几何方程。
3. 本构方程 由于极坐标与直角坐标都是正交坐标,只是通 过同一点的两组坐标架相对转动了一个角度,而材 料又是各向同性的,与方向无关。所以,只须将直
角坐标下本构方程中的x、y用r、替换即得极坐标
下的本构方程如下:
r
1 E
(
r
),
的变化量为
r
r
dr 和
r
r
dr
;
同样两个径向平面由于位置差d,其上正应力和
剪应力的变化分别为 d 和 r d ;
微元体的体力: (Fr、F )
下面研究微元体的平衡,将微元体上所受的力向 微元体中心的径向方向投影,得径向平衡方程:
( r
r
量,就构成了该点的一个局部标架。 在极坐标中,
随点的位置不同局部标架的方向将发生变化。
由于两切线相互垂直,所以极坐标是一种正交 曲线坐标。
图4-1
在极坐标系中,应力分量、应变分量、位移
分量和外力分量的定义、记号和正负号都是参
照局部标架来定义和规定的。比如r 面上的正
应力,用 r 表示,称为径向正应力,其上剪 应力用 r 表示。 面上的正应力,用 表
d )dr cos d
2
dr
cos
d
2
( r
r
r
dr)(r
dr)d
r rd
(r
r
d )dr sin
d
2
r dr sin
d
2
F rddr 0
将微元体上的作用力对中心取矩得:
r r
假定正交线元PA、PB的变形分两步完成:
第1步:只有径向位移,而没有环向位移(图44(a))。
这时,径向线元PA移到PA,环向线元PB移 到PB。;
P点的位移为 A点的位移为 B点的位移为
ur
ur
u r r
dr
ur
u r
d
径向线元PA的正应变:
(1) r
PA PA PA
剪应力互等仍然成立.
由于d是个小量,故有 sin d d 和 cos d 1
22
2
简化以后,除以 rddr ,再略去高阶小量,得:
r
r
1 r r
r
r
Fr
0
1 r
r
r
2 r
r
F
0
这就是平面问题极坐标下的平衡微分方程。
2. 几何方程
下面考察过物体内一点P的两个正交线元
(PA dr和PB rd ) 的变形。 r 和 分别表示线元PA和PB的相对伸长, 即径向和切向正应变, r 表示该两个正交
线元直角的变化,即剪应变。
ur、u 分别表示P点的径向和环向位移。
PA
0
环向线元PB的正应变:
(2)
PB PB
PB
BB PP PB
(u
u
d ) u
1 u
rd
r
直角的改变量(剪应变):
(2)
r
AA AC P C
(u
u r
dr) (r dr
dr)
示,称为环向(或切向)正应力,其上剪应力
表示为
.
r
图4-2
§4-1 极坐标中的基本方程与边界条件
1. 平衡微分方程
根据极坐标的特点,用两个同心圆柱面和两个
径向平面从弹性体中截出一个扇形微单元体PABC。
由于单元体尺寸很小,可以认为各微面上的应
力是均匀分布的。按泰勒级数展开,在两个弧面上,
由于有位置dr的变化,其上相应的正应力和剪应力
