第1章补充例题
《数论》第一章补充例题
《数论》第一章补充例题整除性理论是初等数论的基础.本章要介绍带余数除法,辗转相除法,最大公约数,最小公倍数,算术基本定理以及它们的一些应用.1整数的整除性例1设A={d1,d2,···,dk}是n的所有约数的集合,则}{nnn,,···,B=d1d2dk也是n的所有约数的集合.解由以下三点理由可以证得结论:(i)A和B的元素个数相同;(ii)若di∈A,即di|n,则(iii)若di=dj,则问:d(1)+d(2)+···+d(1997)是否为偶数?n解对于n的每个约数d,有n=d·n,因此,n的正约数d与是成对地出现的.只有n2当d=n,即d=n时,d和才是同一个数.故当且仅当n是完全平方数时,d(n)是奇数.nini|n,反之亦然;=nj.例2以d(n)表示n的正约数的个数,例如:d(1)=1,d(2)=2,d(3)=2,d(4)=3,···.因为442<1997<452,所以在d(1),d(2),···,d(1997)中恰有44个奇数,故d(1)+d(2)+···+d(1997)是偶数.问题d2(1)+d2(2)+···+d2(1997)被4除的余数是多少?例3证明:存在无穷多个正整数a,使得n4+a(n=1,2,3,···)都是合数.??例题中引用的定理或推论可以在教材相应处找到.1解取a=4k4,对任意的n∈N,有n4+4k4=(n2+2k2)2?4n2k2=(n2+2k2+2nk)(n2+2k2?2nk).由n2+2k2?2nk=(n?k)2+k2??k2,所以,对于任意的k=2,3,···以及任意的n∈N,n4+a是合数.例4设a1,a2,···,an是整数,且n∑k=1ak=0,n∏k=1ak=n,则4|n.解如果2??n,则n,a1,a2,···,an都是奇数.于是a1+a2+···+an是奇数个奇数之和,不可能等于零,这与题设矛盾,所以2|n,即在a1,a2,···,an中至少有一个偶数.如果只有一个偶数,不妨设为a1,那么2??ai(2??k??n).此时有等式a2+···+an=?a1,在上式中,左端是(n?1)个奇数之和,右端是偶数,这是不可能的,因此,在a1,a2,···,an 中至少有两个偶数,即4|n.例5若n是奇数,则8|n2?1.解设n=2k+1,则n2?1=(2k+1)2?1=4k(k+1),在k与k+1中有一个偶数,所以8|n2?1.2带余数除法例1设a,b,x,y是整数,k和m是正整数,并且a=a1m+r1,0??r1<m,b=b1m+r2,0??r2<m,则ax+by和ab被m除的余数分别与r1x+r2y和r1r2被m除的余数相同.特别地,ak与k被m 除的余数相同.r1解由ax+by=(a1m+r1)x+(b1m+r2)y=(a1x+b1y)m+r1x+r2y可知,若r1x+r2y被m除的余数是r,即r1x+r2y=qm+r,0??r<m,2则ax+by=(a1x+b1y+q)m+r,0??r<m,即ax+by被m除的余数也是r.例2设a1,a2,···,an为不全为零的整数,以y0表示集合A={y|y=a1x1+···+anxn,xi∈Z,1??i??n}中的最小正数,则对任何的y∈A,y0|y;特别地,y0|ai,1??i??n.′解设y0=a1x′1+···+anxn,?y∈A,由带余除法,?q,r0∈Z,使得y=qy0+r0,0??r0<y0.因此′r0=y?qy0=a1(x1?qx′1)+···+an(xn?qxn)∈A.如果r0=0,那么,因为0<r0<y0,所以r0是A中比y0还小的正数,这与y0的定义矛盾.所以r0=0,即y0|y.显然ai∈A(1??i??n),所以y0整除每个ai(1??i??n).例3任意给出的五个整数中,必有三个数之和被3整除.解设这五个数是ai,i=1,2,3,4,5,记ai=3qi+ri,0??ri<3,i=1,2,3,4,5.分别考虑以下两种情形:(i)若r1,r2,···,r5中数0,1,2都出现,不妨设r1=0,r2=1,r3=2,此时a1+a2+a3=3(q1+q2+q3)+3可以被3整除;(ii)若r1,r2,···,r5中数0,1,2至少有一个不出现,这样至少有三个ri要取相同的值,不妨设r1,r2,r3=r(r=0,1或2),此时a1+a2+a3=3(q1+q2+q3)+3r可以被3整除.例4设a0,a1,···,an∈Z,f(x)=anxn+···+a1x+a0,已知f(0)与f(1)都不是3的倍数,证明:若方程f(x)=0有整数解,则3|f(?1)=a0?a1+a2?···+(?1)nan.证对任意整数x,都有x=3q+r,r=0,1或2,q∈Z.(i)若r=0,即x=3q,q∈Z,则f(x)=f(3q)=an(3q)n+···+a1(3q)+a0=3Q1+a0=3Q1+f(0),3其中Q1∈Z,由于f(0)不是3的倍数,所以f(x)=0;(ii)若r=1,即x=3q+1,q∈Z,则f(x)=f(3q+1)=an(3q+1)n+···+a1(3q+1)+a0=3Q2+an+···+a1+a0=3Q2+f(1),其中Q2∈Z.由于f(1)不是3的倍数,所以f(x)=0.因此若f(x)=0有整数解x,则必是x=3q+2=3q′?1,q′∈Z,于是0=f(x)=f(3q′?1)=an(3q′?1)n+···+a1(3q′?1)+a0=3Q3+a0?a1+a2?···+(?1)nan.其中Q3∈Z.所以3|f(?1)=a0?a1+a2?···+(?1)nan.例5设n是奇数,则16|n4+4n2+11.证我们有n4+4n2+11=(n2?1)(n2+5)+16.由上节例题知道,8|n2?1,由此及2|n2+5得到16|(n2?1)(n2+5).例6证明:若a被9除的余数是3,4,5或6,则方程x3+y3=a没有整数解.证?x,y∈Z,记x=3q1+r1,y=3q2+r2,0??r1,r2<3.则存在Q1,R1,Q2,R2∈Z,使得x3=9Q1+R1,y3=9Q2+R2,3和r3被9除的余数相同,即其中R1和R2被9除的余数分别与r12R1=0,1或8,R2=0,1或8.因此x3+y3=9(Q1+Q2)+R1+R2.(2.1)又由式(2.1)可知,R1+R2被9除的余数只可能是0,1,2,7或8,所以,x3+y3不可能等于a .例7证明:方程22a21+a2+a3=1999(2.2)无整数解.证若a1,a2,a3都是奇数,则存在整数A1,A2,A3,使得22a21=8A1+1,a2=8A2+1,a3=8A3+1,于是22a21+a2+a3=8(A1+A2+A3)+3.4由于1999被8除的余数是7,所以a1为奇数.由式(2.2),a1,a2,a3中只有一个奇数,设a1为奇数,a2,a3为偶数,则存在整数A1,A2,A3,使得22a21=8A1+1,a2=8A2+r,a3=8A3+s,于是22a21+a2+a3=8(A1+A2+A3)+1+r+s,22其中r和s是整数,而且只能取值0或4.这样a21+a2+a3被8除的余数只可能是1或5, 但1999被8除的余数是7,所以这样的a1,a2,a3也不能使式(2.2)成立.3最大公约数例1(105,140,350)=(105,(140,350))=(105,70)=35.21n+4例2证明:若n是正整数,则是既约分数.14n+3证由辗转相除法得到(21n+4,14n+3)=(7n+1,14n+3)=(7n+1,1)=1.??4辗转相除法例1用辗转相除法求(125,17),以及x,y,使得125x+17y=(125,17).解作辗转相除法:125=7×17+6,17=2×6+5,6=1×5+1,5=5×1,q1=7,r1=6,q2=2,r2=5,q3=1,r3=1,q4=5.由推论1.1,(125,17)=r3=1.利用定理1计算(这里n=3)P0=1,P1=7,P2=2·7+1=15,P3=1·15+7=22,Q0=0,Q1=1,Q2=2·1+0=2,Q3=1·2+1=3,取x=(?1)3?1Q3=3,y=(?1)3P3=?22,则125·3+17·(?22)=(125,17)=1.例2在m个盒子中放若干个硬币,然后以下述方式往这些盒子里继续放硬币:每一次在n(n<m)个盒子中各放一个硬币.证明:若(m,n)=1,那么无论开始时每个盒子中有多少个硬币,经过若干次放硬币后,总可使所有盒子含有同样数量的硬币.5证由于(m,n)=1,所以存在整数x,y,使得mx+ny=1.因此对于任意的自然数k,有1+m(?x+kn)=n(km+y),这样,当k充分大时,总可找出正整数x0,y0,使得1+mx0=ny0.上式说明,如果放y0次(每次放n个),那么在使m个盒子中各放x0个后,还多出一个硬币.把这个硬币放入含硬币最少的盒子中(这是可以做到的),就使它与含有最多硬币的盒子所含硬币数量之差减少1.因此经过若干次放硬币后,必可使所有盒子中的硬币数量相同.5素数与算术基本定理例1写出51480的标准分解式.解我们有51480=2·25740=22·12870=23·6435=23·5·1287=23·5·3·429=23·5·32·143=23·32·5·11·13.例2设a,b,c是整数,证明:(i)(a,b)[a,b]=ab;(ii)(a,[b,c])=[(a,b),(a,c)].证为了叙述方便,不妨假定a,b,c是正整数.(i)设a=pααβ11pα22···p1β2βkk,b=p1p2···pkk,其中p1,p2,···,pk是互不相同的素数,αi,βi(1??i??k)都是非负整数.由推论3.3,有(a,b)=pλ11pλ22···pλkk,λi=min{αi,βi},1??i??k,[a,b]=pμ11pμ22···pμkk,μi=max{αi,βi},1??i??k.由此知∏k(a,b)[a,b]=pλi+μi∏kαi=pmin{αi,βi}+max{αi,βi}∏ki=pii+βi=ab;i=1i=1i=1(ii)设a=∏kpα∏kii,b=∏kpβii,c=pγii,i=1i=1i=1其中p1,p2,···,pk是互不相同的素数,αi,βi,γi(1??i??k)都是非负整数.由推论3.3,有(a,[b,c])=∏kpλii,[(a,b),(a,c)]=∏kpμii,i=1i=16其中,对于1??i??k,有λi=min{αi,max{βi,γi}},μi=max{min{αi,βi},min{αi,γi}},不妨设βi??γi,则min{αi,βi}??min{αi,γi},所以μi=min{αi,γi}=λi,即(a,[b,c])=[(a,b),(a,c)].7。
《流体力学与流体机械》计算题及答案
Q v1A1 v2 A2
Q
v2 A2
4
0.12
3
0.0234 m3
/
s
v1
4Q
d12
4 0.0234
0.152
1.3
3
6 m
/
s
编辑ppt
• 习题3-15 判断流动 ux = xy；uy = -xy 是否满足不可压缩流动的连续性条件 。 • 解： 因为 ux = xy；uy = -xy 与时间无关，所以流动定常，根据定常不可压微分形式连续方程，
•
图示为一轴流风机，已测得进口相对压力p1= -103 Pa，出口相对压力p2 = 150 Pa。设截面
1-2间压力损失 100Pa，求风机的全压P ( P为风机输送给单位体积气体的能量 ) 。
• 解：
p1
1
2
v12
z2
z1 ga
p
p2
2
2
v22
ghw
1000 0 p 150100
P 1250 Pa
第一章 流体及其物理性质
•
• 例1－2 相距为h=10 mm的两固定平板间充满动力粘度μ=1.49 Pa·s的甘油， 若两板间甘油的速度分布为u=4000y(h-y)
•
(1) 若上板的面积A=0.2 m2，求使上板固定不动所需的水平作用力F；
•
(2) 求y=h/3和2h/3处的内摩擦应力，
并说明正负号的意义。
有一圆桶，半径R=1m，高H=3.5m，桶内盛有高度h=2.5m的水。圆桶绕中心
轴匀速旋转。问水恰好开始溢出时，转速ω为多少？而此时距中心线r=0.4m处桶底 面上A点的压力是多少?
• 解：(1) 求旋转速度ω
新浙教版八年级上册数学第一章《三角形的初步知识》知识点及典型例题
新浙教版八年级上册数学第一章《三角形的初步知识》知识点及典型例题本文介绍了八年级上册数学第一章《三角形的初步知识》的知识点及典型例题。
其中，三角形按角分类分为锐角三角形、直角三角形和钝角三角形；按边的关系可分为等腰三角形、等边三角形和普通三角形。
文章还介绍了三角形的内角和定理、角平分线、重要线段中线和高线的定义、命题和证明步骤。
此外，文章还讲解了全等三角形、尺规作图、线段垂直平分线和角平分线的性质，以及如何利用这些知识点计算角度和线段长度。
最后，文章列举了八个考点，包括判断三条线段能否组成三角形、求三角形的某一边长或周长的取值范围、证明三角形全等等。
例题部分也包括了两个问题的解答。
1、正确画出AC边上的高的是（C）。
2、工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（B）三角形具有稳定性。
3、不能唯一作出直角三角形的是（C）已知一锐角及其邻边。
4、已知AD、BE、CF是△ABC的三条中线，相交于点O，设△BDO面积为1，则S△ABC=（6）。
5、在图中，由于AB=CD。
AD=BC，所以△ABO≌△CDO，△ABO与△CDO的对应顶点分别为AO和CO，所以全等三角形的对数为1，选项A。
6、根据中线定理可知，DF=EF=BF=AF=1/2AC，所以四边形DCEF是平行四边形，面积为AC的一半，即22.5cm，选项B。
7、根据角平分线定理可知，BP/PC=AB/AC，所以BP/AB=PC/AC，由此可得△BPC与△ABC相似，所以∠BPC=2∠A，选项A。
8、由于BD是BC边上的垂直平分线，所以BD=DC=4，由勾股定理可得AD=3，所以AB=5，所以ΔABD的周长为12，选项D。
9、将三角形按照图中的方式编号，可以发现只有第3块的形状与原来的三角形相同，所以应该带第3块去。
10、以B为顶点的外角为∠ABC=180°-∠A=130°，以C为顶点的外角为∠ACB=180°-∠A=130°，由于外角和等于360°，所以两个外角的平分线的夹角为130°/2=65°，选项A。
(完整版)经济法第一章习题有答案
第一章总论习题第一单元法律基础一、法的本质与特征【例题1·多选题】关于法的本质与特征的下列表述中，正确的有（)。
（2009年)A.法由统治阶级的物质生活条件所决定B.法体现的是统治阶级的整体意志和根本利益C.法是由国家制定或认可的行为规范 D。
法由国家强制力保障其实施【答案】ABCD【解析】（1）选项AB:属于法的本质；(2）选项CD：属于法的特征。
【例题2·多选题】根据我国法律制度的规定,法的特征包括（）。
A.国家强制性B.国家意志性C.明确公开性 D。
规范性【答案】ABCD二、法律关系【例题1·单选题】下列公民中,视为完全民事行为能力人的是（）。
（2017年）A.赵某，9岁,系某小学学生B。
王某，15岁，系某高级中学学生C。
张某，13岁，系某初级中学学生D.李某，17岁，系某宾馆服务员,以自己劳动收入为主要生活来源【答案】D【解析】16周岁以上的未成年人，以自己的劳动收入为主要生活来源的,视为完全民事行为能力人。
【例题2·多选题】下列各项中,属于法律关系客体的有（）。
（2015年）A。
法人 B。
发明 C.行为 D.荣誉称号【答案】BCD【解析】选项A：属于法律关系的主体。
【例题3·多选题】下列可成为法律关系的客体的有（）。
(2016年）A。
土地 B。
荣誉称号 C。
人民币 D.天然气【答案】ABCD【例题4·单选题】甲公司与乙公司签订买卖合同，向乙公司购买了一台设备，价款8万元,该买卖合同的法律关系的主体是（）.（2017年）A。
买卖合同 B.设备 C.8万元价款 D.甲公司与乙公司【答案】D【例题5·多选题】非物质财富可以成为法律关系的客体，下列各项中，属于非物质财富的有( ）。
（2017年)A.著作B.嘉奖表彰C.发明D.荣誉称号【答案】ABCD三、法律事实、【例题1·单选题】下列各项中，会直接引起法律关系发生、变更、消灭的是（)。
南开大学大学物理重点例题
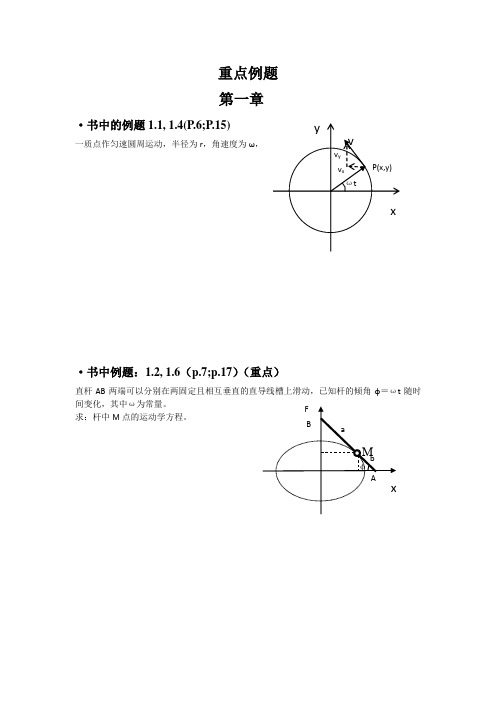
重点例题第一章·书中的例题1.1, 1.4(P.6;P.15)一质点作匀速圆周运动，半径为r，角速度为ω，·书中例题：1.2, 1.6（p.7;p.17）（重点）直杆AB两端可以分别在两固定且相互垂直的直导线槽上滑动，已知杆的倾角φ＝ωt随时间变化，其中ω为常量。
求：杆中M点的运动学方程。
·习题指导P9. 1.4（重点）在湖中有一小船，岸边有人用绳子跨过一高处的滑轮拉船靠岸，当绳子以v 通过滑轮时， 求：船速比v 大还是比v 小？ 若v 不变，船是否作匀速运动？ 如果不是匀速运动,其加速度是多少？·书中例题1.3, 1.5, 1.7（p.7;p.16;p.18）已知：运动学方程：x ＝ －0.31t 2＋7.2t ＋28 y ＝ 0.22t 2－9.1t ＋30 求：t ＝15s 时的位置矢量和方向。
·例题：已知：a ＝100－4t 2，且t ＝0时，v ＝0，x ＝0 求：速度v 和运动学方程x第二章·例题：飞机着陆时受到的阻力为F＝－ct，（c为常数）且t＝0时，v＝v0。
求：飞机着陆时的速度。
·例题：（重点）质量为m的物体以速度v0投入粘性流体中，受到阻力f＝－cv （c为常数）而减速，若物体不受其它力，求：物体的运动速度。
·例题：（重点）光滑的桌面上一质量为M，长为L的匀质链条，有极小一段被推出桌子边缘。
求：链条刚刚离开桌面时的速度。
·例：有一个小球通过一根细线挂在车顶，当车静止时小球铅直向下，当车以加速度a开动时与铅垂线夹角θ。
求：加速度与θ之间的关系。
典型例题·书中例题 2.9（p76 ）（非质点问题的处理方法）试证明在圆柱形容器内，以匀角速度ω绕中心轴作匀速旋转的流体表面为旋转抛物面。
y·书中例题P82，例2.14 (变质量，变力问题)长为L质量为M的均匀柔绳，盘绕在光滑的水平面上，从静止开始，以恒定加速度a竖直向上提绳，当提起的高度为l时，作用在绳端力的大小是多少？当以恒定速度v竖直向上提绳，当提起的高度为l时，作用在绳端力的大小又是多少？第三章·书中例题3.1 (P.95)已知：F＝6x；cosθ＝0.70－0.02x求：质点从x1＝10m到x2＝20m过程中F所作的功。
高中化学必修一第一章物质及其变化知识总结例题(带答案)
高中化学必修一第一章物质及其变化知识总结例题单选题1、钛(Ti)被称为“生物金属”，由TiO 2制取Ti 的主要反应为：①TiO 2 + 2Cl 2 + 2C 高温TiCl 4 + 2CO ，②TiCl 4 + 2Mg 高温2MgCl 2 + Ti ，下列说法不正确的是A ．反应①②都是氧化还原反应B ．反应②是置换反应C ．反应①中TiO 2是氧化剂D ．反应②中每生成1 mol Ti 转移4 mol 电子 答案：CA ．分析题干反应①②可知，两反应中均有元素的化合价发生改变，故都是氧化还原反应，A 正确；B ．置换反应是指一种单质和一种化合物生成另一种单质和另一种化合物的反应，故反应②是置换反应，B 正确；C ．经分析可知，反应①中TiO 2中Ti 和O 的化合价均没有发生改变，故TiO 2既不是氧化剂也不是还原剂，C 错误；D ．反应②中Ti 的化合价由+4价变为0价，故每生成1 mol Ti 转移4 mol 电子，D 正确； 所以答案是：C 。
2、M 是一种可溶性结晶水合物，为了确定M 的组成，取少量M 溶于水配成容液进行如下实验：下列有关M 的推断正确的是A．由实验(1)(2)的现象知，M含Fe2+B．由实验(3)(4)的现象知，该气体显碱性C．由实验(6)的现象知，白色沉淀可能是BaCO3D．由上述实验推知，M可能是(NH4)2Fe(SO4)2⋅6H2O答案：A分析：实验(1)加入KSCN溶液无现象说明无Fe3+，实验(2)加入氯水溶液变红色，说明亚铁离子被氧化生成Fe3+，可推知M溶液含Fe2+；由实验(4)现象可知气体为NH3，说明M中含NH4+，由实验(5)和(6)现象说明M中含SO42-；A．实验(1)加入KSCN溶液无现象说明无Fe3+，实验(2)加入氯水溶液变红色，说明亚铁离子被氧化生成Fe3+，可推知M溶液含Fe2+，A正确；B．由实验(4)现象可知气体为NH3，氨气无碱性，是氨气溶于水得到氨水呈碱性，B错误；C．由实验(5)加入稀盐酸无现象，可排除M中不存在CO32−，根据(6)现象说明M中含SO42-，白色沉淀是BaSO4，C错误；D．由上述实验推知，M含有Fe2+、NH4+、SO42-，但无法确定结晶水的数目，D错误；故选：A。
《高等数学》(一)(2)补充例题及练习题
第八章 空间解析几何与向量代数（6学时）§8.1 向 量 及 其 线 性 运 算一、补充例题例1 已知向量)1,5,3(-=a ，)3,2,2(=b ，)3,1,4(--c，求c b a 432+-。
例2 在yOz 面上，求与三点)2,1,3(A 、)2,2,4(--B 和)1,5,0(C 等距离的点。
例3 已知两点)1,3,2(-A 和)0,2,1(-B ，求与方向相同的单位向量e。
例4 已知两点)2,1,1(-A 和)3,1,0(B ，计算向量的模、方向余弦和方向角。
例5 一向量的终点在点)7,1,2(-B ，它在x 轴、y 轴和z 轴上的投影依次为4，4-和7。
求这向量的起点A 的坐标。
二、练习1312-p 习题8-1 4，5，15，17§8.2 向量的数量积与向量积一、补充例题例1 已知j i a += ，k i b += ，求b a ⋅，∧),(cos b a 及a j bPr 。
例2 已知四点)1,2,2(A 、)2,1,0(B 、)1,1,1(C 、)2,3,3(D ，求AB j CDPr ，∧),(cos 。
例3 记)0,1,3(-=a，)1,2,1(-=b，求b a⨯。
例4 已知ABC ∆的三个顶点为)2,0,3(A ，)1,3,5(B ，)3,1,0(-C ，（1）求垂直于这个三角形所在平面的单位向量；（2）求ABC ∆的面积。
解 （1）因为a ⨯= 垂直于向量与，所以a是一个垂直于三角形ABC 所在平面的向量。
而)1,3,2(-=，)1,1,3(--=，所以k j i kj i a72113132++=---=⨯=。
63712222=++=a ，)7,1,2(631=a e。
所以垂直于三角形ABC 所在平面的单位向量为)7,1,2(631±。
（2）因为ABC ∆的面积S 是以AB ，AC 为邻边的平行四边形面积的一半，所以6237122121222=++===a S 。
应用随机过程第1章补充例题及作业
例 3 已知二维随机变量(X,Y)的联合概率密度函数为：
e x f ( x, y ) 0
（1）问变量 X 与 Y 是否相互独立？ （2）求条件分布密度函数 fY | X ( y | x) ； （3）计算条件期望 E (Y | X ) 。
0 y x other
Y 0 1 2
X
0 0.25 0.05 0.05
10 0.05 0.15 0.10
20 0.05 0.05 0.25
（1）研究吸烟数量多与健康状态差有无关联？要求利用条件分布说明； （2） 研究每天吸 x 支烟 （x = 0,10,20） 的人的平均健康状态值， 并写出条件期望 E (Y | X ) 的分布律。 5. 已知 X
N (0,1) ，U 与 X 相互独立， P{U 0} P{U 1}
1 ，令 2
X Y X
证明： Y
U 0 U 1
。
N (0,1) ，但 ( X , Y ) 不服从二维正态分布。
isX itY
注：( X , Y ) 的二维特征函数为： XY ( s, t ) E (e 为： (t ) exp(i t
1 2
1
（3）计算 E ( X | X Y n) 。 ) 的二项分布。
4. 为研究吸烟与身体健康之间的关系，以 X 表示每人每天吸烟的数量，分为 3 类：0 支、10 支和 20 支；以 Y 表示人的健康状态，分为 3 等：好、中、差，分别表示为 Y=0、Y=1 和 Y=2。在某地区随机抽样调查得到 X 与 Y 的联合分布如下表所示。
1/ 2 1/ 6 1/ 3
2 / 6 1/ 3 0
则有：Y (Y1 , Y2 , Y3 ) K ( X1 , X 2 , X 3 ) KX ，其中 X ( X1 , X 2 , X 3 ) 是三维正态随 机变量。而正态随机变量的线性变换仍为正态随机变量，即 Y (Y1,Y2,Y3) 是三维正态随机 变量，其均值向量与协方差矩阵为： Y K X (0,0,0) ， Y K Y K I 。 所以有 Y1 , Y2 , Y3 相互独立并且都服从标准正态分布。 例 5 假设 E ( X | Y ) EX ，证明随机变量 X 与 Y 不相关。
苏科版八年级物理(上册)课课练[1]
![苏科版八年级物理(上册)课课练[1]](https://img.taocdn.com/s3/m/890e4d004a7302768f993902.png)
第一章 声现象一、声音是什么1．小明将手放在喉咙处，讲话时，感觉到手有点“麻”，说明声音是由于物体 产生的，发声的声带 （是/不是）声源.2．如图1-1所示的“土电话”由两个圆纸盒和一根棉线组成，只要将棉线绷紧，两人就可以通话了，“土电话”是利用________ _原理制成的. 3．声音是由物体的_____产生的，声音的传播需要_______，真空中不能传播声音. 声音不仅可以在空气中传播，还可以在液体和固体中传播，但传播速度不一样，当温度相同时，在_____中传播速度最大.4．发声体振动时压缩了附近的空气形成 相间的波动，并由近及远地向四周传播，这就形成了 .5．宇航员在太空舱中可以直接对话，但在飞船外作业时，他们之间不能直接对话，必须借助电子通信设备进行交流.其原因是 ( )A ．用通信设备对话是为了方便B ．声音的传播需要介质C ．太空中噪声太大D ．声音只能在地面上传播6．以下是关于被埋在城市废墟里的人自救的一些措施，其中最有效的是（ ）A ．大声呼救B ．静等营救人员前来营救C ．见缝隙就钻，从废墟里爬出来D ．硬物敲击预制板或墙壁，向营救人员求救7．将正在发声的手机、电铃或接通电源的音乐芯片悬挂在广口瓶内，如图1-2所示，当把瓶内的空气抽出时，声音会逐渐变小，但始终能听到声音.原因是（ ）A ．声源发声太强B ．瓶内已被抽成真空，真空亦能传声C ．声源离广口瓶太近D ．瓶内仍有少量空气，悬挂声源的固体亦能传声〖课外练习〗1．声音是由发声体的 而产生，人类靠 振动发声的.如图1-3，人耳能听到的鼓声，是由 的振动而产生.水中的鱼会被岸上的人的说话声吓跑，这是因为声音先经 传播到水中，然后再经过 传播而被鱼听到.2．《黄河大合唱》中有一句歌词：“风在吼，马在叫，黄河在咆哮”.这句歌词中的声源分别是 、 、 .3．声音是以 的形式向四周传播的，声音具有 .4．如1-4图是小明所做的一个听声的实验，他将衣架悬空挂在细绳的中央，请小华用铅笔轻轻敲打衣架，使声音通过___________传入他的耳朵.接着，小明将细绳绕在手指上,再用手指堵住双耳来听敲打衣架的声音，通过比较发现,固体传声的本领比空气________(强/弱5．将一支点燃的蜡烛放在喇叭的前方，当喇叭中发出较强的声音时，可以看到烛焰在，这说明：声波具有 .6．能说明液体可以传播声音的现象是（ ）A ．在岸上的人听到河水流动的声音B ．古代枕着牛皮箭筒睡在地上的士兵，能听到夜袭敌人的马蹄声C ．我们能听到波浪排击礁石的声音D ．潜水员能听到岸上的讲话声7．手拨动琴弦，便能听到悦耳的声音，这声音是下列哪个物体振动产生的（ ）A ．手指B ．琴弦C ．空气D ．弦柱8．看图说理：（1）观察图甲得出的结论是： ；（2）观察图乙得出的结论是： .如果按照上图去设计声音传播的实验，有的同学提出这样的想法，左图中怎么知道鱼是听到拍手的声音把鱼吓跑的，而不是看到拍手的动作被吓跑的；中图敲桌面的声音是通过空气传入人耳？还是通过桌子传入人耳？或者两者都有？针对这些疑问，怎样改进实验，使它更完善.（3） ；（4） .9．某课外探究小组做了如图1-6所示的实验：敲响右边的音叉，结果发现左边完全相同的音叉也会发声，并且把泡沫小球弹起，这是为什么呢？假如在月球上做此实验，我们能看到这种现象吗？为什么？二、声音的特征〖补充例题〗 1．东林书院名联“风声、雨声、读书声，声声入耳”表明声音可以在 中传播；用小提琴和二胡演奏“二泉映月”乐曲时，我们可以根据声音的 不同来加以辨别.2． 电子琴能模仿各种乐器发出的声音，在技术上要解决的关键是能模仿各种乐器发出声音的（ ）A ．音调B ．音色C ．响度D ．音色和音调3． 我们平时所说的 “女高音”、“男低音”，这里说的“高”和“低”指的是（ ）A ．音色B ．音调C ．响度D ．速度4．昆虫飞行时翅膀都要振动,蝴蝶每秒振翅5～6次,蜜蜂每秒振翅300～400次,当它们都从你身后飞过时,凭你的听觉（ ）A.能感到蝴蝶从你身后飞过B.能感到蜜蜂从你身后飞过C.都能感到它们从你身后飞过D.都不能感到它们从你身后飞过 〖课内练习〗1．拿一张硬纸片，让它在木梳齿上划过，一次快些，一次慢些，发出声音的__________不同，这是由于_______ ___.2．请在下列各小题中选填声音的特征：“震耳欲聋”说明声音的 ；“悦耳动听”说明声音的 ；“脆如银铃”说明声音的 .3．在听熟人打电话时，从声音的特征上，容易辨别对方是谁，其主要原因（ ）A ．不同的人说话时，声音的音调不同B ．不同的人说话时，声音的频率不同C ．不同的人说话时，声音的音色不同D ．不同的人说话时，声音的响度不同甲 乙图1-54．下列说法正确的是 （ ）A ．收音机中的音量开关是调节音调的B ．收音机中的音量开关是调节响度的C ．一个人音色是不会改变的D ．声音传播的速度是不会改变的5．正在拉二胡的一位同学不断用手指去控制琴弦，这样做的目的是（ ）A ．使二胡发出不同的音调B ．为了获得更好的音色C ．为了获得更大的响度D ．阻止琴弦振动发声6．如图1-7，医生用听诊器检查病人的心脏跳动，主要是为了（ ）A ．适当改变心脏跳动频率，使音调变高B ．缩短和病人之间的距离，增大声音的响度C ．减小声音的分散，增大声音的响度D ．可以增大心脏跳动振幅，使响度增大7．图1-8中，老师用同样的力吹一根吸管，并将它不断剪短，他在探究声音的( )A ．响度与吸管长短的关系B ．音调与吸管材料的关系C ．音调与吸管长短的关系D ．音色与吸管材料的关系8．小明同学在家里找到了一根废钢锯条，请帮助小明设计一个声学实验来验证声音的音调与什么因素有关。
软件工程第1章习题
软件工程第1章例题分析与解答一、填空题1.软件与物质产品有很大的区别，软件是一种____逻辑___产品。
2.软件工程是一门综合性交叉学科，计算机科学着重于理论和原理，软件工程着重于___建造一个软件系统____。
3.概要设计主要是把各项功能需求转换成系统的__体系结构______。
4.最基本、应用广泛、以文档为驱动、适用于开发功能明确的软件项目生存期模型是__瀑布模型_____。
5.简单实用、应用广泛、技术成熟的开发方法是__结构化方法______。
二、选择题1.同一软件的大量软件产品的生产主要是通过( B )而得到。
A.研究B.复制C.开发D.研制2.作坊式小团体合作生产方式的时代是( C )时代。
A.程序设计B.软件生产自动化C.程序系统D.软件工程3.软件工程与计算机科学性质不同，软件工程着重于( C )。
A.理论研究B.原理探讨C.建造软件系统D.原理的理论4.将每个模块的控制结构转换成计算机可接受的程序代码是( A )阶段的任务。
A.编码B.需求分析C.详细设计D.测试5.软件生存周期中时间最长的是( D )阶段。
A.需求分析B.概要设计C.测试D.维护一、填空题答案1.逻辑2.建造一个软件系统3.体系结构4.瀑布模型5.结构化方法二、选择题答案1.B2.C3.C4.A5.D第1章自测题及参考答案一、名称解释1.软件2.文档3.软件工程4.软件生存周期5.软件工程过程6.软件生存周期模型7.软件开发方法8.软件工具二、填空题1.构成一个完整计算机系统的两部分是硬件与_____软件___。
2.程序设计时代的生产方式是___个体手工劳动_____。
3.软件工程涉及到几个学科，它是一门__综合性交叉___学科。
4.软件开发划分的各阶段任务尽可能独立，同一阶段任务性质尽可能_____相同___。
5.将软件生存周期各个活动规定为依线性顺序联接的若干阶段的模型是_瀑布_______模型。
6.喷泉模型是一种以用户需求为动力，以____对象___为驱动的模型。
第一章会计概述例题及详细讲解
【例题2·单选题】下列不属于会计核算的环节的是（）。
A.确认B.计量C.报告D.分析『正确答案』D『答案解析』会计核算职能是会计的基本职能之一，包括对特定主体的经济活动进行确认、计量和报告。
选项D 属于会计拓展职能中的“参与经济决策”职能。
【例题3·多选题】下列各项中，属于会计监督合理性审查内容的有（）。
A.检查各项财务收支是否符合特定对象的财务收支计划B.检查各项财务收支是否符合内部控制制度要求C.检查各项财务收支是否执行了国家的各项方针政策D.检查各项财务收支是否有利于预算目标的实现『正确答案』ABD『答案解析』合理性审查是指检查各项财务收支是否符合特定对象的财务收支计划，是否有利于预算目标的实现，是否有奢侈浪费行为，是否有违背内部控制制度要求等现象，为增收节支、提高经济效益严格把关。
选项C，是否执行国家的各项方针政策属于合法性审查。
【例题4·多选题】下列有关会计基本职能的叙述中，正确的有（）。
A.会计核算是会计监督的基础B.会计监督是会计核算的质量保障C.会计核算与会计监督是相互抵触的D.会计核算与会计监督是相辅相成的『正确答案』ABD『答案解析』会计核算是会计监督的基础，会计监督是会计核算的质量保障，二者是相辅相成、辩证统一的。
【例题5·单选题】根据财务报告等提供的信息，对生产经营过程及其发展趋势进行判断、预计和估测，找到财务方面的预定目标，作为下一个会计期间实行经济活动的指标。
这属于（）职能。
A.参与经济决策B.会计监督C.预测经济前景D.评价经营业绩『正确答案』C『答案解析』题干是对会计预测概念的表述，属于会计拓展职能中“预测经济前景”职能。
【例题6·单选题】会计目标要求会计信息应能充分反映（）受托责任的履行情况，帮助委托者评价企业经营管理和资源使用的有效性。
A.上级部门B.企业管理层C.企业财务人员D.企业各部门『正确答案』B『答案解析』现代企业的所有权和经营权相分离，企业管理层受委托人之托经营和管理企业。
热力学习题答案
第1章 《热力学》习题解答1-1若一打足气的自行车内胎在7.0C 时轮胎中空气压强为54.010Pa ⨯，则在温度变为37.0C 时，轮胎内空气压强为多少？（设内胎容积不变）[解]：轮胎内的定质量空气做等容变化状态1 Pa P K T 511100.4,280⨯== 状态2：?,28022==P K T 由查理定律得Pa Pa P T T P T T P P 55112212121043.4100.4280310⨯=⨯⨯==⇒= 1-2 氧气瓶的容积为233.210m -⨯，其中氧气的压强为71.310Pa ⨯，氧气厂规定压强降到61.010Pa ⨯时，就应重新充气，以免经常洗瓶. 某小型吹玻璃车间平均每天用去30.40m 在51.0110Pa ⨯压强下的氧气，问一瓶氧气能用多少天？（设使用过程中温度不变）[解]：设氧气瓶的容积为320102.3m V -⨯=，使用过程的温度T 保持不变使用前氧气瓶中，氧气的压强为Pa P 71103.1,⨯= 根据克拉帕龙方程nRT PV =得： 使用前氧气瓶中，氧气的摩尔数为RTV P n 011,=氧气压强降到Pa P 62100.1,⨯=时，氧气瓶中，氧气的摩尔数为RTV P n 022,=所以能用的氧气摩尔数为()21021,P P RTV n n n -=-=∆ 平均每天用去氧气的摩尔数RTV P n 333,=故一瓶氧气能用的天数为()()5.91001.140.010113102.3,562332103=⨯⨯⨯-⨯=-=∆=-P V P P V n n N 1-3在湖面下50.0m 深处（温度为4.0C ），有一个体积为531.010m -⨯的空气泡升到湖面上来. 若湖面的温度为17.0C ，求气泡到达湖面的体积.（取大气压为50 1.01310Pa p =⨯）[解]：空气泡在湖面下50.0m 深处时，3511100.1,277m V K T -⨯==Pa P gh P 5530110013.610013.15010100.1⨯=⨯+⨯⨯⨯=+=ρ气泡到达湖面时，Pa P K T 522100.1,290⨯==由理想气体状态方程222111T V P T V P =得： 35351122121029.6100.12772900.1013.6m m V T T P P V --⨯=⨯⨯⨯=⋅=1-4如图所示，一定量的空气开始时在状态为A ，压力为2atm ，体积为l 2, 沿直线AB 变化到状态B 后，压力变为1 atm ，体积变为l 3. 求在此过程中气体所作的功。
高中生物第1章 人体的内环境与稳态人教版必修三
《生物必修3》第1章一、基础知识填空1．单细胞生物〔如草履虫、变形虫〕可以与环境进行物质交换；多细胞生物体内细胞必须通过与外界进行物质交换。
内环境是指，即。
2．体液包括细胞外液〔主要有〕和细胞内液〔约占〕。
细胞外液是细胞所处的内环境，如红细胞的内环境是，毛细胞血管壁细胞的内环境是，大多数组织细胞的内环境是。
三种细胞外液及细胞内液之间的物质转化关系〔如以下图〕。
3．内环境的理化性质主要有三方面。
人体血浆中是维持血浆渗透压的主要因素，人体血浆渗透压约为770KPa；细胞外液的渗透压主要由维持(临床上以N a C l用作生理盐水)；血浆pH为。
人体血浆pH的维持与血浆中含有的等离子有关。
4．假设人体长期供应不足或因肾小球肾炎引起蛋白尿、过敏反应中毛细胞血管通透性增加、淋巴循环受阻等，可能导致血浆蛋白质减少，血浆渗透压，导致组织液，出现组织水肿现象。
5．是机体进行正常生命活动的必要条件，目前普遍认为，内环境稳态的主要调节机制是。
内环境稳态是的结果，是指内环境的各种化学成分和理化性质保持，是一种。
6．多细胞动物〔包括人〕体内细胞与外界物质交换过程〔补充完整〕组织液毛细淋巴管壁细胞组织细胞膜外界环境注：补充完整左图．〔1〕透出毛细胞血管壁的某些小分子蛋白质及由小肠吸收的脂质不能重新透回血浆。
这类物质只能由淋巴循环送回血浆。
〔2〕组织液成分只能透入毛细淋巴管，不能由淋巴透回。
外界环境中的消化系统呼吸系统二、典型例题分析1．以下关于内环境及其稳态的表达中·正确的选项是A．人体代谢中的生物化学反应主要发生在细胞内B．血红蛋白、递质、激素、葡萄糖和CO2都是内环境的成分C．内环境稳态的实质是内环境的渗透压，温度和pH保持不变D2．血液、组织液、淋巴三者关系示意图如右图所示，指出图中哪个箭头表示是错误的A．①血浆B．②组织液C．③水D．④红细胞三、课后习题训练1．医院里医生给病人输液的生理溶液有两种，0.9%的NaCl溶液和5%的葡萄糖溶液，如果把红细胞分别置于这两种溶液中，你预测将会A．前者正常，后者皱缩B．前者皱缩，后者正常C．均正常D．均皱缩2．血浆中的水分来自A．组织液B．血浆、消化道C．淋巴、组织液D．消化道、组织液、淋巴3．稳态是机体进行正常生命活动的必要条件，当稳态遭到破坏，必将引起A．酶促反应速率的加快B．儿童患佝偻病C．细胞代谢紊乱D．成年人患肌无力病4．以下各组物质中全是内环境成分的是：A．O2、CO2、血红蛋白、H+B．过氧化氢酶、抗体、激素、H2OC．血浆蛋白、Ca2+、载体D．Na+、HPO42-、葡萄糖、氨基酸、尿素5．维持血液PH恒定的缓冲物质A．都是由强酸和强碱盐组成的 B．都是由弱酸和弱碱盐组成的C．都是由强酸和弱碱盐组成的 D．都是由弱酸和强碱盐组成的6．有关内环境稳态的实质的描述是A ．是仅在神经和体液共同调节下实现的B ．各个器官系统协调活动的结果C ．温度、PH 值等理化性质呈动态平衡D ．是体内细胞生活不可缺少的条件7．〔多项选择〕右图是人体局部内环境示意图。
电路分析基础例题集(第1-5章)讲解
（b）图中的 、 为关联参考方向，故其功率为
所以
（c）图中的 、 为非关联参考方向，故其功率为
所以
例1.3如图1.3所示电路，已知 ，求 和 。
图1.
解题思路：可由电容的 求出电容电流，由欧姆定律求出电阻电流，然后由后面将要介绍的基尔霍夫电流定律（ ）求出电感电流 ，再由电感的 求出电感电压，最后由基尔霍夫电压定律（ ）求出 。
图2.14 图2.13的等效变换电路
由图2.14可得
例2.10用电源等效变换法求图2.15所示电路中的电流 。
图2.
解题思路：将待求支路左边的电路进行电源等效变换，即可求出电流 。
解：其电源等效变换电路如图2.15所示，由欧姆定律得
例2.11求图2.16（a）所示电路的输入电阻 。
图2.
解题思路：在 端外加一个电压源，用“ ”法求取。为方便计算，假设电压源的极性与 一致，如图2.16（b）所示。
由图2.11可得
各元件的功率为
电压源的功率为
电流源的功率为
电阻的功率为
电阻的功率为
电阻的功率为
因为
所以整个电路的功率是平衡的。
例2.9用电源等效变换法求图2.13所示电路中的电流 。
图2.13
解题思路：根据本题的电路结构，只需将待求支路两边的电路进行电源等效变换，即可求出电流 。
解：将图2.13所示电路进行电源等效变换，如图2.14所示。
图1.9
解题思路：先用 求出 的电压 ，再用电阻功率公式求出 ，最后由欧姆定律和 求出 和 。
解： 、 和 标注如图1.9（b）所示，由题知
，
，
，
例1.10如图1.10（a）所示电路，求 、 和 的值。
电工学复习
本文由402226275贡献doc文档可能在WAP端浏览体验不佳。
建议您优先选择TXT，或下载源文件到本机查看。
选择 20 分填空 10 分计算 70 分第一章直流电路1、理想电压源的（）由外电路决定；理想电流源的（）由外电路决定。
（a）两端电压（b）输出电流2、图示电路中，提供功率的电源是( (a)理想电压源 (b)理想电流源R 2? IS 2A + US 6V（c）两端电压和输出电流 )。
(c)理想电压源与理想电流源3、图示电路中产生功率的元件是。
4、图示电路中，当 R1 增加时，电压 U2 将( (a)变大R1 + IS R2 U2 -)。
(b)变小(c)不变5．在下图电路中，E =2V, R =1Ω。
当 U 为 1V 时，求 I。
a+ +UR R_UI+E_ _b6、对具有 b 条支路 n 个结点的电路，应用基尔霍夫电流定律只能得到（程；再应用基尔霍夫电压定律又能得到（）个独立方程。
）个独立方7、在图示电路中，E =16V， R1 = R2 = R 3 = R4；Uab = 10V。
除去理想电压源后 Uab =? （除去理想电压源即断路）+EaR1IR2IbR3R48、图示电路中，已知：US= 8V，IS1= 2A，IS2= 4A，R1= 4?，R2= 5?，R3= 6?。
用戴维南定理求电流 I，说明电压源是发出还是吸收功率，并计算其数值。
.R2 R1 IS 1I R3 + US IS 2..－第二章正弦交流电路1、已知某正弦电压在 t=0 时为 220V，其初相位为 30o，则它的有效值为（2、对应于u= 311sin(ωt +30°)V 的有效值相量表达式为 V。
）V。
& 3、在 RLC 串联的交流电路中，若电源电压 U = 220∠0 o V，XL=XC=80?，R=22?。
则 P=（）W，cos? =（）。
4．已知复阻抗抗角 ?。
Z ∠? = Z 1 ∠? 1 + Z 2 ∠? 2 ，其中， Z1 = R1 + jX1 ， Z 2 = R2 + jX 2 ，求阻5、在图示正弦交流电路中，各支路电流有效值为 I1＝1A，I2＝1A，I3＝3A，则总电流 i 的有效值 I 为( (a)5Ai + u i1 R i2 L i3 C)。
补充 第1章例题与习题
补充 例题与习题【例1-3】如图1—19a 所示刚架。
在B 处受一水平力刚架自重不计，尺寸如图所示。
试分别用几何法与解析法求解刚架在固定铰链A 和活动铰链D 处的约束反力。
【解】(1)几何法 以刚架为研究对象，取出分离体。
画出主动力FP 和约束反力FND(垂直于支承面，沿DC 方向)，FP 与FND 相交于c 点；根据三力平衡汇交定理，FNA 的作用线必通过C 点，如图l-19b 所示。
最后作力多边形求未知力F ND 和F NA 。
选力比例尺1cm=10kN ，任取一点a ，从a 作FP 的平行线段ab ，并取ab=FP ，再从a 和b 分别作FNA 和FND 的平行线相交于C ，于是得到封闭的力三角形abc ，如图1．19c 所示。
根据力多边形法则，按各力矢量首尾相接的顺序，得出FNA 和FND 的指向。
量出FNA 和FND 的长度经比例尺换算得(2)解析法 以刚架为研究对象，画出受力图如图1-19b 所示。
b)选坐标系xAy 。
列平衡方程︒==565.26)8/4(arctg α由式(1-8)得 36.22565.26cos /==P NA F F KN 由式(1-9)得 kN F F NA ND 10565.26sin 36.22sin =⨯==α解得：均为正值，表示所假设的方向与实际指向相同。
【例1-4】增力机构如图1—20a 所示，已知活塞D 上受到液压力F P =300N ，通过连杆BC 压紧工件。
当压紧平衡时，杆AB 、BC 与水平线的夹角均为α=8°。
不计各杆自重和接触处的摩擦，试求工件受到的压力。
【解】根据作用力与反作用力定律，工件所受的压力可通过求工件对压块的反力F Q 而得到，因已知力F P 作用在活塞上，而活塞杆与压块间有一根二力杆相联系，所以必须分别研究活塞BD 和压块C 的平衡才能解决问题。
图1-20增力机构受力分析(1)取活塞杆BD为研究对象作用在活塞上的力有液压力F P和二力杆AB、BC的约束反力沿着各自杆的中心线，其指向假设如图1-20b所示。
第一章 地球运动知识点例题课件 2022-2023学年高二地理人教版(2019)选择性必修1
黄赤交角及其影响 The angle between yellow and red and its influence
探究四
太阳直射点的移动轨迹图
夏半年
春分
3月21日前后
夏至
6月22日前后
春分
次年3月21日前后
秋分
9月23日前后
冬至
12月22日前后
冬半年
太阳直射点的移动轨迹图
23°26′N 0° 23°26′S
日出/日落
（1）无极昼现象的地区：找准太阳在地平线上的方向
直射北半球：东北升、西北落 直射赤道：正东升、正西落 直射南半球：东南升、西南落
纬度越高，越偏北 纬度越高，越偏南
A点：6.22 vs 5.22 都直射北半球 但 6.22太阳更偏北
直射点越接近北回归线，各地日出/日落越偏北 直射点越接近南回归线，各地日出/日落越偏南
线速度 Linear Velocity
考虑海拔对线速度的影响 • 在纬度相同情况下，海拔越高的地方自转线速度越大。
A2 A1 O
线速度 Linear Velocity
读地球公转轨道局部图和某日光照示意图”（阴影表示夜半球，度数 为经度，箭头表示地球公转方向）
靠近赤道，线速度越大
1、比较图中甲乙丙丁戊五地自转线速度，正确的是（ ） A.丙<甲<乙<戊<丁 B.丁<戊=乙<甲<丙 C. 丙<甲<乙=戊<丁 D.丁<戊<乙<甲<丙
A.1/2 东八区B.2/3
C.3/4
D.1
9.15 20时
1、求0:00经度 118800°
2、求180°地方时 24时
电工电子第1章
2
3
t/ms
1.2.4 电压源
1、理想电压源 、
e + – + E –
图形符号
i + E – + u – 外 电 路 E i u
O
理想电压源的伏安特性
+
+ R0 U
2、实际电压源模型 、
R0 u e – 或
+ E –
–
I RO
U E IR0 U I O
+
U
+ –
RL
E
–
U = E − IRo
伏安特性
b
E2
c
Va = − E1 = −5V, Vb = 0V, Vc = E 2 = 8V U ab = Va − Vb = (−5 − 0)V = −5V U bc = Vb − Vc = (0 − 8)V = −8V
电位计算补充例题
结论：从上述计算结果可以看到， 结论：从上述计算结果可以看到，电位与参考点的 选取有关，参考点不同，各点电位不同； 选取有关，参考点不同，各点电位不同；而电压与 参考点的选取无关，参考点不同， 参考点的选取无关，参考点不同，两点之间的电压 不变，但电压的参考方向不同，则符号不同。 不变，但电压的参考方向不同，则符号不同。
15
u(t ) / V
1 0.5 1.5 2 2.5 3 t/ms
(b)
u(t )
–
R
C
1 0 –15 0.5 1.5
2 2.5
3 t/ms
(a)
i C (t ) / m A
u (t ) iR (t ) = R
du ( t ) iC ( t ) = C dt
2021 第一章 习题班总论
第一章总论【例题·单选题】（2020年）下列规范性文件中，法律效力最高的是（）。
A.全国人民代表大会常务委员会通过的《中华人民共和国劳动合同法》B.财政部发布的《会计基础工作规范》C.国务院发布的《中华人民共和国个人所得税法实施条例》D.全国人民代表大会通过的《中华人民共和国宪法》【正确答案】D【答案解析】宪法是国家的根本大法，具有最高的法律效力。
A选项属于法律；B选项属于部门规章；C选项属于行政法规。
【例题·单选题】（2020年）甲公司和乙公司签订购买20台办公电脑的买卖合同总价款为20万元，该法律关系的主体是（）。
A.甲公司和乙公司B.20台办公电脑C.20万元价款D.买卖合同【正确答案】A【答案解析】法律关系的主体是指参加法律关系，依法享有权利和承担义务的当事人。
【例题·单选题】（2020年）下列法律事实中，属于法律事件的是（）。
A.火山喷发B.书立遗嘱C.赠与房屋D.登记结婚【正确答案】A【答案解析】法律事件是指不以当事人的主观意志为转移，能够引起法律关系发生、变更和消灭的法定情况或者现象。
法律行为是指以法律关系主体意志为转移，能够引起法律后果，即引起法律关系发生，变更和消灭的人们有意识的活动。
（1）选项A：属于法律事件；（2）选项BCD：属于法律行为。
【例题·单选题】（2020年）下列法律事实中，属于法律行为的是（）A.突发地震B.书立遗嘱C.火山喷发D.台风登陆【正确答案】B【答案解析】选项ACD：属于法律事件。
【例题·单选题】（2018年）下列各项中，属于法律行为的是（）。
A.流星陨落B.签发支票C.火山爆发D.台风登陆【正确答案】B【答案解析】选项ACD，属于法律事件。
【例题·单选题】（2020年）下列纠纷中，可以适用《仲裁法》解决的是（）。
A.韩某与杨某的确认收养关系纠纷B.潘某与李某的监护权纠纷C.孙某与郑某的离婚纠纷D.张某与王某的网络购物合同纠纷【正确答案】D【答案解析】仲裁的适用范围：平等主体的公民、法人和其他组织之间发生的合同纠纷和其他财产权益纠纷。
流体力学 第1-2章补充例题
∴
3
4
2、 如图所示,已知h1=20mm，h2=240mm， h3=220mm，求水深H。
p0 h1 H h3 h2 H2O Hg
真空表读数pv=19600Pa L
解：以表压力计算：
p0 Hg h1 p0 H h2 Hg h3
已知如图，试求： ①三测压管L、M、 N的液面高程； ②h?
2 2
PA总 Px Pz 0 2 10900 2 10900N
2 2
17
PC总 的作用线通过球心且与水平线的夹角为： P 2560 arctan Z arctan 7.58 Px 19230
18
9、曲面形状为3/4个圆柱，半径r＝1m，宽度为B＝1m，位于水面下h＝ 3m深处，求曲面所受的液体总压力。 解：根据对称性，bc和cd曲面受水平分力相 抵消，整个曲面abcd受水平分力大小等于 ab曲面所受的水平分力，即：
A
因为： z s 2 z s1 h
2 gh 所以： 0 2 2 r2 r1
15
L p A hA H tan 17755Pa 2 L pB hB H tan 5760Pa 2
另一种解法：根据
2
3 1 4 d h Pz H d 2 2 4 2 3 2 3 1.5 2 1 4 1 9800 2.5 1 2 4 2 3 2 10900N
解：因为各油液厚度很小，所以流速分布可视
牛顿内摩擦定律 液式测压计
重要计算
相对平衡 平面、曲面受力问题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 R1 ( 3) 3 5V R1 1 4
e
（ 4） 1 ( 3) 3 1 R 2 3 0 R2 10
在回路aecda中，利用KVL和欧姆定 律
图1.22
返回 上一节 下一节 上一页 下一页
基尔霍夫定律
求电压 u ed , u b d
[例1.1] 在图1.6(a)中，选c点为参考 点时，已知 V a 30 V , V b 5V , V d 10 V 求：(1)
U ab , U ad , U b c
(2)选择b点为参考点时，求其他 三点的电位值。
解
(1)
以C点为电位参考点
U ab Va Vb 30V 5V 25V
1.8(a)
U4 U5
I1
1
U1
4
I3
5
I2
解：
为负值的电压、电流，表明其实际 方向与参考方向相反。
U2
3
U3
2
电路图 1.8(b)标出了元件的实 际方向，电压也可以用箭头 表示极性由“+”指向“-”
(b)
U4
1.2 电路的基本物理量 功率 例1.3 利用图1.8(a)计算各功率： U
5
4
I1
5
I3
2、求开路电压
I1 20 10 8 10 0 . 556 m
U oc 15 . 56 V
返回
4-6 戴维南定理
a I 8K 8K
RO
10 8 10 8
4 . 45 K
+ + - -
10K 10K + + 12KV
上一节
下一节
上一页
下一页
1.3 理想电路元件 理想电流源
例
计算图示电路各元件的功率。
i 解
2A
i iS 2A
5V
u
_
_
满足：P（发）＝P（吸）
返回
+
+
u 5V
发出
P2 A iS u 2 5 10W
P V uS i 5 (2) 10 W 吸收 5
上一节
下一节
上一页
下一页
1.4 例1.7
基尔霍夫定律 (KCL)
I 2 1A
，
图1.18中已知 I 6 4 A 求电流 I 1 ,
I 4 3A
I1
I2
I3
1
I4
I3 , I5
的值。
I6
[解] :
对节点1有KCL方程：
I1 I 6 I 4
，
2
I5
I1 I 4 I 6 3 4 1A I1 I 3 I 2
I2
解
P U1I1 20 (2)W 40W（提供） 1
U2
1
U1
3
2
U3
P U 2 I 2 14 1W 14W（提供 2
1.8(a)
P U 3 I 3 12 3W 36W（吸收） 3
P U 4 I1 8 (2)W 16W（吸收） 4
求各支路电流。
[解] : 首先设定各支路电流的参考方向 如图1.19所示，由于U U 10 V 根据欧姆定律，有
ab S
，
，
I1 I2
U ab R1 U ab R2
10
A 5A
图1.19 例1.8电路图
2 10 A 2A 5
由KCL，节点a的电流方程有
I1 I 2 I 3 0 I 3 I1 I 2 5A (2)A 7A
∵ U ab 25V ∴ U ab Va 0 Va 25V ∵ U ad Va Vd 40V ∴
V d V a 40 25V 40 V 15V
结论
∵
U bc V b V c 0 V c 5V
∴
V c 5V
电路中电位参考点可任意选择；参考点一经选定，电路中 各点的电位值就是唯一的；当选择不同的电位参考点时， 电路中各点电位值将改变，但任意两点间电压保持不变。
p ui 8 sin t 2 sin t 16 sin t W
2
从0到t期间电阻吸收的电能(W)为
W
t 0
1 1 2 p d 1 6 sin d 1 6 sin 2 0 4 2 0
t
t
8 t 4 sin 2 t J
返回
U ad Va Vd 30V (10V) 40V
U bc V b V c 5V 0 V 5V
图1.6(a)
返回 上一节 下一节 上一页 下一页
1.2 电路的基本物理量 电压
解
(2)
以b点为电位参考点 V 0 b
U ab Va Vb , 任意两点的电压不变
对封闭面有：
3
I 3 I 2 I1 1 1 0A （ ） （ ）
对节点3有KCL方程
I5 I3 I6 I 5 I 6 4A
返回
上一节
下一节
上一页
下一页
1.4 例1.8
基尔霍夫定律 (KCL)
R2 5
R 在图1.19所示电路中， 1 2
U S 10 V
(2) u S1 10 V u S 2 5 V (3)
解：
u S1 2 0 co s t V
u S 2 1 5 sin 2 t V
求电压u
画出分电路图
＋
u H 1u S 1 u H 2 u S 2 2 3 1 2 3 0 .5 2 0 .5
根据叠加定理得
isc i 2 i3 iS 2
返回
上一页
下一页
（2）再求 R o
( R1 R 2 ) R 3 R1 R 2 R 3
Ro
(3)画出诺顿等效电路
返回
上一页
下一页
【例1】 汽车照明用12V蓄电池来供60W车灯， 若蓄电池的额定值为 (安时)，求蓄电池 kW h 的能量？ 解： P / U 60 / 12 5A I 100 A h (安时)表明提供5A可使用20h，因 此储存能量为
W (60 20 60 60)J 4.32 10 J
返回 上一节 下一节 上一页 下一页
1.4
基尔霍夫定律
R1 , R 2
例1.10 在图1.22所示电路中， 求 [解] : 在节点a，利用KCL
和电压 u ed , u b d
I 1 5A ( 4)A 1A
在节点e，利用KCL
，
I 2 1A ( 4)A 3A
，
在回路becb中，利用KVL和欧姆定 律 a
PE 2 E 2 I 2 8 ( 1.25) W 10 W
(负值表示吸收功率，即电池充电)
1.2 电路的基本物理量 电压 4. 电位
为了分析的方便，常在电路 中选某一点为参考点，把任 一点到参考点的电压称为该 点的电位(potential)， 参考点的电位一般选为零， 所以，参考点也称为零电位 点。
在假想回路ecde中，利用KVL和欧姆定律
u ed ( 3) 3 1 R
， ，
2
9 V 1 0 V 1V u b d 1 R u ed
1
1 4 V 1V 1 5 V
图1.22
返回 上一节 下一节 上一页 下一页
叠加定理的应用
已知
(1)
u S1 5V u S 2 1 0 V
- -
4、将待求支路接入等效电路， 由此电路计算待求量I
I a b
12K
3、求等效电阻
a
4.45K 8K Ro 10K
15.56V
+
I 15 . 56 4 . 45 12
0 . 946 m
b
例11
求图 (a)所示单口网络的诺顿等效电路。
解:
（1）先求 i s c
R1 R1 R 2 iS1 uS R3 iS 2
U bd R 3 I 3 1 2 0 .7 5 V 9 V
V b U bd 9 V
故 (2)
U ab R1 I 1 0 .5 2 V 1V
U bc R 2 I 2 0.8 ( 1.25)V 1V
（3） PE1 E1 I 1 10 2 W 20 W
6
【例2】 图1.6电路中，d为电位参考点，各元件的参数值及电压、 电流的参考方向如图所示，并知 I 1 2 A ， I 2 1.25A ， I 3 0.75A ， I 3 0.75A 。试求：(1) a、b、c各点的电位 V a 、 V b 、 V c ；(2) PE 1、 PE 2 。 电压 U ab 、 U b c ；(3) 输出的功率 解：(1) V a E 1 1 0 V V c E 2 8 V ， ，根据欧姆定律
u
R2 R4
R4 R2 R4
iS
( u S R 2 iS )
返回 上一页 下一页
u u u
例10、电路如图，求通过电阻R3的电流I 。
a I 8K 10K
+
20V
+ -
12K
+
R3
8K I1
20V
10K
+
10V
Uoc
10V
-