【学习课件】第四章波形信源和波形信道
合集下载
波形信源和波形信道
电子信息工程学院
信息论
4 连续信道和波形信道的分类
若多维连续信道的传递概率密度函数满足
p( y | x ) p( yi | xi )
i 1 N
则称此信道为连续无记忆信道。 即:若连续信道在任一时刻输出的变量只与对应时刻的输入变 量有关,与以前时刻的输入,输出变量无关,也与以后的输入变量 无关,则此信道为无记忆连续信道。 连续信道任何时刻的输出变量与其他任何时刻的输入,输出变量都 有关。则此信道称为连续有记忆信道。
电子信息工程学院
信息论
4 连续信道和波形信道的分类
输入X 信道
+
噪声n
输出Y
p( x)dx
因此,在加性信道中,Y=X+n ,条件熵为
h( X | Y ) p( xy ) log( y | x)dxdy
R
p( y | x) log p( y | x) dy
XN
Y Y1Y2
波形信道
YN
P( y1 y2
yN | x1 x2
xN )
图4.7 波形信道转化成多维连续信道
电子信息工程学院
信息论
4 连续信道和波形信道的分类
按噪声统计特性分类 1.高斯信道 信道中的噪声是高斯噪声。高斯噪声是平稳遍历的随机过程,其瞬时 值的概率密度函数服从高斯分布(即正态分布)。 一维概率密度函数为 1 ( x m)2 p ( x) exp( ) 2 2 2 2
0 n
信息论
4 连续信道和波形信道的分类
3.高斯白噪声信道
一般情况把既服从高斯分布而功率谱密度又是均匀的噪声称为高斯 白噪声。关于低频限带高斯白噪声有一个很重要的性质,即低频限带高 斯白噪声经过取样函数取样后可分解成N(=2FT)个统计独立的高斯随 机变量(方差为 N0 / 2 ,均值也为零)。 低频限带高斯白噪声可以看成是无限带宽的高斯白噪声通过一 个理想低通滤波器后所得。如果理想低通滤波器其带宽为F 赫兹,那么 它的传递函数的频率响应为 1 2 F 2 F K ( ) 其他 0
信息论第4章(波形信源和波形信道)ppt课件

05-06学年上 2 .
4.1波形信源的统计特性和离散化
随机变量 X
随机矢量X(X1X2 XN)
随机过程{ x ( t ) }
05-06学年上 3 .
表4.1
消息(信号) 消息(信号)取 取值的集合 值时刻的集合
信源种类
离散
离散
离散信源(Discrete source)/ 数字信源(Digital source)
假定连续信源 X 的概率密度 函数p(x)如右 图所示。我们 把取值区间分 割成 n 个等宽 的小区间。X 处于第 i 区间 的概率为
05-06学年上
Pi Pa(i1)xai
ai
7.
a(i1)p(x)dxp(xi)
这样,连续变量 X 就可用取值为 xi 的离 散变量 Xn 来近似。连续信源 X 被量化成 离散信源。
lo2gae
05-06学年上 18 .
4.3具有最大熵的连续信源
离散信源的最大熵问题:离散信源的各 符号为等概率分布时,信息熵有最大值 (最大离散熵定理)。
H(p1, p2,
,
pr
)
H1r,
1, r
r
条件是 pi 1 i1
,1rlogr
05-06学年上 19 .
在什么条件下,连续信源的熵最大?
最大熵为:
N
h(X)log (bi ai)比特 /自由度 i1
05-06学年上 23 .
平均功率受限条件下信源的最大熵 (方差受限)
定理:若一个信源输出信号的平均功率被 限定为P,则其输出信号幅度的概率密度 分布是高斯分布时,信源具有最大熵。
最大熵为:
h (X ) 1 lo 2 e gP 或 h (X ) 1 lo 2 e g 2
4.1波形信源的统计特性和离散化
随机变量 X
随机矢量X(X1X2 XN)
随机过程{ x ( t ) }
05-06学年上 3 .
表4.1
消息(信号) 消息(信号)取 取值的集合 值时刻的集合
信源种类
离散
离散
离散信源(Discrete source)/ 数字信源(Digital source)
假定连续信源 X 的概率密度 函数p(x)如右 图所示。我们 把取值区间分 割成 n 个等宽 的小区间。X 处于第 i 区间 的概率为
05-06学年上
Pi Pa(i1)xai
ai
7.
a(i1)p(x)dxp(xi)
这样,连续变量 X 就可用取值为 xi 的离 散变量 Xn 来近似。连续信源 X 被量化成 离散信源。
lo2gae
05-06学年上 18 .
4.3具有最大熵的连续信源
离散信源的最大熵问题:离散信源的各 符号为等概率分布时,信息熵有最大值 (最大离散熵定理)。
H(p1, p2,
,
pr
)
H1r,
1, r
r
条件是 pi 1 i1
,1rlogr
05-06学年上 19 .
在什么条件下,连续信源的熵最大?
最大熵为:
N
h(X)log (bi ai)比特 /自由度 i1
05-06学年上 23 .
平均功率受限条件下信源的最大熵 (方差受限)
定理:若一个信源输出信号的平均功率被 限定为P,则其输出信号幅度的概率密度 分布是高斯分布时,信源具有最大熵。
最大熵为:
h (X ) 1 lo 2 e gP 或 h (X ) 1 lo 2 e g 2
通信原理第四章 (樊昌信第七版)PPT课件

则接收信号为
2 1
fo(t) = K f(t - 1 ) + K f(t - 2 ) 相对时延差
F o () = K F () e j 1 + K F () e j ( 1 )
信道传输函数
H()F F o(( ))K Keejj 11((1 1 eejj ))
常数衰减因子 确定的传输时延因子 与信号频率有关的复因子
课件
精选课件
1
第4章 信道
通信原理(第7版)
樊昌信 曹丽娜 编著
精选课件
2
本章内容:
第4章 信道
信道分类
信道模型
恒参/随参信道特性对信号传输的影响
信道噪声
信道容量
定义·分类
模型·特性
影响·措施
信道噪声 信道容量
精选课件
3
概述
信道的定义与分类
n 狭义信道:
—传输媒质 有线信道 ——明线、电缆、光纤 无线信道 ——自由空间或大气层
1. 传输特性
H ()H ()ej ()
H() ~ 幅频特性
()~ 相频特性
2. 无失真传输
H()Kejtd
H() K
()td
精选课件
27
n 无失真传输(理想恒参信道)特性曲线:
恒参信道
|H()|
K
() td
td
0
H() K
幅频特性
0
0
()td
()d() d
td
相频特性
群迟延特性
精选课件
28
n 理想恒参信道的冲激响应:
恒参信道
H()Kejtd
h(t)K(ttd)
若输入信号为s(t),则理想恒参信道的输出:
第4章波形信源和波形信道.

X, Y计独立=
©许晓伟 xuxw525@
连续信源和信源的信息测度
连续信源熵的性质(2) 凸状性和极值性 h(X)是p(x)的上凸函数, 对于某一概率密度函数可以h(X)的最大值 证明作为思考题
19
©许晓伟 xuxw525@
连续信源和信源的信息测度
连续信源熵的性质(2) 可为负值 老教材P.231(新教材P.133)
R
©许晓伟 xuxw525@
连续信源和信源的信息测度
连续信源的熵(3) X, Y的联合熵和条件熵
17
h( XY ) p( xy) log p( xy)dxdy
R
h(Y | X ) p( x) p( y | x) log p( y | x)dxdy
R
h( X | Y ) p( x) p( y | x) log p( x | y)dxdy
©许晓伟 xuxw525@
波形信源的统计特性和离散化
3
信源
时间和取值连续的消息
随机过程
©许晓伟 xuxw525@
波形信源的统计特性和离散化
4
消息V=v0 消息T=t0 b
V
随机过程{V(t)}
Vi(t)
a t0 p(V) t
样本函数
a
b
V
随机变量Vt0
©许晓伟 xuxw525@
波形信源的统计特性和离散化
采样定理 (时域) 连续信号f(t)限频F
8
f (t )
n
f(
n sin (2Ft n) ) 2F (2Ft n)
连续信号f(t)限时T
2 FT n1
f (t ) f (
n sin (2Ft n) ) 2F (2Ft n)
©许晓伟 xuxw525@
连续信源和信源的信息测度
连续信源熵的性质(2) 凸状性和极值性 h(X)是p(x)的上凸函数, 对于某一概率密度函数可以h(X)的最大值 证明作为思考题
19
©许晓伟 xuxw525@
连续信源和信源的信息测度
连续信源熵的性质(2) 可为负值 老教材P.231(新教材P.133)
R
©许晓伟 xuxw525@
连续信源和信源的信息测度
连续信源的熵(3) X, Y的联合熵和条件熵
17
h( XY ) p( xy) log p( xy)dxdy
R
h(Y | X ) p( x) p( y | x) log p( y | x)dxdy
R
h( X | Y ) p( x) p( y | x) log p( x | y)dxdy
©许晓伟 xuxw525@
波形信源的统计特性和离散化
3
信源
时间和取值连续的消息
随机过程
©许晓伟 xuxw525@
波形信源的统计特性和离散化
4
消息V=v0 消息T=t0 b
V
随机过程{V(t)}
Vi(t)
a t0 p(V) t
样本函数
a
b
V
随机变量Vt0
©许晓伟 xuxw525@
波形信源的统计特性和离散化
采样定理 (时域) 连续信号f(t)限频F
8
f (t )
n
f(
n sin (2Ft n) ) 2F (2Ft n)
连续信号f(t)限时T
2 FT n1
f (t ) f (
n sin (2Ft n) ) 2F (2Ft n)
第4章波形信源和波形信道(ok)

可用变量的概率密度函数 p(x来) 描述。此时,连续信源
的数学模型为:
X p( x)
( pa(,xb))或
R p( x)
并满足 b p(x)dx 1或 p(x)dx 1
a
R
其中,R是全实数集,是变量X的取值范围。
4.1 连续信源及波形信源的信息测度
连续信源熵:
H
(
X
)
lim
n
H
(
X
C WT log(1 Ps / 2W )(比特 / N自由度) N0 / 2
WT log(1 Ps )(比特 / N自由度) N 0W
4.3 连续信道和波形信道的信道容量
2.高斯加性波形信道的信道容量
要达到这个信道容量要求输入N维随机序列X中每一分量
Xi都是均值为零,方差为Ps,彼此统计独立的高斯变量。
第4章 波形信源和波形信道
4.1 连续信源及波形信源的信息测度 4.2 连续信源熵的性质及最大熵定理 4.3 连续信道和波形信道的信道容量
4.1 连续信源及波形信源的信息测度
实际某些信源的输出常常是时间和取值都是连续的消息。
例如语音信号、电视信号。这样的信源称为随机波形信源。 1、基本概念 模拟信源:信源的输出是时间和取值都连续的消息。即输出
高斯白噪声加性信道的单位时间的信道容量
Ct
lim
T
C T
W
log(1
Ps N0W
)(比特 / 秒)
其中Ps是信号的平均功率, NoW为高斯白噪声在带宽W 内的平均功率。可见,信道容量与信噪功率比和带宽有关。
则当输出信号的概率密度是均匀分布时,信源具有 最大熵。其值等于log(b-a)。
4.2 连续信源熵的性质及最大熵定理
信号波形及频谱ppt课件
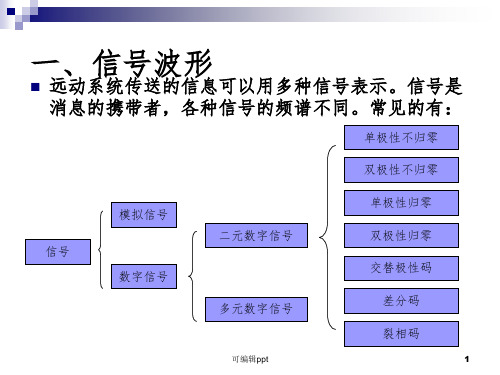
E f 2(t)dt
信号能量在时域和频
域内分布的相互关系
f2(t)dt21 F()2d
所以有
E() F()2
可编辑ppt
21
功率谱密度
功率谱密度是指单位频率间隔内的功率,记 作 P() ,单位是(瓦特每赫兹),信号功率与
信号功率谱P 密 度P的(关)d系f是1:P()d
2
在有限时间内,信号能量一定是有限的。将 f (t) 限定在 T t T 内的函数,叫做截短函数,记
多元数字信号相比二元数字信号来说,每一个码元所含的 信息量提高了,都是随着幅度电平数的增加,在同样的峰 值下,相邻电平的的差值减小了,受到干扰后容易产生译 码错误,使抗干扰性能变差。显然,如果信道干扰小,要 求信息传送速率较高的场合,采用多元数字信号较为合适。
电力系统中常采用二元数字信号。
可编辑ppt
R ( ) F ( ) F ( ) e j1 w F ( t ) e j2 w t F ( ) e jn w 1 t
等式右侧为各个分量的相量和,故一般性随机数字 序列的傅里叶变换后的幅值不会大于各个分量幅值 之和。注意到旋转因子的幅值为1,所以:
R() nF()
可编辑ppt
一、信号波形
远动系统传送的信息可以用多种信号表示。信号是 消息的携带者,各种信号的频谱不同。常见的有:
单极性不归零
双极性不归零
信号
模拟信号 数字信号
二元数字信号 多元数字信号
可编辑ppt
单极性归零 双极性归零 交替极性码
差分码 裂相码
1
一、信号波形
目前远动系统一般都是数字式系统,远动信息以数字信号 方式传送。
处理思想:可以想象成周期趋于无限大的周期矩 形脉冲序列。
信号调制的基本原理PPT

• 根据瞬时相位与瞬时角频率得关系可知,对 式(4-24)积分可得调频波得瞬时相位
• (4-26) t
t
t
f (t)
(t )dt
0
0 c
f u (t)dt
ct f
0 u (t)dt
•
f (t ) f
t
0 u (t )dt
(4-27)
• 表示调频波瞬时相位与载波信号相位得偏
4、2 幅度调制原理及特性
• 4、2、1 普通调幅(AM )
• 1、 普通调幅信号得数学表达式
• 首先讨论调制信号为单频余弦波时得情况, 设调制信号为
• u (t) um cos t cos 2 Ft (4-2)
• 设载波信号为
•
uC (t) Ucm cosct cos 2 fct (4-3)
• 调频信号数学表达式
(4-31)
4、3、2 调频信号分析
• uFM Ucm cos(ct mf sin t) (4-32)
•
mf
k f Um
m
为调频波得最大相移,又称调
频指数。 m值f 可大于1
• 给出了调制信号、瞬时频偏、瞬时相偏、 对应得波形图
4、3、2 调频信号分析
图4-19 调频信号的波形图
• 4、2、3 单边带调幅信号(SSB)
• 由式(4-15)可得SSB调幅信号数学表达式为
• 取上边带时
•
(4-17)
• •
取下边带时
uSSB (t)
1 2
KmaU cm cos (c
)t
(4-18)
uSSB (t )
1 2
KmaU cmcos(c
)t
4、2、3 单边带调幅信号(SSB)
• (4-26) t
t
t
f (t)
(t )dt
0
0 c
f u (t)dt
ct f
0 u (t)dt
•
f (t ) f
t
0 u (t )dt
(4-27)
• 表示调频波瞬时相位与载波信号相位得偏
4、2 幅度调制原理及特性
• 4、2、1 普通调幅(AM )
• 1、 普通调幅信号得数学表达式
• 首先讨论调制信号为单频余弦波时得情况, 设调制信号为
• u (t) um cos t cos 2 Ft (4-2)
• 设载波信号为
•
uC (t) Ucm cosct cos 2 fct (4-3)
• 调频信号数学表达式
(4-31)
4、3、2 调频信号分析
• uFM Ucm cos(ct mf sin t) (4-32)
•
mf
k f Um
m
为调频波得最大相移,又称调
频指数。 m值f 可大于1
• 给出了调制信号、瞬时频偏、瞬时相偏、 对应得波形图
4、3、2 调频信号分析
图4-19 调频信号的波形图
• 4、2、3 单边带调幅信号(SSB)
• 由式(4-15)可得SSB调幅信号数学表达式为
• 取上边带时
•
(4-17)
• •
取下边带时
uSSB (t)
1 2
KmaU cm cos (c
)t
(4-18)
uSSB (t )
1 2
KmaU cmcos(c
)t
4、2、3 单边带调幅信号(SSB)
§4 波形信源与波形信道

h(X|Y)h(X), h(Y|X)h(Y),h (X Y)h (X )h (Y)
2. 可为负
例2. 设 连 续 信 源 x [ a , b ] 均 匀 分 布 , 求 其 熵 。
b1
h (X ) R p (x )lo g p (x )d x ab a lo g (b a )d x
log(ba)
3. 信道带宽受限为B。
§4.2 Shannon公式
二、Shannon公式及其意义
Ct
T 1CBlog1NP0sB
C1t之. 建间立的了定连量续关信系道,的这带三宽者B之,间信可噪以比互P换s/。2,信道容量
➢ 带宽不变(B不变),增加信号功率或者提高信噪比,可
6
使Ct增大;
x 10 10
9
Capacity (bps/Hz)
带宽无B li信道容量( m B l穷i m C 11111大.....44444C 12345t增x 1t0,7 加N P B l是s0 i 带m B l不i m B 宽 l是B o可gN 可P 以s10以lo 增g N 获P 加0s1 B得 信N 无P 道0sB 穷容大量lxi的 m。0信1xl道n(x容量1)?1
且 :Np (x i)Na a (ii 1 )p (x )d x a bp (x )d x 1
i 1
i 1
此信源合理!
§4.1 连续性信源的熵
一、连续信源的熵 〔讨论X之熵〕
N
N
H (X N ) P ilo g P i p (x i)lo g p (x i)
i 1
i 1
N
b
ap(x)logp(x)dx
称为信源X的相对熵〔差熵〕
§4.1 连续性信源的熵
2. 可为负
例2. 设 连 续 信 源 x [ a , b ] 均 匀 分 布 , 求 其 熵 。
b1
h (X ) R p (x )lo g p (x )d x ab a lo g (b a )d x
log(ba)
3. 信道带宽受限为B。
§4.2 Shannon公式
二、Shannon公式及其意义
Ct
T 1CBlog1NP0sB
C1t之. 建间立的了定连量续关信系道,的这带三宽者B之,间信可噪以比互P换s/。2,信道容量
➢ 带宽不变(B不变),增加信号功率或者提高信噪比,可
6
使Ct增大;
x 10 10
9
Capacity (bps/Hz)
带宽无B li信道容量( m B l穷i m C 11111大.....44444C 12345t增x 1t0,7 加N P B l是s0 i 带m B l不i m B 宽 l是B o可gN 可P 以s10以lo 增g N 获P 加0s1 B得 信N 无P 道0sB 穷容大量lxi的 m。0信1xl道n(x容量1)?1
且 :Np (x i)Na a (ii 1 )p (x )d x a bp (x )d x 1
i 1
i 1
此信源合理!
§4.1 连续性信源的熵
一、连续信源的熵 〔讨论X之熵〕
N
N
H (X N ) P ilo g P i p (x i)lo g p (x i)
i 1
i 1
N
b
ap(x)logp(x)dx
称为信源X的相对熵〔差熵〕
§4.1 连续性信源的熵
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于随机过程来说,只要是限频的,它的每个样本函数 也可作同样的取样处理。每个样本函数都可以用一系列
数随t x机2(ntF变)时有量刻无。上限的多样个本,值因此x ,( 2来n取F 表)样征后。瞬因间为随tn机的2过nF样程本的值样是本一函个
.
3
第一节 波形信源的统计特性和离散化
这样,通过取样,随机过程就成为可数的无限维的随
连续信源 的信息熵
b
p(x)logp(x)lim log
a
0
舍弃无穷大的第二项,可得:
连续信源 的差熵
b
h(X)ap(x)logp(x)
.
7
第二节 波形信源和波形信源的信息测度
同理可以定义两个连续变量X、Y的联合熵和条件熵
h(X Y)p(xy)logp(xy)dxdy R
h (Y |X ) p (x)p (y|x)lo gp (y|x)d x d y
.
4
第二节 波形信源和波形信源的信息测度
连续信源的差熵
先看单个变量的基本连续信源的信息测度。基本连续信源 的输出是取值连续的单个随机变量。可用变量的概率密度, 变量间的条件概率密度和联合概率密度来描述。
变量的一维概率密度函数为 pX(x)dF d(xx),pY(x)dF d(yy)
一维概率分布函数为 条件概率密度函数为
第四章 波形信源和波形信道
第一节 第二节 第三节 第四节 第五节 第六节 第七节
波形信源的统计特性和离散化 连续信源和信源的信息测度 具有最大熵的连续信源 连续信道和波形信道的分类 连续信道和波形信道的信息传输率 连续信道和波形信道的信道容量 连续信道编码定理
.
1
第一节 波形信源的统计特性和离散化
h ( X |Y ) h ( X ) 或 h ( Y |X ) h ( Y )
所以可得 h(X Y)h(X )h(Y)
(2)凸状性和极值性
差熵 h(X) 是输入概率密度函数 p(x) 的П型凸函数,对于某一 概率密度函数可以得到差熵的最大。
(3)差熵可为负值
.
9
第二节 波形信源和波形信源的信息测度
F(x1)P [Xx1] x 1pX(x)dx
pX|Y(x| y),pY|X(y|x)
联合概率密度函数为
p X Y (x 1 y 1 ) 2 F (x 1 ,y 1 ) x 1 y 1
.
5
第二节 波形信源和波形信源的信息测度
它们之间的关系为
p X Y ( x y ) p X ( x ) p Y |X ( y |x ) p Y ( y ) p X | Y ( x |y )
波形信源的差熵
实际信源的输入和输出都是平稳随机过程,其 {x(t)}和 {y(t)}可以通过取样,分解成取值连续的无穷平稳随机序列来 表示,所以平稳随机过程的熵就是无穷平稳随机序列的熵。
h ( X ) h ( X 1 X 2 X N ) R p ( x ) l o g p ( x ) d x h ( Y ) h ( Y 1 Y 2 Y N ) R p ( y ) l o g p ( y ) d y h ( Y |X ) h ( Y 1 Y N |X 1X N ) RR p ( x y ) l o g p ( y |x ) d x d y h ( X | Y ) h ( X 1X N | Y 1 Y N ) RR p ( x y ) l o g p ( x |y ) d x d y
R
h (X |Y ) p (x)p (y|x)lo gp (x|信源和波形信源的信息测度
连续信源的差熵只具有熵的部分含义和性质
(1)可加性
h ( X Y ) h ( X ) h ( Y |X ) h ( Y ) h ( X |Y )
并当且仅当 X 与 Y 统计独立时
波形信源的差熵: h{x(t)} limh(X) N
.
10
第二节 波形信源和波形信源的信息测度
当对于限频F/限时T的平稳随机过程,它可以近似地用 有限维N=2FT平稳随机矢量表示。这样,一个频带和时间 都为有限的连续时间过程就转化为有限维时间离散的平稳 随机序列了。 和离散变量中一样, 易于证明:
h ( X ) h ( X 1 X 2 ) h ( X 1 ) h ( X 2 | X 1 ) h ( X 3 | X 1 X 2 ) h ( X N | X 1 X 2 X N )
h ( X ) h ( X 1 X 2X N ) h ( X 1 ) h ( X 2 ) h ( X N )
基本连续信源的数学模型为
XpR (x)并 且 Rp(x)dx1
其中R是全实数集。
.
6
第二节 波形信源和波形信源的信息测度
定义连续信源的熵为:
H (X n) p (xi) lo g [p (xi) ]
i
这样的话:
p (x i) lo g p (x i)p (x i) lo g
i
i
H ( X ) l n i m H ( X n ) l i m 0 i p ( x i) l o g [ p ( x i) ]
机序列 X(X1,X2,。...,Xi ,...)
2F 2F
2F
如果随机过程又是限时的,时间间隔为T,则就成为
2FT个有限维的随机序列。取样之后还要对取值的离散
化。取样加量化才使随机过程变换成时间的取值都是离
散的随机序列。量化必然带来量化噪声,引起信息损失。
随机过程描述输出消息的信源称为随机波形信源。 用连续随机变量描述输出消息的信源称为连续信源。
实际某些信源的输出常常是时间和取值都是连续的消息。例
如语音信号、电视信号。这样的信源成为随机波形信源,其输 出消息可以用随机过程{x(t)}来表示。
随机过程{x(t)}可以看成由一族时间函数
组成 称为样本
函数。每个样本函数是随机过程的一个实现。 { x i ( t ) }
(1)随机波形信源中消息数是无限的。
(2)随机波形信源可用有限维概率密度函数族以及与各维 函数概率密度函数有关的统计量来描述。
.
2
第一节 波形信源的统计特性和离散化
就统计特性的区别来说,随机过程大致可分为平稳随机 过程和非平稳过程两大类。
最常见的平稳随机过程为遍历过程,它不但统计特性不 随时间平移而变化,而且它的集平均以概率1等于时间平均。
数随t x机2(ntF变)时有量刻无。上限的多样个本,值因此x ,( 2来n取F 表)样征后。瞬因间为随tn机的2过nF样程本的值样是本一函个
.
3
第一节 波形信源的统计特性和离散化
这样,通过取样,随机过程就成为可数的无限维的随
连续信源 的信息熵
b
p(x)logp(x)lim log
a
0
舍弃无穷大的第二项,可得:
连续信源 的差熵
b
h(X)ap(x)logp(x)
.
7
第二节 波形信源和波形信源的信息测度
同理可以定义两个连续变量X、Y的联合熵和条件熵
h(X Y)p(xy)logp(xy)dxdy R
h (Y |X ) p (x)p (y|x)lo gp (y|x)d x d y
.
4
第二节 波形信源和波形信源的信息测度
连续信源的差熵
先看单个变量的基本连续信源的信息测度。基本连续信源 的输出是取值连续的单个随机变量。可用变量的概率密度, 变量间的条件概率密度和联合概率密度来描述。
变量的一维概率密度函数为 pX(x)dF d(xx),pY(x)dF d(yy)
一维概率分布函数为 条件概率密度函数为
第四章 波形信源和波形信道
第一节 第二节 第三节 第四节 第五节 第六节 第七节
波形信源的统计特性和离散化 连续信源和信源的信息测度 具有最大熵的连续信源 连续信道和波形信道的分类 连续信道和波形信道的信息传输率 连续信道和波形信道的信道容量 连续信道编码定理
.
1
第一节 波形信源的统计特性和离散化
h ( X |Y ) h ( X ) 或 h ( Y |X ) h ( Y )
所以可得 h(X Y)h(X )h(Y)
(2)凸状性和极值性
差熵 h(X) 是输入概率密度函数 p(x) 的П型凸函数,对于某一 概率密度函数可以得到差熵的最大。
(3)差熵可为负值
.
9
第二节 波形信源和波形信源的信息测度
F(x1)P [Xx1] x 1pX(x)dx
pX|Y(x| y),pY|X(y|x)
联合概率密度函数为
p X Y (x 1 y 1 ) 2 F (x 1 ,y 1 ) x 1 y 1
.
5
第二节 波形信源和波形信源的信息测度
它们之间的关系为
p X Y ( x y ) p X ( x ) p Y |X ( y |x ) p Y ( y ) p X | Y ( x |y )
波形信源的差熵
实际信源的输入和输出都是平稳随机过程,其 {x(t)}和 {y(t)}可以通过取样,分解成取值连续的无穷平稳随机序列来 表示,所以平稳随机过程的熵就是无穷平稳随机序列的熵。
h ( X ) h ( X 1 X 2 X N ) R p ( x ) l o g p ( x ) d x h ( Y ) h ( Y 1 Y 2 Y N ) R p ( y ) l o g p ( y ) d y h ( Y |X ) h ( Y 1 Y N |X 1X N ) RR p ( x y ) l o g p ( y |x ) d x d y h ( X | Y ) h ( X 1X N | Y 1 Y N ) RR p ( x y ) l o g p ( x |y ) d x d y
R
h (X |Y ) p (x)p (y|x)lo gp (x|信源和波形信源的信息测度
连续信源的差熵只具有熵的部分含义和性质
(1)可加性
h ( X Y ) h ( X ) h ( Y |X ) h ( Y ) h ( X |Y )
并当且仅当 X 与 Y 统计独立时
波形信源的差熵: h{x(t)} limh(X) N
.
10
第二节 波形信源和波形信源的信息测度
当对于限频F/限时T的平稳随机过程,它可以近似地用 有限维N=2FT平稳随机矢量表示。这样,一个频带和时间 都为有限的连续时间过程就转化为有限维时间离散的平稳 随机序列了。 和离散变量中一样, 易于证明:
h ( X ) h ( X 1 X 2 ) h ( X 1 ) h ( X 2 | X 1 ) h ( X 3 | X 1 X 2 ) h ( X N | X 1 X 2 X N )
h ( X ) h ( X 1 X 2X N ) h ( X 1 ) h ( X 2 ) h ( X N )
基本连续信源的数学模型为
XpR (x)并 且 Rp(x)dx1
其中R是全实数集。
.
6
第二节 波形信源和波形信源的信息测度
定义连续信源的熵为:
H (X n) p (xi) lo g [p (xi) ]
i
这样的话:
p (x i) lo g p (x i)p (x i) lo g
i
i
H ( X ) l n i m H ( X n ) l i m 0 i p ( x i) l o g [ p ( x i) ]
机序列 X(X1,X2,。...,Xi ,...)
2F 2F
2F
如果随机过程又是限时的,时间间隔为T,则就成为
2FT个有限维的随机序列。取样之后还要对取值的离散
化。取样加量化才使随机过程变换成时间的取值都是离
散的随机序列。量化必然带来量化噪声,引起信息损失。
随机过程描述输出消息的信源称为随机波形信源。 用连续随机变量描述输出消息的信源称为连续信源。
实际某些信源的输出常常是时间和取值都是连续的消息。例
如语音信号、电视信号。这样的信源成为随机波形信源,其输 出消息可以用随机过程{x(t)}来表示。
随机过程{x(t)}可以看成由一族时间函数
组成 称为样本
函数。每个样本函数是随机过程的一个实现。 { x i ( t ) }
(1)随机波形信源中消息数是无限的。
(2)随机波形信源可用有限维概率密度函数族以及与各维 函数概率密度函数有关的统计量来描述。
.
2
第一节 波形信源的统计特性和离散化
就统计特性的区别来说,随机过程大致可分为平稳随机 过程和非平稳过程两大类。
最常见的平稳随机过程为遍历过程,它不但统计特性不 随时间平移而变化,而且它的集平均以概率1等于时间平均。
