第2章原子结构和原子光谱[3]
合集下载
原子结构与光谱：原子光谱与谱线
原子结构与光谱：原子光谱与谱线原子光谱是研究原子结构和性质的重要方法之一。
通过观察原子在光谱仪中经过光激发后产生的谱线，科学家们深入探索了原子的内部构造和粒子行为，为人类认识宇宙提供了重要的线索。
本文将介绍原子结构与光谱的关系，解析原子光谱的特点以及谱线的含义。
一、原子结构与光谱理解原子光谱首先需要了解原子的基本结构。
根据波尔模型，原子由一个中心核和围绕核运动的电子构成。
核内的质子和中子决定了原子的质量，而电子则决定了原子的化学性质。
原子的电子以能级的形式存在，每个能级可以容纳一定数量的电子。
当原子受到外部能量的激发时，电子会从低能级跃迁到高能级。
当电子回到低能级时，会释放出一定的能量，形成光的辐射。
这种辐射所形成的光谱称为原子光谱。
原子光谱可以通过光谱仪进行分析，并确定所观察到的谱线。
二、原子光谱的特点1. 具有特定的波长和颜色：不同元素的原子具有不同的能级结构，因此其光谱也具有独特的波长和颜色。
这使得原子光谱成为元素鉴定和分析的重要手段。
2. 具有离散的谱线：原子的能级是离散的，因此原子光谱呈现出离散的、间隔均匀的谱线。
每个谱线对应着电子跃迁的能级差和能量释放的特定波长。
3. 具有良好的分辨能力：原子光谱仪具有很高的分辨能力，可以准确测量光谱中谱线的波长和强度。
这为科学家们进行精确的光谱分析提供了有力工具。
三、谱线的含义原子光谱中的谱线代表着电子跃迁时产生的辐射能量。
通过观察和分析谱线的特征，可以得出以下信息：1. 波长：谱线的波长可以确定电子跃迁的能级差，从而推测原子的能级结构和电子分布。
2. 强度：谱线的强度反映了电子跃迁的概率，即从高能级到低能级的跃迁概率。
强度较强的谱线对应的跃迁概率较高。
3. 形态：谱线的形态（如单峰、多峰等）可以提供关于原子的电子状态和相应能级的信息。
4. 分裂：有些原子光谱呈现出多条非常接近且微弱的谱线，这是由于原子的内部结构和外界环境的影响导致原子能级的分裂现象。
高中物理第2章原子结构第3节玻尔的原子模型第4节氢原子光谱与能级结构课件鲁科版选修3
跃迁 假设 定频率的光子能量 hν，假如，原子从定态 E2 跃迁到
定态 E1，辐射的光子能量为 hν＝E2－E1
基本 内容
假设
原子的不同能量状态对应于电子的不同运行轨道．原
子的能量状态是不连续的，电子不能在任意半径的轨 轨道 道上运行，只有轨道半径 r 跟电子动量 mev 的乘积满 假设 足下式 mevr＝n2hπ(n＝1，2，3，…)这些轨道才是可
对玻尔原子模型的理解 1.轨道量子化：轨道半径只能够是一些不连续的、某些分立的 数值． 模型中保留了卢瑟福的核式结构，但他认为核外电子的轨道是 不连续的，它们只能在某些可能的、分立的轨道上运动，而不 是像行星或卫星那样，能量大小可以是任意的量值．例如，氢 原子的电子最小轨道半径为 r1＝0.053 nm，其余可能的轨道半 径还有 0.212 nm、0.477 nm、…不可能出现介于这些轨道半径 之间的其他值．这样的轨道形式称为轨道量子化．
按照玻尔原子理论，氢原子中的电子离原子核越远， 氢原子的能量________(选填“越大”或“越小”)．已知氢原 子的基态能量为 E1(E1<0)，电子质量为 m，基态氢原子中的电 子吸收一频率为 ν 的光子被电离后，电子速度大小为 ________(普朗克常量为 h)． [思路点拨] 根据玻尔原子理论与能量守恒定律求解．
得到了氢原子的能级结构图(如图所示)．
n＝∞————————E∞＝0 ⋮
n＝5 ————————E5＝－0.54 eV n＝4 ————————E4＝－0.85 eV n＝3 ————————E3＝－1.51 eV n＝2 ————————E2＝－3.4 eV n＝1 ————————E1＝－13.6 eV
4.原子跃迁时需注意的几个问题 (1)注意一群原子和一个原子 氢原子核外只有一个电子，这个电子在某个时刻只能处在某一 个可能的轨道上，在某段时间内，由某一轨道跃迁到另一个轨 道时，可能的情况只有一种，但是如果容器中盛有大量的氢原 子，这些原子的核外电子跃迁时就会有各种情况出现．
定态 E1，辐射的光子能量为 hν＝E2－E1
基本 内容
假设
原子的不同能量状态对应于电子的不同运行轨道．原
子的能量状态是不连续的，电子不能在任意半径的轨 轨道 道上运行，只有轨道半径 r 跟电子动量 mev 的乘积满 假设 足下式 mevr＝n2hπ(n＝1，2，3，…)这些轨道才是可
对玻尔原子模型的理解 1.轨道量子化：轨道半径只能够是一些不连续的、某些分立的 数值． 模型中保留了卢瑟福的核式结构，但他认为核外电子的轨道是 不连续的，它们只能在某些可能的、分立的轨道上运动，而不 是像行星或卫星那样，能量大小可以是任意的量值．例如，氢 原子的电子最小轨道半径为 r1＝0.053 nm，其余可能的轨道半 径还有 0.212 nm、0.477 nm、…不可能出现介于这些轨道半径 之间的其他值．这样的轨道形式称为轨道量子化．
按照玻尔原子理论，氢原子中的电子离原子核越远， 氢原子的能量________(选填“越大”或“越小”)．已知氢原 子的基态能量为 E1(E1<0)，电子质量为 m，基态氢原子中的电 子吸收一频率为 ν 的光子被电离后，电子速度大小为 ________(普朗克常量为 h)． [思路点拨] 根据玻尔原子理论与能量守恒定律求解．
得到了氢原子的能级结构图(如图所示)．
n＝∞————————E∞＝0 ⋮
n＝5 ————————E5＝－0.54 eV n＝4 ————————E4＝－0.85 eV n＝3 ————————E3＝－1.51 eV n＝2 ————————E2＝－3.4 eV n＝1 ————————E1＝－13.6 eV
4.原子跃迁时需注意的几个问题 (1)注意一群原子和一个原子 氢原子核外只有一个电子，这个电子在某个时刻只能处在某一 个可能的轨道上，在某段时间内，由某一轨道跃迁到另一个轨 道时，可能的情况只有一种，但是如果容器中盛有大量的氢原 子，这些原子的核外电子跃迁时就会有各种情况出现．
选修3-5-2.3~4光谱-玻尔的原子模型
玻尔的原子模型
丹麦物理学家 玻尔
定态（电子处于分立的、特 定 的轨道，不辐射能量） 能级（不同轨道上的能量）
玻尔的原子模型
不同能级的能量：
En=E1/n2 E1= - 13.6 eV 发射的光子的能量： hv= En-Em 不同能级的轨道半径： rn=n2r1
玻尔的原子模型
贡献：很好解释了氢原子的光谱中波长满足的规 律。引入了量子化概念，推动了量子力学发展。
选修3-5 第二章 原子结构
第3节 光谱 氢原子光谱 第4节 玻尔的原子模型 能级
几种光谱
炽热的固体、液体或高压气 体发射的多为连续谱 连续谱
稀薄的气体发射的多为线状谱
线状谱
光谱分析应用广泛
氢原子光谱
观察条件： 真空管充入稀薄氢气 分光仪器观察 现象及规律： 线状谱 各条谱线光波长满足巴尔末公式 2~3kV高压
rn=n2r1
跃迁发射的光子能量 hv= En-Em
不完善：无法说明光谱的强度和偏振情况， 无法解释有两个以上电子的原子复杂光谱。
小结
光谱 定义 将光按波长长短顺序排列 分类 连续谱，线状谱 发射谱，吸收谱
氢原子光谱
观察条件
规律
定态 能级
真空
稀薄氢 气
2~3kV 高压
分光仪器 观察
各条谱线波长满足巴尔末公式
一系列分立的、特定
原子的能级结构与光谱特征
23
但原子实与氢原子核不同，价电子有相当的概率出现在原子实内部。所以平均而言，价 电子感受到的有效核电荷数不是 1，而是大于 1 的值，设为 Z*（>1） 。由此引起的能量降低 称为轨道贯穿。 相同的主量子数 n，角量子数 l 小的电子，出现在原子核附近的概率大，感受到的有效
∗ ∗ ∗ 核电荷数也越大，即 Z ns > Z np > Z nd > .... ，所以碱金属价电子的能级不仅与 n 有关，还显
M
M J 可能取值的个数。
在典型的 LS 耦合下，一个 给定的电子组态可能形成的各 个原子态的能量高低次序， 可以 用洪德 (F.Hund)提出的一个经 验法则来确定。 它的内容可陈述 如下： 图 2.2 2 3 PJ 光谱项及其分裂示意图 （1）对一给定的组态，能 量最低的原子态必定具有泡利 原理所允许的最大 S 值； (2)相同 S 值的状态中，L 值最大的态的能量最低； (c)在电子组态为(nl)v 的情形下，当价电子数 v＜(2l+1)，即不到半满支壳层时，一个 多重态中 J 值最小的状态其能量最低，这称为正常次序；而在 v＞(2l+1)时，即超过半满支 壳层的情形，J 值最大的状态其能量最低，这是倒转次序。 例 1、某原子的一个光谱项为 2 PJ ，试画出其能级图。
25
每个电子的状态仍用四个量子数（n，l，ml，ms）表征。电子在原子中的分布遵从下列 两个原理： 1、泡利不相容原理 在多电子原子中，不能有任何两个电子处于完全相同的状态， 亦即不可能具有相同的四个量子数。 因此，角量子数为 l 的支壳层上可以容纳的最多电子数为 N l = 2（2 l+1） ；当 n 给定时， l 的可能值为 0，1，2，….（n-1）共 n 个，所以，每一个壳层可以容纳的最多电子数目为
选修3-5 第二章 第1讲 原子结构 氢原子光谱
3.光谱分析
特征谱线 可以用来鉴别物质和确定 利用每种原子都有自己的_________
物质的组成成分，且灵敏度很高。在发现和鉴别化学元素上有
着重大的意义。
知识点 2
氢原子的能级结构、能级公式
Ⅰ
1.玻尔理论
不连续 的能量状态中，在这 （1）定态：原子只能处于一系列_______
稳定 的，电子虽然绕核运动，但并不向 些能量状态中原子是_____
表示电子由较高能级向较低能级跃迁，电 子跃迁的条件为hν =Em-En
带箭头的竖线
2.对电子跃迁条件hν =Em-En的说明
（1）电子跃迁条件hν =Em-En只适用于光子和原子作用而使原子
在各定态之间跃迁的情况。
（2）当光子能量大于或等于13.6 eV时，也可以被处于基态的氢 原子吸收，使氢原子电离；当处于基态的氢原子吸收的光子能量 大于13.6 eV时，氢原子电离后，电子具有一定的初动能。 （3）原子还可吸收外来实物粒子（例如自由电子）的能量而被 激发。由于实物粒子的动能可全部或部分被原子吸收，所以只要 入射粒子的能量大于或等于两能级的能量差值（E=Em-En），均
②利用原子能量公式En=Ekn+Epn判断，当轨道半径增大时，原
子能量增大，电子动能减小，故原子的电势能增大。反之，当
轨道半径减小时，原子能量减小，电子动能增大，故原子的电 势能减小。
【典例透析2】氢原子辐射出一个光子后，根据玻尔理论，下 述说法正确的是( )
A．电子绕核旋转的半径增大
B．电子的动能增大
【典例透析1】如图所示为氢原子能级
图，下列说法正确的是(
的光谱
)
A.玻尔理论也能很好地解释复杂原子 B.玻尔理论认为原子的能量是连续的， 电子的轨道半径是不连续的
第二章 原子的结构和性质2.3-2.4
作图方法主要包括：
函数-变量对画图 等值面（线）图 界面图 网格图 黑点图
有些图形只能用某一种方式来画, 有些图形则可 能用几种不同方式来画。作图对象与作图方法结合 起来, 产生了错综复杂的许多种图形。
采用列表的形式, 可使这种关系变得一目了然。
2.3 原子轨道和电子云的图形表示
波函数 ( ，原子轨道) 电子云 ( ||2 ，概率密度)
当n相同，l不同时， l越 大，主峰离核越近； l越小 峰越多，而且第一个峰离 核越近，俗称钻得越深。 钻穿效应
2.3.2 原子轨道 和电子云 ||2 的角度分布
角度分布是以角度波函数 Y ,m ( , ) 在球坐标系中对 θ、角作图，其做法是在坐标系中，选原子核作为 坐标原点，在每一个(θ, )方向上引一条直线，取长 度为|Y|的线段，将这些线段的端点连接起来，在空 间形成一个曲面，根据 Y值的大小标明正负号。若 取直线的长度为|Y|2，所以直线端点构成的曲面称 为电子云 的角2 度分布。
毋庸置疑, Rydberg原子一定是个大胖子. 事实上, 它的半径 大约相当于基态原子的十万倍! 这样一个胖原子, 即使受到微弱 的电场或磁场作用, 也会显著变形.
由于 Yl,m (q ,f )只与角量子数 l 和磁量子数m有关，而 与主量子数n无关，因此 l,m 相同的状态，其原子轨 道的角度分布图都相同。如2pz, 3pz, 4pz角度部分图 形都完全相同。
原子轨道ψ的角度分布
s 00
1
4
对s-型轨道而言，只
与r有关，没有角度依赖
+
性，所以从原点到曲线
数的形式。
5. 磁量子数及角动量在磁场方向的分量
角动量在Z方向(磁场方向)的分量Lz的算符 作用于单电子原子波函数ψ，得：
高中物理第二章原子结构2.3光谱氢原子光谱教科35
审题,然后(ránhòu)利用巴尔末公式1
计算。
RH(212
1 n2
)
进行有关的
第四十四页，共五十五页。
【拓展例题】考查内容(nèiróng):氢原子光谱的问题计算 氢原子光谱在可见光的范围内有两条谱线,其波长分别为 654.55×10-9m和484.85×10-9m,根据巴尔末公式,求所对应的n. 【思路点拨】根据给出的光谱线对应的波长应用巴尔末公 式确定出n。
第二十四页，共五十五页。
【补偿训练】 (多选)下列关于光谱的说法正确的是 ( ) A.连续光谱就是由连续发光的物体产生的光谱,线状谱是线状光 源产生的光谱 B.通过对连续谱的光谱分析(ɡuānɡ pǔ fēn xī),可鉴定物质成分 C.连续光谱包括一切波长的光,线状谱只包括某些特定波长的 光
第二十五页，共五十五页。
第四十二页，共五十五页。
【解析】选A、C。巴尔末公式是分析(fēnxī)氢原子的谱线得到的 一个公式,它只反映氢原子谱线的一个线系,故A对,D错,公式 中的n只能取不小于3的正整数,B错,C对。
第四十三页，共五十五页。
【温馨提示】
对氢原子光谱的理解及其应用是高考的热点,特别是氢
原子光谱的计算问题,在解决本类问题时,一定要仔细
第四页，共五十五页。
二、氢原子光谱 1.许多情况(qíngkuàng)下光是由原子内部电子的运动产生的,因此 光谱研究是探索原子结构的一条重要途径。 2.巴尔末公式: =_1____R__H_(_21_2 (n=n132,)4,5,…)其中RH叫 作里_德__堡__常__数__(_c_há。ngs其hù)值为RH=1.097 373 156 854 8×
第九页，共五十五页。
1.光谱的分类:
print 第2章.原子的结构和性质
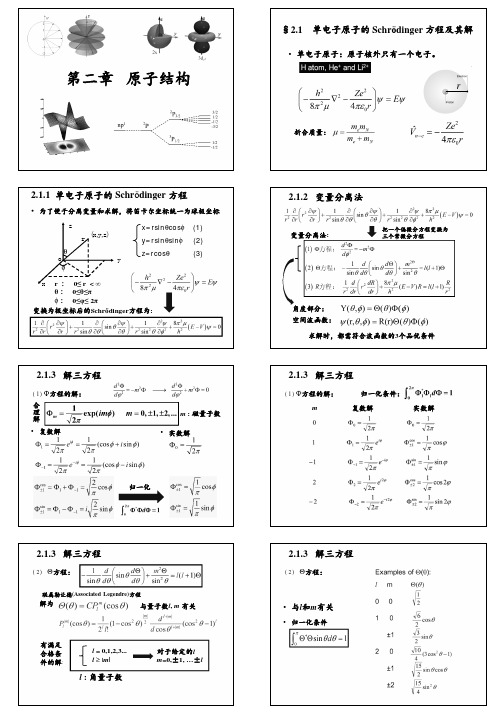
三个量子数n, l和m具有如下的关系
• 主量子数
n = 1, 2, 3, …, n;
• 角量子数
l = 0, 1, 2, …, n-1;
• 磁量子数
m= 0, ±1, ±2,…, ±l
每套量子数n, l和m决定一个波函数ψnlm的形式，即 决定了单电子原子体系的一种状态，因此简称为原子轨
道(AO, Atomic Orbital)。
• 两个径向节面，
3s
即n-l-1=2，所以n=3
§2.4 多电子原子的结构
2.4.1 多电子原子的Schrödinger方程
• 原子单位 atomic unit， a.u.
定核近似
r
2.4.1 多电子原子的Schrödinger方程
两个电子的 电子与原子核相互 两电子之间相互作 动能算符 作用的势能算符 用的势能算符
能级交错
2.4.1 多电子原子的Schrödinger方程
• 单电子波函数求 解结果与类氢粒 子波函数一样
n例：He原子基态
零级近似的计算结果：
实验值：
结论：零级近似的计算结果与实验值相差很大， 说明电子间的相互作用不可忽略。
2.4.2 单电子原子轨道能
和单电子波函数 Ψi 相应的能量 Ei
2. 由屏蔽常数近似计算原子轨道能
l 单电子原子的能级公式：
单电子原子的 能量E只与主量 子数n有关
1. 主量子数
• 能量量子化 • 能量为负，电子离
核无穷远时作为位 能的零点 • 简并度：在相同n 下，而l, m不同的 AO有n2个 例如，n=2时，空间波函数有
2. 角量子数 l：决定电子的原子轨道角动量的大小。
• 原子只要有角动量 也就有磁距
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
pp 3D 1D 3P 1P
3S 1S
m
1 0
l
-1
m
1
l
m
1 1 1 0 0 0 0 0 0 0 0 0 -1 -1 -1
s
↑
↑
-1 0 0 -1 2
↑
1
↓
↓↑
0 1 0 1 0
↑
↓
↓
Atomic terms symbols for two equivalent electrons
12
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
l - l coupling
Summary
s-s coupling
L-S coupling
Magnetic field
20112011-9-30 Chemistry Department of Fudan University 13
L - Scoupling: the orbital momenta for all electrons is coupled to obtain a total orbital angular momentum L and then the individual spin angular momenta is coupled to obtain the total spin angular momentum S. The total angular momentum J is then obtained by vector addition of L and S.
Sz M S M S S , S 1, , S
J LS J
m
s
Total M om e ntum
20112011-9-30
J J 1
J L S , L S 1, , L S
Chemistry Department of Fudan University 5
20112011-9-30
Chemistry Department of Fudan University
11
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
20112011-9-30
Chemistry Department of Fudan University
20112011-9-30 Chemistry Department of Fudan University
7
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Atomic terms symbols for two non-equivalent electrons
M S ms
1 2 0 1 1 1 0 0 1 2 3 2 1 -1 0 1 1 1 0
Slater method
ML
1 0 -1 -2
m
l
L2 S 0
M S ms
1 2 0 1 1 1 0 0 0 1 2 1 0 -1 0 1 1 1 0
1
D
ML
1 0 -1 -2
m
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
1. The term with maximum multiplicity lies lowest in energy. 2. For a given multiplicity, the term with the largest value of L lies lowest in energy. 3. For atoms with less than halffilled shells, the level with the lowest value of J lies lowest in energy. If the subshell is more than half filled, the state with maximum J is lowest in energy.
20112011-9-30
Chemistry Department of Fsical Chemistry I Quantum Numbers of Atom
Electron
Chapter II Atomic Structure and Spectrum
A tom
20112011-9-30 Chemistry Department of Fudan University 6
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
L=0, L=2,
S=0 S=1
1S 3D
singlet triplet
p2
↓
-1 0 -2 -1 -1 0 -2 1
↑
↓
↑
↓↑
0 -1
20112011-9-30
Chemistry Department of Fudan University
8
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Number of possible States of the configuration f7
C
m ( number N ( possible
electrons ) spin orbitals )
max S max L
C
7 14
Count the total ms Count the total ml
20112011-9-30 Chemistry Department of Fudan University 3
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Quantum Numbers of Atom
Electron l Atom L Relation L l
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Physical Chemistry
Chapter II Atomic Structure & Spectrum
20112011-9-30
Chemistry Department of Fudan University
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Spin multiplicity
Atomic Term Symbol
Atomic Levels
2 S 1
L
2 S 1
LJ
If the Pauli principle does not have to be considered, we can write all the term states directly.
20112011-9-30
l
Chemistry Department of Fudan University
9
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
M S ms
1 2 0 1 1 1 0
0 0 1 2 1 0
j - jcoupling: the orbital angular momentum l
and spin angular momentum s of each electron are coupled to obtain a total angular momentum j. The all the individual j are coupled to obtain the total angular momentum J of an atom.
ˆ ' 0 dt E E H
Angular Momentum
l l l 1
lz
L LL 1
LZ
LZ M L
L l1 l2 ,..., l1 l2 Lz lz
Orbital
component
lz ml
M L ml
ml l , l 1,,l M L L, L 1,, L
R elation
s
A ngular M om entum
S S
S
s
s
s s 1
S S 1 S s1 s 2 , , s1 s 2 Sz Sz MS
s 1/ 2
Spin
sz
com ponent
s
z
s z m s m s s , s
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Atomic terms for various configuration
20112011-9-30
Chemistry Department of Fudan University
ˆ H ˆ0H ˆ' H
ˆ 0 0 E 0 0 H
3S 1S
m
1 0
l
-1
m
1
l
m
1 1 1 0 0 0 0 0 0 0 0 0 -1 -1 -1
s
↑
↑
-1 0 0 -1 2
↑
1
↓
↓↑
0 1 0 1 0
↑
↓
↓
Atomic terms symbols for two equivalent electrons
12
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
l - l coupling
Summary
s-s coupling
L-S coupling
Magnetic field
20112011-9-30 Chemistry Department of Fudan University 13
L - Scoupling: the orbital momenta for all electrons is coupled to obtain a total orbital angular momentum L and then the individual spin angular momenta is coupled to obtain the total spin angular momentum S. The total angular momentum J is then obtained by vector addition of L and S.
Sz M S M S S , S 1, , S
J LS J
m
s
Total M om e ntum
20112011-9-30
J J 1
J L S , L S 1, , L S
Chemistry Department of Fudan University 5
20112011-9-30
Chemistry Department of Fudan University
11
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
20112011-9-30
Chemistry Department of Fudan University
20112011-9-30 Chemistry Department of Fudan University
7
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Atomic terms symbols for two non-equivalent electrons
M S ms
1 2 0 1 1 1 0 0 1 2 3 2 1 -1 0 1 1 1 0
Slater method
ML
1 0 -1 -2
m
l
L2 S 0
M S ms
1 2 0 1 1 1 0 0 0 1 2 1 0 -1 0 1 1 1 0
1
D
ML
1 0 -1 -2
m
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
1. The term with maximum multiplicity lies lowest in energy. 2. For a given multiplicity, the term with the largest value of L lies lowest in energy. 3. For atoms with less than halffilled shells, the level with the lowest value of J lies lowest in energy. If the subshell is more than half filled, the state with maximum J is lowest in energy.
20112011-9-30
Chemistry Department of Fsical Chemistry I Quantum Numbers of Atom
Electron
Chapter II Atomic Structure and Spectrum
A tom
20112011-9-30 Chemistry Department of Fudan University 6
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
L=0, L=2,
S=0 S=1
1S 3D
singlet triplet
p2
↓
-1 0 -2 -1 -1 0 -2 1
↑
↓
↑
↓↑
0 -1
20112011-9-30
Chemistry Department of Fudan University
8
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Number of possible States of the configuration f7
C
m ( number N ( possible
electrons ) spin orbitals )
max S max L
C
7 14
Count the total ms Count the total ml
20112011-9-30 Chemistry Department of Fudan University 3
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Quantum Numbers of Atom
Electron l Atom L Relation L l
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Physical Chemistry
Chapter II Atomic Structure & Spectrum
20112011-9-30
Chemistry Department of Fudan University
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Spin multiplicity
Atomic Term Symbol
Atomic Levels
2 S 1
L
2 S 1
LJ
If the Pauli principle does not have to be considered, we can write all the term states directly.
20112011-9-30
l
Chemistry Department of Fudan University
9
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
M S ms
1 2 0 1 1 1 0
0 0 1 2 1 0
j - jcoupling: the orbital angular momentum l
and spin angular momentum s of each electron are coupled to obtain a total angular momentum j. The all the individual j are coupled to obtain the total angular momentum J of an atom.
ˆ ' 0 dt E E H
Angular Momentum
l l l 1
lz
L LL 1
LZ
LZ M L
L l1 l2 ,..., l1 l2 Lz lz
Orbital
component
lz ml
M L ml
ml l , l 1,,l M L L, L 1,, L
R elation
s
A ngular M om entum
S S
S
s
s
s s 1
S S 1 S s1 s 2 , , s1 s 2 Sz Sz MS
s 1/ 2
Spin
sz
com ponent
s
z
s z m s m s s , s
Physical Chemistry I
Chapter II Atomic Structure and Spectrum
Atomic terms for various configuration
20112011-9-30
Chemistry Department of Fudan University
ˆ H ˆ0H ˆ' H
ˆ 0 0 E 0 0 H